常微分方程数值解法欧拉法

微分方程的数值解法微分方程是自然科学和现代技术领域中一种最基本的数学描述工具，它可以描述物理世界中的各种现象。

微分方程的解析解往往很难求出，因此数值解法成为解决微分方程问题的主要手段之一。

本文将介绍几种常见的微分方程的数值解法。

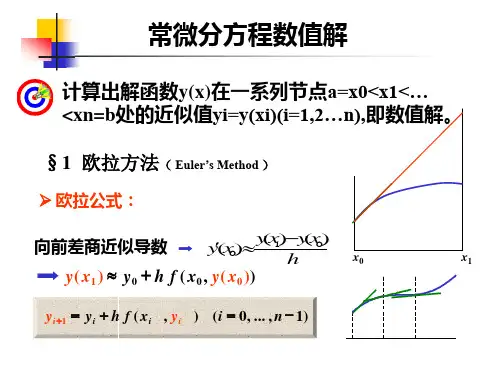
一、欧拉法欧拉法是微分方程初值问题的最简单的数值方法之一，它是由欧拉提出的。

考虑一阶常微分方程：$y'=f(t,y),y(t_0)=y_0$其中，$f(t,y)$表示$y$对$t$的导数，则$y(t_{i+1})=y(t_i)+hf(t_i,y_i)$其中，$h$为步长，$t_i=t_0+ih$，$y_i$是$y(t_i)$的近似值。

欧拉法的精度较低，误差随着步长的增加而增大，因此不适用于求解精度要求较高的问题。

二、改进欧拉法改进欧拉法又称为Heun方法，它是由Heun提出的。

改进欧拉法是在欧拉法的基础上进行的改进，它在每个步长内提高求解精度。

改进欧拉法的步骤如下：1. 根据当前$t_i$和$y_i$估算$y_{i+1}$:$y^*=y_i+hf(t_i,y_i),t^*=t_i+h$2. 利用$y^*$和$t^*$估算$f(t^*,y^*)$:$f^*=f(t^*,y^*)$3. 利用$y_i$、$f(t_i,y_i)$和$f^*$估算$y_{i+1}$:$y_{i+1}=y_i+\frac{h}{2}(f(t_i,y_i)+f^*)$改进欧拉法具有比欧拉法更高的精度，但是相较于其他更高精度的数值方法，它的精度仍然较低。

三、龙格-库塔法龙格-库塔法是一种广泛使用的高精度数值方法，它不仅能够求解一阶和二阶常微分方程，还能够求解高阶常微分方程和偏微分方程。

其中，经典的四阶龙格-库塔法是最常用的数值方法之一。

四阶龙格-库塔法的步骤如下：1. 根据当前$t_i$和$y_i$估算$k_1$:$k_1=f(t_i,y_i)$2. 根据$k_1$和$y_i$估算$k_2$:$k_2=f(t_i+\frac{h}{2},y_i+\frac{h}{2}k_1)$3. 根据$k_2$和$y_i$估算$k_3$:$k_3=f(t_i+\frac{h}{2},y_i+\frac{h}{2}k_2)$4. 根据$k_3$和$y_i$估算$k_4$:$k_4=f(t_i+h,y_i+hk_3)$5. 根据$k_1$、$k_2$、$k_3$和$k_4$计算$y_{i+1}$:$y_{i+1}=y_i+\frac{h}{6}(k_1+2k_2+2k_3+k_4)$龙格-库塔法的精度较高，在求解一些对精度要求较高的问题时，龙格-库塔法是一个比较好的选择。

求常微分方程的数值解一、背景介绍常微分方程（Ordinary Differential Equation，ODE）是描述自然界中变化的数学模型。

常微分方程的解析解往往难以求得，因此需要寻找数值解来近似地描述其行为。

求解常微分方程的数值方法主要有欧拉法、改进欧拉法、龙格-库塔法等。

二、数值方法1. 欧拉法欧拉法是最简单的求解常微分方程的数值方法之一。

它基于导数的定义，将微分方程转化为差分方程，通过迭代计算得到近似解。

欧拉法的公式如下：$$y_{n+1}=y_n+f(t_n,y_n)\Delta t$$其中，$y_n$表示第$n$个时间步长处的函数值，$f(t_n,y_n)$表示在$(t_n,y_n)$处的导数，$\Delta t$表示时间步长。

欧拉法具有易于实现和理解的优点，但精度较低。

2. 改进欧拉法（Heun方法）改进欧拉法又称Heun方法或两步龙格-库塔方法，是对欧拉法进行了精度上提升后得到的一种方法。

它利用两个斜率来近似函数值，并通过加权平均来计算下一个时间步长处的函数值。

改进欧拉法的公式如下：$$k_1=f(t_n,y_n)$$$$k_2=f(t_n+\Delta t,y_n+k_1\Delta t)$$$$y_{n+1}=y_n+\frac{1}{2}(k_1+k_2)\Delta t$$改进欧拉法比欧拉法精度更高，但计算量也更大。

3. 龙格-库塔法（RK4方法）龙格-库塔法是求解常微分方程中最常用的数值方法之一。

它通过计算多个斜率来近似函数值，并通过加权平均来计算下一个时间步长处的函数值。

RK4方法是龙格-库塔法中最常用的一种方法，其公式如下：$$k_1=f(t_n,y_n)$$$$k_2=f(t_n+\frac{\Delta t}{2},y_n+\frac{k_1\Delta t}{2})$$ $$k_3=f(t_n+\frac{\Delta t}{2},y_n+\frac{k_2\Delta t}{2})$$ $$k_4=f(t_n+\Delta t,y_n+k_3\Delta t)$$$$y_{n+1}=y_n+\frac{1}{6}(k_1+2k_2+2k_3+k_4)\Delta t$$三、数值求解步骤对于给定的常微分方程，可以通过以下步骤求解其数值解：1. 确定初值条件：确定$t=0$时刻的函数值$y(0)$。

MATLAB常微分⽅程数值解——欧拉法、改进的欧拉法与四阶龙格库塔⽅法MATLAB常微分⽅程数值解作者：凯鲁嘎吉 - 博客园1.⼀阶常微分⽅程初值问题2.欧拉法3.改进的欧拉法4.四阶龙格库塔⽅法5.例题⽤欧拉法，改进的欧拉法及4阶经典Runge-Kutta⽅法在不同步长下计算初值问题。

步长分别为0.2,0.4,1.0.matlab程序：function z=f(x,y)z=-y*(1+x*y);function R_K(h)%欧拉法y=1;fprintf('欧拉法：x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K=f(x,y);y=y+h*K;fprintf('欧拉法：x=%f, y=%f\n',x+h,y);endfprintf('\n');%改进的欧拉法y=1;fprintf('改进的欧拉法：x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h,y+h*K1);y=y+(h/2)*(K1+K2);fprintf('改进的欧拉法：x=%f, y=%f\n',x+h,y);endfprintf('\n');%龙格库塔⽅法y=1;fprintf('龙格库塔法：x=%f, y=%f\n',0,1);for i=1:1/hx=(i-1)*h;K1=f(x,y);K2=f(x+h/2,y+(h/2)*K1);K3=f(x+h/2,y+(h/2)*K2);K4=f(x+h,y+h*K3);y=y+(h/6)*(K1+2*K2+2*K3+K4);fprintf('龙格库塔法：x=%f, y=%f\n',x+h,y);end结果：>> R_K(0.2)欧拉法：x=0.000000, y=1.000000欧拉法：x=0.200000, y=0.800000欧拉法：x=0.400000, y=0.614400欧拉法：x=0.600000, y=0.461321欧拉法：x=0.800000, y=0.343519欧拉法：x=1.000000, y=0.255934改进的欧拉法：x=0.000000, y=1.000000改进的欧拉法：x=0.200000, y=0.807200改进的欧拉法：x=0.400000, y=0.636118改进的欧拉法：x=0.600000, y=0.495044改进的欧拉法：x=0.800000, y=0.383419改进的欧拉法：x=1.000000, y=0.296974龙格库塔法：x=0.000000, y=1.000000龙格库塔法：x=0.200000, y=0.804636龙格库塔法：x=0.400000, y=0.631465龙格库塔法：x=0.600000, y=0.489198龙格库塔法：x=0.800000, y=0.377225龙格库塔法：x=1.000000, y=0.291009>> R_K(0.4)欧拉法：x=0.000000, y=1.000000欧拉法：x=0.400000, y=0.600000欧拉法：x=0.800000, y=0.302400改进的欧拉法：x=0.000000, y=1.000000改进的欧拉法：x=0.400000, y=0.651200改进的欧拉法：x=0.800000, y=0.405782龙格库塔法：x=0.000000, y=1.000000龙格库塔法：x=0.400000, y=0.631625龙格库塔法：x=0.800000, y=0.377556>> R_K(1)欧拉法：x=0.000000, y=1.000000欧拉法：x=1.000000, y=0.000000改进的欧拉法：x=0.000000, y=1.000000改进的欧拉法：x=1.000000, y=0.500000龙格库塔法：x=0.000000, y=1.000000龙格库塔法：x=1.000000, y=0.303395注意：在步长h为0.4时，要将for i=1:1/h改为for i=1:0.8/h。

数值计算中的常微分方程数值模拟在数值计算中，常微分方程（Ordinary Differential Equations，简称ODE）是一个重要的研究对象。

常微分方程的数值模拟是通过数值方法对其进行近似求解的过程，该过程对于模拟物理系统、生物学过程以及工程问题等具有重要意义。

本文将介绍常微分方程数值模拟的几种常用方法，并分析其特点与应用。

一、欧拉法（Euler's Method）欧拉法是最简单的常微分方程数值模拟方法之一，其基本思想是将连续的微分方程进行离散化，使用一阶差分近似代替微分。

具体步骤如下：1. 建立微分方程：设待求解的微分方程为dy/dx = f(x, y)，其中f(x, y)为已知函数。

2. 初始化：选择初始条件y0 = y(x0)，以及离散步长h。

3. 迭代求解：根据欧拉法的迭代公式yn+1 = yn + h * f(xn, yn)进行近似求解。

欧拉法的优点是简单易实现，但在处理复杂问题和大步长时存在精度较低的问题。

二、改进的欧拉法（Improved Euler's Method）为了提高欧拉法的精度，改进的欧拉法在迭代过程中使用两个不同的斜率近似值，从而对解进行更准确的预测并修正。

具体步骤如下：1. 建立微分方程：同欧拉法。

2. 初始化：同欧拉法。

3. 迭代求解：根据改进的欧拉法的迭代公式yn+1 = yn + h * (k1 +k2)/2进行近似求解，其中k1 = f(xn, yn)，k2 = f(xn + h, yn + h * k1)。

改进的欧拉法在精度上优于欧拉法，但仍然不适用于高精度要求的问题。

三、龙格-库塔法（Runge-Kutta Methods）龙格-库塔法是一类常微分方程数值模拟方法，通过计算多个不同次数的斜率来逼近解。

其中，四阶龙格-库塔方法是最常用的一种方法。

具体步骤如下：1. 建立微分方程：同欧拉法。

2. 初始化：同欧拉法。

3. 迭代求解：根据四阶龙格-库塔方法的迭代公式yn+1 = yn + h * (k1 + 2k2 + 2k3 + k4)/6进行近似求解，其中k1 = f(xn, yn)，k2 = f(xn + h/2, yn + h/2 * k1)，k3 = f(xn + h/2, yn + h/2 * k2)，k4 = f(xn + h, yn + h * k3)。

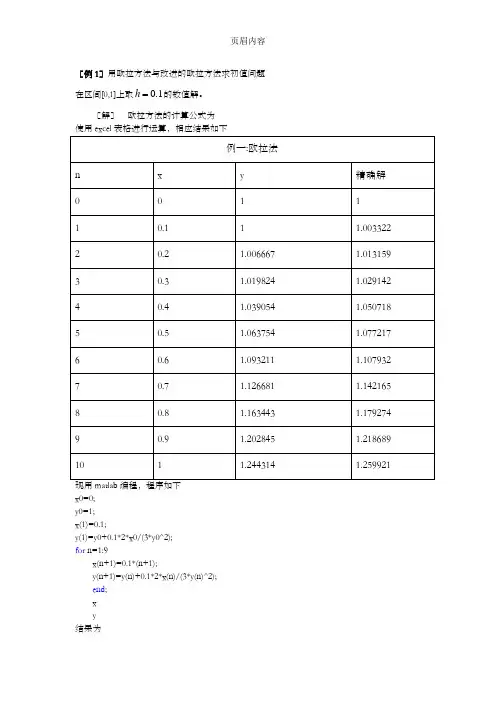
［例1］用欧拉方法与改进的欧拉方法求初值问题h 的数值解。

在区间[0,1]上取0.1［解］欧拉方法的计算公式为x0=0;y0=1;x(1)=0.1;y(1)=y0+0.1*2*x0/(3*y0^2);for n=1:9x(n+1)=0.1*(n+1);y(n+1)=y(n)+0.1*2*x(n)/(3*y(n)^2);end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0067 1.0198 1.0391 1.0638 1.0932 1.1267 1.1634 Columns 9 through 101.2028 1.2443改进的欧拉方法其计算公式为本题的精确解为()y x=x0=0;y0=1;ya(1)=y0+0.1*2*x0/(3*y0^2);y(1)=y0+0.05*(2*x0/(3*y0^2)+2*x0/(3*ya^2));for n=1:9x(n+1)=0.1*(n+1);ya(n+1)=ya(n)+0.1*2*x(n)/(3*ya(n)^2);y(n+1)=y(n)+0.05*(2*x(n)/(3*y(n)^2)+2*x(n+1)/(3*ya(n+1)^2));end;xy结果为x =Columns 1 through 80.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 Columns 9 through 100.9000 1.0000y =Columns 1 through 81.0000 1.0099 1.0261 1.0479 1.0748 1.1059 1.1407 1.1783 Columns 9 through 101.2183 1.2600［例2］用泰勒方法解x＝0.1, 0.2, …, 1.0处的数值解，并与精确解进行比较。

常微分方程的数值解法与实际应用研究引言：常微分方程是数学中一种重要的数学工具，广泛应用于物理、经济、生物等领域的实际问题的数学建模。

在解析求解常微分方程存在困难或不可行的情况下，数值解法提供了一种有效的求解方法，并被广泛应用于实际问题的研究中。

本文将介绍常微分方程的数值解法以及一些实际应用的研究案例。

一、常微分方程的数值解法：1. 欧拉法：欧拉法是一种基础的数值解法，通过将微分方程离散化，近似得到方程的数值解。

欧拉法的基本思想是根据微分方程的导数信息进行近似计算，通过逐步迭代来逼近真实解。

但是欧拉法存在截断误差较大、收敛性较慢等问题。

2. 改进的欧拉法（改进欧拉法推导过程略）：为了解决欧拉法的问题，改进的欧拉法引入了更多的导数信息，改善了截断误差，并提高了算法的收敛速度。

改进欧拉法是一种相对简单而可靠的数值解法。

3. 四阶龙格-库塔法：四阶龙格-库塔法是常微分方程数值解法中最常用和最经典的一种方法。

通过多次迭代，四阶龙格-库塔法可以获得非常精确的数值解，具有较高的精度和稳定性。

二、常微分方程数值解法的实际应用研究：1. 建筑物的结构动力学分析：建筑物的结构动力学分析需要求解一些动力学常微分方程，例如考虑结构的振动和应力响应。

利用数值解法可以更好地模拟建筑物的振动情况，并对其结构进行安全性评估。

2. 生态系统模型分析：生态系统模型通常包含一系列描述物种数量和相互作用的微分方程。

数值解法可以提供对生态系统不同时间点上物种数量和相互作用的变化情况的模拟和预测。

这对于环境保护、物种保护以及生态系统可持续发展方面具有重要意义。

3. 电路模拟与分析：电路模拟与分析通常涉及电路中的电容、电感和电阻等元件，这些元件可以通过常微分方程进行建模。

数值解法可以提供电路中电压、电流等关键参数的模拟和分析，对电路设计和故障诊断具有重要帮助。

4. 化学反应动力学研究：化学反应动力学研究需要求解涉及反应速率、物质浓度等的微分方程。

常微分方程组数值解法一、引言常微分方程组是数学中的一个重要分支，它在物理、工程、生物等领域都有广泛应用。

对于一些复杂的常微分方程组，往往难以通过解析方法求解，这时候数值解法就显得尤为重要。

本文将介绍常微分方程组数值解法的相关内容。

二、数值解法的基本思想1.欧拉法欧拉法是最基础的数值解法之一，它的思想是将时间连续化，将微分方程转化为差分方程。

对于一个一阶常微分方程y'=f(x,y)，其欧拉公式为：y_{n+1}=y_n+hf(x_n,y_n)其中h为步长，x_n和y_n为第n个时间点上x和y的取值。

2.改进欧拉法改进欧拉法是对欧拉法的改良，其公式如下：y_{n+1}=y_n+\frac{h}{2}[f(x_n,y_n)+f(x_{n+1},y_n+hf(x_n,y_n))] 3.四阶龙格-库塔方法四阶龙格-库塔方法是目前最常用的数值解法之一。

其公式如下：k_1=f(x_n,y_n)k_2=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_1)k_3=f(x_n+\frac{h}{2},y_n+\frac{h}{2}k_2)k_4=f(x_n+h,y_n+hk_3)y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)其中，k_i为中间变量。

三、常微分方程组的数值解法1.欧拉法对于一个二阶常微分方程组：\begin{cases} y'_1=f_1(x,y_1,y_2) \\ y'_2=f_2(x,y_1,y_2)\end{cases}其欧拉公式为：\begin{cases} y_{n+1,1}=y_{n,1}+hf_1(x_n,y_{n,1},y_{n,2}) \\y_{n+1,2}=y_{n,2}+hf_2(x_n,y_{n,1},y_{n,2}) \end{cases}其中，x_n和y_{n,i}(i=1, 2)为第n个时间点上x和y_i的取值。

常微分方程与数值解法数学是自然界中最美丽的语言之一，常微分方程是数学中的一个重要分支。

常微分方程是研究随着时间推移而发生的连续变化的数学模型，是许多科学领域的数学基础，如物理学、天文学、生物学、化学、经济学等。

通过对微分方程的求解，我们可以预测未来的变化和趋势，制定相应的政策措施和科学研究方向。

一、常微分方程的基本概念常微分方程是包含未知函数及其导数的方程。

一般形式为dy/dx=f(x,y)，其中y为未知函数，x为自变量，f(x,y)是已知函数，称为方程的右端函数。

常微分方程可以分为初值问题和边值问题。

初值问题是指求解微分方程时需要给出一个特定的初值y(x)=y0，边值问题是指给出方程在一些点的值，而求出未知函数在整个区间上的值。

二、常微分方程的解法常微分方程有许多解法，例如分离变量法、齐次方程、全微分方程、一阶线性方程、变量分离法等。

其中，变量分离法是最基本和最重要的方法之一。

变量分离法的基本思想是将微分方程的未知函数y和自变量x分开，变成dy/g(y)=f(x)dx的形式，然后对两边进行积分。

三、数值解法的发展与应用数值解法是通过数值计算来求解微分方程的，它主要包括欧拉法、改进欧拉法、龙格-库塔法等。

欧拉法最简单、最基本，但精度较低，适用于解决一些简单的微分方程。

改进欧拉法和龙格-库塔法则精度更高，适用于解决较为复杂的微分方程。

数值解法在科学技术中的应用广泛，如气象学、环境保护、物理学、化学等。

以生态学为例，许多生态系统的动态变化可以用微分方程描述，如种群增长、捕食捕获、竞争关系等。

数值解法可以在一定程度上预测未来的生态状态，有助于制定相应的生态保护措施。

四、结论在现代科学技术中，微分方程和数值解法已经成为不可或缺的工具之一。

通过微分方程的求解，可以预测未来的变化和趋势，制定相应的政策措施和科学研究方向。

数值解法则更加精细和灵活，能够解决更为复杂的微分方程，广泛应用于各个领域。

因此，学习微分方程和数值解法，不仅是数学爱好者的追求，更是科学技术工作者不可或缺的技能。