下载文档原格式
实验二MATLAB数值计算常微分方程的求解引言:微分方程是描述物理问题和工程问题的重要工具，也是数学和工程学科中的重要课题。
解析方法可以求得一些简单微分方程的解析解，但对于复杂问题，常常无法得到解析解。
此时，数值求解方法成为一种有效的工具。
MATLAB是一个功能强大的数值计算软件，对于求解常微分方程组也提供了多种数值方法。
本实验将介绍MATLAB中求解常微分方程(组)的方法，并通过实例来演示这些方法的应用。
一、MATLAB的常微分方程(组)求解函数MATLAB提供了多种函数用于求解常微分方程(组)，其中最常用的函数是ode45、ode23和ode15s。
这些函数采用不同的数值方法，精度和效率也不同。
下面分别对这些函数进行简单介绍：1. ode45函数:ode45函数采用了一种自适应的步长控制算法，可以在一个时间段内自动调整步长。
这个函数的语法是：[t,y] = ode45(odefun,tspan,y0,options)其中，odefun是一个函数句柄，表示待解的常微分方程组，tspan是求解区间，y0是初始条件，options是一个结构体，包含其他的参数和选项。
2. ode23函数:ode23函数也采用了自适应的步长控制算法，但相对于ode45，它是一个简化版本，只允许使用比较简单的问题。
这个函数的语法与ode45相似：[t,y] = ode23(odefun,tspan,y0,options)3. ode15s函数:ode15s函数采用了一种隐式数值方法，适用于比较刚性（stiff）的常微分方程。
这个函数的语法与前两个函数也相似：[t,y] = ode15s(odefun,tspan,y0,options)以上是MATLAB提供的三种解常微分方程(组)的函数，根据问题的特点和求解的需求选择相应的函数。
二、实例演示在本实验中，我们将通过一个实例来演示如何使用MATLAB解常微分方程组。
假设有一个简单的线性常微分方程组：dy1/dt = -2y1 + y2dy2/dt = y1 - 2y2给定初始条件为y1(0)=1，y2(0)=0，求在t=[0,5]时，y1和y2的解。
MATLAB是一种用于科学计算和工程应用的高级编程语言和交互式环境。
它在数学建模、模拟和分析等方面有着广泛的应用。
在MATLAB 中，常微分方程的数值求解是一个常见的应用场景。
在实际工程问题中，通常需要对常微分方程进行数值求解来模拟系统的动态行为。
本文将介绍MATLAB中对常微分方程进行数值求解的快速方法。
1. 基本概念在MATLAB中，可以使用ode45函数来对常微分方程进行数值求解。
ode45是一种常用的Runge-Kutta法，它可以自适应地选取步长，并且具有较高的数值精度。
使用ode45函数可以方便地对各种类型的常微分方程进行求解，包括一阶、高阶、常系数和变系数的微分方程。
2. 函数调用要使用ode45函数进行常微分方程的数值求解，需要按照以下格式进行函数调用：[t, y] = ode45(odefun, tspan, y0)其中，odefun表示用于描述微分方程的函数，tspan表示求解的时间跨度，y0表示初值条件，t和y分别表示求解得到的时间序列和对应的解向量。
3. 示例演示为了更好地理解如何使用ode45函数进行常微分方程的数值求解，下面我们以一个具体的例子来进行演示。
考虑如下的一阶常微分方程：dy/dt = -2*y其中，y(0) = 1。
我们可以编写一个描述微分方程的函数odefun：function dydt = odefun(t, y)dydt = -2*y;按照上述的函数调用格式，使用ode45函数进行求解：tspan = [0 10];y0 = 1;[t, y] = ode45(odefun, tspan, y0);绘制出解曲线：plot(t, y);4. 高级用法除了基本的函数调用方式外，MATLAB中还提供了更多高级的方法来对常微分方程进行数值求解。
可以通过设定选项参数来控制数值求解的精度和稳定性，并且还可以对刚性微分方程进行求解。
5. 性能优化在实际工程应用中，常常需要对大规模的常微分方程进行数值求解。
matlab求解微分方程数值解与解析解微分方程是数学中的重要内容，它描述了物理、工程、经济等领域中的许多现象和问题。
在实际应用中，我们经常需要求解微分方程的解析解或数值解。
本文将以Matlab为工具，探讨如何求解微分方程并对比解析解与数值解的差异。
一、引言微分方程是描述自然界中许多现象和问题的数学语言，它包含了未知函数及其导数与自变量之间的关系。
微分方程的求解可以帮助我们了解问题的性质和变化规律，并为实际应用提供参考。
在许多情况下，微分方程的解析解很难求得，这时我们可以利用计算机进行数值求解。
二、微分方程的数值解法1.欧拉法欧拉法是最简单的数值求解微分方程的方法之一。
它通过将微分方程转化为差分方程，然后利用离散的点逼近连续的解。
具体步骤如下：（1）将微分方程转化为差分方程，即用近似的导数代替真实的导数；（2）选择初始条件，即确定初始点的值；（3）选择步长和求解区间，即确定求解的范围和步长；（4）使用迭代公式计算下一个点的值；（5）重复步骤（4），直到达到指定的求解区间。
2.改进的欧拉法欧拉法存在精度较低的问题，为了提高精度，可以使用改进的欧拉法。
改进的欧拉法是通过使用两次导数的平均值来计算下一个点的值，从而提高了数值解的精度。
3.龙格-库塔法龙格-库塔法是一种常用的数值求解微分方程的方法，它通过使用多个点的导数来逼近连续解。
龙格-库塔法的步骤如下：（1）选择初始条件和步长；（2）使用迭代公式计算下一个点的值；（3）计算下一个点的导数；（4）根据导数的值和步长计算下一个点的值；（5）重复步骤（3）和（4），直到达到指定的求解区间。
龙格-库塔法的精度较高，适用于求解一阶和高阶微分方程。
三、微分方程的解析解解析解是指能够用公式或函数表示的方程的解。
有些微分方程具有解析解，可以通过数学方法求得。
例如，一阶线性常微分方程和某些特殊类型的二阶微分方程等。
解析解的优势在于精确性和直观性，能够帮助我们深入理解问题的本质。
matlab求微分方程组的解析解（实用版）目录1.引言2.MATLAB 求微分方程组的解析解的方法3.示例：求解一阶微分方程组4.示例：求解二阶微分方程组5.总结正文一、引言微分方程组在数学建模和实际问题中有着广泛的应用，求解微分方程组对于理解问题的内在机制和预测未来发展趋势具有重要意义。
在众多数学软件中，MATLAB 凭借其强大的数值计算和图形绘制功能，成为求解微分方程组的常用工具。
本文将介绍如何使用 MATLAB 求解微分方程组的解析解。
二、MATLAB 求微分方程组的解析解的方法MATLAB 求解微分方程组的解析解主要依赖于符号计算函数和数值计算函数。
其中，符号计算函数主要用于求解微分方程组的解析解，数值计算函数则用于求解微分方程组的数值解。
在使用这些函数时，需要确保符号计算和数值计算的顺序，以避免计算错误。
三、示例：求解一阶微分方程组考虑如下一阶微分方程组：```dy/dx = x + ydz/dx = x - z```我们可以使用 MATLAB 的符号计算函数`symfun`和`symvar`来求解该方程组。
首先，定义符号变量 x、y、z 和 p（表示参数），然后使用`symfun`函数创建微分方程组的符号表达式。
接着，利用`symvar`函数求解微分方程组，并将结果转换为数值形式。
最后，使用`plot`函数绘制解的图形。
四、示例：求解二阶微分方程组考虑如下二阶微分方程组：```x"" + 3x" + 2x = 0y"" + 3y" + 2y = 0```我们可以使用 MATLAB 的符号计算函数`symfun`和`symvar`来求解该方程组。
首先，定义符号变量 x、y 和 p（表示参数），然后使用`symfun`函数创建微分方程组的符号表达式。
接着，利用`symvar`函数求解微分方程组，并将结果转换为数值形式。
最后，使用`plot`函数绘制解的图形。
MATLAB求微分方程组的解析解引言在科学与工程领域，微分方程组是一种常见的数学模型，用于描述各种物理现象和工程问题。
解析解是指能够用公式表达出来的精确解。
本文将介绍如何使用M ATL A B求解微分方程组的解析解。
1.方程组的建立首先，我们需要确定待求解的微分方程组。
假设我们有一个由n个微分方程组成的方程组，可以写为如下形式：d y1/dt=f1(t,y1,y2,...,yn)d y2/dt=f2(t,y1,y2,...,yn)......d y n/dt=f n(t,y1,y2,...,yn)其中`t`是自变量，`y1,y2,...,y n`是因变量，`f1,f2,...,fn`是给定的函数关系。
我们的目标是求解`y1(t),y2(t),...,yn(t)`的解析解。
2.使用MAT LAB求解M A TL AB提供了强大的求解微分方程组的工具，我们可以使用其中的函数来求解上述方程组的解析解。
首先，我们需要在MA T LA B中定义方程组的函数形式。
可以通过定义一个函数或者使用匿名函数来实现。
例如，我们可以定义一个名为`m yE qu at io ns`的函数，其输入参数为`t`和一个向量`y`，输出为一个向量`d y`，代表方程组的左侧和右侧的变量分别。
函数示例如下：f u nc ti on dy=m yE qua t io ns(t,y)%定义方程组d y=z er os(n,1);d y(1)=f1(t,y(1),y(2),...,y(n));d y(2)=f2(t,y(1),y(2),...,y(n));......d y(n)=fn(t,y(1),y(2),...,y(n));e n d然后，我们可以使用M AT LA B的`d so lv e`函数来求解微分方程组的解析解。
示例如下：s y ms ty1(t)y2(t)...yn(t)a s su me(t,'re al')a s su me(y1(t),'rea l')a s su me(y2(t),'rea l')......a s su me(y n(t),'rea l')e q n1=d if f(y1(t),t)==f1(t,y1(t),y2(t),...,y n(t));e q n2=d if f(y2(t),t)==f2(t,y1(t),y2(t),...,y n(t));......e q nn=d if f(yn(t),t)==fn(t,y1(t),y2(t),...,y n(t));e q ns=[eq n1,e qn2,...,eq nn];S=ds ol ve(e qn s);`S`即为方程组的解析解集合。
matlab 求微分方程组数值解使用Matlab求解微分方程组是一种常见的数值方法。
微分方程组是描述自然界中许多现象的数学模型，它们可以用一组关于未知函数及其导数的方程来表示。
通过求解微分方程组，我们可以得到未知函数在给定条件下的数值解。
在Matlab中，求解微分方程组可以使用ode45函数。
该函数是一个常用的求解常微分方程初值问题的函数，它使用四阶龙格-库塔法（RK4）进行数值求解。
使用ode45函数求解微分方程组的步骤如下：定义微分方程组。
在Matlab中，可以使用匿名函数或函数句柄的方式定义微分方程组。
例如，对于一个二阶微分方程组：dy1/dt = f1(t, y1, y2)dy2/dt = f2(t, y1, y2)可以定义一个匿名函数：f = @(t, y) [f1(t, y(1), y(2)); f2(t, y(1), y(2))]其中，t是自变量，y是未知函数的向量。
接下来，指定求解的时间区间和初值条件。
时间区间可以通过指定起始时间和结束时间来确定。
初值条件是指在起始时间处未知函数的值。
初值条件可以通过一个向量来表示。
例如，对于一个二阶微分方程组，初值条件可以表示为一个长度为2的向量。
然后，调用ode45函数进行求解。
ode45函数的输入参数包括定义的微分方程组、时间区间和初值条件。
该函数会返回数值解和对应的时间点。
可以通过绘制图形或打印数值解来展示结果。
Matlab提供了丰富的绘图函数，可以方便地将数值解可视化。
需要注意的是，求解微分方程组时，应选择合适的数值方法和步长，以保证数值解的精度和稳定性。
对于复杂的微分方程组，可能需要进行参数调整和迭代求解，以得到满意的结果。
使用Matlab求解微分方程组是一种便捷而有效的数值方法。
通过定义微分方程组、指定时间区间和初值条件，调用ode45函数进行求解，可以得到微分方程组的数值解。
这种方法在科学研究和工程实践中具有广泛的应用，可以帮助我们更好地理解和分析自然界中的现象。
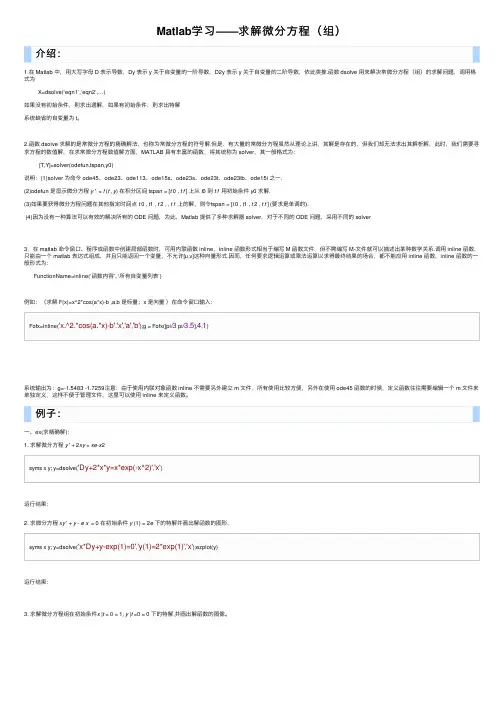
Matlab学习——求解微分⽅程（组）介绍：1.在 Matlab 中，⽤⼤写字母 D 表⽰导数，Dy 表⽰ y 关于⾃变量的⼀阶导数，D2y 表⽰ y 关于⾃变量的⼆阶导数，依此类推.函数 dsolve ⽤来解决常微分⽅程（组）的求解问题，调⽤格式为X=dsolve(‘eqn1’,’eqn2’,…)如果没有初始条件，则求出通解，如果有初始条件，则求出特解系统缺省的⾃变量为 t。
2.函数 dsolve 求解的是常微分⽅程的精确解法，也称为常微分⽅程的符号解.但是，有⼤量的常微分⽅程虽然从理论上讲，其解是存在的，但我们却⽆法求出其解析解，此时，我们需要寻求⽅程的数值解，在求常微分⽅程数值解⽅⾯，MATLAB 具有丰富的函数，将其统称为 solver，其⼀般格式为：[T,Y]=solver(odefun,tspan,y0)说明：(1)solver 为命令 ode45、ode23、ode113、ode15s、ode23s、ode23t、ode23tb、ode15i 之⼀.(2)odefun 是显⽰微分⽅程y ' = f (t , y) 在积分区间 tspan = [t 0 , t f ] 上从t0 到t f⽤初始条件 y0求解.(3)如果要获得微分⽅程问题在其他指定时间点t 0 , t1 , t 2 , , t f上的解，则令tspan = [t 0 , t1 , t 2 , t f ](要求是单调的).(4)因为没有⼀种算法可以有效的解决所有的 ODE 问题，为此，Matlab 提供了多种求解器 solver，对于不同的 ODE 问题，采⽤不同的 solver3．在 matlab 命令窗⼝、程序或函数中创建局部函数时，可⽤内联函数 inline，inline 函数形式相当于编写 M 函数⽂件，但不需编写 M-⽂件就可以描述出某种数学关系.调⽤ inline 函数，只能由⼀个 matlab 表达式组成，并且只能返回⼀个变量，不允许[u,v]这种向量形式.因⽽，任何要求逻辑运算或乘法运算以求得最终结果的场合，都不能应⽤ inline 函数，inline 函数的⼀般形式为：FunctionName=inline(‘函数内容’, ‘所有⾃变量列表’)例如：（求解 F(x)=x^2*cos(a*x)-b ,a,b 是标量；x 是向量）在命令窗⼝输⼊:Fofx=inline('x.^2.*cos(a.*x)-b','x','a','b');g = Fofx([pi/3 pi/3.5],4,1)系统输出为：g=-1.5483 -1.7259注意：由于使⽤内联对象函数 inline 不需要另外建⽴ m ⽂件，所有使⽤⽐较⽅便，另外在使⽤ ode45 函数的时候，定义函数往往需要编辑⼀个 m ⽂件来单独定义，这样不便于管理⽂件，这⾥可以使⽤ inline 来定义函数。
