例题

参考系例题
1. 某人站在一个运动车上，并将车的速度都设为0。

当他看向
窗外时，他看到前方的建筑物静止不动。

他看到相邻车辆正在以相同的速度和方向移动。

这个人所处的参考系是？
答案：该人所处的参考系是运动车。

2. 两辆车同时从同一起点出发，在同一路线上以相同的速度行驶。

车A在某个时刻超过了车B。

这个情况下，哪辆车是相
对静止的？如何确定该车的速度？
答案：相对于车A，车B是相对静止的。

通过测量车B相对
于公路上的某个固定点的位移和时间，可以确定车B的速度。

3. 两个人站在一个静止的火车上，其中一个人向前移动，并距离火车的尾部保持一定的距离。

另一个人则保持原地不动。

当他们观察火车时，两人看到火车的尾部位置是否相同？
答案：是的，两人所看到的火车尾部位置相同。

由于火车是静止的，无论他们在火车上的位置如何，他们都会看到火车尾部的位置不变。

4. 某人站在静止的等车站台上，一辆以10 m/s的速度通过车
站的火车经过他。

这个人看到火车上的旅客以何种速度移动？
答案：这个人看到火车上的旅客以10 m/s的速度相对于车站
台移动，因为火车和火车上的旅客在同一参考系中。

希望以上例题能对你有所帮助！。

20 道条件概率例题例题1袋中有 5 个红球和 3 个白球，从中不放回地依次摸出两个球。

已知第一次摸出红球，求第二次摸出红球的概率。

解：第一次摸出红球后，袋中还有 4 个红球和 3 个白球，所以第二次摸出红球的概率为4/7。

例题2一个盒子里有 6 个黑球和 4 个白球，从中随机取出两个球。

若已知第一个球是黑球，求第二个球也是黑球的概率。

解：第一个球是黑球后，盒子里还有 5 个黑球和 4 个白球，所以第二个球是黑球的概率为5/9。

例题3有三张卡片，分别写着数字1、2、3。

从中随机抽取一张，放回后再抽取一张。

已知第一次抽到数字2，求第二次抽到数字 3 的概率。

解：因为是有放回抽取，所以第一次抽到数字 2 后，第二次抽取时每张卡片被抽到的概率仍为1/3，所以第二次抽到数字 3 的概率为1/3。

例题4一批产品中有合格品和次品，合格品率为80%。

从中随机抽取一件产品，已知是合格品，求该产品是一等品的概率（设合格品中一等品率为60%）。

解：由条件概率公式，所求概率为合格品中的一等品率，即60%。

例题5箱子里有红色球和蓝色球，红色球占总数的40%。

从箱子里随机取出一个球，已知是红色球，求这个球上标有数字 5 的概率（设红色球中有30%标有数字5）。

解：根据条件概率公式，所求概率为红色球中标有数字 5 的比例，即30%。

例题6某班级男生占总人数的60%。

在男生中，喜欢数学的占70%。

从班级中随机抽取一名学生，已知是男生，求该学生喜欢数学的概率。

解：所求概率为男生中喜欢数学的比例，即70%。

例题7有两个盒子，盒子 A 中有 3 个红球和 2 个白球，盒子 B 中有 4 个红球和3 个白球。

从盒子 A 中随机取出一个球放入盒子B，然后从盒子 B 中随机取出一个球。

已知从盒子 B 中取出的是红球，求从盒子 A 中取出的也是红球的概率。

解：设从盒子 A 中取出红球为事件A，从盒子 B 中取出红球为事件B。

先求P(A) = 3/5，P(B|A) = (4 + 1)/(7 + 1) = 5/8。

【例题】某行政村计划15天完成春播任务1500亩，播种5天后，由于更新机械，工作效率提高25%，问这个行政村会提前几天完成这1500亩的春播计划? A.4 B.3 C.2 D.1【例题】某工厂的一个生产小组，当每个工人在自己的工作岗位上工作时，9小时可以完成一项生产任务。

如果交换工人甲和乙的工作岗位，其他人的工作岗位不变时，可提前1小时完成任务；如果交换工人丙和丁的工作岗位，其他人的工作岗位不变时，也可提前1小时完成任务。

如果同时交换甲和乙、丙和丁的工作岗位，其他人的工作岗位不变，可以提前多少小时完成这项任务?A.1.6B.1.8C.2.0D.2.4【例题】有20人修筑一条公路，计划15天完成。

动工3天后抽出5人植树，留下的人继续修路。

如果每人工作效率不变，那么修完这段公路实际用多少天? A.16 B.17 C.18 D.19【例题】单独完成某项工作，甲需要16小时，乙需要12小时，如果按照甲、乙、甲、乙、……的顺序轮流工作，每次1小时，那么完成这项工作需要多长时间?A.13小时40分钟B.13小时45分钟C.13小时50分钟D.14小时【例题】甲、乙两车运一堆货物。

若单独运，则甲车运的次数比乙车少5次；如果两车合运，那么各运6次就能运完，甲车单独运完这堆货物需要多少次? A.9 B.10 C.13 D.15【解析】C。

原来的工作效率为100亩/天，提高25%后则每天播种125亩，剩余的1000亩需要8天播完，因此可以提前2天完成任务。

【解析】【解析】D。

设每人每天干活1个单位，那么，题意可以理解为15人干活需要干满20天。

因为有5个人另干了3天，即相当于15个人干了一天的活，所以15人现在只需干活20-1=19天。

【解析】【解析】【例题】3，6，11，( )，27 A．15 B．18 C．19 D．24【例题】118，199，226，( )，238 A．228 B．230 C．232 D．235【例题】2/3 ，1/2 ，5/9 ，( )，11/15 A．2/5 B．6/11 C．3/4 D．7/12 【例题】2，3，10，23，( ) A．35 B．42 C．68 D．79【例题】8，16，22，24，( ) A．18 B．22 C．26 D．28【解析】B。

100个数论经典例题1. 证明：无理数的十进展开不可能是一个重复的数字序列。

2. 证明：一个正整数为完全平方数的充分必要条件是它的每个质因子的指数都是偶数。

3. 证明：有理数的不循环小数展开是独一无二的。

4. 如果两个整数m和n的最大公约数是1，那么m/n的分数形式是既简单又唯一的。

5. 证明：对于任意自然数n，n²+n+41都是一个质数。

6. 证明：对于任意自然数n，3n²+3n+7都是一个质数。

7. 求1²+2²+3²+...+n²的值，并给出证明。

8. 求1³+2³+3³+...+n³的值，并给出证明。

9. 证明：无穷多个素数是等差数列的形式。

10. 设p是一个素数，证明：x²≡-1(mod p）的解的个数为0或2。

11. 给定一个正整数n，求所有满足φ(x)=n的正整数x，其中φ(x)表示小于x且与x互质的正整数的个数（欧拉函数）。

12. 证明：若p是任意一个素数，则对于任意自然数n，(n+p)!≡n!pⁿ(mod p²)。

13. 证明：若p是任意一个素数，则对于任意自然数n，n!≡-1(mod p)当且仅当p=2或p≡1(mod 4)。

14. 对于任意一个素数p和整数a，证明：x²≡a(mod p）有解的充分必要条件是a^(p-1)/2≡±1(mod p)。

15. 证明：对于任意自然数n，存在无限多个三元组(x,y,z)使得x⁴+y⁴=z³。

16. 证明：对于任意正整数k，存在无限多个素数p，使得p≡1(mod k)。

17. 求2²+4²+6²+...+50²的值，并给出证明。

18. 求1+2+3+...+99+100的值，并给出证明。

19. 给定正整数a、b、n，求aⁿ+bⁿ的最大公因数，并给出证明。

数学例题的分类有哪些
数学例题可以根据不同的标准进行分类。

以下是一些常见的分类方式：
1.按题意分类：包括求解题、求证题、求作题等。

2.按所属数学领域分类：包括代数题、平面几何题、三角题等。

3.按题目综合程度分类：包括单一型题与综合型题，综合题目又分横向综合与纵向综合。

4.按评价的客观性分类：包括主观题与客观题。

5.根据题目要素分类：包括标准型题、训练型题、探索型题、问题型题。

6.根据题目条件与答案的确定性分类：包括开放型题与封闭型题。

7.根据应用范畴分类：包括纯数学题与应用题。

需要注意的是，同一个数学例题可能同时属于多个分类，因此在实际使用时需要根据具体情况进行判断。

典型例题-G-方差分析-2某企业准备用三种方法组装一种新的产品，为确定哪种方法每小时生产的产品数量最多，随机抽取了30名工人，并指定每个人使用其中的一种方法。

通过对每个工人生产的产品数进行方差分析，得到如下表所示的结果。

每个工人生产产品数量的方差分析表(2)若显著性水平为α=0.05，检验三种方法组装的产品数量之间是否有显著差异。

解：(1)完成方差分析表，以表格中所标的①、②、③、④、⑤、⑥为顺序，来完成表格，具体步骤如下： ①求k -1根据题目中“该企业准备用三种方法组装一种新的产品”可知，因素水平(总体)的个数k =3，所以第一自由度df 1=k -1=3-1=2，即SSA 的自由度。

②求n -k由“随机抽取了30名工人”可知，全部观测值的个数n =30，因此可以推出第二自由度df 2=n -k =30-3=27，即SSE 的自由度。

③求组间平方和SSA已知第一自由度df 1=k -1=3-1=2，MSA =210 根据公式1-==k SSAMSA 自由度组间平方和所以，SSA =MSA ×(k -1)=210×2=420④求总误差平方和SST由上面③中可以知道SSA =420；此外从表格中可以知道：组内平方和SSE =3836，根据公式SST =SSA +SSE 可以得出SST =420+3836=4256，即总误差平方和SST=4256 ⑤求SSE 的均方MSE已知组内平方和SSE =3836，SSE 的自由度n -k =30-3=27 根据公式0741.142273836==-==k n SSE MSE 自由度组内平方和所以组内均方MSE =142.0741⑥求检验统计量F已知MSA =210，MSE =142.0741 根据4781.10741.142210===MSE MSA F所以F=1.4781(2)题目中假设α=0.05，根据第一自由度df 1=k -1=3-1=2和第二自由度df 2=n -k =30-3=27，查F 分布表得到临界值F 0.05(2,27)=3.354131，所以F =1.4781<F α=3.354131，所以接受原假设，即μ1=μ2=μ3成立，表明μ1、μ2、μ3之间没有显著差异，也就是说，用三种方法组装的产品数量之间没有显著差异。

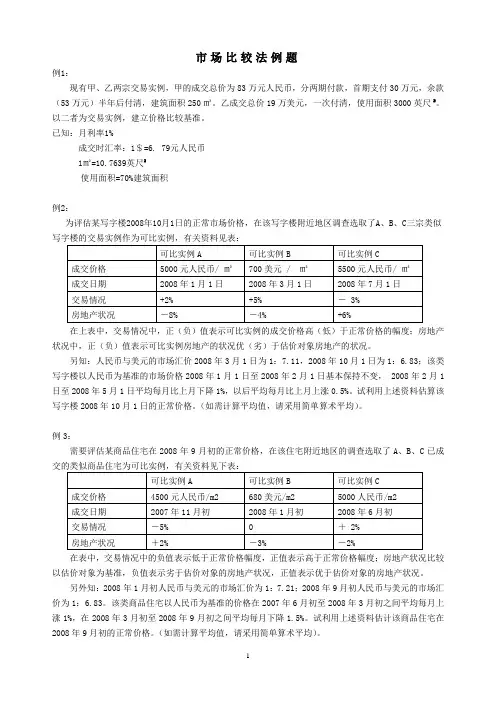
市场比较法例题例1：现有甲、乙两宗交易实例，甲的成交总价为83万元人民币，分两期付款，首期支付30万元，余款（53万元）半年后付清，建筑面积250㎡。

乙成交总价19万美元，一次付清，使用面积3000英尺2。

以二者为交易实例，建立价格比较基准。

已知：月利率1%成交时汇率：1＄=6. 79元人民币1㎡=10.7639英尺2使用面积=70%建筑面积例2：为评估某写字楼2008年10月1日的正常市场价格，在该写字楼附近地区调查选取了A、B、C三宗类似在上表中，交易情况中，正（负）值表示可比实例的成交价格高（低）于正常价格的幅度；房地产状况中，正（负）值表示可比实例房地产的状况优（劣）于估价对象房地产的状况。

另知：人民币与美元的市场汇价2008年3月1日为1：7.11，2008年10月1日为1：6.83；该类写字楼以人民币为基准的市场价格2008年1月1日至2008年2月1日基本保持不变， 2008年2月1日至2008年5月1日平均每月比上月下降1%，以后平均每月比上月上涨0.5%。

试利用上述资料估算该写字楼2008年10月1日的正常价格。

（如需计算平均值，请采用简单算术平均）。

例3：需要评估某商品住宅在2008年9月初的正常价格，在该住宅附近地区的调查选取了A、B、C已成在表中，交易情况中的负值表示低于正常价格幅度，正值表示高于正常价格幅度；房地产状况比较以估价对象为基准，负值表示劣于估价对象的房地产状况，正值表示优于估价对象的房地产状况。

另外知：2008年1月初人民币与美元的市场汇价为1：7.21；2008年9月初人民币与美元的市场汇价为1：6.83。

该类商品住宅以人民币为基准的价格在2007年6月初至2008年3月初之间平均每月上涨1%，在2008年3月初至2008年9月初之间平均每月下降1.5%。

试利用上述资料估计该商品住宅在2008年9月初的正常价格。

（如需计算平均值，请采用简单算术平均）。

例4：需要评估某商品住宅在2008年8月31日的正常价格，在该住宅附近地区的调查了A、B、C、D、E已成上表中，交易情况、房地产状况中的各正、负值都是按直接比较所得结果。

例题：求下列各物质的质子化常数：（1）氟离子，（2）氨分子，（3）S2-解例题：已知Zn2+-NH3溶液中，锌的分析浓度0.020mol/l，游离氨[NH3]的浓度0.10mol/l，计算溶液中锌－氨配合物中各型体的浓度。

锌－氨配合物的lg?1~ lg?4分别为2.27、4.61、7.01、9.06例：计算pH=5时，EDTA的酸效应系数，若此时EDTA各种型体总浓度为0.02mol/L，求[Y4 -]题：例求pH = 5.00 时 NH3 的酸效应系数。

计算pH=9.0,CNH3 =0.10mol/L时的lgK’ZnYpH = 9.0,pH = 9.0从前面的例题， pH = 9.0, CNH3 = 0.10 mol/L例题：pH = 9.0 的氨性缓冲溶液中，用0.02 mol / L EDTA 滴定 0.02 mol / L Zn2+ 溶液，用铬黑 T 为指示剂，终点 CNH3 = 0.1 mol / L, 求pZn’ep解：终点时， pH = 9.0， CNH3 = 0.1 mol / L,求出查表pH = 9.0 时，铬黑 T 作为滴定Zn2+的指示剂变色点的pMep 值例：设计0.020mol/LEDTA→同浓度Bi3+,Pb2+混合溶液方法(1)滴定铋离子假设Mg2+和EDTA的浓度皆为0.02mol/L，在pH=6时条件稳定常数K’MY为多少？说明此pH值条件下能否用EDTA标液准确滴定Mg2+？若不能滴定，求其允许的最小pH？为什么以EDTA滴定Mg2+时，通常在pH=10而不是在pH=5的溶液中进行；但滴定Zn2+时，则可以在pH=5的溶液中进行？用2×10-2mol/L的EDTA滴定2×10-2mol/L的Fe3+溶液，要求膒M’=±0.2，TE%=0.1%，计算滴定适宜酸度范围?例题：用0.02 mol / L EDTA滴定 0.02 mol / L Pb2+和0. 02 mol / L Mg2+混合物中的Pb2+ 。

数学11个例题
1.有一根长为20cm的绳子，将其剪成两段，其中一段是另一段的3倍，请求出两段的长度。

2. 某超市打折，原价为80元的商品，现在打7折，请问现在的价格是多少？
3. 如果 a+b=5，a-b=3，请问a和b分别是多少？
4. 一辆汽车以每小时60km的速度行驶，行驶10小时后行驶了多少公里？
5. 如果 x:y=2:3，且x=12，请问y是多少？
6. 有一组数据：2, 4, 6, 8, 10，请问这组数据的平均数是多少？
7. 如果a是奇数，b是偶数，且a+b=13，请问a和b可能是哪些数？
8. 有一组数据：5, 7, 9, 11，请问这组数据中的最小值是多少？
9. 如果一个圆的半径为4cm，请问这个圆的周长是多少？
10. 有一组数据：2, 4, 6, 8, 10，请问这组数据的中位数是多少？
11. 如果一张纸的长是10cm，宽是8cm，请问这张纸的面积是多少平方厘米？
- 1 -。

第3章例：某银行同时贷给两个工厂各1000万元，年利率均为12%。

假如甲厂单利计息，乙厂复利计息，问五年后，该银行应从两个工厂各提取多少资金？ 从甲厂提取资金：()16005%1211000)1(=⨯+=+=in P F从乙厂提取资金：从乙厂多提了162.34万元资金。

例：某银行同时贷给两个工厂各1000万元，年利率均为12%。

甲厂每年结算一次，乙厂每月结算一次。

问一年后，该银行从两个工厂各提出了多少资金？已知：r=12%,m 甲=1， m 乙=12，p=1000,n=1F 甲=1000*（1+12%）=1120（万元）F 乙=1000*（1+12.7%）=1127（万元）1、一次支付类型⑴一次支付终值公式例1：某企业为开发新产品，向银行借款100万元，年利率10%，借期五年，问五年后一次归还银行的本利和是多少？F=P （1+i ）n =100(1+0.1)5=100×1.611 =161.1(万元)⑵一次支付现值公式例2-6：准备10年后从银行取10万元，银行存款年利率为10%，采取定期一年、自动转存方式存款，年初应存入银行多少元？例2-7：准备10年后从银行取10万元，银行存款年利率为10%，采取定期一年、自动转存方式存款，如果年末存款，应存入银行多少元？例：如果银行利率为12%，某人计划5 年后从银行提取10000元款项，现应存入银行多少钱？ 解:P=F(1+i)-5=10000(1+0.12)-5 =5674(元)2、等额分付系列⑴ 等额分付终值公式（已知A ，求F ）例：某人每年末在银行存款1万元，存款期一年，自动转存，连续十年。

问十年后可从银行取出多少元？()())(487.14487.14110%,8,/1,,/万元=⨯=⨯==A F n i A F A F⑵ 等额分付偿债基金公式（已知F ，求A ）例：某企业计划自筹资金，在5年后扩建厂房，估计那时需资金1000万元，问从现在起平均每年应积累多少资金？年利率6％。

1、如果消费者对某商品的偏好增加，同时这种产品的生产技术有很大改进，我们可以预料（）A．该商品的需求曲线和供给曲线都向右移动并使均衡价格和产量提高B．该商品的需求曲线和供给曲线都向右移动并使均衡价格和产量下降C．该商品的需求曲线和供给曲线都向左移动并使均衡价格上升而均衡产量下降D．该商品的需求曲线和供给曲线都向右移动并使均衡产量增加，但均衡价格可能上升也可能下降2、下列哪种情况不正确？（）。

A、如果供给减少，需求不变，均衡价格将上升B、如果供给增加，需求减少，均衡价格将下降C、如果需求增加，供给减少，均衡价格将上升D、如果需求减少，供给增加，均衡价格将上升3．在需求和供给同时减少的情况下（）A．均衡价格和均衡交易量都将下降B．均衡价格将下降，均衡交易量的变化无法确定C．均衡价格的变化无法确定，均衡交易量将减少D．均衡价格在上升，均衡交易量将下降4．均衡价格随着（）A．需求和供给的增加而上升B．需求和供给的减少而上升C．需求的减少和供给的增加而上升D．需求的增加和供给的减少而上升5、假设有一个竞争的公寓市场,在发生了下列变化(其他条件相等)之后,对均衡价格和数量会发生什么影响?A、消费者收入增加；B、对公寓租金每月征收100元税金；C、政府出台限购令；D、新建筑技术是公寓的建筑成本降10%；E、建筑工人工资提高10%；F、房屋动迁费每平方米提高2000元。

政府对卖者出售的商品每单位征税5美元，假定这种商品的需求价格弹性为零，可以预料价格的上升（）A．小于5美元B．等于5美元C．大于5美元D．不可确定设供给函数为S =2 +3P；需求函数为D=10 -P。

(1)求解市场均衡的价格与产量水平；(2;8)(2)求在此均衡点的供给弹性与需求的价格弹性；(0.75;-0.25)(3)若征收从量税t=1，求此时新的均衡价格与产量水平；(2.75;7.27)(4)求消费者和厂商各承受了多少税收份额；(0.75;0.25)(5)用图来表示上述的结论。

例1：一个小于80的自然数与3的和是5的倍数，与3的差是6的倍数，这个自然数最大是多少？A.32B.47C.57D.72例2：某零件加工厂按照工人完成的合格零件盒不合格零件数支付工资，工人每做出一个合格零件能得到工资10元，每做出一个不合格零件将扣除5元。

已知某人一天一共做了12个零件，得到工资90元，那么他在这一天作了多少个不合格零件？A. 2B.3C.4D.6练习：1999年，一个青年说：“今年我的生日已过了，我现在的年龄正好是我出生的年份的四个数之和”，这个青年是哪年出生的？A.1975B.1976C.1977D.1978例3：一个五位数，左边三位数是右边两位数的5倍，如果把右边的两位数移到前面，则所得新的五位数要比原来的五位数的2倍还多75，则原五位数是多少？A.12525B.13527C.17535D.22545例4：一个三位数，百位数比十位上的数大4，个位上的数比十位上的数大2，这个三位数恰好是后两个数字组成的两位数的21倍，那么，这个三位数是？A.532B.476C.676D.735练习1、编一本书的书页，用了270个数字(重复的也算。

如页码115用了2个1和1个5共3个数字)，问这本书一共多少页?（）A.117B.126C.127D.1892、有粗细不同的两支蜡烛，细蜡烛的长度是粗蜡烛长度的2倍，点完细蜡烛需要1小时，点完粗蜡烛需要2小时。

有一次停电，将这样两支蜡烛同时点燃，来电时，发现两支蜡烛所剩长度一样，则此次停电共停了（）A．10分钟B．20分钟C．40分钟D．60分钟例1：现有一种药物配置成的甲、乙两种不同浓度的消毒溶液。

若从甲中取2100克、乙中取700克混合而成的消毒溶液的浓度为3%；若从甲中取900克、乙中取2700克，则混合而成的消毒溶液的浓度为5%。

则甲、乙两种消毒溶液的浓度分别为？A.3%、6%B.3%、4%C.2%、6%D.4%、6%练习1：两个相同的瓶子装满盐水溶液，一个瓶子中盐和水的比例是3:1，另一个瓶子中盐和水的比例是4:1，若把两瓶盐水溶液混合，则混合液中盐和水的比例是？A.31:9B. 4：55C.31:40D.5:4练习2：甲班与乙班同学同时从学校出发去某公园，甲班步行的速度是每小时4千米。

典型例题分析例、请你分别计算出下面每个长方体或正方体向上、向左的面的面积。

5厘米厘米7厘米5厘米①②分析与解：首先要弄清楚每个长方体（含正方体）向上、向左的面是哪个面，如果是长方形，长和宽分别是多少厘米；如果是正方形，边长又是多少厘米，这样即可求出所求面的面积。

图①向上的面积是7×2 = 14（平方厘米），向左的面积是2×5 = 10（平方厘米）。

图②向上、向左的面积都是5×5 = 25（平方厘米）。

例、江宁体育馆有一个长方体形状的游泳池，长50米，宽30米，深3米，现在要在游泳池的各个面上抹上一层水泥，抹水泥的面积有多少平方米？如果每平方米用水泥12千克，22吨够吗？分析与解：求水泥的面积有多少平方米，实际就是求这个长方体游泳池的表面积。

要计算前、后、左、右、下这5个面的面积之和。

再根据每平方米用水泥的千克数，算出这个游泳池共用水泥多少千克，即可知道22吨水泥够不够用。

50×30 + 50×3×2 + 30×3×2= 1500 + 300 + 180= 1980（平方米）12×1980=23760（千克）=23.76（吨）23.76 > 22 所以，22吨水泥不够用。

答：抹水泥的面积有1980平方米。

22吨水泥够不够用。

例4、厂商生产的一幅扑克牌长9厘米、宽6.5厘米、高2厘米，现在要把相同的两幅扑克牌放在一起包装（如右图），请问这个包装盒的表面积至少是多少平方厘米？分析与解：由上图可知，这个长方体包装盒的长是13厘米（6.5×2=13厘米），宽应是9厘米，高为2厘米，根据分析结果，能准确算出这个包装盒的表面积。

（13×9 + 13×2 + 9×2）×2=（117 + 26 + 18）×2= 161×2= 322（平方厘米）答：这个包装盒的表面积是322平方厘米。

向阳客车厂原计划生产客车 5000 辆，实际生产 5500 辆。

实际比计划多生产百分之几？向阳客车厂原计划生产客车 5000 辆，实际生产 5500 辆。

计划比实际少生产百分之几？一筐苹果比一筐梨重 20％，那么一筐梨就比一筐苹果轻 20％一种电子产品，原价每台 5000 元，现在降低到 3000 元。

降价百分之几？一项工程，原计划 10 天完成，实际 8 天就完成了任务，实际每天比原计划多修百分之几？益民五金公司去年的营业总额为 400 万元。

如果按营业额的 3％缴纳营业税，去年应缴纳营业税多少万元？王叔叔买了一辆价值 16000 元的摩托车。

按规定，买摩托车要缴纳 10％的车辆购置税。

王叔叔买这辆摩托车一共要花多少钱？李明把 500 元钱按三年期整存整取存入银行，到期后应得利息多少元？根据国家税法规定，个人在银行存款所得的利息要按 5％的税率缴纳利息税。

例 1 中纳税后李明实得利息多少元？方明将 1500 元存入银行，定期二年，年利率是 4.50％。

两年后方明取款时要按 5％缴纳利息税，到期后方明实得利息多少元？一本书现价 6.4 元，比原价便宜 1.6 元。

这本书是打几折出售的？“国庆”商场促销，一套西服打八五折出售是 1020 元，这套西服原价多少元？一台液晶电视 6000 元，若打七五折出售，可降价 2000 元？一批电冰箱，原来每台售价 2000 元，现促销打九折出售，有一顾客购买时，要求再打九折，如果能够成交，售价是多少元？商店以 40 元的价钱卖出一件商品，亏了 20％。

这件商品原价多少元，亏了多少元？某商店同时卖出两件商品，每件各得 30 元，其中一件盈利 20％，另一件亏本 20％。

这个商店卖出这两件商品总体上是盈利还是亏本？具体是多少？一根绳子长 48 米，截成甲、乙两段，其中乙绳长度是甲绳的 60％。

甲、乙两绳各长多少米？体育馆内排球的个数是篮球的 75％，篮球比排球多 6 个。