圆弧齿锥齿轮传动设计几何计算过程
- 格式:docx
- 大小:10.72 KB
- 文档页数:2

弧齿锥齿轮铣齿计算弧齿锥齿轮是传动行业中常用的一种齿轮,其结构相对复杂,铣齿计算难度较大。
本文将围绕弧齿锥齿轮铣齿计算进行分步骤的阐述。
第一步:确定齿轮参数在进行弧齿锥齿轮铣齿计算之前,需要确定齿轮参数,包括轴距、锥距、锥度、压力角等参数。
这些参数需要在设计时给出,或者由实际应用中的传递比、轴功率等参数推算得出。
第二步:计算齿数弧齿锥齿轮铣齿计算的第一步是计算齿数。
通常情况下,弧齿锥齿轮的齿数较小,一般不超过20个。
计算齿数需要使用弧齿锥齿轮铣刀的几何参数,以及齿面曲线的基本方程。
每个齿面曲线可以看做一条螺旋线,其截面积呈三角形状。
根据这些参数计算得出的齿数,不一定是整数,需要舍入到最接近的整数。
第三步:计算铣刀参数在确定齿数之后,就可以开始计算铣刀参数了。
铣刀的参数包括齿宽、齿高、齿间隙等。
齿宽可以由齿数和啮合角度计算得出;齿高可以由矢高、压力角等参数计算得出;齿间隙可以采用经验数据或理论计算得出。
第四步:计算加工参数铣齿前需要确定加工参数,包括进给量、转速等。
这些参数需要根据加工机床和工件材质等具体情况进行选取,以获得最佳的加工效果。
进给量的选择要尽量保证加工效率和质量,而转速的选择则要考虑切削油,刀具材料等方面的因素。
第五步:检验加工精度最后一步是检验加工精度。
通过测量齿轮的齿高、齿宽、轴向距离、齿距等参数,可以判断齿轮加工的精度是否符合要求。
如果齿轮加工精度不足,则需要对铣刀的加工参数进行调整,并重新进行铣齿计算。
综上所述,弧齿锥齿轮铣齿计算需要经过齿轮参数计算、齿数计算、铣刀参数计算、加工参数选择和加工精度检验等多个步骤,这些步骤需要根据具体的工件、机床和材料等因素进行调整。
只有经过认真的计算和精细的加工,才能获得符合要求的弧齿锥齿轮。

弧齿锥齿轮几何参数设计分解————————————————————————————————作者:————————————————————————————————日期:ﻩ第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
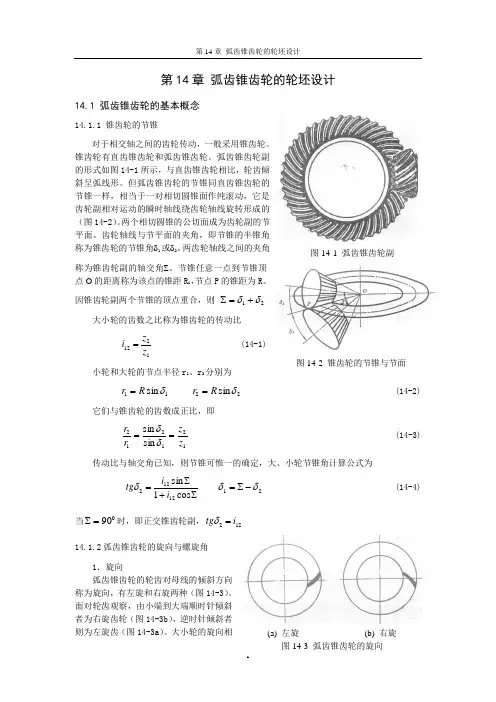
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距Ri ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1)小轮和大轮的节点半径r1、r 2分别为11sin δR r = 22sin δR r =(14-2)它们与锥齿轮的齿数成正比,即121212sin sin z z r r ==δδ (14-3)传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑=(14-4)当090=∑时,即正交锥齿轮副,122i tg =δ14.1.2弧齿锥齿轮的旋向与螺旋角图14-2 锥齿轮的(a) 左旋图14-1 弧齿锥1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b),逆时针倾斜者则为左旋齿(图14-3a )。
大小轮的旋向相反时,才能啮合。
一般情况下,工作面为顺时针旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。


第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
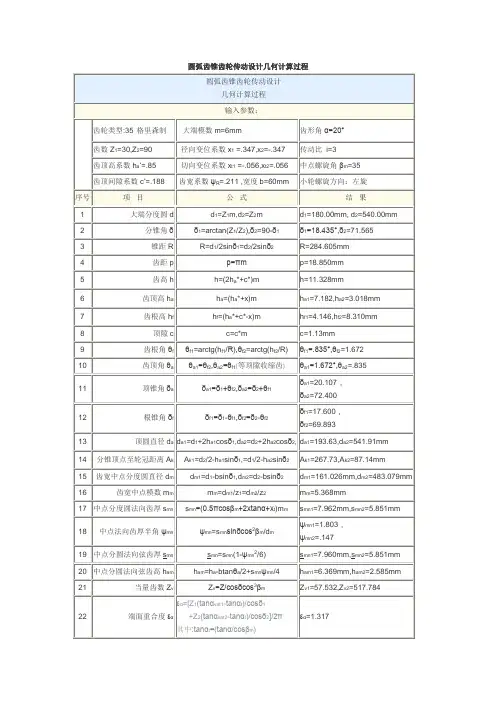
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比,即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时,即正交锥齿轮副,122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b ),逆时针倾斜者则为左旋齿(图14-3a )。
大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-3 弧齿锥齿轮的旋向图14-1 弧齿锥齿轮副反时,才能啮合。
一般情况下,工作面为顺时针旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。


圆弧齿轮曲率半径计算公式圆弧齿轮是一种常见的齿轮传动装置,其曲率半径是一个重要的参数,对于齿轮的设计和制造具有重要的意义。
在工程实践中,需要根据齿轮的模数、齿数、齿轮的压力角等参数来计算圆弧齿轮的曲率半径。
本文将介绍圆弧齿轮曲率半径的计算公式及其应用。
圆弧齿轮曲率半径的计算公式如下:R = (m + d) / 2 cos(α)。
其中,R为圆弧齿轮的曲率半径,m为齿轮的模数,d为齿轮的分度圆直径,α为齿轮的压力角。
在实际的工程设计中,需要根据齿轮的参数来计算曲率半径。
首先需要确定齿轮的模数m,然后根据齿轮的齿数和模数来计算分度圆直径d,最后根据齿轮的压力角α来计算曲率半径R。
通过这个公式,可以方便地计算出圆弧齿轮的曲率半径,为齿轮的设计和制造提供了重要的参考。
圆弧齿轮曲率半径的计算公式是根据齿轮的几何特征和力学性能推导而来的,具有一定的理论基础。
在工程实践中,这个公式被广泛应用于圆弧齿轮的设计和制造中。
通过计算曲率半径,可以确定齿轮的齿形和尺寸,保证齿轮的传动性能和工作稳定性。
圆弧齿轮曲率半径的计算公式还可以帮助工程师进行齿轮的优化设计。
通过调整齿轮的模数、齿数和压力角等参数,可以得到不同的曲率半径,从而满足不同的工程需求。
在实际的工程设计中,工程师可以根据具体的传动要求和工作条件,选择合适的曲率半径,从而设计出性能更优越的圆弧齿轮。
除了圆弧齿轮的设计和制造,曲率半径的计算公式还可以应用于齿轮的检测和评估。
通过测量齿轮的实际曲率半径,可以对齿轮的质量和性能进行评估,保证齿轮的可靠运行。
这对于工程装备和机械传动的安全性和稳定性具有重要的意义。
总之,圆弧齿轮曲率半径的计算公式是齿轮设计和制造中的重要工具,具有广泛的应用价值。
通过这个公式,可以方便地计算出圆弧齿轮的曲率半径,为齿轮的设计、制造、检测和评估提供了重要的参考。
在工程实践中,工程师可以根据具体的需求和条件,灵活运用这个公式,设计出性能更优越的圆弧齿轮,保证齿轮的可靠运行。
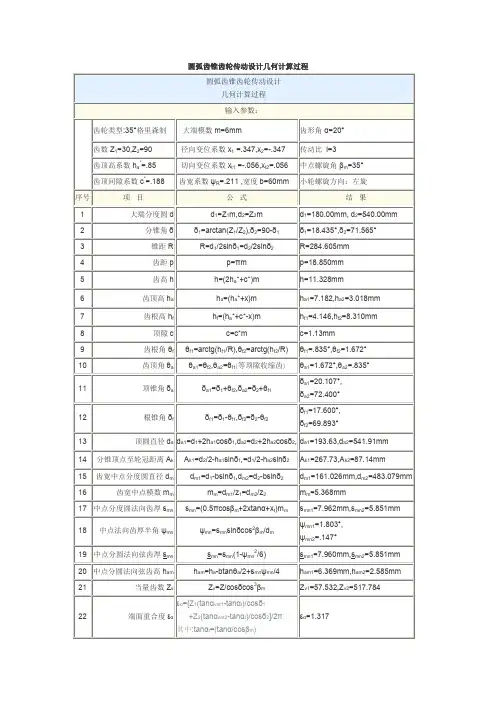
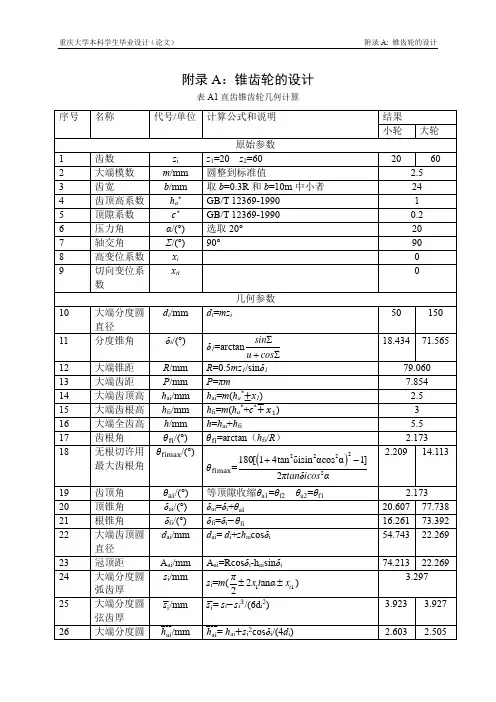
圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分。
通常的已知条件是由水平线除2组成的大边和以垂直线组成的小边。
圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1-θf1,δf2=δ2-θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2-ha1sinδ1,=d1/2-ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1-ψmn2/6)20中点分圆法向弦齿高hamham=ha-btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1-tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分。
通常的已知条件是由水平线除2组成的大边和以垂直线组成的小边。
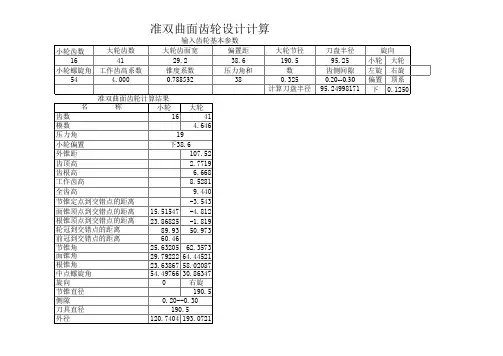
(i)轴交角工两锥齿轮轴线之间的夹角;⑵传动比i:被动轮转速与主动轮转速之比。
可表示为:/ = d =旦(3)公称模数m-:法向圆弧螺旋锥齿轮的小端法向模数;(4)分度锥:锥齿轮设计时所依据的一个基准分度圆锥面。
锥齿轮轴线与分度锥母线之间的夹角称为分锥角,用6表示。
由此,锥齿轮副的轴交角和传动比尚可sin<5tsin(£ —务)用两锥齿轮的分锥角表示为:(5)节锥:锥齿轮副传动时作纯滚动的一对圆锥。
锥齿轮轴线与节锥母线之间的夹角称为节锥角。
一般情况下,节锥与分度锥重合,在工程习惯上往往将二者混用;(6)节线与节平面:节线是指两个节锥相切的公共母线;节平面是指经过节线所作的两个节锥的公共切平面;(7)大端基面:锥齿轮的大端垂直于轴线的平面。
它是锥齿轮设计、加工及安装时的基准面;(8)顶锥和根锥:锥齿轮的齿顶面和齿根面所在的圆锥分别称为顶锥和根锥。
由于法向圆弧螺旋锥齿轮为等高齿,其顶锥角、根锥角和分锥角相等,顶锥、根锥和分度锥的锥顶不重合;(9)节锥距r:分度锥上任意点到锥点的距离。
当参考点分别为小端及大端点时,则称为小端锥矩rs和大端锥矩rb(10)公称齿向线与公称螺旋角刀:表征轮齿齿向特征的原型准线称为公称齿向线其螺旋角称为公称螺旋角刀;(11)实际齿向线和实际螺旋角B :决定实际齿廓面的准线称为实际齿向线,分别对应左右廓面的实际齿向线称为左齿向线和右齿向线,它们所对应的螺旋角称为左螺旋角B和右螺旋角Br,斜航式法向圆弧锥齿轮的实际齿向线是依据等强度原则设计的,这样形成的凸齿廓,从小端到大端齿厚相等,齿槽逐渐变大,凹齿廓齿槽相等,齿厚逐渐变大,这样齿厚和齿槽宽占的角度比值趋于合理;(12)齿形线实际齿向线的法面与齿廓面的交线(13)压力角an:齿形线上理论接触点处的法向压力角;(14)接触迹:凸凹齿廓面啮合过程中理论接触点在各自廓面上的轨迹统称为接触迹(15)齿宽b:锥齿轮大端与小端之间在节锥母线上的距离,即大端节锥距vb 与小端节锥距vs之差;(16)齿厚s:锥齿轮理论啮合点处的固定弦齿厚。
圆弧齿锥齿轮传动设计几何计算过程
圆弧齿锥齿轮传动设计
几何计算过程
输入参数:
齿轮类型:35。
格里森制
大端模数m=6mm
齿形角a =20°
齿数 Z 1=30,Z 2=90
径向变位系数X 1 =.347,x 2=-.347 传动比i=3
齿顶高系数 h a*=.85 切向变位系数 x t1 =-.056,x t2=.O56 中点螺旋角3m =35°
齿顶间隙系数c *=.188
齿宽系数tpR =.211 ,宽度b=60mm
小轮螺旋方向:左旋
序号 项目
公式 结果
1 大端分度圆d
d 1=Z 1m,d 2=Z 2m
d 1=180.00mm, d 2=540.00mm
2 分锥角S 81 =arctan(Z 1/Z 2), 2=90- 8
81=18.435 ° ,2=71.565 °
3 锥距R R=d 1/2sin 81=d 2/2sin 82
R=284.605mm 4 齿距p p= nm p=18.850mm 5 齿高h h=(2h a *+c*)m h=11.328mm
6 齿顶高h a h a =(h a *+x)m h a1=7.182,h a2=3.018mm
7 齿根高h f
h f =(h a *+c*-x)m
h f1 =4.146,h f2=8.310mm 8 顶隙c c=c*m
c=1.13mm
9 齿根角9f Q f1=arctg(h f1/R), Q =arctg(h f2/R) 0f1 =.835 ° ,f2=1.672 ° 10 齿顶角Q a Q a 1= Q f2, Q 2=Q f1(等顶隙收缩齿)
0a1=1.672 ° 戶陆.835 ° 11
顶锥角8a
8a1= 81+ Q f2, 82= 82+Q f1
81=20.107 °, 82=72.400 ° 12 根锥角8 8f1= 81- Q f1, f2= 82- 02
8f1=17.600 °, 8(2=69.893 °
13
顶圆直径d a d a1=d 1+2h a1COS 81,d a2=d 2+2h a2COS
82,
d a1=193.63,d a2=541.91mm
14 分锥顶点至轮冠距离 A k A k1 =d 2/2-h a1Sin 81,=d 1/2-h a2Sin 82
A k1=267.73,A k2=87.14mm 15 齿宽中点分度圆直径 d m d m1=d 1-bsin 81,d m2=d 2-bsin 82
d m1=161.026mm,d m2=483.079mm 16
齿宽中点模数m m
m m =d m1/z 1=d m2/z 2
m m =5.368mm
17 中点分度圆法向齿厚s mn S mn =(0.5 n COS 唱+2xtan a +x»m m
s mn1 =7.962mm,s mn2=5.851mm
18
中点法向齿厚半角书mn
, 2
^mn =S mn Sin 8 COS 旳/d m
ipmn1 =1.803 ° 书 mn 2=.147
19 中点分圆法向弦齿厚S mn 2
_S mn =S mn (1-书mn /6) S mn1 =7.960mm 丄 mn2=5.851mm 20 中点分圆法向弦齿高h am h am =h a -btan 0a /2+S mn ^mn /4
h am1 =6.369mm,h am2=2.585mm 21
当量齿数Z v
3
Z v =Z/cos 8 cos (3m
Z v1=57.532,Z v2=517.784
22
端面重合度£a e«=[Z 1(tan a at1 -tan a )/cos 1 +Z 2(tan a at2-tan a )/cos 2]/2 n 其中:tan a =(tan a /cos m j
&z =1.317
n
COS a vat=[ZCOS l/(Z+2(h a*+X)COS
S )]
23 齿线重合度邙£B=btan 3m n /m £=2.491
24 总重合度 2 2 1/2
£ =(a 才£|3 ) £ =2.818。