信号与系统分析第四章部分答案 许信玉
- 格式:pdf
- 大小:162.39 KB
- 文档页数:14





第4章拉普拉斯变换与连续系统复频域分析4.6本章习题全解4.1 求下列函数的拉普拉斯变换(注意:为变量,其它参数为常量)。
(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)解:(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18) ()(19)(20)(21)(22)(23)(24)4.2 已知,求下列信号的拉普拉斯变换。
(1)(2)(3)(4)(5)解:(1)(2)(3)(4)(5)所以4.3 已知信号的拉普拉斯变换如下,求其逆变换的初值和终值。
(1)(2)(3)(4)解(1)初值:终值:(2)初值:终值:(3)初值:终值:(4)初值:终值:4.4 求题图4.4所示信号的单边拉普拉斯变换。
题图4.4解(1)所以根据微分性质所以注:该小题也可根据定义求解,可查看(5)小题(2)根据定义(3)根据(1)小题的结果再根据时移性质所以根据微分性质得(4)根据定义注:也可根据分部积分直接求取(5)根据单边拉氏变换的定义,本小题与(1)小题的结果一致。
(6)根据单边拉氏变换的定义,在是,对比(3)小题,可得4.5 已知为因果信号,,求下列信号的拉普拉斯变换。
(1)(2)(3)(4)解:(1)根据尺度性质再根据s域平移性质(2)根据尺度性质根据s域微分性质根据时移性质(3)根据尺度性质再根据s域平移性质(4)根据时移性质再根据尺度性质本小题也可先尺度变化得到,再时移单位,得到结果4.6 求下列函数的拉普拉斯逆变换。
(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14)(15)(16)(17)(18)(19)(20)(21)(22)(23)(24)解:(1)(2)(3)(4)(5)(6)(7)(8)(9)(10)(11)(12)(13)(14){} =(15){} =(16){}=(17){}=(18){}=(19){}=(20){}=(21){}=(22){}=(23) {}=(24) ()=4.7 求如题图4.7所示的单边周期信号的拉普拉斯变换。




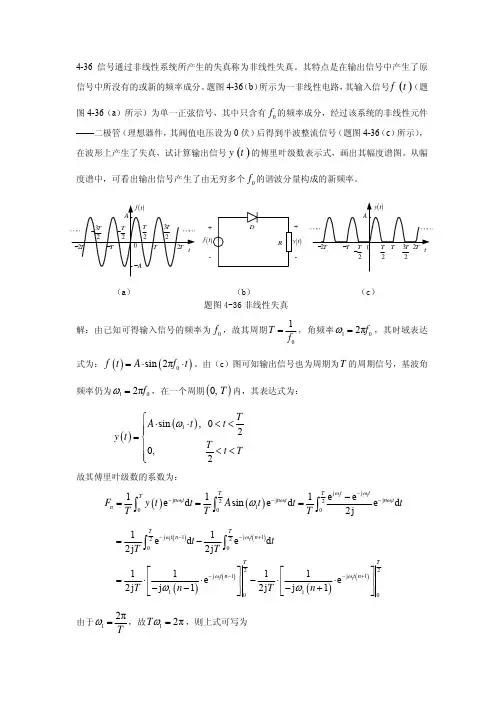
信号与系统课后习题参考答案精心整理1-试分别指出以下波形是属于哪种信号?题图1-11-2试写出题1-1图中信号的函数表达式。
1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示,试作出下列各信号的波形图,并加以标注。
题图1-3⑴(1x ⑷2x ⑺1x 1-4 题图1-4⑴(1x ⑷2x ⑺1x 1-51-6⑴(t x 2⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t t t x =1-7试画出下列信号的波形图:⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --= ⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角,并画出模与幅角的波形图。
⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X1-9已知信号)]()([sin )(π--=t u t u t t x ,求出下列信号,并画出它们的波形图。
⑴)()()(221t x dtt x d t x +=⑵ττd x t x t ?∞-=)()(21-101-11⑴?∞-⑶?∞-⑸?∞-1-12⑴x 1⑶x 31-13⑴t y =)(⑶)2()(t x t y =⑷)1()1()(t x t x t y ---=⑸?∞-=2)()(t d x t y ττ⑹2()(n x n y =⑺)()(n nx n y =⑻)1()()(-=n x n x n y1-14如题图1-14中已知一线性时不变系统当输入为)(t x 时,响应为)(t y 。
试做出当输入为)(1t x 时,响应)(1t y 的波形图。
第4章习题答案4-1 判断以下系统是线性的还是非线性的,是时变的还是非时变的。
〔1〕1()4(3)2(2)()()(3)()()(4)()()tt t y t x t y t x t y t e x t y t x d ττ--=+===⎰121212*********[()()]4[(3)(3)]2()()=4(3)2+4(3)]2=4[(3)(3)]4[()()]()()T x t x t x t x t y t y t x t x t x t x t T x t x t y t y t +=+++++++∴+≠+∴()但:系统解:是非线性的000000T[()]4(3)2,()4[3()]2T[()](),x t t x t t y t t x t t x t t y t t -=-+-=-+∴-≠-所以系统是时变的。
1212121212122[()()]()()()()=()()[()()]()()T x t x t x t x t y t y t x t x t T x t x t y t y t +=+++∴+≠+∴()但:系统是非线性的000000T[()](),()()T[()]=(),x t t x t t y t t x t t x t t y t t -=--=-∴--所以系统是时不变的。
1212121212123[()()][()()]()()=()()[()()]()()t t t T x t x t e x t x t y t y t e x t e x t T x t x t y t y t ---+=+++∴+=+∴()系统是线性的0()000000T[()](),()()T[()](),t t t x t t e x t t y t t e x t t x t t y t t ----=--=-∴-≠-所以系统是时变的。
1212121211112124[()()][()()]()()=()()[()()]()()tttt t t T x t x t x x y t y t x x T x t x t y t y t τττττττ---+=+++∴+=+∴⎰⎰⎰()d d d 系统是线性的000000011100T[()]()(),()()T[()](),tt t t t t t t t t x t t x t d x u du y t t x d x t t y t t ττττ--------=-=-=∴-=-⎰⎰⎰所以系统是时不变的。