四边形的中位线定理

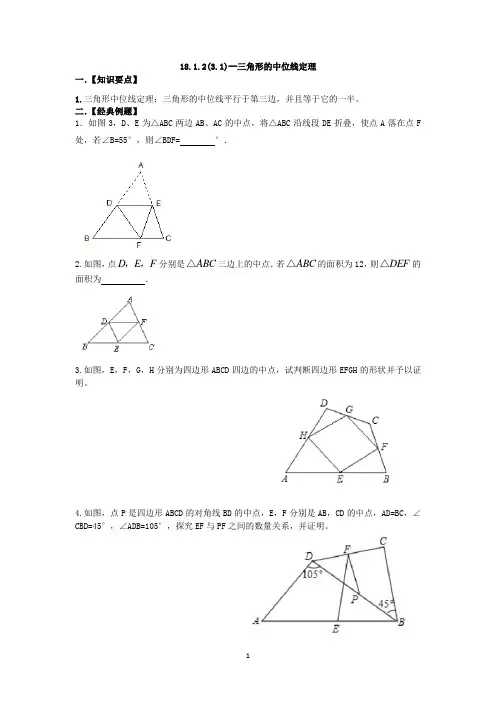
18.1.2(3.1)--三角形的中位线定理一．【知识要点】1.三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。

二．【经典例题】1．如图3，D 、E 为△ABC 两边AB 、AC 的中点，将△ABC 沿线段DE 折叠，使点A 落在点F 处，若∠B=55°，则∠BDF= °．2.如图，点分别是三边上的中点．若的面积为12，则的面积为 ．3.如图，E ，F ，G ，H 分别为四边形ABCD 四边的中点，试判断四边形EFGH 的形状并予以证明。

4.如图，点P 是四边形ABCD 的对角线BD 的中点，E ，F 分别是AB ，CD 的中点，AD=BC ，∠CBD=45°，∠ADB=105°，探究EF 与PF 之间的数量关系，并证明。

D E F ，，ABC △ABC △DEF△5.如图，∠ACB=∠BCD=90°，AC=BC，点E在BC上，CD=CE，点P，M，N分别为AB，AD，BE 的中点，试探究:PM与PN之间的数量关系和位置关系.6.如图，四边形ABCD中，∠A＝90°，AB＝8，AD＝6，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为（）A．8B．7C．6D．57．如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，连接DC，点M，P，F分别为DE，DC，BC的中点，△ADE可以绕点A在平面内自由旋转，若AD＝4，AB＝10，则△PMF的面积S的变化范围是．三．【题库】【A】1.在ABCD中，点O是对角线AC.BD的交点，点E是边CD的中点，且AB=6，BC=10，则OE=______________．2．如图，要测量的A、C两点被池塘隔开，李师傅在AC外任选一点B，连接BA和BC，分别取BA和BC的中点E、F，量得E、F两点间的距离等于23米，则A、C两点间的距离= ．3.如图，A.B两点被池塘隔开，在AB外选一点C ，连结AC 和BC，并分别找出AC 和BC的中点M.N，如果测得MN=20 m，那么 A.B两点的距离是，依据是．4.如图,ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.【B】1．如图，在△ABC中，AB=5，AC=3，AD是角平分线，AE是中线，过点C作CG⊥AD于点F，AB CDO E交AB 于点G ，连接EF ，则线段EF 的长为 ．3．如图，△ABC 中，D 、E 分别是BC 、AC 的中点，BF 平分∠ABC ，交DE 于点F ，若BC=6，则DF 的长是（ ） A. 2 B. 3 C.25D. 4 4.已知：三角形的各边分别为8cm ,10cm 和12cm ，求连结各边中点所成三角形的周长_____. 5. 如图，ABCD 的周长为36，对角线AC ，BD 相交于点O ．点E 是CD 的中点，BD=12，则△DOE 的周长为 ．【C 】1.如图，在四边形ABCD 中，DC ∥AB ，CB ⊥AB ，AB=AD ，CD=12AB ，点E 、F 分别为AB 、AD 的中点，则△AEF 与多边形BCDFE 的面积之比为 （ ） A ．17B ．16C ．15D ．142．如图，在矩形ABCD 中，P 、Q 分别是BC 、DC 上的点，E 、F 分别是AP 、PQ 的中点．BC =12，第24题图FE DCBADQ =5，在点P 从B 移动到C （点Q 不动）的过程中，则下列结论正确的是 ( )A. 线段EF 的长逐渐增大,最大值是13B. 线段EF 的长逐渐减小，最小值是6.5C. 线段EF 的长始终是6.5D. 线段EF 的长先增大再减小，且6.5≤EF ≤133.如图，在四边形ABCD 中，AD ∥BC ，AB ＝AD ，∠C ＝60°，∠ABD ＝30°AE ⊥BD 于点E ，F 是CD 的中点. 求证：四边形AEFD 是平行四边形.3.如图①，已知正方体ABCD ﹣A 1B 1C 1D 1的棱长为4cm ，E ，F ，G 分别是AB ，AA 1，AD 的中点，截面EFG 将这个正方体切去一个角后得到一个新的几何体（如图②），则图②中阴影部分的面积为 cm 2．4.如图，在△ABC 中，AB ＝AC ，∠BAC ＝90°，直角∠EPF 的顶点P 是BC 的中点，两边PE 、PF 分别交于点E ，F ，现给出一下四个结论：①AE ＝CF ，②△EPF 是等腰直角三角形，③S 四边形AEPF＝，④当∠EPF 在△ABC 内绕顶点P 旋转时始终有EF ＝AP （点E 不与A 、B 重合），上述结论中是正确的结论有（ ）A ．1个B ．2个C ．3个D ．4个【D 】1.已知,在平行四边形ABCD 中,连接对角线AC , ∠CAD 的平分线AF 交CD 于点F ，∠ACD 平分线CG 交AD 于点G, AF.CG 交于点O,点E 为BC 上一点,且 ∠BAE=∠GCD, （12分） (1)如图1,若△ACD 是等边三角形,OC=2 ,求平行四边形ABCD 的面积; (2)如图2,若△ACD 是等腰直角三角形∠CAD=90O, ,求证：CE + 2 OF = AC:2.（绵阳2018年第18题）如图，在△ABC 中，3=AC ，4=BC ,若AC ，BC 边上的中线BE ，垂直相交于O 点，则=AB __________。

梯形中位线定理证明方法一、梯形中位线定理的表述及含义梯形是一种特殊的四边形，它有两条平行边，分别称为上底和下底；另外还有两条非平行的边，称为腰。

梯形的两个对角线分别是连接两个非平行边的线段。

梯形中位线定理表述如下：梯形两个对角线的长度之和等于梯形两条平行边长度之和。

这个定理的含义是，梯形的两个对角线之间的距离，即对角线的长度之和，等于梯形两条平行边的长度之和。

这个定理在解决梯形相关的几何问题时非常有用。

二、梯形中位线定理的证明方法下面将介绍一种证明梯形中位线定理的方法，该证明方法基于几何的基本原理和定理。

证明思路如下：步骤一：画出梯形ABCD我们画出一个任意的梯形ABCD，其中AB和CD是平行边，AD和BC 是非平行边。

步骤二：连接梯形的两个对角线AC和BD我们需要连接梯形的两个对角线AC和BD。

通过连接AC和BD，我们可以将梯形分成两个三角形，分别是三角形ABC和三角形ACD。

步骤三：证明三角形ABC与三角形ACD全等接下来，我们需要证明三角形ABC与三角形ACD全等。

根据几何的基本原理，我们可以通过证明它们的对应边相等来证明它们全等。

我们观察到AB和CD是梯形的两条平行边，根据平行线的性质，我们可以得出AB与CD平行。

又因为AC和BD是梯形的两个对角线，根据梯形的性质，我们可以得出AC与BD相交于一点，且互相平分。

接下来，我们观察到AB和CD是梯形的两条平行边，而AC和BD是梯形的两个对角线，根据平行线的性质和对角线的性质，我们可以得出三角形ABC与三角形ACD有以下对应边相等的关系：AB=CD，AC=BD。

因此，根据三角形全等的判定条件，我们可以得出三角形ABC与三角形ACD全等。

步骤四：根据三角形全等的性质，证明对角线长度之和等于平行边长度之和根据三角形全等的性质，我们知道如果两个三角形全等，那么它们的对应边的长度是相等的。

因此，根据三角形ABC与三角形ACD全等，我们可以得出AC=BD。

第四章四边形性质探索知识点归纳 一．四边形的相关概念和性质（1）在同一平面内，由不在同一直线上的四条线段首尾顺次相接组成的图形叫做四边形．四边形用表示它的各顶点的字母来表示．注意：表示四边形必须按顶点的顺序书写，可按照顺时针或逆时针的顺序．如图读作“四边形ABCD ” ．（2）在四边形中，连结不相邻两个顶点的线段叫做四边形的对角线．注意：①四边形共有两条对角线．②连结四边形的对角线也是一种常用的辅助线作法．（3）四边形的不稳定性：三角形的三边如果确定后，它的形状、大小就确定了，这是三角形的稳定性．但是，四边形四边长确定后，它的形状不能确定．这就是四边形具有不稳定性，它在生产、生活方面有很多的应用．（4）四边形的内角和等于 360．（5）四边形的外角和等于 360．注意：1、四边形内角中最多有三个钝角，四个直角，三个锐角；2、四边形外角中最多有三个钝角、四个直角、三个锐角，最少没有钝角，没有直角，没有锐角；3、四边形内角与同一个顶点的一个外角互为邻补角．二．多边形的概念和性质：（1）n 边形的内角和等于 180)2(⋅-n ．（2）任意多边形的外角和等于 360．（3）n 边形共有2)3(-n n 条对角线．（4）在平面内，内角都相等且边都相等的多边形叫做正多边形。

（5）正多边形的每个内角等于n n 180).2(-三、平行四边形．1．平行四边形的性质(1)平行四边形的邻角互补，对角相等．(2)平行四边形的对边平行且相等．(3)夹在两条平行线间的平行线段相等．(4)平行四边形的对角线互相平分．（5）中心对称图形，对称中心是对角线的交点。

(6)若一直线过平行四边形两对角线的交点，则这直线被一组对边截下的线段以对角线的交点为中点，且这条直线二等分四边形的面积．2．平行四边形的判定(1)定义：两组对边分别平行的四边形是平行四边形．(2)定理1：两组对角分别相等的四边形是平行四边形．(3)定理2：两组对边分别相等的四边形是平行四边形．(4)定理3：对角线互相平分的四边形是平行四边形．(5)定理4：一组对边平行且相等的四边形是平行四边形．3．两条平行线的距离两条平行线中，一条直线上的任意一点到另一条直线的距离，叫做这两条平行线的距离．平行线间的距离处处相等．注意：(1)距离是指垂线段的长度，是正值．(2)两条平行线的位置确定后，它们的距离是定值，不随垂线段位置改变．(3)平行线间的距离处处相等，因此在作平行四边形的高时，可根据需要灵活选择位置．4．平行四边形的面积S=底边长×高=ah(a是平行四边形任何一边长，h必须是a边与其对（1）、平行四边形边的距离)．（2）、同底(等底)同高(等高)的平行四边形面积相等．四．矩形、1．矩形的定义：_________________________________2．矩形的性质：(1)对边平行且相等。

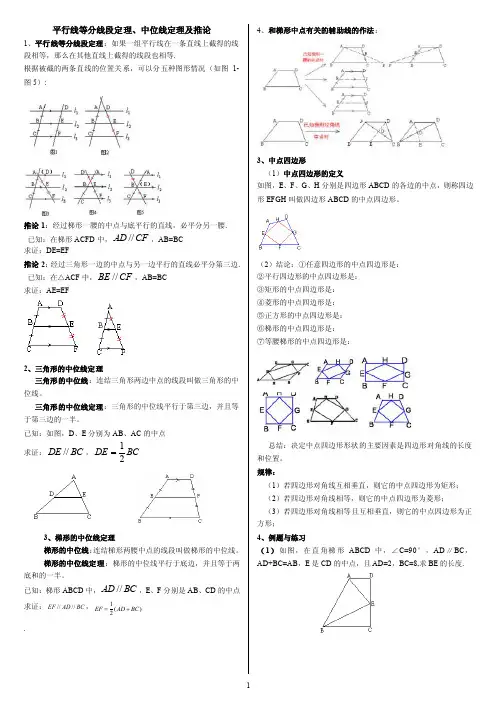
平行线等分线段定理、中位线定理及推论1、平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等.根据被截的两条直线的位置关系，可以分五种图形情况（如图1-图5）:推论1：经过梯形一腰的中点与底平行的直线，必平分另一腰. 已知：在梯形ACFD 中，CF AD //，AB=BC 求证：DE=EF推论2：经过三角形一边的中点与另一边平行的直线必平分第三边. 已知：在△ACF 中，CF BE //，AB=BC求证：AE=EF2、三角形的中位线定理三角形的中位线：连结三角形两边中点的线段叫做三角形的中位线。

三角形的中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半。

已知：如图，D 、E 分别为AB 、AC 的中点 求证：BC DE //，BC DE21=3、梯形的中位线定理梯形的中位线：连结梯形两腰中点的线段叫做梯形的中位线。

梯形的中位线定理：梯形的中位线平行于底边，并且等于两底和的一半。

已知：梯形ABCD 中，BC AD //，E 、F 分别是AB 、CD 的中点 求证：////EF AD BC ，1()2EF AD BC =+. 4、和梯形中点有关的辅助线的作法：3、中点四边形（1）中点四边形的定义如图，E 、F 、G 、H 分别是四边形ABCD 的各边的中点，则称四边形EFGH 叫做四边形ABCD 的中点四边形。

（2）结论：①任意四边形的中点四边形是： ②平行四边形的中点四边形是： ③矩形的中点四边形是： ④菱形的中点四边形是： ⑤正方形的中点四边形是： ⑥梯形的中点四边形是： ⑦等腰梯形的中点四边形是：总结：决定中点四边形形状的主要因素是四边形对角线的长度和位置。

规律：（1）若四边形对角线互相垂直，则它的中点四边形为矩形； （2）若四边形对角线相等，则它的中点四边形为菱形； （3）若四边形对角线相等且互相垂直，则它的中点四边形为正方形； 4、例题与练习（1）如图，在直角梯形ABCD 中，∠C=90°，AD ∥BC ，AD+BC=AB ，E 是CD 的中点，且AD=2，BC=8,求BE 的长度.（2） 如图，梯形ABCD 中，AB ∥DC ，M 是腰BC 的中点，MN ⊥AD 于N 。

初中中位线教案一、教学目标1. 知识与技能：（1）理解中位线的概念，掌握中位线的性质；（2）学会用直尺和圆规作三角形的中位线；（3）能够运用中位线定理证明四边形的性质。

2. 过程与方法：（1）通过观察、操作、思考、交流等活动，培养学生的空间想象能力和逻辑思维能力；（2）学会合作学习，提高学生的团队协作能力。

3. 情感、态度与价值观：（1）培养学生对数学的兴趣，激发学生探究数学问题的热情；（2）培养学生勇于尝试、克服困难的自信心；（3）培养学生严谨治学、追求真理的科学态度。

二、教学内容1. 中位线的概念：三角形的中位线是指连接一个三角形两个中点的线段。

2. 中位线的性质：（1）中位线等于第三边的一半；（2）中位线平行于第三边；（3）中位线等于对应角的平分线。

3. 作中位线的方法：（1）先画出三角形；（2）找出三角形的中点；（3）用直尺和圆规连接中点，画出中位线。

4. 中位线定理：在一个四边形中，连接对边中点的线段互相平分。

三、教学过程1. 导入新课：通过复习三角形的中位线性质，引出四边形的中位线定理。

2. 探究中位线的性质：（1）让学生自己动手画出一个任意的三角形，找出中点，画出中位线；（2）观察中位线与第三边的关系，引导学生发现中位线的性质；（3）通过几何画板软件，动态展示中位线的性质，加深学生理解。

3. 学习作中位线的方法：（1）讲解作中位线的基本步骤；（2）让学生动手实践，独立完成作中位线的过程；（3）互相交流，分享作中位线的心得。

4. 应用中位线定理：（1）让学生画出一个任意的四边形，找出对边中点，连接中点，画出中位线；（2）证明中位线互相平分；（3）引导学生发现中位线在几何证明中的应用。

5. 课堂小结：通过本节课的学习，让学生总结中位线的性质和作法，以及中位线定理的应用。

四、作业布置1. 画出一个任意的三角形，作出中位线，并标注中位线的性质；2. 画出一个任意的四边形，作出中位线，并证明中位线互相平分。

1.中线定理：(巴布斯定理)设三角形ABC的边BC的中点为P，则有AB2+AC2=2(AP2+BP2)初中竞赛需要，重要2.托勒密定理：设四边形ABCD内接于圆，则有AB×CD+AD×BC=AC初中竞赛需要，重要3.梅涅劳斯定理：设△ABC的三边BC、CA、AB或其延长线和一条不经过它们任一顶点的直线的交点分别为P、Q、R则有BPPC×CQQA×ARRB=1初中竞赛需要，重要4.梅涅劳斯定理的逆定理：(略)初中竞赛需要，重要5.梅涅劳斯定理的应用定理1：设△ABC的∠A的外角平分线交边CA于Q、∠C的平分线交边AB于R，、∠B的平分线交边CA于Q，则P、Q、R三点共线。

不用掌握6.梅涅劳斯定理的应用定理2：过任意△ABC的三个顶点A、B、C作它的外接圆的切线，分别和BC、CA、AB的延长线交于点P、Q、R，则P、Q、R三点共线不用掌握7.、塞瓦定理：设△ABC的三个顶点A、B、C的不在三角形的边或它们的延长线上的一点S连接面成的三条直线，分别与边BC、CA、AB或它们的延长线交于点P、Q、R，则BPPC×CQQA×ARRB()=1.初中竞赛需要，重要8.塞瓦定理的应用定理：设平行于△ABC的边BC的直线与两边AB、AC的交点分别是D、E，又设BE和CD交于S，则AS一定过边BC的中心M不用掌握9.塞瓦定理的逆定理：(略)初中竞赛需要，重要10.塞瓦定理的逆定理的应用定理1：三角形的三条中线交于一点这个定理用塞瓦定理来证明将毫无几何美感，应该用中位线证明才漂亮11.塞瓦定理的逆定理的应用定理2：设△ABC的内切圆和边BC、CA、AB分别相切于点R、S、T，则AR、BS、CT交于一点。

不用掌握12.西摩松定理：从△ABC的外接圆上任意一点P向三边BC、CA、AB或其延长线作垂线，设其垂足分别是D、E、R，则D、E、R共线，(这条直线叫西摩松线)初中竞赛的常用定理13.西摩松定理的逆定理：(略)初中竞赛的常用定理14.切线长定理从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角15.圆的外切四边形的两组对边的和相等16.弦切角定理弦切角等于它所夹的弧对的圆周角17.推论如果两个弦切角所夹的弧相等，那么这两个弦切角也相等18.相交弦定理圆内的两条相交弦，被交点分成的两条线段长的积相等19.推论如果弦与直径垂直相交，那么弦的一半是它分直径所成的两条线段的比例中项20.切割线定理从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项21.推论从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等斯特瓦特定理有三角形ABC，D为角A平分线与BC边的交点，则有以下定理：AB （2）·DC＋AC（2）·BD－AD（2）·BC=BC·BD·DC托勒密定理：圆内接四边形中，两条对角线的乘积(两对角线所包矩形的面积)等于两组对边乘积之和(一组对边所包矩形的面积与另一组对边所包矩形的面积之和)．已知：圆内接四边形ABCD，求证：AC·BD＝AB·CD＋AD·BC．证明：如图1，过C作CP交BD于P，使∠1=∠2，又∠3=∠4，∴△ACD∽△BCP．得AC：BC=AD：BP，AC·BP=AD·BC ①。

第 1 页 共 3 页第九讲 中位线定理温馨提示：⏹ 如果下载讲义后部分内容无法显示，解决办法：进入 ，点击页面右上方的“帮助中心——新手帮助——热门问题——下载的讲义乱码不能看？”，或通过 页面右侧的“在线咨询”联系客服人员。

⏹ 解题分析和答案请观看配套视频。

——————————————————————————————————————一、知识提要1. 三角形的中位线：连接三角形两边中点的线段.2. 梯形的中位线：连接梯形两腰中点的线段.3. 三角形中位线定理：三角形的中位线平行于第三边，且等于第三边的一半.4. 梯形中位线定理：梯形中位线平行于上下底，且等于上下底和的一半.5. 补充定理：平行线等分线段定理（1）经过三角形一边中点，平行于另一边的直线必平分第三边； （2）经过梯形一腰中点，平行于上下底的直线必平分另一腰.二、 专项训练【板块一】三角形中位线1. （2011安徽）如图，D 是△ABC 内一点，BD ⊥CD ，AD =6，CD =3，BD =4，E 、F 、G 、H 分别是AB 、AC 、CD 、BD 的中点，则四边形EFGH 的周长是( ) A.7 B.9 C.10 D.11H GFED CBA2. （2010锦州）如图所示，在△ABC 中，AB =AC ，M 、N 分别是AB ，AC 的中点，D 、E 为BC 上的点，连接DN 、EM ，若AB =5cm ，BC =8cm ，DE =4cm ，则图中阴影部分的面积为（ ） A ．1cm 2 B ．1.5cm 2 C ．2cm 2 D ．3cm 2NM EABCD第 2 页 共 3 页A DBCE MN3. 求证：三角形的一条中位线与第三边上的中线互相平分.【板块二】梯形中位线4. （2011江苏）如图，DE 是△ABC 的中位线，M 、N 分别是BD 、CE 的中点，MN =6，则BC =_______.N M E D CBA5. 直角梯形的一条对角线将它分成两个三角形，其中一个是等边三角形，如果它的中位线长为a ，那么它的下底长是______.6. 在如图所示的梯形ABCD 中，AD ∥BC ，AD =5，BC =11，①中A 1B 1是连接两腰中点的线段，易知A 1B 1=8，②中A 1B 1，A 2B 2是连接两腰三等分点且平行于底边的线段，可求出A 1B 1+A 2B 2的值，照此规律下去，③中A 1B 1，A 2B 2，…A 10B 10是连接两腰十一等分点且平行于底边的线段，则A 1B 1+A 2B 2+…+A 10B 10的值为（ ）A ．50B ．80C ．96D ．1007. （2011河南）如图，在梯形ABCD 中，AD ∥BC ，延长CB 到点E ，使BE =AD ，连接DE 交AB 于点M . （1）求证:△AMD ≌△BME ；（2）若N 是CD 的中点，且MN =5，BE =2，求BC 的长.B 10A 10B 1A 1D CBA A 2B 2③②①B 2A 2A BC D A 1B 1B 1A 1D CBA第 3 页 共 3 页8. 如图，已知MN 是梯形ABCD 的中位线，AC 、BD 与MN 交于F 、E ，AD=18cm ，BC =40cm ，求EF 的长.【板块三】综合提高9. 如图，M 是△ABC 的边BC 的中点，AN 平分∠BAC ，BN ⊥AN 于点N ，且AB =10，BC =15，MN =3，则△ABC 的周长等于（ ）A.38B.39C.40D.4110. 如图，四边形ABCD 中，对角线AC 、BD 交于O ，已知AC =BD ，M 、N 分别是AD 、BC 中点，MN 与AC 、BD 分别相交于E ，F .求证：OE =OF .11. 如图，以△ABC 的边AB 、AC 为斜边向外作Rt △ABD 、Rt △ACE ，且使∠ABD =∠ACE ，M 是BC 中点，求证：DM=ME .MEDCBAN M A BCD EFNMCBANMOFEDCB A。

四边形知识点总结大全1.四边形的内角和与外角和定理：四边形的内角和等于360度；四边形的外角和等于360度。

2.多边形的内角和与外角和定理：n边形的内角和等于(n-2)180度；任意多边形的外角和等于360度。

3.平行四边形的性质：两组对边分别平行；两组对边分别相等；两组对角分别相等；对角线互相平分；邻角互补。

4.平行四边形的判定：若两组对边分别平行、相等、对角分别相等或一组对边平行且相等，则四边形为平行四边形。

5.矩形的性质：具有平行四边形的所有通性；四个角都是直角；对角线相等。

6.矩形的判定：若四边形为平行四边形且至少有一个直角，则为矩形；若对角线相等且为平行四边形，则为矩形。

7.菱形的性质：具有平行四边形的所有通性；四个边都相等；对角线垂直且平分对角。

8.菱形的判定：若四边形为平行四边形且一组邻边相等，则为菱形；若四边形四边相等且对角线垂直，则为菱形。

9.正方形的性质：具有平行四边形的所有通性；四个边都相等，四个角都是直角；对角线相等垂直且平分对角。

10.正方形的判定：若四边形为平行四边形且至少有一组邻边相等且有一个直角，则为正方形；若为菱形且有一个直角，则为正方形；若为矩形且一组邻边相等，则为正方形。

11.等腰梯形的性质：两底平行，两腰相等；同一底上的底角相等；对角线相等。

12.等腰梯形的判定：若四边形两底平行且两腰相等，则为等腰梯形；若同一底上的底角相等且对角线相等，则为等腰梯形。

1.等腰梯形的定义：一个四边形，其中两边是平行的且相等，另外两边也相等，但不平行。

根据这个定义，可以得出等腰梯形的性质：底角相等，对角线相等。

2.三角形中位线定理：三角形的中位线是连接一个角的顶点和对边中点的线段。

根据中位线定理，三角形的中位线平行于第三边，并且等于它的一半。

3.梯形中位线定理：梯形的中位线是连接两个非平行边中点的线段。

根据梯形中位线定理，梯形的中位线平行于两底，并且等于两底和的一半。

公式部分：1.菱形的面积公式：S=ab=ch，其中a、b为菱形的对角线，c为菱形的边长，h为c边上的高。

中位线定理三角形的中位线：连接三角形两边中点的线段梯形的中位线：连接梯形两腰中点的线段中位线定理：1、三角形的中位线平行于第三边，且等于第三边的一半2、梯形的中位线平行于两底，且等于两底和的一半例1、△ABC 的三条边AB 、AC 、BC 的中点分别是点D 、E 、F ，且DE=4，EF=3，DF=6，则△ABC 的周长为（ ）A 、22B 、26C 、20D 、24例2、如图，DE 是△ABC 的中位线，下面的结论中错误的是（ ）A 、AB DE 21 B 、AB//DEC 、BC=2DED 、AB=2DE例3、如图，在四边形ABCD 中，∠C=60°，AD//BC ，AD=DC=8，E 、F 分别为AB 和DC 的中点，则EF 的长为___________1、如图，已知△ADE周长为4，且DE是△ABC的中位线，则△ABC的周长为（）A、6B、8C、12D、162、在△ABC中，D、E、F分别是AB、BC、CA的中点，AB=6，AC=4，则四边形AEDF的周长是（）A、10B、20C、30D、403、如图，在菱形ABCD中，E、F分别是AB、AC的中点，如果EF=2，则菱形ABCD的周长是（）A、4B、8C、12D、162cm，则这个等边三角形的中位线为（）4、等边三角形的一边上的高为3A、3cmB、2.5cmC、2cmD、4cm5、若三角形的三边分别是6cm、8cm、10cm，则分别连接三边中点所组成的三角形的周长是（）A、24cmB、48cmC、12cmD、无法确定6、如图，△ABC 的周长为a ，以各边中点为顶点组成一个新三角形，以新三角形各边中点为顶点又组成一个三角形，则这个小三角形的周长等于（ ）A 、2aB 、3aC 、4a D 、6a7、如图，D 、E 分别为△ABC 的AC 、BC 边的中点，将此三角形沿DE 折叠，使点C 落在AB 边上的点P 处。

若∠CDE=48°，则∠APD 等于（ ）A 、42°B 、48°C 、52°D 、58°8、如图，△ABC 中，D 、E 分别是BC 、AC 的中点，BF 平分∠ABC ，交DE 于点F ，若BC=6，则DF 的长是（ ）A 、2B 、3C 、25D 、49、如图，△ABC 中，AB=AC=8，BC=6，AD 平分∠BAC 交BC 于点D ，点E 为AC 的中点，连接DE ，则△CDE 的周长为（ ）A 、10B 、11C 、12D 、1310、如图，△ABC中，D、E、F、G分别是AB、AC、AD、AE的中点，若BC=8，则DE+FG等于（）A、4.5B、6C、7D、811、如图，D是△ABC内一点，BD⊥CD，AD=6，BD=4，CD=3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是（）A、7B、9C、10D、1112、如图，平行四边形ABCD的对角线AC、BD相交于点O，点E、F分别是线段AO，BO的中点。

例谈中位线定理在几何问题中的应用作者：***来源：《中学教学参考·理科版》2024年第02期［摘要］中位线定理是初中数学的重要定理，它在平面几何问题的解决中有广泛的应用。

文章通过分析典型例题，介绍一些中位线定理的应用方法，旨在帮助学生提高解题效率，提升解题能力。

［关键词］中位线定理；几何问题；应用［中图分类号］ G633.6 ［文献标识码］ A ［文章编号］ 1674-6058（2024）05-0009-03中位线定理是初中数学的重要定理，它在平面几何问题的解决中有广泛的应用。

下面笔者结合一些典型例题介绍一些中位线定理的应用方法。

一、利用中位線定理求线段的长因为中位线定理反映两条线段之间的数量关系，所以已知三角形中位线与第三边中的其中一个量，就可以求得另一个量。

［例1］（1）课本再现：如图1所示，[D]、[E]分别是[△ABC]的边[AB]、[AC]的中点。

求证：[DE]∥[BC]，且[DE=12BC]。

定理证明：如图2所示，延长[DE]至点[F]，使得[EF=DE]，连接[CF]。

请你写出完整的证明过程。

（2）知识应用：如图3所示，在四边形[ABCD]中，[AB=6]，[CD=8]，[∠BAC=30°]，[∠ACD=120°]，点[E]、[F]、[M]分别是[AD]、[BC]、[AC]的中点，求[EF]的长。

（1）证明：在[△AED]和[△CEF]中，[DE=FE，∠AED=∠CEFAE=CE，]，∴[△AED ]≌[△CEF]（SAS），∴[AD=CF]，[∠A=∠ECF]，∴[AB]∥[CF]，∵[AD=BD]，∴[BD=CF]，∴四边形[DBCF]为平行四边形，∴[DF]∥[BC]，[DF=BC]，∴[DE]∥[BC]，[DE=12BC]。

（2）解：∵点[E]、[M]分别是[AD]、[AC]的中点，∴[EM]是[△ADC]的中位线，∴[EM=12CD=4]，[EM]∥[CD]，∴[∠EMC+∠ACD=180°]，∵[∠ACD=120°]，∴[∠EMC=60°]。