高三第一次调研考试试卷分析(数学)

高三第一次月考数学试卷分析高三第一次月考数学试卷分析本次月考是高三学生进入高三阶段的第一次考试，旨在检验学生的数学学习情况和综合素质。

本次考试试卷难度适中，考察了学生对高中数学基础知识的掌握和应用能力。

一、试卷分析本次月考试卷分为选择题和解答题两个部分，总分为100分。

其中选择题共12道，每题5分，共计60分；解答题共4道，每题20分，共计80分。

试题难度逐步提升，注重考察学生的基础知识和应用能力。

选择题部分主要考察学生对基础知识的掌握和理解，包括函数、数列、三角函数、平面几何等知识点。

其中，第1题考察数列的通项公式，第2题考察函数的单调性，第3题考察三角函数的图像和性质，第4题考察不等式的解法，第5题考察平面几何中的圆和直线等知识点。

这些题目难度较低，学生基本能够正确解答。

解答题部分主要考察学生对数学知识的综合应用能力。

其中，第6题考察函数的奇偶性和单调性，第7题考察数列的通项公式和前n项和，第8题考察三角函数的图像和周期，第9题考察平面几何中的直线和圆的位置关系。

这些题目难度适中，需要学生具备一定的分析和解决问题的能力。

二、学生表现从学生的表现来看，大部分学生能够正确理解题意，灵活运用所学知识进行解答。

其中，选择题部分正确率较高，学生对于基础知识的掌握比较扎实；解答题部分，部分学生能够较好地运用所学知识进行解答，但也有部分学生存在思路不清晰、解题不规范等问题。

三、教学启示根据本次月考试卷的分析，我们可以得出以下教学启示：1.夯实基础：高三阶段已经进入复习阶段，但学生的数学基础还是需要不断夯实。

在教学过程中，应该注重基础知识的讲解和训练，让学生更好地掌握和理解高中数学的基础知识和基本技能。

2.强化应用：数学是一门应用性很强的学科，应该注重培养学生的应用能力。

在教学过程中，可以通过一些实际问题或应用场景来引导学生运用所学知识进行解决，增强学生的实践能力和解决问题的能力。

3.规范解题：解题规范是数学学习中非常重要的一环。

一、试题整体特点2023年全国高三数学一模试卷在贯彻党的教育方针、落实立德树人根本任务的基础上，深入挖掘数学学科的育人价值，全面贯彻“四基”，培养“四能”，促进学生数学学科核心素养的形成和发展。

试卷加大开放题的创新力度，突出理性思维，考查关键能力，发挥了选拔功能。

试题倡导理论联系实际，利用真实问题情境，体现数学思想方法在解决实际问题中的价值和作用，考查考生利用数学工具解决实际问题的能力。

试卷结构和高考的模拟试卷基本保持一致，主要体现在大纲理念、试卷结构、题目数量以及题型等方面。

二、试题分析1. 试题难度适中，注重基础知识的考查。

试卷难度先后呈现合理，注重基础知识的考查，使学生在面对新高考时能够更好地应对。

2. 试题结构稳定，题型多样。

试卷结构基本保持稳定，解答题题型与顺序基本保持稳定，分别是立体几何、解三角形、概率统计、解析几何、导数、数列。

同时，试题注重考查学生综合运用所学知识解决问题的能力，题型多样。

3. 试题注重考查数学思想方法。

试卷强调知识之间的内在联系，引导学生形成学科知识系统，强调对通性通法的深入理解和综合运用，促进学生将知识和方法内化为自身的知识结构。

4. 试题突出数学应用价值。

试题倡导理论联系实际、学以致用，关注我国社会主义建设和科学技术发展的重要成果，设计真实问题情境，体现数学的应用价值。

5. 试题注重考查学生的创新能力。

试卷加大开放题的创新力度，突出理性思维，考查关键能力，发挥了选拔功能。

三、备考建议1. 复习时注重基础知识的学习。

在复习过程中，要注重对基础知识的学习，尤其是对基础概念、基本方法和基本技能的掌握。

2. 加强数学思想方法的训练。

要注重培养学生的数学思维，提高学生的数学素养，使学生在面对问题时能够灵活运用数学思想方法。

3. 注重数学应用能力的培养。

在复习过程中，要关注数学与实际生活的联系，提高学生的数学应用能力。

4. 加强模拟试题的练习。

通过模拟试题的练习，可以让学生熟悉高考题型，提高解题速度和准确率。

高三数学试卷分析与反思
一、试卷分析
1、本次考试题型分布：
本次考试的题型主要包括7道选择题和2道填空题。

其中，选择题主要包括有关数轴，抛物线，函数，初等三角函数等代数和几何方面的内容；填空题主要考查有关统计，概率等的内容。

2、整体难度分析：
从整体来看，本次考试的难度主要处于中等水平，其中有些复杂的题目很难，但还有不少简单题，整体难度属于中等偏上，考生应根据自己的能力情况，善加利用有限的时间，熟以下每一类试卷的知识点，重视题型转换等方面的练习，在有限的时间内应能做出较优的答案。

二、反思：
试卷分析后，我发现参加高三数学考试，我存在着一些问题，比如：
1、对代数和几何的数学知识的理解存在着较大的差距，而且一些基础的题目我也可能有时会做错。

2、统计和概率作为一个新学科，我在应用和计算有一定的困难。

3、我在做题过程中，把每一道题跳过或者写错的可能性较大，从而影响我有效利用时间取得好成绩。

从上面的反思来看，我要尽快补上这些知识点，加强练习，加强自己临场作答的锻炼，以便取得较好的数学考试成绩。

高三下学期新高考第一次调研测试数学试卷-带参考答案与解析注意专项：1．答卷前 考生务必将自己的姓名 考生号 考场号 座位号填写在答题卡上。

2．回答选择题时 选出每小题答案后 用铅笔把答题卡上对应题目的答案标号涂黑。

如简改动 用橡皮擦干静后 再选涂其他答案标号回答非选择题时 将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后 将本试卷和答题卡一并交回。

一、选择题（本大题共8小题 每小题5分 共40分．在每小题给出的四个选项中 只有一项是符合题目要求的．）1．设复数1i z =+，则复数1z z +（其中z 表示z 的共轭复数）表示的点在（ ）上 A ．x 轴B ．y 轴C ．y x =-D ．y x =2．已知角α和β，则“αβ=”是“tan tan αβ=”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件3 侧面展开图是一个半圆面，则该圆锥的体积为（ ）A ．12πB ．9πC ．3πD 4．已知双曲线()222106x y b b -=>的一条渐近线的倾斜角为π6，则此双曲线的右焦点到一条渐近线的距离为（ ）A B ．2CD ．5．一对夫妻带着3个小孩和一个老人 手拉着手围成一圈跳舞 3个小孩不相邻的站法种数是（ ） A ．6B ．12C ．18D ．366．已知递增的等比数列{}n a 10a > 公比为q 且1a 3a 4a 成等差数列，则q 的值为（ ）A B C D 7．已知平面内的三个单位向量a b c 且12a b ⋅=32a c ⋅=，则b c ⋅=（ ）A ．0B ．12C D 0 8．设方程22log 1xx ⋅=的两根为1x ()212x x x <，则（ ）A ．101x << 22x >B ．121x x >C ．1201x x <<D ．123x x +>二 选择题（本大题共3小题 每小题6分 共18分．在每小题给出的选项中 有多项符合题目要求．全部选对的得6分 部分选对的得部分分 有选错的得0分．）9．下列说法正确的是（ ）A ．若事件A 和事件B 互斥 ()()()P AB P A P B = B ．数据4 7 5 6 10 2 12 8的第70百分位数为8C ．若随机变量ξ服从()217,N σ ()17180.4P ξ<≤=，则()180.1P ξ>=D ．已知y 关于x 的回归直线方程为0.307ˆ.yx =-，则样本点()2,3-的残差为 1.9- 10．设函数()f x ()g x 的定义域都为R 且()f x 是奇函数 ()g x 是偶函数，则下列结论正确的是（ ）A ．()()f x g x 是奇函数B ．()()f x g x 是偶函数C ．若()()321g x f x x x -=++，则()()111f g +=D ．若函数()f x 在(),-∞+∞上单调递减且()11f =-，则满足()121f x -≤-≤的x 的取值范围是[]1,3 11．已知体积为2的四棱锥P ABCD - 底面ABCD 是菱形 2AB = 3PA =，则下列说法正确的是（ ）A ．若PA ⊥平面ABCD ，则BAD ∠为π6B ．过点P 作PO ⊥平面ABCD 若AO BD ⊥，则BD PC ⊥C ．PA 与底面ABCD 所成角的最小值为6πD ．若点P 仅在平面ABCD 的一侧 且AB AD ⊥，则P点轨迹长度为三 填空题（本大题共3小题 每小题5分 共15分．）12．已知关于x 的不等式10ax ->的解集为M 2M ∈且1M ∉，则实数a 的取值范围是______． 13．已知抛物线22y x =的弦AB 的中点的横坐标为2，则弦AB 的最大值为______． 14．已知()1cos 3αβ+=-cos cos 1αβ+=，则cos cos 22αβαβ-+=______()sin sin sin αβαβ+=+______． 四 解答题（本大题共5小题 共77分．解答应写出文字说明 证明过程或演算步骤．）15．（本小题满分13分）在如图所示的ABC △中 sin 0B =． （1）求B ∠的大小（2）直线BC 绕点C 顺时针旋转π6与AB 的延长线交于点D 若ABC △为锐角三角形 2AB = 求CD 长度的取值范围．16．（本小题满分15分）已知椭圆()2222:10x y W a b a b+=>>的右顶点为A 左焦点为F 椭圆W 上的点到F 的最大距离是短半轴长倍 且椭圆W 过点31,2⎛⎫⎪⎝⎭．记坐标原点为O 圆E 过O A 两点且与直线6x =相交于两个不同的点P Q （P Q 在第一象限 且P 在Q 的上方） PQ OA = 直线QA 与椭圆W 相交于另一个点B ． （1）求椭圆W 的方程 （2）求QOB △的面积． 17．（本小题满分15分）如图 在四棱锥P ABCD -中 AB CD ∥ 4AB = 2CD = 2BC = 3PC PD == 平面PCD ⊥平面ABCD PD BC ⊥． （1）证明：BC ⊥平面PCD（2）若点Q 是线段PC 的中点 M 是直线AQ 上的一点 N 是直线PD 上的一点 是否存在点M N 使得MN =请说明理由．18．（本小题满分17分）已知函数()ln f x x x =的导数为()f x '．（1）若()1f x kx ≥-恒成立 求实数k 的取值范围（2）函数()f x 的图象上是否存在三个不同的点()11,A x y ()22,B x y ()33,C x y （其中123x x x <<且1x2x 3x 成等比数列） 使直线AC 的斜率等于()2f x '?请说明理由．19．（本小题满分17分）2023年10月11日 中国科学技术大学潘建伟团队成功构建255个光子的量子计算机原型机“九章三号” 求解高斯玻色取样数学问题比目前全球是快的超级计算机快一亿亿倍．相较传统计算机的经典比特只能处于0态或1态 量子计算机的量子比特（qubit ）可同时处于0与1的叠加态 故每个量子比特处于0态或1态是基于概率进行计算的．现假设某台量子计算机以每个粒子的自旋状态作为是子比特 且自旋状态只有上旋与下旋两种状态 其中下旋表示“0” 上旋表示“1” 粒子间的自旋状态相互独立．现将两个初始状态均为叠加态的粒子输入第一道逻辑门后 粒子自旋状态等可能的变为上旋或下旋 再输入第二道逻辑门后 粒子的自旋状态有p 的概率发生改变 记通过第二道逻辑门后的两个粒子中上旋粒子的个数为X ． （1）若通过第二道逻辑门后的两个粒子中上旋粒子的个数为2 且13p = 求两个粒子通过第一道逻辑门后上旋粒子个数为2的概率（2）若一条信息有()*1,n n n >∈N 种可能的情况且各种情况互斥 记这些情况发生的概率分别为1p2p … n p ，则称()()()12n H f p f p f p =++⋅⋅⋅+（其中()2log f x x x =-）为这条信息的信息熵．试求两个粒子通过第二道逻辑门后上旋粒子个数为X 的信息熵H（3）将一个下旋粒子输入第二道逻辑门 当粒子输出后变为上旋粒子时则停止输入 否则重复输入第二道逻辑门直至其变为上旋粒子 设停止输入时该粒子通过第二道逻辑门的次数为Y （1Y = 2 3 ⋯ n ⋯）．证明：当n 无限增大时 Y 的数学期望趋近于一个常数． 参考公式：01q <<时 lim 0nn q →+∞= lim 0nn nq →+∞=．2024届新高考教学教研联盟高三第一次联考数学参考答案一 选择题（本大题共8小题 每小题5分 共40分．）1．C 【解析】11331i i 1i 22z z +=+-=-+ 所以对应的点33,22⎛⎫- ⎪⎝⎭在直线y x =-上． 2．D 【解析】当2παβ==时 tan α tan β没有意义 所以由αβ=推不出tan tan αβ=当tan tan αβ=时()πk k αβ=+∈Z所以由tan tan αβ=推不出αβ=故“αβ=”是“tan tan αβ=”的既不充分也不必要条件． 3．C 【解析】设圆锥的底面半径为r 母线为l 由于圆锥的侧面展开图是一个半圆面，则2ππr l = 所以2l r =所以圆锥的高h ==圆锥的体积为2211ππ3π33V r h ==⨯⨯⨯=．4．A 【解析】因为双曲线()222106x y b b -=>的一条渐近线的倾斜角为π6 πtan 6= 所以该渐近线的方程为3y x = 所以2263b ⎛= ⎝⎭解得b =（舍去） 所以c =此双曲线的右焦点坐标为()30y -==5．B 【解析】3232A A 12=．6．A 【解析】由题意知1432a a a += 即321112a a q a q += 又数列{}n a 递增 10a > 所以1q > 且3212q q += 解得q =7．D 【解析】如图 a OA = c OC = b OB =（或b OD =）由32a c ⋅=得cos COA ∠= 又[]0,πCOA ∠∈ 所以π6COA ∠=由12a b ⋅=得1cos 2BOA ∠= 又[]0,πBOA ∠∈ 所以π3BOA ∠=（或1cos 2DOA ∠= 又[]0,πDOA ∠∈ 所以π3DOA ∠=）所以b c 夹角为π6或π2所以32b c ⋅=或0．8．C 【解析】由题意得 120x x << 由22log 1xx ⋅=得21log 02xx ⎛⎫-= ⎪⎝⎭令()()21log 02xf x x x ⎛⎫=-> ⎪⎝⎭，则()1102f =-< ()1321044f =-=> 1102f ⎛⎫=-> ⎪⎝⎭由()1102f f ⎛⎫⋅<⎪⎝⎭ ()()120f f ⋅<得11,12x ⎛⎫∈ ⎪⎝⎭()21,2x ∈ 故A 错 由21222111log log 022xxx x ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭得21222111log log 22xxx x ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭由11,12x ⎛⎫∈ ⎪⎝⎭ ()21,2x ∈得21222111log log 022x xx x ⎛⎫⎛⎫+=-< ⎪ ⎪⎝⎭⎝⎭所以1201x x << 故C 对 B 错由11,12x ⎛⎫∈ ⎪⎝⎭()21,2x ∈ 所以123x x +< D 错误．二 选择题（本大题共3小题 每小题6分 共18分．）9．BCD 【解析】对于A 若事件A 和事件B 互斥 ()0P AB = 未必有()()()P AB P A P B = A 错 对于B 对数据从小到大重新排序 即：2 4 5 6 7 8 10 12 共8个数字 由870% 5.6⨯= 得这组数据的第70百分位数为第6个数8 B 正确 对于C 因为变量ξ服从()217,N σ 且()17180.4P ξ<≤=，则()()()181717180.50.40.1P P P ξξξ>=>-<≤=-= 故C 正确对于D 由0.307ˆ.yx =- 得样本点()2,3-的残差为()30.30.72 1.9---⨯=- 故D 正确 故选BCD ． 10．ACD 【解析】令()()()F x f x g x =，则()()()F x f x g x -=-- 因为()f x 是奇函数 ()g x 是偶函数 所以()()f x f x -=- ()()g x g x -= 所以()()()()F x f x g x F x -=-=- 所以()()()F x f x g x =是奇函数 A 正确同样 令()()()F x f x g x =，则()()()()()()F x f x g x f x g x F x -=--=-=- 所以()F x 是奇函数 B 错误令1x =-代入()()321g x f x x x -=++，则()()()()32111111g f ---=-+-+= 又()()11g g -=()()11f f -=- 所以()()111g f += C 正确因为()f x 为奇函数 又()11f =- 所以()11f -=由于()f x 在(),-∞+∞上单调递减 要使()121f x -≤-≤成立，则121x -≤-≤ 所以13x ≤≤ D 正确．11．BCD 【解析】114sin sin 2333P ABCD NBCD V S h AB AD BAD h h BAD -=⋅=⋅∠⋅=∠=，则当PA ⊥平面ABCD 时 3h PA ==，则1sin 2BAD ∠= 即BAD ∠为π6或5π6A 错误如图1 若PO ⊥平面ABCD ，则PO BD ⊥ 又AO BD ⊥则BD ⊥平面PAO 有BD PA ⊥ 又BD AC ⊥ 所以BD ⊥平面PAC BD PC ⊥ B 正确 设PA 与底面ABCD 所成角为θ 又11sin 233P ABCD ABCD ABCD V S h S PA θ-===则2sin ABCDS θ=因为4sin 4ABCD S BAD =∠≤，则1sin 2θ≥则PA 与底面ABCD 所成角的最小值为π6C 正确如图2 当AB AD ⊥ 根据123P ABCD ABCD V S h -== 得32h = 即P 点到底面ABCD 的距离为32过A 点作底面ABCD 的垂线为l 过点P 作PO l ⊥交l 于点O，则PO ===点P 的轨迹是以O 为圆心为半径的圆轨迹长度为 D 正确．三 填空题（本大题共3小题 每小题5分 共15分．）12．1,12⎛⎤⎥⎝⎦【解析】2M ∈且1M ∈ 所以210,10,a a ->⎧⎨-≤⎩所以112a <≤．13．5 【解析】方法一：当直线AB 的斜率不存在时 直线AB 的方程为2x = 代入22y x =得2y =或2y =- 所以4AB =当直线AB 的斜率存在时 显然不为零 设直线AB 的方程为y kx b =+代入22y x =消y 并整理得()222220k x kb x b +-+=设()11,A x y ()22,B x y 判别式480kb ∆=->时有122212222,,kb x x k b x x k -⎧+=-⎪⎪⎨⎪=⎪⎩因为弦AB 的中点的横坐标为2 所以2224kb k --= 所以212kb k =-21AB x =-==所以2211145AB k k ⎛⎫⎛⎫=≤++-= ⎪ ⎪⎝⎭⎝⎭当且仅当221114k k +=-即223k =时取到等号 故弦AB 的最大值为5．方法二：设抛物线的焦点为F ，则AB AF BF ≤+又121211122AF BF x x x x +=+++=++当弦AB 的中点的横坐标为2时 有124x x += 所以5AB ≤当直线过焦点F 时取到等号 故弦AB 的最大值为5．14．12 23（任意填对一空给3分） 【解析】由()1cos 3αβ+=-得212cos 123αβ+-=-，则21cos 23αβ+=由cos cos 1αβ+=得2cos cos 122αβαβ-+=，则1cos cos 222αβαβ-+=所以3cos cos222αβαβ-+=()2sin cos cos sin 2222sin sin 32sin cos cos 222αβαβαβαβαβαβαβαβ++++===+--+． 四 解答题（本大题共5小题 共77分．解答应写出文字说明 证明过程或演算步骤．）15．【解析】（1sin 0B =sin B = 两边同时平方可得：2cos 1sin 2B B += 由22sin cos 1B B +=整理得22cos cos 10B B +-= 解得1cos 2B =或cos 1B =- 又()0,πB ∈，则π3B =．sin 0B -=2sin cos 022B B=得cos 02B =或1sin 22B = 又()0,πB ∈，则π26B = π3B =．（2）由（1）得π3ABC ∠=，则2π3CBD ∠= 由题可知π6BCD ∠=，则π6D ∠=设BC a =，则BD BC a ==由余弦定理有2222cos CD BC BD BC BD CBD =+-⋅∠所以CD =由正弦定理有sin sin BC ABA ACB =∠所以2sin 2sin 31sin sin ACB A a ACB ACB π⎛⎫+∠ ⎪⎝⎭====∠∠ 因为ABC △为锐角三角形，则π0,2π0,2ACB A ⎧<∠<⎪⎪⎨⎪<∠<⎪⎩得ππ62ACB <∠<所以tan 3ACB ⎛⎫∠∈+∞ ⎪⎝⎭，则(1tan ACB ∈∠所以3tan CD ACB==+∠即CD的取值范围为．16．【解析】（1）依题有a c += 又222a b c =+所以2,a cb =⎧⎪⎨=⎪⎩所以椭圆W 的方程为2222143x y c c +=又点31,2⎛⎫⎪⎝⎭在椭圆W 上 所以221191434c c +⨯=解得1c =所以椭圆W 的方程为22143x y +=． （2）设()6,P P y ()6,Q Q y 0P Q y y >> ()0,0O ()2,0A因为PQ OA = 所以2P Q y y -= ①圆E 过点O 与A 且与直线6x =相交于两个不同的点P Q ，则圆心E 的坐标为1,2P Q y y +⎛⎫⎪⎝⎭又EO EP = =解得24P Q y y = ②（另法一：设直线6x =与x 轴交于点G ，则有GA GO GQ GP =又4GA = 6GO = 所以24P Q y y = ② 另法二：由OA PQ =知 612P Qy y +=- 10P Q y y += ②）由①②解得6P y = 4Q y =所以()6,4Q 40162M k -==-所以直线QA 的方程为2y x =-与椭圆方程联立消去y 得271640x x -+= 解得B 点的横坐标27B x =所以267Q B QB x x =-=-=又O 到直线QA 的距离d ==所以QOB △的面积11402277S QB d =⋅=⨯=．17．【解析】（1）如图 取CD 的中点O 因为3PC PD ==，则PO CD ⊥因为平面PCD ⊥平面ABCD 平面PCD 平面ABCD CD = PO ⊂平面PCD所以PO ⊥平面ABCD 又BC ⊂平面ABCD所以PO BC ⊥ 又BC PD ⊥ PO ⊂平面PCD PD ⊂平面PCD PD PO P =所以BC ⊥平面PCD ．（2）因为3PC PD == O 为CD 的中点 1OC =所以PO ==过点O 作OE BC ∥交AB 于点E ，则由BC ⊥平面PCD 可得BC CD ⊥，则以O 为原点 OE OCOP 分别为x 轴 y 轴 z 轴建立如图所示的空间直角坐标系则()0,0,0O ()2,3,0A -10,2Q ⎛ ⎝()0,1,0D -(P所以72,2AQ ⎛=- ⎝(DP = ()2,2,0AD =-设与AQ DP 都重直的向量为(),,n x y z =，则720,2220,n AQ x y nDP y ⎧⋅=-++=⎪⎨⎪⋅=+=⎩得3,2,x y z y ⎧=⎪⎪⎨⎪=⎪⎩令4y =，则(6,4,n =设直线AQ与直线DP 的距离为d则12cos ,36AD n d AD AD n n⋅-=⋅===>则不存在点M 和N 使得MN =． 18．【解析】（1）()1f x kx ≥-恒成立即ln 1x x kx ≥-恒成立 又0x > 所以1ln x k x+≥恒成立今()()1ln 0g x x x x =+> 所以()22111x g x x x x ='-=-当01x <<时 ()0g x '< 函数()g x 单调递减 当1x >时 ()0g x '> 函数()g x 单调递增所以当1x =时 ()g x 取到极小值也是最小值 且()11g =所以1k ≤故实数k 的取值范围为(],1-∞．（2）1x 2x 3x 成等比数列且123x x x << 设公比为()1q q >，则21x qx = 231x q x =()ln f x x x =求导得()1ln f x x ='+ 所以()2211ln 1ln ln f x x q x =+=++'直线AC 的斜率为()21131331123131ln 2ln ln ln ln 1q x q x y y x x x x x x x x q +---==---若存在不同的三点A B C 使直线AC 的斜率等于()2f x '则有()21112ln 2ln ln 1ln ln 1q x q x q x q +-=++-整理成221ln 01q q q --=+． 令()()221ln 11x h x x x x -=->+，则()()()()222222114011x xh x x x x x -=-=+'≥+所以()221ln 1x h x x x -=-+在1x >时单调递增 而()10h = 故方程221ln 01q q q --=+在1q >时无实数解 所以不存在不同的三点A B C 使直线AC 的斜率等于()2f x '．19．【解析】（1）设i A =“两个粒子通过第一道逻辑门后上旋粒子个数为i 个” 0i = 1 2B =“两个粒子通过第二道逻辑门后上旋粒子个数为2个” 则()()2021124P A P A ⎛⎫=== ⎪⎝⎭ ()221211C 22P A ⎛⎫== ⎪⎝⎭()019P B A =∣ ()129P B A =∣ ()249P B A =∣则()()()211121414929494i i i P B P A P BA ===⨯+⨯+⨯=∑∣故()()()()()()222214449194P A P BA P AB P A B P B P B ⨯====∣∣． （2）由题知0X = 1 2由（1）知()()()2211112114244P X p p p p ==+-+-=同理可得()()()()21212211111C 11C 14242P X p p p p p p ⎡⎤==-++-+-=⎣⎦则()()()101124P X P X P X ==-=-==故X 的信息熵22111111132log log 42444222H f f f ⎛⎫⎛⎫⎛⎫⎛⎫=++=⨯--=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． （3）由题知()()11n P Y n p p -==- 其中1n = 2 3 …则()()()01111211n EY p p p p n p p -=⋅-+⋅-+⋅⋅⋅+⋅-+⋅⋅⋅又()()111111nni i i i i p p p i p --==⋅-=⋅-∑∑则()()()()1111111211ni n i i p p p n p --=⋅-=⋅-+⋅-+⋅⋅⋅+⋅-∑ ①()()()()()11211111211ni ni p i p p p n p -=-⋅⋅-=⋅-+⋅-+⋅⋅⋅+⋅-∑ ②-①②得：()()()()()1011111111ni n ni p i p p p p n p --=⋅-=-+-+⋅⋅⋅+---∑()()()()111111nnn np p n p n p p p p ---=--=---由题知 当n 无限增大时 ()1np -趋近于零 ()1nn p -趋近于零，则EY 趋近于1p． 所以当n 无限增大时 Y 的数学期望䞨近于一个常数．。

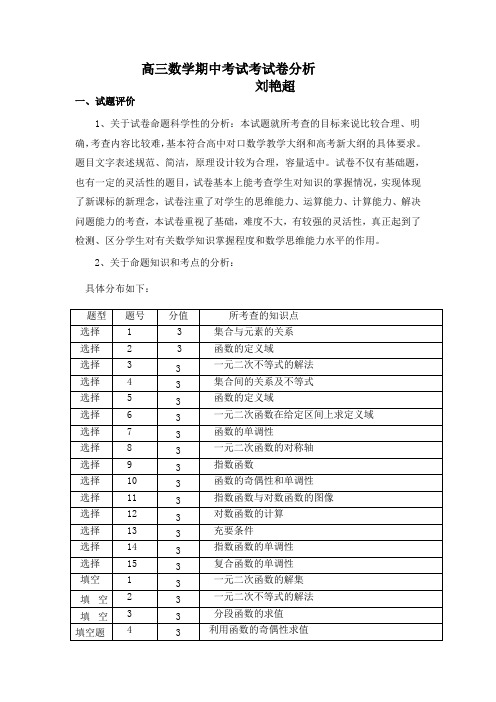
高三数学期中考试考试卷分析刘艳超一、试题评价1、关于试卷命题科学性的分析：本试题就所考查的目标来说比较合理、明确，考查内容比较难，基本符合高中对口数学教学大纲和高考新大纲的具体要求。

题目文字表述规范、简洁，原理设计较为合理，容量适中。

试卷不仅有基础题，也有一定的灵活性的题目，试卷基本上能考查学生对知识的掌握情况，实现体现了新课标的新理念，试卷注重了对学生的思维能力、运算能力、计算能力、解决问题能力的考查，本试卷重视了基础，难度不大，有较强的灵活性，真正起到了检测、区分学生对有关数学知识掌握程度和数学思维能力水平的作用。

2、关于命题知识和考点的分析：具体分布如下：式进行设计，整个卷面分为客观题和主观题两部分。

其中客观题分为选择题15道，每题3分，填空题10道，每题3分，共计75分。

主观题6道，共计45分。

卷面总分120分。

本试题总体卷面设计规范、标准、科学、合理，题型设置严格按照高考真题式样，其中三种题型中基础题、中档题和难题所占的比例也较为适宜，但整个题的计算程度较高二、存在的主要问题与建（一）考试结果分析：本班共35人，18人优秀，优秀率22.3%；及格共25人，及格率71.4%。

（二）通过对本试题的教学导向性的认真分析，我们就会发现，本试题设计具有以下几个方面的特点对教学产生了积极的引导作用：1、注重考查对知识概念的本质理解及运用；2、注重对于计算基本功和带有字母式子的化简变形能力的考查；3、注重对公式结构特点和本质特征的理解与套用；4、注重各个知识点之间的巧妙结合与综合运用；（三）通过对学生答卷情况的认真分析，我们不难发现，目前学生在数学学习方面仍旧存在以下几个方面的问题：1、学生的学习态度、习惯和责任感均有一定的问题；2、对于典型题型和基本题型的基本思路和解法掌握不熟练；3、书面表达和做题基本功不过硬，书写格式不规范，逻辑混乱；4、计算基本功和变形能力欠佳；5、观察分析问题的能力不够，思维推理的能力和层次太简单；6、克服困难、摆脱困境、积极寻找思路的信心、勇气不足。

高三下学期第一次调研测试数学试卷-带参考答案和解析考生注意：1.试卷分值：150分 考试时间：120分钟.2.考生作答时 请将答案答在答题卡上.选择题每小题选出答案后 用2B 铅笔把答题卡上对应题目的答案标号涂黑 非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答案区域内作答 超出答题区域书写的答案无效 在试题卷､草稿纸上作答无效.3.所有答案均要答在答题卡上 否则无效.考试结束后只交答题卡.一､单选题（本大题共8小题 每小题5分 共40分.在每小题给出的四个选项中 只有一个选项是符合题目要求的.）1.已知集合{}{}{}1,2,3,4,5,2,3,2,U A B xx k k ====∈Z ∣，则U B A ⋂=（ ）A.{}4B.{}2,4C.{}1,2D.{}1,3,5 2.复数31i i ⎛⎫- ⎪⎝⎭的虚部为（ ）A.8B.-8C.8iD.8i -3.已知向量()()0,2,1,a b t =-= 若向量b 在向量a 上的投影向量为12a -，则ab ⋅=（ ） A.2 B.52-C.-2D.1124.在ABC 中 “π2C =”是“22sin sin 1A B +=”的（ ） A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.过点()0,2-与圆22410x y x +--=相切的两条直线的夹角为α，则cos α=（ ）A.4B.14-C.4D.14 6.,,,,A B C D E 五人站成一排 如果,A B 必须相邻 那么排法种数为（ ）A.24B.120C.48D.607.若系列椭圆()22*:101,n n n C a x y a n +=<<∈N 的离心率12nn e ⎛⎫= ⎪⎝⎭，则n a =（ ）A.114n ⎛⎫- ⎪⎝⎭B.112n ⎛⎫- ⎪⎝⎭ 8.已知等差数列{}n a （公差不为0）和等差数列{}n b 的前n 项和分别为n n S T ､ 如果关于x 的实系数方程21003100310030x S x T -+=有实数解 那么以下1003个方程()201,2,,1003i i x a x b i -+==中 有实数解的方程至少有（ ）个A.499B.500C.501D.502 二､多选题（本大题共3小题 每小题6分 共18分.在每小题给出的选项中 有多项符合题目要求 全部选对得6分 部分选对得部分 有选错的得0分）9.已知一组数据：12,31,24,33,22,35,45,25,16 若去掉12和45，则剩下的数据与原数据相比 下列结论正确的是（ ）A.中位数不变B.平均数不变C.方差不变D.第40百分位数不变10.双曲线2222:1(0,0)x y C a b a b-=>> 左､右顶点分别为,,A B O 为坐标原点 如图 已知动直线l 与双曲线C 左､右两支分别交于,P Q 两点 与其两条渐近线分别交于,R S 两点，则下列命题正确的是（ ）A.存在直线l 使得AP ∥ORB.l 在运动的过程中 始终有PR SQ =C.若直线l 的方程为2y kx =+ 存在k 使得ORB S取到最大值D.若直线l 的方程为(),22y x a RS SB =--=，则双曲线C 11.如图所示 有一个棱长为4的正四面体P ABC -容器 D 是PB 的中点 E 是CD 上的动点，则下列说法正确的是（ ）A.直线AE 与PB 所成的角为π2B.ABE 的周长最小值为4C.如果在这个容器中放入1D.如果在这个容器中放入4个完全相同的小球(三､填空题（本大题共3小题 每小题5分 共15分）12.小于300的所有末尾是1的三位数的和等于__________.13.已知函数()()ln 11ax f x x x =+-+ 若()0f x 恒成立，则a =__________. 14.已知抛物线2:2(0)C y px p => 点P 为抛物线上的动点 点4,02p A ⎛⎫- ⎪⎝⎭与点P 的距离AP 的最小值为2，则p =__________.四､解答题（本大题共5小题 共77分.解答应写出必要的文字说明､证明过程或演算步骤）15.（13分）在ABC 中 ,,A B C 的对边分别为,,a b c 已知4,cos 0b c a C b ==+=. （1）求a（2）已知点D 在线段BC 上 且3π4ADB ∠= 求AD 长. 16.（15分）甲､乙两人进行射击比赛 每次比赛中 甲､乙各射击一次 甲､乙每次至少射中8环.根据统计资料可知 甲击中8环､9环､10环的概率分别为0.7,0.2,0.1 乙击中8环､9环､10环的概率分别为0.6,0.2,0.2 且甲､乙两人射击相互独立.（1）在一场比赛中 求乙击中的环数少于甲击中的环数的概率（2）若独立进行三场比赛 其中X 场比赛中甲击中的环数多于乙击中的环数 求X 的分布列与数学期望. 17.（15分）如图 圆台12O O 的轴截面为等腰梯形11111,224A ACC AC AA AC === B 为底面圆周上异于,A C 的点.（1）在平面1BCC 内 过1C 作一条直线与平面1A AB 平行 并说明理由.（2）设平面1A AB ⋂平面11,,C CB l Q l BC =∈与平面QAC 所成角为α 当四棱锥11B A ACC -的体积最大时 求sin α的取值范围.18.（17分）已知函数()()ln 1f x x ax x =--.（1）当0a <时 探究()f x '零点的个数（2）当0a >时 证明：()22328af x a a +-+. 19.（17分）阿波罗尼斯是古希腊著名数学家 他的主要研究成果集中在他的代表作《圆锥曲线》一书中.阿波罗尼斯圆是他的研究成果之一 指的是已知动点M 与两定点,Q P 的距离之比(0,1),MQ MP λλλλ=>≠是一个常数 那么动点M 的轨迹就是阿波罗尼斯圆 圆心在直线PQ 上.已知动点M 的轨迹是阿波罗尼斯圆其方程为224x y += 定点分别为椭圆2222:1(0)x y C a b a b +=>>的右焦点F 与右顶点A 且椭圆C 的离心率为12e =.（1）求椭圆C 的标准方程（2）如图 过右焦点F 斜率为(0)k k >的直线l 与椭圆C 相交于,B D （点B 在x 轴上方） 点,S T 是椭圆C 上异于,B D 的两点 SF 平分,BSD TF ∠平分BTD ∠.①求BS DS 的取值范围②将点S F T ､､看作一个阿波罗尼斯圆上的三点 若SFT 外接圆的面积为81π8求直线l 的方程.。

20XX学年度第一学期学期高三期末调研考试数学试卷分析一、试卷总体评价本次试卷是文理合卷，共有三大题22小题（选择题10题共50分，填空题7小题共28分，解答题5题共72分），其中有12题（选择5题、填空4题、解答题3题共83分）是文理分开做，还有第22题是文科只做理科的三分之二，试卷的题型和结构符合是按照20XX年高考数学卷要求设计的。

（一）重基础，重主干本学期期末试题总体难度适中，知识涵盖基本合理，有利于对学生情况的测试了解，有利于中学数学教学，全卷没有偏题、难题，更没有怪题。

与去年同期相比文、理科难度都相当。

选择题、填空题的前几题运用基础知识即可一望而解。

突出数学知识的基础性和综合性，注重数学主干知识的考查。

如涉及函数概念、函数性质和图像、数列、三角函数、立体几何、解析几何等。

（二）重考纲，重平稳1．题型题量稳定。

选择题、填空题和解答题三种题型结构、题量、排列次序仍然保持不变；内容分布合理，考核内容大约分布为(以理科为例)：新增内容约占37分，传统内容中代数占61分，立体几何占28分，解析几何占24分。

2．试题层次分明。

继续坚持多角度、多层次的考查方式，延续了去年分步设问、分散难点的做法，进一步体现了多题把关的命题特点，易、中、难题比例大致符合考试说明中的3：5：2。

各类题型的起点难度较低，阶梯递进，由浅入深，拾级而上。

3．能力方法并重。

继续坚持能力立意的命题指导思想下，一如继往贯穿逻辑思维能力的考查。

尤其突出了基本的数式计算、变形及计算方法的考查以及空间想象能力的考查。

（三）重变化，重新意1．题型设计新颖别致。

例如第（7）题看似简单、但由于设问的角度新颖、涵盖丰富，解答时对函数定义、反函数概念要有一个深刻理解，要把握数形结合思想，要不厌其烦地枚举验证，充分考查思维的条理性、深刻性。

2．试题简洁清爽明快。

通览全卷，试卷一改往年试题叙述冗长，信息繁多的做法，通过简明的语言描述、常用的数学符号及匹配的图形组成题目，显得干净利落，体现了命题者关注数学本身的意义及形式化的语言，更加注重了数学基础，适度地追求形式化以及数学和谐，强调数学本质，达到数学本质与数学形式的辩证统一。

2006学年年第一学期学期高三期末调研考试数学试卷分析一、试卷总体评价本次试卷是文理合卷，共有三大题20小题（选择题10题共50分，填空题4小题共16分，解答题6题共84分），其中有5题（选择3题、填空1题、解答题1题共29分）是文理分开做，还有第18、19题是文科只做理科的三分之二，试卷的题型和结构符合是按照2006年高考数学卷要求设计的。

（一）立足基础，注重主干本学期期末试题总体难度适中，知识涵盖基本合理，有利于对学生情况的测试了解，有利于中学数学教学，全卷没有偏题、难题，更没有怪题。

与去年同期相比文、理科难度都有所下降（文科今年P=0.587，去年P=0.542；理科今年P=0.701，去年P=0.657）。

选择题、填空题的前几题运用基础知识即可一望而解。

突出数学知识的基础性和综合性，注重数学主干知识的考查。

如涉及函数概念、函数性质和图像、数列、三角函数、立体几何、解析几何等。

（二）紧扣考纲，保持稳定1．题型题量稳定。

选择题、填空题和解答题三种题型结构、题量、排列次序仍然保持不变；内容分布合理，考核内容大约分布为(以理科为例)：新增内容约占37分，传统内容中代数占61分，立体几何占28分，解析几何占24分。

2．试题层次分明。

继续坚持多角度、多层次的考查方式，延续了去年分步设问、分散难点的做法，进一步体现了多题把关的命题特点，易、中、难题比例大致符合考试说明中的3：5：2。

各类题型的起点难度较低，阶梯递进，由浅入深，拾级而上。

3．能力方法并重。

继续坚持能力立意的命题指导思想下，一如继往贯穿逻辑思维能力的考查。

尤其突出了基本的数式计算、变形及计算方法的考查以及空间想象能力的考查。

（三）稳中有变，变中求新1．题型设计新颖别致。

例如第（9）题看似简单、但由于设问的角度新颖、涵盖丰富，解答时对函数定义、复合函数概念、圆的方程要有一个深刻理解，要把握数形结合思想，要不厌其烦地枚举验证，充分考查思维的条理性、深刻性。

一、考试概况本次高三数学考试，试卷分为选择题、填空题、解答题三个部分，共50题，总分150分。

考试内容涵盖了高中数学的各个模块，包括函数、数列、三角函数、立体几何、解析几何、概率统计等。

试题难度适中，既有基础知识的考查，也有综合能力的考察。

二、试卷分析1.选择题选择题共10题，主要考查学生对基础知识的掌握程度。

题目难度不高，但部分题目具有一定的迷惑性。

从学生的答题情况来看，大部分学生对基础知识的掌握较好，但仍有部分学生对某些概念、公式、定理的理解不够深入。

例如，在函数的单调性、奇偶性、周期性等方面，部分学生存在混淆的情况。

2.填空题填空题共10题，主要考查学生对基础知识的运用能力。

题目难度较选择题略高，需要学生在短时间内进行计算和推理。

从学生的答题情况来看，大部分学生对基础知识的运用能力较好，但仍有部分学生在计算、推理等方面存在不足。

例如，在解方程、不等式、三角函数的计算过程中，部分学生容易出现错误。

3.解答题解答题共30题，包括以下三个部分：（1）计算题：主要考查学生对基础知识的运用能力和计算能力。

题目难度适中，但部分题目具有一定的难度。

从学生的答题情况来看，大部分学生在计算题上表现较好，但仍有部分学生在计算过程中出现错误。

（2）证明题：主要考查学生的逻辑推理能力和空间想象能力。

题目难度较高，需要学生在短时间内进行推理和证明。

从学生的答题情况来看，部分学生在证明题上表现较好，但仍有部分学生在推理过程中出现错误。

（3）应用题：主要考查学生的综合运用能力。

题目难度较高，需要学生在理解题意的基础上，运用所学知识解决问题。

从学生的答题情况来看，部分学生在应用题上表现较好，但仍有部分学生无法准确把握题意，导致解题过程出现偏差。

三、学生分析1.基础知识掌握较好，但运用能力不足从整体来看，学生在基础知识方面掌握较好，但部分学生在运用知识解决实际问题的能力上存在不足。

这主要表现在以下两个方面：（1）计算能力不足：部分学生在计算题上出现错误，主要原因是基础知识掌握不牢固，计算方法不熟练。

高三数学学情调研考试试卷分析本次学情调研数学试卷，能以大纲为本，以教材为基准，基本覆盖了平时所学的知识点，试卷不仅有基础题，也有一定的灵活性的题目，能考查学生对知识的掌握情况，实现体现了新课标的新理念，试卷注重了对学生的思维能力、运算能力、计算能力、解决问题能力的考查，且难度也不大，在出题发面应该是一份很成功的试卷。

但整体的考试结果却不是很让人满意，通过分析试卷主要存在以下问题：选择题部分：10题学生忘记双曲线的数量关系并且不能正确认识题目所组成的图形与结论之间的关系到底是什么，无从下手。

11题已知与结论找不到联系，大部分学生不会做，12题几何概率模型忘了。

填空题部分：15题16题出错率比较高，运用转化思想解比较容易。

解答题部分：17题是考查等差数列和等比数列基本概念和基本运算的题目，题目源于课本，略高于课本，难度不大，均分约10分。

运算存在问题，少数学生列出了方程组后求解不正确。

18题立体几何题，不少学生用常规方法解费时费力答案也不对，建系解就容易多了。

20题是一道函数综合题，绝大部分学生没有足够的时间取做，实验班学生会做但步骤欠规范，所以得分较低。

21题是解析几何题，第二问难度较大，技巧性高，运算量也大，本题得分率最低。

分析出错的原因，主要归纳为以下几点：一学生对基础知识的掌握不扎实一些易得分的题也出现失分现象，对所学知识不能熟练运用，对知识的掌握也不是很灵活，造成容易的失分难的攻不下的两难状况。

二一些学生的学习方法有待改进一些同学平时学习也挺认真，日常练习也不错，但一遇上综合性的考试就不行，像这样的状况主要是因为学生的复习方法不对，作为一名高三的学生应该学会自己归纳总结，可以把相似和有关联的一些题总结在一起，也可以把知识点相同或做题方法相同的题总结在一块，这样便于复习，也省时。

三同学们的应试技巧也有待提高，翻看这次学生们的试卷会发现有些学生的题还没做完，前面难的没拿下后面容易的没时间做。

拿不到高分认为是自己时间不够，这就是考试技巧的问题。