浙教版七年级数学上《6.3线段的长短比较》分层训练含答案

6．3 线段的长短比较知识点一线段长短的比较方法比较两条线段的长短有两种方法：叠合法和度量法．1．如图6－3－1，比较线段AB与线段CD的长短．图6－3－1知识点二线段的基本事实在所有连结两点的线中，线段最短．简单地说，两点之间线段最短．连结两点的线段的______叫做这两点间的距离．2．把一条弯曲的河道改成直道，可以缩短航程，其中的道理可以解释为________________________________________________________________________．类型一线段的画法例1 教材例题针对训练已知三角形ABC(如图6－3－2)，用直尺和圆规作一条线段，使它等于图中线段AB的长．图6－3－2【归纳总结】画一条线段等于已知线段的依据就是叠合法．类型二线段的基本事实的应用例2 教材补充例题如图6－3－3所示，直线l是一条平直的公路，A，B是公路两旁的两个工厂，现要在A，B两厂之间建一个货运站C，使两工厂到货运站C的距离之和最小(公路宽不计)，请你找出货运站C的位置，并说明理由．图6－3－3小结◆◆◆)反思◆◆◆)如图6－3－4，小明认为从A到B的最短路线是A—C—E—B，你认为正确吗？如果不正确，请你帮忙改正．图6－3－4详解详析【学知识】知识点一1．解：方法一：如图所示，将线段CD移到线段AB所在的直线上，使点C与点A重合，点D与点B在点A的同侧，因为点D在线段AB外，所以AB<CD.方法二：用刻度尺分别量出线段AB与线段CD的长度，得AB<CD.知识点二长度2．[答案] 两点之间线段最短【筑方法】例1解：步骤：如图．(1)画一条射线AM；(2)用圆规量取已知线段AB的长度；(3)以A为端点，用圆规在射线AM上截取AD＝AB.则线段AD就是所求作的线段．例2[解析] 根据“两点之间线段最短”，只需连结A，B，与l的交点便是它到A，B 两点距离和最小的点．解：如图，连结AB，与l的交点C就是货运站的位置．理由：两点之间线段最短．【勤反思】[反思] 不正确，从A到B的最短路线是A—F—E—B.。

最新精选初中数学七年级上册6.3 线段的长短比较浙教版课后练习第四十三篇第1题【单选题】已知线段AB=6 cm，在直线AB上画线段AC=2 cm，则线段BC的长是( )A、4 cmB、4 cm或8 cmC、8 cmD、3 cm或8 cm【答案】：【解析】：第2题【单选题】下列语句：①两点之间，线段最短．②线段AB是点A与点B两点间的距离．③对顶角相等．④同位角相等．其中正确的有( )A、①②③④B、②③④C、①③D、②④【答案】：第3题【单选题】如图，线段CD在线段AB上，且CD=2，若线段AB的长度是一个正整数，则图中以A，B，C，D这四点中任意两点为端点的所有线段长度之和可能是( )A、28B、29C、30D、31【答案】：【解析】：第4题【单选题】点A、B、C在同一条数轴上，其中点A、B表示的数分别为﹣3、1，若BC=2，则AC等于( )A、3B、2C、3或5D、2或6【解析】：第5题【单选题】把弯曲的河道改直，能够缩短航程，这样做的道理是( )A、两点之间，射线最短B、两点之间，线段最短C、两点确定一条直线D、两点之间，直线最短【答案】：【解析】：第6题【单选题】如图，直线l外有不重合的两点A，B．在直线l上求一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B＇．②连接AB＇交直线l于点C，则点C即为所求．在解决这个问题时，没有用到的知识点是( )A、线段的垂直平分线性质B、两点之间线段最短C、三角形两边之和大于第三边D、角平分线的性质【答案】：【解析】：第7题【解答题】如图，B，C是线段AD上任意两点，B在A，C之间．M、N分别是AB，CD的中点．已知AD=a，MN=b．求BC．【答案】：【解析】：第8题【解答题】如图，M是线段AC中点，点B在线段AC上，且AB=4cm，BC=2AB，求线段MC和线段BM的长．【答案】：【解析】：第9题【解答题】如图，已知点A、B、C、D、E在同一直线上，且AC=BD，E是线段BC的中点．（1）点E是线段AD的中点吗？说明理由；（2）当AD=10，AB=3时，求线段BE的长度．【答案】：【解析】：第10题【解答题】如图，P是线段AB上一点，M，N分别是线段AB，AP的中点，若AB=16，BP=6，求线段MN的长．【答案】：【解析】：第11题【解答题】如图，D是AB的中点，E是BC的中点，BE=有误AC=2cm，求线段DE的长．【答案】：【解析】：第12题【解答题】2014年7月18日下午至19日早晨，超强台风“威马逊”先后在中国海南、广东、广西三省区三次登陆，并造成多人伤亡，多地遭受重创．武警某部队接到救灾命令后火速携带救灾物资乘车赶往省道AB两侧的村庄M、N．已知汽车在直线形的公路AB上由A向B行驶，由于道路泥泞，汽车无法直接到达村庄，需把物资卸在道路上，请你分析：救灾物资应分别卸在什么地方，才能使两村的群众各自在最近的距离拿到救灾物资．请在图上标出这两个位置，并说明理由．【答案】：【解析】：第13题【作图题】一辆货车在公路（直线CD）上由点C向点D方向行驶，村庄A、B分别位于道路CD的两侧，司机师傅要在公路上选择一个货物的下货点．请在CD上确定一个下货点E，使点E到村庄A的距离最近，画出图形并写出画图的依据；请在直线CD上确定一点O，使点O到村庄A、B的距离之和最小，画出图形并写出画图的依据．【答案】：【解析】：第14题【综合题】已知线段AB=6cm，在直线AB上画线段BC=2cm．画出线段AC；（有几种情况就画几种）求出线段AC的长；（要求有计算过程）在以上条件下，点M、N分别是线段AB、AC的中点，求线段MN的长．（要求有计算过程）【答案】：【解析】：第15题【综合题】如图，已知线段AB的长为a，延长线段AB至点C，使BC=有误．求线段AC的长（用含a的代数式表示）；取线段AC的中点D，若DB=3，求a的值．最新教育资料精选【答案】：【解析】：11/ 11。

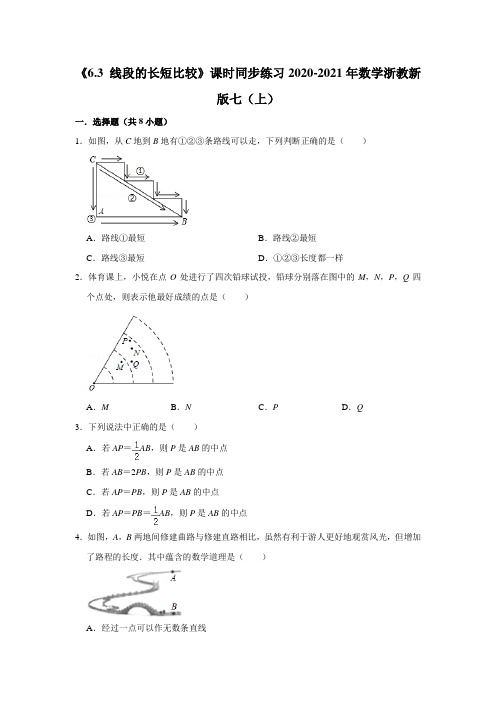
《6.3 线段的长短比较》课时同步练习2020-2021年数学浙教新版七（上）一．选择题（共8小题）1．如图，从C地到B地有①②③条路线可以走，下列判断正确的是（）A．路线①最短B．路线②最短C．路线③最短D．①②③长度都一样2．体育课上，小悦在点O处进行了四次铅球试投，铅球分别落在图中的M，N，P，Q四个点处，则表示他最好成绩的点是（）A．M B．N C．P D．Q3．下列说法中正确的是（）A．若AP＝AB，则P是AB的中点B．若AB＝2PB，则P是AB的中点C．若AP＝PB，则P是AB的中点D．若AP＝PB＝AB，则P是AB的中点4．如图，A，B两地间修建曲路与修建直路相比，虽然有利于游人更好地观赏风光，但增加了路程的长度．其中蕴含的数学道理是（）A．经过一点可以作无数条直线B．经过两点有且只有一条直线C．两点之间，有若干种连接方式D．两点之间，线段最短5．点C为线段AB的三等分点，D为射线BA上一点，若AB＝6，BD＝8，则CD的长为（）A．4B．4或6C．12D．10或126．如图，某工厂有三个住宅区，A、B、C各区分别住有职工15人、20人、45人，且这三个区在一条大道上（A、B、C三点共线），已知AB＝1500m，BC＝1000m，为了方便职工上下班，该工厂打算从以下四处中选一处设置接送车停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（）A．A住宅区B．B住宅区C．C住宅区D．B、C住宅区中间D处7．如图，点A、B、C在同一直线上，H为AC的中点，M为AB的中点，N为BC的中点，则下列说法：①MN＝HC；②MH＝（AH﹣HB）；③MN＝（AC+HB）；④HN＝（HC+HB），其中正确的是（）A．①②B．①②④C．②③④D．①②③④8．如图，在线段AB上有C、D两点，CD长度为1cm，AB长为整数，则以A，B，C，D 为端点的所有线段长度和不可能为（）A．16cm B．21cm C．22cm D．31cm二．填空题（共6小题）9．M、N是数轴上的二个点，线段MN的长度为3，若点M表示的数为﹣1，则点N表示的数为．10．下列三个日常现象：其中，可以用“两点之间线段最短”来解释的是（填序号）．11．如图，琵岩山旅游风景区里有一条曲折迂回的路，这样虽然有利于游人更好的观赏风景，但增加了路程的长度，其中蕴含的数学道理是．12．如图，已知，E、F分别是AD、BC的中点，且BF＝20cm，则EF的长度为cm．13．在直线m上取A、B、C三点，使得AB＝10cm，BC＝4cm，如果点O是线段AC的中点，则线段OC的长度为．14．如图，点B是线段AC上一点，且AB＝15cm，，点O是线段AC的中点，则线段OB＝．三．解答题（共8小题）15．如图，C为线段AD上一点，B为CD的中点，AD＝20cm，AC＝12cm．（1）图中共有条线段；（2）求BD的长；（3）若点E在线段BD上，且BE＝3cm，求AE的长．16．如图，C为线段AB上一点．AB＝m，BC＝n，M，N分别为AC，BC的中点．（1）若m＝8，n＝2，求MN的长；（2）若m＝3n，求的值．17．已知直线l依次三点A、B、C，AB＝6，BC＝m，点M是AC点中点（1）如图，当m＝4，求线段BM的长度（写清线段关系）．（2）在直线l上一点D，CD＝n＜m，用m、n表示线段DM的长度．18．如图，C是线段AB的中点．（1）若点D在CB上，且DB＝1.5cm，AD＝6.5cm，求线段CD的长度．（2）若将（1）中的“点D在CB上”改为“点D在CB的延长线上”，其它条件不变，请画出相应的示意图，并求出此时线段CD的长度．19．如图，线段AB＝20cm，线段AB上有一点C，BC：AC＝1：4，点D是线段AB的中点，点E是线段AC的中点．（1）求线段AC的长度；（2）求线段DE的长度．20．如图，线段AB＝10cm，C是线段AB上一点，AC＝4cm，M是AB的中点，N是AC的中点．求（1）线段CM的长；（2）求线段MN的长．21．（1）如图，已知点C在线段AB上，且AC＝6cm，BC＝4cm，点M、N分别是AC、BC 的中点，求线段MN的长度；（2）若点C是线段AB上任意一点，且AC＝a，BC＝b，点M、N分别是AC、BC的中点，请直接写出线段MN的长度；（用a、b的代数式表示）（3）在（2）中，把点C是线段AB上任意一点改为：点C是直线AB上任意一点，其他条件不变，则线段MN的长度会变化吗？若有变化，求出结果．22．如图，点C在线段AB上，AC＝8cm，CB＝6cm，点M、N分别是AC、BC的中点．（1）求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB＝a cm，其它条件不变，你能猜想MN的长度吗？并说明理由；（3）若C在线段AB的延长线上，且满足AC﹣BC＝b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？并说明理由；参考答案一．选择题（共8小题）1．解：利用线段的性质可得路线②最短，故选：B．2．解：如图所示，OP＞ON＞OQ＞OM，∴表示他最好成绩的点是点P，故选：C．3．解：A答案错误，当P点在BA的延长线上时不成立．B答案错误，当P点在AB的延长线上时不成立C答案不成立，没有强调A、B、P三点在同一直线上用排除法得：D答案正确．故选：D．4．解：A，B两地间修建曲路与修建直路相比，虽然有利于游人更好地观赏风光，但增加了路程的长度．其中蕴含的数学道理是两点之间，线段最短，故选：D．5．解：如图1，当AC＝AB＝×6＝2时，CD＝BD﹣AB+AC＝8﹣6+2＝4；如图2，当AC＝AB＝×6＝4时，CD＝BD﹣AB+AC＝8﹣6+4＝6．故CD的长为4或6．故选：B．6．解：当停靠点在A区时，所有员工步行到停靠点路程和是：20×1500+45×2500＝142500m；当停靠点在B区时，所有员工步行到停靠点路程和是：15×1500+45×1000＝67500m；当停靠点在C区时，所有员工步行到停靠点路程和是：15×2500+20×1000＝57500m；当停靠点在D区时，设距离B区x米，所有员工步行到停靠点路程和是：15×（1500+x）+20x+45（1000﹣x）＝﹣10x+67500，由于k＝﹣10，所以，x越大，路程之和越小，∴当停靠点在C区时，所有员工步行到停靠点路程和最小．故选：C．7．解：∵H为AC的中点，M为AB的中点，N为BC的中点，∴AH＝CH＝AC，AM＝BM＝AB，BN＝CN＝BC，∴MN＝MB+BN＝（AB+BC）＝AC，∴MN＝HC，①正确；（AH﹣HB）＝（AB﹣BH﹣BH）＝MB﹣HB＝MH，②正确；MN＝AC，③错误；（HC+HB）＝（BC+HB+HB）＝BN+HB＝HN，④正确，故选：B．8．解：由题意可得，图中以A，B，C，D这四点中任意两点为端点的所有线段长度之和是：AC+CD+DB+AD+CB+AB＝（AC+CD+DB）+（AD+CB）+AB＝AB+AB+CD+AB＝3AB+CD，∴以A、B、C、D为端点的所有线段长度和为长度为3的倍数多1，∴以A、B、C、D为端点的所有线段长度和不可能为21．故选：B．二．填空题（共6小题）9．解：如图，N的位置不确定：（1）N在M的左边，可以看出点N表示的数为﹣4；（2）N在M的右边，可以看出点N表示的数为2．∴点N表示的数为﹣4或2．10．解：图①利用垂线段最短；图②利用两点之间线段最短；图③利用两点确定一条直线；故答案为：②．11．解：其中蕴含的数学道理是两点之间线段最短，故答案为：两点之间，线段最短．12．解：∵点F是BC的中点，且BF＝20cm，∴BC＝2BF＝40cm，∵CD＝AD＝BC，∴CD＝×40＝10（cm），AD＝30cm，∵E、F分别是AD、BC的中点，∴EC＝AD﹣CD＝5cm，CF＝BF＝20cm，∴EF的长度为CE+CF＝25cm，故答案为：25．13．解：如图所示，AC＝10+4＝14（cm），∵点O是线段AC的中点，∴AO＝AC＝7cm，∴OC＝AO＝7cm，∵AC＝AB﹣BC＝10﹣4＝6cm，∴AO＝AC＝3cm，∴OC＝AO＝3cm．故答案为：7cm或3cm．14．解：∵AB＝15cm，BC＝AB＝5cm，∴AC＝AB+BC＝15+5＝20（cm）；∵点O是线段AC的中点，∴CO＝AC＝×20＝10（cm），∴OB＝CO﹣BC＝10﹣5＝5（cm）．故答案为：5cm．三．解答题（共8小题）15．解：（1）图中共有1+2+3＝6条线段．故答案为：6；（2）∵AD＝20cm，AC＝12cm．∴CD＝AD﹣AC＝8cm．∵B为CD的中点．∵BD＝CD＝4cm，（3）AB＝AD﹣BD＝20﹣4＝16（cm），AE＝AB+BE＝16+3＝19（cm）．故AE的长是19cm．16．解：（1）∵M，N分别为AC，BC的中点，∴MC＝AC，NC＝BC，∵AB＝m，BC＝n，∴AC＝AB﹣BC＝m﹣n∵m＝8，n＝2，∴MC＝AC＝3NC＝BC＝1∴MN＝MC+CN＝3+1＝4；答：MN的长为4；（2）∵M，N分别为AC，BC的中点，m＝3n，∴MC＝AC＝n，NC＝BC＝∴MN＝MC+NC＝n+＝n∴＝＝．答：的值为．17．解：（1）当m＝4时，BC＝4，又∵AB＝6，∴AC＝4+6＝10，又M为AC中点，∴AM＝MC＝5，∴BM＝AB﹣AM，＝6﹣5＝1；（2）∵AB＝6，BC＝m，∴AC＝6+m，∵M为AC中点，∴，①当D在线段BC上，M在D的左边时，CD＝n，MD＝MC﹣CD＝＝；②当D在线段BC上，M在D的右边边时，CD＝n，MD＝DC﹣MC＝n﹣＝；③当D在l上且在点C的右侧时，CD＝n，MD＝MC+CD＝+n＝．18．解：（1）AB＝AD+BD＝6.5cm+1.5cm＝8cm，∵C是线段AB的中点，∴CB＝AB＝4cm，∴CD＝CB﹣BD＝4cm﹣1.5cm＝2.5cm；（2）∵AB＝AD﹣BD＝6.5cm﹣1.5cm＝5cm，∴CB＝AB＝2.5cm，∴CD＝CB+BD＝4cm．19．解：（1）∵AB＝20cm，BC：AC＝1：4，∴BC＝4cm，AC＝16cm；（2）∵点D是线段AB的中点，∴BD＝AB＝10cm，∴CD＝BD﹣BC＝6cm，∵点E是线段AC的中点，∴CE＝AC＝8cm，∴DE＝CE﹣CD＝2cm．20．解：（1）由AB＝10，M是AB的中点，所以AM＝5，又AC＝4，所以CM＝AM﹣AC＝5﹣4＝1（cm）．所以线段CM的长为1cm；（2）因为N是AC的中点，所以NC＝2，所以MN＝NC+CM，2+1＝3（cm），所以线段MN的长为3cm．21．解：（1）∵AC＝6cm，点M是AC的中点∴CM＝AC＝3cm∵BC＝4cm，点N是BC的中点∴CN＝BC＝2cm∴MN＝CM+CN＝5cm∴线段MN的长度为5cm．（2）．（3）线段MN的长度会变化．当点C在线段AB上时，由（2）知当点C在线段AB的延长线时，如图：则AC＝a＞BC＝b∵AC＝a点M是AC的中点∴CM＝AC＝a∵BC＝b点N是BC的中点∴CN＝BC＝b∴MN＝CM﹣CN＝当点C在线段BA的延长线时，如图：则AC＝a＜BC＝b同理可求：CM＝AC＝aCN＝BC＝b∴MN＝CN﹣CM＝∴综上所述，线段MN的长度变化，，，．22．解：（1）∵点M、N分别是AC、BC的中点，AC＝8cm，CB＝6cm，∴CM＝AC＝4cm，CN＝BC＝3cm，∴MN＝CM+CN＝4+3＝7cm，即线段MN的长是7cm；（2）∵点M、N分别是AC、BC的中点，AC+CB＝acm，∴CM＝AC，CN＝BC，∴MN＝CM+CN＝AC+BC＝（AC+BC）＝acm，即线段MN的长是acm；（3）如图：MN＝b，理由是：∵点M、N分别是AC、BC的中点，AC﹣CB＝bcm，∴CM＝AC，CN＝BC，∴MN＝CM﹣CN＝AC﹣BC＝（AC﹣BC）＝bcm，即线段MN的长是bcm．。

第6章 图形的初步知识6. 3线段的长短比较知识要点分类练 务实塞敲 知识点1线段的长短比较1. 下列各种图形中，可以比较大小的是（ ）A .两条射线B .两条直线C .直线与射线D .两条线段2. [2018台州乐清模拟改编]如图6-3 —1,( )A . A'B '> ABB . A' B ' = ABC. A'B'v ABD .没有刻度尺，无法确定图6 —3—13 .如图6—3—2所示，用刻度尺测量图中AB,AC,BC的长度，可以得出AB _________ AC,AC _______ BC, AB+ BC _______ A C.（填“〉” 或＜” = ”）知识点2两点之间线段最短及两点间的距离4. A, B两点间的距离是指（）A .连结A, B两点的线段的长度C .连结A, B两点的线段B .过A, B两点的直线D .直线AB的长5. [2018北京丰台区期末]如图6 —3—3,小红用剪刀沿直线将一片平整的树叶剪掉一部分，发现剩下树叶的周长比原树叶的周长要小，能解释这一现象的数学知识是（）A .经过一点能画无数条直线B .两点之间线段最短C .两点确定一条直线D .连结两点的线段的长度叫做这两点间的距离6. __________________________________________________ 如图6- 3 —4,数轴上A, B两点之间的距离为_____________________1 ._____ L-io 5图6—3—4知识点3线段作图AB,使AB = c.7.如图6—3 —5所示，已知线段c,利用尺规，求作一条线段规律方｝£综合练&以下说法正确的是（）A .两点之间直线最短B .延长直线AB到点E,使BE = ABC. A, B两点间的距离是2 cmD •连结两点的线段就是这两点间的距离9•如图6—3—6所示，某同学的家在A处，书店在B处，星期日他到书店去买书，想尽快赶到书店，请你帮他在图中所示的路线中选择一条最近的路线( )A • A T C T D TB B • A TC T F T BC • A T C T E T F T BD • A T C T M T B10. ____________ 已知线段AB,延长AB到点C,使BC = AB,在AB的反向延长线上截取AD = AC, 贝y DB : AB = __ , CD : BD = ________ .11. 如图6 —3—7所示，已知A, B, C, D四个村庄，为解决当地缺水问题，政府准备投资修建一个蓄水池，不考虑其他因素，请你画图确定蓄水池点H的位置，使它与四个村庄的距离之和最小.A拓广探究创新练12. 已知四边形ABCD（如图6—3 —8 所示）,若用直尺和圆规画线段a, b,使a = AB +BC+ CD + DA , b = AC+ BD ,贝U a ______ b_（填“〉” 或A C D＜” = ”）教师详解详析1. D2. A3. < > =4. A ［解析］连结两点的线段的长度叫做这两点间的距离.5. B6. 4 ［解析］AB = 3—( —1) = 4•故答案为4.7. 略& C ［解析］两点之间线段最短，故A项错误，不符合题意；延长线段AB到点E,使BE= AB,故B项错误，不符合题意；C项中的说法正确，符合题意；连结两点的线段的长度叫做这两点间的距离，故D项错误，不符合题意.故选C.9. B ［解析］根据两点之间线段最短的原理可知，由C到B的各条线路中，线段BC最短，则B项符合题意•故选 B.10. 3 : 1 4 : 311. 解：连结AC, BD ,交点H即为所求•图略.12. > ［解析］可以先画线段a, b,再比较a与b的大小.作法：(1)在射线MN 上顺次截取MA'= AB, A' B'= BC, B' C '= CD , C D'= DA, 则线段MD ' = a；⑵在射线PQ上顺次截取PE = AC, EF = BD,则线段PF = b.如图所示,a>b.。

6.3 线段的长短比较1．一般地，如果两条线段____________，那么我们就说这两条线段相等．2．在所有连结两点的线中，____________最短，简单地说，____________.3．____________叫做这两点间的距离．A组基础训练1．下列说法正确的是()A．直线可以比较长短B．直线比射线长C．线段可以比较长短D．线段可能比直线长2．已知线段AB和线段CD，使A与C重合，若点D在AB的延长线上，则() A．AB＞CDB．AB＝CDC．AB＜CDD．无法比较AB与CD的长短3．已知A，B是数轴上的两点，AB＝2，点B表示－1，则点A表示()A．1 B．－3 C．1或－3 D．3或14．A，B两点间的距离是指()A．连结A，B两点间的线段长度B．过A，B两点间的直线C．连结A，B两点间的线段D．直线AB的长5．为了估计池塘两岸A，B间的距离，小明在池塘一侧选取了一点P，测得PA＝16m，PB＝12m，那么A，B间的距离不可能是()A．5m B．15m C．20m D．30m6．如图所示，比较图中AB，AC，BC的长度，可以得出AB____________AC，AC____________BC，AB＋BC____________AC.第6题图7．某工程队在修建高速公路时，将如图的弯曲的道路改直，这样做的理由是____________．第7题图8．用”＞”、”＜”或”＝”填空：(1)如果点C在线段AB上，那么AC____________AB，AB____________BC；(2)如果点D在线段AB的延长线上，那么AD____________AB，BD____________AD；(3)如果点C在线段AB的反向延长线上，则BC____________AC.9．如图，利用圆规比较四边形ABCD中四条边的长短，并用”>”连接．第9题图10．如图，线l表示一条小河，点A，点B表示两个村庄，在何处架桥才能使A村到B 村的路程最短？第10题图11．如图所示，沿大街AB段上有四处居民小区A，B，C，D，且有AC＝CD＝DB.为了改善每个小区的居民的购物环境，想在AB上建一家超市，每个小区的居民各执一词，难以定下具体建设位置，如果由你出任超市负责人．从便民、获利的角度考虑，你将把超市建在哪里？第11题图B组自主提高12．为解决村庄用电问题，政府投资在已建电厂与A，B，C，D这四个村庄之间架设输电线路．现已知这四个村庄及电厂之间的距离(单位：km)如图所示，则把电力输送到这四个村庄的输电线路的总长度最短应是()第12题图A．19.5km B．20.5km C．21.5km D．24.5km13．如图所示，有一正方体纸盒，在点C′处有一只小虫，它要爬到点A吃食物，应该沿着怎样的路线才能使行程最短？你能设计出这条路线吗？第13题图C组综合运用14．如图，一条街道旁有A，B，C，D，E五幢居民楼，其中BC＝DE＝2AB＝2CD.某大桶水经销商统计各居民每周所需大桶水的数量如下表：第14题图他们计划在这五幢楼中租赁一间门市房，设立供水点．若仅考虑这五幢楼内的居民取水所走路程之和最小，你将把门市房选择在哪幢楼中？参考答案6．3线段的长短比较【课堂笔记】1．长度相等 2.线段两点之间线段最短 3.连结两点的线段的长度【分层训练】1．C 2.C 3.C 4.A 5.D6．＜＞＝7.两点之间线段最短8．(1)＜＞(2)＞＜(3)＞9．BC>CD>AD>AB10．连结AB，线段AB与线l的交点P就是架桥之处．第10题图11．超市应建在CD段上12．C13．答案不唯一，如图虚线为一种．第13题图14．设AB＝a，则BC＝2a，CD＝a，DE＝2a.若供水点在A楼，则55a＋50(a＋2a)＋72(a＋2a＋a)＋85(a＋2a＋a＋2a)＝1003a；若供水点在B楼，则38a＋50×2a＋72(2a＋a)＋85(2a＋a＋2a)＝779a；若供水点在C楼，则38(a＋2a)＋55×2a＋72a＋85(a＋2a)＝551a；若供水点在D楼，则38(a＋2a＋a)＋55(2a＋a)＋50a＋85×2a＝537a；若供水点在E楼，则38(a＋2a＋a＋2a)＋55(2a＋a＋2a)＋50(a＋2a)＋72×2a＝797a. ∴桶装水供应点设在D楼时总路程最小．。

《6.3线段的长短比较》同步练习1. 下列说法错误的是（ ）A. 平面内过一点有且只有一条直线与已知直线垂直B. 两点之间的所有连线中，线段最短C.经过两点有且只有一条直线D. 过一点有且只有一条直线与已知直线平行2．平面上的三条直线最多可将平面分成（ ）部分 A ．3 B ．6 C ． 7 D ．93．如果A BC 三点在同一直线上，且线段AB=4CM ，BC=2CM ，那么AC 两点之间的距离为（ ）A ．2CMB ． 6CMC ．2 或6CMD ．无法确定4．下列说法正确的是（ ）A ．延长直线AB 到C ； B ．延长射线OA 到C ； C ．平角是一条直线；D ．延长线段AB 到C5．如果你想将一根细木条固定在墙上，至少需要几个钉子（ ）A ．一个B ．两个C ．三个D ．无数个6．点P 在线段EF 上，现有四个等式①PE=PF;②PE=12EF;③12EF=2PE;④2PE=EF;其中能表示点P 是EF 中点的有（ ）A ．4个B ．3个C ．2个D ．1个7. 如图所示，从A 地到达B 地，最短的路线是（ ）．A ．A →C →E →B B ．A →F →E →BC ．A →D →E →B D ．A →C →G →E →B8．如果AB=8，AC=5，BC=3，则（ ）A ． 点C 在线段AB 上 B ． 点B 在线段AB 的延长线上C ． 点C 在直线AB 外D ．点C 可能在直线AB 上，也可能在直线AB 外9．两点间的距离是指（ ）．A ．连接两点的线段B ．连接两点的直线的长度C ．连接两点的直线的长度D ．连接两点的直线10．如果点B 在线段AC 上，那么下列各表达式中，AB=12AC=BC ，AC=2AB ，AB+BC=AC ，能表示B 是线段AC 的中点的有（ ）．A ．1个B ．2个C ．3个D ．没有11．若线段AB=a，C是线段AB上的任意一点，M、N分别是AC和CB的中点，则MN=_______. 12．经过１点可作________条直线；如果有3个点，经过其中任意两点作直线，可以作______条直线；经过四点最多能确定条直线。

6.3线段的长短比较同步测试【浙教版】参考答案与试题解析一．选择题1．（2019秋•房山区期末）如图，用圆规比较两条线段AB和A′B′的长短，其中正确的是（）A．A′B′＞AB B．A′B′＝ABC．A′B′＜AB D．没有刻度尺，无法确定【思路点拨】根据比较线段的长短进行解答即可．【答案】解：由图可知，A′B′＜AB；故选：C．【点睛】本题主要考查了比较线段的长短，解题的关键是正确比较线段的长短．2．（2020•密云区二模）如图，小林利用圆规在线段CE上截取线段CD，使CD＝AB．若点D恰好为CE的中点，则下列结论中错误的是（）A．CD＝DE B．AB＝DE C．CE＝CD D．CE＝2AB【思路点拨】根据线段中点的定义即可得到结论．【答案】解：∵点D恰好为CE的中点，∴CD＝DE，∴AB＝DE＝CE，故A，B，D选项正确，C选项错误，故选：C．【点睛】本题考查了线段中点的定义，正确的理解题意是解题的关键．3．（2019秋•厦门期末）下列4个生产、生活现象中，可用“两点之间线段最短”来解释的是（）A．用两根钉子就可以把木条固定在墙上B．植树时，只要选出两棵树的位置，就能确定同一行树所在的直线C．把弯曲的公路改直，就能缩短路程D．砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线【思路点拨】直接利用线段的性质以及直线的性质分别分析得出答案．【答案】解：A、用两根钉子就可以把木条固定在墙上，利用的是两点确定一条直线，故此选项不合题意；B、植树时，只要选出两棵树的位置，就能确定同一行树所在的直线，利用的是两点确定一条直线，故此选项不合题意；C、把弯曲的公路改直，就能缩短路程，可用“两点之间线段最短”来解释，符合题意；D、砌墙时，经常在两个墙角的位置分别插一根木桩拉一条直的参照线，利用的是两点确定一条直线，故此选项不合题意；故选：C．【点睛】此题主要考查了线段的性质以及直线的性质，正确掌握相关性质是解题关键．4．（2019秋•越秀区期末）如图，从A地到B地有四条路线，由上到下依次记为路线①、②、③、④，则从A地到B地的最短路线是路线（）A．①B．②C．③D．④【思路点拨】由题意从A到B，肯定要尽量缩短两地之间的里程，就用到线段的性质：两点之间线段最短．【答案】解：根据两点之间线段最短可得，从A地到B地的最短路线是路线③．故选：C．【点睛】本题考查了线段的性质．解题的关键是掌握线段的性质：两点之间线段最短，本题比较基础．5．（2019秋•无锡期末）已知点A，B，C为平面内三点，给出下列条件：①AC＝BC；②AB＝2BC；③AC ＝BC＝AB．选择其中一个条件就能得到“点C是线段AB中点”的是（）A．①B．③C．①或③D．①或②或③【思路点拨】利用线段中点的意义：在线段上平分线段的点判定即可．【答案】解：①点C在线段AB上，且AC＝BC，则C是线段AB中点故①不符合题意；②AB＝2BC，C不一定是线段AB中点故②不符合题意；③AC＝BC＝AB，则C是线段AB中点，故③符合题意．故选：B．【点睛】本题考查了对线段中点定义的应用，注意：如果一个点把一条线段分成相等的两条线段，那么这个点就叫作这条线段的中点．6．（2020秋•铁西区期中）已知线段AB＝9，点C是AB的中点，点D是AB的三等分点，则C，D两点间距离为（）A．3B．1.5C．1.2D．1【思路点拨】根据线段中点、三等分点的概念计算即可．【答案】解：∵点C是AB的中点，AB＝9，∴AC＝CB＝AB＝5.5，∴CD＝4.5﹣3＝1.5，∴CD′＝4.8﹣3＝1.5，故选：B．【点睛】本题考查的是两点间的距离，掌握线段中点、三等分点的概念是解题的关键．7．（2020秋•江阴市期中）如图，在公路MN两侧分别有A1，A2…A7，七个工厂，各工厂与公路MN（图中粗线）之间有小公路连接．现在需要在公路MN上设置一个车站，选择站址的标准是“使各工厂到车站的距离之和越小越好”．则下面结论中正确的是（）①车站的位置设在C点好于B点；②车站的位置设在B点与C点之间公路上任何一点效果一样；③车站位置的设置与各段小公路的长度无关；④车站的位置设在BC段公路的最中间处要好于设在点B及点C处．A．①③B．③④C．②③D．②【思路点拨】可结合题意及图，直接对四个选项本身进行分析，确定对错．【答案】解：①通过测量发现车站的位置设在C点好于B点，故原来的结论正确；②车站设在B点与C点之间公路上，车站朝M方向始终有4个工厂，车站朝N方向始终有3个工厂，所以在这一段任何一点，效果一样，故原来的结论错误；③工厂到车站的距离是线段的长，和各段的弯曲的小公路无关，故原来的结论正确；④车站的位置设在BC段公路的最中间处与设在点B及点C处一样好，故原来的结论错误．故选：A．【点睛】本题考查了两点之间线段最短的问题，解题关键是具有较强的理解能力及分析能力，实际这道题根本不需要计算．二．填空题8．（2018秋•庆阳期末）如图，用圆规比较两条线段A'B'和AB的长短，则AB＜A'B'．（填“＞”“＝”或“＜”）【思路点拨】比较两条线段长短的方法有两种：度量比较法、重合比较法．根据重合比较法进行解答即可．【答案】解：由图可知，AB＜A'B'，故答案为：＜．【点睛】本题主要考查了比较线段的长短，解题的关键是正确比较线段的长短．9．（2019春•普陀区期末）如果点C在线段AB上，且点C不与点A、B重合，那么AB＞BC．（填“＞”或“＜”）【思路点拨】根据题意画出图形，根据图象即可得到结论．【答案】解：由图形可知，AB＞BC，故答案为＞．【点睛】本题考查了比较线段的大小，解题的关键是结合图形．10．（2019秋•永吉县期末）长度12cm的线段AB的中点为M，C点将线段MB分成MC：CB＝1：2，则线段AC的长度为8cm．【思路点拨】先由中点的定义求出AM，BM的长，再根据MC：CB＝1：2的关系，求MC的长，最后利用AC＝AM+MC得其长度．【答案】解：∵线段AB的中点为M，∴AM＝BM＝6cm∴x+2x＝6，解得x＝4∴AC＝AM+MC＝6+2＝8cm．【点睛】利用中点性质转化线段之间的倍分关系是解题的关键，同时灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．11．（2019秋•兰州期末）点A、B、C在直线l上，AB＝4cm，BC＝6cm，点E是AB中点，点F是BC的中点，EF＝5cm或1cm．【思路点拨】因为A、B、C三点位置不明确，分点B在A、C之间和点A在B、C之间两种情况讨论，①根据中点定义先求出BE、BF的长，BE+BF＝EF；②根据中点定义先求出BE、BF的长，BF﹣BE＝EF．【答案】解：如图，∵AB＝4cm，BC＝6cm，点E是AB中点，点F是BC的中点，∴BE＝AB＝2cm，BF＝BC＝3cm，①点B在A、C之间时，EF＝BE+BF＝2+3＝6cm；②点A在B、C之间时，EF＝BF﹣BE＝3﹣2＝1cm．故答案为：2cm或1cm．【点睛】本题利用线段中点定义，需要分两种情况讨论．12．（2020春•大丰区期中）如图，长度为12cm的线段AB的中点为M，C点将线段MB分成MC：CB＝1：2，则线段MC的长度为2cm．【思路点拨】先由中点的定义求出AM，BM的长，再根据MC：CB＝1：2的关系，求MC的长．【答案】解：∵线段AB的中点为M，∴AM＝BM＝6cm∴x+2x＝6，解得x＝3故答案为：2．【点睛】考查了两点间的距离，本题的关键是根据图形弄清线段的关系，求出AC的长．利用中点性质转化线段之间的倍分关系是解题的关键，在不同的情况下灵活选用它的不同表示方法，有利于解题的简洁性．同时灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点．13．（2020春•香坊区校级期中）已知：线段AB＝5cm，在直线AB上有一点C，并且BC＝3cm，则AC＝2cm 或8cm．【思路点拨】本题没有给出图形，在画图时，应考虑到A、B、C三点之间的位置关系的多种可能，再根据题意正确地画出图形解题．【答案】解：本题有两种情形：①当点C在线段AB上时，如图1，又∵AB＝5cm，BC＝3cm，②当点C在线段AB的延长线上时，如图2，又∵AB＝5cm，BC＝7cm，综上可得：AC＝2cm或8cm．故答案为：2cm或8．【点睛】本题考查的是两点间的距离，在画图类问题中，正确画图很重要，本题渗透了分类讨论的思想，体现了思维的严密性，在今后解决类似的问题时，要防止漏解．14．（2019秋•崇川区校级期末）已知点C在直线AB上且BC＝2AB，取AC的中点D，已知线段BD的长为6，则线段AB的长为4或12．【思路点拨】根据题意画出草图，根据线段中点的性质计算即可．【答案】解：点C在A的左边，如图，∴AD＝AC，∴AC＝AB，∴BD＝AB AB＝6，C在A的右边，∵且BC＝2AB，∵D是AC的中点，∴BD＝AD﹣AB＝AB＝6，综上所述，AB的长为4或12，故答案为：4或12．【点睛】本题考查的是两点间的距离的计算，注意数形结合思想在求两点间的距离中的应用．15．（2020春•武邑县校级月考）某公司员工分别在A、B、C三个住宅区，A区有30人，B区有15人，C，区有10人，三个区在一直线上，位置如图所示，公司的接送车打算在此间只设一个停靠点，为要使所有员工步行到停靠点的路程总和最少，那么停靠点的位置应在A区．【思路点拨】根据题意分别计算停靠点分别在A、B、C各点时员工步行的路程和，选择最小的即可求解．【答案】解：∵当停靠点在A区时，所有员工步行到停靠点路程和是：15×100+10×300＝4500m，当停靠点在B区时，所有员工步行到停靠点路程和是：30×100+10×200＝5000m，∴当停靠点在A区时，所有员工步行到停靠点路程和最小，那么停靠点的位置应该在A区．故答案为A．【点睛】本题主要考查了比较线段的长短，正确理解题意是解题的关键，要能把线段的概念在现实中进行应用，比较简单．16．（2019秋•毕节市期末）下列有四个生活、生产现象：其中可用基本事实“两点之间，线段最短”来解释的现象有②④（填序号）．①有两个钉子就可以把木条固定在墙上；②A从地到B地架设电线，总是尽可能沿着线段AB架设；③植树时，只要定出两棵树的位置，就能确定同一行所在的直线；④把弯曲的公路改直，就能缩短路程，【思路点拨】分别利用直线的性质以及线段的性质分析得出答案．【答案】解：①有两个钉子就可以把木条固定在墙上，原理：两点确定一条直线；②A从地到B地架设电线，总是尽可能沿着线段AB架设，原理：两点之间，线段最短；③植树时，只要定出两棵树的位置，就能确定同一行所在的直线，原理：两点确定一条直线；④把弯曲的公路改直，就能缩短路程，原理：两点之间，线段最短；故答案为：②④．【点睛】此题主要考查了直线的性质以及线段的性质，正确区分直线与线段的性质是解题关键．三．解答题17．（2019秋•历下区期末）如图所示，工厂A与工厂B想在公路m旁修建一座共用的仓库O，并且要求O 到A与O到B的距离之和最短，请你在m上确定仓库应修建的O点位置，同时说明你选择该点的理由．【思路点拨】根据两点之间线段最短，连接AB与直线m的交点即为所求．【答案】解：如图，连接AB交直线m于点O，则O点即为所求的点．∴OA+OB最短．【点睛】本题主要考查了线段的性质，熟记两点之间线段最短并灵活运用是解题的关键．18．（2018秋•南关区校级月考）请你判断下列两个生活情景所蕴含的数学道理．情景一：如图，小明家到学校有3条路可走，一般情况下，小明通常走第二条路，其中的数学道理是两点之间线段最短．情景二：同学们做体操时，为了保证一队同学站成一条直线，先让两个同学站好不动，其他同学依次往后站，要求目视前方只能看到各自前面的那个同学，请你说明其中的道理：两点确定一条直线．【思路点拨】根据线段的性质和直线的性质填空即可．【答案】解：情景一：如图，小明家到学校有3条路可走，一般情况下，小明通常走第二条路，其中的数学道理是两点之间线段最短；故答案为：两点之间线段最短；故答案为：两点确定一条直线．【点睛】此题主要考查了线段和直线的性质，关键是掌握定理．19．（2020秋•锦江区校级期中）如图，线段AB＝8cm，C是线段AB上一点，AC＝3cm，M是AB的中点，N是AC的中点．（1）求线段CM、NM的长；（2）若线段AC＝m，线段BC＝n，求MN的长度（m＜n用含m，n的代数式表示）．【思路点拨】（1）求出AM长，代入CM＝AM﹣AC求出即可；分别求出AN、AM长，代入MN＝AM﹣AN求出即可；【答案】解：（1）∵AB＝8cm，M是AB的中点，∴AM＝AB＝6cm，∴CM＝AM﹣AC＝4﹣3＝1（cm）；∴AM＝AB＝4cm，AN＝AC＝1.6cm，（2）∵AC＝m，BC＝n，∵M是AB的中点，N是AC的中点，∴MN＝AM﹣AN＝（m+n）﹣m＝n．【点睛】本题考查了两点之间的距离，线段中点的定义的应用，解此题的关键是求出AM、AN的长．20．（2020秋•锦江区校级期中）（1）如图1，已知点C在线段AB上，线段AC＝10厘米，BC＝6厘米，点M，N分别是AC，BC的中点，求线段MN的长度；（2）已知点C在线段BA的延长线上，点M，N分别是AC，BC的中点，设BC﹣AC＝a，请根据题意画出图形并求MN的长度；（3）在（1）的条件下，动点P、Q分别从A、B同时出发，点P以2cm/s的速度沿AB向右运动，终点为B，点Q以1cm/s的速度沿AB向左运动，终点为A，当一个点到达终点，另一个点也随之停止运动，求运动多少秒时，C、P、Q三点有一点恰好是以另两点为端点的线段的中点？【思路点拨】（1）根据中点的定义、线段的和差，可得答案；（2）根据中点的定义、线段的和差，可得答案；（3）根据线段中点的性质，可得方程，根据解方程，可得答案．【答案】解：（1）∵线段AC＝10厘米，BC＝6厘米，点M，N分别是AC，BC的中点，∴CM＝AC＝5厘米，CN＝BC＝3厘米，（2）如图，∵点M，N分别是AC，BC的中点，∴MN＝CN﹣CM＝（BC﹣AC）＝a；（3）①当0＜t≤8时，C是线段PQ的中点，得10﹣2t＝6﹣t，解得t＝4；②当5＜t≤时，P为线段CQ的中点，2t﹣10＝16﹣3t，解得t＝；③当＜t≤6时，Q为线段PC的中点，6﹣t＝3t﹣16，解得t＝；④当3＜t≤8时，C为线段PQ的中点，2t﹣10＝t﹣6，解得t＝4（舍），综上所述：t＝4或或．【点睛】本题考查了两点间的距离，利用线段中点的性质得出关于t的方程是解题关键，要分类讨论，以防遗漏．。

七年级数学上册 6.3 线段的长短比较同步练习（1）（新版）浙教版【课前热身】1.比较两条线段的长短有两种方法：一种方法是利用，另一种方法是通过来比较.2.下列图形中，可以比较长短的是 ( )A.两条射线B.两条线段 c.两条直线 D.直线与射线3.比较线段AB与线段CD的长度，结果会有种，它们是 .4.如图，线段AC的长度是线段AB，BC长度的和，记做；类似地，线段AB的长度是线段AC与BC的差，记做 .5.已知线段a，用直尺和圆规画一条线段使它等于已知线段a.【课堂讲练】典型例题1 比较下列各组线段的长度.巩固练习2 如图，比较四边形四条边的长短，并用“<’’进行连接.典型例题2 已知线段a ，利用尺规，求作一条线段AB ，使AB=2a.巩固练习2 已知线段a ，b ，用尺规画一条直线c ，使c=a+2b.【跟踪演练】一、选择题1.如图，线段AB=CD ，那么AC 与BD 的大小关系为 ( )A.AC<BDB.AC>BDC.AC=BDD.无法判断2.如图，C ，D 将线段AB 平均分成3份，点E 为CD 中点，已知BE=m ，那么AD 的长为 ( )A.mB.m 34 C.2m D.无法判断 3.为比较两条线段AB 与CD 的大小，小明将A 与C 点重合使两条线段在一条直线上，结果点B 在CD 的延长线上，则 ( )A.AB<CDB.AB>CDC.AB=CDD.以上都有可能4.如果线段AB=5cm ，BC=4cm ，且A ，B ，C 三点在同一直线上，则线段AC 的长为 ( )A.1cmB.9cmC.1cm 或9cmD.以上答案都不对二、填空题5.如下图，AC= + ，BD= － + .6.已知线段AB ，反向延长AB 到C ，使BC=3AB ，那么AB ：AC= .7.如图，点C，D，E是线段AB上的三个点，下面是关于线段CE的表示：①CE=CD+DE；②CE=BC－EB；③CE=CD+BD－AC；④CE=AE+BC－AB.其中正确的是 .(填序号)三、解答题8.小明将一根长2m的木棒和一根长1.5m的木棒捆在一起，长度为3.2m，求这两根木棒捆在一起时公共部分的长度.9.如图三角形，用直尺和圆规画出一条线段a，使a=AC+BC，然后比较a与AB的长短.10.如图，点C，D在线段AB上，CD=4cm，AB=12cm，则图中所有线段的和是多少?参考答案：【课前热身】1.圆规量出各条线段的长度2.B3.3AB>CD，AB<CD，AB=CD4.AC=AB+BC AB=AC－BC5.作图略【课堂讲练】典型例题l (1)a<6；(2)a>6；(3)a=b；(4)a<b.巩固练习l AB<BC=AD<DC.典型例题2 略巩固练习2 略【跟踪演练】1.C2.B3.B4.C5.AB BC AC AB CD6. 1 ：27.①②④ 8.L=2+1.5－3.2=0.3m 9.作图略，a>AB l0.40cm。

七年级数学上册第6章图形的初步知识6.3 线段的长短比较分层训练（新版）浙教版编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（七年级数学上册第6章图形的初步知识6.3 线段的长短比较分层训练（新版）浙教版）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为七年级数学上册第6章图形的初步知识6.3 线段的长短比较分层训练（新版）浙教版的全部内容。

6.3 线段的长短比较1．一般地，如果两条线段____________，那么我们就说这两条线段相等．2．在所有连结两点的线中，____________最短，简单地说，____________。

3．____________叫做这两点间的距离．A组基础训练1．下列说法正确的是( )A．直线可以比较长短B．直线比射线长C．线段可以比较长短D．线段可能比直线长2．已知线段AB和线段CD,使A与C重合,若点D在AB的延长线上，则（）A．AB＞CDB．AB＝CDC．AB＜CDD．无法比较AB与CD的长短3．已知A,B是数轴上的两点，AB＝2，点B表示－1，则点A表示（）A．1 B．－3 C．1或－3 D．3或14．A，B两点间的距离是指（)A．连结A，B两点间的线段长度B．过A，B两点间的直线C．连结A，B两点间的线段D．直线AB的长5．为了估计池塘两岸A，B间的距离，小明在池塘一侧选取了一点P,测得PA＝16m,PB＝12m,那么A，B间的距离不可能是（)A．5m B．15m C．20m D．30m6．如图所示，比较图中AB，AC，BC的长度，可以得出AB____________AC，AC____________BC，AB＋BC____________AC。

6.3线段的长短比较01基础题知识点1线段的长短比较1．从直观上看，下列线段中最长的是(B)A．________ B．____________________C．______ D．________________2．下列图形中，可以比较长短的是(B)A．两条射线B．两条线段C．两条直线D．直线与射线3．为比较两条线段AB与CD的大小，小明将点A与点C重合使两条线段在一条直线上，点B在CD的延长线上，则(B)A．AB＜CD B．AB＞CD C．AB＝CD D．以上都有可能4．如图，用刻度尺量一量，比较下列线段的大小：AB＝AC；CB>AC.5．比较图中以A为一个端点的线段的大小，并把它们用“＜”号连接起来．解：AB＜AC＜AD.6．如图，四条线段AB、BC、CD、DA，用圆规截取的方法比较图中的线段的大小．解：通过用圆规比较图中的四条线段，可得DA＞CD＞BC＞AB.知识点2线段的基本事实及两点间的距离7．A，B两点间的距离是(D)A．连结两点间的直线B．连结两点的线段C．连结两点间的直线的长度D．连结两点的线段的长度8．(嵊州期末)如图，从A到B有三条路径，最短的路径是③，理由是(C)A．两点确定一条直线B．过一点有无数条直线C．两点之间，线段最短D．因为直线比曲线和折线短9．如图，数轴上A，B两点之间的距离为4．10．如图，直线AB表示一条公路，公路两旁各有一个工厂，用点M、N表示，要在公路旁建一个货场，使它到两个工厂的距离之和最小，问这个货场应建在什么地方．解：图略．连结MN，与AB的交点即为所求．02中档题11．(徐州中考)点A、B、C在同一条数轴上，其中点A、B表示的数分别为－3，1，若BC＝2，则AC等于(D)A．3 B．2 C．3或5 D．2或6 12．如图，小华的家在A处，书店在B处，星期日小华到书店去买书，他想尽快赶到书店，请你帮助他选择一条最近的路线(B)A．A→C→D→B B．A→C→F→B C．A→C→E→F→B D．A→C→M→B 13．如图所示，正方形ABCD的边长为1 cm，现将正方形ABCD沿水平方向翻滚15次，那么图中点A翻滚后所在的位置与A点开始位置之间的距离为(B)A．15 cm B．16 cm C．30 cm D．45 cm14．如图，按下面语句画图．(1)分别延长线段AD和BC，使它们相交于点M；(2)延长AB至点N，使BN＝CD，再连接DN交线段BC于点P；(3)用刻度尺比较线段DP和PN的大小．解：图略．用刻度尺测量得DP＝PN.15．如图，平面上有A、B、C、D 4个村庄，为解决当地缺水问题，政府准备修建一个蓄水池，不考虑其他因素，请你画出蓄水池P的位置，使它与4个村庄的距离之和最小．解：如图所示，连结AC、BD的交点即为P点的位置．03综合题16．如图所示，有一个正方体盒子，一只虫子在顶点A处，一只蜘蛛在顶点B处，蜘蛛沿着盒子准备偷袭虫子．蜘蛛想要最快地捉住虫子，应怎样走？解：略．。