§2.9曲线的曲率

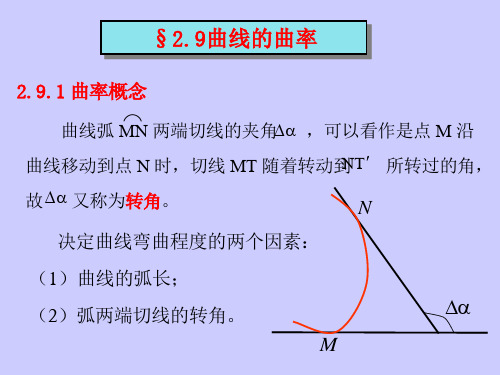
曲线的曲率推导曲线的曲率是曲线局部上的一种本质性质，它描述了曲线的弯曲程度。

在工程、物理、生物学等领域，曲率的概念都有着广泛的应用。

在本文中，我们将从几何和数学角度出发，详细介绍曲线的曲率的定义、性质以及推导过程。

一、曲率的定义假设我们有一条平面曲线C，并以P为曲线上的一个点，同时过该点P可以画出曲线的切线L。

记曲线C在点P处的曲率为k，则有如下公式：k = |\frac{d\boldsymbol{T}}{ds}|其中，T是曲线在点P处的切向量，s为曲线上从起点到点P的弧长，d\boldsymbol{T}/ds为切向量在弧长方向的导数。

此处符号“| |”表示向量的模长。

从上述定义中可以看出，曲率k刻画的是曲线在局部上的弯曲情况。

当k值越大时，曲线的弯曲程度越大；反之，当k值越小或为0时，曲线的弯曲程度越小或没有弯曲。

二、曲率的推导过程现在，我们来推导一下曲率的公式。

在P处切线L上选取一个点A，并以AP为半径画出一个圆弧BC，其中B和C分别是圆弧上AP两侧的点。

则有如下关系：AC = 2APsin(\theta/2)其中，\theta是圆弧BC对应的圆心角的大小，即∠BPC。

又有：\boldsymbol{T} = \frac{\boldsymbol{AP}}{AP}此处的AP是向量AP的模长。

考虑将\boldsymbol{AP}写成曲线上的表示，即\boldsymbol{AP} = s\boldsymbol{T}。

因此，我们可以得到：AC = 2s\sin(\theta/2)根据三角函数的定义，可以得到：\frac{\mathrm{d}\theta}{\mathrm{d}s} =\frac{2}{AC}\cdot\frac{\mathrm{d}AC}{\mathrm{d}s}将上述两式相乘并代入之前的定义公式中，得到：k = \frac{1}{s}\cdot\frac{\mathrm{d}\theta}{\mathrm{d}s} = \frac{\dot{\boldsymbol{T}}}{s}其中，符号“·”表示向量的点积，\dot{\boldsymbol{T}}是切向量在固定坐标系下的导数（即加速度）。

曲线的曲率计算公式
首先，我们来看曲线的参数方程表示，假设曲线由参数方程 x = f(t) 和 y = g(t) 给出，其中 t 是参数。

曲线上任意一点的曲率可以用以下公式来计算：
\[ k = \frac{|f'(t)g''(t) g'(t)f''(t)|}{(f'(t)^2 +
g'(t)^2)^{3/2}} \]
在这个公式中，f'(t) 和 g'(t) 分别表示 x 和 y 对参数 t 的导数，而 f''(t) 和 g''(t) 则分别表示它们的二阶导数。

这个公式可以用来计算曲线在参数 t 处的曲率。

另外，如果曲线由函数表达式 y = f(x) 给出，那么可以使用以下公式来计算曲线在某一点的曲率：
\[ k = \frac{|f''(x)|}{(1 + (f'(x))^2)^{3/2}} \]
在这个公式中，f'(x) 和 f''(x) 分别表示 y 对 x 的一阶和二阶导数。

这个公式适用于描述用函数表达式给出的曲线的曲率。

需要注意的是，曲率描述了曲线在某一点处的弯曲程度，而曲线可能在不同点具有不同的曲率。

因此，为了全面地描述曲线的曲率特性，需要对曲线上的各个点分别计算曲率。

总之，曲线的曲率计算公式可以根据曲线的参数方程或者函数表达式来推导，通过计算导数和二阶导数，然后代入相应的公式来求得曲率。

这些公式在实际问题中具有重要的应用，能够帮助我们理解和分析曲线的性质。