高数c1期末试卷

高等数学c1期末考试试卷和答案**高等数学C1期末考试试卷**一、选择题（每题4分，共20分）1. 函数f(x)=x^2-4x+3的零点个数为（）。

A. 0B. 1C. 2D. 32. 极限lim(x→0) (1-cosx)/x的值为（）。

A. 0B. 1C. -1D. 23. 以下哪个函数是偶函数（）。

A. f(x) = x^3B. f(x) = x^2C. f(x) = x^2 + xD. f(x) = x^2 - x4. 以下哪个积分是发散的（）。

A. ∫(0,1) 1/x dxB. ∫(0,1) x dxC. ∫(0,1) 1/√x dxD. ∫(0,1) x^2 dx5. 以下哪个级数是收敛的（）。

A. 1 + 1/2 + 1/4 + 1/8 + ...B. 1 - 1/2 + 1/3 - 1/4 + ...C. 1 + 1/2^2 + 1/3^2 + 1/4^2 + ...D. 1 + 1/2 + 1/3 + 1/4 + ...二、填空题（每题4分，共20分）6. 函数f(x)=x^3-3x的导数为______。

7. 函数f(x)=e^x的不定积分为______。

8. 函数f(x)=ln(x)的不定积分为______。

9. 函数f(x)=x^2+3x+2的极值点为______。

10. 函数f(x)=x^3-3x的拐点为______。

三、计算题（每题10分，共30分）11. 计算极限lim(x→∞) (x^2-3x+2)/(x^2+x-2)。

12. 计算定积分∫(0,2) (x^2-2x+1) dx。

13. 计算二重积分∬(D) x^2+y^2 dA，其中D是由x^2+y^2≤1所定义的区域。

四、证明题（每题10分，共20分）14. 证明函数f(x)=x^3在(-∞,+∞)上是增函数。

15. 证明对于任意x∈(0,1)，有ln(x)<x-1。

**高等数学C1期末考试试卷答案**一、选择题1. C2. B3. B4. A5. C二、填空题6. 3x^2-37. e^x + C8. x*ln(x) - x + C9. x=-3/2 或 x=110. x=0 或x=±√3三、计算题11. 极限lim(x→∞) (x^2-3x+2)/(x^2+x-2) = 1。

《高等数学Ⅰ（一）》课程期末考试试卷（模拟卷C ）一、选择题（每题4分，共40分） 1．设函数()f x 在0x 处可导，则极限000()()lim2h f x h f x h h→+−−=A ．0()f x ′B ．02()f x ′C ．01()2f x ′D ．20[()]f x ′2．函数11(e e)tan ()(e e)xxx f x x +⋅=−在区间[π,π]−上的第一类间断点是A ．0B ．1C．．π23．设sin 20()sin d xf x t t =∫，34()g x x x =+，则当0x →时，()f x 是()g x 的A ．等价无穷小B ．同阶但非等价无穷小C ．高阶无穷小D ．低阶无穷小4．设()d arcsin xf x x x C =+∫，则1d ()x f x =∫A ．3223(1)4x C −−+B ．2233(1)4x C −+C ．3221(1)3x C −−+D ．2232(1)3x C −+5．微分方程3232e x y y y x ′′′−+=−有特解形式 A ．e x ax b + B ．e x ax b c ++ C ．e x ax bx + D ．e x ax b cx ++6．已知函数()f x 在[0,1]上二阶可导，且10()d 0f x x =∫，则A ．当()0f x ′<时，102f<B ． 当()0f x ′′<时，102f<C ．当()0f x ′>时，102f<D ． 当()0f x ′′>时，102f<7．已知1()(12ln )f x x x ′=+，且(1)1f =，则()f x =A ．ln |12ln |1x ++B ．1ln |12ln |12x ++C ．1ln |12ln |2x +．2ln |12ln |1x ++8．把24y ax =及00(0)xx x >所围成的图形绕x 轴旋转，所得旋转体的体积V =A ．20πaxB ．02πaxC ．30πaxD ．202πax9．设π40ln sin d I x x =∫，π40ln cos d J x x =∫，π40ln cot d K x x =∫，则 A ．I J K << B ．I J K >> C ．J I K << D ．J I K >>10．函数()f x 为连续函数，则21d ()d d f x t t x +=∫ A ．0B ．(2)(1)f f −C ．(2)(1)f x f x +−+D ．(2)f x +二、填空题（每题4分，共24分）1．极限30tan sin lim ln(1)x x xx →−=+___________．2．设函数()f x 连续，20()()d x x xf t t ϕ=∫，若(1)1ϕ=，(1)5ϕ′=，则(1)f =___________．3．已知2121x y f x − = +，2()arctan f x x ′=，则0d x y ==___________．4．定积分41220201sin 3||d 1x x x x x x − += +∫___________．5．广义积分2=∫___________．6．设()d ()f x x F x C =+∫，则(2)d f x x =∫___________．三、解答题（每题6分，共36分）1．设函数()y f x =是由方程21e yx y −+=所确定的隐函数，求22d d x yx=．2． 由3y x =，2x =，0y =所围成的平面图形分别绕x 轴和y 轴旋转一周，计算所得几何体的体积．3．计算定积分．（1）10x x ∫．（2）x ∫．4．求微分方程d 24d yxy x x=−+满足(0)0y =的特解．5．证明：当0x >时，arctan ln(1)1xx x+>+．6．设函数()f x 在[,]a b 上连续，在(,)a b 内具有一阶和二阶导数．证明：若在(,)a b 内()0f x ′′>，则对12[,]x x a b ∀∈，有12121212()()3333f x x f x f x +<+ ．《高等数学Ⅰ（一）》课程期末考试试卷（模拟卷C ）解答参考一、选择题（每题4分，共40分） 1．设函数()f x 在0x 处可导，则极限000()()lim2h f x h f x h h→+−−=A ．0()f x ′B ．02()f x ′C ．01()2f x ′D ．20[()]f x ′答案 A 解析 000000000()()()()()()1limlim ()22h h f x h f x h f x h f x f x h f x f x h h h →→+−−+−−−′=+= −，故本题选A ． 2．函数11(e e)tan ()(e e)xxx f x x +⋅=−在区间[π,π]−上的第一类间断点是A ．0B ．1C．．π2答案 A解析 在区间[π,π]−上()f x 的间断点有0，π2±，显然，π2±均为第二类间断点（无穷间断点），下面考察0x =．因1100e e e e lim ()lim lim 1e e e e txt t x x x f x ++→+∞→→++===−−，1100e e e elim ()lim lim 1e e e et xt t x x x f x −−→−∞→→++===−−−， 所以0x =是函数的第一类间断点（跳跃间断点），故本题选A ． 3．设sin 20()sin d xf x t t =∫，34()g x x x =+，则当0x →时，()f x 是()g x 的A ．等价无穷小B ．同阶但非等价无穷小C ．高阶无穷小D ．低阶无穷小答案 B 解析 因sin 2222043323232000000sin d ()sin(sin )sin 11lim lim limlim lim lim ()434343433xx x x x x x t t f x x x x g x x x x x x x x x x →→→→→→======+++++∫， 所以当0x →时，()f x 是()g x 的同阶但非等价无穷小，故选B 项．4．设()d arcsin xf x x x C =+∫，则1d ()x f x =∫A ．3223(1)4x C −−+B ．2233(1)4x C −+C ．3221(1)3x C −−+D ．2232(1)3x C −+答案 C解析 因为()d arcsin xf x x x C =+∫，两边求导得()xf x =所以1()f x =．因此3222111d )(1)()23x x x x C f x =−−=−−+∫∫，5．微分方程3232e x y y y x ′′′−+=−有特解形式 A ．e x ax b +B ．e x ax b c ++C ．e x ax bx +D ．e x ax b cx ++答案 D解析 原方程对应齐次方程的特征方程为21232012r r r r −+=⇒==，．考虑2112323e e x x y y y x y ax b c c ′′′−+⇒+++，考虑2112322e e e e x x x x y y y y cx c c ′′′−+=−⇒=++，根据线性微分方程的叠加原理可知，原方程通解为212e e e x x x ax b cx c c ++++，故选D 项．6．已知函数()f x 在[0,1]上二阶可导，且10()d 0f x x =∫，则A ．当()0f x ′<时，102f<B ． 当()0f x ′′<时，102f<C ．当()0f x ′>时，102f<D ． 当()0f x ′′>时，102f<答案 D思路分析 条件中出现二阶可导，可尝试泰勒公式．解析 将()f x 泰勒展开：21111()()2222f x f f x f x ξ ′′′=+−+−  ，(0,1)ξ∈，所以 21101111()d ()d 2222f x x ff x f x x ξ′′′=+−+− ∫∫ 21110001111d d ()d 2222f x f x x f x x ξ ′′′+−+−  ∫∫∫210110()d 022f f x x ξ′′++−=∫，所以当()0f x ′′>时，102f< ，故本题选D ．7．已知1()(12ln )f x x x ′=+，且(1)1f =，则()f x =A ．ln |12ln |1x ++B ．1ln |12ln |12x ++C ．1ln |12ln |2x +．2ln |12ln |1x ++答案 B 解析 因为111111()(1)()d (1)d 1d(12ln )(12ln )212ln xx x f x f f t t f t t t t t=+=+=++++∫∫∫ 1111[ln(12ln )]ln |12ln |122x t x =++=++，8．把24y ax =及00(0)xx x >所围成的图形绕x 轴旋转，所得旋转体的体积V =A ．20πaxB ．02πaxC ．30πaxD ．202πax答案 D解析 由旋转体体积公式可得022πd π4d 2πx x V y x ax x ax ==⋅=∫∫，故本题选D ． 9．设π40ln sin d I x x =∫，π40ln cos d J x x =∫，π40ln cot d K x x =∫，则 A ．I J K <<B ．I J K >>C ．J I K <<D ．J I K >>答案 A解析 当π0,4x∈时，1cos sin 0x x >>>，cos cot cos sin x x x x =>，所以I J K <<，故本题选A ．10．函数()f x 为连续函数，则21d ()d d f x t t x +=∫ A ．0 B ．(2)(1)f f − C ．(2)(1)f x f x +−+ D ．(2)f x +答案 C解析 令u x t =+，则2211()d ()d x x f x t t f u u +++=∫∫，所以2211d d ()d()d (2)(1)d d x x f x t t f u u f x f x x x +++==+−+∫∫， 故本题选C ．二、填空题（每题4分，共24分）1．极限30tan sin lim ln(1)x x xx →−=+___________．答案12解析 方法一 由泰勒公式知，当0x →时，33tan ()3x x x o x =++，33sin ()6x x x o x =−+，故3333331tan sin ()()()362x x x x x o x x o x x o x −=++−−+=+ ，于是可知31tan sin ~2x x x −，又33ln(1)~x x +，故 333001tan sin 12lim lim ln(1)2x x xx x x x →→−==+． 方法二 2332200001tan sin sin (1cos )1cos 12lim lim lim lim ln(1)cos 2x x x x xx x x x x x x x x x →→→→−−−====+⋅． 2．设函数()f x 连续，2()()d x x xf t t ϕ=∫，若(1)1ϕ=，(1)5ϕ′=，则(1)f =___________．答案 2解析 由题可知20()()d x x x f t t ϕ=∫，220()()d 2()x x f t t x f x ϕ′=+∫，故1(1)()d 2(1)f t t f ϕ′=+∫，1(1)()d 1f t t ϕ==∫， 则(1)(1)2(1)5f ϕϕ′=+=，所以(1)2f =．3．已知2121x y f x − = +，2()arctan f x x ′=，则0d x y ==___________．答案 πd x解析 令21212121x u x x −==−++，故 2d 4d (21)u x x =+， 当0x =时，1u =−，所以000d d d ()(1)πd d d x x x y u u f u f xx x ===′′=⋅=−⋅= ，因此0d πd x y x ==．4．定积分41220201sin 3||d 1x x x x x x − += +∫___________． 答案32解析 441112220202020111sin sin 3||d d 3||d 11x x x x x x x x x x x x x −−− +=+ ++∫∫∫． 第一个积分被积函数是奇函数，积分区间对称，故积分值为0；第二个积分被积函数为偶函数，积分区间对称，所以14112342020100sin 333||d 23d 2142x x x x x x x x x − +==⋅= + ∫∫． 5．广义积分2=∫___________．答案 π思路分析 该积分为无界函数的反常积分，且有两个瑕点，于是由定义，当且仅当2∫3∫均收敛时，原反常积分才收敛．解析 因为32222π[arcsin(3)]lim arcsin(3)2xx x++→=−=−−=∫∫，43334π[arcsin(3)]lim arcsin(3)2xx x−−→−=−=∫∫，所以2πππ22=+=∫．6．设()d()f x x F x C=+∫，则(2)df x x=∫___________．答案1(2)2F x C+解析令2t x=，则111(2)d()d()(2)222f x x f t t F t C F x C==+=+∫∫．三、解答题（每题6分，共36分）1．设函数()y f x=是由方程21e yx y−+=所确定的隐函数，求22ddxyx=．解将0x=代入方程21e yx y−+=解得0y=．对方程21e yx y−+=两边求导得2e yx y y′′−=①将0x=，0y=代入①得(0)0y′=．式①两端再求导得22e e()y yy y y′′′′′−=+②将0x=，0y=，(0)0y′=代入②得22d1dxyx==．2．由3y x=，2x=，0y=所围成的平面图形分别绕x轴和y轴旋转一周，计算所得几何体的体积．解所求体积为222600128ππdπd7xV y x x x===∫∫．1258882228333000564ππ28πd32ππ()d32ππd32ππ[]35yV x y y y y y y=⋅⋅−=−=−=−⋅=∫∫∫．或用柱壳法计算2224500164π2πd2πd2π55yV xy x x x x====∫∫．3．计算定积分．（1）1x x ∫．解令sinx t=，则ππ1424222000sin cos d sin(1sin)dx x t t t t t t=−∫∫∫ππ46220031π531ππsin d sin d422642232t t t t=−=⋅⋅−⋅⋅⋅=∫∫．注这里用到了华里士公式ππ22001321,123sin d cos d131π,222n nnn n nn nI x x x xn n nn n−−××××−===−−××××−∫∫为大于的奇数为正偶数．（2）x∫．解令tanx t=，则πππ2444000sec1ππd d csc d(1tan)sec sin cos44tx t t t tt t t t==++++ ∫∫∫π4ππln csc cot44t t+−+=．4．求微分方程d24dy xy xx=−+满足(0)0y=的特解．解易知该方程对应的齐次方程d2dy xyx=−的通解为2e xy C−=，设原方程的解为2()e xy u x−=，代入原方程整理得2()4e xu x x′=，两端积分得2()2e xu x C=+，进而可得原方程的通解为22e xy C−=+．又因为(0)20y C=+=，故2C=−．所以满足条件的特解为222e xy−=−．5．证明：当0x>时，arctanln(1)1xxx+>+．证令()(1)ln(1)arctanf x x x x=++−，[0,)x∈+∞．显然函数()f x在[0,)x∈+∞时可导，且7 21()ln(1)10(0)1f x x x x ′=++−>>+， 所以函数()f x 在[0,)+∞上单调增加，故()(0)0f x f >=，从而 arctan ln(1)1x x x+>+． 6．设函数()f x 在[,]a b 上连续，在(,)a b 内具有一阶和二阶导数．证明：若在(,)a b 内()0f x ′′>，则对12[,]x x a b ∀∈，有12121212()()3333f x x f x f x +<+ ． 证 设12x x <．令0121233x x x =+，根据拉格朗日中值定理可得，110202(,)(,)x x x x ξξ∃∈∈，，使得 011011212()()()()()()3f x f x f x x f x x ξξ′′−=−=−， 202012211()()()()()()3f x f x f x x f x x ξξ′′−=−=−． 于是01202112211222[()()]2[()()]()[()()]()()()033f x f x f x f x x x f f x x f ξξξξξ′′′′−−−=−−=−−<． 故0123()()2()0f x f x f x −−<，所以01212()()()33f x f x f x <+，即得 12121212()()3333f x x f x f x +<+ ．。

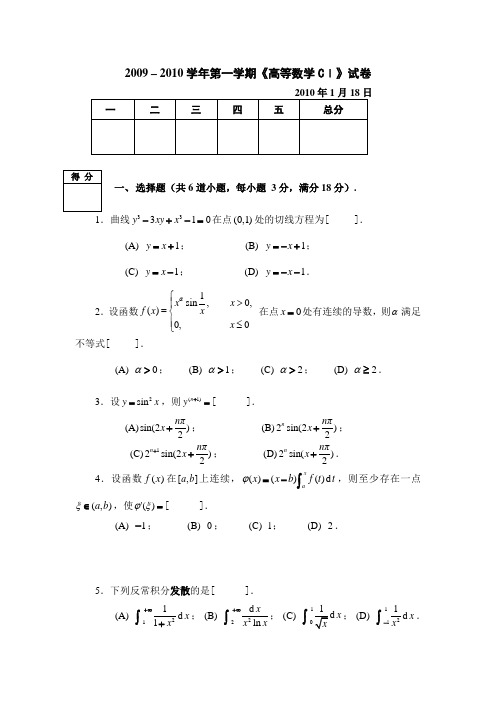
2009 – 2010学年第一学期《高等数学C Ⅰ》试卷2010年1月18日一 二 三 四 五 总分一、 选择题（共6道小题，每小题 3分，满分18分）.1．曲线33310y xy x -+-=在点(0,1)处的切线方程为[ ]．(A) 1y x =+； (B) 1y x =-+；(C) 1y x =-； (D) 1y x =--．2．设函数1sin ,0,()0,x x f x x x α⎧>⎪=⎨⎪≤⎩ 在点0x =处有连续的导数，则α满足不等式[ ]．(A) 0α>； (B) 1α>； (C) 2α>； (D) 2α≥．3．设2sin y x =，则(1)n y +=[ ]．(A)sin(2)2n πx +； (B)2sin(2)2n n πx +； (C)12sin(2)2n n πx ++； (D)2sin()2n n πx +．4．设函数()f x 在[,]a b 上连续，()()()d xax x b f t t ϕ=-⎰，则至少存在一点(,)a b ξ∈，使()'ϕξ=[ ]．(A) 1-； (B) 0； (C) 1； (D) 2．5．下列反常积分发散的是[ ]．(A)211d 1x x+∞+⎰； (B)22d ln xx x+∞⎰； (C)101d x x⎰； (D)1211d x x -⎰．得 分6．若函数()y f x =有01()2f x '=，则当0x ∆→时，()f x 在点0x x =处微分d y 是[ ]．（A ）与x ∆等价的无穷小;（B ）比x ∆低阶的无穷小;（C ）比x ∆高阶的无穷小; （D ）与x ∆同阶的无穷小，但不是等价的无穷小.二、填空题（共6小题，每小题 3分，满分18分）.1．设 0tan sin 1lim 2p x x x x →-=，则常数p = ___ ____．2．函数sin ()e x xf x =的第一类间断点为x =____ ____．3．设函数()f x 连续且0()lim1x f x x→=，则(0)'=f ___ ___． 4．设函数()f x 连续，0()()()d x F x x t f t t =-⎰，则d ()F x =___ __． 5．曲线2sin 3cos x xy x x+=+的水平渐近线为y =___ __．6．设()f x 在[0,)+∞上连续，且230()d 1x f t t x =+⎰，则(2)f =___ __．.三、解答题（共6道题，每小题7分，满分42分）. 1．求 21ln(1)0arcsin lim x x x x +→⎛⎫ ⎪⎝⎭．得 分得 分2．设()f x 在点1x =处有连续的导数，且(1)1'=f ，求201dlim (cos 2)d x f x x x→．3．已知(sin ),(1cos ),x a t t y a t =-⎧⎨=-⎩ 求22d d yx ．4．计算21e d x x -⎰．5．设e ,0,()1,10,1cos x x f x x x -⎧≥⎪=⎨-<<⎪+⎩ 求41(2)d -⎰f x x ．6．求函数24(1)()2x f x x+=-的极值，并求曲线()y f x =的拐点．四、 （本题满分10分）设曲线2e -=xy ，过原点作其切线．求 (1) 切线方程；(2)由上述曲线、切线及y 轴围成的平面图形的面积；(3) 由上述曲线、切线及y 轴围成的平面图形绕x 轴旋转所生成的旋转体的体积．得 分五、（共2道题，每小题6分，满分12分）1．某商品需求量Q是价格p的单调减少函数：()Q Q p=．其需求弹性222192ppη=>-，()R R p=为总收益函数．（1）证明()d1dRQpη=-．（2）求6=p时，总收益对价格的弹性．得分2．设()f x 在[,]a b 上连续(0)a >，在(,)a b 内可导，证明：在(,)a b内必存在,ξη，使得()()2ξηη+''=a bf f ．。

拟题学院（系）：数理学院 适用专业： 机专、自专、营专等相关专业 2012-2013 学年 1 学期 高等数学C1 （B 卷） 题库标准答案（答案要注明各个要点的评分标准）一、填空题（每小题3分，共15分）1．1x ≥-； 2．2x ； 3．2； 4．2； 5．0二、选择题（每小题3分，共15分）1．B ； 2．D ； 3．D ； 4．C ； 5．B三、计算题（每小题8分，共24分）1. 解：20(1)lim2xx t dtx x→++⎰()()02(1)lim2xx t dtx x →'+='+⎰ ---------------------------------------2分01lim22x x x →+=+ ---------------------------------------5分12=--------------------------------------8分 2. 解：cos ,0()1,0x x f x x x <⎧=⎨+≥⎩ 当 0<x 时，()sin .f x x '=-当0>x 时，()(1)1f x x ''=+= ---------------------------------------2分又()()()000lim++→-'=-x f x f f x11lim 10x x x +→+-==- 拟 题 人： 杨树国书写标准答案人： 杨树国()()()001lim 0--→-'=-x f x f f xcos 1lim 00x x x -→-==- --------------------4分由()()00f f +-''≠，得：(0)f '不存在 --------------------5分 所以-sin , 0,() 1, 0.x x f x x <⎧'=⎨>⎩--------------------8分3．解： 22tx t t y e⎧=+-⎨=⎩ 2()(2)t dy e dx t t '='+- --------------------3分 21te t =+ --------------------8分 四、计算题（每小题10分，共20分）1．解：(sin )x x x e dx +⎰xxdcosx e dx =-+⎰⎰cos cos x x x xdx e =-++⎰ --------------------5分cos sin x x x x e C =-+++ --------------------10分2．解：cos 2xdx π⎰01sin 22d x π=⎰ --------------------5分 01sin 202x π== --------------------10分五、计算题（10分）1. 求曲线22y x x =+上横坐标为0x =的点处的切线方程和法线方程； 解：当0=x 时，0=y 。

同济大学 2019-2020 学年第一学期高等数学 C(上)期终试卷一. 填空题( 4'⨯6 = 24' )13 1. 已知当 x → 0 时, (1+ ax 2 )3-1与cos x -1是等价无穷小, 则a = - .22. lim( n - 2)n=e -3n →∞ n +13. 已知 f '(3) = 2 , 则lim f (3 - h ) - f (3)= -1 .h →0 2hx4. 曲线 y =⎰(t -1)(t - 2)dt 在点(0, 0) 处的切线方程是y = 2x5. 已知 f '(x ) =2x 则 df (x 2) =dx 36. 若函数 f (x ) = a ln x + bx 2+ x 在 x =1及 x = 2 取得极值, 则a = - 3 , b = - 126二． 计算题( 5'⨯9 = 45' )e x - e - x - 2x1. 求 limx →0 x - sin x[ 2 ]2. 求 lim(1- cot 2 x ) [ 2]x →0x 233. 求 lim(1- 2)5 x -2[ e -10 ]x →∞x4. 设 y = ln(cos 2x +, 求 y ' [ y ' -sin 2x ) ]5. 设y =1- x , 求 1+ xy (n )[ y(n ) =(-1)n 2n !(1+ x )n +1 ]6. 设 y = (tan x )sin x, 求 dy [ y ' = (tan x )sin x(cos x ln tan x + sec x ) ]9. 求,[ 2a 2 - x 2dt = 7. 求a + xdx a - x[ a a rcsinx- ac ]8. 求 ⎰x arctan xdx[ 1x 2arctan x - x + 1arctan x + c ]22 2⎰adx= ⎰πcos t πx +0 sin t + c os t 4三. 解答题( 31' )1. ( 7' )求曲线 xy + 2 ln x = y 4 在点(1, 1) 处的切线与法线方程[ y ' (1, 1) = 1⇒ y = x ;x + y = 2 ]sin t x2. ( 7' )设 f (x ) = lim( )sin t -sin x , 求 f (x ) 的间断点及其类型t →x sin xx[ f (x ) = esin x⇒ x = 0 可去;x = k π (k ≠ 0) 第二类]3. ( 7' )求正数a , 使 axdx1 +∞xdx , 并说出它的几何意义⎰(1+ x 2 )22 ⎰0 (1+ x 2 )2[a xdx = 1(1-1),+∞xdx = 1⇒ a = 1 ]⎰(1+ x 2 )221+ a 2⎰(1+ x 2 )2 24. (10' )设曲线 y = ax 2 (a > 0, x ≥ 0) 与 y = 1- x 2 交于点 A , 过坐标原点O 和点 A 的直线与曲线 y = ax 2围成一个平面图形. 问: a 为何值时, 该图形绕 x 轴旋转一周所得的旋转体体积最大.ax 1ax 2 - 5[ OA : y = , v = π ⎰ 1+a [( )2 - (ax 2 )2 ]dx = π a 2 (1+ a ) 21+ a 0 1+ a15 = a 2 - x 2 ]⇒V ' =0 ⇒a = 4 ⇒V " < 0 ]。

练习一一、选择题（在每小题的四个备选答案中选出一个正确答案，并将正确答案的序号填入题后的括号内。

（每小题3分，共24分 ） 1. 函数xx f -=11arctan )(当1→x 时的极限是( C ). (A)2π (B) 2π- (C) 0 (D) 不存在. 2. 若c x F dx x f +=⎰)()(，若0a ≠，则=+⎰xdx b ax f )(2( ). (A)cb ax F ++)(2(B))(212b ax F a+ (C)c b ax F a++)(212 (D)c b ax aF ++)(22.3. 若函数 ()⎩⎨⎧>-≤=0)1(02x x b x e x f ax 在x =0处可导，则( ). (A) 1==b a (B) 0,1==b a (C) 1,0==b a (D) 1,2-=-=b a .4. 函数11x x e y e +=- 是( ).(A)偶函数 (B)奇函数 (C)非奇非偶函数； (D)既是奇函数又是偶函数.5. 设函数)(x f 在点a x =处可导，则=--+→xx a f x a f x )()(lim( ).(A) )(2a f ' (B) )(a f ' (C) )2(a f ' (D) 0. 6. 已知x y sin =，则=)10(y( )。

(A) x sin (B) x cos (C) x sin - (D) x cos -. 7. 若()f x 和()g x 均为区间I 内的可导函数,则在I 内,下列结论中正确的是( ). （A ）若'()'()f x g x =,则 ()()f x g x = （B ）若()()f x g x >,则'()'()f x g x > （C ）若'()'()f x g x =,则 ()()f x g x c =+ （D ）若'()'()f x g x >,则()()f x g x >. 8.若()(1)(2)(3)f x x x x x =---,则方程'()0f x =根的个数为( ). （A ） 0个 (B) 1个 (C) 2个 (D) 3个.二、填空题（每题3分，共18分。

高数c下学期期末考试试题及答案一、选择题（每题5分，共30分）1. 若函数f(x)在点x=a处可导，则以下说法正确的是：A. f(x)在x=a处连续B. f(x)在x=a处不可导C. f(x)在x=a处不连续D. f(x)在x=a处的导数为0答案：A2. 极限lim(x→0)(sin x/x)的值为：A. 0B. 1C. -1D. 2答案：B3. 函数f(x)=x^3-6x^2+11x-6的导数为：A. 3x^2-12x+11B. x^3-6x^2+11C. 3x^2-12x+6D. 3x^2-6x+11答案：A4. 定积分∫(0,1)x^2dx的值为：A. 1/3B. 1/2C. 1D. 2答案：B5. 若级数∑(n=1 to ∞)(1/n^2)收敛，则以下级数收敛的是：A. ∑(n=1 to ∞)(1/n)B. ∑(n=1 to ∞)(1/n^3)C. ∑(n=1 to ∞)(1/n^4)D. ∑(n=1 to ∞)(1/n^5)答案：C6. 函数y=e^x的不定积分为：A. e^x + CB. ln(x) + CC. x * e^x + CD. 1/e^x + C答案：A二、填空题（每题5分，共20分）1. 函数f(x)=x^2-4x+4的最小值为________。

答案：02. 曲线y=x^3在x=1处的切线斜率为________。

答案：33. 定积分∫(0,2)x dx的值为________。

答案：44. 若函数f(x)=ln(x)，则f'(x)=________。

答案：1/x三、解答题（每题10分，共50分）1. 求函数f(x)=x^3-3x+1在x=2处的导数。

答案：f'(x)=3x^2-3，所以f'(2)=9。

2. 计算定积分∫(1,2)(2x-1)dx。

答案：[(2x^2-x)](1,2) = (2*2^2-2) - (2*1^2-1) = 4。

3. 求级数∑(n=1 to ∞)(1/n^2)的和。

同济大学2021-2021学年第二学期高等数学C(下)期终试卷一、选择题.〔此题共有5小题，每题3分，总分值15分，每题只有一个正确答案〕1、以下微分方程为一阶线性方程的是：【D】y A:yy'1；B:y'e1；C:2y'yy；D:2y'yx。

2、假设向量a2,1,0,b1,1,2,c0,1,2k，且abc0，那么k【B】A；B:2；C:3；D:4。

:13、假设向量a1,2,k在向量b2,1,2上的投影为2，那么k【C】A；B:2；C:3；D:4。

:1xx 4、设ecoszxyy，那么zy【A】A:xx2esinyy ；B:xx1esin2yy ；C:12yxesin y ；D:xx2esinyy 。

5、交换二次积分的次序：22yd,dyfxyx【A】20y4xA:dxfx,ydy；x2x4Bx2fxyy；:d,dBx2fxyy；0x22x Cxfxyy；:d,d20x22x Dxfxyy。

:d,d0x二、填空题〔此题共4小题，每题4分，总分值16分，只需将答案填入空格〕6、微分方程y"2y'2y0的通解为y x ecossincxcx.127、设向量a2,3,2,b2,3,0，假设xax,b，且x7。

那么向量x3,2,6。

8、空间直线2x4yz03x y2z9在xoy面上的投影直线方程为：7x9y9z0。

9、设函数zf2xy，其中函数f具有二阶导数，那么2zxy2f"2xy。

1三、解答题〔此题共有6小题，每题7分，总分值42分，需写出具体解题过程〕10、求微分方程：dyxydx2 1的通解。

[1d ydx2yxyxc]tanln11、一平面过原点及点6,3,2，且与另一平面4xy2z8垂直，求平面方程。

[n6,3,24,1,24,4,62x2y3z0]12、函数zzx,y由zlnz1sinxy所确定，求d z。

[z1cosxydzydxxdyz]13、求函数22fx,y4xyxy的极值点。