递归算法与递归程序

C语言常用算法程序汇总C语言是一门广泛应用于计算机编程的语言，具有较高的效率和灵活性。

在C语言中，常见的算法程序包括排序算法、查找算法、递归算法等等。

以下是一些常用的C语言算法程序的汇总：1.排序算法：-冒泡排序：通过多次迭代比较相邻元素并交换位置，将最大的元素逐渐移动到正确的位置。

-插入排序：将待排序的元素与已排序的部分依次比较并插入到正确的位置。

-选择排序：每次从待排序的元素中选择最小的元素并与已排序的部分交换位置。

-快速排序：通过选择一个基准元素，将数组划分为两个子数组进行递归排序。

2.查找算法：-顺序查找：逐个比较数组中的元素，直到找到目标元素或到数组末尾。

-二分查找：通过比较目标元素与数组中间元素的大小，逐步缩小范围，直到找到目标元素。

-哈希查找：通过散列函数将目标元素映射到哈希表的索引位置进行查找。

3.递归算法：-阶乘：通过递归调用自身计算一个正整数的阶乘。

-斐波那契数列：通过递归调用自身计算斐波那契数列的第n个数。

-二叉树遍历：通过递归调用自身遍历二叉树的各个节点。

4.图算法：- 最短路径算法：如Dijkstra算法和Floyd算法，用于计算图中两个节点之间的最短路径。

-拓扑排序：通过对有向无环图进行排序，使得所有的边从排在前面的节点指向排在后面的节点。

- 最小生成树：如Prim算法和Kruskal算法，用于找到图中连接所有节点的最小子树。

5.动态规划：-最长公共子序列：通过寻找两个字符串中的最长公共子序列，解决字符串匹配问题。

-背包问题：通过动态规划解决在给定容量下选取物品使得总价值最大的问题。

-最大子序列和：通过动态规划解决一个数组中选取连续子序列使得和最大的问题。

以上只是一些C语言中常用的算法程序的汇总，实际上，还有很多其他的算法，如逆波兰表达式、霍夫曼编码、最小割等等。

通过学习这些算法，可以更好地理解C语言的应用和开发。

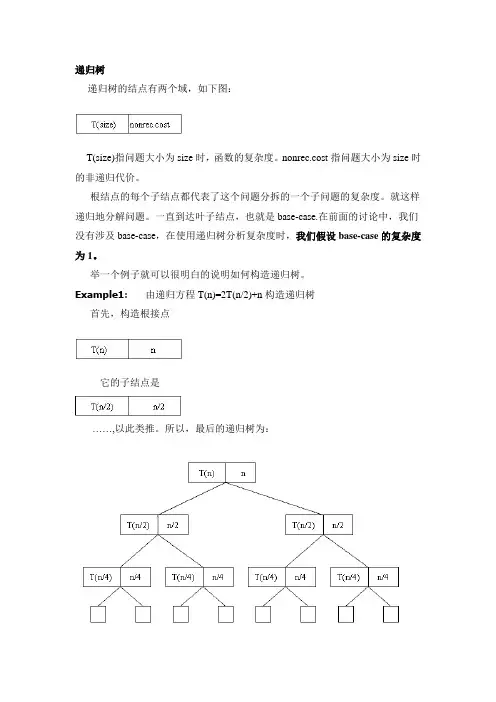
递归树
递归树的结点有两个域，如下图：
T(size)指问题大小为size时，函数的复杂度。

nonrec.cost指问题大小为size时的非递归代价。

根结点的每个子结点都代表了这个问题分拆的一个子问题的复杂度。

就这样递归地分解问题。

一直到达叶子结点，也就是base-case.在前面的讨论中，我们没有涉及base-case，在使用递归树分析复杂度时，我们假设base-case的复杂度为1。

举一个例子就可以很明白的说明如何构造递归树。

Example1: 由递归方程T(n)=2T(n/2)+n构造递归树
首先，构造根接点
它的子结点是
……,以此类推。

所以，最后的递归树为：
递归树规则:
根结点的复杂度=所有非叶结点的非递归复杂度+叶子结点的复杂度。

所以，在上面的例子中，每层的非递归复杂度为n,而base-case出现在大约lgn 层(n/2^d =1;d = lgn)。

由于base-case的复杂度为1，所以T(n)≈nlgn，即递归树是分析和计算递归方程的一个重要工具。

它可以直观地表示出递归函数的复杂度，并使人易于理解。

【关键字】分析《算法分析与设计》作业参考答案作业一一、名词解释：1.递归算法：直接或间接地调用自身的算法称为递归算法。

2.程序：程序是算法用某种程序设计语言的具体实现。

2、简答题：1.算法需要满足哪些性质？简述之。

算法是若干指令的有穷序列，满足性质：1）输入：有零个或多个外部量作为算法的输入。

2）输出：算法产生至少一个量作为输出。

3）确定性：组成算法的每条指令清晰、无歧义。

4）有限性：算法中每条指令的执行次数有限，执行每条指令的时间也有限。

2.简要分析分治法能解决的问题具有的特征。

分析分治法能解决的问题主要具有如下特征：1）该问题的规模缩小到一定的程度就可以容易地解决；2）该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；3）利用该问题分解出的子问题的解可以合并为该问题的解；4）该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子问题。

3.简要分析在递归算法中消除递归调用，将递归算法转化为非递归算法的方法。

将递归算法转化为非递归算法的方法主要有：1）采用一个用户定义的栈来模拟系统的递归调用工作栈。

该方法通用性强，但本质上还是递归，只不过人工做了本来由编译器做的事情，优化效果不明显。

2）用递推来实现递归函数。

3）通过Cooper变换、反演变换能将一些递归转化为尾递归，从而迭代求出结果。

后两种方法在时空复杂度上均有较大改善，但其适用范围有限。

三、算法编写及算法应用分析题：1.冒泡排序算法的基本运算如下：for i ←1 to n-1 dofor j ←1 to n-i doif a[j]<a[j+1] then交换a[j]、a[j+1]；分析该算法的时间复杂性。

解答：排序算法的基本运算步为元素比较，冒泡排序算法的时间复杂性就是求比较次数与n的关系。

1）设比较一次花时间1；2）内循环次数为：n-i次,（i=1,…n），花时间为：3）外循环次数为：n-1，花时间为：2.设计一个分治算法计算一棵二叉树的高度。

c语言九连环← 递归程序算法描述一、概述九连环是一种经典的益智游戏，通过递归的方式可以有效地解决该问题。

本文档将详细描述如何使用C语言实现九连环的递归算法。

二、问题描述九连环是一个由9个环相连构成的环状结构，要求通过递归的方式求解九连环的解法。

每个环可以取下来再重新放上去，每次只能将相邻的两个环取下或放上，目标是找出一种方法将所有环都正确放置。

三、算法设计递归是一种解决问题的有效方法，可以解决九连环问题。

通过递归的方式，我们可以将九连环分解为两个部分：当前环和其它八个环。

当当前环放置好时，就可以将其取下来并处理其它八个环，这就是递归的基本思想。

具体的算法流程如下：1. 判断当前环是否能够放置到正确的位置上，如果不能则返回错误信息；2. 将当前环取下来，并递归处理其它八个环；3. 将当前环重新放置到正确的位置上；4. 返回当前环的状态信息。

四、代码实现以下是一个使用C语言实现九连环递归算法的示例代码：```c#include <stdio.h>#include <stdlib.h>#define MAX_NUMBER 9 // 九连环的最大环数#define MAX_SIZE 100 // 存储状态的数组大小// 存储状态的数组int state[MAX_NUMBER][MAX_SIZE];// 递归函数，求解九连环的解法int solve(int num, int pos, int size) {// 边界条件：当只有一个环时，已经成功放置了if (num == 1) {return 1;}// 当前环无法放置到正确位置上，返回错误信息if (state[num-1][pos] == -1) {return -1;}// 将当前环取下来，并处理其它八个环int ret = solve(num-1, pos+1, size); // pos+1表示下一个位置可以放置当前环if (ret == -1) { // 如果无法放置其它八个环，则返回错误信息return -1;} else { // 否则将当前环重新放置到正确位置上，并返回当前环的状态信息state[num-1][pos] = ret; // 将当前环的状态标记为已放置return ret+1; // 返回当前环的状态信息（已放置）}}int main() {// 初始化状态数组，表示每个位置上是否有环以及是否成功放置了for (int i = 0; i < MAX_NUMBER; i++) {for (int j = 0; j < MAX_SIZE; j++) {state[i][j] = -1; // 初始状态为未放置状态（-1）或错误状态（-2）}}// 设置第一个环成功放置的状态为已放置状态（0）和下一个位置可以放置下一个环的状态为已放置状态（1）state[0][0] = 0; // 第一个环成功放置状态为已放置状态（0）state[0][9] = 1; // 下一个位置可以放置下一个环的状态为已放置状态（1）// 通过递归求解九连环的解法，并输出结果信息（已放置的环数）int count = solve(MAX_NUMBER, 0, MAX_SIZE); // 从第一个位置开始求解九连环的解法，输出已放置的环数即可得到最终结果信息（即成功的解法） printf("成功解法：%d\n", count); // 将已放置的环数输出即可得到最终结果信息（即成功的解法）return 0;}```五、总结本文档详细描述了如何使用C语言实现九连环的递归算法，通过递归的方式将九连环分解为两个部分：当前环和其它八个环，并实现了相应的代码实现。

C语言中的递归程序可以用非递归算法实现吗C语言中的递归程序可以用非递归算法来实现。

递归是一种使用函数自身调用的编程技巧，通过将一个问题拆分成更小的子问题来解决。

然而，递归在处理大规模问题或者嵌套过深的情况下会导致栈溢出，并且递归调用的开销较大。

因此，一些复杂的递归程序可以通过非递归算法来重新实现，以降低开销和避免栈溢出。

一种常见的非递归替代方法是使用循环结构和栈数据结构来模拟递归函数的行为。

栈的数据结构可以保存每次递归调用过程中的参数和局部变量，从而避免函数调用的开销。

下面以经典的阶乘函数为例，展示如何将递归程序转化为非递归算法。

递归版阶乘函数：```cint factorial(int n)if (n == 0)return 1;} elsereturn n * factorial(n-1);}```非递归版阶乘函数：```cint factorial(int n)int result = 1;while (n > 0)result *= n;n--;}return result;```这个非递归版本的阶乘函数使用了一个循环来迭代计算乘法，并使用一个变量 `result`来保存当前的结果。

每次迭代，`n` 减1，并将当前结果乘以 `n`，直到 `n` 为0。

类似的，其他的递归函数也可以通过类似的方式来转化为非递归版本。

需要注意的是，非递归版本通常需要额外的变量来保存中间结果，并使用循环结构来模拟函数的递归调用过程。

通过将递归程序转化为非递归算法，可以避免栈溢出和函数调用开销，从而提高程序的效率和性能。

但是非递归算法通常会增加代码的复杂度和可读性，因此开发者在选择使用递归还是非递归算法时应该权衡这些因素。

总而言之，C语言中的递归程序可以通过非递归算法来实现。

通过使用循环结构和栈数据结构，可以模拟递归函数的行为，并避免由于递归调用导致的栈溢出和函数调用开销。

但是需要注意的是，非递归算法可能会增加代码的复杂度和可读性，开发者需要在性能和代码清晰度之间进行权衡。