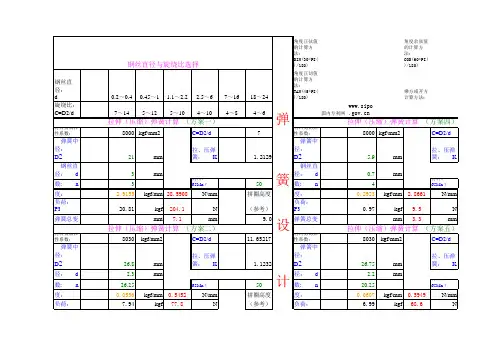
弹簧刚度计算
- 格式:xls
- 大小:55.00 KB
- 文档页数:12
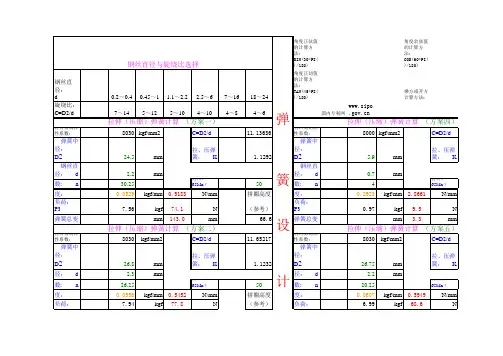

弹簧的k值计算公式(二)弹簧的k值计算公式弹簧的k值(弹性系数)是衡量弹簧强度和刚度的重要参数。
在弹簧的设计和应用过程中,计算k值是必不可少的步骤。
本文将列举几种常见的弹簧k值计算公式,并用例子进行说明。
1. 无扭转弹簧的k值计算公式线圈弹簧(拉伸弹簧)的k值计算公式:k = (G * d⁴) / (8 * D³ * n)其中:k:弹簧的k值(N/m)G:弹簧材料的剪切模量(N/m²)d:弹簧线径(m)D:弹簧直径(m)n:弹簧总匝数(个)例如,假设有一个线径为(5mm)、直径为(40mm)的线圈弹簧,弹簧材料的剪切模量为80 × 10^9 N/m²,总匝数为10个。
那么可以通过上述公式计算出该弹簧的k值:k = (80 × 10^9 * ()^4) / (8 * ()^3 * 10)≈ 15784 N/m因此,该线圈弹簧的k值约为15784 N/m。
扭转弹簧(扭簧)的k值计算公式:k = (G * d⁴) / (32 * D³ * n)其中的符号意义与线圈弹簧的公式相同。
2. 有扭转弹簧的k值计算公式杆弹簧(压簧)的k值计算公式:k = (E * d⁴) / (8 * D³ * n)其中:k:弹簧的k值(N/m)E:弹簧材料的弹性模量(N/m²)d:弹簧线径(m)D:弹簧直径(m)n:弹簧总匝数(个)例如,假设有一个线径为(5mm)、直径为(40mm)的杆弹簧,弹簧材料的弹性模量为200 × 10^9 N/m²,总匝数为20个。
那么可以通过上述公式计算出该弹簧的k值:k = (200 × 10^9 * ()^4) / (8 * ()^3 * 20)≈ 312500 N/m因此,该杆弹簧的k值约为312500 N/m。
总结弹簧的k值计算公式是根据弹簧的材料、几何尺寸和总匝数等参数进行推导的。

串联弹簧刚度计算公式
弹簧串联同时应用,总劲度系数变小,弹簧并联同时应用,总劲度系数增大。
弹簧产生弹性形变时,弹力的大小F跟弹簧伸展(或宿短)的总长度x成正比,即F=kx,式中的k称之为弹簧的劲度系数,的单位是牛頓每米。
假如把弹簧串联或是是并联同时同时应用,这一个串联或是并联的总体的劲度系数,和一种弹簧的劲度系数中间有怎样的关联。
为了能简便考虑,让我们假定把完全一致的弹簧串联或并联。
设将两个劲度系数均为k的弹簧,串联同时成为一种总体应用,这一个总体的劲度系数是多少呢?因为F=kx,如果我们还是应用同样大小的力F去拉这一个弹簧,这一个总体将会伸展2x,那么这一个串联同时的弹簧总体,其劲度系数为1/2倍k,就是说串联同时应用的弹簧的劲度系数变小了。
设将两个劲度系数均为k的弹簧,并联同时成为一种总体应用。
同样的道理,如果我们还是应用同样大小的力F去拉这一个弹簧,两个弹簧分别分担了F的一半,这一个总体只能伸展1/2倍x,那么,这一个并联同时的弹簧总体,其劲度系数为2k,就是说并联同时应用的弹簧的劲度系数变为了原来的2倍,比一种弹簧的劲度系数大了。
弹簧串联公式计算
从公式计算而言,弹簧的刚度计算公式为:Gd^4/8/D^3/n。
弹簧串联时,作用力是作用在一个弹簧的端面上的,此时串联同时的
两个弹簧可以看成是一个弹簧的高度和圈数成倍数增加,此时弹簧刚度公式计算中除圈数成倍增加外,其化所有条件没有发生变化,那么此时刚度值是缩小的,由此可见弹簧串联时力度会变小。
弹簧并联公式计算
弹簧并联时,作用力是作用在两个并列的弹簧端面上的,此时并联同时的两个弹簧同时作用在一个物体时,此时弹簧是两个独立工作时,因此弹簧的力是成倍增加的。

滑块弹簧计算公式(一)滑块弹簧计算公式在机械工程中,滑块弹簧系统是一种常见的结构,用于实现线性运动的弹簧振动系统。
在设计和分析这种系统时,需要使用一些计算公式来计算相关参数。
以下是一些常用的滑块弹簧计算公式,以及实际应用的例子。
弹簧刚度的计算公式弹簧刚度可以用来描述弹簧的硬度,即在单位位移下产生的弹力。
常用的计算弹簧刚度的公式有:1.钢丝弹簧的刚度公式:弹簧刚度(K)等于弹簧材料的剪切弹性模量(G)除以弹簧材料的截面面积(A),即K = G/ A。
例如,对于一个钢丝弹簧,如果弹簧材料的剪切弹性模量为^11 Pascal,而弹簧的截面面积为2x10^-4 平方米,那么弹簧的刚度为:K = ^11 / 2x10^-4 = 6x10^14 N/m。
2.压缩弹簧的刚度公式:弹簧刚度(K)等于弹簧的导程(C)除以弹簧的刚度系数(S),即K = C / S。
例如,对于一个压缩弹簧,如果弹簧的导程为10 cm,而弹簧的刚度系数为200 N/mm,那么弹簧的刚度为:K = 10 cm / 200 N/mm = N/mm。
滑块运动的计算公式滑块运动是弹簧振动系统中的核心部分,常用的计算滑块运动的公式有:1.滑块位移公式:滑块的位移(x)等于弹簧的变形量(δ)减去补偿长度(l),即x = δ - l。
例如,如果弹簧发生了20 cm的压缩变形,并且补偿长度为5 cm,那么滑块的位移为:x = 20 cm - 5 cm = 15 cm。
2.滑块速度公式:滑块的速度(v)等于滑块的位移(x)对时间(t)的导数,即v = dx / dt。
例如,如果滑块的位移随时间变化的函数为x(t) = 4t^2 cm,那么滑块的速度为:v = d(4t^2) / dt = 8t cm/s。
3.滑块加速度公式:滑块的加速度(a)等于滑块的速度(v)对时间(t)的导数,即a = dv / dt。
例如,如果滑块的速度随时间变化的函数为v(t) = 8t cm/s,那么滑块的加速度为:a = d(8t) / dt = 8 cm/s^2。

拉簧及扭簧弹力、刚度计算公式一、拉伸弹簧弹力、刚度计算公式1.拉伸弹簧一已知自由长度,弹簧刚度和初始拉力时,某一工作长度负荷的计算公式如下:P=(Rx F)+I.T.P是指负荷(磅);R是指弹簧刚度(磅/英寸);F是指距自由长度的变形量;I.T.是指初拉力。
例如:已知自由长度为1英寸、刚度为6.9磅/英寸和初始张力为0.7磅,工作长度为1.500英寸时,负荷计算公式如下:P= [6.9 x(1.500-1.000)l+0.7= (6.9x 0.500) +0.7= 3.45+0.7= 4.15磅2.如何计算刚度一弹簧刚度是指使弹簧产生单位变形的负荷,可通过以下步骤测试:1>弹簧变形约为最大变形的20%(自由长度藏去压并高度)时,测量弹簧负荷(P1)及弹簧长度(L1)。
2>弹簧变形不超过最大变形的80%时,测量弹簧负荷(P2)及弹簧长度(L2)。
务必确保弹簧长度为L2时任意两个簧圈(闭合收口除外)都没有发生接触。
3>计算刚度(R)(磅/英寸)R=(P2-P1)/(L1-L2)二、扭簧设计需要的技术参数扭簧的工作状态和拉伸弹簧及压缩弹簧有所不同,其更为复杂和多变,其中包括了很多参数指标,下面一一讲解:d (弹簧线径) :该参数描述了弹簧线的直径,也就是我们说的弹簧钢丝的粗细,默认单位mm。
Dd (心轴最大直径):该参数描述的是工业应用中弹簧轴的最大直径,公差±2%。
D1 (内径): 弹簧的内径等于外径减去两倍的线径。
扭簧在工作过程中,内径可以减小到心轴直径,内径公差±2%。
D (中径): 弹簧的中径等于外径减去一个线径。
D2 (外径) : 等于内径加上两倍的线径。
扭簧在工作过程中,外径将变小,公差(±2%±0.1)mm。
L0 (自然长度):注意:在工作过程中自然长度会减小,公差±2%。
Tum (扭转圈数):弹簧绕制的圈数,圈数的不同直接影响扭簧的性能。

弹簧刚度计算公式推导摘要:1.弹簧刚度的定义与意义2.弹簧刚度计算公式的推导3.弹簧刚度计算公式的应用4.弹簧刚度在工程中的重要性正文:一、弹簧刚度的定义与意义弹簧刚度是指弹簧在受到外力作用时,其变形量与所受外力之比。
具体来说,就是单位变形所需的载荷。
弹簧刚度是弹簧的一个重要特性,它直接影响弹簧在实际应用中的性能和效果。
在工程中,弹簧刚度要求严格,因为刚度不足或过大都会导致弹簧性能不佳,影响设备的运行和使用寿命。
二、弹簧刚度计算公式的推导弹簧刚度计算公式是f"df/d,其中f 表示载荷增量,d 表示变形增量。
这个公式是从弹簧的工作原理和力学原理推导得出的。
弹簧刚度与弹簧的材料、尺寸、形状等因素有关。
在实际应用中,弹簧刚度的计算需要考虑这些因素,以确保弹簧的性能和使用效果。
三、弹簧刚度计算公式的应用弹簧刚度计算公式在工程中具有广泛的应用。
在设计弹簧时,工程师需要根据弹簧的工作环境和性能要求,确定弹簧的材料、尺寸和形状,然后利用刚度计算公式计算弹簧的刚度,以确保弹簧在实际应用中具有良好的性能。
在制造和使用弹簧时,工程师也需要根据弹簧的刚度要求,进行质量检测和性能测试,确保弹簧的质量和使用效果。
四、弹簧刚度在工程中的重要性弹簧刚度在工程中具有重要意义。
它直接影响弹簧的性能、使用寿命和设备的运行效果。
在工程设计中,工程师需要根据弹簧的工作环境和性能要求,合理选择弹簧的材料、尺寸和形状,以确保弹簧具有良好的刚度性能。
在制造和使用过程中,工程师也需要根据弹簧的刚度要求,进行质量检测和性能测试,确保弹簧的质量和使用效果。

弹簧常数和刚度关系公式引言弹簧是一种常见的力学元件,广泛应用于各个领域,例如机械、汽车、电子等。
在研究弹簧的性能和行为时,了解弹簧常数和刚度的关系是十分重要的。
本文将介绍弹簧常数和刚度之间的关系,并给出相应的公式。
弹簧常数弹簧常数是衡量弹簧刚度程度的物理量,用符号"k"表示,单位是牛顿/米(N/m),通常用于描述弹簧线性弹性行为的程度。
弹簧常数越大,代表弹簧的刚度越大,同样的外力作用下,弹簧变形的程度较小。
刚度刚度是弹簧的物理特性之一,用于衡量弹簧对外力的抵抗能力。
刚度可以用弹簧变形量与施加在弹簧上的力的比值来表示。
刚度越大,弹簧对外力的抵抗能力越强。
弹簧常数和刚度的关系弹簧常数和刚度之间存在着密切的关系。
根据牛顿第二定律,弹簧受力与弹簧的变形量成正比,且弹簧常数是比例系数。
弹簧的刚度可以通过弹簧常数来计算,其公式为:刚度=弹簧常数×弹簧变形量根据这个公式,我们可以看到刚度和弹簧常数成正比。
当弹簧常数增大时,刚度也随之增大;反之,当弹簧常数减小时,刚度也随之减小。
刚度的影响因素除了弹簧常数的影响外,刚度还受到其他因素的影响,例如弹簧的形状、材料和长度等。
下面将介绍这些因素对刚度的影响。
弹簧形状弹簧的形状对刚度有很大的影响。
通常情况下,弹簧的刚度与其形状相关,例如螺旋弹簧的刚度与螺旋线的直径、线径和螺距等有关。
弹簧材料弹簧的材料也会对刚度产生影响。
不同材料的弹簧具有不同的弹性模量,从而影响刚度的大小。
材料的选择应根据具体的工程需求和弹簧的使用条件。
弹簧长度弹簧长度对刚度同样有影响。
一般来说,弹簧长度越长,刚度越小;反之,弹簧长度越短,刚度越大。
因此,在设计弹簧系统时,需要考虑弹簧的长度对刚度的影响。
总结弹簧常数和刚度之间存在着正比关系,弹簧常数越大,刚度也越大。
但是,刚度还受到其他因素的影响,如弹簧形状、材料和长度等。
在实际应用中,我们需要根据具体的需求和条件选择合适的弹簧常数和刚度。

恒力弹簧计算公式恒力弹簧是一种力学零件,它的作用是通过给定的力,提供恒定的弹力。
在使用恒力弹簧时,我们需要知道它的力学特性,包括弹簧刚度、伸长和弹力等。
下面将介绍常用的恒力弹簧计算公式。
首先,我们来讨论弹簧的刚度。
弹簧的刚度是指单位长度或单位变形量所产生的弹力。
它常用刚度系数表示,即弹簧的弹力与弹簧伸长量的比值。
刚度系数(K)的计算公式如下:K=F/ΔL其中,K为刚度系数,F为弹簧的弹力,ΔL为弹簧的伸长量。
其次,我们来讨论弹簧的伸长量。
伸长量是指弹簧在承受外力后产生的长度变化。
当弹簧受到外力F时,弹簧的伸长量ΔL可以通过以下公式计算:ΔL=F/K其中,ΔL为弹簧的伸长量,F为弹簧的外力,K为弹簧的刚度系数。
接下来,我们来讨论弹簧的弹力。
弹力是指弹簧所产生的恢复力。
弹力的计算公式如下:F=K*ΔL其中,F为弹簧的弹力,K为弹簧的刚度系数,ΔL为弹簧的伸长量。
除了上述的计算公式,我们还可以通过Hooke定律来计算弹簧的力学特性。
Hooke定律是指在弹性变形范围内,弹簧的变形与所受力成正比。
根据Hooke定律,我们可以得到以下公式:F=k*Δx其中,F为弹簧的外力,k为弹簧的弹性系数,Δx为弹簧的变形量。
在实际计算中,我们通常会根据实际需求选择恒力弹簧的参数,并利用上述的计算公式进行计算。
需要注意的是,不同类型的弹簧具有不同的计算公式,因此在具体计算时需要根据实际情况选择正确的公式。
此外,还有其他与恒力弹簧相关的计算公式,包括弹簧的自然长度、位移等。
但是这些内容超过了1200字的限制,因此在这里无法一一介绍。
总结起来,恒力弹簧的计算公式是设计和制造弹簧过程中必不可少的工具。
了解和掌握这些公式可以帮助我们计算弹簧的力学特性,从而正确选择和应用弹簧。
当然,除了理论计算,我们还需要进行实际测试和验证,以确保弹簧的性能符合需求。

弹簧刚度计算公式推导【实用版】目录1.弹簧刚度的定义与意义2.弹簧刚度计算公式的推导3.弹簧刚度计算公式的应用举例4.弹簧刚度在工程中的重要性正文一、弹簧刚度的定义与意义弹簧刚度是指在弹性范围内,弹簧所产生的弹力与其伸长量或压缩量之比。
弹簧刚度是弹簧材料本身的一种特性,它反映了弹簧在受到外力作用时,单位变形所需的载荷。
在工程中,弹簧刚度对于保证弹簧正常工作和准确测量力的大小具有重要意义。
二、弹簧刚度计算公式的推导弹簧刚度计算公式为:f"df/d。
其中,f 表示弹力,d 表示伸长量或压缩量,f"表示弹力对伸长量或压缩量的导数。
根据胡克定律,弹力 f 与伸长量或压缩量 d 成正比,即 f=kd,其中 k 为弹簧的弹性系数。
对 f 关于 d 求导,可得 f"=k。
将 f"代入弹簧刚度公式,可得弹簧刚度f"df/d=k。
三、弹簧刚度计算公式的应用举例假设一条弹簧的线径为 1000,弹簧中径为 C,弹簧外径为 D,工作圈数为 n。
根据弹簧刚度计算公式,可以计算出弹簧刚度 k:k = F"dF/d = (D^2 - C^2) / (4 * π * d^3 * n)其中,F 为弹簧的弹力,d 为弹簧的伸长量或压缩量。
四、弹簧刚度在工程中的重要性弹簧刚度在工程中有着广泛的应用,如在测量力、减震、控制机构等方面。
弹簧刚度对于保证弹簧的正常工作和准确测量力的大小具有重要意义。
在设计弹簧时,需要根据工程需求和实际工作条件,选择合适的弹簧材料和结构,以满足所需的弹簧刚度。

弹簧总刚度"弹簧总刚度" 是一个工程力学和弹性力学领域的概念,通常涉及到弹簧的设计和性能分析。
弹簧总刚度表示弹簧在受力时的整体刚度,是弹簧系统对外界加载的响应的一个重要参数。
以下是关于弹簧总刚度的一些基本概念和相关信息:1. 弹簧总刚度的定义弹簧总刚度是指弹簧在受到一定的外力或位移作用时,所表现出的整体刚度。
刚度通常用弹性系数(弹性常数)来表示,它是弹簧的材料和几何特性的函数。
2. 弹簧总刚度的计算弹簧总刚度的计算涉及到弹簧的材料、几何形状、工作原理等多个因素。
对于一些简单的情况,弹簧总刚度可以通过胡克定律(Hooke's Law)计算,即刚度等于受力与位移的比值:是弹簧总刚度(弹性系数)。
是作用在弹簧上的力。
是由于受力而发生的弹簧的位移。
对于复杂的弹簧系统,可能需要考虑弹簧的材料特性、弯曲形状、叠加效应等因素,使用更复杂的数学模型和方法进行计算。
3. 弹簧总刚度与刚度的变化弹簧总刚度可能会受到温度、疲劳、变形等因素的影响而发生变化。
在一些情况下,这些因素可能导致弹簧的刚度减小,甚至失去其弹性性能。
因此,在设计和使用弹簧系统时,需要考虑这些因素,以确保系统的性能和可靠性。
4. 工程应用弹簧总刚度的概念在各种工程应用中都有重要的作用,如机械工程、汽车工程、建筑工程等。
在这些领域,弹簧总刚度的准确计算和控制对于系统的正常运行和性能至关重要。
总结弹簧总刚度是描述弹簧系统刚性的重要参数,对于设计和分析弹簧系统的性能至关重要。
在实际应用中,需要考虑多种因素,使用适当的数学模型和方法来计算和控制弹簧总刚度,以确保系统的可靠性和稳定性。
弹簧k计算弹簧是一种常见的力学元件,也是物理学中研究的重要对象之一。
弹簧的刚度常数k是衡量弹簧刚度的参数,也是计算弹簧变形和弹性力的重要依据。
弹簧是一种可以储存弹性势能的装置,它具有一定的弹性,可以在受力作用下发生形变,并且当力消失时能够恢复原状。
弹簧的变形与受力之间存在着一定的关系,而弹簧的刚度常数k就是描述这种关系的参数。
弹簧刚度常数k的计算方法有多种,下面将分别介绍几种常见的计算方法。
1. 钢丝弹簧刚度常数的计算:钢丝弹簧是一种常见的弹簧类型,其刚度常数的计算可以通过弹簧的材料特性和几何参数来进行。
首先,需要知道弹簧的材料的弹性模量E和截面积A,然后利用公式k = (E * A) / L来计算弹簧的刚度常数,其中L为弹簧的长度。
2. 压缩弹簧刚度常数的计算:压缩弹簧是一种能够在压缩力作用下发生形变的弹簧,其刚度常数的计算可以通过弹簧的材料特性和几何参数来进行。
首先,需要知道弹簧的材料的弹性模量E、截面积A和弹簧的原始长度Lo,然后利用公式k = (E * A) / Lo来计算弹簧的刚度常数。
3. 扭转弹簧刚度常数的计算:扭转弹簧是一种能够在扭转力作用下发生形变的弹簧,其刚度常数的计算可以通过弹簧的材料特性和几何参数来进行。
首先,需要知道弹簧的材料的剪切模量G、扭转半径R和弹簧的长度L,然后利用公式k = (G * R^4) / (32 * L)来计算弹簧的刚度常数。
弹簧刚度常数的计算方法虽然各异,但都依赖于弹簧的材料特性和几何参数。
在实际应用中,我们可以通过测量弹簧的力和变形来确定刚度常数,也可以通过材料的物理性质和弹簧的几何参数来计算刚度常数。
无论是计算还是测量,都需要准确的数据和严密的计算方法,以确保得到准确可靠的结果。
弹簧刚度常数k的计算在工程设计和科学研究中具有重要的意义。
它不仅可以用于弹簧的设计和选择,还可以用于弹簧系统的分析和优化。
在机械设计中,合理选择和使用弹簧刚度常数可以提高产品的性能和寿命;在物理实验中,准确测量和计算弹簧刚度常数可以帮助我们理解物体的弹性性质和力学行为。
压力弹簧刚度计算压力弹簧是一种常见的弹性元件,可以用于各种场合,例如汽车悬挂系统、机械设备、电子产品等。
计算压力弹簧的刚度是衡量其性能的重要指标之一,也是设计过程中必须考虑的参数之一压力弹簧的刚度可以用以下公式来计算:K=(Gd^4)/(8ND^3)其中,K是压力弹簧的刚度(N/mm),G是弹性模量(N/mm^2),d是线径(mm),N是圈数,D是直径(mm)。
在计算压力弹簧的刚度时,首先需要获得弹簧材料的弹性模量。
弹性模量是材料的重要力学特性之一,表示了材料在受力时的变形能力和恢复能力。
不同的材料具有不同的弹性模量,常见的弹簧材料有钢、铜、合金等。
在得到弹性模量后,可以开始计算压力弹簧的刚度了。
首先,需要测量弹簧的线径和直径。
线径是弹簧丝线的直径,直径是弹簧的外径。
在测量线径和直径时,需要使用准确的测量工具,例如游标卡尺、微量卡尺等,确保测量结果的准确性。
接下来,需要测量压力弹簧的圈数。
圈数是指弹簧的螺旋圈数,可以通过数圈的方式进行测量。
可以使用标尺或线尺量取弹簧两端之间的距离,然后除以弹簧的线径,得到圈数。
将测得的线径、直径和圈数代入上述的刚度计算公式中,就可以计算得到压力弹簧的刚度值。
刚度值的单位是N/mm,表示单位弹性变形时所受到的力大小。
在实际的工程应用中,压力弹簧的刚度是设计中的重要参数之一、根据实际需求和设计要求,可以通过调整材料、线径、直径等参数,来改变压力弹簧的刚度,从而满足不同的应用需求。
需要注意的是,压力弹簧的刚度计算是一个理论计算,并且只考虑了弹簧的几何尺寸和材料等因素。
实际应用中,考虑到各种实际因素的影响,例如弯曲、扭转、疲劳等,需要进行更为复杂的分析和计算。
因此,在实际工程中,常常需要进行试验和验证,以确保设计的可靠性和合理性。
总结起来,压力弹簧的刚度计算是压力弹簧设计中的关键步骤之一、通过计算,可以得到弹簧的刚度值,从而为设计和应用提供参考依据。
需要注意的是,在实际应用中,需要综合考虑各种因素的影响,并进行试验和验证,以确保设计的合理性和可靠性。
弹簧组刚度计算公式弹簧是一种常见的机械元件,广泛应用于工业、汽车、航空航天等领域。
弹簧的主要作用是储存和释放能量,用于各种机械装置的控制和调节。
在设计和制造弹簧时,计算其刚度是非常重要的一步,因为刚度直接影响到弹簧的性能和工作效果。
本文将介绍弹簧组刚度的计算公式及其应用。
弹簧组刚度是指多个弹簧组合在一起后的整体刚度。
在实际工程中,常常需要将多个弹簧组合在一起,以满足特定的工作要求。
在这种情况下,需要计算弹簧组的整体刚度,以确保其能够正常工作并承受所需的载荷。
弹簧组刚度的计算公式可以通过以下步骤得到:1. 首先,需要计算每个弹簧的刚度。
弹簧的刚度通常用弹簧系数(K)来表示,即单位长度内的弹簧受力与变形之间的比值。
弹簧系数可以通过实验测定或理论计算得到。
2. 然后,将每个弹簧的刚度进行叠加,得到整个弹簧组的刚度。
如果弹簧组是串联排列的,则整体刚度为各个弹簧刚度的总和;如果弹簧组是并联排列的,则整体刚度需要根据并联弹簧的公式进行计算。
对于串联排列的弹簧组,整体刚度K_total可以通过以下公式计算得到:1/K_total = 1/K1 + 1/K2 + ... + 1/Kn。
其中,K1、K2、...、Kn分别为每个弹簧的刚度。
对于并联排列的弹簧组,整体刚度K_total可以通过以下公式计算得到:K_total = K1 + K2 + ... + Kn。
其中,K1、K2、...、Kn分别为每个弹簧的刚度。
通过以上公式,可以计算出弹簧组的整体刚度,从而为工程设计和制造提供参考依据。
在实际应用中,需要根据具体情况选择合适的弹簧组合方式,并进行刚度计算,以确保弹簧组能够满足工作要求。
除了上述的计算公式外,还需要注意以下几点:1. 弹簧的刚度受到材料、形状、工艺等因素的影响,因此在计算刚度时需要准确掌握弹簧的相关参数,并进行合理的估算和计算。
2. 弹簧在工作过程中会受到外部载荷的作用,因此在计算刚度时需要考虑弹簧的变形和受力情况,以确保计算结果准确可靠。
弹簧刚度计算公式推导摘要:I.引言- 弹簧刚度的重要性- 弹簧刚度的定义II.弹簧刚度计算公式- 弹簧刚度计算公式推导- 公式中各参数的含义III.弹簧刚度计算公式的应用- 在实际工程中的运用- 举例说明IV.结论- 弹簧刚度计算公式的重要性- 总结弹簧刚度计算公式的应用正文:I.引言弹簧是一种常见的机械元件,用于储存和释放能量。
在各种工程应用中,弹簧的刚度是一个重要的性能指标。
弹簧刚度计算公式可以帮助工程师快速、准确地计算弹簧的刚度,从而优化设计。
弹簧刚度是指在一定范围内,弹簧受到外力作用发生变形时,所产生单位变形所需的载荷。
通常用公式F" = kx 来表示,其中F" 是弹簧所受的力,k是弹簧刚度,x 是弹簧的变形量。
II.弹簧刚度计算公式弹簧刚度计算公式为:k = F" / x其中,k 是弹簧刚度,F" 是弹簧所受的力,x 是弹簧的变形量。
这个公式可以通过胡克定律推导出来。
胡克定律是指在弹性范围内,弹簧的伸长量与所受力成正比。
即F = kx,其中F 是弹簧所受的力,k 是弹簧的弹性系数,x 是弹簧的伸长量。
将公式两边同时除以x,得到k = F" / x。
III.弹簧刚度计算公式的应用弹簧刚度计算公式在实际工程中有广泛的应用,例如在汽车、火车等交通工具的悬挂系统设计中,弹簧的刚度是一个重要的参数。
此外,在机械设备、电子产品等各行各业中,弹簧刚度计算公式也发挥着重要作用。
以汽车悬挂系统为例,设计师需要根据汽车的行驶条件,计算出合适的弹簧刚度。
如果弹簧刚度太大,汽车在行驶过程中会感到颠簸;如果弹簧刚度太小,汽车的行驶稳定性会受到影响。
因此,设计师需要通过弹簧刚度计算公式,选择合适的弹簧刚度,以保证汽车的舒适性和行驶稳定性。
IV.结论弹簧刚度计算公式是工程设计中一个重要的工具,可以帮助工程师快速、准确地计算弹簧的刚度,从而优化设计。
在实际应用中,弹簧刚度计算公式被广泛应用于各种领域,如汽车、火车、机械设备等。
弹簧种类和计算公式弹簧是一种能够储存和释放机械能的装置,广泛应用于各种机械设备和工程中。
根据其工作原理和结构特点,弹簧可以分为多种类型,每种类型都有其特定的计算公式。
本文将介绍几种常见的弹簧类型及其计算公式。
1. 螺旋弹簧。
螺旋弹簧是最常见的一种弹簧类型,其结构简单,使用广泛。
螺旋弹簧的计算公式主要包括弹簧刚度、变形量和应力等参数。
其中,弹簧刚度K的计算公式为:K = Gd^4 / (8D^3n)。
其中,G为材料的剪切模量,d为线径,D为螺旋弹簧的平均直径,n为有效圈数。
螺旋弹簧的变形量可以通过以下公式计算:δ = F / K。
其中,F为外力,K为弹簧刚度,δ为变形量。
螺旋弹簧的应力计算公式为:σ = 8Fd / (πD^3n)。
其中,σ为应力,F为外力,d为线径,D为螺旋弹簧的平均直径,n为有效圈数。
2. 压缩弹簧。
压缩弹簧是一种短小粗的弹簧,通常用于承受压缩力的场合。
压缩弹簧的计算公式与螺旋弹簧类似,主要包括弹簧刚度、变形量和应力等参数。
压缩弹簧的弹簧刚度K的计算公式为:K = (Gd^4) / (8D^3n)。
压缩弹簧的变形量和应力计算公式与螺旋弹簧相似,不再赘述。
3. 张力弹簧。
张力弹簧是一种受拉力的弹簧,通常用于吊挂和支撑等场合。
张力弹簧的计算公式与压缩弹簧类似,也包括弹簧刚度、变形量和应力等参数。
张力弹簧的弹簧刚度K的计算公式为:K = (Gd^4) / (8D^3n)。
张力弹簧的变形量和应力计算公式与螺旋弹簧相似,不再赘述。
4. 扭转弹簧。
扭转弹簧是一种受到扭转力的弹簧,通常用于扭转传递和控制等场合。
扭转弹簧的计算公式主要包括弹簧刚度、变形角度和应力等参数。
扭转弹簧的弹簧刚度K 的计算公式为:K = (Gd^4) / (32D^3n)。
扭转弹簧的变形角度和应力计算公式为:θ = T / K。
τ = 16T / (πd^3nD)。
其中,θ为变形角度,T为扭矩,K为弹簧刚度,τ为应力。
·压力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;
拉力弹簧
拉力弹簧的k值与压力弹簧的计算公式相同
·拉力弹簧的初张力:初张力等于适足拉开互相紧贴的弹簧并圈所需的力,初张力在弹簧卷制成形后发生。
拉力弹簧在制作时,因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同,使得每个拉力弹簧初始拉力产生不平均的现象。
所以安装各规格的拉力弹簧时,应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。
·初张力=P-(k×F1)=最大负荷-(弹簧常数×拉伸长度)
·拉力弹簧的设计数据,除弹簧尺寸外,更需要计算出最大负荷及变位尺寸的负荷;
·弹簧常数:以k表示,当弹簧被拉伸时,每增加1mm距离的负荷(kgf/mm);
·弹簧常数公式(单位:kgf/mm):
G=线材的钢性模数:碳钢丝G=79300 ;不锈钢丝G=697300 ,磷青铜线G=4500 ,黄铜线G=350 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径=Do-d
N=总圈数
扭力弹簧
·弹簧常数:以k 表示,当弹簧被扭转时,每增加1°扭转角的负荷(kgf/mm).
·弹簧常数公式(单位:kgf/mm):
E=线材之钢性模数:琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200,黄铜线E=11200 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径=Do-d
N=总圈数
R=负荷作用的力臂
p=3.1416。