关于弹簧的刚度系数计算

弹簧刚度科技名词定义中文名称：弹簧刚度英文名称：stiffness of spring定义：产生单位变形量的弹簧载荷。

应用学科：机械工程（一级学科）；机械零件（二级学科）；弹簧（三级学科）以上内容由全国科学技术名词审定委员会审定公布1、弹簧的刚度是载荷增量dF与变形增量dλ之比，即产生单位变形所需的载荷，弹簧的刚度计算公式为F'=dF/dλ。

特性线为渐增型的弹簧，刚度随着载荷的增加而增大；而渐减型的弹簧，刚度随着载荷的增加而减少。

至于直线型的弹簧，刚度则不随载荷变化而变化，即F'=dF/dλ=F/λ=常数。

因此，对于具有直线型特性线的弹簧，其刚度也成为弹簧常数。

2、单位力使弹簧所产生的变形，即刚度的倒数称为弹簧的柔度。

3、计算：弹簧刚度是指使弹簧产生单位变形的载荷，用C和CT分别表示拉（压）弹簧的刚度与扭转弹簧的刚度，其表达式如下：对于拉压弹簧其中：F --- 弹簧轴向拉（压）力；λ --- 弹簧轴向伸长量或压缩量；对于扭转弹簧T --- 扭转弹簧的扭矩；Φ--- 扭转弹簧的扭转角。

[1]20.3.2 弹簧刚度1、定义：弹簧刚度是指使弹簧产生单位变形的载荷，用K和K T分别表示拉（压）弹簧的刚度与扭转弹簧的刚度，其表达式如下：对于拉压弹簧对于扭转弹簧其中：F --- 弹簧轴向拉（压）力；λ--- 弹簧轴向伸长量或压缩量；T --- 扭转弹簧的扭矩；ø--- 扭转弹簧的扭转角。

2、弹簧刚度与弹簧特性的关系图a）所示的直线型弹簧，其刚度为一常数。

这种弹簧的特性曲线越陡，弹簧刚度相应愈大，即弹簧愈硬；反之则愈软。

图b）所示的弹簧特性曲线为刚度渐增型，即弹簧随变形量的增大其刚度越大，且在最大或冲击载荷作用时，仍具有较好的缓冲减振性能，故多使用弹簧特性曲线具有该型曲线的走向。

图c）所示弹簧特性曲线为刚度渐减型，即弹簧刚度随变形的增大而越小。

为了在冲击动能一定时，获得较小冲击力，则应使用具有刚度渐减型特性曲线的弹簧为宜。

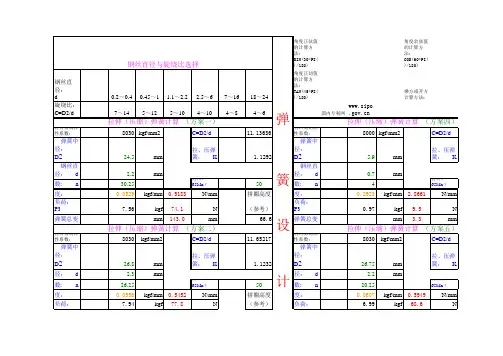
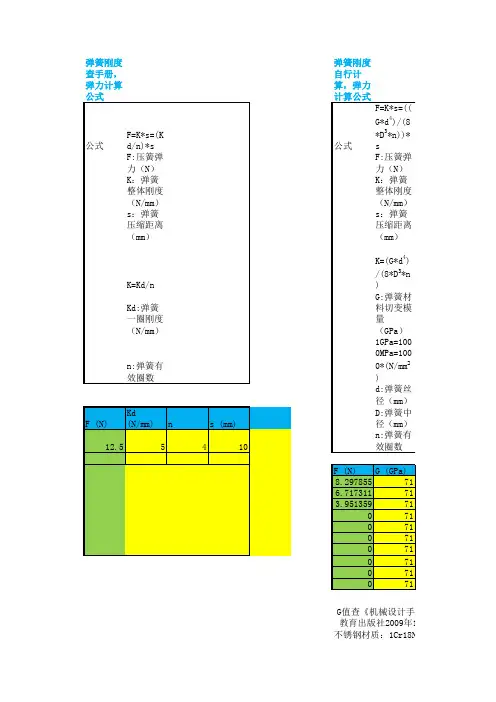
弹簧刚度查手册，弹力计算公式弹簧刚度自行计算，弹力计算公式
公式F=K*s=(Kd/n)*s公式F=K*s=((G*d4)/(8*D3*n))*s F:压簧弹力（N）F:压簧弹力（N）
K：弹簧整体刚度（N/mm）K：弹簧整体刚度（N/mm）
s：弹簧压缩距离（mm）s：弹簧压缩距离（mm）
K=Kd/n K=(G*d4)/(8*D3*n)
Kd:弹簧一圈刚度（N/mm）G:弹簧材料切变模量（GPa）
n:弹簧有效圈数1GPa=1000MP2)
d:弹簧丝径（
D:弹簧中径（mm）
n:弹簧有效圈数
G值查《机械设计手册（
教育出版社2009年1月第2版）P313，表1
不锈钢材质：1Cr18Ni9
自行计算，弹力计算公式
((G*d4)/(8*D3*n))*s
弹力（N）
K：弹簧整体刚度（N/mm）
s：弹簧压缩距离（mm）
4)/(8*D3*n)
材料切变模量（GPa）
000MPa=1000*(N/mm2)
丝径（mm）
D:弹簧中径（mm）
n:弹簧有效圈数
手册（第2版）吴宗泽 高志 主编》（高等版社2009年1月第2版）P313，表14-2 弹簧常用材料18Ni9Ti。

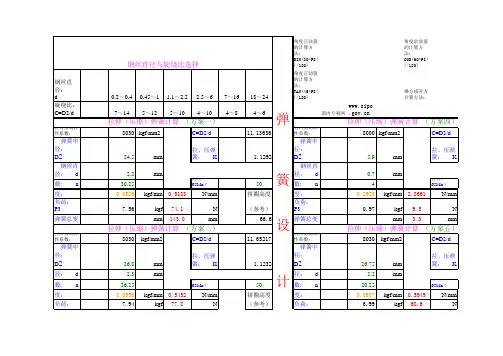
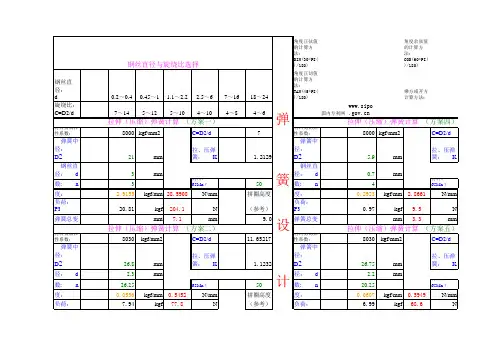
调压弹簧旋绕比 C D/d 3.9曲度系数 k1(4C-1)/(4C-4) +0.615/C 1.415弹簧刚度 K G×d4/(8×n×D3)36.4予压缩量H1P/(K*π*(d2*d2-d1*d1)/4)0.010最小工作载荷 F1K×H10.4最大工作载荷F2K×（H1+△H） 2.18平均载荷Fm(F2+F1)/2 1.27载荷幅Fa(F2-F1)/20.91平均剪切应力τm8 *k1*D*F m/π*d314.75切应力幅τa8 *k1*D*F a/π*d310.59 最大切应力τmaxτm+τa25.34最小切应力τmixτm-τa 4.16疲劳强度安全系数S(τo+0.75τmix)/ τmax27.21弹簧的高径比b H0/D 2.56弹簧的自振频率γn 3.56×105 ×d/n D24235.80弹簧的强迫机械振动频率γr油泵转速/6030.00γn/γr141.19工作时最小高度Hb1H0-△H -H110.94压并高度Hb n1*d7.7弹簧节距t(Ho-1.5×d)/n 1.87螺旋角 αarctg(t/(Dπ))7.9弹簧展开长度LπDn1/cos(α)95.42临界载荷Fc Cb*K*H00电磁阀弹簧项目调压弹簧电磁阀弹簧3.5#DIV/0!钢丝直径 d 1.111.476#DIV/0!弹簧中径 D 4.3 3.546.1#DIV/0!有效圈数 n550.000#DIV/0!总圈数 n1770.0#DIV/0!自由高度 H01110.82.30#DIV/0!升程 △H0.050.051.15#DIV/0!抗拉强度 σb196119611.15#DIV/0!许用剪切应力τ0686.35686.3515.15#DIV/0!发动机转速3600360015.15#DIV/0!开启压力 P 3.0030.31#DIV/0!针阀密封交线直径 d1 2.30.00#DIV/0!针阀导向直径 d2422.65#DIV/0!切变模量 G79000790003.09#DIV/0!弹簧安装高度8.958.975812.24#DIV/0!不稳定系数Cb30.000.00193.74#DIV/0!10.75#DIV/0!701.86#DIV/0!9.6#DIV/0!78.02#DIV/0!。

弹簧刚度计算公式推导【原创版】目录1.弹簧刚度的定义与意义2.弹簧刚度计算公式的推导3.弹簧刚度计算公式的应用举例4.弹簧刚度在工程中的重要性正文一、弹簧刚度的定义与意义弹簧刚度是指弹簧在受到外力作用下，产生单位变形所需的载荷。

它反映了弹簧的弹性特性，是弹簧材料、弹簧形状和弹簧尺寸等因素综合影响的结果。

在工程中，弹簧刚度是设计弹簧的重要参数，直接影响弹簧的性能和使用寿命。

二、弹簧刚度计算公式的推导弹簧刚度计算公式为：f"df/d。

其中，f 表示载荷增量，d 表示变形增量。

弹簧刚度是产生单位变形所需的载荷，因此可以用载荷增量与变形增量的比值来表示。

在具体计算时，需要知道弹簧的工作状态、配装尺寸限制、工作频率、疲劳要求、耐蚀性等信息。

对于一般力度计算公式，可以表示为：pp"fp0(p 拉力、p"刚度、p0 初拉力）p"gd4/8/d3/n(g 材料弹性模量、d 材料直径、d 弹簧中径、n 有效圈数)。

其中，g 表示材料弹性模量，d 表示材料直径，d 表示弹簧中径，n 表示有效圈数。

三、弹簧刚度计算公式的应用举例假设弹簧的材料弹性模量为 g=78500（碳素钢丝），材料直径为 d=4mm，弹簧中径为 d=3mm，有效圈数为 n=4，弹簧受到的拉力为 p=100N，弹簧的初拉力为 p0=0，我们可以根据公式计算出弹簧的刚度 p"：p" = f"df/d = (p*d^3)/(8*n*g*d^4) = (100*3^3)/(8*4*78500*3^4) = 12.5 N/mm因此，弹簧的刚度为 12.5 N/mm。

四、弹簧刚度在工程中的重要性弹簧刚度在工程中具有重要意义，它直接影响弹簧的性能和使用寿命。

在设计弹簧时，需要根据工程实际需求，合理选择弹簧材料、弹簧形状和弹簧尺寸，以达到合适的弹簧刚度。

在实际应用中，弹簧刚度过大会导致弹簧变形困难，影响弹簧的使用寿命；弹簧刚度过小会导致弹簧变形过大，影响弹簧的性能。

弹簧刚度计算公式推导【实用版】目录1.弹簧刚度的定义与意义2.弹簧刚度计算公式的推导3.弹簧刚度计算公式的应用举例4.弹簧刚度在工程中的重要性正文一、弹簧刚度的定义与意义弹簧刚度是指在弹性范围内，弹簧所产生的弹力与其伸长量或压缩量之比。

弹簧刚度是弹簧材料本身的一种特性，它反映了弹簧在受到外力作用时，单位变形所需的载荷。

在工程中，弹簧刚度对于保证弹簧正常工作和准确测量力的大小具有重要意义。

二、弹簧刚度计算公式的推导弹簧刚度计算公式为：f"df/d。

其中，f 表示弹力，d 表示伸长量或压缩量，f"表示弹力对伸长量或压缩量的导数。

根据胡克定律，弹力 f 与伸长量或压缩量 d 成正比，即 f=kd，其中 k 为弹簧的弹性系数。

对 f 关于 d 求导，可得 f"=k。

将 f"代入弹簧刚度公式，可得弹簧刚度f"df/d=k。

三、弹簧刚度计算公式的应用举例假设一条弹簧的线径为 1000，弹簧中径为 C，弹簧外径为 D，工作圈数为 n。

根据弹簧刚度计算公式，可以计算出弹簧刚度 k：k = F"dF/d = (D^2 - C^2) / (4 * π * d^3 * n)其中，F 为弹簧的弹力，d 为弹簧的伸长量或压缩量。

四、弹簧刚度在工程中的重要性弹簧刚度在工程中有着广泛的应用，如在测量力、减震、控制机构等方面。

弹簧刚度对于保证弹簧的正常工作和准确测量力的大小具有重要意义。

在设计弹簧时，需要根据工程需求和实际工作条件，选择合适的弹簧材料和结构，以满足所需的弹簧刚度。

弹簧总刚度"弹簧总刚度" 是一个工程力学和弹性力学领域的概念，通常涉及到弹簧的设计和性能分析。

弹簧总刚度表示弹簧在受力时的整体刚度，是弹簧系统对外界加载的响应的一个重要参数。

以下是关于弹簧总刚度的一些基本概念和相关信息：1. 弹簧总刚度的定义弹簧总刚度是指弹簧在受到一定的外力或位移作用时，所表现出的整体刚度。

刚度通常用弹性系数（弹性常数）来表示，它是弹簧的材料和几何特性的函数。

2. 弹簧总刚度的计算弹簧总刚度的计算涉及到弹簧的材料、几何形状、工作原理等多个因素。

对于一些简单的情况，弹簧总刚度可以通过胡克定律（Hooke's Law）计算，即刚度等于受力与位移的比值：是弹簧总刚度（弹性系数）。

是作用在弹簧上的力。

是由于受力而发生的弹簧的位移。

对于复杂的弹簧系统，可能需要考虑弹簧的材料特性、弯曲形状、叠加效应等因素，使用更复杂的数学模型和方法进行计算。

3. 弹簧总刚度与刚度的变化弹簧总刚度可能会受到温度、疲劳、变形等因素的影响而发生变化。

在一些情况下，这些因素可能导致弹簧的刚度减小，甚至失去其弹性性能。

因此，在设计和使用弹簧系统时，需要考虑这些因素，以确保系统的性能和可靠性。

4. 工程应用弹簧总刚度的概念在各种工程应用中都有重要的作用，如机械工程、汽车工程、建筑工程等。

在这些领域，弹簧总刚度的准确计算和控制对于系统的正常运行和性能至关重要。

总结弹簧总刚度是描述弹簧系统刚性的重要参数，对于设计和分析弹簧系统的性能至关重要。

在实际应用中，需要考虑多种因素，使用适当的数学模型和方法来计算和控制弹簧总刚度，以确保系统的可靠性和稳定性。

弹簧k值计算公式
弹簧k值是衡量弹簧特性的重要参数，它可以反映弹簧的强度和刚性。

弹簧k值的计算公
式为：k=F/Δx，其中F表示施加到弹簧上的力，Δx表示弹簧在受力后变形的量。

通常情况下，弹簧k值越大，弹簧的刚度就越大，也就是说弹簧变形越小，承载能力就越强。

反之，弹簧k值越小，弹簧的刚度就越小，也就是说弹簧变形越大，承载能力就越弱。

弹簧k值可以由弹簧的材料、尺寸和形状等参数来决定，因此在设计应用弹簧时，需要根据应用需要，选择合适的弹簧参数，以保证弹簧的功能。

弹簧力量计算
力=弹簧刚度（kg/mm）*压缩量（mm）
弹簧刚度=线径*刚性模数/(8*旋绕比C的3次方*工作圈数)
工作圈数=总圈数-2
旋绕比C=弹簧中径/线径
弹簧中径=弹簧外径-线径
刚性模数：弹簧钢(常用)8000，不锈钢7000，铜4000
用0.8mm不锈钢丝缠绕外径5.8mm的弹簧，缠绕30圈，总长度80mm，完全压缩到60mm时的压力计算
刚性模数取8000
弹簧中径=5.8-0.8=5mm
旋绕比=5/0.8=6.25
工作圈数=30（为了便于计算）
弹簧刚度=1*8000/(8*6.25^3*30)=0.52
力=0.52*50=26kg
如果弹簧中径增加1mm，则
旋绕比=5/1=5
弹簧刚度=1*8000/(8*5^3*30)=0.047
力=0.047*20=0.94kg
用2.5mm不锈钢丝缠绕外径49.5mm的弹簧，缠绕6圈，总长度70mm，完全压缩到50mm时的压力计算
刚性模数取8000
弹簧中径=49.5-2.5=47mm
旋绕比=47/2.5=18.8
工作圈数=6（为了便于计算）
弹簧刚度=1*8000/(8*18.8^3*6)=0.025
力=0.025*20=0.5kg。

·压力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；
拉力弹簧
拉力弹簧的k值与压力弹簧的计算公式相同
·拉力弹簧的初张力：初张力等于适足拉开互相紧贴的弹簧并圈所需的力，初张力在弹簧卷制成形后发生。

拉力弹簧在制作时，因钢丝材质、线径、弹簧指数、静电、润滑油脂、热处理、电镀等不同，使得每个拉力弹簧初始拉力产生不平均的现象。

所以安装各规格的拉力弹簧时，应预拉至各并圈之间稍为分开一些间距所需的力称为初张力。

·初张力=P-（k×F1）=最大负荷-（弹簧常数×拉伸长度）
·拉力弹簧的设计数据，除弹簧尺寸外，更需要计算出最大负荷及变位尺寸的负荷；
·弹簧常数：以k表示，当弹簧被拉伸时，每增加1mm距离的负荷(kgf/mm)；
·弹簧常数公式（单位：kgf/mm）：
G=线材的钢性模数：碳钢丝G=79300 ；不锈钢丝G=697300 ，磷青铜线G=4500 ，黄铜线G=350 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径=Do-d
N=总圈数
扭力弹簧
·弹簧常数：以k 表示,当弹簧被扭转时，每增加1°扭转角的负荷(kgf/mm).
·弹簧常数公式（单位：kgf/mm）:
E=线材之钢性模数：琴钢丝E=21000 ,不锈钢丝E=19400 ,磷青铜线E=11200，黄铜线E=11200 d=线径
Do=OD=外径
Di=ID=内径
Dm=MD=中径=Do-d
N=总圈数
R=负荷作用的力臂
p=3.1416。

压力弹簧计算公式压力弹簧是一种用于储存弹性能量并提供稳定力的装置。

它由硬质材料制成，通常用于工业和机械应用中。

在设计和使用压力弹簧时，计算其弹性特性是非常重要的。

本文将介绍压力弹簧的计算公式及其相关概念。

接下来，我们可以利用胡克定律（Hooke's law）来计算压力弹簧的刚度。

根据胡克定律，弹簧恢复的力与其压缩或伸长的距离成正比。

通常用以下公式表示：F=K*x其中，F是弹簧恢复的力，K是弹簧的刚度，x是压缩或伸长的距离。

在计算压力弹簧的弹性特性时，我们通常会考虑材料的弹性模量（elastic modulus）和截面形状。

压力弹簧的截面形状可以是圆形、方形或其他形状，因此我们需要根据实际情况选择适当的公式。

在研究圆形截面的弹簧时，我们可以利用以下公式来计算刚度K：K=(G*d^4)/(8*D^3*n)其中，K是弹簧的刚度，G是材料的剪切模量，d是弹簧的线径，D是弹簧的外径，n是绕制圈数。

当研究方形截面的弹簧时，我们可以利用以下公式来计算刚度K：K=(G*b*h^3)/(12*L)其中，K是弹簧的刚度，G是材料的剪切模量，b是弹簧的边宽，h是弹簧的边高，L是弹簧的长度。

计算初始压缩量Lo时，我们可以利用以下公式：Lo=n*h其中，Lo是初始压缩量，n是绕制圈数，h是弹簧的边高。

需要注意的是，以上计算公式仅适用于理想的理论计算。

在实际应用中，还需要考虑材料的非线性特性、压缩或伸长的极限以及边界条件等因素。

综上所述，压力弹簧的计算公式涉及到刚度和初始压缩量的计算。

这些公式可以帮助工程师和设计师在设计和使用压力弹簧时更好地了解其弹性特性，并进行相应的优化和调整。

但需要注意的是，在实际应用中，还需考虑其他因素的影响，以确保弹簧的性能和可靠性。

普通弹簧刚度摘要：I.普通弹簧刚度简介- 定义与概念- 计算公式II.弹簧刚度的影响因素- 材料- 弹簧圈数- 弹簧直径III.弹簧刚度的应用领域- 工程机械- 汽车工业- 电子产品IV.弹簧刚度的测量与测试- 测量方法- 测试设备- 数据处理与分析正文：普通弹簧刚度是指在弹性范围内，弹簧产生单位变形所需的载荷。

它是一个重要的力学参数，用于描述弹簧的弹性特性。

在实际应用中，弹簧刚度的大小直接影响到系统的稳定性和性能。

弹簧刚度的计算公式为：F"dF/d，其中F 为载荷增量，d 为变形增量。

根据这个公式，我们可以看出，弹簧刚度与载荷和变形之间呈线性关系。

此外，根据弹簧的特性线，弹簧刚度还可以分为渐增型、渐减型和直线型。

弹簧刚度受到多种因素的影响，包括材料、弹簧圈数和弹簧直径。

首先，材料的弹性模量是决定弹簧刚度的主要因素。

通常，弹簧采用高弹性钢材制成，如碳素钢丝、不锈钢丝和琴钢丝等。

其次，弹簧圈数和直径也会影响弹簧刚度。

在相同的材料和载荷条件下，弹簧圈数越多，弹簧刚度越大；弹簧直径越大，弹簧刚度也越大。

弹簧刚度在许多领域都有广泛的应用，如工程机械、汽车工业和电子产品等。

在工程机械中，弹簧刚度用于设计各种弹性元件，如减震器、悬挂系统和离合器等。

在汽车工业中，弹簧刚度用于设计汽车悬挂系统、制动系统和座椅等部件。

在电子产品中，弹簧刚度用于设计各种振动器件和减震器件等。

弹簧刚度的测量与测试是保证弹簧性能的关键环节。

常用的测量方法有静态测量法和动态测量法。

静态测量法是通过测量弹簧在静态载荷下的变形量来计算弹簧刚度。

动态测量法则是通过测量弹簧在动态载荷下的响应来计算弹簧刚度。

测试设备包括万能试验机、动态试验机和电子测量仪等。

波簧力值计算公式
公式：k=Gd^4/8nD^3
上面公式里每项代表的含义为：
G=剪切弹性模量[MPa]（G值大小为：碳钢，不锈钢）
d=线径[mm，in]
n=有效率圈数[-]
D=中心直径[mm，in]
k=弹簧系数[N/mm，lb/in]
这个公式是弹簧刚度的计算公式，刚度乘以工作行程就等于这个弹簧的工作力度。

通过上式，我们可以得出结论，放大弹簧的参数必须由：材料、线径、中心直径、有
效率圈数、弹簧总长，工作高度，市场需求力度这些参数共同组成。

如果对力度没特别建
议的'弹簧，可以不提供更多弹簧的工作高度和市场需求力度的参数。

什么是弹力
物体在力的促进作用下出现的形状或体积发生改变叫作应力。

在外力暂停促进作用后，能恢复原状的应力叫作弹性应力。

出现应力的物体，由于必须恢复原状，必须对跟它碰触
的物体产生力的促进作用。

这种促进作用叫做弹力。

即为，在弹性限度范围之内，物体对
并使物体出现应力的施力物产生的力叫做弹力。

日常生活中观察到的相互作用，无论是推、拉、提、举，还是牵引列车、锻打工件、
击球、弯弓射箭等，都是在物体与物体接触时才会发生的，这种相互作用可称为接触力。

接触力按其性质可归纳为弹力和摩擦力，它们本质上都是由电磁力引起的。

弹力就是接触力，弹力就可以存有于物体的相互碰触处，但相互碰触的物体之间，并
不一定存有弹力的促进作用。

因为弹力的产生不仅必须碰触，还要存有相互作用。

弹簧力值的计算通常涉及弹簧的刚度（弹性系数）和变形量。

下面是一些常见的弹簧力值计算公式和相关参数：
弹簧力值公式：F = k * x
其中，F表示弹簧的力值，k表示弹簧的刚度（弹性系数），x表示弹簧的变形量。

弹性系数（刚度）：弹性系数表示弹簧单位变形量产生的力值。

它可以通过实验测试或根据弹簧的材料和几何参数计算得出。

变形量：变形量是指弹簧在受力下发生的形变或压缩量。

它可以是弹簧的线性变化（如拉伸或压缩）或非线性变化（如弯曲）。

需要注意的是，弹簧力值的计算涉及到弹簧的特性和受力情况，具体的计算方法和参数选择应根据实际情况进行。

如果涉及到复杂的弹簧系统或非线性变形，可能需要进行更复杂的数学建模和分析。