第二章例题
- 格式:ppt
- 大小:940.00 KB
- 文档页数:37


第二章增值税法【例题1】某商城以旧换新销售5台电冰箱,新冰箱每台零售价3000元,旧冰箱每台作价100元,每台冰箱收取差价2900元,计算该项业务的增值税的销项税额。
【例题2】某首饰商城为增值税一般纳税人,2012年5月发生以下业务:采取“以旧换新”方式向消费者销售金项链2000条,新项链每条零售价0.25万元,旧项链每条作价0.22万元,每条项链取得差价款0.03万元. 计算该项业务的增值税的销项税额。
【例题3】某企业收购一批免税农产品用于生产,在税务机关批准使用的专用收购凭证上注明价款100000元,其可计算抵扣多少增值税进项税?记账采购成本是多少?【例题4】某厂一个月前外购一批材料因保管不善毁损,账面成本10000元,其购进的增值税应如何处理?【例题5】某厂的一批产成品因保管不善毁损,账面成本10000元,外购比例60%,其购进的增值税应如何处理?【例题6】某生产企业属增值税小规模纳税人,2012年6月销售使用过的小汽车1辆,取得含税收入72100元,计算该企业应缴纳增值税。
【练习题1】某制造设备的生产企业2009年业务如下(所含该抵税的凭证均经过认证):①购入一批原材料用于生产,价款200000元,增值税34000元;②外购一批床单用于职工福利,价款10000元,增值税1700元;③外购一批涂料用于装修办公室,价款50000元,增值税8500元;④外购一批食品用于交际应酬,价款3000元,增值税510元⑤外购一批办公用品用于管理部门使用,价款4000元,增值税680元计算该企业当月可抵扣的增值税进项税。
【练习题2】某生产果酒企业为增值税一般纳税人,月销售收入为140.4万元(含税),当期发出包装物收取押金为4.68万元, 当期逾期未归还包装物押金为2.34万元。
该企业本期应申报的销项税额为多少?【作业题】某商业企业是增值税一般纳税人,2009年4月初留抵税额2000元,4月发生下列业务:(1)购入商品一批,取得认证税控发票,价款10000元,税款1700元;(2)3个月前从农民手中收购的一批粮食毁损,账面成本5220元;(3)从农民手中收购大豆1吨,税务机关规定的收购凭证上注明收购款1500元;(4)从小规模纳税人处购买商品一批,取得税务机关代开的发票,价款30000元,税款900元,款已付,货物未入库,发票已认证;(5)购买建材一批用于修缮仓库,价款20000元,税款3400元;(6)零售日用商品,取得含税收入150000元;(7)将2个月前购入的一批布料捐赠受灾地区,账面成本20000元,同类不含税销售价格30000元。

第二章负债例题【例1】甲公司为增值税一般纳税人,适用的增值税税率为17%。
2010年12月甲公司董事会决定将本公司生产的500件产品作为福利发放给公司人员,其中生产工人400人,总部管理人员100人。
该批产品单件成本为1.2万元,市场销售价格为每件2万元(不含增值税),不考虑其他相关税费。
【例2】B公司2010年7月有关职工薪酬业务如下:(1)为生产工人100人提供免费住宿,月计提折旧合计为3万元。
(2)为总部部门经理级别以上职工每人提供一辆汽车免费使用,该公司总部共有部门经理以上职工10名,假定每辆汽车每月计提折旧0.2万元;【例3】企业缴纳的下列税金,应通过“应交税费”科目核算的有()。
(多选)A.印花税B.耕地占用税C.房产税D.土地增值税【例4】不通过“应交税费”科目核算?【例5】某企业为增值税一般纳税人,2010年实际已交纳税金情况如下:房产税850万元,消费税150万元,城市维护建设税70万元,车船税0.5万元,耕地占用税1.5万元,所得税120万元。
上述各项税金应记入“应交税费”科目的金额是()万元。
(单选)A.1 190B.1 190.5C.1 191.5D.1 192【例6】(单选)甲公司因意外火灾(管理不善导致)毁损一批存货,其中原材料的成本为100万元,增值税额l7万元;库存商品的实际成本800万元,经确认损失外购材料的增值税34万元。
该企业的有关会计分录不正确的是()。
A.借记“待处理财产损溢”科目951万元B.贷记“原材料”科目l00万元C.贷记“库存商品”科目800万元D.贷记“应交税费——应交增值税(进项税额转出)科目17万元【例7】【思考问题】如果为自然灾害造成的损失,如何处理?【例8】(多选)下列各项,增值税一般纳税企业需要转出进项税额的有()。
A.自制产成品用于职工福利B.自制产成品用于对外投资C.外购的生产用原材料发生非正常损失D.外购的生产用原材料改用于自建厂房【例9】(单选)2010年乙公司发出原材料一批,成本为100万元,其购入时支付的增值税为17万元。


第二章 恒定电流经典例题典型例题1——电流的计算例:某电解池,如果在1秒钟内共有5×1018个二价正离子和1.0×1019个一价负离子通过面积为0.1米2的某截面,那么通过这个截面的电流强度是( )(A)0安培; (B)0.8安培; (C)1.6安培; (D)3.2安培。
【课堂练习】有一横截面积为S 的铜导线,流经其中的电流为I ,设每单位体积的导线有n 个自由电子,电子电量为e ,此时电子的定向转动速度为υ,在△t 时间内,通过导体横截面的自由电子数目可表示为( )A .n υS △tB .n υ△tC .I △t/eD .I △t/(Se)典型例题2——关于白炽灯使用实际伏安特性曲线一个标有“220V ,60W ”的白炽灯泡,加上的电压U 由零逐渐增大到220V ,在此过程中电压U 和电流I 的关系可用图线表示,在留给出的四个图中,肯定不符合实际情况的是( )典型例题3——关于电流表的改装有一只满偏电流Ig=5mA ,内阻Ω=400Rg 的电流表G .若把它改装成量程为10V 的电压表,应______联一个______Ω的分压电阻.该电压表的内阻为______Ω;若把他改装成量程为3A 的电流表,应______联一个____Ω的分流电阻,该电流表的内阻为_____Ω.典型例题4——关于直流电动机的线圈电阻例:某一用直流电动机提升重物的装置如图所示,重物质量m=50kg ,电源提供恒定电压U=110V ,不计各处摩擦。
当电动机以v=0.90m/s 的恒定速度向上提升重物时,电路中的电流强度I=5A ,由此可知电动机线圈的电阻R=____Ω。
【讨论】如果电动机的转子被卡住,则通过电动机线圈的电流多大?线圈上的发热功率多大?【课堂练习】如图所示的电路中,某录音机用的直流电机通过一串联电阻R =5Ω接在电动势为ζ=6V ,内阻r 2=0.5Ω的电池上,流过电机的电流强度为I =0.3A ,电动机绕组的电阻为r 1=1Ω,求:(1)电动机消耗的电功率; (2)电机每分钟产生的热量Q ;(3)电动机的机械功率; (4)电源的输出功率;(5)电源的效率; (6)电机的效率.典型例题5——电源的外特性曲线如图所示中的图线a 是某电源的外特性曲线,图线b 是电阻R 的伏安特性曲线,这个电源的电动势为________V ,内阻等于________Ω.用这个电源和两个电阻R 串联形成闭合电路,电源的输出功率为______W .典型例题6——闭合电路的欧姆定律如图所示,Ω=51R ,Ω=92R .当开关S 断开时,电流表的示数为A 2.0=I ,当开关S 闭合时,电流表的示数为A 3.0='I .求:(1)电源的电动势和内阻.(2)S 断开和闭合两种情况下,电源的输出功率.典型例题7——电容器在电路中的连接如图所示,电阻Ω=21R ,Ω=42R ,Ω=63R .电容F 5μ=C .电源电压V 6=U 不变,分别求电键S 断开和闭合两种情况下,电路达稳定状态后电容器的带电量.典型例题8——可变电阻的阻值变化对电流以及电压的影响1、如图所示的电路中,当可变电阻R的值增大时()A、ab两点间的电压增大B、ab两点间的电压减小C、通过电阻R的电流增大D、通过电阻R的电流减小2、如图所示的电路中,当滑动变阻器的滑动头向上移动时,下列结论正确的是()A.电压表的示数增大,电流表的示数减小.B.电压表和电流表的示数都增大.C.电压表的示数减小,电流表的示数增大.D.电压表和电流表的示数都减小.3、如图所示,用两节干电池点亮几个小灯泡,当逐一闭合电键,接入灯泡增多时,以下说法正确的是()A.灯少时各灯较亮,灯多时各灯较暗B.各灯两端的电压在灯多时较低C.通过电池的电流在灯多时较大D.电池输出功率灯多时较大答案:例题1、D 课堂练习AC例题2、ACD例题3、串1600 2000 并0.67 0.67例题4、4 27.5A,3025W 课堂练习:1.305W,5.4J,1.215W,1.755W,97.5%,93% 例题5、6,2,2.88例题6、3V,1,断开0.56 闭合0.81例题7、断开10-5C,闭合2*10-5C例题8、AD A ABC。



市场证券组合的报酬率为13%,国库券的利息率为5%。
要求:(1)计算市场风险报酬率;(2)当β值为1.5时,必要报酬率应为多少?(3)如果一个投资计划的β值为0.8,期望报酬率为11%,是否应当进行投资?(4)如果某种股票的必要报酬率为12.2%,其β值应为多少?(10分)1.市场风险报酬率=市场证券组合的报酬率-国库券的利息率=13%-5%=8%.2.必要报酬率=无风险利率+β*(预期报酬率-无风险利率)=8%+1.5*(13%-8%)=15.5%3投资计划必要报酬率=无风险利率+β*(预期报酬率-无风险利率)=8%+0.8*(11%-8%)=10.4%投资计划必要报酬率10.4%<期望报酬率为11%,所以不应当进行投资;4.12.2%=8%+β*(12.2%-8%)β=1第二章例题总结例一、将1000元钱存入银行,年利息率为7%,按复利计算,5年后终值应为多少?解答:FV5=P V·(1+i)5=1000*(1+7%)5=1403元或FV5=PV·FVIF5,%,7=1000*1.403=1043元例二、若计划在3年以后得到2000元,年利息率为8%,复利计息,则现在应存金额为多少?解答:PV=FVn ·PVIF3%,8=2000*0.794=1588元例三、某人在5年中每年年底存入银行1000元,年存款利率8%,复利计息,则第5年年末年金终值为多少元钱?解答:FV A5=A·FVIFA5,%,8=1000*5.867=5867元例四、某人准备在今后5年中每年年末从银行取1000元,如果利息率为10%,则现在应存入多少元钱?解答:PVA5=A·PVIFA5%,10=1000*3.791=3791元例五、某人每年年初存入银行1000元,银行年存款利率为8%,则第10年年末约本利和应为多少?解答:XFVA10=1000·FVIFA10%,8·(1+8%)=1000*14.487*1.08=15646元或XFVA10=1000*(FAIFA11%,8-1)=1000*(16.645-1)=15645元例六、某企业租用一套设备,在10年中每年年初要支付租金5000元,年利息率为8%,则这些租金的现值为多少?解答:XPVA10=5000·PVIFA10%,8·(1+8%)=5000*6.71*1.08=36234元或XPVA10=5000·(PVIFA9%,8+1)=5000*(6.247+1)=36235元例七、某企业向银行借入一笔款项,银行贷款的年利息率为8%,银行规定前10年不需要还本付息,但第11-12年每年年末偿还本息1000元,则这笔款项的现值是多少?解答:V0=1000·PVIFA10%,8·PVIF10%,8=1000*6.710*0.463=3107元或V0=1000·(PVIFA20%,8- PVIFA10%,8)=1000*(9.818-6.710)=3108元例八、一项每年年底的收入为800元的永续年金投资,利息率为8%,则其现值为多少?解答:V0=800*%81=10000元例九、某人每年年末都将节省下来的工资存入银行,其存款额如下表所示,贴现率为5%,求这笔不等额存款的现值。


例1-1某台离心泵进、出口压力表读数分别为220mmHg(真空度)及1.7kgf/cm2(表压)。
若当地大气压力为760mmHg,试求它们的绝对压力各为若干(以法定单位表示)?解泵进口绝对压力P1=760-220=540mmHg=7.2*104Pa泵出口绝对压力P2=1.7+1.033=2.733kgf/cm2=2.68*105Pa例1-2如附图所示,常温水在管道中流过。
为测定a、b两点的压力差,安装一U型压差计,试计算a、b两点的压力差为若干?已知水与汞的密度分别为1000kg/m3及13600kg/m3。
解取管道截面a、b处压力分别为pa与pb。
根据连续、静止的同一液体内同一水平面上各点压力相等的原理,则p 1'=p1(a)因 p1'=pa-xρH2Ogp1=RρHgg+2=RρHgg+p2'=R ρHg g+p b -(R +x )ρH2Og根据式(a ),则 p a -p b =x ρH2Og +R ρHg g -(R +x )ρH2Og=R ρHg g -(R +x )ρH2Og=0.1(13600-1000)9.81 =1.24*104Pa例1-3 为了确定容器中石油产品的液面,采用如附图所示的装置。
压缩空气用调节阀1调节流量,使其流量控制得很小,只要在鼓泡观察器2内有气泡缓慢逸出即可。
因此,气体通过吹气管4的流动阻力可忽略不计。
吹气管内压力用U 管压差计3来测量。
压差计读数R 的大小,反映贮罐5内液面高度。
指示液为汞。
1.分别由a 管或由b管输送空气时,压差计读数分别为R 1或R 2,试推导R 1、R 2分别同Z 1、Z 2的关系。
2.当(Z 1-Z 2)=1.5m ,R 1=0.15m ,R 2=0.06m 时,试求石油产品的密度ρP 及Z 1。
解 (1)在本例附图所示的流程中,由于空气通往石油产品时,鼓泡速度很慢,可以当作静止流体处理。
因此可以从压差计读数R 1,求出液面高度Z 1,即(a )(b)(2)将式(a)减去式(b)并经整理得故例1-4以内径105mm的钢管输送压力为2atm、温度为120℃的空气。
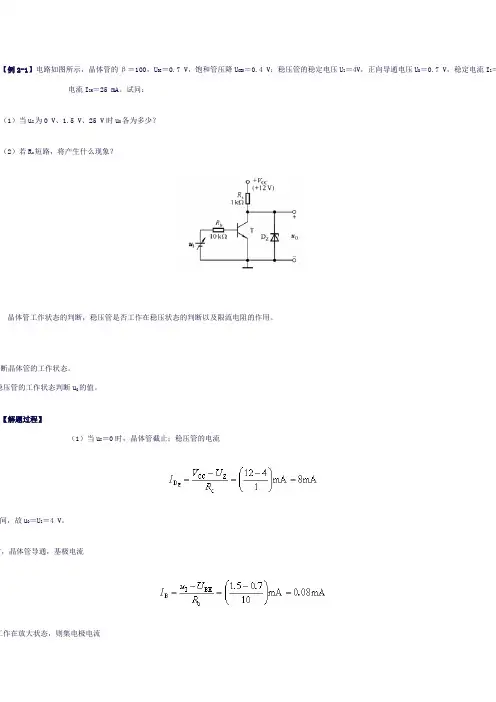
【例2-1】电路如图所示,晶体管的β=100,U BE=0.7 V,饱和管压降U CES=0.4 V;稳压管的稳定电压U Z=4V,正向导通电压U D=0.7 V,稳定电流I Z=5 mA,最大稳定电流I ZM=25 mA。
试问:(1)当u I为0 V、1.5 V、25 V时u O各为多少?(2)若R c短路,将产生什么现象?【相关知识】晶体管工作状态的判断,稳压管是否工作在稳压状态的判断以及限流电阻的作用。
【解题思路】(1)根据u I的值判断晶体管的工作状态。
(2)根据稳压管的工作状态判断u O的值。
【解题过程】(1)当u I=0时,晶体管截止;稳压管的电流在I Z和I ZM之间,故u O=U Z=4 V。
当u I=15V时,晶体管导通,基极电流假设晶体管工作在放大状态,则集电极电流由于u O>U CES=0.4 V,说明假设成立,即晶体管工作在放大状态。
值得指出的是,虽然当u I为0 V和1.5 V时u O均为4 V,但是原因不同;前者因晶体管截止、稳压管工作在稳压区,且稳定电压为4 V,使u O=4 V;后者因晶体管工作在放大区使u O=4 V,此时稳压管因电流为零而截止。
当u I=2.5 V时,晶体管导通,基极电流假设晶体管工作在放大状态,则集电极电流在正电源供电的情况下,u O不可能小于零,故假设不成立,说明晶体管工作在饱和状态。
实际上,也可以假设晶体管工作在饱和状态,求出临界饱和时的基极电流为I B=0.18 mA>I BS,说明假设成立,即晶体管工作在饱和状态。
(2)若R c短路,电源电压将加在稳压管两端,使稳压管损坏。
若稳压管烧断,则u O=V CC=12 V。
若稳压管烧成短路,则将电源短路;如果电源没有短路保护措施,则也将因输出电流过大而损坏【方法总结】(1)晶体管工作状态的判断:对于NPN型管,若u BE>U on(开启电压),则处于导通状态;若同时满足U C≥U B>U E,则处于放大状态,I C=βI B;若此时基极电流则处于饱和状态,式中I CS为集电极饱和电流,I BS是使管子临界饱和时的基极电流。
第二章 运动和力【例题精讲】例2-1 两个质量相等的小球由一轻弹簧相连接,再用一细绳悬挂于天花板上,处于静止状态,如图所示。
将绳子剪断的瞬间,球1和球2的加速度分别为 A. a 1=g,a 2=g B. a 1=0,a 2=gC. a 1=g,a 2=0D. a 1=2g,a 2=0 [ D ] 例2-2质量为m 的物体自空中落下,它除受重力外,还受到一个与速度平方成正比的阻力的作用,比例系数为k ,k 为正值常量。
该下落物体的收尾速度(即最后物体作匀速运动时的速度)将是A.k mg B. kg2 C. gk D. gk [ A ]例2-3如图所示,质量为m 的物体A 用平行于斜面的细线连结置于光滑的斜面上,若斜面向左方作加速运动,当物体开始脱离斜面时,它的加速度的大小为(A) g sinθ (B) g cos θ (C) g cot θ(D) g tan θ[ C ] 例2-4 判断下列说法是否正确?说明理由。
(1) 质点作圆周运动时受到的作用力中,指向圆心的力便是向心力,不指向圆心的力不是向心力。
(2) 质点作圆周运动时,所受的合外力一定指向圆心。
【答】 (1) 不正确。
向心力是质点所受合外力在法向方向的分量。
质点受到的作用力中,只要法向分量不为零,它对向心力就有贡献,不管它指向圆心还是不指向圆心,但它可能只提供向心力的一部分。
即使某个力指向圆心,也不能说它就是向心力,这要看是否还有其它力的法向分量。
(2) 不正确。
作圆周运动的质点,所受合外力有两个分量,一个是指向圆心的法向分量,另一个是切向分量,只要质点不作匀速率圆周运动,它的切向分量就不为零,所受合外力就不指向圆心。
例2-5 如图所示,用一斜向上的力F (与水平成30°角),将一重为G 的木块压靠在竖直壁面上,如果不论用怎样大的力F ,都不能使木块向上滑动,则说明木块与壁面间的静摩擦系数μ的大小为 A. 21≥μ B. 31≥μ C. 3≥μ D. 32≥μ [ B ]例2-6 质量为m 的子弹以速度v 0水平射入沙土中,设子弹所受阻力与速度反向,大小与速度成正比,比例系数为k ,忽略子弹的重力,求:(1)子弹射入沙土后,速度随时间变化关系式;(2)子弹进入沙土的最大深度。
【例1·单选题】已知(F/A,10%,9)=13.579,(F/A,10%,11)=18.531。
则10年,利率10%的预付年金终值系数为( A )。
A.17.531B.15.937C.14.579D.12.579【解析】预付年金终值系数与普通年金终值系数相比期数加1,系数减1,所以10年,10%的预付年金终值系数=18.531-1=17.531【例2·计算题】某人拟购房,开发商提出两种方案,一是5年后一次性付120万元,另一方案是从现在起每年年初付20万元,连续5年,若目前的银行存款利率是7%,应如何付款?【答案】方案1终值:F1=120万元方案2的终值:F2=20×(F/A,7%,5)×(1+7%)=123.065(万元)或 F2=20×(F/A,7%,6)-20=123.066(万元)所以应选择5年后一次性付120万元。
【例3·计算题】某人拟购房,开发商提出两种方案,一是现在一次性付80万元,另一方案是从现在起每年年初付20万元,连续支付5年,若目前的银行贷款利率是7%,应如何付款?【答案】方案1现值:P1=80万元方案2的现值:P2=20×(P/A,7%,5)×(1+7%)=87.744(万元)或 P2=20+20×(P/A,7%,4)=87.744(万元)应选择现在一次性付80万元。
【例4·单选题】有一项年金,前3年无流入,后5年每年年初流入500万元,假设年利率为10%,其现值为(B)万元。
A.1994.59B.1565.68C.1813.48D.1423.21【解析】本题是递延年金现值计算的问题,对于递延年金现值计算关键是确定正确的递延期。
本题总的期限为8年,由于后5年每年年初有流量,即在第4~8年的每年年初也就是第3~7年的每年年末有流量,从图中可以看出与普通年金相比,少了第1年末和第2年末的两期A,所以递延期为2,因此现值=500×(P/A,10%,5)×(P/F,10%,2)=500×3.791×0.826=1565.68(万元)。
第二章、一元函数微分学题型一、导数与微分的计算【例题2.2】设函数f (x )在(0,+∞)内有定义,且对任意的x >0,y >0,都有f (xy )=f (x )+f (y ),又f (1)存在且等于a ,求f ′(x )和f (x )【例题2.4】设函数f (x )=g (x )−cos x x,x =00,x =0其中,g (x )具有二阶连续导数,且g (0)=1,确定a 的值,使得f (x )在点x 0=0处连续,并求出f ′(x ),同时讨论f ′(x )在点x =0处的连续性【例题2.11】(利用Taylor 公式求高阶导数)设函数f (x )=sin 6x +cos 6x ,求f (n )(x )【例题2.13】设函数f (x )=11−x −x2求f (n )(0)题型二、微分中值定理的应用【例题2.21】求极限lim n →∞n n √n +1−n +1√n n √2−1 ln n 【例题2.22】求极限I =limx →0+e (1+x )1x−(1+x )exx 2【例题2.23】设函数f (x ),g (x )均为(0,+∞)上的非常数可导函数,且对任意的x,y ∈(−∞,+∞),恒有f (x +y )=f (x )f (y )−g (x )g (y ),g (x +y )=f (x )g (y )+g (x )f (y )已知f ′(0)=0,证明:对一切x ∈(−∞,+∞),恒有f 2(x )+g 2(x )=1【例题2.25】设n 为正整数,证明:对任意实数λ≥1,有nk =11(1+k )k√λ<λ【例题2.28】设f (x )在区间[−a,a ]上具有二阶连续导数,f (0)=0,(1)写出f (x )的带拉格朗日余项的一阶麦克劳林公式;(2)证明:在区间[a,a ]上至少存在一点η,使得a 3f ′′(η)=3a−a f(x )dx【例题2.29】设函数y =f (x )((−1,1)内具有二阶连续导数,且f ′′(x )=0,证明:(1)对于(−1,1)内任意x =0,存在唯一的θ(x ),使得f (x )=f (0)+xf ′(θ(x )x )(2)lim x →0θ(x )=12题型三、导数的应用【例题2.30】设在(−∞,+∞)上f ′′(x )>0,f (0)<0,证明:f (x )x分别在(−∞,0)和(0,+∞)上单调递增【例题2.31】设函数f (x )=(1+x )1x ,x >0确定常数A,B,C ,使得当x →0+时,f (x )=Ax 2+Bx +C +o x 2【例题2.43】设函数f (x )在区间(−π,π)内连续可导,且满足f ′′(x )=sin 2x −[f ′(x )]2=13xg (x ),其中g (x )为连续函数,满足当x =0,g (x )x >0且lim x →0g (x )x =34,证明:(1)点x =0是f (x )在区间(−π,π)内唯一的极值点,且是极小值点;(2)曲线g =f (x )在区间(−π,π)内是向上凹的题型四、介值定理的论证方法【例题2.54】设函数f (x )在[0,1]上连续,(0,1)可导,并且f (0)=f (1)=0,已知对任意的x ∈(0,1),都有f ′′(x )>0,且f (x )在[0,1]上的最小值m <0,求证:(1)对任意正整数n 都存在唯一的x n ∈(0,1),使得f ′(x n )=m n;(2)数列{x n }收敛,且flim n →∞x n=m【例题2.58】设0<a <b,f (x )在[a,b ]上连续,在(a,b )内可导,求证:存在ξ,ηϵ(a,b ),使得f ′(ξ)=a +b 2ηf ′(η)【例题2.60】设函数f (x )在[a,b ]上连续, ba f (x )dx =b a f (x )e x dx =0,求证:f (x )在(a,b )内至少存在两个零点【例题2.61】f (x )在区间[a,b ]上连续,在(0,1)内可导,f ′(x )>0,f (0)=0,f (1)=1,证明:对任意给定的正数λ1,λ2,λ3···λn ,在(0,1)内存在不同的数,x 1,x 2,x 3···x n 使得ni =1λif ′(x i )=ni =1λi【例题2.62】设函数f (x )=x n +x −1,其中n 为正整数,证明:(1)若n 为奇数,则存在唯一的正实数x n ,使得f (x n )=0(2)若n 为奇数,则存在两个实数根x n ,y n ,且x n <0,y n >0(3)极限lim n →∞x n ,lim n →∞y 2n 都存在,并求出它们的值【例题2.63】设实数a,b ,满足b −a >π,函数f (x )在开区间(a,b )内可导,证明:至少存在一点ξ∈(a,b ),使得f 2(ξ)+1>f ′(ξ)。
第二章例题题1 评定土的密实度条件:某工程房心填土经夯实后取土样做实验,环刀容积为200cm 3,环刀内土重368g 。
从环内取土29.4g ,烘干后干土重25.2g 。
房心填土夯实后干密度要求达到1.55g/cm 3。
要求:确定房心填土密度是否符合要求。
答案:1. 求填土密度3/84.1200368cm g v m ===ρ2. 求土的含水量%7.16%1002.252.254.29%100=⨯-=⨯=s W m m ω333.求土的干密度 33/55.1/58.1167.0184.11cm g cm g w d >=+=+=ρρ符合要求。
题2 土的物理指标计算(一)条件:某填土工程的填方量为V=30000m 3,压实后的干密度要求不小于3/70.1m t d =ρ,压实时的最优含水量为%18=op w ,取土现场土料,天然含水量%15=w ,天然密度3/64.1m t =ρ。
要求:确定1.需运来多少立方米的土料?2.为使土料达到最优含水量,在压实前需加多少吨水? 答案:解法一:1. 当土料为最优含水量%18=op ω是填土夯实后的密度1ρ和总土重1m31/006.2)18.01(70.1)1(m t w op d =+=+=ρρt V m 6018030000006.211=⨯==ρ 2. 求当土料为天然含水量%15=w 时,压实后密度2ρ和总土重2m 32/955.1)15.01(70.1)1(m t w d =+=+=ρρt V m 5865030000955.122=⨯==ρ3. 求需运来土料数量323576264.158650m m V ===ρ 4. 求压实前需加水量t m m m w 1530586506018021=-=-=解法二: 1. 求取土现场土料的干密度 3/4261.115.0164.11m t w d =+=+=ρρ 2. 压实后填土的干土重t V m d s 510003000070.12=⨯==ρ 3. 取土现场待运土的总体积 32357624261.151000m m V ds ===ρ 4. 压实前所需加水数量t w V m d w 1530%)15%18(357624261.1=-⨯⨯=∆∙∙=ρ题3 土的物理指标计算(二)条件:由钻探取得某原装土样,经试验测得土的天然密度3/70.1m t =ρ,含水量%2.13=w ,土粒相对密度69.2=s d 。