一位插值、二维插值
- 格式:ppt
- 大小:159.50 KB
- 文档页数:28

二维插值原理
二维插值是一种基于已知数据点的二维曲线或曲面估计方法。
它广泛应用于图像处理、地理信息系统、物理模拟等领域。
在二维插值中,我们假设已知的数据点位于一个二维平面上,每个数据点都有一个对应的数值。
我们的目标是通过这些已知数据点,来推断出未知位置上的数值。
常见的二维插值方法包括线性插值、拉格朗日插值和样条插值等。
线性插值是最简单的二维插值方法之一。
它假设在两个相邻数据点之间,数值的变化是线性的。
我们可以通过这两个相邻数据点之间的线段来估计未知位置上的数值。
拉格朗日插值则使用一个多项式来拟合已知数据点。
该多项式会经过所有已知数据点,并通过它们来估计未知位置上的数值。
它的优点是能够完全通过已知数据点来插值,但在高维情况下容易产生过拟合问题。
样条插值是一种基于局部插值的方法。
它通过在每个局部区域上拟合一个低阶多项式来实现插值。
这些局部多项式在相邻区域处满足平滑和连续性条件,从而得到整体平滑的插值结果。
除了上述方法外,还有其他一些二维插值方法,如反距离加权插值和克里金插值等。
总的来说,二维插值通过已知数据点之间的关系来估计未知位置上的数值。
不同的插值方法在计算复杂度、精度和平滑性等方面存在差异,根据具体应用场景的需求,选择合适的插值方法是非常重要的。


二维插值算法原理二维插值算法是一种在二维空间中根据已知的数据点来估计未知位置上的数值的算法。
它广泛应用于图像处理、地理信息系统和数值模拟等领域。
其原理是基于数学上的连续性和局部平滑性假设,通过利用已知数据点的信息,对未知位置上的数值进行估计。
二维插值算法的基本思想是根据已知的数据点的数值和位置,构建出一个合适的数学模型。
对于每一个未知位置,通过模型可以预测其数值。
这个模型常常是一个多项式函数或者其它形式的连续函数,以便于能够在整个二维空间中插值。
其中最常见的二维插值算法是双线性插值。
双线性插值法假设每个未知位置上的数值都是由其相邻四个已知点的数值线性插值得到的。
具体而言,假设已知的四个点为A、B、C、D,它们的数值分别为f(A)、f(B)、f(C)、f(D)。
对于未知位置P,可以通过以下公式计算得到其数值f(P):f(P) = (1 - u)(1 - v) f(A) + u(1 - v) f(B) + (1 - u)v f(C) + uv f(D)其中,u和v是分别表示未知位置在水平和垂直方向上的相对位置的权重。
这种方法实现简单,计算效率高,可以较为准确地插值出未知位置上的数值。
除了双线性插值之外,还有其它一些更复杂的二维插值算法,如三次样条插值、Kriging插值等。
这些算法在不同的应用场景下具有不同的优势。
例如,三次样条插值在处理光滑函数时效果较好,而Kriging插值则适用于处理具有空间相关性的数据。
选择适合的插值算法可以提高插值结果的质量。
在实际应用中,二维插值算法在处理图像、地理数据和模拟结果等方面具有重要意义。
通过插值算法,可以将有限的离散数据转换为连续的函数,从而对未知位置上的数值进行预测和分析。
同时,它也为数据的可视化提供了基础,使得我们能够更直观地理解数据的分布和变化规律。
总之,二维插值算法是一种有指导意义的数学工具,它通过在二维空间中根据有限的已知数据点估计未知位置上的数值。

MATLAB中的插值函数命令1:interp1功能:一维数据插值(表格查找)。
该命令对数据点之间计算内插值。
它找出一元函数f(x)在中间点的数值。
其中函数f(x)由所给数据决定。
x:原始数据点Y:原始数据点xi:插值点Yi:插值点格式(1) yi = interp1(x,Y,xi) 返回插值向量yi,每一元素对应于参量xi,同时由向量x 与Y 的内插值决定。
参量x 指定数据Y 的点。
若Y 为一矩阵,则按Y 的每列计算。
yi 是阶数为length(xi)*size(Y,2)的输出矩阵。
(2) yi = interp1(Y,xi) 假定x=1:N,其中N 为向量Y 的长度,或者为矩阵Y 的行数。
(3) yi = interp1(x,Y,xi,method) 用指定的算法计算插值:’nearest’:最近邻点插值,直接完成计算;’linear’:线性插值(缺省方式),直接完成计算;’spline’:三次样条函数插值。
对于该方法,命令interp1 调用函数spline、ppval、mkpp、umkpp。
这些命令生成一系列用于分段多项式操作的函数。
命令spline 用它们执行三次样条函数插值;’pchip’:分段三次Hermite 插值。
对于该方法,命令interp1 调用函数pchip,用于对向量x 与y 执行分段三次内插值。
该方法保留单调性与数据的外形;’cubic’:与’pchip’操作相同;’v5cubic’:在MATLAB 5.0 中的三次插值。
对于超出x 范围的xi 的分量,使用方法’nearest’、’linear’、’v5cubic’的插值算法,相应地将返回NaN。
对其他的方法,interp1 将对超出的分量执行外插值算法。
(4)yi = interp1(x,Y,xi,method,'extrap')对于超出x 范围的xi 中的分量将执行特殊的外插值法extrap。
(5)yi = interp1(x,Y,xi,method,extrapval)确定超出x 范围的xi 中的分量的外插值extrapval,其值通常取NaN 或0。

simulink中查表模块的用法Simulink中查表模块的用法Simulink是一款广泛应用于系统建模与仿真的软件,其中查表模块是其常用的一个功能模块之一。
查表模块可以将输入信号映射到输出信号,通过预先定义好的表格来实现非线性函数的计算。
在本文中,我们将详细介绍Simulink中查表模块的用法。
一、查表模块概述1.1 查表模块的作用查表模块可以将输入信号映射到输出信号,通过预先定义好的表格来实现非线性函数的计算。
在实际应用中,我们常常需要对非线性函数进行处理,例如三角函数、指数函数等等。
此时就可以使用查表模块来进行处理。
1.2 查表模块的分类在Simulink中,查表模块主要分为两类:一维查找和二维插值。
其中一维查找主要适用于单变量情况下进行处理;而二维插值则适用于多变量情况下进行处理。
二、一维查找2.1 一维查找原理在一维情况下,我们可以将输入信号映射到输出信号上。
具体来说,在一维情况下,我们需要定义一个输入向量和一个输出向量,并且将它们存储在一个表格中。
当输入信号进入查表模块时,查表模块会根据输入信号在输入向量中的位置,找到对应的输出向量中的值,并将其作为输出信号输出。
2.2 一维查找实现在Simulink中,我们可以使用“Lookup Table”模块来实现一维查找。
具体步骤如下:(1)打开Simulink软件,在工具栏中选择“Sinks”下的“Scope”模块和“Sources”下的“Sine Wave”模块,并将它们连接起来。
(2)在工具栏中选择“Lookup Tables”下的“1-D L ookup Table”模块,并将其连接到Sine Wave模块的输出端口上。
(3)打开1-D Lookup Table模块,设置输入向量和输出向量,并保存设置。
(4)运行Simulink程序,观察Scope窗口中的波形图,即可看到一维查找结果。
三、二维插值3.1 二维插值原理在多变量情况下,我们需要使用二维插值来进行处理。
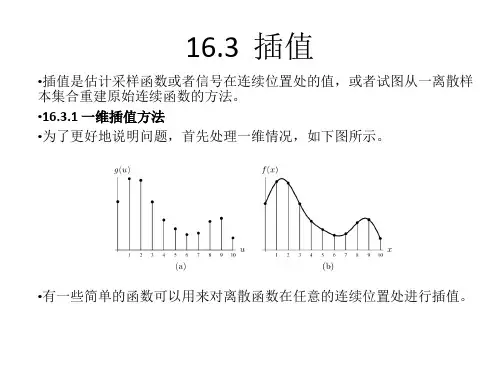

二维插值算法是一种用于在二维空间中估计未知数据点的方法。
它基于已知数据点的值和位置来推断未知数据点的值。
以下是常见的二维插值算法原理之一:双线性插值。
双线性插值是一种基于四个最近邻数据点进行估计的方法。
假设我们有一个二维网格,已知在四个顶点上的数据点的值和位置。
要估计某个位置处的未知数据点的值,双线性插值算法按照以下步骤进行:
1.找到目标位置的最近的四个已知数据点,通常称为左上、右上、左下和右下。
2.计算目标位置相对于这四个已知数据点的相对位置权重。
这可以通过计算目标位置到每个已知数据点的水平和垂直距离,然后根据距离来计算相对权重。
3.根据权重对四个已知数据点的值进行加权平均。
这里的加权平均可以使用线性插值进行计算。
4.得到目标位置的估计值作为插值结果。
双线性插值算法基于以下两个假设:
-在目标位置的附近,插值曲面在水平和垂直方向上是一致的,即呈现线性关系。
-已知数据点之间的变化不会很剧烈,即目标位置与附近已知数据点的值之间存在一定的连续性。
双线性插值算法是一种简单而有效的二维插值方法,适用于平滑、连续变化的数据。
但对于非线性、不规则的数据分布,或者存在边界情况的情况下,可能需要使用其他更复杂的插值算法来获得更准确的估计结果。

一维、二维与多维插值插值就是已知一组离散的数据点集,在集合内部某两个点之间预测函数值的方法。
一、一维插值插值运算是根据数据的分布规律,找到一个函数表达式可以连接已知的各点,并用此函数表达式预测两点之间任意位置上的函数值。
插值运算在信号处理和图像处理领域应用十分广泛。
1.一维插值函数的使用若已知的数据集是平面上的一组离散点集(x,y),则其相应的插值就是一维插值。
MATLAB中一维插值函数是interp1。
y=interp([x,]y,xi,[method],['extrap'],[extrapval]),[]代表可选。
method:'nearest','linear','spline','pchip','cubic','v5cubic'。
此m文件运行结果:放大π/2处:2.内插运算与外插运算(1)只对已知数据点集内部的点进行的插值运算称为内插,可比较准确的估测插值点上的函数值。
(2)当插值点落在已知数据集的外部时的插值称为外插,要估计外插函数值很难。
MATLAB对已知数据集外部点上函数值的预测都返回NaN,但可通过为interp1函数添加'extrap'参数指明也用于外插。
MATLAB的外插结果偏差较大。
二、二维插值已知点集在三维空间中的点的插值就二维插值问题,在图像处理中有广泛的应用。
二维插值函数是interp2,用法与一维插值函数interp1类似。
ZI=interp2(X, Y, Z, XI, YI, method, extrapval):在已知的(X,Y,Z)三维栅格点数据上,在(XI, YI)这些点上用method指定的方法估计函数值,外插使用'extrapval'。
二维插值中已知数据点集(X, Y)必须是栅格格式,一般用meshgrid函数产生。


图像插值算法总结插值指的是利⽤已知数据去预测未知数据,图像插值则是给定⼀个像素点,根据它周围像素点的信息来对该像素点的值进⾏预测。
当我们调整图⽚尺⼨或者对图⽚变形的时候常会⽤到图⽚插值。
⽐如说我们想把⼀个4x4的图⽚,就会产⽣⼀些新的像素点(如下图红点所⽰),如何给这些值赋值,就是图像插值所要解决的问题, 图⽚来源常见的插值算法可以分为两类:⾃适应和⾮⾃适应。
⾃适应的⽅法可以根据插值的内容来改变(尖锐的边缘或者是平滑的纹理),⾮⾃适应的⽅法对所有的像素点都进⾏同样的处理。
⾮⾃适应算法包括:最近邻,双线性,双三次,样条,sinc,lanczos等。
由于其复杂度, 这些插值的时候使⽤从0 to 256 (or more) 邻近像素。
包含越多的邻近像素,他们越精确,但是花费的时间也越长。
这些算法可以⽤来扭曲和缩放照⽚。
⾃适应算法包括许可软件中的许多专有算法,例如:Qimage,PhotoZoom Pro和正版Fractals。
这篇博客通过opencv中cv.resize()函数介绍⼀些⾮⾃适应性插值算法cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]]) → dst其中interpolation的选项包括,图⽚来源我们主要介绍最近邻,线性插值,双三次插值三种插值⽅式,下图是对双三次插值与⼀些⼀维和⼆维插值的⽐较。
⿊⾊和红⾊/黄⾊/绿⾊/蓝⾊点分别对应于插值点和相邻样本。
点的⾼度与其值相对应。
图⽚来源于最近邻顾名思义最近邻插值就是选取离⽬标点最近的点的值(⿊点,原来就存在的点)作为新的插⼊点的值,⽤opencv进⾏图像处理时,根据srcX = dstX* (srcWidth/dstWidth)srcY = dstY * (srcHeight/dstHeight)得到来计算⽬标像素在源图像中的位置,dstY代表输出图Y的坐标,srcY代表原图Y的坐标,srcX、srcY同理。
二维插值原理1. 插值的概念在数学和计算机科学中,插值是指根据已知数据点的值,通过构造合适的函数或曲线来估计未知数据点的值。
插值可以用于处理各种问题,如信号处理、图像处理、地理信息系统等。
2. 二维插值的基本原理二维插值是一种在二维空间中对离散数据进行估计的方法。
它可以用于网格数据、图像处理、地理信息系统等领域。
2.1 网格数据的插值在网格数据中,每个数据点都有一个坐标和一个数值。
通过已知数据点之间的数值关系,可以推断出其他位置上的数值。
二维插值方法通常使用邻近点之间的数值关系来进行估计。
2.1.1 最近邻插值最近邻插值是最简单和最直观的二维插值方法之一。
它假设目标位置上的数值与离其最近的已知数据点相同。
即将目标位置上最近的已知数据点的数值赋给目标位置。
最近邻插值适用于离散分布、边界清晰且没有明显趋势变化的数据。
但它的缺点是无法对目标位置周围的数据进行考虑,容易产生锯齿状的估计结果。
2.1.2 双线性插值双线性插值是一种基于线性关系的二维插值方法。
它假设目标位置上的数值与其周围四个已知数据点之间的线性关系相同。
双线性插值首先在目标位置周围找到最近的四个已知数据点,然后根据这四个点之间的数值关系进行估计。
具体而言,它使用目标位置距离四个已知数据点的距离来计算一个权重,然后将这四个点的数值按权重进行加权平均。
双线性插值适用于边界较为平滑、变化趋势较为连续的数据。
它能够考虑目标位置周围数据的变化情况,因此结果更加平滑。
但对于非线性或不规则分布的数据,双线性插值可能导致估计结果不准确。
2.1.3 其他插值方法除了最近邻插值和双线性插值外,还有许多其他二维插值方法。
例如:•双三次插值:基于三次多项式的插值方法,可以更好地拟合数据的曲线变化。
•样条插值:通过构造光滑的曲线来估计数据点之间的数值关系。
•克里金插值:基于空间自相关性的插值方法,可以考虑数据点之间的空间关系。
这些方法各有优缺点,适用于不同类型的数据和问题。
matlab插值函数用法在MATLAB 中,插值函数用于根据已知数据点的值,估计在这些数据点之间的位置的值。
MATLAB 提供了多种插值函数,常用的包括`interp1`、`interp2`、`interp3` 等。
下面是一些常见的MATLAB 插值函数的用法:1. interp1:一维插值函数,用于对一维数据进行插值。
```matlab% 创建一些示例数据x = 1:5;y = [3 7 2 5 8];% 定义插值点xi = 1:0.1:5;% 进行线性插值yi = interp1(x, y, xi, 'linear');```2. interp2:二维插值函数,用于对二维数据进行插值。
```matlab% 创建一些示例数据[X, Y] = meshgrid(1:5, 1:5);Z = peaks(5);% 定义插值点[XI, YI] = meshgrid(1:0.1:5, 1:0.1:5);% 进行二维插值ZI = interp2(X, Y, Z, XI, YI, 'linear');```3. interp3:三维插值函数,用于对三维数据进行插值。
```matlab% 创建一些示例数据[X, Y, Z] = meshgrid(1:5, 1:5, 1:5);V = rand(5, 5, 5);% 定义插值点[XI, YI, ZI] = meshgrid(1:0.1:5, 1:0.1:5, 1:0.1:5);% 进行三维插值VI = interp3(X, Y, Z, V, XI, YI, ZI, 'linear');```这些函数中的`'linear'` 参数表示使用线性插值方法,你也可以选择其他插值方法,比如`'nearest'`、`'spline'` 等。
此外,还可以根据需要进行更高级的插值操作,比如多项式插值、样条插值等。
二维数组使用拉格朗日插值算法拉格朗日插值算法是一种用于二维数组的插值方法。
它通过对已知数据点的函数值进行逼近,可以在缺失数据的位置上给出一个合理的函数值。
这种方法是一种非常常用的数值分析算法,它可以广泛应用于工程、科学和其他领域。
下面我们将详细介绍二维数组使用拉格朗日插值算法的原理和步骤。
1. 基本原理拉格朗日插值算法的基本原理是通过已知数据点的函数值,对未知的函数值进行逼近。
具体来说,对于一组给定的插值点:(x0, y0), (x1, y1), (x2, y2), ..., (xn, yn)我们要在这些点的函数值上进行插值,在某个未知点(x, y)处给出一个函数值f(x, y)。
这个问题的解决方法就是求出一个多项式P(x, y),满足在插值点处P(x0, y0) = y0,P(x1, y1) = y1,..., P(xn, yn) = yn,并且f(x, y) = P(x, y)。
拉格朗日插值算法的多项式表达式如下:P(x, y) = Σ yiLi(x, y)其中Li(x, y)表示拉格朗日基函数,它的表达式为:Li(x, y) = Π(j ≠ i) (x - xj) / (xi - xj) * Π(k ≠ i) (y - yk) / (yi - yk)2. 插值方法具体来说,二维数组的拉格朗日插值算法分为下面四个步骤:(1) 选择一组插值点,构造出拉格朗日插值多项式。
(2) 在未知点(x, y)处代入多项式,求出函数值。
(3) 去掉一些离未知点较远的数据点,加入离未知点较近的数据点,重新构造出拉格朗日插值多项式。
(4) 重复执行第二步和第三步,直到满足一定的误差要求。
3. 算法实现(1) 定义一个数组data[N][N],存储网格的值,其中N为网格大小。
(2) 定义插值点的坐标(xi, yi),插值点的函数值fi。
可以选择一个较小的插值点集,并且随着插值迭代的进行,插值点的数量会不断增加。
(4) 定义一个函数Lagrange(data, xi, yi),求出在(x, y)处的函数值。
Excel表格中二维数值插值的操作方法
我们进行了只有一个方向数据是数值型的数据检索时的插值方法,将对两个方向均为插值的情况进行分析。
今天,店铺就教大家在Excel 表格中二维数值插值的操作方法。
Excel表格中二维数值插值的操作步骤如下:
源数据表如下。
检索要求:根据温度厚度检索有关数据并进行双向插值。
思路:首先要获取有关的四个数据(红圈内)及相应的X,Y对应的四个数据,
然后进行插值计算。
X方向索引位置:=MATCH(B1,Sheet1!B2:I2,1),
Y方向索引位置:=MATCH(B2,Sheet1!A3:A12,1)。
对应的轴数值,
X1,=INDEX(Sheet1!B2:I2,B4)。
X2,=INDEX(Sheet1!B2:I2,B4+1)
Y1,=INDEX(Sheet1!A3:A13,B7)
Y2,=INDEX(Sheet1!A3:A13,B7+1)
对应数据,
D11,=INDEX(Sheet1!B3:I11,B7,B4),
D12,=INDEX(Sheet1!B3:I11,B7+1,B4),
D21,=INDEX(Sheet1!B3:I11,B7,B4+1),
D22,=INDEX(Sheet1!B3:I11,B7+1,B4+1)。
X方向插值计算,
y插1:=(B2-B8)/(B9-B8)*(B11-B10)+B10,
y插2:=(B2-B8)/(B9-B8)*(B13-B12)++B12,
最终值:=(B1-B5)/(B6-B5)*(B15-B14)+B14。
Excel表格中二维数值插值的操作。
matlab基于多维插值方法
在MATLAB中,多维插值是一种常见的数据处理方法,它可以用来估计在给定数据点之间的数值。
多维插值在处理图像处理、数值模拟和科学计算等领域都有广泛的应用。
MATLAB提供了几种多维插值的函数,包括interp1、interp2、interp3和griddedInterpolant等。
interp1函数可用于一维插值,interp2函数可用于二维插值,interp3函数可用于三维插值。
这些函数可以根据给定的数据点,通过线性插值、最近邻插值、三次样条插值等方法,计算出指定位置的插值结果。
例如,interp2可以用于在二维平面上进行插值计算,可以通过设置不同的插值方法和参数来获得不同的插值效果。
另外,griddedInterpolant函数提供了更加灵活和高效的多维插值方式。
它可以创建一个插值对象,通过指定不同的插值方法和边界条件,可以在多维数据点上进行插值计算。
这种方式相比于传统的interp函数,可以更好地处理不规则的数据点分布和高维数据的插值计算。
除了内置的插值函数,MATLAB还提供了丰富的可视化工具,可
以帮助用户分析和理解多维插值的结果。
用户可以通过绘制插值曲面、比较不同插值方法的效果等方式,对多维插值的结果进行直观的展示和分析。
总之,MATLAB提供了多种多维插值的方法和工具,用户可以根据具体的需求和数据特点,选择合适的插值函数和参数,进行高效准确的多维插值计算。
希望这些信息能够帮助你更好地理解MATLAB 中基于多维插值的方法。