下载文档原格式
二认识多位数教学目标：1.使学生结合现实的问题情境，了解十进制计数法，认识万级和亿级的计数单位，掌握千亿以内的数位顺序表；理解并掌握含有万级和亿级的数的组成，能正确地读、写多位数；会用算盘表示多位数；会比较多位数的大小，会把整万或整亿的数改写成“万”或“亿”作单位的数；理解近似数的含义，会用“四舍五入”法求一个数的近似数。
2.使学生经历从现实情境中抽象出数的过程，感受大数目的实际大小，能用大数目描述生活中一些事物的具体数量，获得良好的数感；能有根有据、有条有理地思考和表达，发展思维能力和解决问题的能力。
3.使学生在认识多位数的过程中，感受大数目在日常生活中的广泛应用，培养独立思考和合作交流的习惯；增强克服困难的勇气，树立学好数学的信心。
第一课时亿以内数的认识（1）教学目标：1.认识计数单位，知道亿以内各个计数单位的名称和相邻两个单位之间的关系。
2.掌握亿以内的数位顺序表和分级的方法，学会整万数的读法和写法。
教学重点：掌握亿以内的数位顺序表，学会整万数的读法和写法。
教学难点：理解亿以内数所表示的含义。
教学准备：课件教学过程：一、谈话引入1.引入：在日常生活和生产中，我们常常遇到、用到比万大的数，谁来读一读下列几组数据？课件出示图片及文字。
：（1）我国的领土面积约为九百六十万平方公里，位居世界第三位。
（2）世界上现存最大的皇宫是北京的故宫。
它的占地面积约为七十二万平方米。
（3）2011年，我国芝麻、茶叶和油菜籽的总产量如下：芝麻六十一万吨、茶叶一百六十二万吨、油菜籽一千三百四十三万吨。
让学生根据课件出示的内容读数。
2.揭题：今天这节课，我们就来学习比万更大的数。
（板书课题）二、交流共享1.复习万以内数的知识。
（1）指名学生说出万以内数的计数单位有哪些。
（2）课件出示：填一填，说一说。
10个一是（）；10个十是（）；10个一千是（）。
说一说：每相邻两个计数单位之间的进率是多少？读一读下列各数：2362、1002、8945。
2.6近似数（教案）-四年级下册数学苏教版教学目标：1. 理解近似数的概念，能够正确判断一个数是不是近似数。
2. 学会使用四舍五入法求一个数的近似数，并能解决实际问题。
3. 培养学生的估算能力和应用意识。
教学重点：1. 近似数的概念。
2. 四舍五入法的应用。
教学难点：1. 如何判断一个数是不是近似数。
2. 如何正确使用四舍五入法求一个数的近似数。
教学过程：一、导入1. 复习导入：请同学们回顾一下我们之前学过的数的概念，比如整数、小数、分数等。
2. 提问：我们在日常生活中，经常会遇到一些不是精确的数，而是接近精确数的数，这样的数叫做什么数呢？二、新课讲解1. 讲解近似数的概念：近似数就是接近精确数的数，它通常用来表示测量数据或者计算结果。
2. 举例说明：比如，我们测量一根绳子的长度，得到的结果可能是2.6米，这个2.6米就是一个近似数，因为它接近绳子的真实长度，但并不完全精确。
3. 讲解四舍五入法：四舍五入法是一种常用的求近似数的方法，它的规则是：当一个数的小数部分大于等于5时，就向前一位进1；小于5时，就直接舍去。
4. 举例说明：比如，我们要把2.6米精确到0.1米，那么我们就看2.6的小数部分0.6，因为0.6大于等于5，所以我们就把2.6米四舍五入为2.6米。
三、课堂练习1. 判断题：请同学们判断下列各数中，哪些是近似数，哪些是精确数。
（1）2.6米（2）2.60米（3）2.600米2. 求解题：请同学们使用四舍五入法，把下列各数精确到指定的位数。
（1）2.6米，精确到0.1米（2）2.65米，精确到0.01米（3）2.648米，精确到0.001米四、课堂小结通过本节课的学习，我们了解了近似数的概念，学会了使用四舍五入法求一个数的近似数。
希望同学们能够灵活运用这些知识，解决实际问题。
五、课后作业1. 请同学们完成课后练习题。
2. 请同学们观察一下日常生活中，哪些地方会用到近似数，并记录下来，下节课分享。
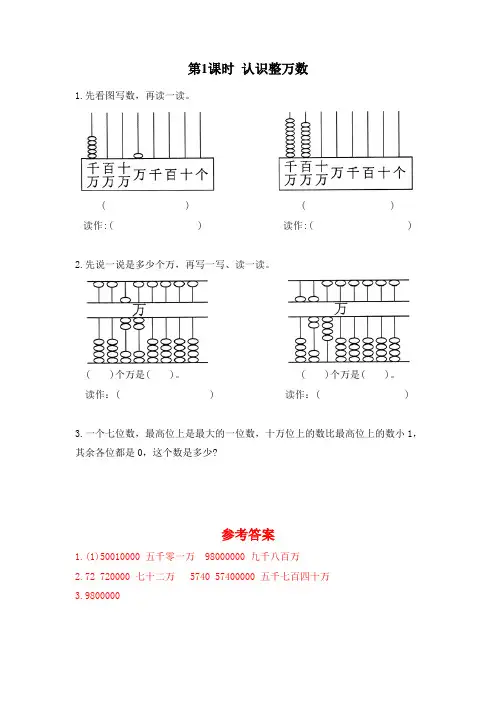
第1课时认识整万数1.先看图写数，再读一读。
( ) ( )读作:( ) 读作:( )2.先说一说是多少个万，再写一写、读一读。
( )个万是( )。
( )个万是( )。
读作：( ) 读作：( )3.一个七位数，最高位上是最大的一位数，十万位上的数比最高位上的数小1，其余各位都是0，这个数是多少?参考答案1.(1)50010000 五千零一万 98000000 九千八百万2.72 720000 七十二万 5740 57400000 五千七百四十万3.9800000第2课时认识含有万级和个级的数1.写出下面横线上的数。
(1)太阳中心的温度大约为一千五百万开。
写作：( )(2)我国维吾尔族大约有一千二百八十四万七千人。
写作：( )(3)一台电脑一万四千元。
写作：( )2.鸟巢(国家体育场)是2008年第29届奥运会的主体育场，它的建筑面积达258000平方米，鸟巢内观众席为91000个，其中临时座席为11000个。
258000 读作：( )91000 读作：( )11000 读作：( )3.用4个“8”和4个“0”按要求组成数。
(1)一个“零”都不读出来的八位数：( )、( )、( )、( )。
(2)只读出一个“零”的八位数：( )、( )、( )、( )、( )……(3)读出两个“零”的八位数：( )、( )、( )、( )、( )……(4)读出三个“零”的八位数：( )、( )、( )。
参考答案1.(1)15000000 (2)12847000 (3)140002.二十五万八千九万一千一万一千3.(1)88880000 88008800 88808000 80008880(2)80088800 80808800 80008088 88008008 80008808(3)80808080 80800880 80080880 88000808 80080088(4)80800808 88080808 80080808第3课时认识整亿数1.读出横线上的数。
第1课时图形的平移1、下面哪些图形可以通过平移与绿色的图形重合？并标上记号。
2、填一填。
（1）长方形向（）平移了（）格。
（2）六边形向（）平移了（）格。
（3）五角星向（）平移了（）格。
3、画一画。
（1）房子向右平移5格，小船向下平移5格。
（2）①将三角形向左平移8格。
②将梯形向下平移4格。
4、将下面平行四边形中的三角形（红色部分）向右平移多少厘米，可以使平行四边形转化为长方形？5、许力把一条小帆船先向右平移5格，再向下平移2格，到达现在的位置。
你能在图中画出这条小船平移之前的位置吗？第2课时图形的旋转1、填空。
（1）与时针旋转方向相同的是（）旋转，相反的是（）旋转。
（2）下图中转盘的指针绕点（）旋转，从点E到点C顺时针旋转了（）°；指针从点B逆时针旋转90°到点（）。
2、下面的图形是怎样得到的？连一连。
3、如图，甲梯形绕点A（）时针方向旋转（）就得到乙梯形。
4、将平行四边形绕点A顺时针旋转90°，将三角形绕点B逆时针旋转90°。
5、按要求画一画。
（1）将直角三角形绕点A逆时针旋转90°。
（2）将等腰三角形绕点O顺时针旋转90°。
（3）长方形是由原来的长方形绕着点B逆时针旋转90°得到的，画出原来的长方形。
6、通过旋转把方格中的两个三角形变成一个长方形，并用文字叙述旋转过程。
第3课时轴对称图形1、下面的图形各有几条对称轴？填一填。
2、画出下面各图形的所有对称轴。
3、判断。
（1）平行四边形有2条对称轴。
（）（2）等边三角形一定有3条对称轴。
（）（3）梯形是轴对称图形。
（）（4）等腰梯形有2条对称轴。
（）4、下面的图形中哪些是轴对称图形？是轴对称图形的分别画出它们所有的对称轴。
5、画出下面图形的另一半，使它成为一个轴对称图形。
6、下面的图形分别是从哪张对折的纸上剪下来的？连一连。
在分别画出每个图形的一条对称轴。
7、从镜子中看到的图形是样子是什么？请画“√”。
苏教版四年级下《近似数》在我们的日常生活和数学学习中，近似数是一个非常重要的概念。
它不仅能帮助我们更方便地处理和表达数量，还能让我们对事物的估计和描述更加接近真实情况。
那么，什么是近似数呢？近似数就是与准确数相近的一个数。
比如说，我们学校大约有 1000 名学生，这里的“1000 名”就是一个近似数，因为学校学生的实际人数可能不是正好 1000 人，而是接近 1000 人的某个数字。
近似数的产生通常有两种情况。
一种是因为测量工具的精度有限，导致测量结果无法得到准确值，只能得到一个近似数。
比如我们用尺子测量一个物体的长度，尺子的最小刻度是 1 厘米，而测量的结果在两个刻度之间，这时我们就只能给出一个近似数。
另一种情况是在某些情况下，不需要知道非常精确的数值，只需要一个大概的估计就可以了，这时候也会用到近似数。
在苏教版四年级下册的数学教材中，对于近似数的学习，孩子们会接触到如何用“四舍五入”法来求一个数的近似数。
“四舍五入”法是一种常用的求近似数的方法。
简单来说，如果要省略的尾数的最高位上的数字小于5，就把尾数舍去；如果尾数的最高位上的数字大于或等于5，就把尾数舍去并且在它的前一位进 1。
比如说，要将 3827 省略到百位求近似数。
首先找到百位，百位上是 8，然后看它后面一位，也就是十位上的数字 2。
因为 2 小于 5，所以把十位和个位上的数字舍去，得到近似数 3800。
再比如，将 76548 省略到万位求近似数。
找到万位上的数字 6，再看它后面一位千位上的数字 5。
因为 5 等于 5，所以要把万位上的数字6 进1，变成7，同时把千位及后面的数字都舍去，得到近似数80000。
学会了“四舍五入”法求近似数后，孩子们还需要能够区分近似数和准确数。
这在解决实际问题中非常重要。
比如，一个商店里有 158 个苹果，这就是一个准确数；而如果说这个商店里大约有 160 个苹果，这就是一个近似数。
近似数在我们的生活中有着广泛的应用。
芦草沟镇小学数学集体备课教案课题第六课时用“四舍五入”法求近似数学习目标知识与技能1、学生理解准确数、近似数的含义，知道它们与日常生活的联系。
2、学会用“四舍五入”法把一个亿以内的数的万位后面的尾数省略，求出它的近似数。
过程与方法在探究求亿以内数近似数方法的过程中，渗透比较的思维方法，培养初步的观察、比较及概括的能力和符号意识。
情感态度与价值观在认识和应用大数知识的过程中，培养认真仔细的学习习惯与严谨的学习态度。
重点：用“四舍五入”法求亿以内数的近似数。
难点：省略尾数时怎样进行“舍”和“入”。
教法、学法教法：演示讲解法。
学法：独立思考与小组合作相结合法。
教具小黑板、教学课件授课类型定稿备课时间2018年8月24日授课时间主备人贺晓梅授课人新课引入旁批（一）认识近似数1．课件出示2．这里有一些数据，比较这些数据有什么不同？（准确数，近似数）3．有些数据前有“约”字，或后面有“多”字，这是什么意思？4．我们的日常生活离不开数，但有时有些数不需要知道到底是多少，如在整个2014年世界杯赛事举行期间，共有大约150万人通过航空电子系统在飞机上收看球赛。
这时就需要近似数。
图中这些画横线的数，哪些是近似数？哪些是准确数？(二）点明课题怎么求近似数呢？这节课我们就学习求亿以内数近似数的方法。
设计意图：通过问题引发学生思考，引入新课。
探究新知（一）求近似数设计意图：放手让学生自主解决求近似数问题，让学生亲历学习数学的方法和过程。
1．课件出示：（1）从图中你知道了哪些信息？要我们解决什么问题？（2）你是从哪儿看出来的（圈出题中的“大约”、“万”）。
这说明要省略这两个数万位后面的尾数，还要把它们改写成用“万”作单位的数。
（3）这两个数都不是整万的数。
把不是整万的数写成整万数，这个整万数与原来的数有什么关系呢？2．求12756的近似数（1）12756千米大约是多少千米？你是怎么想的？（2）是这样吗？我们来看图。
①课件出示：②在这条数线上，用这个点表示10000，这个点表示20000，这两个点中间的点表示多少？（15000）③请你在这条数线上找一找12756大约在什么位置。
