声场图

Pm
nP0 r
sin nd / sin n sin d / sin
图3.21 线阵换能器声场坐标系统
二、多阵元超声换能器的声场
2、声束指向性 （1）指向性函数Ds
Ds
P r P0r
sin
n
d
n
sin
d
sin
sin
式3.47
（2）主瓣、栅瓣的位置以及消除栅瓣的条件，Ds
半功率点开角的条件：
Ds
sin
nd
n
sin
d
sin sin
'3dB '3dB
1 2
式3.51
二、多阵元超声换能器的声场
波束宽度：
0
2 arcsin
nd
2 arcsin
n
1
nL
3dB
2
arcsin
0.42
nd
2 arcsin
0.42
n
1
nL
式3.52
L是阵的长度d＝L/（n－1）
二、多阵元超声换能器的声场
（4）定向准确度Δθ 当超声设备用极大值法定向时，能发现声束偏离极
大值方向的最小偏角称为准确度，用Δθ表示，一 般情况下，
0.25sin0 / 2 0.60sin 3dB / 2 式3.53
第九讲 超声换能器的声场特性 器
第九讲 超声换能器的声场特性
本章主要内容 一、单阵元换能器的声场 二、多阵元超声换能器的声场 三、凹型压电材料聚焦声场的数值模拟
一、单阵元换能器的声场
一、单阵元换能器的声场 （一）平面圆形换能器的超
声场 1、声源轴线上的声压分布
点状声源在空间的 声场分布表达式

第六章 室内声场6.1 驻波声场6.1.1 室内驻波6.1.2 简正频率的分布6.1.3 声源的影响6.1.1 室内驻波[ 返回本节目录]我们先以一种极端的边界作为讨论的开始，即假设房间的内壁是刚性的。

设房间的长、宽、高分别为 。

如果把坐标原点取在房间的一个角上，可以写出刚性壁面的边界条件为（ 6-1-1 ）这里 分可得满足上述边界条件的特解为（ 6-1-2 ）其中 ，， ，而 ，或表示成（ 6-1-3 ）由于如下关系再设 ，那么对应每一组 数值决（ 6-1-4 ）此式表明在矩形房间中存在大量的简正波。

6.1.2 简正频率的分布[ 返回本节目录 ]式 （ 6-1-3 ） 表示，我们可以将频率人表示成一个矢量形式这里 i ， j ， k 可分别表示在 z ， y ， z 方向的单位矢量，其分量为这一 fn 矢量的方向代表了相应简正波的行进方向，其大小表示该简正波的频率数值。

如果我们以 构的整（ 1 ）轴向波——与两个 n 等于零对应的驻波：x 轴向波，其行进方向与 x 轴平行 ；y 轴向被，其行进方向与 y 轴平行 ；z 轴向波，其行进方向与 z 轴平行 。

（ 2 ）切向波——与一个 n 等于零对应的驻波：yz 切向波，其行进方向与 yz 平面平行 ；xz 切向波，其行进方向与 xz 平面平行 ；xy 切向波，其行进方向与 xy 平面平行 。

（ 3 ）斜向波一一与三个 n 都不等于零对应的驻波。

要分别计算以上各类被在某一频率 f 以下，或者在某个频带 df 内的准确数目是比较困难的。

因此，需要有一近似计算公式。

我们设每一特征点占有频率空间中的边长分别为一个的矩形体积被小矩形格子体积 来目应等于这里 代表圆面积乘上厚度为 的圆。

用同样的方法可算出 xz 与 xy 切向波的平均数，于是频率低于 f 的所有切向波平均数就等于这里 代表由此可得频率低于 f 的各类波的平均总数为（ 6-1-5 ）公式 （ 6-1-5 ） 代表的是各类波的平均数，它同准确数之间自然有一偏差。

YOUR SITE HERE
室内声场的统计分析
LOGO
从以上分析可知，除声源发出的直达声外，还存在着大量反射 声。这些反射声在到达边界面并经过每次反射之前，均有一段自由传 播的路程，称为自由程。经过这一自由程后，声波就要反射一次，而 每次反射，因边界面的吸收就要损失一部分能量。在声源不断发声的 情况下，损失的这部分能量将不断获得补充，直至声场达到稳态。一 旦声源停止发声，虽然损失的能量得不到补充，但室内的声音并不会 马上消失。这是很显然的，因为这时直达声虽然没有了，但反射声继 续存在，这些反射声是由声源停止发声之前的直达声形成的，它不因 声源停止发声而立即消失，而是按照原有的规律——每反射一次损失 部分能量，持续进行下去，其声能不断减小，直至全部丧失殆尽。这 时由于不再有新的反射声产生，因而封闭空间中的总声级也就逐渐降 低，直至最后消失。这种在声源停止发声后仍然存在的声延续现象称 为混响。混响的概念在封闭空间声场的统计研究中具有特殊的意义， 它对室内的听闻条件有着重大的影响。
YOUR SITE HERE
声波在室内的传播
LOGO 直达声、近次反射声和混响声 直达声：声源直接到达接受点的声音。 近次反射声：相对直达声延时小雨50ms的反射声。 混响声：延时超过50ms以后到达接受点的多重反射声。
YOUR SITE HERE
声波在室内的传播
LOGO
室内声场的几何图解
几何声学是一门运用“声线”的概念研究声学问题的 学科，采用声线研究分析室内声场，主要了解声波在室内 经各反射面反射后的反射声分布情况。它的理论基础就是 惠更斯原理。
YOUR SITE HERE
室内声场的几何图解
LOGO 凸面的反射 条件：q<0 反射结果： 效果

第二章声波的基本性质及其传播规律在日常生活中存在各种各样的声音。

例如，人们的交谈声、汽车喇叭声、机器运转声、演奏乐器的乐声等等。

在所有各种声音中，凡是有人感到不需要的声音，对这些人来说，就是噪声。

简单地讲，噪声就是指不需要的声音。

为了对噪声进行测量、分析、研究和控制，需要了解声音的基本特性。

本章介绍声波的基本性质及其传播规律。

2. 1 声波的产生及描述方法2. 1. 1 声波的产生各种各样的声音都起始于物体的振动。

凡能产生声音的振动物体统称为声源。

从物体的形态来分，声源可分成固体声源、液体声源和气体声源等。

例如，锣鼓的敲击声、大海的波涛声和汽车的排气声都是常见的声源。

如果你用手指轻轻触及被敲击的鼓面，就能感觉到鼓膜的振动。

所谓声源的振动就是物体（或质点）在其平衡位置附近进行往复运动。

当声源振动时，就会引起声源周围空气分子的振动。

这些振动的分子又会使其周围的空气分子产生振动。

这样，声源产生的振动就以声波的形式向外传播。

声波不仅可以在空气中传播，也可以在液体和固体中传播。

但是，声波不能在真空中传播。

因为在真空中不存在能够产生振动的媒质。

根据传播媒质的不同，可以将声分成空气声、水声和固体（结构）声等类型。

在噪声控制工程中主要涉及空气媒质中的空气声。

在空气中，声波是一种纵波，这时媒质质点的振动方向是与声波的传播方向相一致。

与之对应，将质点振动方向与声波传播方向相互垂直的波称为横波。

在固体和液体中既可能存在纵波，也可能存在横波。

需要注意，声波是通过相邻质点间的动量传递来传播能量的。

而不是由物质的迁移来传播能量的。

例如，若向水池中投掷小石块，就会引起水面的起伏变化，一圈一圈地向外传播，但是水质点（或水中的飘浮物）只是在原位置处上下运动，并不向外移动。

2. 1. 2 描述声波的基本物理量当声源振动时，其邻近的空气分子受到交替的压缩和扩张，形成疏密相间的状态，空气分子时疏时密，依次向外传播（图2－1）。

图2－1 空气中的声波当某一部分空气变密时，这部分空气的压强P变得比平衡状态下的大气压强（静态压强）P0大；当某一部分的空气变疏时，这部分空气的压强P变得比静态大气压强P o小。

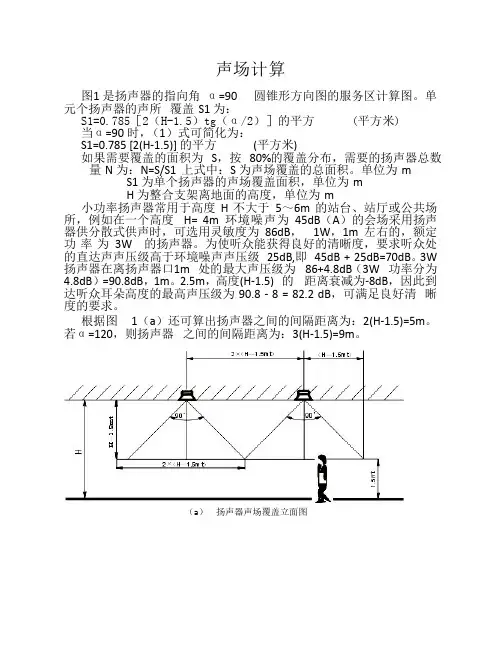
声场计算
图1 是扬声器的指向角 α=90 圆锥形方向图的服务区计算图。

单元个扬声器的声所 覆盖 S1 为：
S1=0.785［2（H-1.5）tg（α/2）］的平方 (平方米)
当α=90 时，（1）式可简化为：
S1=0.785 [2(H-1.5)] 的平方 (平方米)
如果需要覆盖的面积为 S，按 80%的覆盖分布，需要的扬声器总数量 N 为：N=S/S1 上式中：S 为声场覆盖的总面积。

单位为 m S1 为单个扬声器的声场覆盖面积，单位为 m
H 为整合支架离地面的高度，单位为 m
小功率扬声器常用于高度 H 不大于 5～6m 的站台、站厅或公共场所，例如在一个高度 H= 4m 环境噪声为 45dB（A）的会场采用扬声器供分散式供声时，可选用灵敏度为 86dB， 1W，1m 左右的，额定功率为 3W 的扬声器。

为使听众能获得良好的清晰度，要求听众处的直达声声压级高于环境噪声声压级 25dB,即 45dB + 25dB=70dB。

3W 扬声器在离扬声器口1m 处的最大声压级为 86+4.8dB（3W 功率分为4.8dB）=90.8dB，1m。

2.5m，高度(H-1.5) 的 距离衰减为-8dB，因此到达听众耳朵高度的最高声压级为 90.8 - 8 = 82.2 dB，可满足良好清 晰度的要求。

根据图 1（a）还可算出扬声器之间的间隔距离为：2(H-1.5)=5m。

若α=120，则扬声器 之间的间隔距离为：3(H-1.5)=9m。

（a） 扬声器声场覆盖立面图
（b）80%的水平覆盖图 （c）100%的水平覆盖图 图
1 扬声器的分散式供声系统。

2
• 极大值对应的距离为：
D (2n 1) x 4 (2n 1)
2 s 2
2
• 式中n=0,1…(Ds-λ)/2λ ，共有n+1个极大值，其中n=0是 最后一个极大值。
3.1.1 圆盘波源辐射的纵波声场
• 因此近场长度为：
Ds2 2 Ds2 RS2 FS2 N 4 4
3.1.1 圆盘波源辐射的纵波声场
r • 由图中的位置关系可知，面元至Q点的距离 ：
R e jk0 c0ua jt 2 P e 0 d 0 RdR 2 2 2 R x jk R 2 x 2
0
R2 x2
jk0c0ua e jt

2 2 Rs e jk R x
jt jt
U Rs2 x 2

Rs2 x 2
x
e jkU UdU U

Rs2 x 2
x
e jkU dU
Rs2 x 2
jk 0 c0ua e jt
1 jk [e jk
e jkx ]
0 c0ua e jt [(cosk Rs2 x 2 j sin k Rs2 x 2 ) (cos kx j sin kx) 0 c0ua e jt [(cosk Rs2 x 2 cos kx) j (sin k Rs2 x 2 sin kx)] k k k 0 c0ua e jt [2 sin ( Rs2 x 2 x)(sin ( Rs2 x 2 x) cos ( Rs2 x 2 x) j ] 2 2 2 k j( ( R x x) k 2 0 c0ua e jt [sin ( Rs2 x 2 x)e 2 2 ] 2 k j [ t ( R x x )] k 2 2 2 0 c0ua sin ( Rs x x)e 2 2 2

EASE4.0声场模拟分析图
EASE4.0声学软件
我们采用EASE4.0音场模拟软件可以协助我们设计及解决声学上的问题，只需绘制相应的建筑结构图纸，放置好音箱的位置及型号，此系统便可以协助您计算出不同声频反射情况，由此可知反射问题最严重的部分。

我们可以针对这些部分加上吸音材料，从而得到最好的声学效果；同时，此系统更可以计算声场平均情况，在音箱的位置及选择等设计上会否出现问题，更可做前期的时差报告，只有国际公司才会拥有如此先进的器材。

特此我们针对小剧场的布局和摆位，测出以下信息。

1000hz直达声
2000hz直达声
4000hz直达声
6300hz直达声。

R 11 r22Hz0z2
R 12r24Hz0z2
p R e R e R e R e R e R e 1 j0 k1 R 1 j0 k2 R 1 j0 k3 R 1 j0 k4 R 1 j1 k 1 R 1 j1 k 2 R 01 02 03 04 11 12
College of Underwater Acoustic Engineering
College of Underwater Acoustic Engineering
HEU
7
三、浅海声场的虚源表示
基本思想
将海面和海底的反射声线视为由各自的虚源发出的声线， 虚源数目与考虑的声线反射次数有关，数目趋于无穷， 则可求得浅海总声场。
O03
R03 > >
O01
R01
>
R02
H
O02 z
HEU
19
三、浅海声场的虚源表示
弹性海底均匀浅海 声场计算：
College of Underwater Acoustic Engineering
HEU
20
三、浅海声场的虚源表示
弹性海底楔形海域
(G. B. Deane and M. J. Buckingham. An analysis of the three-dimensional sound field in penetrable wedge with a stratified fluid or elastic basement[J]. J. Acoust. Soc. Am., 1993,93(3):1319-1328P. )
r (r, z)
College of Underwater Acoustic Engineering

单击模型界面空白地方，点Options
打开显示扬声器覆盖角的声线图 ：
界面上可以选择不同 的频率
声场覆盖线有： 3dB/6dB/9dB
相对大的分贝音箱 的声场扩散范围比 较大
红色的声场线：3dB 黄色的声场线：6dB 绿色的声场线：9dB 通常我们选用的3dB时所产生的声场覆盖线
放置主音箱：打开声场线，布置好部分音箱，调整好音箱的位置、倾斜 以及旋转的角度。
下面是我们行业在投标时候最常用到我一些音响模 拟效果的一些图片：
• 1、直达声
• 2、混合声
3、ALC
4、C50
5、STI
下面我们就来开始接触EASE这个软 件，如何运用这软件来进行音响声 音模拟
利用EASE进行音响声音模拟绘图的思路：
• 1：建筑舞台模型的建立 • 2：模型建好后为整个厅堂吸音材质的添加 • 3：音响布置、根据要求选择音响 • 4：出声音模拟图纸
音响声场分析—EASE软件
声音模拟绘图
EASE软件的10项主要功能：
1、计算和显示厅堂混响时间与频率的关系曲线； 2、计算和显示厅堂听众区域在不同频率下的直达声声场声压级分布曲线； 3、计算和显示厅堂听众区域在不同频率下的直达声混响声总声场的声压
级分布曲线； 4、计算和显示厅堂听众区辅音清晰度损失率分布曲线； 5、计算和显示厅堂听众区快速语言传递分布曲线； 6、计算和显示声音的清晰度：
EASE软件声学建筑设计中的重要性
• EASE做为建筑电声计算机辅助设计软件，能使声学顾问、建筑师、 音响工程师、建筑装修设计师可以预计建筑的声学、扩声系统包括扬 声器布置方案等特性，通过EASE模拟设计可以直观的看到所设计项 目的厅堂扩声系统预期的声学特性效果图，了解厅堂建筑内所采用的 吸声材料、扬声器型号、摆放位置、角度、以及扬声器的相关数据， 对实际的建设项目具有良好的指导作用。

实验二 单阵元圆形超声换能器辐射声场分布特性测试与分析李武松 生基硕81 08123011一、实验目的1、 复习单阵元超声换能器声场分布特性的理论知识，包括单阵元圆形聚焦和非聚焦换能器。

2、 学习利用针式水听器测试换能器声场特性的原理及方法。

3、 利用实验室Panametrics 多扫描系统测量5 MHz 、3.5MHz 、2.25 MHz 、1MHz 聚焦或非聚焦Panametircs 换能器声场分布，掌握实验过程和数据的计算机处理方法。

4、 比较同频率聚焦换能器与非聚焦换能器的声场特性；比较不同频率的聚焦换能器的声场特性、不同频率的非聚焦换能器的声场特性，并分析声场特性随频率的变化规律；二、数学物理原理Ⅰ 诊断超声换能器的声场特性超声辐射场是指超声能量分布的空间，即超声换能器所发射的超声波到达的区域，接受超声治疗与检测的区域均属于超声场的部分。

各种换能器辐射的超声场取决于换能器本身的特性、尺寸、形状等。

1. 单阵元非聚焦超声换能器的声场特性根据声学理论，一个有限尺寸的换能器或阵的辐射声场，可以按照惠更斯原理进行分析，即将换能器或阵的有效辐射面，看作是无数点声源的组合。

辐射声场中某一点的声压是辐射面上所有的点源在该点产生的声压叠加的结果，因而可以通过对整个辐射面的积分来计算，如图1所示。

图1 圆片换能器轴向辐射对于实验所用的单源圆形平面换能器，其轴线上任意一点的声压公式为：122202sin[()]sin()z p p a z z t ka πωλ=+-- (1)其中，0p 为声源处起始声压；a 为圆片半径；z 为该点距离声源的距离；ω为角频率；2k πλ=，λ为波长，声压随时间作周期性变化。

声压振幅：122202sin[()]m p p a z z πλ=+- (2)当2z a >时， 202sin()2m a p p zπλ= (3)又当23a z λ>时，22sin()22a a z z ππλλ≈，所以200m p a p S p z zπλλ==（2S a π=，即圆盘面积） (4) 从上式可以看出，m p 与z 成反比，即当z 足够大(23a z λ>)时，圆形声源轴线上的声压随距离的增加而衰减，如图2：图2 圆片换能器（a ）声束（b ）轴线上声压分布在近场有极大极小值，这是由于在靠近声源处，换能器平面边缘和平面中心辐射声波到达轴线上某点波程差不同引起声波相互干涉的结果。

声场报告图是一种用于表示声音分布和传播的有力工具。

它可以帮助我们更好地理解声音在不同环境中的传播方式，从而为声学设计和音频工程提供指导。

在本文中，我们将逐步介绍如何创建声场报告图。

第一步：收集数据要创建声场报告图，我们首先需要收集声音数据。

可以使用专业的声学设备，如麦克风阵列或声音传感器，来测量不同位置的声音强度。

在测量过程中，我们需要确保在不同位置均匀分布测量点，以获得准确的数据。

第二步：处理数据一旦我们收集到声音数据，接下来需要对数据进行处理。

首先，我们可以将数据导入到数据处理软件中，如MATLAB或Python中的科学计算库。

然后，我们可以使用平均值或加权平均值来计算每个位置的声音强度。

这将帮助我们得到一个声音分布的整体概览。

第三步：绘制声场图一旦数据处理完成，我们可以开始绘制声场图。

可以使用专业的声学分析软件，如COMSOL Multiphysics或CAD软件，来绘制声场图。

在绘制过程中，我们需要将测量点的声音强度数据与相应的坐标进行关联，并使用合适的颜色映射将声音强度可视化。

第四步：分析声场图通过观察声场图，我们可以得出一些有关声音传播的重要信息。

首先，我们可以看到声音在不同位置的强度分布，从而了解声音在空间中的传播方式。

其次，我们可以分析声音的反射和衍射现象，从而预测声音在特定环境中的回音和阴影区域。

第五步：优化声学设计最后，基于声场图的分析结果，我们可以针对特定环境进行声学设计的优化。

例如，我们可以通过调整音源位置或添加声音吸收材料来改善声音分布的均匀性。

此外，我们还可以使用声场图来评估不同设计方案的效果，并选择最佳方案。

总结：声场报告图是一种强大的工具，可以帮助我们更好地理解声音在不同环境中的传播方式。

通过收集数据、处理数据、绘制声场图、分析声场图和优化声学设计，我们可以更好地利用声场报告图进行声音分布和传播的研究和应用。

无论是在音频工程领域还是在其他领域，声场报告图都具有广泛的应用前景。

2.近场区长度 横波声场近场区长度为 式中 N—近场区长度，由假想波源算起 由以上公式可知，横波声场的近场区长度和纵波声场一样，与波长成反比，与波源面积成正比。
第三章 超声波发射声场 与规则反射体的分回波声压
主要内容： 纵波发射声场 横波发射声场 规则反射体的回波声压 AVG曲线
超声波探头（波源）发射的超声场具有特殊的结构。只有当缺陷位于超声场内时，才有可能被发现。 由于液体介质中的声压可以进行线性叠加，并且测试比较方便。因此对声场的理论分析研究常常从液体介质入手，然后在一定条件下过渡到固体介质。
横波声场中，第二介质中的近场区长度为 式中 FS—波源的面积； λS2—第二介质中横波波长； L1—入射点至波源的距离； L2 —入射点至假想波源的距离。
例：用2.5MHz，直径14mm纵波直探头水浸探伤钢板，已知水层厚度为20mm，钢中纵波声速5900m/s，水中纵波声速1480m/s，求钢中近场区长度N。 解： 钢中纵波波长 （mm） 钢中近场区长度： （mm）
四、实际声场与理想声场
以上讨论的是液体介质，波源作活塞振动，辐射连续波等理想条件下的声场，简称理想声场。实际检测往往是固体介质，波源非均匀激发，辐射脉冲波声场，简称实际声场。它与理想声场是不完全相同的。
由图可知，实际声场与理想声场在远场区轴线上声压分布基本一致。这是因为，当至波源的距离足够远时，波源各点至轴线上某点的波程明显减少，从而使波的干涉大大减弱，甚至不产生干涉。 但在近场区内，实际声场与理想声场存在明显区别。理想声场轴线上声压存在一系列极大极小值，且极大值为2P0，极小值为零。实际声场轴线上声压虽然也存在极大极小值，但波动幅度小，极大值远小于2P0。极小值也远大于零，同时极值点的数量明显减少。这可从以下几方面来分析其原因。

第四章声波的衰减§4.1概述到目前为止，我们讨论的声波一直是在理想介质中传播，即声波在传播过程中不存在任何形式的能量耗损。

实际上，严格的理想介质是不存在的，声波在介质中传播的过程总会伴随不同程度、不同形式的能量损耗，声衰减就是声波在介质中传播时其强度随传播距离的增加而逐渐减弱的现象。

声衰减具体表现主要有：随着声波在介质中传播距离的增加，声波动的振幅减小；声强或（平均）声能密度下降；色（频）散或声速变化等，其实色（频）散程度本身就反映声传播能耗的大小。

声波衰减的程度不仅与声波动的物理量（如频率、波矢等）有关，还与介质的特性（如均匀程度、完整程度、连续程度、介质微观粒子的质量密度和弹性性质等）密切相关。

同时还严重依赖声波长与介质内不均匀区域尺度的相对大小。

根据引起声衰减的原因或微观机制的不同，可以把声衰减划分为①几何衰减；②散射衰减；③吸收衰减。

几何衰减主要考虑声波传播中因波阵面的面积扩大而导致的声强（或声能密度）减弱。

它仅取决于声源辐射的波形及声束状况，而与介质特性无关，如球面波的声强反比于传播距离的平方。

声波的扩散衰减因其不符合指数衰减规律而无法纳入衰减系数中，因此在讨论与介质特性相关的声波衰减问题时，通常不考虑扩散衰减。

对扩散衰减的分析只能根据具体波型及其相应的指向特性单独来进行估算。

另外从能量的角度看，扩散衰减过程声源辐射声波的总能量并未变化，只不过因声扰动体积的扩大而使声能密度减小，即使在理想介质中，扩散衰减也照样可以发生。

散射衰减是指声波在介质中传播时，因碰到由另外一种介质组成的障碍物而使部分声波偏离原方向，从而导致原方向声波减弱的现象。

因此广义的散射可以认为是声传播过程中，由于遇到各种散射体而发生的反射、折射和衍射的总效应。

所谓的散射波是指在声传播方向有散射时实际接收到的波与假设无散射时应收到的波之差。

散射衰减不仅与介质的性质、状况有关，还与障碍物的性质、形状、尺寸、分布和数量有关。

ppt课件
24
其有效声压的数学表达式为：
p e
1 T p2 (t)dt T0
将（2－7）式代入，可得
Pe P0 / 2
同理可得
Ue U0 / 2
ppt课件
25
在自由声场中，单位时间在垂直于声波的传播方 向上单位面积所通过的声能量，称为声强，用I 表示。由（2－10）可得
振幅声波的波动方程是：
2 p 2 p 2 p 1 2 p x2 y2 z 2 c2 t 2
ppt课件
9
一、平面声波含义
当声波的波阵面是垂直于传播方向的一系列平面时， 就称其为平面声波。
定义声音传播方向为x，声场在空间的y、z两个方向 上是均匀的，即声压、质点振动速度等物理量在垂
面声波的声阻抗率为
Zs=ρc 只与媒质的密度ρ和媒质中的声速c有关，而与声波的
频率、幅值等无关，故又称ρc为媒质的特性声阻抗。
ppt课件
19
2.2.2 球面声波、柱面声波
1、球面声波
当声源的几何尺寸比声波波长小得多时，或者测量 点离开声源相当远时，则可以将声源看成一个点， 称为点声源。
在各向同性的均匀媒质中，从一个表面同步胀缩的 点声源发出的声波是球面声波，也就是在以声源点 为球心，以任何r值为半径的球面上声波的相位相同。
n
p=p1+p2+…+pn=
pi
i 1
式中：pi----第i列的瞬时声压。
ppt课件
29
设两声源频率相同，到声场中某点s的距离分别为x1 和x2，则两列波在s点的瞬时声压分别为
p1＝P01cos(ωt－kx1)=P01cos(ωt-φ1)

声场分析计算机模拟声场分析 21. EASE 4.3电脑设计系统简介 22. 分析依据: 23. 电视电话会议室声场分析 44. 电视电话会议室分析结果 115. 作战指挥室声场分析 126. 作战指挥室分析结果 19计算机模拟声场分析为使武警水电会场声学方案设计更好地符合实际的效果，运用当代先进的计算机模拟技术，根据实际尺寸建立计算机建筑模型，对方案设计的音响效果进行计算机模拟验证，以确认设计的合理性，以及能满足技术要求，达到预期效果。

设计运用的是著名的声场分析软件——EASE4.3。

1. EASE 4.3电脑设计系统简介EASE（全称ELECHO ACOUSTIC SIMNLATOR FOR ENGINEER）是由德国人在九十年代中期开发的通用数据库，现已成为世界上最为广泛使用的声学设计软件。

EASE是采用计算机CAD技术进行模拟声场的模型建设、声学设计、声学计算与声学分析的综合设计软件。

我们现在使用的是EASE 4.3版本，主要用它进行模拟验算的声学参数有：• 声场声压的分布——对声场的均匀度、频率响应及分布进行分析计算• 声场清晰度的计算——对声音清晰度的分析计算2. 分析依据:武警水电电视电话会议室以及作战指挥室扩声系统属厅堂扩声。

声学特性指标采用广播电影电视部部分标准GYJ25-86<<厅堂电声系统声学特性指标>>中语言和音乐兼用的电声系统二级（语言扩声一级）声学特性指标。

RASTI----快速语言传输指数（rapid speech transmission index）是语言传输指数法（STI法）在某些条件下的一种简化形式，用来测定与可懂度有关的语言传输质量。

在EASE中0.75～1（含0.75）为优,0.6～0.75（含0.6）为良好,0.45～0.6（含0.6）为一般,0.3～0.45（含0.3）为较差,小于0.3为差.一般大于0.5为好.ALC-----辅音清晰度损失百分比（%ALCONS）是一种语言可懂度的度量方法。