当前位置：文档之家 › 定积分的概念：求曲边梯形的面积 PPT

定积分的概念：求曲边梯形的面积 PPT

  • 格式：pptx
  • 大小：1.20 MB
  • 文档页数：38

下载文档原格式

  / 38

合集下载

数学分析完整版本ppt课件

数学分析完整版本ppt课件


返回
牛 顿（I.Newton 1642.12.25—1727.3.3）
英国数学家和物理学家出生在一个农民家庭，出生前父亲就去世了， 三岁母亲改嫁，由外祖母抚养。1661年入剑桥大学，1665年获学士学位， 1668年获硕士学位。由于他出色的成就，1669年巴鲁（Barrow）把数学 教授的职位让给年仅26岁的牛顿。1703 年被选为英国皇家学会会长。牛 顿一生成就辉煌，堪称科学巨匠。最突出的有四项重大贡献：创立微积 分，为近代数学奠定了基础，推动了整个科学技术的发展。他发现了力 学三大定律，为经典力学奠定了基础；他发现了万有引力为近代天文学 奠定了基础；他对光谱分析的实验，为近代光学奠定了基础 。他的巨著 《自然哲学的数学原理》影响深远，他被公认为历史上伟大的科学家。可 惜他晚年研究神学，走了弯路。
n
n
1
i
2
n
1 n
它的面积
ΔSi
(1
i2 n2
)
1 n
所求的总面积
Sn
n (1 i1
i2 n2
)
1 n
1
1 n3
n
i
2
i 1
1
2n
2 3n 6n 2
1
2 3
我 们 分 别 取 n=10, 50, 100 用 计 算 机 把 它 的 图 象 画 出 来 ， 并 计
算出面积的近似值：
clf, n=10; x=0:1/n:1;
四．小结： 学习定积分，不仅要理解、记住定积分的定义，还要学习建立定积分概念
的基本思想，我们以后的学习中还会遇到其它类型的积分，比如勒贝格积分、
斯蒂疌斯积分等，只要理解了定积分的思想，其他类型的积分就很容易理解了。
现在我们再来总结一下定积分建立的的思想和方法：从定积分的实例和概念中
1.5定积分的概念(4课时)ppt课件

1.5定积分的概念(4课时)ppt课件


作业： P45练习：2 .
1.5.3 定积分的概念
问题提出 1.求曲边梯形的面积和求变速直线运
动的路程，都可以通过“四步曲”解决， 这四个步骤是什么？其中哪个步骤是难 点？
分割→近似代替→求和→取极限.
2.求曲边梯形的面积与求变速直线运 动的路程是两类不同的问题，但它们有 共同的解决途径，我们可以此为基点， 构建一个新的数学理论，使得这些问题 归结为某个数学问题来解决，并应用于 更多的研究领域.
x 3)dx
(2x x )dx . 1
0
y sin( .x
)3
0
1
(2x
x 3)dx
0
1
2xdx
0
1x 3dx 1 1 3
0
44
小结作业
1.定积分是一个特定形式和的极限，其 几何意义是曲边梯形的面积，定积分的 值由被积函数，积分上限和下限所确定.
2.在实际问题中，定积分可以表示面积、 体积、路程、功等等，求定积分的值目 前有定义法和几何法两种，有时利用定 积分的性质进行计算，能简化解题过程.
B组：2，3.
i)
，那么
当n→∞时，Sn的极限是否一定存在？
一定存在
思 做考 函数4：f(数x)学在上区，间把[a，nlimb]in上1 b的n定a f积( i )分，叫
记作
b
f (x)dx，即
a b
f (x)dx
a
lim
n
n i1
b
af( n
i)
其中a与b分别叫做积分下限与积分上限，
பைடு நூலகம்
区间[a，b]叫做积分区间，函数f(x)叫
2
(x 1)dx 的值.
1
高二数学定积分概念.pptx

高二数学定积分概念.pptx


lim 0
n
ei
i 1
1 n
lim
iY
n n1
1
e lim
ni
en
n i1
n n n i1
1
1
lim
n
1 n
1
(e
n)
1
n
1
en
(1 e) lim n
n
1
1 en
1 en
e 1
第7页/共91页
第二节 定积分的性质
定积分的性质
第8页/共91页
规定：(1)当a b时，b f (x)dx 0; a
1
xdx
1ln(1 x)dx.又在[0，1]上，x ln(1 x) 0，
0
0
故
1
xdx
1
ln(1 x)dx.
0
0
例2：估计下列积分值
（1）4 (x2 1)dx；（2）0 ex2xdx.
1
2
第12页/共91页
解： (1)2 x2 1 17，
2 (4 1) 4 (x2 1)dx 17 (4 1) 1
b
n
a
f (x)dx I
lim 0
i 1
f (i )xi
这里f(x)叫做被积函数，f(x)dx叫做被积表达式，x叫做积
分变量，a,b叫做积分下限和上限，[a,b]叫做积分区间。
n
Y
注意:(i) 当和 f (i )xi的极限存在时，其极限I仅与被积函数
i 1
f (x)及积分区间[a,b]有关，而与积分变量的记法无关，即
x f (t)dt也是f (x)的a一个原函数，从而
a
F(x) (x) C.令x a有F(a) C.即F(x) (x) F(a)
定积分的概念PPT课件

定积分的概念PPT课件


（3 ）
a
f ( x )dx
f ( x )dx
b a
f (x )dx
性质4： 性质5： 性质6：


a
a
b
f ( x )dx 0.
a
dx b a .

b
a
f ( x )dx f ( x )dx .
b
a
思考4：
r 0
2 xdx
2
？
r
2


1
0
1 x dx ？

i 1
b n
a
f ( i ) ，那么
当n→∞时，Sn的极限是否一定存在？
一定存在
n
思考4：数学上，把
n
lim
i 1
b n
a
f( i)
叫
做函数f(x)在区间[a，b]上的定积分， 记作 即
a
b a
b
f (x )dx ，
n
f (x )dx
n
lim
i 1
b n
a
f( i)
b a
f (x )dx 其中
---积分号 a---积分下限 b---积分上限 区间[a，b] ---积分区间 函数f(x) ---被积函数 x---积分变量 f(x)dx---被积式
v＝v(t)
n
s
n
lim
i 1
b n
a
v( i )
O a
i
b t
思考3：一般地，如果函数f(x)在区间[a， b]上连续，用分点 a＝x0＜x1＜x2＜„＜xi＜„＜xn＝b将区 间[a，b]等分成n个小区间，在每个小区 间[xi－1，xi](i＝1，2,„，n)上任取一
定积分的概念ppt课件

定积分的概念ppt课件


2
2
b a
(b
x)( x
a)dx
1
2
(b a )2 2
(b a)2
8
.
17
例1 利用定义计算定积分 1 x2dx. 0
解 因为y x2在[0,1]上连续，积分存在.
将[0,1]n 等分，分点为 xi
i ，( i n
0,1,2,
,n
)
小区间[ xi1 ,
xi ]的长度xi
1 ，(i n
b
a
f
(u)du
（2）定义中区间的分法和介点i 的取法是任意的.
（3）当函数 f ( x)在区间[a,b]上的定积分存在时，
称 f ( x)在区间[a, b]上可积. 也称定积分为
Riemann 积分.
11
对定积分的补充规定:
（1）当a
b时， b a
f
(
x)dx
0；
（2）当a
b时， b a
f
( x)dx
1
一、问题的提出
实例1 （求曲边梯形的面积）
y
曲边梯形由连续曲线
y f (x)
y f ( x)( f ( x) 0)、
x轴与两条直线x a 、
x b所围成.
A?
oa
bx
2
用矩形面积近似取代曲边梯形面积
y
y
oa
b xo a
bx
（四个小矩形）
（九个小矩形）
显然，小矩形越多，矩形总面积越接近 曲边梯形面积．
0
证明 利用对数的性质得
lim n f 1 f 2 f n n n n n
eln lim n n
f
1 n
定积分的概念及性质课件

定积分的概念及性质课件

度、磁场强度等；在弹性力学中，定积分可以用于求解应力和应变等问题。
06
定积分的进一步应用
积分变换
积分变换的定义
积分变换是一种将函数在某一区间内的行为转化为另一种函数的方法，常见的积分变换包括傅里叶变换和拉普拉斯变 换等。
积分变换的性质
积分变换具有一些重要的性质，例如线性性质、时间平移性质和微分性质等，这些性质在解决实际问题中具有广泛的 应用。
积分变换的应用
积分变换在信号处理、图像处理和控制系统等领域有着广泛的应用，通过积分变换可以将复杂的信号或 系统转换为易于分析和处理的函数形式。
傅里叶变换
傅里叶变换的定义
傅里叶变换是一种将时间域函数转换为频域函数的方法， 它可以将一个时间函数分解成一系列不同频率的正弦和余 弦函数的线性组合。
傅里叶变换的性质
傅里叶变换具有一些重要的性质，例如线性性质、对称性 质和微分性质等，这些性质在解决实际问题中具有广泛的 应用。
傅里叶变换的应用
傅里叶变换在信号处理、图像处理和控制系统等领域有着 广泛的应用，通过傅里叶变换可以将复杂的信号或系统转 换为易于分析和处理的频域函数形式。
反常积分
反常积分的定义
反常积分是一种在无穷区间上定 义的积分，它通常用于处理一些 在无穷远处收敛的函数。
符号的意义
定积分的符号表示一个函 数在一个区间上的总值， 其中“∫”表示积分号。
计算公式
定积分可以通过一个公式
来计算x，其中a和b
是区间的端点。
02
定积分的性质
连续函数的积分性质
积分区间可加性
对于任意两个不相交的区间[a,b]和[b,c]，有$\int_{a}^{c}f(x)dx = \int_{a}^{b}f(x)dx + \int_{b}^{c}f(x)dx$。
定积分概念、性质ppt课件

定积分概念、性质ppt课件


上例曲边图形的面积用定积分表示
S1x2d x lin m (n 1 )2 (n 1 )1
0
n 6 n 3
3
注意：据定义有如下说明:
(1)定积分是特殊和式极限,它是一个定数;
(2)定积分的大小仅与区间[a,b]和被积函数f(x)有关；
(3)规定：
a
f(x)d x0,
b
a
f(x)d x f(x)dx
b f (x)dx
b
g ( x)dx
a
a
推2 论 ：b
.
f(x)d
x
b
f（ x） dx,(ab)
a
a
因f(x)f(x)f(x)
.
性质6（介值定理）：设f(x)在[a,b]上可取得最大值M和最
小值m， 于是， 由性质5有
b
m (ba)af(x)d xM (ba)
几何意义也很明显
性质 7（积分中值若定函理 f(数 x)） 在[a： ,b]上连续，
S曲
lim n
n i 1
S i矩
lim
n
(n
1)( 2n 6n 2
1)
1 0.333 3
.
总结：求曲边梯形面积的步骤 v
引例1——曲边梯形的面积（演示） 引例2——变速直线运动的路程
设物体的运动速度 vvt
分割区间 作和
取近似值 取极限
T1
ti-1 i ti T2 t
（1）细分区间 [ T 1 ,T 2 ] [ T 1 ,t 1 ] U [ t 1 ,t2 ] U L U [ tn 1 ,T 2 ]
曲边梯形的面积，即：
n
S曲
.
lim
n i1
人教版高中数学选修2-2第一章导数及其应用第五节(第一课时)曲边梯形的的面积和定积分的概念(共19张

人教版高中数学选修2-2第一章导数及其应用第五节(第一课时)曲边梯形的的面积和定积分的概念(共19张


n nn
nn
nn
每个区间的长度为 x i i 1 1 nn n
过各区间端点作x轴的垂线，从而得到n 个小曲边梯形，他们的面积分别记作
S1, S2,, Si ,, Sn.
2、近似代替
S第i个黄色矩形
1 n
f
(i-1) n
10
S第1个黄色矩形
n
f
() n
0
S第2个黄色矩形
1 n
f
(1) n
1 n3
凡 事 都是 多 棱 镜 ， 不 同 的 角 度 会 看 到 不 同 的 结果 。 若 能 把 一 些 事 看 淡 了 ，就 会 有 个 好 心 境 ， 若 把 很 多事 看 开 了 ， 就 会有 个 好 心 情 。 让 聚 散 离 合 犹 如 月 缺 月 圆那 样 寻 常 ， 让 得 失 利 弊 犹 如花 开 花 谢 那 样 自 然 ， 不 计 较， 也 不 刻 意 执 着； 让 生 命 中 各 种 的 喜 怒 哀 乐 ， 就 像 风 儿一 样 ， 来 了 ， 不 管 是 清 风 拂面 ， 还 是 寒 风 凛 冽 ， 都 报 以自 然 的 微 笑 ， 坦然 的 接 受 命 运 的 馈 赠 ， 把 是 非 曲 折 ， 都当 作 是 人
n
i 1
f i x
n i 1
ba n
f i
当n→∞时,上式无限接近某个常数,这个常数叫做函数
f
(x)在区间[a,b]上的定积分
记作 b a
f
xdx
b a
f xdx lim n
n i 1
ba n
f i
定积分的定义：即
b a
f
(x)dx
lim
n
n i1
最新人教版高中数学选修1.5.3定积分的概念 (7)ppt课件

最新人教版高中数学选修1.5.3定积分的概念 (7)ppt课件

Ｂ
Ｄ
Ｃ
y=f２(x)
o
a
b
x
例题
例1:利用定积分的定义，计算 1 x3dx的值. 0 解：令f x x3
(1)分割
在区间[0,1]上等间割地插入n-1个分点，把区间[0,1]等分成n个小区
间
每个小区 i间n-的1 ,长ni 度（为i = 1, 2, ,n）
Δx = i - i - 1 = 1 nn n
解:(1)曲线所围成的平面区域如下图所示,设此面积为S,则
2
S 0 xdx.
题型二 利用定积分表示曲边梯形的面积
例2 : 利用定积分表示下列曲线围成的平面区域的面积 :
2 y x 2, x y2.
(2)曲线所围成的平面区域如下图所示.
记S A1 A2 , A1由y x , y x , x 1围成;
f (i )
变速直线运动路程
S

lim
t 0
n i 1
v(i )t
lim n
n i 1
1 n
v(i )
概念
一、定积分的概念
一般地，如果函数f（x）在区间[a，b]上连续，用分点
a x0 x1 xi1 xi xn b
将区间[a，b]等分成n个小区间，在每个小区间[ xi1，xi ]
(3)
9
( x )dx
S=________4.
题型三 利用定积分的几何意义求定积分
例3:利用定积分的几何意义,求下列各式的值.
2
(1)
4 x2 dx;
2
分析:定积分
b f ( x的)几dx何意义是:介于直线x=a,x=b,x轴及y=f(x)所围成图形面积的代数和, a
定积分定义

定积分定义


b
a
f
(x)dx
abg(x)dx
.
上页 下页 返回 退出
•性质5 如果在区间[a, b]上 f (x)0, 则
b
a
f
(x)dx
0
(a<b).
•推论1 如果在区间[a, b]上 f (x)g(x), 则
b
a
f
(x)dx
abg(x)dx
(a<b).
•推论2
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
(a<b).
01(1
x)dx
1 11 2
1 2
.
首页
上页 下页 返回 退出
三、定积分的性质
❖两点规定
(1)当 ab 时,
b
a
f
(x)dx
0
;
(2)当 ab 时,
b
a
f
(x)dx ba
f
(x)dx
.
上页 下页 返回 退出
三、定积分的性质
性 •性质质11
ab[
f
(x)
g(x)]dx
b
a
f
(x)dx
abg(x)dx
线xa、xb与x轴所围成的曲边梯形的面积.
当f(x)0时, f(x)在[a, b]上的定积分表示曲边梯形面积的
负值.
这是因为
b
a
f
n
(x)dx lim 0 i1
f
n
(xi
)Dxi
lim
0
[
i1
f
(xi )]Dxi
ab[
f
(x)]dx
定积分的性质 课件

定积分的性质 课件

定积分的概念之
定积分的性质
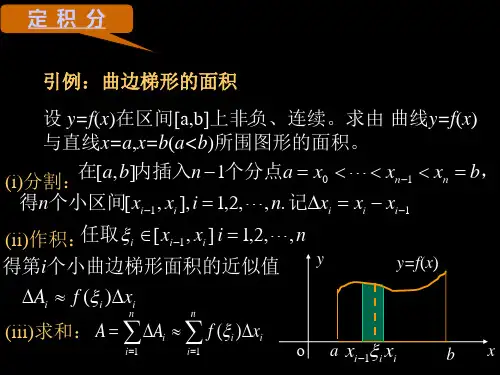
一、定积分问题举例
1.曲边梯形的面积
•曲边梯形 设函数yf(x)在区间[a, b]上非负、连续. 由直线xa、xb、
y0及曲线yf (x)所围成的图形称为曲边梯形, 其中曲线弧称 为曲边.
•观察与思考 在曲边梯形内摆满小的矩形, 当小矩形的宽度减少时,
小矩形面积之和与曲边梯形面积之间的误差将如何变化?
e 1
n n
1
1e n
n
1
n(1e n )
利用几何意义求定积分
例例22 用定积分的几何意义求01(1 x)dx .
解 函数 y1x在区间[0, 1]上的定积分是以y1x为曲边, 以区间[0, 1]为底的曲边梯形的面积.
因为以y1x为曲边, 以区间[0, 1]为底的曲边梯形是一个 直角三角形, 其底边长及高均为1, 所以
b
a
f
(x)dx
abg(x)dx
(a<b).
•推论2
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
(a<b).
这是因为|f(x)|f(x)|f(x)|, 所以
ab|
f
(x)|dx
b
a
f
(x)dx
ab|
f
(x) | dx
,
即
|
b
a
f
(x)dx|
ab|
f
(x)|
dx
.
•性质5 如果在区间[a, b]上 f (x)0, 则
f(x) ———被积函数, i1
f(x)dx ——被积表达式,
x ————积分变量,
a ————积分下限,

5-1定积分的概念与性质(1)



i 1
n
f ( i )xi i xi xi2 xi ,
2 i 1
i 1
n
n
1 n 2 1 n( n 1)(2n 1) i 1 3 i 3 n n i 1 n 6 i 1 n
n
2
1 1 1 1 2 , 6 n n
设某物体作直线运动，已知速度v v ( t ) 是 t 的一个连续函数，且 时 间 间 隔 [T1 , T2 ] 上 v ( t ) 0 ，求物体在这段时间内所经过的路程.
思路：把整段时间分割成若干小段，每小段上 速度看作不变，求出各小段的路程再相加，便 得到路程的近似值，最后通过对时间的无限细 分过程求得路程的精确值．
第一节 定积分的概念

一、问题的提出 二、定积分的定义 三、存在定理 四、定积分的几何意义 五、小结
一、问题的提出
实例1 （求曲边梯形的面积）
曲边梯形由连续曲线 y f ( x ) ( f ( x ) 0) 、
x 轴与两条直线 x a 、
y
y f ( x)
A?
o
a b
Ai f ( i )xi
曲边梯形面积的近似值为
A f ( i )xi
i 1
n
当分割无限加细 ,即小区间的最大长度
max{x1 , x2 ,xn }
趋近于零 ( 0) 时，
曲边梯形面积为 A lim f ( i )xi
变速直线运动的路程）
四、定积分的几何意义
f ( x ) 0, f ( x ) 0,
a f ( x )dx A
b
b
曲边梯形的面积

定积分的概念和性质课件

i 1
f(ξｉ )
0
a x0 x1
x2 xi 1 ξｉxi
xn 1 x b n
x
（4）取极限：当分割无限时，所有小矩形的面积之
分割越细， f (i )xi 就越接近于曲边梯形的面积A，当
和的极限 就是曲边梯形面积A的精确值。 n
i 1
小区间长度最大值趋近于零，即
n
0（ 表示 这些小区间的长度最大者）时，和式 f ( i )xi 的
b
• 证
[ f ( ) g ( )]x [ f ( x) g ( x)]dx lim
b a 0 i 1 n i i
n
i
lim f ( i )xi lim g ( i )xi
0
b i 1
n
0
i 1
f ( x)dx g ( x)dx
a
f ( x)dx f ( )(b a) ( a b)
这个公式叫积分中值公 式。
证 由性质6，有
m(b a) f ( x)dx M (b a)
a b
即有
1 b m f ( x)dx M a ba
因m、M分别是f ( x)的最小值和最大值，由 连续函数的介值定理知 ，在[a，b]上至少存 在一点，使得 1 b f ( x)dx f ( ) ba a
若f(x)≥0，则 a f ( x)dx 的几何意义表示 由曲线y=f(x)，直线x=a，x=b与x轴所围成 的曲边梯形的面积。
b
一般情形,a f ( x)dx 的几何意义为：它 是介于x轴，曲线y=f(x)，直线x=a，x=b 之 间的各部分面积的代数和。
b
y

《定积分的概念》参考省名师优质课赛课获奖课件市赛课一等奖课件


g(x)dx
a
S1
b
y a
fg((x))dx
b
S2
g ( x)dx
a
O aa
bx
（三）、定积分旳基本性质
性质1.
b
b
a kf ( x )dx k a f ( x )dx
性质2.
b
b
b
[ f ( x ) g( x )]dx f ( x )dx g( x )dx
a
a
a
三：定积分旳基本性质 性质3. 定积分有关积分区间具有可加性
积分上限
n
b
f ( x)dx I
a
lim
n
i 1
f (i )xi
积分 下限
积分变量 被积体现式 被积函数
阐明：
(1) 定积分是一种数值,
它只与被积函数及积分区间有关，
而与积分变量旳记法无关，即
b f(x)dx
b
f (t)dt
b f(u)du。
a
a
a
（2）定义中区间的分法和 i 的取法是任意的.
a
定积分旳定义：
即
b a
f
( x)dx
lim
n
n i1
b
n
a
f
(i )
定积分旳有关名称：
———叫做积分号， y
f(x) ——叫做被积函数，
y f (x)
f(x)dx —叫做被积体现式，
x ———叫做积分变量，
a ———叫做积分下限， O a
b ———叫做积分上限，
bx
[a, b] —叫做积分区间。
a
Oa
b
c
f (x)dx =-Sf (x)dx

5.1 定积分的概念与性质

2
0 x dx lim 0 i 1
2
1
n
i x i
1 1 1 1 lim 1 2 . n 6 n n 3
15 上一页 下一页
四、定积分的性质
对定积分的补充规定:
（1）当a b 时，a f ( x )dx 0 ；
a 1 dx a
b a
b
b
dx b a .
性质5 如果在区间[a, b] 上 f ( x ) 0 ，
则 f ( x )dx 0 . (a < b)
证
f ( x ) 0, f ( i ) 0, ( i 1,2,L, n)
xi 0,
n

max{x1 , x2 ,L, xn }
故 x 为极大点，x 为极小点, 4 2
26 上一页 下一页
2 2 M f( ) , 4
2 m f( ) , 2
ba , 2 4 4
2 sin x 2 2 2 dx , 4 4 x 4 1 sin x 2 2 dx . 2 4 x 2
称 f ( x ) 在区间[a , b] 上可积.
11 上一页 下一页
三、定积分的几何意义
f ( x ) 0, f ( x ) < 0,
a f ( x )dx A
b
b
曲边梯形的面积
的负值
a f ( x )dx A 曲边梯形的面积
A3
A1
A2
A4
a f ( x )dx A1 A2
7 上一页 下一页
（1）分割
T1 t0 < t1 < t 2 < L < t n1 < t n T2 t i t i t i 1

定积分的概念-PPT精选

b
s a v(t)dt;
密 度 为 ( x ) 线 状 物 体 的 质 量 为
m b(x)dx. a 前页 后页 返回
关于定积分定义，应注意以下几点：
n
注1 表 达 式 JlT im 0i1f(i)xi 不 仅 与 n和 T有
关 , 还 与 { 1 ,2 , ,n } 有 关 , 因此定积分既不是数 列极限，也不是函数极限.
区 间 [xi1, xi]的长度不趋于 0 . 要 保 证 每 个 区 间 [ x i 1 , x i ] 的 长 度 趋 于 0 , 需 引 入 分 割 T 的 细 度 ( 模 ) :
T m a x x i i 1 ,2 , ,n .
则 当T0时 ,就能保证分割越来越细.
n
当v(t)v0为 匀 速 运 动 时 ， s v 0 ( b a ) ; 当质量是
均 匀 分 布 时 ， 即 x 为 常 数 时 , m(ba).
这就是说,在“常值”、“均匀”、“不变”的情况下
前页 后页 返回
可以用简单的乘法进行计算. 而现在遇到的问题 是“非常值” 、“不均匀”、“有变化”的情形， 如来何解决这些问题呢？ 以下我们以求曲边梯形的面积为例，把这类问题 合理地归为一类特殊的和式的极限. 中心思想： 把曲边梯形看作许许多多小的曲边梯形之和，每 个小曲边梯形面积，可近似地用矩形的面积来替
与S的差距就会越来越小.
i 1
问题是：
(1 )如 何 刻 划 分 割 越 来 越细？
n
(2 )如 何 刻 划 f(i)x i越 来 越 逼 近 于 S ? i 1
下面依次讨论这两个问题.
前页 后页 返回
( 1 ) 对 于 一 般 的 T : a 0 x 0 x 1 x n b , 不 能 用n来表示分割 T 越来越细,因为可能某些

定积分的概念

a a
b
特别地： 若f x 在[a , b]上连续, f x 0, 且f x 不恒为零， 则 f 0.
a
例 比较积分值 e dx和 e x dx的大小.
x 0 0
1
1
解 因为当x [0,1]时，x x , 所以e x e
x
,

1
0
e dx e x dx.
2

sinxd x0
(2)
2

1
1
x dx 2 x 2dx
2 0
a a
a
1
f ( x )在 a, a 上连续且为奇函数时， f ( x)dx 0.
f ( x )在 a , a 上连续且为偶函数时， f ( x )dx 2 f ( x )dx
0 a a
性质5 （保向性） 若f x , g x 在a , b上均可积, 且恒有 f x g x , x a , b , 则 f

b
a
f x轴上方图形总面积 x轴下方图形总面积
b 1 a 0
例1.由几何意义求 dx, 其中b a;
2 2
1 x 2 dx.
key 1 ） 矩形面积： b a； 2 ） 单位圆x y 1的1 / 4面积： 4
例2 根据定积分几何意义， 说明下列各式成立 .

(1)

b
(i ) f ( x ) g( x ) 在[a, b]上可积，并且
(i i ) f ( x ) g( x )在a, b上也可积，但一般地
[ f ( x) g( x)]dx
a
a
f ( x )dx g( x )dx
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 6
(n
1)n(2n
1)
1 (1 1 )(2 1 ) 1 6n n3
S= lim x0
Sn
lim
x0
n i1
f(
i-1) n
1= n
lim
x0
1 6
(1
1 )(2 n
1) n
1 3
所以S 1，即所求曲边三角形的面积为 1。
3
3
分割
以曲代直
求和
取极限
两个结论
• （1）在分割时一定要等分吗？不等分影响 结果吗？
以“直”代“曲” 无限逼近
刘徽的这种研究方法对你有什么启示?
案例探究
如何求由直线 x 0, x 1, y 0 与抛物线
y x2 所围成的平面图形的面积 S？ y
思考1：怎样“以直代曲”？ 能整体以“直”代“曲吗？ 思考2：怎样分割最简单？
y x2
o
1x
案例探究
1、分割 把底边[0,1]分成n等份, 在每个分点作底边
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
当分割点无限增多时，小矩形的面积和=曲边梯形的面积
深入思考
• 通过动画演示我们可以看出，n越大， 区间分的越细，各个结果就越接近真 实值。为此，我们让n无限变大，这 就是一个求极限的过程。
1.在分割时，不管采用等分与不等分，结果一样。
• （2）在近似代替时用小区间内任一点处的 函数值影响结果吗 ？
2. 在近似代替时，用小区间内任 一点处的函数值作 为近似值，结果也是一样的。
• （3）总结一般曲边梯形面积的表达式？
归纳概括
一般曲边梯形的面积的表达式
S
n
lim n i1
ba n
和曲线 y f (x) 所围成的图形称为曲边梯形。
思维导航
看看怎样求出下列图形的面积?从中你有何启示？
y
y
A
A
∟
∟
o
B
x
o
B
x
不规则的几何图形可以分割成 若干个规则的几何图形来求解
思维导航
-----割圆术
魏晋时期的数学家刘徽的割圆术
“…割之弥细，所 失弥少，割之又割， 以至于不可割，则 与圆周合体而无所 失矣…” ——刘徽
1.5.1定积分的 概念：曲边梯 形的面积
一,学习目标:
1、掌握曲边梯形面积的求法. 2、深刻理解化曲为直的思想. 3、初步认识定积分的概念.
二,重点:
1、曲边梯形的面积 2、化曲为直的思想 3、定积分的概念
三,难点:
化曲为直的思想及定积分概念
情境创设
金门大桥 （美国）
概念形成
曲边梯形的定义：由直线 x a, x b(a b), y 0
i1 n n i1 n n
02 1 ( 1 )2 1 ( 2 )2 1 ( n 1 )2 1
nnnnn
nn
1 n3
[02
12
22
(n
1)2 ]
1 n3
n(n
1)(2n 6
1)
（4）取极限
当分割无限变细，即x 0(亦即n )时，
1 n3
[02
12
22
(n
1)2 ]
1 n3
案例探究
2、近似代替(以直代曲）思考3：对每个小曲边梯形
y
如何“以直代曲”？
y=x2
f ( i ) ( i )2 nn
f (i 1) (i 1)2
n
n
f ( i ) ( i )2 nn
O i 1 i
1x
nn
方案. 方案.. 方案… 方案….
深入思考
怎样使各个结果更接近真实值？
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
（2）近似代替(以直代曲）
Si
f
(i
1)x n
(i
1)2 n
1 n
（3）求和
于是图中曲线之下小矩形面积依次为
02 1 , ( 1 )2 1 , ( 2 )2 1 , ,( n 1)2 1 ,
nn nn n
nn
所有这些小矩形的面积的和为
n
S S1 S2 Sn Si
i1
n f( i-1) 1 n ( i-1)2 1
• 有位成功人士曾说过：“做事业的 过程就是在求解一条曲线长度的过 程。每一件实实在在的小事就是组 成事业曲线的直线段。”想想我们 的学习过程、追求理想的过程又何 尝不是这样？希望大家能用微积分 的思想去学习、去做事！
的垂线, 这样[0,1]区间
分成n个小区间：0,
1 n
,
1 n
,
2 n
,
n
1 n
,1
记第i个区间为 i
1 n,i n源自i1,2,,n
y
长度: x i i 1 1
y=x2
nn n
对应的小曲边梯形面积为△Si
Sn S1 S2 Si Sn
O 1 2 i 1 i n 11 x
n n nn n
刘徽的这种研究方法 对你有什么启示?
思维导航
-----割圆术
魏晋时期的数学家刘徽的割圆术
“…割之弥细，所 失弥少，割之又割， 以至于不可割，则 与圆周合体而无所 失矣…” ——刘徽
刘徽的这种研究方法 对你有什么启示?
思维导航
-----割圆术
割圆术：刘徽在《九章算术》注中讲到
“…割之弥细，所 失弥少，割之又割， 以至于不可割，则 与圆周合体而无所 失矣…” ——刘徽
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
观察下列演示过程，注意当分割加细时， 矩形面积和与曲边梯形面积的关系．
f
i
即时小结
以上计算曲边三角形面积的过程可以用流程图表示：
分割
近似代替
求和 取极限
y
y
y
y
O
xO
xO
xO
x
学以致用
假设上半部分的抛物线的方程为y 1- x2，x [0,1], 求抛物线部分的断面面积。
y
o
1
x
一个案例 两种思想 三个方案 四个步骤
课堂小结
求一个具体曲边梯形的面积 “以直代曲”和“无限逼近”思想 方案一、方案二、方案三 分割、近似代替、求和、求极限