2016年桂林电子科技大学考博试题3002现代控制理论

格式：doc
大小：167.50 KB
文档页数：2

下载文档原格式

桂林电子科技大学博士研究生入学考试最优化方法试题

桂林电子科技大学博士研究生入学考试试题
科目代码： 2002 科目名称：最优化方法
请注意：答案必须写在答题纸上（写在试题上无效）。
1.（本题满分 10 分）函数 f ( x1 , x2 ) x1e ( x1 x2 ) 是否为凸函数？说明理由. 2.（本题满分 10 分）用最速下降法解问题 2 min f ( x) x12 4x2 2x1 x2 x1 3x2 .（取初点 x (1) (1,1)T ，迭代 1 次）
x12 x2 0 s.t. 2 x1 x2 3 0
5.（本题满分 15 分）用梯度投影法求解问题（取初始点 x (1) (0,0)T ，迭代 1 次）
2 min f ( x ) 2 x12 2 x2 2 x1 x2 4 x1 6 x2 2 x1 x2 0 s. t. 5 x1 5 x2 0 x , x 0 1 2
min x1 x2 3 3 7.（本题满分 10 分）证明点 x ( , ) T 是优化问题 4 2 s.t. 2 x1 x2 3 0
的局部最优解.
1 min x T Ax 2 8.（本题满分 10 分）设 x 是问题的最优解，其中 A 为 n 阶正定矩阵. s. t. x b
证明 x 与 x b 关于 A 共轭.
第 1 页共 1 页
3. （本题满分 10 分）设 k 满足 f ( xk k d k ) min f ( xk d k ) . 证明：若对 0 ，
0
2 1 有 2 f ( xk d k ) 1 ，则 f ( xk ) f ( xk k d k ) [d kT f ( xk )]2 / d k . 2 4.（本题满分 20 分）求解问题 min f ( x ) ( x1 3) 2 ( x2 1) 2

桂林电子科技大学博士研究生入学考试随机过程试题

桂林电子科技大学博士研究生入学考试试题科目代码：2001 科目名称：随机过程请注意：答案必须写在答题纸上（写在试题上无效）。

一、填空题（每小题4分，共32分）1、机变量X特征函数，随机变量X的数学期望= 。

2、已知随机变量X服从均值为3的指数分布，随机变量Y服从[0,X]上的均匀分布，则= 。

3、设随机过程是均值函数为0，方差函数为的正交增量过程，且，则= 。

4、设是参数为的Wiener过程，令，对，的相关函数= 。

5、设随机过程，其中是均值函数为2，方差为1的随机变量，则随机过程的相关函数= 。

6、设为一齐次马氏链，其步转移概率为，状态是正常返态非周期的，若在0时刻从状态出发经过1,2,3步首次返回的概率分别为，则。

7、设是一平稳随机序列，其谱密度为，则的相关函数= 。

8、设平稳过程的谱密度为，则的相关函数= 。

二、解答题（共68分）1、（12分）设随机变量Y服从均值为1的指数分布，令求（1）随机过程X(t)的一维概率密度函数，（2）X(t)的相关函数。

2、（12分）设随机过程，其中A,B都是均值为零，方差为且不相关的随机变量，证明：（1）是宽平稳随机过程,(2)的均值是各态历经的。

3、（12分）设震动按参数为的泊松过程发生，并记内发生震动次数为。

(1)若震动在内已经发生n次，且，对于，求；(2)若某装置在k次震动后失灵，求该装置寿命T的密度函数。

4、（12分）在电路系统中，若输入电压是一实平稳过程，输出电压满足随机微分方程，其中为常数，且的均值为0，相关函数，。

求（1）输出过程；（2）的谱密度及相关函数。

5、（10分）设齐次马尔可夫链的状态空间为，其转移概率矩阵为试：（1）正确分解此链并指出各状态的常返性和周期；（2）求不可约闭集的平稳分布。

6、（10分）设群体中各个成员独立地活动且以指数率λ生育。

若假设没有任何成员死亡，以X(t)记时刻t群体的总量，则X(t)是一个纯生过程，其，状态空间，设转移为，试计算(1);（2）。

桂林电子科技大学博士研究生入学考试现代控制理论试题

?101??0????010?x??1?uyt??111?xx???????100???1??1求该系统的闭环和开环传递函数
桂林电子科技大学博士研究生入学考试试题
科目代码：3002 科目名称：现在试题上无效）。
一、（15 分）机械系统如下图 1 所示（不考虑轮子与地面摩擦力），其中，物体的质量为 mkg ,弹簧钢度为 kN / m ，阻尼系数为
y (t )
k
f
m
u (t )
图1
二、（15 分）已知某单位负反馈系统状态空间方程如下：
1 0 x 1 0 1 0 1 0 0 x 1 u , y (t ) 1 1 1 x 0 1
（1）求该系统的闭环和开环传递函数；（2）试分析该闭环系统的能控性、能观测性；（3）试求该闭环系统的能控标准型。三、（15 分）对下列连续时间时不变系统，判断平衡状态是否为大范围渐近稳定：
试证明受控系统 0 的传递函数 G0 (s) 与受控系统 yf 的传递函数 GF (s) 之间的关系如下：
GF (s) G0 (s)[I FG0 (s)]1 或者 GF (s) [ I G0 (s) F ]1G0 (s)
五、(20 分)已知系统的传递函数 Y (s)
U ( s)
第 1 页共 2 页
1 x2 x
3 2 x1 x x2
四、（15 分）设线性时不变系统
0 :
Ax Bu, x y Cx x(0) x0 , t 0
经输出反馈 u Fy v 后，可以导出如下输出反馈系统 yf
yf ：
( A BFC ) x Bv, x y Cx x(0) x0 , t 0

2016年桂林电子科技大学考博试题1001英语

A) lingers
B) invests
C) deserves
D) thrives
8. You should ________ your letter with a phone call.
A) follow
B) lift up
C) follow up
D) pass along
9. Bob’s __________comments insulted me
things about the meal I’d cooked.
A）complimentary B）complimented
C）complementary D）complement
5. He has some ________ ideas about what to do, but nothing specific.
本大题共 20 小题，每小题 0.5 分，本大题共 10 分
1. Their study shows that sports skills_________ into personal life.
A) take over
B) carry over
C) turn over
D) come over
2. A similar ___________of female to male students has been observed in law and medical school
14. Typical jokes or ______ stories have a three-part anatomy that is easily recognized.
A) humorist B) humorous C) humorless

2018年桂林电子科技大学考博真题309计算机网络博士研究生考试试题

A、减小了路由表的规模。
B、去掉了路由表中关于相同路径的冗余信息。
C、使路由表变得简单，便于维护。
D、以上皆是
7、Internet的网络层含有四个重要的协议，分别为（）。
A、IP，ICMP，ARP，UDP B、ARP，RARP，IP，ICMP
C、TCP，ICMP，UDP，ARP D、UDP，IP，ICMP，RARP
桂林电子科技大学
2018年硕士研究生入学考试复试试题
科目代码
309
科目名称计算机网络
A卷
适用学院
信息与通信学院
请注意：答案必须写在答题册上（写在试题上无效）。答题纸请注明页码与总页数。
一、单选题（每题2分，共20分）
1、以下关于ARQ协议类型和特点的描述中，错误的是（）
A、ARQ实现方法有两种：单帧的停止等待方式和多帧的连续发送方式。
10、HDLC协议对0111 1100 0111 1110 组帧后对应的比特串为（）。
A、01111100 00111110 10 B、01111100 01111101 01111110
C、01111100 01111101 0 D、01111100 01111110 01111101
二、填空题（每空2分，共20分）
7、在滑动窗口流量控制（假设发送窗口大小为8）中，若已发送5帧，只收到前3帧的确认，则还可以发送的帧数是。
三、简答题（每题6分共30分）
1、计算以下三种情况之下每个结点可以得到的平均带宽。
（1）10个节点接到一台10Mbps的Ethernet集线器上。
（2）10个节点接到一台100Mbps的Ethernet集线器上。
1、UDP协议在IP协议的数据报服务的之上增加了功能和功能。

2016年桂林电子科技大学考博试题3004数字信号处理

2.在对连续信号进行均匀采样时，要从离散采样值不失真恢复原信号，则采样角频率 s 与信
号最高截止频率 h 应满足关系
。
（1） s 2h
（2） s h
（3) s 2h
(4) s h
3. 以下对实平稳随机过程 X (t) 的自相关函数 RX ( ) 的论述不正确的是
是
， X (t0 ) 是
， A0 cos(0t ) 是
。
（1）样本函数（2）随机过程
（3）随机变量
7．下面哪一种滤波器能用于处理非平稳随机信号？
（1）维纳滤波器
（2）卡尔曼滤波器
第1页共5页
8. 特征分解法进行谱分析时，要划分出信号子空间和噪声子空间，组成噪声子空间的特征向
量对应于自相关矩阵的
白噪声过程 w(n) 激励时，它们的输出功率谱密度 Sxx (z) 和 Sxx () 的公式。
4．写出经典谱估计中周期图法的谱估计公式，并说明经典谱估计存在哪些缺点？ 5. 写出用自相关序列的离散傅里叶变换表示的离散随机序列功率谱密度公式，同时写出逆变
换公式。
四、计算题（共 41 分）
1.（6 分）设一个 AR（3）模型为 x(n) 0.9x(n 1) 0.36x(n 2) 0.145x(n 3) w(n) ，
求与其等价的 ARMA（1，1）模型的参数。
2.
（6
分）考虑随机过程
x(n)

A exp(n0
)

w(n)
，其中
w(n)
是均值为零、方差为
2 w
的高斯白噪声，是在区间[ , ]上均匀分布的随机变量， A 和是常量。求 x(n) 的
自相关序列及其功率谱密度。

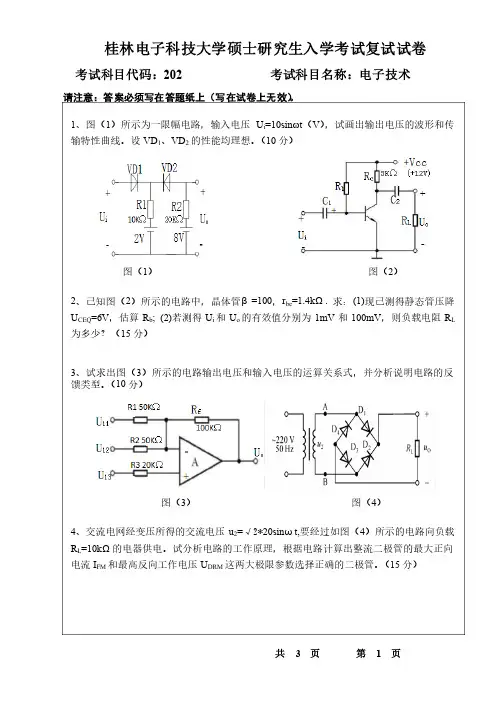
桂林电子科技大学硕士研究生入学考试复试试卷考试电子技术B卷

桂林电子科技大学硕士研究生入学考试复试试卷考试科目代码：202 考试科目名称：电子技术请注意：答案必须写在答题纸上（写在试卷上无效）。

1、图（1）所示为一限幅电路，输入电压U i=10sin w t（V），试画出输出电压的波形和传分）输特性曲线。

设VD1、VD2的性能均理想。

（10分）图（1）图（2）2、已知图（2）所示的电路中，晶体管β=100，r be=1.4kΩ. 求：(1)现已测得静态管压降U CEQ=6V，估算R b; ; (2)(2)若测得U i和U o的有效值分别为1mV和100mV，则负载电阻R L分）为多少？（15分）3、试求出图（3）所示的电路输出电压和输入电压的运算关系式，并分析说明电路的反分）馈类型。

（10分）图（3）图（4）4、交流电网经变压所得的交流电压u2=√2*20sinωt,要经过如图（4）所示的电路向负载R L=10kΩ的电器供电。

试分析电路的工作原理，根据电路计算出整流二极管的最大正向分）电流I FM和最高反向工作电压U DRM这两大极限参数选择正确的二极管。

（15分）共3 页第1 页请注意：答案必须写在答题纸上（写在试卷上无效）。

5、试分析图（5）给出的逻辑电路，列出真值表和输出P 、Q 逻辑表达式，说明该电路实现了什么功能功能。

（10分）分）&>=1&=100=1AB CPQ&&==11=1>11图 (5) 6、说明图（6）示电路的功能。

要求：（1）写出每个触发器的驱动方程、状态方程；（2）列出状态转换表；画出状态图；根据给定CP 信号的波形画出各触发器输出端Q 1、Q 2、Q 3的波形。

（设各触发器的初始状态均为“0”）（15分）分）图（6）7、格雷码又称循环码，只有4位，见下表1，从0000开始，最右边的一位按状态0110顺序循环，右边第二位按00111100循环，右边第三位按0000111111110000顺序循环，可见，自右向左，每一位的状态循环中的0、1数目增加一倍。

2017年桂林电子科技大学考博真题专业英语A卷博士研究生考试试题

5.Theorem 1. A monotonic sequence converges if only if it is bounded.
Note: A sequence is called bounded if there exists a positive number M such that
A sequence that is not bounded is called unbouned.
3.A circle is a closed curve lying in one plane, all points of which are equidistant from a fixed point called the center.
4.Two sets A and B are said to be equal if they consist of exacly the same elements, in which case we write A=B. If one of the sets contains and element not in the other, we say the sets are unequal and we write .
Proof: It is clear that an unbounded sequence cannot converge. Therefore, all we need to prove is that a bounded monotonic sequence must converge.
Assume and let L denote the least upper bound of the set of function values. Then for all n, and we shall prove that the sequence converges to L.

广西大学现代控制理论期末考试题库之填空题含答案

广西大学现代控制理论期末考试题库之填空题含答案1. 对任意传递函数00()m nj j j j j j G s b sa s ===∑∑，其物理实现存在的条件是。

(传递函数为s 的真有理分式函数或m n ≤)2. 系统的状态方程为齐次微分方程x Ax =，若初始时刻为0，x (0)=x 0则其解为___________。

其中， _____称为系统状态转移矩阵。

(0()e ,0A x x t t t =≥；e A t )3. 对线性连续定常系统，渐近稳定等价于大范围渐近稳定，原因是___________________。

(线性系统的稳定性与初值无关，只与系统的特征根有关)4. 系统1111(,,)∑=A B C 和2222(,,)∑=A B C 是互为对偶的两个系统，若1∑使完全能控的，则2∑是__________的。

(能观)5. 能控性与能观性的概念是由__________提出的，基于能量的稳定性理论是由__________构建的。

(卡尔曼李亚普诺夫)6. 线性定常连续系统x Ax Bu =+，系统矩阵是___________，控制矩阵是__________。

(A ； B )7. 系统状态的可观测性表征的是状态可由完全反映的能力。

(输出)8. 线性系统的状态观测器有两个输入，即_________和__________。

(原系统的输入和原系统的输出)状态空间描述包括两部分，一部分是_________，另一部分是__________。

(状态微分方程；输出方程)9. 系统状态的可控性表征的是状态可由完全控制的能力。

(输入)10. 由系统的输入-输出的动态关系建立系统的_______________，这样的问题叫实现问题。

(状态空间描述)11. 某系统有两个平衡点，在其中一个平衡点稳定，另一个平衡点不稳定，这样的系统是否存在？__________。

(存在)12. 对线性定常系统，状态观测器的设计和状态反馈控制器的设计可以分开进行，互不影响，称为______原理。

桂林电子科技大学2016年考研试题801机械设计(2016-B)

第1页共3页
5. 轴承材料的主要性能要求有哪些？
6. 为何大多数轴呈阶梯形？
四、计算题（66 分，每小题 22 分） 1. 图为一个托架的边板用 8 个普通螺栓与相邻机架联接。托架受一大小为 4400N 的载荷 F 作用，该载荷与边板螺栓组的竖直对称轴线平行，距离为 330mm。托架与机架间的摩擦系数 f=0.15，结合面数目为 2，防滑系数 Ks =1.2，螺栓材料许用拉应力[σ]=400MPa。试确定为确保螺栓组连接可靠需选用的螺栓直径。
桂林电子科技大学
2016 年研究生统一入学考试试题
科目代码：801
科目名称：机械设计（A）
请注意：答案必须写在答题纸上（写在试题上无效）。答题纸请注明页码与总页数。
一、选择题（20 分，每小题 2 分）
1. 塑性材料在脉动循环变应力作用下的极限应力为
。
A. σb B. σs C. σ0 D. σ-1 2. 在同一螺栓组中，螺栓的材料、直径和长度均应相同，这主要是为了
A. 受力均匀 B. 便于装配. C. 外形美观 D. 降低成本
3. 平键连接与花键连接相比较，
。
A．承载能力较大 B．对中性比较好 C．对轴的削弱比较严重
4. 能用于螺纹连接的放松装置中的是
。
A.安全销 B.圆柱销 C.圆锥销 D.开口销
5. 能用于需要保证严格传动比的场合的是
A. 同步带传动 B. 圆带传动 C. 多楔带传动 D. 平带传动
8. 对轮齿进行齿顶修缘的目的是
。
A.提高轮齿的弯曲强度
B.减少动载荷
C.改善载荷沿接触线分布不均匀 D.使齿轮装配方便
9.
联轴器是有弹性元件的挠性联轴器的—种。
A. 弹性柱销 B. 齿式 C.十字轴式万向 D. 凸缘

桂林电子科技大学硕士研究生入学考试复试试卷2014控制专业综合

G0 ( s)
H 2 ( s) Qi ( s)
h1
h2 C1 R1 Q 2
2
C2 图1
R2
Q0
四、（20 分）已知系统结构图如图 4 所示，其中采样周期 T=1，试求系统对单位阶跃输入下系统无稳态误差、过渡过程在最少拍内结束的 D ( z ) 。
r (t )
_
T
D( z )
T
ZOH
K s
c(t )
图4
共
2
页
第
1
页
请注意：答案必须写在答题纸上（写在试卷上无效）。
五、（10 分）已知线性定常系统的状态方程为
0 1 x x 2 3试应用李雅普诺夫来自二法判别系统稳定性。共
2
页
第
2
页
三、（20 分）已知两只水箱串联工作（如图 1），其输入量为 Qi，流出量为 Q2, Q0；h1, h2 分别为两只水
箱的水位，h2 为被控量，C1, C2 分别为水箱的底面积（即容量系数），假设 R1, R2,Rs 为线性液阻。要求：（1）列写过程的微分方程组；（2）求液位过程的传递函数 Rs Qi
考试科目名称：控制专业综合
请注意：答案必须写在答题纸上（写在试卷上无效）。
二、判断题（下列各题中，描述正确的在括号中打：；错误打：）（每小题 4 分）
1、在选择单回路调节系统的调节参数时，应尽量使干扰远离调节阀。 2、增大干扰通道的时间常数，可以减小系统的超调，改善系统的平稳性。 3、均匀调节系统的目的是协调前后设备供求，使两个参数缓慢地在允许的范围内变化。 4、引入积分调节器的目的是利用调节器的低频幅值较大特性，来消除静差。 5、工程上，引入前馈调节器的主要原因是它能精确的补偿扰动的影响。（（（（（）））））

2016年桂林电子科技大学考博试题3003通信原理

B. 根据载波的不同可分为以正弦波作为载波的连续载波调制和以脉冲串作
为载波的脉冲调制
C. 根据调制器频谱搬移特性的不同可分为线性调制和非线性调制
D. 按调制信号频率的高低分为高频调制和低频调制
E. 按照输出已调信号和输入调制信号的时域关系不同可为线性调制和非线
性调制
4.高斯过程的性质有
【】
A．宽平稳和严平稳是等价的。
。
3.部分响应系统的最高频带利用率为
。
4.线性分组码（n，k），若要求它能纠正 2 个随机错误，同时检测 3 个随机错误，
则其最小码距为
。
5.非相干解调是在接收端解调信号时不需要本地载波，而是利用已调信号中
的
来恢复原基带信号。
第1页共4页
6. PCM30/32 路基群系统中，第 20 路话路的信令码的传输位置在
。
7.部分响应技术对输入序列进行预编码是为了防止
。
8. 某信源的信息速率为 28kbit/s，通过一个码率为 4/7 的循环码编码器，采用滚降
系数为 1 的频谱成形，再进行 4PSK 调制。则 4PSK 的符号速率是
波特。
9.已知某信号经抽样后，用 A 律 13 折线法编码，得到八位代码为 01110001，则
六、（12 分）某通信系统发送部分框图如图 2 所示，已知 s(t) m1(t) cosct m2 (t)sin ct Acosct ，其中 fc 50 KHz ，A 为常数；m1(t) 和
m2 (t) 是要传送的两个不包含直流分量的带调制信号，它们的傅氏频谱分别为
M1( f ) 和 M 2 ( f ) ，它们的带宽分别为 5KHz 与 10KHz。
第3页共4页

2016年桂林电子科技大学考研试题806信号系统与电路(B)

2
n
y t t cos f t
2．积分（A）0
t
t
2
2t 3 t 1 dt 的值为：
（B） 2 (D)
（C） 2U t
2U t 1
3．设 y t f1 t * f 2 t ， t0 为实常数，则下列式子成立的是：
第 2 页共 5 页
三、（本题 15 分）已知某因果 LTI 系统，当 f t e U t 时，全响应为 y1 t e te
t t
当 f t e U t 时，全响应为 y2 t 2e e
2 t t

2t
U t 。求：
出电压 U o 的值；
Rd 3k + V DD (+12V) C2 + V DD (+12V) R g2 100k C1 R g1 100k Rs 3k Ro ( b)
R g2 100k C1 R g1 u i 100k
C2
Rs 3k Ro (a)
uo
ui
uo
图1
图2
二、（本题 15 分）设图 2 所示各电路的静态工作点均合适。晶体管的 1 、 2 、 rbe 1 、
7．已知 f1 n 1, 2,3,1 , 0 n 3 ； f 2 n 1,1,1 , 0 n 2 ， f n f1 n * f 2 n ，那么
f 5 等于：
（A）0 （C）4
n 1
（B） 1 (D) 5
8． f n
（A）
dy t dt

2018年广西桂林电子科技大学电子技术综合(A)考研真题

2021年广西桂林电子科技大学电子技术综合(A)考研真题第一部分模拟电子技术〔总分值75分〕一、选择题〔每题2分共20分〕1、由NPN 管组成的单管共射放大电路，当输入正弦波电压时，输出u O 如下图，可确定输出波形产生的失真为〔〕。

A 、饱和失真B 、截止失真C 、交越失真D 、频率失真2、某传感器产生的电压信号〔几乎不能提供电流〕，进过放大后希望输出电压信号成正比，这时放大电路应选〔〕A ．电流串联负反应B ．电压并联负反应C ．电流并联负反应D ．电压串联负反应 3、工作在电压比拟器中的运放与工作在运算电路中的运放的主要区别是：A ．开环或正反应状态B ．深度负反应状态C ．放大状态D ．线性工作状态 4、某负反应放大电路，其开环增益9.9mS iu A =，反应系数10ui F k =Ω，开环输入电阻5.0i R K '=Ω，可推算出其闭环输入电阻ifR '=〔〕。

A. 500k Ω；B. 50k Ω；C.50Ω；D. 5Ω5、有两个增益一样，输入电阻和输出电阻不同的放大电路A 和B ，对同一个具有内阻的信号源电压进展放大。

在负载开路的条件下，测得A 放大器的输出电压小，这说明A 的〔〕 A ．输入电阻大 B ．输入电阻小 C ．输出电阻大 D ．输出电阻小6、在负反应电路中自激振荡的平衡条件是〔〕。

A 、附加相移2,1n AF ϕπ∆=±≥B 、附加相移2(1),1n AF ϕπ∆=±+=C 、附加相移2,1n AF ϕπ∆=±<D 、附加相移2(1),1n AF ϕπ∆=±+< 7、放大电路产生零点漂移的主要原因是〔〕 A ．采用了直接耦合方式 B ．采用了阻容耦合方式 C ．采用了正、负双电源供电 D ．增益太大8、二阶压控电压源低通有源滤波器通带外幅频响应曲线的斜率为〔〕A ．20dB/十倍频程B ．-20dB/十倍频程C ．40dB/十倍频程D ．-40dB/十倍频程 9、甲乙类互补对称电路与乙类互补对称电路相比，主要优点是〔〕。

电子科技大学《自动控制理论》20春期末考试

(单选题)1: 线性定常控制系统的微分方程或差分方程的系数是（）。

A: 常数
B: 函数
C: 随时间变化的函数
D: 都不对
正确答案: C
(单选题)2: 在直流电动机的电枢回路中，以电流为输出，电压为输入，两者之间的传递函数是( )。

A: 比例环节
B: 积分环节
C: 惯性环节
D: 微分环节
正确答案: A
(单选题)3: 现代控制理论主要以（）为数学模型。

A: 频域分析
B: 根轨迹
C: 时域分析法
D: 状态方程
正确答案: D
(单选题)4: 信号流图中，（）的支路称为混合节点。

A: 只有信号输入
B: 只有信号输出
C: 既有信号输入又有信号输出
D: 任意
正确答案: C
(单选题)5: 经典控制理论主要以（）为数学模型，研究单输入单输出系统的分析和设计问题。

A: 传递函数
B: 微分方程
C: 状态方程
D: 差分方程
正确答案: A
(单选题)6: 在正弦输入信号的作用下，系统输出的（）称为频率响应。

A: 稳态响应
B: 参量
C: 暂态响应
D: 以上都不对
正确答案: A。

桂林电子科技大学3009先进功能材料与传感器技术2016年考博真题

桂林电子科技大学博士研究生入学考试试题科目代码：3009 科目名称：先进功能材料与传感器技术请注意：答案必须写在答题纸上（写在试题上无效）。

一、选择题（每题2分，合计20分）1、电池是人类生产和生活中的重要能量来源，各式各样电池的发明是化学对人类的一项重大贡献。

下列有关电池的叙述正确的是( )A. 锌锰干电池工作一段时间后碳棒变细B．氢氧燃料电池可将热能直接转变为电能C. 氢氧燃料电池工作时氢气在负极被氧化D．太阳能电池的主要材料是高纯度的二氧化硅材料2、氢镍电池的总反应式是H2＋2NiO(OH)2Ni(OH)2。

根据此反应判断，下列叙述中不正确的是( )A. 电池放电时，镍元素被氧化B. 电池充电时，氢元素被还原C. 电池放电时，镍元素被还原D. 电池放电时，H2在负极放电3、微型锂碘电池可用于植入某些心脏病人体内的心脏起搏器所用的电源。

这种电池中的电解质是固体电解质LiI，其中的导电离子是I-。

下列有关说法正确的是( ) A. 正极反应：2Li-2e- =2Li＋ B. 负极反应：I2＋2e- =2I-C. 总反应是：2Li＋I2 =2LiID. 金属锂作正极4、生物材料植入人体后，与机体组织直接接触，在生理环境作用下逐渐被腐蚀，将这种反应称为：（）A. 宿主反应B. 过敏反应C. 生理腐蚀反应D. 失效反应5、下列不属于传感器基本组成部分的是（）A. 电源电路B. 敏感元器件C. 转换电路D. 转换元器件6、下面是物理传感器的是（）A. 热电偶B. 酶传感器C. 湿度传感器D. 气体传感器7、下列不属于固体燃料电池的是（）A. 质子交换膜燃料电池B. 硫酸燃料电池C. 碱性燃料电池D. 固体氧化物燃料电池。

杭州电子科技大学2015现代控制理论期末考试试卷B

5．（10分）如下RLC电网络系统，试以电流u(t)为输入，电压y(t)为输出，电容电压uC(t)及电感电流iL(t)为状态变量，写出系统的状态空间模型。
6．（10分）试证明线性定常连续系统的下列不变性：
(a) 线性变换不改变系统的传递函数；
(b) 线性变换不改变系统的能观性。
7．（10分）分析下面两个线性定常系统是否渐近稳定：
杭州电子科技大学学生考试卷（B）卷
考试课程
现代控制理论
考试日期
年月日
成绩
课程号
教师号
任课教师姓名
考生姓名
学号（8位）
年级
专业
1．（10分求以下传递函数模型对应的能控标准Ⅰ型
2．（20分）给定线性定常连续系统，其中：
，，，，
（1）求系统的特征多项式及特征值；
（2）求系统的状态转移矩阵；
（1）
（2）
8．（10分）求下列系统的平衡态，并判断其稳定性。
（提示：取李亚普诺夫函数为V(x1,x2)x12x22）
（3）设，，求，和。
3．（20分）给定系统为：
其状态不能直接测得，试设计一个观测器——状态反馈系统，使其具有期望的闭环极点23j和23j，观测器的特征值为1和3，并计算整个闭环系统的传递函数。
4．（10分）给定系统
求出系统的能控性矩阵Qc、能观性矩阵Qo以及它们的秩，并判断系统的能控性和能观性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第 1 页共 2 页
1 x2 x 2 x13 x2 x
四、（15 分）设线性时不变系统
0 :
Ax Bu, x y Cx x(0) x0 , t 0
经输出反馈 u Fy v 后，可以导出如下输出反馈系统 yf
yf ：
( A BFC ) x Bv, x y Cx x(0) x0 , t 0
统输出。（1）写出系统以位移和速度为状态变量的状态空间方程；（2）若 m 1, k 1, f 2 ，求当 u(t ) 1(t ) ，初始条件为 y(0) y(0) 1时状态方程的解及 y(t ) 的表达式。
y (t )
k
fቤተ መጻሕፍቲ ባይዱ
m
u (t )
图1
二、（15 分）已知某单位负反馈系统状态空间方程如下：
2016 年桂林电子科技大学博士研究生入学考试试题
科目代码：3002 科目名称：现代控制理论
请注意：答案必须写在答题纸上（写在试题上无效）。
一、（15 分）机械系统如下图 1 所示（不考虑轮子与地面摩擦力），其中，物体的质量为 mkg ,弹簧钢度为 kN / m ，阻尼系数为
fNs / m ； u(t ) 为外力作用力，为系统输入； y(t ) 表示位移，为系
试证明受控系统 0 的传递函数 G0 (s) 与受控系统 yf 的传递函数 GF (s) 之间的关系如下：
GF (s) G0 (s)[I FG0 (s)]1 或者 GF (s) [ I G0 (s) F ]1G0 (s)
五、(20 分)已知系统的传递函数 Y (s)
U ( s)
g ( s) 1 s( s 1)( s 2)
（1）确定一个状态反馈增益矩阵 K，使闭环系统极点为 -3,
1 3 j ； 2 2
（ 2）确定一个全维状态观测器，并使观测器的特征值均为-5；（3）求出闭环传递函数。
第 2 页共 2 页
sa ( s 1)( s 2)( s 2 2s 2)
（1）确定实数 a 为何值时，系统不能控或不能观；（2）选择一组系统变量，使系统在（ 1）确定的 a 值下能控而不能观；（3）选择一组系统变量，使系统在（ 1）确定的 a 值下能观而不能控。六、(20 分)已知线性时不变系统传递函数：
1 0 x 1 0 1 0 1 0 0 x 1 u , y (t ) 1 1 1 x 0 1
（1）求该系统的闭环和开环传递函数；（2）试分析该闭环系统的能控性、能观测性；（3）试求该闭环系统的能控标准型。三、（15 分）对下列连续时间时不变系统，判断平衡状态是否为大范围渐近稳定：