三角函数公式默写模版

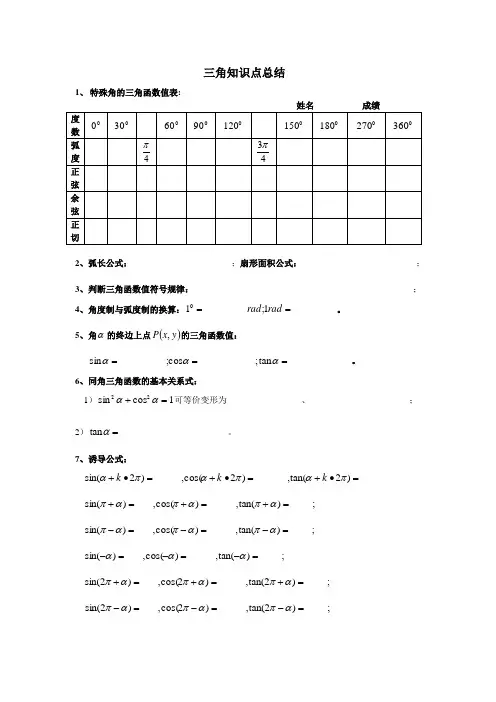
三角知识点总结1、 特殊角的三角函数值表:2、弧长公式：___________________；扇形面积公式：______________________；3、判断三角函数值符号规律：___________________________________________；4、角度制与弧度制的换算：________1;________10==rad rad 。

5、角α的终边上点()y x P ,的三角函数值：____________tan _;__________cos _________;sin ===ααα。

6、同角三角函数的基本关系式：1）1cos sin 22=+αα可等价变形为______________、___________________；2）_____________________tan =α。

7、诱导公式：____)2tan(______,)2cos(_____,)2sin(=∙+=∙+=∙+παπαπαk k k ____;)tan(_____,)cos(___,)sin(=+=+=+απαπαπ ____;)tan(_____,)cos(___,)sin(=-=-=-απαπαπ ____;)tan(_____,)cos(___,)sin(=-=-=-ααα____;)2tan(_____,)2cos(___,)2sin(=+=+=+απαπαπ____;)2t a n (_____,)2c o s (___,)2s i n (=-=-=-απαπαπ_____;)2cos(_____,)2sin(=+=+απαπ_____;)2cos(_____,)2sin(=-=-απαπEx ：______)23cos(_______,)23sin(=+=+απαπ ______)23cos(_______,)23sin(=-=-απαπ对于απ±2n 中其记忆规律是________________________________________。

1《三角函数与解三角形》公式默写1.设任意α的终边上一点P (),x y ， OP r =，则sin α= ，cos α= ，tan α= ．2.角三角函数的基本关系：()221sin cos αα+= ；()sin 2cos αα= ．3.函数的诱导公式：()()1sin 2k πα+= ，()cos 2k πα+= ，()tan 2k πα+= ． ()()2sin πα+= ，()cos πα+= ，()tan πα+= ． ()()3sin α-= ，()cos α-= ，()tan α-= ．()()4sin πα-= ，()cos πα-= ，()tan tan παα-=-．()5sin 2πα⎛⎫-=⎪⎝⎭ ，cos 2πα⎛⎫-= ⎪⎝⎭ ．()6sin 2πα⎛⎫+= ⎪⎝⎭ ，cos 2πα⎛⎫+= ⎪⎝⎭． 4.函数()()sin 0,0y x ωϕω=A +A >>的性质：①振幅： ；②周期：T = ；③频率：f = ；④相位：x ωϕ+；⑤初相： ．5.6.两角和与差的正弦、余弦和正切公式：⑴()cos αβ-= ；⑵()cos αβ+= ； ⑶()sin αβ-= ；⑷()sin αβ+= ； ⑸()tan αβ-= ；⇒（tan tan αβ-= ）； ⑹()tan αβ+= ；⇒（tan tan αβ+= ）． 7.二倍角的正弦、余弦和正切公式： ⑴sin2α= ．⑵cos2α= = =⇒降幂公式2cos α= ，2sin α= ．⑶tan 2α= ． 8.合一变形：()sin cos sin αααϕA +B =+，其中tan ϕB =A． 9.=12sinπ；cos15= ；10.正弦定理：在C ∆AB 中，则有sin sin a b ===AB(R 为C ∆AB 的外接圆的半径) 11.正弦定理的变形公式：①2sin a R =A ， b =，2sin c R C =；用途（ ）②sin A =，sin 2b R B =， s i n 2c C R =；用途（ ） ③ ::a b c =12.三角形面积公式：C S ∆AB = = = ．13.余弦定理：在C ∆AB 中，有2222cos a b c bc ⎧=+-A ⎪⎪⎨⎪⎪⎩，用途余弦定理推论：222cos 2b c a bc+-A =，，；用途。

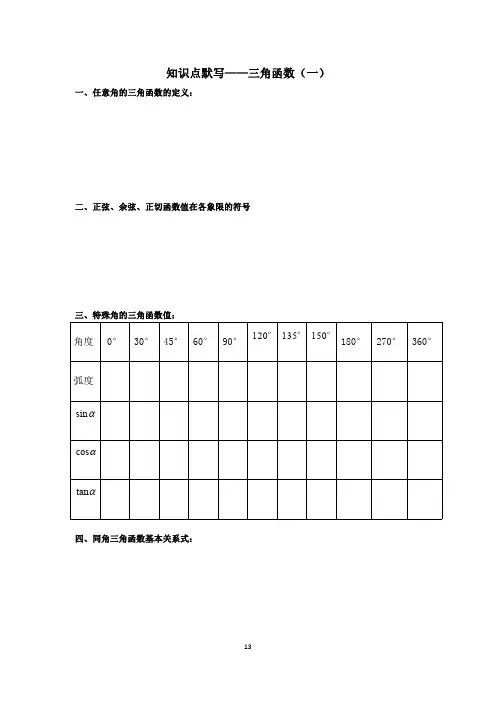
知识点默写——三角函数（一）一、任意角的三角函数的定义：二、正弦、余弦、正切函数值在各象限的符号三、特殊角的三角函数值：角度0°30°45°60°90°120o135o150o180°270°360°弧度αsinαcosαtan四、同角三角函数基本关系式：五、诱导公式（1）()()()sin 2sin ;co s 2co s ;tan 2tan ;k k k πααπααπαα+=+=+=()Z k ∈（2）();sin sin αα-=-();cos cos αα=-();tan tan αα-=-（3）();sin sin ααπ-=+();cos cos ααπ-=+();tan tan ααπ=+（4）();sin sin ααπ=-();cos cos ααπ-=-();tan tan ααπ-=-（5）;cos 2sin ααπ=⎪⎭⎫⎝⎛-;sin 2cos ααπ=⎪⎭⎫⎝⎛-（6）;cos 2sin ααπ=⎪⎭⎫ ⎝⎛+;sin 2cos ααπ-=⎪⎭⎫⎝⎛+六、和角公式sin()αβ+=sin()αβ-=cos()αβ+=cos()αβ-=tan()αβ+=tan()αβ-=七、二倍角公式sin 2α=；cos α2===；tan 2α=.补充：1、辅助角公式=+x b x a cos sin 2、（1）90,90=+βα即两角相加为互余：()ββαβαcos 90sin sin cos sin =-== 理由：(2)两角相加和为180，互补：()()⎩⎨⎧-=-==-=ββαββαcos 180cos cos sin 180sin sin3、“ααcos sin -”与“ααcos sin +”的正负判断cos sin >-αα-y x =sin cos 0αα+>y x=0cos sin <-ααsin cos 0αα+<4、降幂公式：①2sin x =cos 2x 例1、角2017o 是（）A.第一象限角B.第二象限角C.第三象限角D.第四象限角例2、如果sin tan 0θθ⋅<，则θ是第象限角，如果θ是第四象限角，则点(sin ,cos )P θθ在第象限.例3、如果角α的终边过点P (2sin 30°，－2cos 30°)，则cos α的值等于()A.12B ．－12C ．－32D.32例4、已知4sin 5α=，(,)2παπ∈，求cos ,tan αα.例5、求下列各三角函数式的值：(1)sin 1320°；(3)tan(－945°)．例6、设αsin α＝35，则2cos ()A.75B.15C.－75 D.－15例7、22cos 18π-的值是（）A.2B.2-C.12D.12-知识点默写——三角函数（二）八、正弦函数的图象与性质（1）、“五点法”画sin ,[0,2]y x x π=∈的图象1、列表x sin y x=2、描点；3、连线（2）、正弦函数在R 上图象函数y ＝sin x图象定义域值域对称性对称轴：对称中心：奇偶性周期性最小正周期：单调性在上单调递增；在上单调递减最值当x =时，max y =；当x =时，min y =；九、正弦型函数的图象与性质（1）正弦型函数：sin()y A x ωϕ=+①定义域：②值域：③最小正周期：④辅助角公式：由sin cos y a x b x ωω=+=可知该函数最大值，最小值，周期.（2）用“五点法”画出正弦型函数3sin(23)y x =+的图象1、列表x23x π+2ππ32π2πsin(2)3x π+3sin(2)3y x π=+2、描点；3、连线（3）函数图象的移动怎么样由sin y x =的图象变换到13sin()23y x π=+的图象？1、先平移后伸缩：2、先伸缩后平移：例8、函数42sin y x =+，当x =时，y 取最小值；当x =时，y 取最大值.例9、求函数sin 22y x x =-的最小正周期和值域.十、余弦定理余弦定理的表示及其推论文字语言三角形中任何一边的平方等于其他两边的平方的和减去这两边与它们的夹角的余弦的积的两倍符号语言a 2＝，b 2＝，c 2＝.推论cos A ＝，cos B ＝，cos C ＝十一、正弦定理文字语言在一个三角形中，各边和它所对角的正弦的比都相等，该比值为三角形外接圆的直径符号语言在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，则十二、三角形面积公式三角形面积公式：ABC S ∆===课外补充：余弦函数：cos y x =的图象与性质；余弦型函数：cos()y A x ωϕ=+的图象与性质；正切函数：tan (,)2y x x k k Z ππ=≠+∈的图象与性质；正切型函数：tan()y A x ωϕ=+的性质.。

高中三角函数公式大全整理版（可编辑修改word版）高中三角函数公式大全sin30°=1/2sin45°=√2/2 sin60°=√3/2 cos30°=√3/2cos45°=√2/2 cos60°=1/2 tan30°=√3/3tan45°=1 tan60°=√3 cot30°=√3cot45°=1 cot60°=√3/3 sin15°=（√6-√2）/4 sin75°=（√6+√2）/4 cos15°=（√6+√2）/4cos75°=（√6-√2）/4（这四个可根据sin （45°±30°）=sin45°cos30°±cos45°sin30°得出）sin18°=(√5-1)/4 (这个值在高中竞赛和自招中会比较有用，即黄金分割的一半)正弦定理：在△ABC 中，a / sin A = b / sin B = c / sin C = 2R (其中，R 为△ABC 的外接圆的半径。

)两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinBcos(A+B) = cosAcosB-sinAsinBcos(A-B) = cosAcosB+sinAsinB tan(A+B) = tanA + tanB 1- tanAtanBtan(A-B) = tanA - tanB 1+ tanAtanBcot(A+B) = cotAcotB-1 cotB + c otAcot(A-B) = cotAcotB +1 cotB - cotA 倍角公式 tan2A =2tanA1- tan 2ASin2A=2SinA?CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3cos3A = 4(cosA)3-3cosATan3A= 3 t an 3A - (tan A )3 1- (tan A )2tan A t an( 3 A ) tan( 3 + A ) 半角公式= -sin( A )= 2 cos( A )= 2 tan( A )= 2 cot( A )= 2 tan( A )= 1- cos A =sin A2 sin A 和差化积 1+ cos Asina+sinb=2sin a + b cos a - b2 2 sina-sinb=2cos a + b sin a - b22cosa+cosb = 2cos a + b cos a - b2 2cosa-cosb = -2sin a + b sin a - b2 2tana+tanb= sin(a + b )cos a cos b积化和差1sinasinb = - [cos(a+b)-cos(a-b)]2 cosacosb = sinacosb = cosasinb = 诱导公式1 [cos(a+b)+cos(a-b)]21 [sin(a+b)+sin(a-b)]21 [sin(a+b)-sin(a-b)]2sin(-a) = -sinacos(-a) = cosasin( -a) = cosa2cos( -a) = sina2sin( +a) = cosa2 1- cos A 2 1+ cos A 2 1- cos A 1+ cos A 1+ cos A1- cos A(a 2 + b 2 ) (a 2 + b 2 ) cos( +a) = -sina 2sin(π-a) = sinacos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA = sin acos a万能公式 2 tan a sina=2 1+ (tan a )2 21- (tan a )2cosa=2 1+ (tan a )2 2 2 tan a tana=2 1- (tan a )2 2其它公式a?sina+b?cosa= ×sin(a+c) [其中b tanc= ] aa?sin(a)-b?cos(a) = ×cos(a-c) [其中 a tan(c)= ] b a a 2 1+sin(a) =(sin +cos )2 2 a a 2 1-sin(a) = (sin -cos ) 2 2其他非重点三角函数csc(a) = sec(a) = 1 sin a 1 cos a公式一：设α 为任意角，终边相同的角的同一三角函数的值相等：sin （2kπ＋α）= sinαcos （2kπ＋α）= cosαtan （2kπ＋α）= tanαcot （2kπ＋α）= cotα公式二：设α 为任意角，π+α 的三角函数值与α 的三角函数值之间的关系： sin （π＋α）= -sinαA 2 +B 2 + 2A B c os(?) t + arcsin[(Asin + Bsin ) A 2 + B 2 + 2 A B c os(?)cos （π＋α）= -cosαtan （π＋α）= tanαcot （π＋α）= cotα公式三：任意角α 与 -α 的三角函数值之间的关系：sin （-α）= -sinαcos （-α）= cosαtan （-α）= -tanαcot （-α）= -cotα公式四：利用公式二和公式三可以得到π-α 与α 的三角函数值之间的关系：sin （π-α）= sinαcos （π-α）= -cosαtan （π-α）= -tanαcot （π-α）= -cotα公式五：利用公式-和公式三可以得到2π-α 与α 的三角函数值之间的关系：sin （2π-α）= -sinαcos （2π-α）= cosαtan （2π-α）= -tanαcot （2π-α）= -cotαA?sin(ωt+θ)+ B?sin(ωt+φ) = ×sin。

高一数学校本作业22（三角函数公式默写）班级： 姓名： 座号： 1.三角函数的定义：已知角α的终边与单位圆交于一点P ()y x ,，则αin s = ；αcos = ；αtan = 推广：已知角α的终边上一点P ()y x ,，若P 点到坐标原点的距离为r ，其中r= ，则αin s = ；αcos = ；αtan = 2.写出三角函数的正负象限αsin 在第象限为正；在第 象限为负； αcos 在第象限为正；在第 象限为负； αtan 在第象限为正；在第 象限为负；3.写出1弧度的定义：4.写出弧度制与角度制的互化公式1=rad ；1rad= ；5.写出弧长公式和扇形的面积公式=l；=S =6.写出特殊三角函数的值：7.写出同角三角函数的公式：平方关系： ；商数关系： 8.写出ααcos sin +、ααcos -sin 、ααcos sin 三者之间的关系：2cos sin ）（αα+=；2cos -sin ）（αα=ααcos sin = =9.写出下列诱导公式：()=α-sin；()=α-cos ；()=α-tan ； ()=απ-sin ；()=απ-cos ；()=απ-tan ； ()=+απsin；()=+απcos ；()=+απtan ； ()=απ-2sin ；()=απ-2cos ；()=απ-2tan ；=⎪⎭⎫⎝⎛+απ2sin ；=⎪⎭⎫⎝⎛+απ2cos ；=⎪⎭⎫ ⎝⎛απ-2sin ；=⎪⎭⎫⎝⎛απ-2cos ；10.已知02πα<<，且4sin 5α. （1）求tan α的值；（2）求23sin cos sin()cos 2cos sin(3)cos 2πααπααπααπα⎛⎫--- ⎪⎝⎭⎛⎫+++ ⎪⎝⎭的值.10【分析】（1）由同角三角函数关系，利用正弦值，求解正切值即可；（2）用诱导公式对代数式进行化简，再用同角商数关系，转化为齐次式求值.【详解】（1）因为4 sin5α，所以3 cos5α===±，因为02πα<<，所以cos0α>，则3cos5α=.故sin4tancos3ααα==.（2）23sin cos sin()cos2cos sin(3)cos2πααπααπααπα⎛⎫---⎪⎝⎭⎛⎫+++⎪⎝⎭sin cossin cosαααα+=-tan1tan1αα+=-4137413+==-.。

必修四第一章2、诱导公式=+)2sin(απk =+)2(c o s απk =+)2(tan απk =+)sin(απ =+)(c o s απ =+)(tan απ =)-sin(α =)-(cos α =)-tan(α =)-sin(απ =)-(c o s απ =)-(tan απ =-)2sin(απ=-)2(c o s απ =-)2(t a n απ=+)2sin(απ =+)2(c o s απ =+)2(t a n απ3、扇形公式：扇形所对圆心角为α，半径为r扇形的弧长公式 ，周长公式 ，面积公式 . 4、三角函数的定义：角α的终边上有任意一点),(y x P则=αsin ，=αc o s ，=αt a n. 5、同角三角函数之间的关系：+ 1=，=αt a n. 6、知一求二：=+2)cos (sin αα =2)c o s -(s i n αα7、齐次式：已知x =αtan=-+ααααcos sin cos sin ，=--αααα22c o s c o s s i n s i n .8、正弦曲线的周期为 ，单调递增区间为 ， 单调递减区间为 ，值域为 ，定义域为 。

9、余弦曲线的周期为 ，单调递增区间为 ， 单调递减区间为 ，值域为 ，定义域为 。

10、正切曲线的周期为 ，单调递增区间为 ， 值域为 ，定义域为 。

必修四第二章1、b 在a 方向上的投影为 ；a 在b 方向上的投影为2、设θ是与的夹角，则=θcos3、向量a 与b 的数量积=∙b a4、若),(),,(2211y x y x == 则=∙______________________________5、向量的模长公式：设),(y x ==__________6、两点间距离公式：设A （),11y x B ),(22y x 则=__________7、向量的夹角公式：设a = （),11y x ，),(22y x = ，a 与b 的夹角为θ ，则有=θcos __________8、两个向量垂直：设= （),11y x ，),(22y x =，,≠≠，⇔⊥ _____________注意：对零向量只定义了平行，而不定义垂直。

1、终边相同的角（弧度制表示）：所有与α终边相同的角连同α在内可以构成一个集合 若βα和是终边相同的角。

那么βα-终边在2、终边在坐标轴上的点（弧度制表示）：终边在x 轴正半轴上的角的集合： 终边在x 轴负半轴上的角的集合： 终边在y 轴正半轴上的角的集合： 终边在y 轴负半轴上的角的集合： 终边在x 轴上的角的集合： 终边在y 轴上的角的集合： 终边在坐标轴上的角的集合： 3、终边共线且反向的角（弧度制表示）：终边在y =x 轴上的角的集合： 终边在x y -=轴上的角的集合： 4、区域角（弧度制表示）第一象限角的集合： 第二象限角的集合： 第三象限角的集合： 第四象限角的集合：5、 角度与弧度的互换关系：6、弧长公式和扇形面积公式__________,__________===扇S l7、特殊角的三角函数值8、三角函数的定义（1）用终边与单位圆交点坐标）（y x ,定义三角函数 ____tan ____,cos ____,sin ===ααα（2）用终边上任意点坐标）（y x ,定义三角函数 ____tan ____,cos ____,sin ===ααα9、三角函数的定义域、值域____________1,____________1,___180,___360'︒≈︒≈︒=≈=︒=︒=︒rad rad rad rad rad10、口诀：一（ ）正，二（ ）弦，三（ ）切，四（ ）弦 11、三角函数线（分别在单位圆中画出终边在第一、第二、第三、第四象限时，所对应的正弦线，余弦线，正切线） (1) (2) (3) (4)12、简要写出π20-范围内随着角的变化角的正弦值，余弦值，正切值变化情况(看三角函数线的变化情况) （1）正弦： （2）余弦： （3）正切：13、同角三角函数的基本关系（1）平方关系:_______ 商数关系：______（2）αααααααααcos sin tan tan sin cos tan cos sin 求求知求求知求求知→→→→→→→→→→→→→→→→→→（3）________)cos (sin 2=±αα14、奇变偶不变，符号看象限____,)tan(______,)cos(_____,)sin()(____,)tan(______,)cos(_____,)sin()(____,)2tan(______,)2cos(_____,)2sin()(____,)tan(_________,)cos(________,)sin()(____,)tan(_______,)cos(______,)sin()(____,)tan(_______,)cos(______,)sin()(___,)2tan(_____,)2cos(_____,)2sin()(2,2=+-=+-=+-=--=--=--=-=-=-=-=-=-=+=+=+=-=-=-=+=+=++-----+-+απαπαπαπαπαπαπαπαπααααπαπαπαπαπαππαπαπααπαπαπααπαππαα七六五四三二一终边，并写出下列公式，，，，，在同一坐标系下画出定是锐角）看成锐角（实际并非一将k k k k __,)23cos(___,)23sin()(_,)23cos(___,)23sin()(__,)2cos(___,)2sin()(__,)2cos(___,)2sin()(__,)23cos(____,)23sin()(___,)23cos(___,)23sin()(__,)2cos(____,)2sin()(____,)2cos(____,)2sin()(23,23,2,2,23,23,2,2=+-=+-=--=--=+-=+-=--=--=+=+=-=-=+=+=-=-+---+---+-+-απαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπαπα八七六五四三二一并写出下列公式在同一坐标第下画出定是锐角）看成锐角（实际并非一将。

②终边在x 轴上的角的集合：③终边在y 轴上的角的集合：2. 角度与弧度的互换关系： 180°= （rad ） 弧度与角度互换公式： 1rad ＝ °3、弧长公式：=l. 扇形面积公式：4、三角函数：设α是一个任意角，在α的终边上任取（异于原点的）一点P （x,y ）P 与原点的距离为r ，则=αsin ； =αcos ； =αtan写出正弦是正数的角所在的象限： 写出余弦是正数的角所在的象限： 写出正切是正数的角所在的象限：=+=+=+)2tan()2cos()2sin(x k x k x k πππ =-=-=-)tan()cos()sin(x x x=+=+=+)tan()cos()sin(x x x πππ =-=-=-)tan()cos()sin(x x x πππ=-=-)2cos()2sin(x x ππ=+=+)2cos()2sin(x x ππ=+)cos(βα =α2sin=-)cos(βα （三个公式）=α2cos =+)sin(βα =α2tan =-)sin(βα=+)tan(βα =-)tan(βα正弦、余弦、正切函数的图象的性质：注意：①x y sin -=与x y sin =的单调性正好相反；x y cos -=与x y cos =的单调性也同样相反.一般地，若)(x f y =在],[b a 上递增（减），则)(x f y -=在],[b a 上递减（增）.②x y sin =与x y cos =的周期是π.③)sin(ϕω+=x y 或)cos(ϕω+=x y （0≠ω）的周期ωπ2=T .⑤当αtan ·,1tan =β)(2Z k k ∈+=+ππβα；αtan ·,1tan -=β-βα⑥x y cos =与⎪⎭⎫ ⎝⎛++=ππk x y 22sin 是同一函数,而)(ϕω+=x y 是偶函数，则)cos()21sin()(x k x x y ωππωϕω±=++=+=.⑦函数x y tan =在R 上为增函数.（×） [只能在某个单调区间单调递增. 若在整个定义域，x y tan =为增函数，同样也是错误的].⑧定义域关于原点对称是)(x f 具有奇偶性的必要不充分条件.（奇偶性的两个条件：一是定义域关于原点对称（奇偶都要），二是满足奇偶性条件，偶函数：)()(x f x f =-，奇函数：)()(x f x f -=-）奇偶性的单调性：奇同偶反. 例如：x y tan =是奇函数，)31tan(π+=x y 是非奇非偶.（定义域不关于原点对称）奇函数特有性质：若x ∈0的定义域，则)(x f 一定有0)0(=f .（x ∉0的定义域，则无此性质）⑨x y sin =不是周期函数；x y sin =为周期函数（π=T ）x y cos =是周期函数（如图）；x y cos =为周期函数（=T 三角函数的图象变换有振幅变换、周期变换和相位变换等．函数y ＝Asin （ωx ＋φ）的振幅|A|，周期2||T πω=，频率1||2f Tωπ==，相位;x ωϕ+初相ϕ（即当x ＝0时的相位）．（当A ＞0，ω＞0 时以上公式可去绝对值符号），由y ＝sinx 的图象上的点的横坐标保持不变，纵坐标伸长（当|A|＞1）或缩短（当0＜|A|＜1）到原来的|A|倍，得到y ＝Asinx 的图象，叫做振幅变换或叫沿y 轴的伸缩变换．（用y/A 替换y ）由y ＝sinx 的图象上的点的纵坐标保持不变，横坐标伸长（0＜|ω|＜1）或缩短（|ω|＞1）到原来的1||ω倍，得到y＝sin ω x 的图象，叫做周期变换或叫做沿x 轴的伸缩变换．(用ωx 替换x)由y ＝sinx 的图象上所有的点向左（当φ＞0）或向右（当φ＜0）平行移动｜φ｜个单位，得到y ＝sin （x ＋φ）的图象，叫做相位变换或叫做沿x 轴方向的平移．(用x ＋φ替换x)由y ＝sinx 的图象上所有的点向上（当b ＞0）或向下（当b ＜0）平行移动｜b ｜个单位，得到y ＝sinx ＋b 的图象叫做沿y 轴方向的平移．（用y+(-b)替换y ）由y ＝sinx 的图象利用图象变换作函数y ＝Asin （ωx ＋φ）（A ＞0，ω＞0）（x ∈R ）的图象，要特别注意：当周期变换和相位变换的先后顺序不同时，原图象延x 轴量伸缩量的区别。

一． 扇形的中心角的弧度数为α，半径为r ，则弧长l= ；扇形面积S= = 二． 六个三角比的定义：已知点P （x ，y ）是角α终边上一点，点P 到原点的距离为r ，则=αsin ；αcos = ；αtan = ；αcot = ；αsec = ；αcsc = 。

三．四个常用三角比的符号分布：四．同角三角比的关系： （1）倒数关系： （2）商数关系： （3）平方关系：五．常用角的弧度数与三角比六．诱导公式：1. Z k ∈，)2sin(παk += ；)2cos(παk += ；)2tan(παk += ；)2cot(παk += 2．若Z n ∈(且n 为奇数），则)sin(παn += ；)cos(παn += ；)tan(παn += ；)cot(παn +=3． )sin(α-= ；)cos(α-= ；)tan(α-= ；)cot(α-=4． )sin(απ-= ；)cos(απ-= ；)tan(απ-= ；)cot(απ-= 5． )2sin(απ-= ；)2cos(απ-= ；)2tan(απ-= ；)2cot(απ-=6． )2sin(απ+= ；)2cos(απ+= ；)2tan(απ+= ；)2cot(απ+= 七．两角和与差的公式)sin(βα±= ；)cos(βα±= ；)tan(βα±=八．二倍角公式=α2sin ；α2cos = = = 。

α2tan =九．万能公式（用αtan 表示α2sin 与α2cos ）=α2sin ；α2cos =十．常用公式1． 2)cos (sin αα±= ；ααcot tan += 2． 降次公式：=α2sin ；α2cos = 3．=-+ααtan 1tan 1 ；=+-ααtan 1tan 14． 当∈α 时，0cos sin >-αα；当∈α 时，0cos sin >+αα 十一.在ABC ∆中：1． 正弦定理： ；面积公式：S= = = 2． 余弦定理：=A cos ；2b = ；222c b a -+=。