信号与线性系统习题解

第三章习题答案da3.1 计算下列各对信号的卷积积分()()()y t x t h t =*：(a) ()()()()t tx t e u t h t e u t αβ==（对αβ≠和αβ=两种情况都做）。

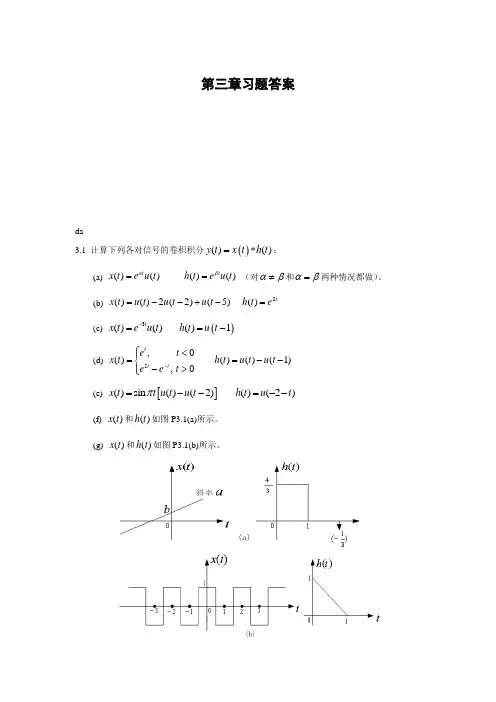
(b) 2()()2(2)(5)()tx t u t u t u t h t e =--+-=(c) ()3()()()1tx t eu t h t u t -==-(d) 5,0()()()(1),0tt t e t x t h t u t u t e e t -⎧<⎪==--⎨->⎪⎩(e) []()sin ()(2)()(2)x t t u t u t h t u t π=--=--(f) ()x t 和()h t 如图P3.1(a)所示。

(g) ()x t 和()h t 如图P3.1(b)所示。

图P3.1 解：(a) ()()0()()()(0)t ttty t x t h t eed eed t βτατβαβτττ------=*==>⎰⎰当αβ≠时，()1()()ttey t e u t αβββα----=-当αβ=时，()()t y t te u t α-=(b) 由图PS3.1(a)知， 当1t ≤时，252()2()22(2)2(5)021()22t t t t t y t ed ed e e e ττττ----⎡⎤=-=-+⎣⎦⎰⎰ 当13t ≤≤时，252()2()22(2)2(5)121()22t t t t t y t ed ed e e e ττττ-----⎡⎤=-=-+⎣⎦⎰⎰ 当36t ≤≤时，52()2(5)211()2t t t y t ed e e ττ---⎡⎤=-=-⎣⎦⎰ 当6t >时，()0y t =(c) 由图PS3.1(b)知，当1t ≤时，()0y t = 当1t >时，133(1)01()13t t y t ed e ττ----⎡⎤==-⎣⎦⎰3(1)1()1(1)3t y t e u t --⎡⎤∴=--⎣⎦(d) 由图PS3.1(d)知： 当0t ≤时，11()tt t t y t e d e eττ--==-⎰当01t <≤时，055(1)1014()(2)255t ttt t y t e d e e d e eeτττττ-----=+-=+--⎰⎰当1t >时，555(1)(1)111()(2)2255t tt tt t y t e ed eeeeτττ------=-=-+-⎰(e) 如下图所示：(f) 令()11()(2)3h t h t t δ⎡⎤=+--⎢⎥⎣⎦，则11()()()(2)3y t x t h t x t =*-- 由图PS3.1(h)知，11424()()()()(21)333t t y t x t h t a b d a t b ττ-=*=+=-+⎰2411()(21)(2)()3333a y t tb a t b a t b x t ∴=-+---=+= (g) ()x t 是周期信号，由此可推知()()()y t x t h t =*也是周期的，且周期也为2。

第1章基本概念K第1章习题k1.1解：（1）x(t)为周期信号，周期为T=10。

（2）x(t)为非周期信号。

（3）x[n]为非周期信号。

（4）x[n]为周期信号，周期为N=2。

（5）x(t)为非周期信号。

（6）x[n]为周期信号，周期为N=2。

1.2解：（1）x(t)为功率信号。

（2）x(t)既不是能量信号也不是功率信号。

（3）x[n]为能量信号。

（4）x(t)为能量信号。

（5）x(t)为能量信号。

（6）x[n]为能量信号。

1.3略。

1.4略。

1.5（原题有误）一个离散时间系统的激励与响应的关系为y[n]=M∑i=0b i x[n−i]。

用算符S−k代表将信号x[n]平移k个单位时间得到输出信号x[n−k]的系统，即x[n−k]=S−k(x[n])。

写出联系y[n]与x[n]的系统算符T及其可逆系统的算符T inv。

解：提示：可逆系统为y[n]−M∑i=1b i x[n−i]=b0x[n]。

1.6解：（1）因果、无记忆、非线性、时不变、BIBO稳定系统。

（2）因果、无记忆、线性、时变和BIBO稳定系统。

（3）因果、无记忆、线性、时变和非稳定系统。

（4）因果、记忆、线性、时不变和BIBO稳定系统。

（5）因果、无记忆、线性、时变和BIBO稳定系统。

（6）因果、记忆、时不变、非稳定系统。

–2/48–第1章基本概念（7）因果、无记忆、线性、时不变和BIBO稳定系统。

（8）非因果系统、无记忆、线性、时不变、BIBO稳定系统。

1.7证明略。

1.8解：（1）x[n]的响应为{1,1,−1,2,n=0,1,2,3}。

（2）x[n]的响应为{1,1,−3,1,3,−5,2,n=−3∼3}。

（3）x[n]的响应为{1,0,−1,4,−3,2,n=−2∼3}。

1.9证明提示：根据微积分的极限定义证明。

1.10解：（1）x(t)的响应为4(1−e−t)u(t)−6(1−e−t+1)u(t−1)。

（2）x(t)的响应为[2(t+e−t)−2]u(t)。

标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。

它的调制方式有调幅、调频、调相。

2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。

3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。

4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。

5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。

6、调频电路有直接调频、间接调频两种方式。

7、检波有同步、和非同步检波两种形式。

8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。

9、变频器可由混频器、和带通滤波器两部分组成。

10、列出三个常见的频谱搬移电路调幅、检波、变频。

11、用模拟乘法器非线性器件实现调幅最为理想。

二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。

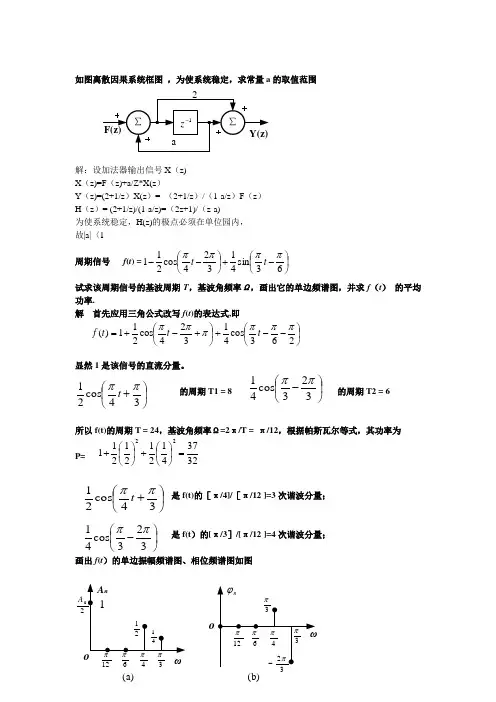
专业课习题解析课程第1讲第一章信号与系统（一）专业课习题解析课程第2讲第一章 信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)tf=r)(sin(t（7）)f kε=t)(2(k（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

专业课习题解析课程第1讲第一章信号与系统（一）. 学习参考.专业课习题解析课程第2讲. 学习参考.. 学习参考 .第一章 信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(. 学习参考.（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=. 学习参考.（5）)(sin )(t r t f =（7）)(2)(k t f k ε=. 学习参考.（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f. 学习参考 .（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f. 学习参考.（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε. 学习参考.（11）)]7()()[6sin()(--=k k k k f εεπ. 学习参考 .（12）)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。

习题六题6.1 求下列序列的双边z 变换，并注明收敛域 (1) 1(),0()20,0k k f k k ⎧<⎪=⎨⎪≥⎩ (3) ||1()(,0,1, (2)k f k k ==± 解: (1) 11()((1),||1222k z f k k z z ε−=−−↔<− (3) 11()2(1)()(),||213233k k z z f k k k z z z εε−=−−+↔+<<−−题6.2求下列序列的z 变换，并注明收敛域 (1) 1()(()3k f k k ε= (2) 1()()()3k f k k ε−=− (5) ()cos()()4k f k k πε= 解： (1) 11()((),||1333k z f k k z z ε=↔>− (2) 1()()(),||333k z f k k z z ε−=−↔>+(5) 222cos ()cos()()|142cos 1z z k z z f k k z z z πβεβ−−=↔=>−+题6.4 根据下列象函数及所标注的收敛域，求其所对应得原序列(2) 3(),||F z z z =<∞ (5) 11(),||||1F z z a az−=>− (6) 11(),||||1F z z a az −=<− 解：(2) 3()(3)F z z k δ=↔+(5) 11(),||||()1k F z z a a k azε−=>↔− (6) 11(),||||(1)1k F z z a a k azε−=<↔−−−− 题6.5 已知2()1,(),()(1)k z z k a k k k z a z δεε↔↔↔−−试利用z 变换的性质求下列序列的z 变换，并注明收敛域。

(2) ()2(4)(8)k k k εεε−−+−(4) (1)(1)k k ε−−(6) 2(1)(1)k k ε−− (8) cos(()2k k πε 解： (2) 48()2(4)(8)2111z z z k k k z z z z z εεε−−−−+−↔−+−−− 48(12)1z z z z −−=−+− 441||01z z z z z−=>− (4) ()()d k k zF z dz ε↔− 2()(1)z k k z ε↔− 1221(1)(1),||1(1)(1)z k k z z z z ε−−−↔=>−− (6) 2133(1)(1)(1)(1)(1)(1)z z z k k z z z ε−++−−↔=−− (8) 2222cos cos()(),||122cos 11k z z z k z z z z πβεβ−↔=>−++题6.9求下列象函数的逆z 变换 (2) 311(),||122z F z z z +=>+232z z ++(6) 2(),||0.5(0.5)(0.25)z F z z z z =>−− 解： (2) 01()3111()22k k F z z z z z z z +==+++ 000()31||2()2z z F z z k z z z ==+=•==+ 1121312|21()2z z z k z z z =++=∗=−+ 2221()**22()()()11222k z F z z z k k z z z δε−=+=−↔+−++ (4) 212()(1)(2)12k k F z z z z z z z z ==+++++ 2111*|1(1)(2)z z z k z z z z =−+==−++ 222(2)*|2(1)(2)z z k z z z z =−=+=++ 22()(1)()2(2)()[(1)2(2)]()12k k k k z z F z k k k z z εεε−=+↔−+−=−+−++ (6) ()(0.5)(0.25)F z z z z z =−− 10.5()(0.5)|2z F z k z z==−= 20.25()(0.25)|1z F z k z z==−=− 211()[2()()]()0.50.2524k k z z F z k z z ε−=+↔−−−题6.11求下列象函数的逆z 变换 (1) 21(),||11F z z z =>+(5) 2(),||1(1)(1)z F z z z z =>−− 解： (1)0122()1(1)k k k F z z z z z z j z j ==+++−+ 00()*|1z F z k z z=== 12()1*()|2z j F z k z j k z ==−=−= 1122()1z zF z z j z j−−=++−+ 1()()2*||cos()*()k f k k k k k δαβθε=++()cos *()2k k k πδε=−(3) ()|1F z z z =>61,2|22j z e π±=±=21()1*()||2233j F z j j k z e z π=−−=−=− 12()2*||cos()cos()()362k f k k e k k k αππβθε=+=+ (5) 1212222()1(1)(1)1(1)1k k k F z z z z z z z ==++−−+−− 11()1*(1)|4z F z k z z =−=+= 2211()1*(1)|2z F z k z z ==−= 2214k =− 2111422(),||11(1)1z z zF z z z z z =++>+−− 1111[(1)]()[(1)21]()4244k k k k k k εε↔−+−=−+−题6.16 用z 变换法求下列非齐次方程的全解(2) ()3(1)2(2)(),(1)0,(2)0.5y k y k y k k y y ε+−+−=−=−=(3) (2)(1)2()(),(0)1,(1)1y k y k y k k y y ε+−+−===解：(2) 121()3[()(1)]2[()(2)(1)]()Y z z Y z y z Y z y y z F z −−−++−++−+−=121()[132][3(1)2(2)2(1)]1z Y z z z y y y z z −−−+++−+−+−=− 3121211()[]13212112k k k z Y z z z z z z z −−=+=++++−−++ 2111(31)1*|2(1)(1)(2)6z z z z k z z z z =−−==−++ 2211(31)1*|2(1)(1)(2)2z z z z k z z z z =−+−==−++ 2322(31)2*|2(1)(1)(2)3z z z z k z z z z =−+−==−−++ 112()[(1)(2)]()623k k y k k ε=+−−− (3) 22()(0)(1)[()(0)]2()1z Y z z z y zy zY z zy Y z z −−−−−=− 22()[2][2]1z Y z z z z z z −−−+−=− 231112()1(1)(1)(2)112k k k Y z z z z z z z z z z −+==++−+−−+− 22221112()111(1)(1)|(1)(2)(2)2z Y z z z z z k z z z z z z =−+−+=−=−==−−−− 21212(21)(2)(1)1|(2)3z z z z z k z =−−−−+==−− 232(2)(1)|1(1)(1)z z z z k z z =−−+==−+ 1132()112z z z Y z z z z −−=++−+− 11()[(1)(2)]()23k k y k k ε=−−−+题6.17 描述某LTI 离散系统的差分方程为()(1)2(2)()y k y k y k f k −−−−=已知1(1)1,(2),()()4y y f k k ε−=−−==，求该系统的零输入响应，零状态响应和全响应。

第一章 信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)tf=r)(sin(t（7）)f kε=t)(2(k（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=kkkkfεεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

专业课习题解析课程第2讲第一章 信号与系统（二）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t et f t,)( （3）)()sin()(t t t f επ=（4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f kε= （10）)(])1(1[)(k k f kε-+=解：各信号波形为 （2）∞<<-∞=-t et f t,)(（3）)()sin()(t t t f επ=（4）)(sin )(t t f ε=（5）)tf=r(t(sin)（7）)f kε=t(k2)(（10）)(])1(1[)(k k f k ε-+=1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε （11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k---=εε 解：各信号波形为（1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(kkkf k---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

如果是，确定其周期。

信号与线性系统题解 阎鸿森 第二章 习题答案2.1 (1) 已知连续时间信号()x t 如图P2.1(a)所示。

试画出下列各信号的波形图，并加以标注。

(a) (2)x t - (b) (1)x t - (c) (22)x t +(2) 根据图P2.1(b)所示的信号()h t ，试画出下列各信号的波形图，并加以标注。

(a) (3)h t + (b) (2)2t h - (c) (12)h t -(3) 根据图P2.1(a)和(b)所示的()x t 和()h t ，画出下列各信号的波形图，并加以标注。

(a) ()()x t h t - (b) (1)(1)x t h t -- (c) (2)(4)2t x h t -+图P2.1 解：(1) 各信号波形如下图所示：(a)(b)(c)12(2)x t -(1)x t -(22)x t +ttt22221111121001-1-1-2-2-35(2) 各信号波形如下图所示：(a)(b)(c)1212-32(3)h t +(2)2t h -(12)h t -t tt00111124681-2-3-4-5-(3) 各信号波形如下图所示：()()x t h t -(1)(1)x t h t --(2)2t x -(a)(b)(c)ttt∴(2/2)(4)0x t h t -+=00111112222221-1-462-2.2 已知信号(52)x t -的波形图如图P2.2所示，试画出的波形图，并加以标注。

j Ωσa-图P2.2解：波形如下图所示：j Ωσ2.3 (1) 已知离散时间信号如图P2.3(a)所示，试画出下列各信号的波形图，并加以标注。

(a) (b)(c)(2) 对图P2.3(b)所示的信号，试画出下列个信号的波形，并加以标注。

(a) (b)(c)(3) 根据图P2.3(a)和(b)所示的和()h n ，画出下列各信号的波形图，并加以标注。

(a) (2)(12)x n h n +- (b) (1)(4)x n h n -+ (c) (1)(3)x n h n --()x n n()h n n1212-3232-12(a)(b)4-1-1-1-2-0011122334421图P2.3 解：(1) 各信号波形图如下图所示：(4)x n -n(a)1/22-1-01123456(21)x n+ˆ()xn nn(b)(c)2-1-1-0011112233(2) 各信号波形图如下图所示：(2)(1)h n h n ++--n1/2(c)6-5-4-3-2-2-2-1-0123(3) 各信号波形如下图所示：(2)(12)x n h n +-(1)(4)x n h n -+(a)(b)nn1/21/2-3/23/21/43/4-1-1-001112232(1)(3)x n h n --(c )n1/21/2-3/2-1-1-012345672.4 画出图P2.4所给各信号的奇部和偶部。