计量经济学(第3版)习题数据
- 格式:doc
- 大小:1.59 MB
- 文档页数:38

目 录第1章 绪 论第2章 经典单方程计量经济学模型:一元线性回归模型第3章 经典单方程计量经济学模型:多元线性回归模型第4章 经典单方程计量经济学模型:放宽基本假定的模型第5章 经典单方程计量经济学模型:专门问题第6章 联立方程计量经济学模型:理论与方法第7章 扩展的单方程计量经济学模型第8章 时间序列计量经济学模型第9章 计量经济学应用模型第1章 绪 论1什么是计量经济学?计量经济学方法与一般经济数学方法有什么区别?答:(1)计量经济学是经济学的一个分支学科,以揭示经济活动中客观存在的数量关系为主要内容,是由经济理论、统计学和数学三者结合而成的交叉学科。
(2)计量经济学方法通过建立随机的数学方程来描述经济活动,并通过对模型中参数的估计来揭示经济活动中各个因素之间的定量关系,是对经济理论赋予经验内容;而一般经济数学方法是以确定性的数学方程来描述经济活动,揭示的是经济活动中各个因素之间的理论关系。
2计量经济学的研究对象和内容是什么?计量经济学模型研究的经济关系有哪两个基本特征?答:(1)计量经济学的研究对象是经济现象,主要研究的是经济现象中的具体数量规律,即是利用数学方法,依据统计方法所收集和整理到的经济数据,对反映经济现象本质的经济数量关系进行研究。
(2)计量经济学的内容大致包括两个方面:一是方法论,即计量经济学方法或理论计量经济学;二是应用计量经济学。
任何一项计量经济学研究和任何一个计量经济学模型赖以成功的三要素是理论、方法和数据。
(3)计量经济学模型研究的经济关系的两个基本特征是随机关系和因果关系。
3为什么说计量经济学在当代经济学科中占据重要地位?当代计量经济学发展的基本特征与动向是什么?答:(1)计量经济学自20世纪20年代末30年代初形成以来,无论在技术方法还是在应用方面发展都十分迅速,尤其是经过20世纪50年代的发展阶段和60年代的扩张阶段,使其在经济学科占据重要的地位,主要表现在:①在西方大多数大学和学院中,计量经济学的讲授已成为经济学课程表中最具有权威的一部分;②从1969~2003年诺贝尔经济学奖的53位获奖者中有10位是与研究和应用计量经济学有关;③计量经济学方法与其他经济数学方法结合应用得到了长足的发展。

封面作者:Pan Hongliang仅供个人学习第一章绪论参考重点:计量经济学的一般建模过程第一章课后题(1.4.5)1.什么是计量经济学?计量经济学方法与一般经济数学方法有什么区别?答:计量经济学是经济学的一个分支学科,是以揭示经济活动中客观存在的数量关系为内容的分支学科,是由经济学、统计学和数学三者结合而成的交叉学科。
计量经济学方法揭示经济活动中各个因素之间的定量关系,用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各个因素之间的理论关系,用确定性的数学方程加以描述。
4.建立与应用计量经济学模型的主要步骤有哪些?答:建立与应用计量经济学模型的主要步骤如下:(1)设定理论模型,包括选择模型所包含的变量,确定变量之间的数学关系和拟定模型中待估参数的数值范围;(2)收集样本数据,要考虑样本数据的完整性、准确性、可比性和—致性;(3)估计模型参数;(4)检验模型,包括经济意义检验、统计检验、计量经济学检验和模型预测检验。
5.模型的检验包括几个方面?其具体含义是什么?答:模型的检验主要包括:经济意义检验、统计检验、计量经济学检验、模型的预测检验。
在经济意义检验中,需要检验模型是否符合经济意义,检验求得的参数估计值的符号与大小是否与根据人们的经验和经济理论所拟订的期望值相符合;在统计检验中,需要检验模型参数估计值的可靠性,即检验模型的统计学性质;在计量经济学检验中,需要检验模型的计量经济学性质,包括随机扰动项的序列相关检验、异方差性检验、解释变量的多重共线性检验等;模型的预测检验主要检验模型参数估计量的稳定性以及对样本容量变化时的灵敏度,以确定所建立的模型是否可以用于样本观测值以外的范围。
第二章经典单方程计量经济学模型:一元线性回归模型参考重点:1.相关分析与回归分析的概念、联系以及区别?2.总体随机项与样本随机项的区别与联系?3.为什么需要进行拟合优度检验?4.如何缩小置信区间?(P46)由上式可以看出(1).增大样本容量。

第一章绪论(一)参考重点:计量经济学的一般建模过程第一章课后题(1.4.5)1.什么是计量经济学?计量经济学方法与一般经济数学方法有什么区别?答:计量经济学是经济学的一个分支学科,是以揭示经济活动中客观存在的数量关系为内容的分支学科,是由经济学、统计学和数学三者结合而成的交叉学科。
计量经济学方法揭示经济活动中各个因素之间的定量关系,用随机性的数学方程加以描述;一般经济数学方法揭示经济活动中各个因素之间的理论关系,用确定性的数学方程加以描述。
4.建立与应用计量经济学模型的主要步骤有哪些?答:建立与应用计量经济学模型的主要步骤如下:(1)设定理论模型,包括选择模型所包含的变量,确定变量之间的数学关系和拟定模型中待估参数的数值范围;(2)收集样本数据,要考虑样本数据的完整性、准确性、可比性和—致性;(3)估计模型参数;(4)检验模型,包括经济意义检验、统计检验、计量经济学检验和模型预测检验。
5.模型的检验包括几个方面?其具体含义是什么?答:模型的检验主要包括:经济意义检验、统计检验、计量经济学检验、模型的预测检验。
在经济意义检验中,需要检验模型是否符合经济意义,检验求得的参数估计值的符号与大小是否与根据人们的经验和经济理论所拟订的期望值相符合;在统计检验中,需要检验模型参数估计值的可靠性,即检验模型的统计学性质;在计量经济学检验中,需要检验模型的计量经济学性质,包括随机扰动项的序列相关检验、异方差性检验、解释变量的多重共线性检验等;模型的预测检验主要检验模型参数估计量的稳定性以及对样本容量变化时的灵敏度,以确定所建立的模型是否可以用于样本观测值以外的范围。
第二章经典单方程计量经济学模型:一元线性回归模型参考重点:1.相关分析与回归分析的概念、联系以及区别?2.总体随机项与样本随机项的区别与联系?3.为什么需要进行拟合优度检验?4.如何缩小置信区间?(P46)由上式可以看出(1).增大样本容量。
样本容量变大,可使样本参数估计量的差减小;同时,在同样置信水平下,n越大,t分布表中的临界值越小。

计量经济学李⼦奈(第3版)例题+习题数据计量经济学(第3版)例题和习题数据表表2.1.1 某社区家庭每⽉收⼊与消费⽀出统计表表2.3.1 参数估计的计算表表2.6.1 中国各地区城镇居民家庭⼈均全年可⽀配收⼊与⼈均全年消费性⽀出(元)资料来源:《中国统计年鉴》(2007)。
表2.6.3 中国居民总量消费⽀出与收⼊资料单位:亿元年份GDP CONS CPI TAX GDPC X Y 19783605.6 1759.1 46.21519.28 7802.5 6678.83806.7 19794092.6 2011.5 47.07537.828694.2 7551.64273.2 19804592.9 2331.2 50.62571.70 9073.7 7944.24605.5 19815008.8 2627.951.90629.899651.8 8438.05063.9 19825590.0 2902.9 52.95700.02 10557.3 9235.25482.4 19836216.2 3231.154.00775.5911510.8 10074.65983.2 19847362.7 3742.0 55.47947.35 13272.8 11565.06745.7 19859076.7 4687.460.652040.79 14966.8 11601.77729.2 198610508.5 5302.1 64.572090.37 16273.7 13036.58210.9 198712277.4 6126.1 69.302140.36 17716.3 14627.78840.0 198815388.6 7868.1 82.302390.47 18698.7 15794.09560.5 198917311.3 8812.6 97.002727.40 17847.4 15035.59085.5 199019347.8 9450.9 100.002821.86 19347.8 16525.99450.9 199122577.4 10730.6 103.422990.17 21830.9 18939.610375.8 199227565.2 13000.1 110.033296.91 25053.0 22056.511815.3 199336938.1 16412.1 126.204255.30 29269.1 25897.313004.7 199450217.4 21844.2 156.655126.88 32056.2 28783.413944.2 199563216.9 28369.7 183.416038.04 34467.5 31175.415467.9 199674163.6 33955.9 198.666909.82 37331.933853.717092.5 199781658.5 36921.5 204.218234.04 39988.5 35956.218080.6 199886531.6 39229.3 202.599262.80 42713.1 38140.919364.1 199991125.0 41920.4 199.7210682.58 45625.8 40277.020989.3 200098749.0 45854.6200.5512581.51 49238.0 42964.622863.9 2001108972.4 49213.2 201.9415301.38 53962.5 46385.424370.1 2002120350.3 52571.3 200.3217636.45 60078.0 51274.026243.2 2003136398.8 56834.4 202.7320017.31 67282.2 57408.128035.0 2004160280.4 63833.5 210.6324165.68 76096.3 64623.130306.2 2005188692.1 71217.5 214.4228778.54 88002.1 74580.433214.4 2006221170.5 80120.5 217.6534809.72 101616.3 85623.136811.2资料来源:根据《中国统计年鉴》(2001,2007)整理。

第一章 绪论(一)基本知识类题型1-1. 什么是计量经济学?1-2. 简述当代计量经济学发展的动向。
1-3. 计量经济学方法与一般经济数学方法有什么区别?1-4.为什么说计量经济学是经济理论、数学和经济统计学的结合?试述三者之关系。
1-5.为什么说计量经济学是一门经济学科?它在经济学科体系中的作用和地位是什么?1-6.计量经济学的研究的对象和内容是什么?计量经济学模型研究的经济关系有哪两个基本特征?1-7.试结合一个具体经济问题说明建立与应用计量经济学模型的主要步骤。
1-8.建立计量经济学模型的基本思想是什么?1-9.计量经济学模型主要有哪些应用领域?各自的原理是什么?1-10.试分别举出五个时间序列数据和横截面数据,并说明时间序列数据和横截面数据有和异同?1-11.试解释单方程模型和联立方程模型的概念,并举例说明两者之间的联系与区别。
1-12.模型的检验包括几个方面?其具体含义是什么?1-13.常用的样本数据有哪些?1-14.计量经济模型中为何要包括随机误差项?简述随机误差项形成的原因。
1-15.估计量和估计值有何区别?哪些类型的关系式不存在估计问题?1-16.经济数据在计量经济分析中的作用是什么?1-17.下列假想模型是否属于揭示因果关系的计量经济学模型?为什么?⑴ t 年农村居民储蓄增加额(亿元)t 年城镇居民可支配收入总额(亿元)。
⑵ (1-t )年底农村居民储蓄余额为第t 年农村居民纯收入总额(亿元)。
1-18.指出下列假想模型中的错误,并说明理由:(1t 年社会消费品零售总额(亿元)t 年居民收入总额(亿元)(城镇居民可支配收入总额与农村居民纯收入总额之和)t 年全社会固定资产投资总额(亿元)。
(2)t t Y C 2.1180+=其中,C 、Y 分别是城镇居民消费支出和可支配收入。
(3)t t t L K Y ln 28.0ln 62.115.1ln -+=其中,Y 、K 、L 分别是工业总产值、工业生产资金和职工人数。
第2章 一元线性回归模型习 题3.简答题、分析与计算题(12)表1数据是从某个行业的5个不同的工厂收集的,请回答以下问题:①估计这个行业的线性总成本函数: tt x b b y 10ˆˆˆ+= ②0ˆb 和1ˆb 的经济含义是什么? ③估计产量为10时的总成本。
表1 某行业成本与产量数据(13)有10户家庭的收入(x ,百元)与消费(y ,百元)的资料如表2。
表2 家庭的收入与消费的资料要求:①建立消费(y )对收入(x )的回归直线。
②说明回归直线的代表性及解释能力。
③在95%的置信度下检验参数的显著性。
④在95%的置信度下,预测当x =45(百元)时,消费(y )的可能区间 (14)假设某国的货币供给量(y )与国民收入(x )的历史数据如表3所示:表3 货币供给量(y )与国民收入(x )数据请回答以下问题:①作出散点图,然后估计货币供给量y 对国民收入x 的回归方程,并把加归直线画在散点图上。
②如何解释回归系数的含义?③如果希望1997年国民收入达到15.0,那么应该把货币供应量定在什么水平上? (15)我国1978-2011年的财政收入y 和国内生产总值x 的数据资料如表4所示。
表4 我国1978-2011年中国财政收入和国内生产总值数据试根据资料完成下列问题:①建立财政收入对国内生产总值的一元线性回归方程,并解释回归系数的经济意义;②求置信度为95%的回归系数的置信区间;③对所建立的回归方程进行检验(包括经济意义检验、估计标准误差评价、拟合优度检验、参数的显著性检验);④若2012年国内生产总值为117253.52亿元,求2002年财政收入预测值及预测区间(05.0=α)。
(16)表5是1960-1981年间新加坡每千人电话数y 与按要素成本x 计算的新加坡元人均国内生产总值。
这两个变量之间有何关系?你怎样得出这样的结论?表5 1960-1981年新加坡每千人电话数与人均国内生产总值第3章 多元线性回归模型习 题3.简答题、分析与计算题(12)表1给出某地区职工平均消费水平t y ,职工平均收入t x 1和生活费用价格指数t x 2,试根据模型:t t t t u x b x b b y +++=22110作回归分析。
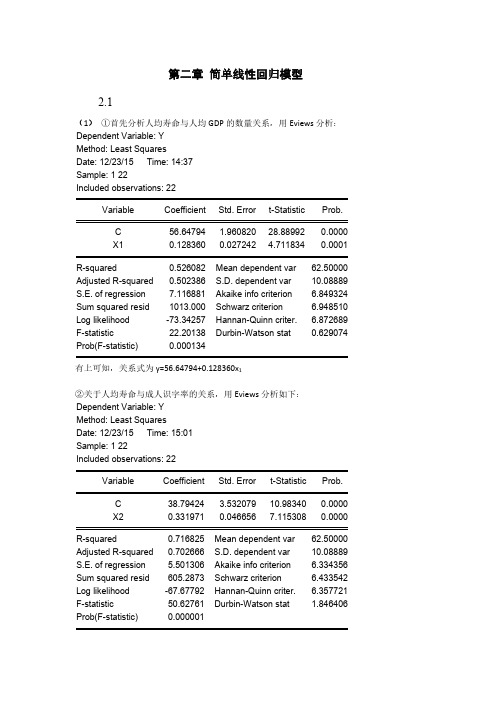
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
第二章简单线性回归模型2.1(1)①首先分析人均寿命与人均GDP的数量关系,用Eviews分析:Dependent Variable: YMethod: Least SquaresDate: 12/23/15 Time: 14:37Sample: 1 22Included observations: 22Variable Coefficient Std. Errort-Statistic Prob.C56.64794 1.96082028.889920.0000X10.1283600.027242 4.7118340.0001R-squared0.526082 Mean dependent var62.50000 Adjusted R-squared0.502386 S.D. dependent var10.08889S.E. of regression7.116881 Akaike infocriterion 6.849324Sum squared resid1013.000 Schwarz criterion 6.948510Log likelihood-73.34257 Hannan-Quinncriter. 6.872689F-statistic22.20138 Durbin-Watson stat0.629074 Prob(F-statistic)0.000134有上可知,关系式为y=56.64794+0.128360x1②关于人均寿命与成人识字率的关系,用Eviews分析如下:Dependent Variable: YMethod: Least SquaresDate: 12/23/15 Time: 15:01Sample: 1 22Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C38.79424 3.53207910.983400.0000X20.3319710.0466567.1153080.0000R-squared0.716825 Mean dependent var62.50000 Adjusted R-squared0.702666 S.D. dependent var10.08889S.E. of regression 5.501306 Akaike infocriterion 6.334356Sum squared resid605.2873 Schwarz criterion 6.433542 Log likelihood-67.67792 Hannan-Quinn 6.357721criter.F-statistic50.62761 Durbin-Watson stat 1.846406 Prob(F-statistic)0.000001由上可知,关系式为y=38.79424+0.331971x2③关于人均寿命与一岁儿童疫苗接种率的关系,用Eviews分析如下:Dependent Variable: YMethod: Least SquaresDate: 12/23/14 Time: 15:20Sample: 1 22Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C31.79956 6.536434 4.8649710.0001X30.3872760.080260 4.8252850.0001R-squared0.537929 Mean dependent var62.50000 Adjusted R-squared0.514825 S.D. dependent var10.08889S.E. of regression7.027364 Akaike infocriterion 6.824009Sum squared resid987.6770 Schwarz criterion 6.923194Log likelihood-73.06409 Hannan-Quinncriter. 6.847374F-statistic23.28338 Durbin-Watson stat0.952555Prob(F-statistic)0.000103由上可知,关系式为y=31.79956+0.387276x3(2)①关于人均寿命与人均GDP模型,由上可知,可决系数为0.526082,说明所建模型整体上对样本数据拟合较好。
第二章练习题及参考解答表中是1992年亚洲各国人均寿命(Y)、按购买力平价计算的人均GDP(X1)、成人识字率(X2)、一岁儿童疫苗接种率(X3)的数据表亚洲各国人均寿命、人均GDP、成人识字率、一岁儿童疫苗接种率数据(1)分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。
(2)对所建立的回归模型进行检验。
【练习题参考解答】(1)分别设定简单线性回归模型,分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系(2)对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显着影响.(3)分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为人均寿命与成人识字率回归的可决系数为人均寿命与一岁儿童疫苗接种率的可决系数为相对说来,人均寿命由成人识字率作出解释的比重更大一些为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:表浙江省财政预算收入与全省生产总值数据的显着性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年,全省生产总值为32000 亿元,比上年增长%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显着性,并解释所估计参数的经济意义【练习题参考解答】建议学生独立完成由12对观测值估计得消费函数为:(1)消费支出C的点预测值;(2)在95%的置信概率下消费支出C平均值的预测区间。
第2章 一元线性回归模型习 题3.简答题、分析与计算题(12)表1数据是从某个行业的5个不同的工厂收集的,请回答以下问题:①估计这个行业的线性总成本函数: tt x b b y 10ˆˆˆ+= ②0ˆb 和1ˆb 的经济含义是什么? ③估计产量为10时的总成本。
表1 某行业成本与产量数据(13)有10户家庭的收入(x ,百元)与消费(y ,百元)的资料如表2。
表2 家庭的收入与消费的资料要求:①建立消费(y )对收入(x )的回归直线。
②说明回归直线的代表性及解释能力。
③在95%的置信度下检验参数的显著性。
④在95%的置信度下,预测当x =45(百元)时,消费(y )的可能区间 (14)假设某国的货币供给量(y )与国民收入(x )的历史数据如表3所示:表3 货币供给量(y )与国民收入(x )数据请回答以下问题:①作出散点图,然后估计货币供给量y 对国民收入x 的回归方程,并把加归直线画在散点图上。
②如何解释回归系数的含义?③如果希望1997年国民收入达到15.0,那么应该把货币供应量定在什么水平上? (15)我国1978-2011年的财政收入y 和国内生产总值x 的数据资料如表4所示。
表4 我国1978-2011年中国财政收入和国内生产总值数据试根据资料完成下列问题:①建立财政收入对国内生产总值的一元线性回归方程,并解释回归系数的经济意义;②求置信度为95%的回归系数的置信区间;③对所建立的回归方程进行检验(包括经济意义检验、估计标准误差评价、拟合优度检验、参数的显著性检验);④若2012年国内生产总值为117253.52亿元,求2002年财政收入预测值及预测区间(05.0=α)。
(16)表5是1960-1981年间新加坡每千人电话数y 与按要素成本x 计算的新加坡元人均国内生产总值。
这两个变量之间有何关系?你怎样得出这样的结论?表5 1960-1981年新加坡每千人电话数与人均国内生产总值第3章 多元线性回归模型习 题3.简答题、分析与计算题(12)表1给出某地区职工平均消费水平t y ,职工平均收入t x 1和生活费用价格指数t x 2,试根据模型:t t t t u x b x b b y +++=22110作回归分析。
表1 某地区职工收入、消费和生活费用价格指数(13)设有模型t t t t u x b x b b y +++=22110,试在下列条件下: ①121=+b b ;②21b b =,分别求出1b 和2b 的最小二乘估计量。
(14)某地区统计了机电行业的销售额y (万元)和汽车产量x 1(万辆)以及建筑业产值x 2(千万元)的数据如表2所示。
试按照下面要求建立该地区机电行业的销售额和汽车产量以及建筑业产值之间的回归方程,并进行检验(显著性水平05.0=α)。
表2 某地区机电行业的销售额、汽车产量与建筑业产值数据①根据上面的数据建立对数模型:t t t t u x b x b b y +++=22110ln ln ln (1)②所估计的回归系数是否显著?用p 值回答这个问题。
③解释回归系数的意义。
④根据上面的数据建立线性回归模型:t t t t u x b x b b y +++=22110 (2)⑤比较模型(1)、(2)的2R 值。
⑥如果模型(1)、(2)的结论不同,你将选择哪一个回归模型?为什么? (15)对下列模型进行适当变换化为标准线性模型: ①u xb x b b y +⋅+⋅+=221011 ②u e K AL Q βα= ③ux b b e y ++=10④)(1011u x b b ey ++-+=(16)表3给出了一个钢厂在不同年度的钢产量。
找出表示产量和年度之间关系的方程:bx ae y =,并预测2002年的产量。
表3 某钢厂1991-2001年钢产量(单位:千吨)(17)某产品的产量与科技投入之间呈二次函数模型:u x b x b b y +++=2210其统计资料如表4所示,试对模型进行回归分析。
表4 某产品产量与科技投入数据(18)表5给出了德国1971-1980年间消费者价格指数y (1980=100)及货币供给x (亿德国马克)的数据。
表5 德国1971-1980年消费者价格指数与货币供给数据①根据表5数据进行以下回归:①y 对x ;②lny 对lnx ;③lny 对x ;④ y 对lnx 。
②解释各回归结果;③对每一个模型求y 对x 的变化率; ④对每一个模型求y 对x 的弹性;⑤根据这些回归结果,你将选择那个模型?为什么? (19)根据表6的数据估计模型t t tu x b b y ++=101表6 样本数据①解释1b 的含义; ②求y 对x 的变化率; ③求y 对x 的弹性;④用相同的数据估计下面的回归模型:t tt u x b b y ++=110 ⑤你能比较这两个模型的2R 值吗?为什么? ⑥如何判断哪一个模型更好一些?(20)表7给出了1960-1982年间7个OECD 国家(美国、加拿大、德国、意大利、英国、日本、法国)的能源需求指数(y)、实际的GDP 指数(x 1)、能源价格指数(x 2)的数据,所有指数均以1970为基准(1970=100)。
表7 7个OECD 国家能源需求指数、实际GDP 指数与能源价格指数①运用柯布——道格拉斯生产函数建立能源需求与收入、价格之间的对数需求函数:t t t t u x b x b b y +++=22110ln ln ln (3)②所估计的回归系数是否显著?用p 值回答这个问题; ③解释回归系数的意义;④根据上面的数据建立线性回归模型:t t t t u x b x b b y +++=22110 (4)⑤比较模型(3)、(4)的2R 值;⑥如果模型(3)、(4)的结论不同,你将选择哪一个回归模型?为什么?(21)表8列出了中国2000年按行业分的全部制造业国有企业及规模以上企业制造业非国有企业的工业总产值Y ,资产合计K 及职工人数L 。
设定模型为u e L AK Y βα=①利用表8资料,进行回归分析;②中国2000年的制造业总体呈现规模报酬不变状态吗?表8 中国2000年制造业业总产值、资产、职工人数统计资料(22)表9列出了某地区家庭人均鸡肉年消费量Y 与家庭月平均收入X ,鸡肉价格1P 、猪肉价格2P 与牛肉价格3P 的相关数据。
①利用表9资料,求出该地区家庭鸡肉消费需求模型:u P b P b P b X b b Y +++++=34231210ln ln ln ln ln②试分析该地区家庭鸡肉消费需求是否受猪肉价格2P 与牛肉价格3P 的影响。
表9 相关统计数据(23)在一项对某社区家庭对某种商品需求调查中,得到表10的统计数据。
请用手工与软件两种方式对该社区家庭对某种商品需求支出作二元线性回归分析,其中手工方式要求以矩阵表达式进行运算。
表10 某社区家庭某商品消费需求统计调查数据(单位:元)①估计回归方程的参数及随机误差项的方差2ˆσ,计算2R 及2R 。
其中已知: 1)(-'X X =⎪⎪⎪⎭⎫--- ⎝⎛-00000011.00005958.000053817.00005958.003381604.036302110.000053817.03630211.032536028.5②对方程进行F 检验,对参数进行t 检验,并构造参数95%的置信区间。
③如果商品价格变为35元,则某一月收入为20000元的家庭对其消费支出估计是多少?构造该估计值的95%的置信区间。
第4章 异方差性习 题3.简答题、分析与计算题(10)建立住房支出模型:t t t u x b b y ++=10,样本数据如表1(其中:y 是住房支出,x 是收入,单位:千美元)。
表1 住房支出与收入数据请回答下列问题:①用最小二乘法估计10,b b 的估计值、标准差、拟合优度;②用Goldfeld-Quandt 检验异方差性(假设分组时不去掉任何样本值),取05.0=α; ③如果存在异方差性,假设222t t x σσ=,用加权最小二乘法重新估计10,b b 的估计值、标准差、拟合优度。
(11)试根据表2中消费(y)与收入(x)的数据完成以下问题:①估计回归模型:t t t u x b b y ++=10;②检验异方差性;(3)选用适当的方法修正异方差性。
表2 消费与收入数据(12)考虑表3中的数据。
①估计OLS 回归方程:t t t u x b b y ++=10表3 样本数据②估计:tttttttu x b b y σσσσ++=11分析两个回归方程的结果,你认为哪个回归方程更好?为什么? (13)现有20个家庭的年收入和消费支出资料如表4(单位:千元)。
表4 20个家庭年收入和消费支出资料①用普通最小二乘法估计家庭消费函数:t t t u x b b y ++=10;②利用Goldfeld-Quandt检验进行异方差性检验;③利用White检验、Park检验和Glejser检验进行异方差性检验;④用加权最小二乘法估计家庭消费函数。
(14)表5列出了1995年北京市规模最大的20家百货零售商店的商品销售收入x和销售利润y的统计资料。
表5 20家百货商店商品销售收入与利润(单位:千万元)①根据y、x的相关图分析异方差性;②利用White检验、Park检验和Glejser检验进行异方差性检验;③利用WLS方法估计利润函数。
(15)表6列出了2000年中国部分省市城镇居民每个家庭平均全年可支配收入x与消费性支出y的统计数据。
①利用OLS法建立人均消费支出与可支配收入的线性模型和对数线性模型;②检验模型是否存在异方差性;③如果存在异方差性,试采用适当的方法加以消除。
表6 中国城镇居民人均可支配收入与消费性支出(单位:元)(16)已知某地区的个人储蓄y,可支配收入x的截面样本数据见表7。
①利用OLS法建立个人储蓄与可支配收入的线性模型;②利用White检验、Park检验和Glejser检验、Goldfeld-Quandt检验对模型进行异方差性检验;③如果存在异方差性,试采用适当的方法加以消除。
表7 某地区个人储蓄、可支配收入数据第5章 自相关性习 题3.简答题、分析与计算题(10)表1给出了美国1958-1969年期间每小时收入指数的年变化率(y )和失业率(x ) 请回答以下问题:①估计模型t tt u x b b y ++=110中的参数10,b b ②计算上述模型中的DW 值。
③上述模型是否存在一阶自相关性?如果存在,是正自相关还是负自相关? ④如果存在自相关,请用DW 的估计值估计自相关系数ρ。
⑤利用广义差分法重新估计上述模型,自相关问题还存在吗?表1 美国1958-1969年每小时收入指数变化率和失业率(11)考虑表2中所给数据:表2 美国股票价格指数和GNP 数据注:y-NYSE 复合普通股票价格指数(1965年12月31日=100);x-GNP (单位:10亿美元)①利用OLS 估计模型:tt t u x b b y ++=10。