连续梁的内力包络图(参考学习)
- 格式:ppt
- 大小:680.00 KB
- 文档页数:9


一、判断题(题数10,共10.0分)1.风对结构的作用属于直接作用。
对2.单向板肋梁楼盖采用的弯矩调幅法,没有考虑活荷载的最不利布置。
错3.按弹性方法计算时,只要板的长边与短边之比不大于2,这种板就称为两向受力的双向板。
错4.单层厂房排架柱的总高度是由柱顶标高减去基础底面标高求得的。
错5.单层厂房预制柱吊装验算时,柱身自重应乘以1.5的动力系数。
对6.排架计算时,屋面均布活荷载不与雪荷载同时组合。
对7.柱上的短牛腿的计算简图可简化为一个以纵筋为拉杆,以混凝土斜撑为压杆的三角形桁架。
对8.框架内力组合时,采用满布荷载法,所得到的梁跨中弯矩最不利。
错9.框架结构梁端弯矩调幅降低后,应对梁跨中弯矩作相应的提高。
错10.一般而言,对于超高层建筑,框架是一个合适的结构选型。
错11.单向板为仅仅在一个方向弯曲的板。
错12.梁的计算跨度,理论上就是支座转动点之间的距离。
对13.钢筋混凝土连续梁考虑塑性内力重分布后,梁截面承载力的计算值有所提高。
对14.荷载按刚度分配原理是结构设计中的一个重要概念,贯穿结构设计的一条主线。
对15.单层厂房中的柱间支撑应设置在伸缩缝区段两端。
对16.塑性铰只能单向转动,并能承受一定的极限弯矩。
对17.现浇楼盖中的连续梁,在进行正截面承载力计算时,跨中按T形截面计算,而支座按矩形截面计算。
对18.单层厂房排架计算的主要内容是:确定计算简图,确定计算荷载,内力分析和组合,必要时还应验算排架的水平位移值。
对19.吊车的竖向荷载不可能脱离横向水平荷载而单独存在。
错二、单选题(题数10,共20.0分)1.计算现浇单向板肋梁楼盖时,对板和次梁可采用折算荷载来计算,这是考虑到。
()A、在板的长跨方向也能传递一部分荷载B、塑性内力重分布的有利影响C、支座的弹性转动约束D、出现活载最不利布置的可能性较小2.五等跨连续梁,为使边支座出现最大剪力,活荷载应布置在()。
A、1、2、5跨B、1、2、4跨C、1、3、5跨D、2、4跨3.即使塑性铰具有足够的转动能力,弯矩调幅值也必须加以限制,主要是考虑到()。

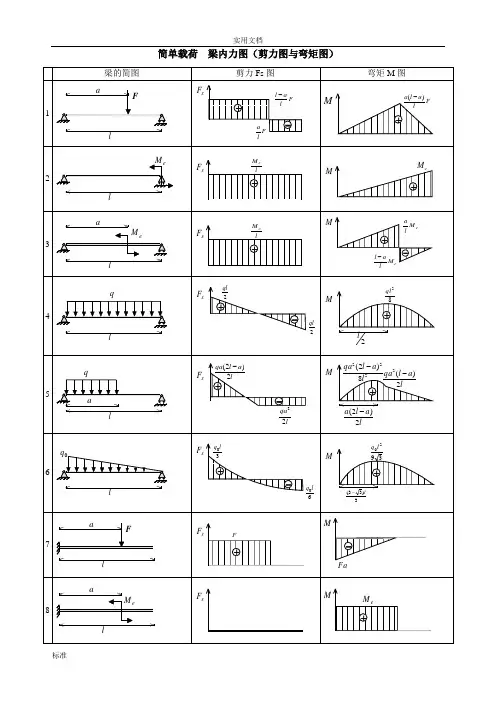
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
实用文档2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。


一、填空题(共48题)1.单向板肋梁楼盖荷载的传递途径为 楼面(屋面)荷载 → 次梁 → 主梁 →柱 → 基础 → 地基。
2.在钢筋混凝土单向板设计中,板的短跨方向按 计算 配置钢筋,长跨方向按_ 构造要求 配置钢筋。
3.多跨连续梁板的内力计算方法有_ 弹性计算法__和 塑性计算法___ 两种方法。
4.四边支承板按弹性理论分析,当L 2/L 1≥_2__时为_单向板_;当L 2/L 1<__2 _时为_双向板 。
5.常用的现浇楼梯有__板式楼梯___和___梁式楼梯___两种。
6.对于跨度相差小于10%的现浇钢筋混凝土连续梁、板,可按等跨连续梁进行内力计算。
7、双向板上荷载向两个方向传递,长边支承梁承受的荷载为 梯形 分布;短边支承梁承受的荷载为 三角形 分布。
8、按弹性理论对单向板肋梁楼盖进行计算时,板的折算恒载 p g g 21'+=, 折算活载p p 21'= 9、对结构的极限承载力进行分析时,需要满足三个条件,即 极限条件 、 机动条件 和平衡条件 。
当三个条件都能够满足时,结构分析得到的解就是结构的真实极限荷载。
10、对结构的极限承载能力进行分析时,满足 机动条件 和 平衡条件 的解称为上限解,上限解求得的荷载值大于真实解;满足 极限条件 和 平衡条件 的解称为下限解,下限解求得的荷载值小于真实解。
11、在计算钢筋混凝土单向板肋梁楼盖中次梁在其支座处的配筋时,次梁的控制截面位置应取在支座 边缘 处,这是因为 支座边缘处次梁内力较大而截面高度较小。
12、钢筋混凝土超静定结构内力重分布有两个过程,第一过程是由于 裂缝的形成与开展 引起的,第二过程是由于 塑性铰的形成与转动 引起的。
13、按弹性理论计算连续梁、板的内力时,计算跨度一般取 支座中心线 之间的距离。
按塑性理论计算时,计算跨度一般取 净跨 。
14、在现浇单向板肋梁楼盖中,单向板的长跨方向应放置分布钢筋,分布钢筋的主要作用是:承担在长向实际存在的一些弯矩、抵抗由于温度变化或混凝土收缩引起的内力、将板上作用的集中荷载分布到较大面积上,使更多的受力筋参与工作、固定受力钢筋位置。

21、连续梁(板)塑性设计应遵循的原则之一是(C ).A。
必须采用折算荷载B。
不考虑活荷载的不利位置C。
截面受压区相对高度22、整浇楼盖的次梁搁置在钢梁上时(B )A.板和次梁均可采用折算荷载B。
仅板可以采用折算荷载C。
仅次梁可以用折算荷载D.二者均不可用折算荷载23、雨篷梁支座截面承载力计算时,应考虑(B )A。
弯、扭相关B。
剪、弯、扭相关C.弯、剪相关D.弯、压、剪相关25、弹性方法设计的连续梁、板各跨跨度不等,但相邻两跨计算跨度相差<10%,仍作为等跨计算,这时,当计算支座截面弯矩时,则应按( C )计算。
A。
相邻两跨计算跨度的最大值B。
两邻两跨计算跨度的最小值C。
相邻两跨计算跨度的平均值D。
无法确定31、关于折算荷载的叙述,哪一项不正确(D )A.为了考虑支座抵抗转动的影响,采用增大恒载和相应减少活荷载的办法来处理B。
对于板其折算荷载取:折算恒载g/=g+ ,折算活载q/=C。
对于次梁其折算荷载取:折算恒载g/=g+ ,折算活载q/=D. 对于主梁其折算荷载按次梁的折算荷载采用32、关于塑性较,下面叙述正确的是(C )A.塑性较不能传递任何弯矩而能任意方向转动B。
塑性较转动开始于Ia,终止于IIIaC。
塑性较处弯矩不等于0而等于该截面的受弯承载力Mu D. 塑性较与理想铰基本相同37、在单板肋梁楼盖设计中,一般楼面板的最小厚度h可取为(B )A。
≥50mm B. ≥60mm C. ≥80mm D。
没有限制38、对于板内受力钢筋的间距,下面哪条是错误的(D )A。
间距s≥70mm B. 当板厚h≤150mm,间距不应大于200mmC.当板厚h>150mm,间距不应大于1。
5h,且不应大于250mmD。
当板厚h>150mm时,间距不应大于1.5h,且不应大于300mm39、对于连续板受力钢筋,下面哪条是错误的( B )A。
连续板受力钢筋的弯起和截断,一般可不按弯矩包络图确定B。
连续板跨中承受正弯矩的钢筋可在距离支座C.连续板支座附近承受负弯矩的钢筋,可在距支座边缘不少于D。

第八节 简支梁的内力包络图在移动荷载作用下,将各截面产生的最大内力值和最小内力值分别连成一条光滑的曲线,称为内力包络图。
梁的内力包络图有弯矩包络图和剪力包络图。
下面先以简支梁在移动的单个集中荷载F 作用下的内力包络图为例加以说明。
图10-30(a)所示简支梁承受单个移动集中荷载F 作用,某截面C 的弯矩及剪力的影响线分别如图10-30(b)和10-30(c)所示。
由影响线的的形状可知:1、当F 恰好作用于C 点时,C M 达到最大,且max /C M Fab l =;2、当F 恰好作用于C 点左侧时,SC F 达到负最大值(或最小值),且min /SC F Fa l =-3、当F 恰好作用于C 点右侧时,SC F 达到最大值,且max /SC F Fb l =。
由此可见,荷载F 从左向右移动时,只要逐个算出荷载作用点处的弯矩值和剪力值,便可分别得到弯矩包络图和剪力包络图。
这里可以选取一系列截面(如将梁段分成10等分),逐个算出每个截面处的弯矩和剪力的最大(小)值。
每个等分点截面处弯矩和剪力的最大值(小)计算结果见表10-1。
表10-1 max M 、max SC F 及min SC F 的计算根据逐点算出的最大弯矩值而连成的图形即为弯矩包络图,如图10-30(d)所示。
根据逐点算出的最大(小)剪力值分别连成的图形即为剪力包络图,如图10-30(e)所示。
图10-30 简支梁的内力包络图(a)简支梁计算简图 (b)C M 影响线 (c)弯矩包络图 (d)SC F 影响线 (e)剪力包络图 在实际工程结构计算中,必须要求出在恒载和活载共同作用下各个截面的最大(小)内力值,作为结构设计的依据。
活载还须考虑其动力影响,通常是将静活载所产生的内力值乖以冲击系数,关于冲击系数的确定详见相关规范。
将各截面最大(或最小)内力值连成曲线所得到的内力包络图,是结构设计的重要工具,在吊车梁、楼盖的连续梁和桥梁的设计中应用很多。

二级注册结构工程师-钢筋混凝土结构3(总分120, 做题时间90分钟)一、单项选择1.条件相同的四边支承双向板,采用上限解法求得的极限荷载一般要比采用下限解法求得的极限荷载( )。
SSS_SINGLE_SELA 大;B 小;C 相等;D 无法比较。
该题您未回答:х该问题分值: 1答案:A2.在确定梁的纵筋弯起奌时,要求抵抗弯矩图不得切入设计弯矩图以内,即应包在设计弯矩图的外面,这是为了保证梁的( )。
SSS_SINGLE_SELA 正截面受弯承载力;B 斜截面受剪承载力;C 受拉钢筋的锚固;D 箍筋的强度被充分利用。
该题您未回答:х该问题分值: 1答案:A3.在结构的极限承载能力分析中,正确的叙述是( )。
SSS_SINGLE_SELA 若同时满足极限条件、变形连续条件和平衡条件的解答才是结构的真实极限荷载;B 若仅满足极限条件和平衡条件的解答则是结构极限荷载的下限解;C 若仅满足变形连续条件和平衡条件的解答则是结构极限荷载的上限解;D 若仅满足极限条件和机动条件的解答则是结构极限荷载的上限解。
该题您未回答:х该问题分值: 1答案:B4.按弯矩调幅法进行连续梁、板截面的承载能力极限状态计算时,应遵循下述规定( )。
SSS_SINGLE_SELA 受力钢筋宜采用I、II级或III级热轧钢筋;B 截面的弯矩调幅系数< >宜超过0.25;C 弯矩洞整后的截面受压区相对计算高度< >一般应超过0.35,但不应超过< >;D 按弯矩调幅法计算的连续紧、板,可适当放宽裂缝宽度的要求。
该题您未回答:х该问题分值: 1答案:A5.钢筋混凝土连续梁的中间支座处,当配置好足够的箍筋后,若配置的弯起钢筋不能满足要求时,应增设( )来抵抗剪力。
SSS_SINGLE_SELA 纵筋B 鸭筋C 浮筋D 架立钢筋该题您未回答:х该问题分值: 1答案:B6.承受均布荷载的钢筋混凝土五跨连续梁(等跨),在一般情况下,由于塑性内力重分布的结果,而使 ( )SSS_SINGLE_SELA 跨中弯矩减少,支座弯矩增加B 跨中弯矩增大,支座弯矩减小C 支座弯矩和跨中弯矩都增加该题您未回答:х该问题分值: 1答案:B7.按弹性方法计算现浇单向肋梁楼盖时,对板和次梁采用折算荷载来进行计算,这是因为考虑到 ( )SSS_SINGLE_SELA 在板的长跨方向能传递一部分荷载B 塑性内力重分布的影响C 支座转动的弹性约束将减少活荷载布置对跨中弯矩的不利影响该题您未回答:х该问题分值: 1答案:C8.求连续梁跨中最小弯矩时,可变荷载(活载)的布置应该是 ( )SSS_SINGLE_SELA 本跨布置活载,然后隔跨布置活载B 本跨不布置活载,相邻两跨布置活载,然后隔跨布置活载C 本跨及相邻两跨布置活载,然后隔跨布置活载该题您未回答:х该问题分值: 1答案:B9.按单向板进行设计( )。
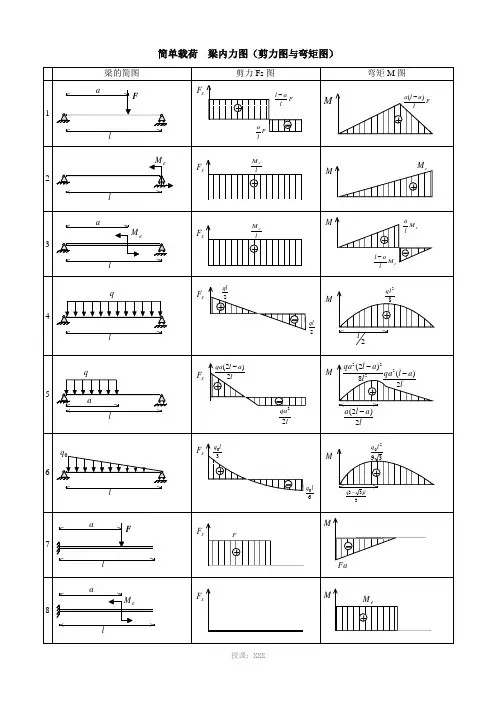
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5授课:XXX授课:XXX授课:XXX授课:XXX授课:XXX授课:XXX授课:XXX注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。

任务三十一多跨连续梁的内力包络图一、填空题1.( 影响线 )是在竖向单位移动荷载作用下,结构内力、反力或变形的量值随竖向单位荷载位置移动而变化的规律。
2.影响线的横坐标表示 ( 单位移动荷载作用位置 ),纵坐标表示单位移动荷载作用下结构某一指定位置某一量值的大小。
3. 绘制影响线有 ( 静力法 ) 和 ( 机动法 )两种。
4.根据静力平衡条件建立量值关于单位移动荷载作用位置的函数方程,据此函数绘制影响线的方法称为 ( 静力法 )。
5.由虚位移原理,撤除与所求量值对应的约束,沿量值正向给出单位位移,根据约束条件作出机构的位移图来绘制影响线的方法称为 ( 机动法 )。
6.静定结构的影响线由 ( 直线段 )组成,超静定结构的影响线由 ( 曲线 )构成。
7.荷载的不利位置:(1)单个集中力的荷载不利位置在影响线的 ( 顶点 );(2)一组等间距的集中力,其荷载不利位置是临界荷载(有时临界荷载不止一个)作用在影响线的 ( 顶点时的位置 );8.各截面内力最大值的连线与各截面内力最小值的连线称为 ( 内力包络图 );弯矩包络图上的最大弯矩称为 ( 绝对最大弯矩 )。
二、画影响线1.作出下列结构支座A左截面的剪力影响线VA左影响线4m 4m 2mA11/2--VA 影响线3.作出下列结构A 截面的剪力影响线。
MA 影响线4.作出下列结构A 截面的剪力影响线。
VA 影响线5.作出下列结构A 截面的剪力影响线。
MA 影响线A2m2m 4m2m A1/2 1/21/2 +- +-2m2m3m3mAAP=1P=11/21/2MA 影响线7.作出单跨梁的影响线A-+8.作图 a)所示多跨静定梁C支座反力FCy和K截面内力MK、FQK的影响线。
解: 对于多跨静定梁来说,在绘制虚位移图时要注意几何位移协调,满足剩余约束条件。
由于A为固定支座,不允许发生位移和转角,所以在作图过程中,画C支座反力的影响线时,AB段没有刚体位移,同样,画K截面内力影响线时,AK段也没有刚体位移,注意到这一点,再根据约束条件,可得出欲求量值的影响线,如图(c)(e)(g)所示。
结构力学课程作业——连续梁的影响线、最不利荷载布置及内力包络图班级道桥1001班学号U201015341姓名名夺独世华中科技大学土木工程与力学学院二0一二年十月结构力学课程作业一. 题目具体数据见下表二.计算书的要求1、用力法计算求得支点弯矩1M 、2M 的影响线;2、用挠度法计算求得支点弯矩1M 、2M 的影响线;3、求第二跨内截面K 的弯矩,剪力影响线及支座1的反力影响线;4、在求影响线的基础上,进行均布移动荷载的最不利布置;5、连续梁承受均布活荷载18p KN m =及恒载12q KN m =时,绘出弯矩、剪力包络图。
6、计算书要求步骤清晰,绘图准确,电子文档,A4打印纸输出,正文:宋体,小四字,单倍行距;页面设置:页边距上下2.6cm 、左右2.8cm 。
三. 计算书1、用力法计算求得支点弯矩1M 、2M 的影响线;① 去除支点弯矩约束,代之以未知力1M 、2M ,建立基本结构如图:② 建立力法方程⎪⎩⎪⎨⎧=∆++=∆++0022222211212111p p M M M M δδδδ ③ 作出1M 、2M 图如下1M 图2M 图④ 求方程的系数 利用图乘法可以算出:CEI l l l l EI 103)3212113221(1212111=+=⨯⨯⨯+⨯⨯⨯=δC EI l l l l EI 113)3212113221(1323222=+=⨯⨯⨯+⨯⨯⨯=δCEI l l EI 26)13121(12212==⨯⨯⨯=δ⑤ 求方程的自由项a. 移动荷载0.1=p F 作用在第一跨上Cx x l x l l l x l x x l l x l x l x x EI p 108324)3)(2)()(2132)(21(1311111111111111111111-=--⨯-⨯-⨯+⨯-⨯⨯=∆02=∆p∴代入力法方程得⎪⎪⎩⎪⎪⎨⎧=+=--+011201083242102113121M C M C C x x M C M C 解得:⎪⎪⎩⎪⎪⎨⎧-=-=5724324)(11448)324(11)(3111221111x x x M x x x M b. 移动荷载0.1=p F 作用在第二跨上Cx x x l x l l x l x x l l x l l x l x x EI p 72)24)(12()3)()(2)(21)32()(21(1222222222222222222221--=-⨯-⨯-⨯+-⨯-⨯⨯=∆Cx x l x l l l x l x x l l x l x l x x EI p 72)144()3)(2)()(2132)(21(1222222222222222222222-=--⨯-⨯-⨯+⨯-⨯⨯=∆∴代入力法方程得⎪⎪⎩⎪⎪⎨⎧=-++=--++072)144(112072)24)(12(2102222122221C x x M C M CCx x x M C M C 解得:222221()2222()(12)(24013)7632(12)(6)636X X x x x M x x x M --⎧=⎪⎪⎨-+⎪=⎪⎩c. 移动荷载0.1=p F 作用在第三跨上Cx x x l x l l x l x x l l x l l x l x x EI p p 126)42)(21()3)()(2)(21)32()(21(103333333333333333333321--=-⨯-⨯-⨯+-⨯-⨯⨯=∆=∆∴代入力法方程得⎪⎪⎩⎪⎪⎨⎧=--++=+0126)42)(21(11202103332121C x x x M C M CM C M C 解得:⎪⎪⎩⎪⎪⎨⎧--=--=6678)42)(21(5)(6678)42)(21()(3333233331x x x x M x x x x M ⑥ 绘出支点弯矩1M 、2M 的影响线根据弯矩函数式求得:1M 影响线3821.02M 影响线2、用挠度法计算求得支点弯矩1M 、2M 的影响线; (1) 用挠度法计算求得支点弯矩1M 的影响线① 去除1点支座弯矩约束,代之以一对力偶m KN M ⋅=11② 使体系沿1M 的正方向发生位移,作出荷载作用的挠度图③ 用力矩分配法求出力偶m KN M ⋅=11所引起的弯矩图第一跨:两端弯矩为m KN ⋅0和m KN ⋅0.1,挠度方程为:[]Cx x x l x l EIl x l x x y 108)324()(1)2(06)()(2111111111111-=+⨯+-⨯⨯-=第二跨:两端弯矩为m KN ⋅1和m KN ⋅-112,挠度方程为:Cx x x x l x l EIl x l x x y 792)24013()12()(112)2(16)()(2222222222221--=⎥⎦⎤⎢⎣⎡+⨯--⨯⨯-=第三跨:两端弯矩为m KN ⋅-112和m KN ⋅0,挠度方程为: Cx x x x l x l EIl x l x x y 693)42)(21()(0)2()112(6)()(3333333333331--=⎥⎦⎤⎢⎣⎡+⨯+-⨯-⨯-=⑤ 将相应的x 值代入后,求得)(1x EIy 如图所示,此即1p EI δ图1p EI δ图⑥ 求11δ11106)1122(612)02(618''11'1111=-+-=+=EI EI δδδ⑦ 将1p δ除以)(11δ-即得:第一跨:11448)324(11)(21111-=x x x M第二跨:7632)13240)(12()(22221x x x x M --=第三跨:6678)42)(21()(33331--=x x x x M∴支点弯矩1M 的影响线如图弯矩M的影响线1(2) 用挠度法计算求得支点弯矩M的影响线2①去除2点支座弯矩约束,代之以一对力偶m=1M⋅KN2②使体系沿M的正方向发生位移,作出荷载作用的挠度图2⑧用力矩分配法求出力偶m所引起的弯矩图=1KNM⋅1第一跨:两端弯矩为m KN ⋅0和m KN ⋅-51,挠度方程为:Cx x x l x l EIl x l x x y 540)324()(51)2(06)()(2111111111112-=⎥⎦⎤⎢⎣⎡+⨯--⨯⨯-=第二跨:两端弯矩为m KN ⋅-51和m KN ⋅1,挠度方程为:Cx x x x l x l EIl x l x x y 60)6()12()(1)2()51(6)()(2222222222222+-=⎥⎦⎤⎢⎣⎡+⨯+-⨯-⨯-=第三跨:两端弯矩为m KN ⋅1和m KN ⋅0,挠度方程为:[]Cx x x x l x l EIl x l x x y 126)42)(21()(0)2(16)()(3333333333332--=+⨯+-⨯⨯-=⑩ 将相应的x 值代入后,求得)(2xEIy 如图所示,此即2p EI δ图2p EI δ图11 求22δ553)02(621)2.02(612''22'2222=-+-=+=EIEI δδδ12 将2p δ除以)(22δ-即得:第一跨:5724)324()(21112x x x M -=第二跨:636)6)(12()(22222+-=x x x x M第三跨:6678)42)(21(5)(33332x x x x M --=∴支点弯矩2M 的影响线如图3821.0弯矩2M 的影响线3.1求第二跨内截面K 的弯矩影响线;由对1-2杆的力学分析知: 0120.550.45k k M M M M =++04.46 6.6124.46 5.4k x M x ⎧⎪⎪⎪=⨯⎨⎪-⎪⨯⎪⎩由上述公式可得::311222232223335.151668.40~111448(12)(272.47.6) 4.46~k 7632 6.64.46(12)(12)(272.47.6)k~27632 5.41.7(21)(42)~36678K x x p x x x x p M x x x x p x x x p ⎧-⎪⎪--⎪+⎪=⎨⨯---⎪+⎪⎪--⎪⎩作用于跨间作用于1跨间作用于跨间作用于2跨间根据此方程可得影响线如下1.270.860.743.4221.9251.8760.8840.5790.6143.2求第二跨内截面K 的剪力影响线;由对1-2杆的力学分析得到0211()K K V V M M l=+-由于000~12~30.55~k 6.6120.45k~25.4k p x V p x p ⎧⎪⎪⎪=-⨯⎨⎪-⎪⨯⎪⎩作用于和之间作用于1之间作用于之间所以2x x-324~206064(12)(25168)0.55~k 91632 6.6(12)(25168)0.45(12)~91632 5.4(21)(42)~13356K p x x x x p V x x x x p x x x p ⎧⎪⎪--⎪-⎪=⎨---⎪-⎪⎪--⎪⎩(-324)(11)作用于01作用于1作用于k 2作用于23影响线如下0.2650.1820.1770.549-0.4510.2650.1530.1793.3求支座1的反力影响线根据力学分析得到下式其中01R如下图所示:012带入相应的数据可以得到R1的影响线方程为21294(1)0~1114481141(1)(10197)~27632359(21)(1)~36678x xx pR x x x a px x a p⎧-+⎪⎪⎪=----⎨⎪⎪--⎪⎩作用于之间作用于1之间作用于2之间影响线如下23 0+M2min55. 连续梁承受均布活荷载18p KN m =及恒载12q KN m =时,绘出弯矩、剪力包络图。
第九章渐进法§9-1 概述现代工程结构中出现了越来越多的超静定结构,其中大多数是梁和刚架(组合结构),如:教学楼,图书馆、外招、科学馆、电教馆等。
基本解法:力法,位移法但是我们发现:无论是力法或位移法,如果未知量数目在三个以内,算起来比较容易,三个—五个,有点费劲,五个以上—十个,比较困难,而十个以至更多未知量,很困难或无法用力法或位移法计算,而工程实际结构,也就是横向三跨七层刚架4×7+7=35个(位移法)7×3×3=63个(力法)。
纵向连续梁,七跨或八跨,也有7、8个未知量。
用力法及位移法求解十分困难,逼的人们又想其它方法,于是近几十年来,在力法几位移法的基础上,又发展了许多实用的计算方法:(渐进法,数值法)。
力矩分配法:适用于无结点线位移的刚架AND多跨连续梁力矩分配法和位移法联合应用:有侧移刚架(线位移较多时,也很麻烦)主要用在单层多跨刚架无剪力分配法:一些特殊的有侧移刚架。
迭代法:多层多跨刚架力矩分配法和位移法联合求解:单层多跨刚架,有侧移电算:(矩阵位移法OR有限元法)手算:1、精确力法、位移法、混合法缺点:当未知量较多时2、渐进法力矩分配法、无剪力分配法、迭代法、反弯点(D值法)、弯矩二次分配法、联合法优点:避免求解联立方程组,但又能满足工程需要电算:矩阵力法、矩阵位移法、矩阵混合法力矩分配法:;无剪力分配法:单层多跨对称刚架(工业厂房)和一些特殊的有侧移刚架和力矩分配法类似的渐进法迭代法:多层刚架(多个线位移),有、无侧移刚架均可。
(有铰接点,简式刚架,复式刚架和变截面杆件组成的刚架。
)这两种方法的理论基础均是位移法,在计算中采用逐次修正的步骤,一轮一轮的提高计算精度。
机械→简单。
其他对于多层多跨刚架近似方法:分层法:多层多跨刚架在竖向荷载作用下;反弯点法:水平荷载,层数不多的多层多跨刚架;D值法:水平荷载作用下层数较多的高层多跨刚架;弯矩二次分配法:竖向荷载作用下多层多跨刚架;§9-2 转动刚度、传递系数理论基础是位移法,解题方法是渐进法。