最新中考数学二轮复习压轴专题：三角形(含答案解析)

专题06三角形的内角和与外角压轴题六种模型全攻略考点一三角形内角和定理的证明考点二与平行线有关的三角的内角和问题考点三与角平分线有关的三角的内角和问题考点四三角形折叠中的角度问题考点五三角形内角和定理的应用考点六三角形外角的定义和性质考点一三角形内角和定理的证明例题：（2021·广西·靖西市教学研究室八年级期末）（1）如图①，直线DE 经过点A ，DE ∥BC ．若∠B ＝45°，∠C ＝58°，那么∠DAB ＝；∠EAC ＝；∠BAC ＝．(在空格上填写度数）（2）求证：在△ABC 中，∠A +∠B +∠C ＝180°．【答案】（1）45°；58°；77°（2）见解析【解析】【分析】（1）通过平行线的性质，两直线平行，内错角相等，可分别求出：45DAB ，58EAC ．由图可知：180DAB BAC EAC ，可求出：77BAC ．（2）过点A 作//DE BC ，通过平行线的性质，可得：B DAB ，C EAC所以180BAC B C BAC DAB EAC ．【详解】（1）解：∵//DE BC ，45B ，58C45B DAB ，=58C EAC∵180BAC DAB EAC18077BAC DAB EAC ，故答案是：45°，58°，77°；典型例题（2）证明：过点A 作//DE BC∵//DE BCB DAB ，C EAC∵180BAC DAB EAC180BAC B C BAC DAB EAC【点睛】本题主要考查知识点为，平行线的性质．即：两直线平行，同位角相等，内错角相等，同旁内角互补．熟练掌握平行线的性质是解决本题的关键．【变式训练】1．（2022·全国·八年级专题练习）在小学，我们曾经通过动手操作，利用拼图的方法研究了三角形三个内角的数量关系．如图，把三角形ABC 分成三部分，然后以某一顶点（如点B ）为集中点，把三个角拼在一起，观察发现恰好构成了平角，从而得到了“三角形三个内角的和是180°”的结论．但是，通过本学期的学习我们知道：由观察、实验、归纳、类比、猜想得到的结论还需要通过证明来确认它的正确性．小聪认真研究了拼图的操作方法，形成了证明命题“三角形三个内角的和是180°”的思路：①画出命题对应的几何图形；②写出已知，求证；③受拼接方法的启发画出辅助线；④写出证明过程．请你参考小聪解决问题的思路，写出证明该命题的完整过程．【答案】见解析【解析】【分析】根据要求画出△ABC ，写出已知，求证．构造平行线，利用平行线的性质解决问题即可．解：已知：△ABC ．求证：∠A +∠B +∠C =180°．证明：如图，延长CB 到F ，过点B 作BE ∥AC ．∵BE ∥AC ，∴∠1=∠4，∠5=∠3，∵∠2+∠4+∠5=180°，∴∠1+∠2+∠3=180°，即∠A +∠ABC +∠C =180°．【点睛】本题考查三角形内角和定理的证明，平行线的性质，平角的定义等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题．2．（2022·北京·中考真题）下面是证明三角形内角和定理的两种添加辅助线的方法，选择其中一种，完成证明．三角形内角和定理：三角形三个内角和等于180°，已知：如图，ABC ,求证：180.A B C方法一证明：如图，过点A 作.DE BC ∥方法二证明：如图，过点C 作.CD AB ∥【答案】答案见解析【解析】选择方法一，过点A 作//DE BC ，依据平行线的性质，即可得到B BAD ，C EAC ，再根据平角的定义，即可得到三角形的内角和为180 ．【详解】证明：过点A 作//DE BC ，则B BAD ，C EAC ．(两直线平行，内错角相等）∵点D ，A ，E 在同一条直线上，180DAB BAC C ．（平角的定义）180B BAC C ．即三角形的内角和为180 ．【点睛】本题主要考查了平行线的性质以及三角形内角和定理的运用，熟练掌握平行线的性质是解题的关键．考点二与平行线有关的三角的内角和问题例题：（2022·山东泰安·一模）如图，AB ∥CD ，EF 分别与AB ，CD 交于点B ，F ．若30E ，130EFC ，则A ______．【答案】20【解析】【分析】通过两直线平行，同位角相等，求出∠ABE 的度数，再利用三角形内角和定理求解．【详解】解：//AB CD ∵，130ABE EFC ，在△ABE 中，30E ，1801803013020A E ABE ，20A ．故答案为：20 ．【点睛】本题考查平行线的性质，三角形的内角和定理，灵活运用平行线的性质和三角形内角和定理是解题的关键．【变式训练】1．（2022·江西南昌·模拟预测）如图，直线AB ，CD 被直线BC ，EG 所截．若AB //CD ，176 ，236 ，则3 的度数为（）A ．30°B ．36C ．40D ．45【答案】C【解析】【分析】由两直线平行，同旁内角互补求出∠CGE 的度数，再由三角形的内角和定理求得∠3的度数．【详解】解：∵AB //CD ，176 ，∴∠CGE ＝180°－∠1＝104°，∵∠2＋∠3＋∠CGE ＝180°，236 ，∴∠3＝180°－∠2－∠CGE ＝40°．故选：C【点睛】此题考查了平行线的性质、三角形的内角和定理，熟练掌握相关性质和定理是解题的关键．2．（2022·全国·八年级课时练习）如图所示，直线a b ∥，直线c 与直线a ，b 分别相交于点A 、点B ，AM ⊥b ，垂足为点M ，若∠1＝56°，则∠2＝______．【答案】34°##34度【解析】【分析】先根据平行线的性质得出∠ABM 的度数，再由三角形内角和定理求出∠2的度数即可．【详解】：解：∵直线a b ∥，∠1＝56°，∴∠ABM ＝∠1＝56°，∵AM ⊥b ，垂足为点M ，∴∠AMB ＝90°，∴∠2＝180°−∠AMB −∠ABM ＝180°−56°−90°＝34°，故答案为：34°．【点睛】本题考查三角形中求角度问题，涉及到平行线的性质、三角形内角和定理，在求角度问题中，熟练运用三角形内角和是180°是解决问题的关键．考点三与角平分线有关的三角的内角和问题例题：（2022·江苏·南京市第十三中学七年级期中）在△ABC 中，∠ABC 与∠ACB 的平分线相交于点P ，若∠P =125°，则∠A =_____°【答案】70【解析】【分析】依据BP 、CP 分别平分∠ABC 、∠ACB ，可得∠PBC =12∠ABC ，∠PCB =12∠ACB ，再根据三角形内角和定理，即可求得∠ABC +∠ACB =110°，即可求得∠A 的度数．【详解】解：∵BP 、CP 分别平分∠ABC 、∠ACB ，∠PBC =12∠ABC ，∠PCB =12∠ACB ，=180=180125=55PBC PCB P ∵，∠PBC +∠PCB =12∠ABC +12∠ACB =55°， ∠ABC +∠ACB =110°，=180=180110=70ABC ACB A ，故答案为：70．【点睛】本题考查了三角形内角和定理，角平分线定义，能正确运用定理进行推理是解此题的关键．【变式训练】1.（2022·福建省福州屏东中学七年级期末）如图，在ABC 中，AD 是高，AE 是角平分线．(1)若32B ∠，60C °，求DAE 的度数；(2)若18C B ，求DAE 的度数．【答案】(1)14°(2)9°【解析】【分析】先求∠DAC =30°，再求∠BAC =180°-32°-60°=88°，根据角的平分线计算∠EAC =1442BAC ，求得∠DAE =14°．(2)根据∠DAE =12BAC DAC =1(180)(90)2B C C =11909022B C C =12()C B ，代入计算即可．(1)∵AD 是高，AE 是角平分线，32B ∠，60C °，∴∠DAC =30°，∠BAC =180°-32°-60°=88°，∴∠EAC =1442BAC ，∴∠DAE =∠EAC -∠DAC =44°-30°=14°．(2)∵∠DAE =12BAC DAC =1(180)(90)2B C C =11909022B C C =12()C B ，18C B ，∴∠DAE =9°．【点睛】本题考查了三角形内角和定理，直角三角形性质，角的平分线意义，熟练掌握三角形内角和定理，直角三角形性质是解题的关键．2．（2022·黑龙江·哈尔滨工业大学附属中学校七年级期中）如图，ABC 中，AD BC 于点D ，E 为AC 上任意一点，连接BE 交AD 于点F ．(1)若4070ABD AFE ，，求证：BE 平分ABC ．(2)如图2，在（1）的条件下，若AFE AEF ，请直接写出图中所有直角三角形．【答案】(1)证明见解析；(2)△ABC 、△ABE 、△ABD 、△ACD 、△BDF 都是直角三角形．【解析】【分析】（1）AD ⊥BC ，得∠ADB =90°，进而得∠DBF =20°，又由∠ABD =40°即可得∠DBF = 12ABD ，即可证明结论成立；（2）由AD ⊥BC 得△ABD 、△ACD 、△BDF 是直角三角形，另由∠ABE +∠AEF =20°+70°=90°，可得∠BAE =90°得△ABE 、△ABC 是直角三角形．(1)解：∵AD ⊥BC ，∴∠ADB =90°，∴在Rt △BDF 中，∠DBF +∠BFD =90°，∴∠BFD +∠AFE =70°，∴∠DBF =20°，∵∠ABD =40°，∴∠DBF = 12ABD ，∴BE 平分∠ABC ；(2)解：∵AD ⊥BC ，∴△ABD 、△ACD 、△BDF 是直角三角形，∵∠ABE =∠CBE =20°，∴∠AEF =∠AFE =70°，∴∠ABE +∠AEF =20°+70°=90°，∴.在△ABE 中，∠BAE =90°，∴△ABC 、△ABE 是直角三角形，综上所述△ABC 、△ABE 、△ABD 、△ACD 、△BDF 都是直角三角形．【点睛】本题主要考查了直角三角形及角平分线与垂直，熟练掌握直角三角形的概念是解题的关键．考点四三角形折叠中的角度问题例题：（2022·河南·南阳市第三中学七年级阶段练习）如图，在三角形纸片ABC 中，65A ，75B ，将纸片的一角折叠，使点C 落在ABC 外的点C 处．若225 ，则1 的度数为（）A ．115°B ．100°C ．105°D ．95°【答案】C【解析】【分析】在△ABC 中利用三角形内角和定理可求出∠C 的度数，由折叠的性质，可知：∠CDE ＝∠C ′DE ，∠CED ＝∠C ′ED ，结合∠2的度数可求出∠CED 的度数，在△CDE 中利用三角形内角和定理可求出∠CDE 的度数，再由∠1＝180°﹣∠CDE ﹣∠C ′DE 即可求出结论．【详解】解：在△ABC 中，∠A ＝65°，∠B ＝75°，∴∠C ＝180°﹣∠A ﹣∠B ＝40°．由折叠，可知：∠CDE ＝∠C ′DE ，∠CED ＝∠C ′ED ，∴∠CED ＝18022＝102.5°，∴∠CDE ＝180°﹣∠CED ﹣∠C ＝37.5°，∴∠1＝180°﹣∠CDE ﹣∠C ′DE ＝180°﹣2∠CDE ＝105°．故选：C．【点睛】本题考查了三角形内角和定理以及折叠的性质，利用三角形内角和定理及折叠的性质求出∠CDE的度数是解题的关键．【变式训练】1．（2022·全国·八年级课时练习）如图，在△ABC中，∠A＝30°，∠B＝50°，将点A与点B分别沿MN和EF折叠，使点A、B与点C重合，则∠NCF的度数为（）.A．22°B．21°C．20°D．19°【答案】C【解析】【分析】根据三角形的内角和定理可得∠ACB＝100°，再由折叠的性质可得∠ACN＝∠A＝30°，∠FCE＝∠B＝50°，即可求解．【详解】解：∵∠A＝30°，∠B＝50°，∴∠ACB＝100°，∵将点A与点B分别沿MN和EF折叠，使点A、B与点C重合，∴∠ACN＝∠A＝30°，∠FCE＝∠B＝50°，∴∠NCF＝20°，故选：C．【点睛】本题主要考查了图形的折叠的性质、三角形内角和定理、熟练掌握图形的折叠的性质、三角形内角和定理是解题的关键．2．（2022·江苏·南京市第十三中学七年级期中）如图1，△ABC中，D是AC边上的点，先将ABD沿看BD翻折，使点A落在点A＇处，且A′D∥BC，A′B交AC于点E（如图2），又将△BCE沿着A′B翻折，使点C落在点C′处，若点C′恰好落在BD上（如图3），且∠C′EB=75°，则∠C=___°【答案】80°##80度【解析】【分析】先由平行线性质得：A =∠CBE ，再由折叠可得：∠A =∠A ，∠ABD =∠DBE =∠CBE ，BC E =∠C ，则∠A =∠ABD =∠DBE =∠CBE ，由三角形内角和定理知180BC E C EB DBE ，而75C EB ，可求得105C DBE ，然后由∠A +∠C +∠ACB =180°，则∠C +4∠DBE =180°，即可求出∠C 度数．【详解】解：∵A ′D ∥BC ，∴A =∠CBE ，由折叠可得：∠A =∠A ，∠ABD =∠DBE =∠CBE ，BC E =∠C ，∴∠A =∠ABD =∠DBE =∠CBE ，∵180BC E C EB DBE ，75C EB ，∴105BC E DBE ，∴105C DBE ，∵∠A +∠C +∠ACB =180°，∴∠C +4∠DBE =180°，∴∠C =80°，故答案为：80°．【点睛】本题考查平行线的性质，折叠性质，三角形内角和定理，求出105C DBE 和∠C +4∠DBE =180°是解题的关键．考点五三角形内角和定理的应用例题：（2022·河南南阳·二模）小明把一副三角板按如图所示方式摆放，直角边CD 与直角边AB 相交于点F ，斜边∥DE BC ，∠B ＝30°，∠E ＝45°，则∠CFB 的度数是（）A ．95°B ．115°C ．105°D ．125°【答案】C【解析】【分析】根据等腰直角三角形的性质可得45D ，再由平行线的性质得出45BCF ，再由三角形的内角和定理进行求解即可．【详解】CDE ∵是直角三角形，∠E ＝45°，45D ，∵∥DE BC ，45BCF D ，180,30B BCF BFC B ∵，105CFB ，故选：C ．【点睛】本题考查了等腰直角三角形的性质，平行线的性质及三角形的内角和定理，熟练掌握知识点是解题的关键．【变式训练】1．（2022·福建省福州第十六中学七年级期中）如图，直线MN PQ ∥，点A 在直线MN 与PQ 之间，点B 在直线MN 上，连接AB ．ABM 的平分线BC 交PQ 于点C ，连接AC ，过点A 作AD PQ 交PQ 于点D ，作AF AB 交PQ 于点F ，AE 平分DAF 交PQ 于点E ，若45CAE ，52ACB DAE ，则ACD 的度数是（）A ．18B ．27C ．30°D ．45【答案】B【解析】【分析】设DAE ，则EAF ，52ACB ，先求得180BCE CEA ，即可得到AE BC ∥，进而得出ACB CAE ，即可得到18DAE ，再依据Rt ACD △内角和即可得到∠ACD 的度数．【详解】设DAE ，则EAF ，52ACB ，∵,AD PQ AF AB ，∴90BAF ADE ，∴90BAE BAF EAF ，90CEA ADE DAE ，∴BAE CEA ，∵MN PQ ∥，BC 平分∠ABM ，∴BCE CBM CBA ，又∵360ABC BCE CEA BAE ，∴180BCE CEA ，∴AE BC ∥，∴ACB CAE ，即5452，∴18 ，∴18DAE ，∴在Rt ACD △中，9090)451827(ACD CAD ，故答案为：B ．【点睛】此题考查平行线的性质，三角形内角和定理，解题关键在于得出ACB CAE ．2．（江西省吉安市六校联谊联考2021-2022学年七年级下学期期中考试数学试题）如图，在ABC 中，点D 在边BC 上，点G 在边AB 上，点E 、F 在边AC 上，70AGF ABC ，12180(1)试判断BF 与DE 的位置关系，并说明理由；(2)若DE AC ，30 CDE ，求A 的度数．【答案】(1)BF ∥DE ，理由见解析(2)50【解析】【分析】（1）先证FG CB ∥，得出∠1=∠3，进而得出23180 ，最后证得DE BF ；（2）由DE AC ，可知∠DEC =90°，进而∠C =60°，根据三角形内角和定理最后求得∠A 的度数．(1)解：BF DE ，理由如下：∵70AGF ABC ，∴FG CB ∥，∴13 ，又12180 ，∴23180 ，∴DE BF ．(2)解：∵DE AC ，∴90CED ，30CDE ∵，60C ，∴180180706050A ABC C ．【点睛】本题考查了平行线的判定和性质，三角形内角和定理，熟练地掌握平行线的判定和性质是解决问题的关键．考点六三角形外角的定义和性质例题：（2022·四川·成都七中七年级期中）如图，已知7AOB ，一条光线从点A 出发后射向OB 边．若光线与OB 边垂直，则光线沿原路返回到点A ，此时90783A ．当83A 时，光线射到OB 边上的点1A 后，经OB 反射到线段AO 上的点2A ，易知12 ．若12A A AO ，光线又会沿21A A A 原路返回到点A ，此时A ______°．若光线从A 点出发后，经若干次反射能沿原路返回到点A ，则锐角A 的最小值 ______°．【答案】766【解析】【分析】根据入射角等于反射角得出1290783 ，再由1 是1AA O 的外角即可得A 度数；如图，当MN OA 时，光线沿原路返回，分别根据入射角等于反射角和外角性质求出5 、9 的度数，从而得出与A 具有相同位置的角的度数变化规律，即可解决问题．【详解】解：12A A AO ∵，7AOB ，1290783 ，176A AOB ，如图：当MN OA 时，光线沿原路返回，4390783 ，654837769027AOB ，8767679037AOB ，98697629047AOB ，由以上规律可知，9027A n ，当6n 时，A 取得最小值，最小度数为6 ，故答案为：76，6．【点睛】本题主要考查直角三角形的性质和三角形的外角性质及入射角等于反射角，根据三角形的外角性质及入射角等于反射角得出与A 具有相同位置的角的度数变化规律是解题的关键．【变式训练】1．（2021·广西·靖西市教学研究室八年级期末）如图，∠BCD ＝145°，则∠A +∠B +∠D 的度数为_____．【答案】145°【解析】【分析】连接AC 并延长，延长线上一点为E ．由三角形外角的性质可得：DCE D DAC ，BCE E BAC ．所以可得：145DAB B D DAC BAC B D DCE BCE BCD【详解】解：连接AC 并延长，延长线上一点为E∵DCE 是ACD △的外角DCE D DAC同理可得：BCE B BAC145DAB B D DAC BAC B D DCE BCE BCD故答案为145 ．【点睛】本题主要考查知识点为，三角形中外角的性质．即：三角形的一个外角等于不相邻的两个内角的和．本题需根据已知和所求作出辅助线．掌握外角的性质是解决本题的关键．2．（2022·江苏·淮安市淮安区教师发展中心学科研训处七年级期中）平面内的两条直线有相交和平行两种位置关系．(1)如图1，AB∥CD，点P在AB、CD内部，∠B＝55°，∠D＝40°，则∠BPD＝°；(2)如图2，AB∥CD，点P在AB、CD外部（CD的下方），则∠BPD、∠B、∠D之间的数量关系为；(3)如图3，直接写出∠BPD、∠B、∠D、∠BQD之间的数量关系为；(4)如图4，计算∠A+∠B+∠C+∠D+∠E+∠F的度数是°．【答案】(1)95(2)∠BPD+∠D=∠B(3)∠BQD+∠QBP+∠PDQ=∠BPD(4)360【解析】【分析】（1）延长BP交CD于点E，根据平行线的性质、三角形外角的性质即可求解；（2）根据AB∥CD，得∠B=∠BOD，再由三角形外角的性质即可求证；（3）连接BD，由∠BQD+∠QBP+∠DBP+∠BDP+∠PDQ=180°，∠DBP+∠BDP+∠BPD=180°即可求解；（4）连接AD，由∠B+∠F=∠EHF，∠GAD+∠ADG=∠EGH，∠EHF+∠EGH+∠E=180°，∠CAD+∠ADC+∠C=180°，即可求解；(1)解：延长BP交CD于点E，∵AB∥CD，∠B＝55°，∴∠B=∠BED=55°，∵∠D＝40°，∴∠BPD＝∠D+∠BED＝95°．故答案为：95．(2)∵AB∥CD，∴∠B=∠BOD，∵∠BPD+∠D=∠BOD，∴∠BPD+∠D=∠B．故答案为：∠BPD+∠D=∠B．(3)连接BD，∵∠BQD+∠QBP+∠DBP+∠BDP+∠PDQ=180°，∠DBP+∠BDP+∠BPD=180°，∴∠BQD+∠QBP+∠PDQ-∠BPD=0，∴∠BQD+∠QBP+∠PDQ=∠BPD．故答案为：∠BQD+∠QBP+∠PDQ=∠BPD．(4)如图，连接AD，∵∠B+∠F=∠EHF，∠GAD+∠ADG=∠EGH，∠EHF+∠EGH+∠E=180°，∴∠B+∠F+∠GAD+∠ADG+∠E=180°，∵∠CAD+∠ADC+∠C=180°，∴∠B+∠F+∠GAD+∠ADG+∠CAD+∠ADC+∠C+∠E=360°．故答案为：360．【点睛】本题主要考查平行线的性质、三角形的内角和定理、三角形外角的性质，掌握相关知识并结合题意正确做出辅助线是解题的关键．一、选择题1．（2022·河南平顶山·七年级期末）如图，直线a b ∥，若∠1＝70°，∠2＝30°则∠3的度数是（）A ．40°B ．50°C ．60°D ．无法计算【答案】A 【分析】如图，根据平行线的性质求出∠4＝∠1＝70°，然后根据三角形外角的性质得出答案．【详解】解：如图．∵a ∥b ，∠1＝70°，∴∠4＝∠1＝70°，∵∠4＝∠3＋∠2，∠2＝30°，∴∠3＝∠4−∠2＝70°−30°＝40°，故选：A ．【点睛】本题考查了平行线的性质、三角形外角的性质，熟知三角形的一个外角等于与它不相邻的两个内角和是解答本题的关键．2．（2022·湖北·武汉市光谷实验中学七年级阶段练习）如图，已知AB CD ∥，1113 ，265 ，则C 的度数是（）A ．43B ．58C ．48D ．65【答案】C 【分析】根据平行线的性质，由AB CD ，得1113EGD ．根据三角形外角的性质，得2EGD C ，那么248C EGD ．【详解】解：AB CD ∥∵，1113 ，课后训练1113EGD ．2EGD C ∵，265 ，21136548C EGD ．故选：C ．【点睛】本题主要考查平行线的性质、三角形外角的性质，熟练掌握平行线的性质、三角形外角的性质是解决本题的关键．3．（2022·山东聊城·七年级期末）如图，将直尺与含30°角的三角尺叠放在一起，若∠2=50°，则∠1的大小是（）A ．40°B ．50°C ．70°D ．80°【答案】C 【分析】根据三角形内角和定理得360 ，根据平行线的性质得4250 ，根据平角定义即可求解．【详解】解：如图所示，由题意得，3180903060 ，∵AB CD ∥，250 ，∴4250 ，∴11804370 ，故选：C ．【点睛】本题考查了三角形内角和定理，平行线的性质，解题的关键是掌握这些知识点．4．（2022·江苏连云港·七年级阶段练习）如图所示，将长方形纸片ABCD 折叠，使点D 与点B 重合，点C 落在点C 处，折痕为EF ，若∠ABE =20°，那么EFC 的度数为（）A．115°B．120°C．125°D．130°【答案】C【分析】根据折叠的性质知∠BEF=∠DEF，而∠AEB的度数可在Rt△ABE中求得，由此可求出∠DEF的度数，再根据平行线的性质即可得解．【详解】解：Rt△ABE中，∠ABE=20°，∴∠AEB=70°，由折叠的性质知：∠BEF=∠DEF，∠EFC=EFC，而∠BED=180°-∠AEB=110°，∴∠DEF=55°，∵AD∥BC，∴∠EFC=180°-∠DEF=125°．=125°．∴EFC故选：C．【点睛】本题考查了平行线的性质以及图形的翻折变换，折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．5．（2022·四川眉山·七年级期末）如图，△ABC中CD平分∠ACB，点M在线段CD上，且MN⊥CD交BA 的延长线于点N．若∠B=30°，∠CAN=96°，则∠N的度数为（）A．22°B．27°C．30°D．37°【答案】B【分析】由∠CAN是△ABC的外角可得∠ACB，由CD平分∠ACB可得∠BCD；再由∠CDN是△BCD的外角求得∠CDN；△DMN中再由三角形内角和定理即可解答；【详解】解：∵∠CAN是△ABC的外角，∴∠CAN=∠B+∠ACB，∵∠B=30°，∠CAN=96°，【答案】28°##28度【分析】根据折叠的性质得出∠【详解】解：过E点将∠A∴∠DEN=∠HEN，∠AEM=【答案】11或29【分析】讨论：如图1，△COD绕点O顺时针旋转得到△C′OD′，C′D′交OB于E，根据平行线的判定，当∠OEC′=∠B=40°时，C′D′∥AB，则根据三角形外角性质计算出∠C′OC=110°，从而可计算出此时△COD绕点O顺时针旋转110°得到△C′OD′所需时间；如图2，△COD绕点O顺时针旋转得到△C″OD″，C″D″交直线OB于F，利用平行线的判定得当∠OFC″=∠B=40°时，C″D″∥AB，根据三角形内角和计算出∠C″OC=70°，则△COD绕点O顺时针旋290°得到△C″OD″，然后计算此时旋转的时间．【详解】如图1，△COD绕点O顺时针旋转得到△C′OD′，C′D′交OB于E，则∠C′OD′=∠COD=90°，∠OC′D=∠C=70°，当∠OEC′=∠B=40°时，C′D′∥AB，∴∠C′OC=∠OEC′+∠OC′E=40°+70°=110°，∴△COD绕点O顺时针旋转110°得到△C′OD′所需时间为110÷10=11（秒）；如图2，△COD绕点O顺时针旋转得到△C″OD″，C″D″交直线OB于F，则∠C″OD″=∠COD=90°，∠OC″D″=∠C=70°，当∠OFC″=∠B=40°时，C″D″∥AB，∴∠C″OC=180°-∠OFC″-∠OC″F=180°-40°-70°=70°，∴△COD绕点O顺时针旋转的角度为：360°-70°=290°，∴△COD绕点O顺时针旋得到△C″OD″所需时间为290÷10=29（秒）；综上所述，在旋转的过程中，在第11秒或29秒时，边CD恰好与边AB平行．故答案为：11或29【答案】1207或22.5【分析】设BAE x，EDF y，根据题意可用中有两个内角相等可分类讨论，结合三角形内角和定理列出方程组，即可解答．【详解】设BAE x，EDF y，∵13BAE BAC，14EDF∵AE 是BC 边上的高线，∴∠BEA =90°，∴∠BAE =180°-∠B -∠BEA =55°，∵∠DAE =∠BAE -∠BAD ，∴∠DAE =55°-40°=15°，即∠DAE 为15°．【点睛】本题主要考查了三角形内角和定理以及角平分线的知识，掌握三角形内角和为180°是解答本题的关键．12．（2022·陕西·武功县教育局教育教学研究室七年级期末）如图，已知直线,,AB CD AC 上的点M ，N ，E 满足ME NE ，90,AME CNE ACD 的平分线CG 交MN 于G ，作射线GF AB ∥．(1)直线AB 与CD 平行吗？为什么？(2)若66CAB ，求CGF 的度数．【答案】(1)平行，理由见解析(2)123【分析】（1）利用已知条件和三角形内角和定理，通过等量代换可得180A ACD ，由同旁内角互补，两直线平行，可得//AB CD ；（2）利用,66AB CD CAB ∥，求出ACD ，再利用角平分线的定义求出GCD ，再证GF CD ∥，利用两直线平行，同旁内角互补，即可求出CGF ．（1）解：//AB CD ．理由如下：∵ME NE ，∴90MEN ，∴90AEM CEN ，∵180A AEM AME ，180ACD CEN CNE ，∴360A ACD AEM CEN AME CNE ，∵90AME CNE ，90AEM CEN ，∴180A ACD ，∴//AB CD ；（2）解：∵66AB CD CAB ∥， ，360A A A DA A EA ，12360A DA A EA ∵，12A A ，由折叠可得：A A ，212A ，故答案为：212A ；（3）如图③，2DME A ∵，1A DME ，由折叠可得：A A ，1222A A A ，212802456A ，28A ．故答案为：28 ．【点睛】本题是四边形综合题，考查了折叠的性质，三角形外角性质，三角形内角和定理的应用，本题主要考查运用定理进行推理和计算的能力．解题的关键是结合图形运用外角的性质列等式求解．14．（2022·江苏·沭阳县外国语实验学校七年级阶段练习）已知ABC 、DEF 是两个完全一样的三角形，其中90ACB DFE ，30A D ．(1)将它们摆成如图①的位置（点E 、F 在AB 上，点C 在DF 上，DE 与AC 相交于点G ）．求AGD 的度数．(2)将图①的ABC 固定，把DEF 绕点F 按逆时针方向旋转(0180)n n ．①当DEF 旋转到DE ∥AB 的位置时（如图2），n _________；②若由图①旋转后的EF 能与ABC 的一边垂直，则n 的值为_________．【答案】(1)∠AGD ＝150°；(2)①60；②60或90或150．【分析】（1）根据三角形外角的性质先求出∠DEA ，再求出∠AGD 即可；（2）①根据平行线的性质求出∠E＝∠EFA＝60°可得答案；②分情况讨论：当EF⊥AC时；当EF⊥AB时；当EF⊥BC时，分别作出图形求解即可．（1）解：∵∠DFE＝90°，∠D＝30°，∴∠DEA＝30°＋90°＝120°，∵∠A＝30°，∴∠AGD＝∠DEA＋∠A＝120°＋30°＝150°；（2）①∵∠DFE＝90°，∠D＝30°，∴∠E＝60°，∵DE∥AB，∴∠E＝∠EFA＝60°，∴n＝60；故答案为：60；②分情况讨论：当EF⊥AC于点G时，如图，则∠AGF＝90°，由三角形内角和定理可得：∠EFA＝180°−90°−30°＝60°，∴n＝60；当EF⊥AB时，如图，∴∠EFA＝90°，∴n＝90；当EF⊥BC于点H时，如图，则∠BHF＝90°，∴∠EFA＝∠B＋∠BHF＝60°＋90°＝150°，∴n＝150；综上，n的值为60或90或150，故答案为：60或90或150．【点睛】此题主要考查了三角形内角和定理，三角形外角的性质，平行线的性质等知识，解题的关键是要考虑全面，不要漏解，作出图形会更加直观．15．（2022·山西·测试·编辑教研五七年级期末）教材呈现：如图是华师版七年级下册数学教材第76页的部分内容．如图，已知ABC 分别用1 、2 、3 表示ABC 的三个内角，证明123180 ．解：延长BC 至点E ，以点C 为顶点，在BE 的上侧作2DCE ，则CD ∥BA （同位角相等，两直线平行）(1)请根据教材提示，结合图一，将证明过程补充完整．(2)结论应用：①如图二，在ABC 中，60A ，BP 平分ABC ，CP 平分ACB ，求BPC 的度数；②如图三，将ABC 的A 折叠，使点A 落在ABC 外的1A 处，折痕为DE ．若A ，1BDA ，1CEA ，则 、 、 满足的等量关系为______（用含 、 、 的代数式表示）．【答案】(1)见解析(2)①120 ；②2【分析】（1）利用平行线的性质得2DCE ，1ACD 即可解答；（2）①利用角平分线的定义和三角形内角和定理可得；②根据四边形BCFD 内角和为360 ，分别表示出各角得出等式即可．（1）。

中考数学复习---二次函数中三角形存在性问题压轴题练习（含答案解析）一．相似三角形的存在性1．（2022•陕西）已知抛物线y＝ax2+bx﹣4经过点A（﹣2，0），B（4，0），与y 轴的交点为C．（1）求该抛物线的函数表达式；（2）若点P是该抛物线上一点，且位于其对称轴l的右侧，过点P分别作l，x 轴的垂线，垂足分别为M，N，连接MN．若△PMN和△OBC相似，求点P的坐标．【解答】解：（1）把A（﹣2，0），B（4，0）代入y＝ax2+bx﹣4得：，解得，∴抛物线的函数表达式为y＝x2﹣x﹣4；（2）如图：∵y＝x2﹣x﹣4＝（x﹣1）2﹣，∴抛物线y＝x2﹣x﹣4的对称轴是直线x＝1，在y＝x2﹣x﹣4中，令x＝0得y＝﹣4，∴C（0，﹣4），∴OB＝OC＝4，∴△BOC是等腰直角三角形，∵△PMN和△OBC相似，∴△PMN是等腰直角三角形，∵PM⊥直线x＝1，PN⊥x轴，∴∠MPN＝90°，PM＝PN，设P（m，m2﹣m﹣4），∴|m﹣1|＝|m2﹣m﹣4|，∴m﹣1＝m2﹣m﹣4或m﹣1＝﹣m2+m+4，解得m＝+2或m＝﹣+2或m＝或m＝﹣，∵点P是该抛物线上一点，且位于其对称轴直线x＝1的右侧，∴P的坐标为（+2，+1）或（，1﹣）．2．（2022•绵阳）如图，抛物线y＝ax2+bx+c交x轴于A（﹣1，0），B两点，交y轴于点C（0，3），顶点D的横坐标为1．（1）求抛物线的解析式；（2）在y轴的负半轴上是否存在点P使∠APB+∠ACB＝180°，若存在，求出点P的坐标，若不存在，请说明理由；（3）过点C作直线l与y轴垂直，与抛物线的另一个交点为E，连接AD，AE，DE，在直线l下方的抛物线上是否存在一点M，过点M作MF⊥l，垂足为F，使以M，F，E三点为顶点的三角形与△ADE相似？若存在，请求出M点的坐标，若不存在，请说明理由．【解答】解：（1）∵顶点D的横坐标为1，∴抛物线的对称轴为直线x＝1，∵A（﹣1，0），∴B（3，0），∴设抛物线的解析式为：y＝a（x+1）（x﹣3），将C（0，3）代入抛物线的解析式，则﹣3a＝3，解得a＝﹣1，∴抛物线的解析式为：y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3．（2）存在，P（0，﹣1），理由如下：∵∠APB+∠ACB＝180°，∴∠CAP+∠CBP＝180°，∴点A，C，B，P四点共圆，如图所示，由（1）知，OB＝OC＝3，∴∠OCB＝∠OBC＝45°，∴∠APC＝∠ABC＝45°，∴△AOP是等腰直角三角形，∴OP＝OA＝1，∴P（0，﹣1）．（3）存在，理由如下：由（1）知抛物线的解析式为：y＝﹣x2+2x+3，∴D（1，4），由抛物线的对称性可知，E（2，3），∵A（﹣1，0），∴AD＝2，DE＝，AE＝3．∴AD2＝DE2+AE2，∴△ADE是直角三角形，且∠AED＝90°，DE：AE＝1：3．∵点M在直线l下方的抛物线上，∴设M（t，﹣t2+2t+3），则t＞2或t＜0．∴EF＝|t﹣2|，MF＝3﹣（﹣t2+2t+3）＝t2﹣2t，若△MEF与△ADE相似，则EF：MF＝1：3或MF：EF＝1：3，∴|t﹣2|：（t2﹣2t）＝1：3或（t2﹣2t）：|t﹣2|＝1：3，解得t＝2（舍）或t＝3或﹣3或（舍）或﹣，∴M的坐标为（3，0）或（﹣3，﹣12）或（﹣，）．综上，存在点M，使以M，F，E三点为顶点的三角形与△ADE相似，此时点M的坐标为（3，0）或（﹣3，﹣12）或（﹣，）．3．（2022•恩施州）在平面直角坐标系中，O为坐标原点，抛物线y＝﹣x2+c与y 轴交于点P（0，4）．（1）直接写出抛物线的解析式．（2）如图，将抛物线y＝﹣x2+c向左平移1个单位长度，记平移后的抛物线顶点为Q，平移后的抛物线与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C．判断以B、C、Q三点为顶点的三角形是否为直角三角形，并说明理由．（3）直线BC与抛物线y＝﹣x2+c交于M、N两点（点N在点M的右侧），请探究在x轴上是否存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似，若存在，请求出点T的坐标；若不存在，请说明理由．（4）若将抛物线y＝﹣x2+c进行适当的平移，当平移后的抛物线与直线BC最多只有一个公共点时，请直接写出抛物线y＝﹣x2+c平移的最短距离并求出此时抛物线的顶点坐标．【解答】解：（1）∵抛物线y＝﹣x2+c与y轴交于点P（0，4），∴c＝4，∴抛物线的解析式为y＝﹣x2+4；（2）△BCQ是直角三角形．理由如下：将抛物线y＝﹣x2+4向左平移1个单位长度，得新抛物线y＝﹣（x+1）2+4，∴平移后的抛物线顶点为Q（﹣1，4），令x＝0，得y＝﹣1+4＝3，∴C（0，3），令y＝0，得﹣（x+1）2+4＝0，解得：x1＝1，x2＝﹣3，∴B（﹣3，0），A（1，0），如图1，连接BQ，CQ，PQ，∵P（0，4），Q（﹣1，4），∴PQ⊥y轴，PQ＝1，∵CP＝4﹣3＝1，∴PQ＝CP，∠CPQ＝90°，∴△CPQ是等腰直角三角形，∴∠PCQ＝45°，∵OB＝OC＝3，∠BOC＝90°，∴△BOC是等腰直角三角形，∴∠BCO＝45°，∴∠BCQ＝180°﹣45°﹣45°＝90°，∴△BCQ是直角三角形．（3）在x轴上存在点T，使得以B、N、T三点为顶点的三角形与△ABC相似．∵△ABC是锐角三角形，∠ABC＝45°，∴以B、N、T三点为顶点的三角形与△ABC相似，必须∠NBT＝∠ABC＝45°，即点T在y轴的右侧，设T（x，0），且x＞0，则BT＝x+3，∵B（﹣3，0），A（1，0），C（0，3），∴∠ABC＝45°，AB＝4，BC＝3，设直线BC的解析式为y＝kx+b，则，解得：，∴直线BC的解析式为y＝x+3，由，解得：，，∴M（﹣，），N（，），∴BN＝×＝，①当△NBT∽△CBA时，则＝，∴＝，解得：x＝，∴T（，0）；②当△NBT∽△ABC时，则＝，∴＝，解得：x＝，∴T（，0）；综上所述，点T的坐标T（，0）或（，0）．（4）抛物线y＝﹣x2+4的顶点为P（0，4），∵直线BC的解析式为y＝x+3，∴直线BC与y轴的夹角为45°，当抛物线沿着垂直直线BC的方向平移到只有1个公共点时，平移距离最小，此时向右和向下平移距离相等，设平移后的抛物线的顶点为P′（t，4﹣t），则平移后的抛物线为y＝﹣（x﹣t）2+4﹣t，由﹣（x﹣t）2+4﹣t＝x+3，整理得：x2+（1﹣2t）x+t2+t﹣1＝0，∵平移后的抛物线与直线BC最多只有一个公共点，∴Δ＝（1﹣2t）2﹣4（t2+t﹣1）＝0，解得：t＝，∴平移后的抛物线的顶点为P′（，），平移的最短距离为．二．直角三角形的存在性4．（2022•广安）如图，在平面直角坐标系中，抛物线y＝ax2+x+m（a≠0）的图象与x轴交于A、C两点，与y轴交于点B，其中点B坐标为（0，﹣4），点C 坐标为（2，0）．（1）求此抛物线的函数解析式．（2）点D是直线AB下方抛物线上一个动点，连接AD、BD，探究是否存在点D，使得△ABD的面积最大？若存在，请求出点D的坐标；若不存在，请说明理由．（3）点P为该抛物线对称轴上的动点，使得△P AB为直角三角形，请求出点P 的坐标．【解答】解：（1）∵抛物线y＝ax2+x+m（a≠0）的图象经过点B（0，﹣4），点C（2，0），∴，解得，∴抛物线的解析式为y＝x2+x﹣4；（2）存在．理由：如图1中，设D （t ，t 2+t ﹣4），连接OD ．令y ＝0，则x 2+x ﹣4＝0，解得x ＝﹣4或2，∴A （﹣4，0），C （2，0），∵B （0，﹣4），∴OA ＝OB ＝4，∵S △ABD ＝S △AOD +S △OBD ﹣S △AOB ＝×4×（﹣﹣t +4）+×4×（﹣t ）﹣×4×4＝﹣t 2﹣4t ＝﹣（t +2）2+4，∵﹣1＜0，∴t ＝﹣2时，△ABD 的面积最大，最大值为4，此时D （﹣2，﹣4）； （3）如图2中，设抛物线的对称轴交x 轴于点N ，过点B 作BM ⊥抛物线的对称轴于点M ．则N （﹣1.0）．M （﹣1，﹣4）；∵OA＝OB＝4，∠AOB＝90°，∴∠OAB＝∠OBA＝45°，当∠P1AB＝90°时，△ANP1是等腰直角三角形，∴AN＝NP1＝3，∴P1（﹣1，3），当∠ABP2＝90°时，△BMP2是等腰直角三角形，可得P2（﹣1，﹣5），当∠APB＝90°时，设P（﹣1，n），设AB的中点为J，连接PJ，则J（﹣2，﹣2），∴PJ＝AB＝2，∴12+（n+2）2＝（2）2，解得n＝﹣2或﹣﹣2，∴P3（﹣1，﹣2），P4（﹣1，﹣﹣2），综上所述，满足条件的点P的坐标为（﹣1，3）或（﹣1，﹣5）或（﹣1，﹣2）或（﹣1，﹣﹣2）．5．（2022•辽宁）如图，抛物线y＝ax2﹣3x+c与x轴交于A（﹣4，0），B两点，与y轴交于点C（0，4），点D为x轴上方抛物线上的动点，射线OD交直线AC 于点E，将射线OD绕点O逆时针旋转45°得到射线OP，OP交直线AC于点F，连接DF．（1）求抛物线的解析式；（2）当点D在第二象限且＝时，求点D的坐标；（3）当△ODF为直角三角形时，请直接写出点D的坐标．【解答】解：（1）将点A（﹣4，0），C（0，4）代入y＝ax2﹣3x+c，∴，解得，∴y＝﹣x2﹣3x+4；（2）过点D作DG⊥AB交于G，交AC于点H，设直线AC的解析式为y＝kx+b，∴，解得，∴y＝x+4，设D（n，﹣n2﹣3n+4），H（n，n+4），∴DH＝﹣n2﹣4n，∵DH∥OC，∴＝＝，∵OC＝4，∴DH＝3，∴﹣n2﹣4n＝3，解得n＝﹣1或n＝﹣3，∴D（﹣1，6）或（﹣3，4）；（3）设F（t，t+4），当∠FDO＝90°时，过点D作MN⊥y轴交于点N，过点F作FM⊥MN交于点M，∵∠DOF＝45°，∴DF＝DO，∵∠MDF+∠NDO＝90°，∠MDF+∠MFD＝90°，∴∠NDO＝∠MFD，∴△MDF≌△NOD（AAS），∴DM＝ON，MF＝DN，∴DN+ON＝﹣t，DN＝ON+（﹣t﹣4），∴DN＝﹣t﹣2，ON＝2，∴D点纵坐标为2，∴﹣x2﹣3x+4＝2，解得x＝或x＝，∴D点坐标为（，2）或（，2）；当∠DFO＝90°时，过点F作KL⊥x轴交于L点，过点D作DK⊥KL交于点K，∵∠KFD+∠LFO＝90°，∠KFD+∠KDF＝90°，∴∠LFO＝∠KDF，∵DF＝FO，∴△KDF≌△LFO（AAS），∴KD＝FL，KF＝LO，∴KL＝t+4﹣t＝4，∴D点纵坐标为4，∴﹣x2﹣3x+4＝4，解得x＝0或x＝﹣3，∴D（0，4）或（﹣3，4）；综上所述：D点坐标为（，2）或（，2）或（0，4）或（﹣3，4）．三．等腰三角形的存在性6．（2022•百色）已知抛物线经过A（﹣1，0）、B（0，3）、C（3，0）三点，O 为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM，交BC于点F．（1）求抛物线的表达式；（2）求证：∠BOF＝∠BDF；（3）是否存在点M，使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长．【解答】（1）解：设抛物线的表达式为y＝ax2+bx+c，把A（﹣1，0）、B（0，3）、C（3，0）代入得：，解得，∴抛物线的表达式为：y＝﹣x2+2x+3；（2）证明：∵正方形OBDC，∴∠OBC＝∠DBC，BD＝OB，∵BF＝BF，∴△BOF≌△BDF，∴∠BOF＝∠BDF；（3）解：∵抛物线交正方形OBDC的边BD于点E，∴令y＝3，则3＝﹣x2+2x+3，解得：x1＝0，x2＝2，∴E（2，3），①如图，当M在线段BD的延长线上时，∠BDF为锐角，∴∠FDM为钝角，∵△MDF为等腰三角形，∴DF＝DM，∴∠M＝∠DFM，∴∠BDF＝∠M+∠DFM＝2∠M，∵BM∥OC，∴∠M＝∠MOC，由（2）得∠BOF＝∠BDF，∴∠BDF+∠MOC＝3∠M＝90°，∴∠M＝30°，在Rt△BOM中，BM＝，∴ME＝BM﹣BE＝3﹣2；②如图，当M在线段BD上时，∠DMF为钝角，∵△MDF为等腰三角形，∴MF＝DM，∴∠BDF＝∠MFD，∴∠BMO＝∠BDF+∠MFD＝2∠BDF，由（2）得∠BOF＝∠BDF，∴∠BMO＝2∠BOM，∴∠BOM+∠BMO＝3∠BOM＝90°，∴∠BOM＝30°，在Rt△BOM中，BM＝，∴ME＝BE﹣BM＝2﹣，综上所述，ME的值为：3﹣2或2﹣．7．（2022•山西）综合与探究如图，二次函数y＝﹣x2+x+4的图象与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．点P是第一象限内二次函数图象上的一个动点，设点P的横坐标为m．过点P作直线PD⊥x轴于点D，作直线BC交PD于点E．（1）求A，B，C三点的坐标，并直接写出直线BC的函数表达式；（2）当△CEP是以PE为底边的等腰三角形时，求点P的坐标；（3）连接AC，过点P作直线l∥AC，交y轴于点F，连接DF．试探究：在点P 运动的过程中，是否存在点P，使得CE＝FD，若存在，请直接写出m的值；若不存在，请说明理由．【解答】解：（1）在y＝﹣x2+x+4中，令x＝0得y＝4，令y＝0得x＝8或x＝﹣2，∴A（﹣2，0），B（8，0），C（0，4），设直线BC解析式为y＝kx+4，将B（8，0）代入得：8k+4＝0，解得k＝﹣，∴直线BC解析式为y＝﹣x+4；（2）过C作CG⊥PD于G，如图：设P（m，﹣m2+m+4），∴PD＝﹣m2+m+4，∵∠COD＝∠PDO＝∠CGD＝90°，∴四边形CODG是矩形，∴DG＝OC＝4，CG＝OD＝m，∴PG＝PD﹣DG＝﹣m2+m+4﹣4＝﹣m2+m，∵CP＝CE，CG⊥PD，∴GE＝PG＝﹣m2+m，∵∠GCE＝∠OBC，∠CGE＝90°＝∠BOC，∴△CGE∽△BOC，∴＝，即＝，解得m＝0（舍去）或m＝4，∴P（4，6）；（3）存在点P，使得CE＝FD，理由如下：过C作CH⊥PD于H，如图：设P（m，﹣m2+m+4），由A（﹣2，0），C（0，4）可得直线AC解析式为y＝2x+4，根据PF∥AC，设直线PF解析式为y＝2x+b，将P（m，﹣m2+m+4）代入得：﹣m2+m+4＝2m+b，∴b＝﹣m2﹣m+4，∴直线PF解析式为y＝2x﹣m2﹣m+4，令x＝0得y＝﹣m2﹣m+4，∴F（0，﹣m2﹣m+4），∴OF＝|﹣m2﹣m+4|，同（2）可得四边形CODH是矩形，∴CH＝OD，∵CE＝FD，∴Rt△CHE≌Rt△DOF（HL），∴∠HCE＝∠FDO，∵∠HCE＝∠CBO，∴∠FDO＝∠CBO，∴tan∠FDO＝tan∠CBO，∴＝，即＝，∴﹣m2﹣m+4＝m或﹣m2﹣m+4＝﹣m，解得m＝2﹣2或m＝﹣2﹣2或m＝4或m＝﹣4，∵P在第一象限，∴m＝2﹣2或m＝4．8．（2022•东营）如图，抛物线y＝ax2+bx﹣3（a≠0）与x轴交于点A（﹣1，0），点B（3，0），与y轴交于点C．（1）求抛物线的表达式；（2）在对称轴上找一点Q，使△ACQ的周长最小，求点Q的坐标；（3）点P是抛物线对称轴上的一点，点M是对称轴左侧抛物线上的一点，当△PMB是以PB为腰的等腰直角三角形时，请直接写出所有点M的坐标．【解答】解：（1）将点A（﹣1，0），点B（3，0）代入y＝ax2+bx﹣3，∴，解得，∴y＝x2﹣2x﹣3；（2）连接CB交对称轴于点Q，∵y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴抛物线的对称轴为直线x＝1，∵A、B关于对称轴x＝1对称，∴AQ＝BQ，∴AC+AQ+CQ＝AC+CQ+BQ≥AC+BC，当C、B、Q三点共线时，△ACQ的周长最小，∵C（0，﹣3），B（3，0），设直线BC的解析式为y＝kx+b，∴，解得，∴y＝x﹣3，∴Q（1，﹣2）；（3）当∠BPM＝90°时，PM＝PB，∴M点与A点重合，∴M（﹣1，0）；当∠PBM＝90°时，PB＝BM，如图1，当P点在M点上方时，过点B作x轴的垂线GH，过点P作PH⊥GH 交于H，过点M作MG⊥HG交于G，∵∠PBM＝90°，∴∠PBH+∠MBG＝90°，∵∠PBH+∠BPH＝90°，∴∠MBG＝∠BPH，∵BP＝BM，∴△BPH≌△MBG（AAS），∴BH＝MG，PH＝BG＝2，设P（1，t），则M（3﹣t，﹣2），∴﹣2＝（3﹣t）2﹣2（3﹣t）﹣3，解得t＝2+或t＝2﹣，∴M（1﹣，﹣2）或（1+，﹣2），∵M点在对称轴的左侧，∴M点坐标为（1﹣，﹣2）；如图2，当P点在M点下方时，同理可得M（3+t，2），∴2＝（3+t）2﹣2（3+t）﹣3，解得t＝﹣2+（舍）或t＝﹣2﹣，∴M（1﹣，2）；综上所述：M点的坐标为（1﹣，﹣2）或（1﹣，2）或（﹣1，0）．9．（2022•枣庄）如图①，已知抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），过点A作AC∥x轴交抛物线于点C，∠AOB的平分线交线段AC于点E，点P是抛物线上的一个动点．（1）求抛物线的关系式；（2）若动点P在直线OE下方的抛物线上，连结PE、PO，当△OPE面积最大时，求出P点坐标；（3）将抛物线L向上平移h个单位长度，使平移后所得抛物线的顶点落在△OAE 内（包括△OAE的边界），求h的取值范围；（4）如图②，F是抛物线的对称轴l上的一点，在抛物线上是否存在点P，使△POF成为以点P为直角顶点的等腰直角三角形？若存在，直接写出所有符合条件的点P的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线L：y＝x2+bx+c经过点A（0，3），B（1，0），∴，解得，∴抛物线的解析式为：y＝x2﹣4x+3；（2）如图，过P作PG∥y轴，交OE于点G，设P（m，m2﹣4m+3），∵OE平分∠AOB，∠AOB＝90°，∴∠AOE＝45°，∴△AOE是等腰直角三角形，∴AE＝OA＝3，∴E（3，3），∴直线OE的解析式为：y＝x，∴G（m，m），∴PG＝m﹣（m2﹣4m+3）＝﹣m2+5m﹣3，∴S△OPE ＝S△OPG+S△EPG＝PG•AE＝×3×（﹣m2+5m﹣3）＝﹣（m2﹣5m+3）＝﹣（m﹣）2+，∵﹣＜0，∴当m＝时，△OPE面积最大，此时，P点坐标为（，﹣）；（3）由y＝x2﹣4x+3＝（x﹣2）2﹣1，得抛物线l的对称轴为直线x＝2，顶点为（2，﹣1），抛物线L向上平移h个单位长度后顶点为F（2，﹣1+h）．设直线x＝2交OE于点M，交AE于点N，则E（3，3），∵直线OE的解析式为：y＝x，∴M（2，2），∵点F在△OAE内（包括△OAE的边界），∴2≤﹣1+h≤3，解得3≤h≤4；（4）设P（m，m2﹣4m+3），分四种情况：①当P在对称轴的左边，且在x轴下方时，如图，过P作MN⊥y轴，交y轴于M，交l于N，∴∠OMP＝∠PNF＝90°，∵△OPF是等腰直角三角形，∴OP＝PF，∠OPF＝90°，∴∠OPM+∠NPF＝∠PFN+∠NPF＝90°，∴∠OPM＝∠PFN，∴△OMP≌△PNF（AAS），∴OM＝PN，∵P（m，m2﹣4m+3），则﹣m2+4m﹣3＝2﹣m，解得：m＝（舍）或，∴P的坐标为（，）；②当P在对称轴的左边，且在x轴上方时，同理得：2﹣m＝m2﹣4m+3，解得：m1＝（舍）或m2＝，∴P的坐标为（，）；③当P在对称轴的右边，且在x轴下方时，如图，过P作MN⊥x轴于N，过F作FM⊥MN于M，同理得△ONP≌△PMF，∴PN＝FM，则﹣m2+4m﹣3＝m﹣2，解得：m1＝或m2＝（舍）；P的坐标为（，）；④当P在对称轴的右边，且在x轴上方时，如图，同理得m2﹣4m+3＝m﹣2，解得：m＝或（舍），P的坐标为：（，）；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．方法二：作直线DE：y＝x﹣2，E（1，﹣1）是D点（2，0）绕O点顺时针旋转45°并且OD缩小倍得到，易知直线DE即为对称轴上的点绕O点顺时针旋转45°，且到O点距离缩小倍的轨迹，联立直线DE和抛物线解析式得x2﹣4x+3＝x﹣2，解得x1＝，x2＝，同理可得x3＝或x4＝；综上所述，点P的坐标是：（，）或（，）或（，）或（，）．10．（2023•澄城县一模）如图，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣1，0）、B，与y轴交于点C（0，3），直线l是抛物线的对称轴．（1）求抛物线的函数解析式；（2）在对称轴l上是否存在点M，使△MAC为等腰三角形，若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．【解答】解：（1）把点A（﹣1，0）、点C（0，3）分别代入y＝﹣x2+bx+c，得．解得．故该抛物线解析式为：y＝﹣x2+2x+3；（2）由（1）知，该抛物线解析式为：y＝﹣x2+2x+3．则该抛物线的对称轴为直线x＝﹣＝1．故设M（1，m）．∵A（﹣1，0）、点C（0，3），∴AC2＝10，AM2＝4+m2，CM2＝1+（m﹣3）2．①若AC＝AM时，10＝4+m2，解得m＝±．∴点M的坐标为（1，）或（1，﹣）；②若AC＝CM时，10＝1+（m﹣3）2，解得m＝0或m＝6，∴点M的坐标为（1，0）或（1，6）．当点M的坐标为（1，6）时，点A、C、M共线，∴点M的坐标为（1，0）；③当AM＝CM时，4+m2＝1+（m﹣3）2，解得m＝1，∴点M的坐标为（1，1）．综上所述，符合条件的点M的坐标为（1，）或（1，﹣）或（1，0）或（1，1）．11．（2023•碑林区校级一模）二次函数y＝ax2+bx+2的图象交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，动点M从点A出发，以每秒2个单位长度的速度沿AB方向运动，过点M作MN⊥x轴交直线BC于点N，交抛物线于点D，连接AC，设运动的时间为t秒．（1）求二次函数y＝ax2+bx+2的表达式；（2）在直线MN上存在一点P，当△PBC是以∠BPC为直角的等腰直角三角形时，求此时点D的坐标．【解答】解：（1）将点（﹣1，0），B（4，0）代入y＝ax2+bx+2，∴a＝﹣，b＝，∴y＝﹣x2+x+2；（2）∵BM＝5﹣2t，∴M（2t﹣1，0），设P（2t﹣1，m），∵PC2＝（2t﹣1）2+（m﹣2）2，PB2＝（2t﹣5）2+m2，∵PB＝PC，∴（2t﹣1）2+（m﹣2）2＝（2t﹣5）2+m2，∴m＝4t﹣5，∴P（2t﹣1，4t﹣5），∵PC⊥PB，∴×＝﹣1，∴t＝1或t＝2，∴M（1，0）或M（3，0），∴D（1，3）或D（3，2）．12．（2023•东洲区模拟）抛物线y＝ax2+bx+3经过A（﹣1，0），B（3，0）两点，与y轴正半轴交于点C．（1）求此抛物线解析式；（2）如图①，连接BC，点P为抛物线第一象限上一点，设点P的横坐标为m，△PBC的面积为S，求S与m的函数关系式，并求S最大时P点坐标；（3）如图②，连接AC，在抛物线的对称轴上是否存在点M，使△MAC为等腰三角形？若存在，请直接写出符合条件的点M的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+bx+3经过A（﹣1，0），B（3，0）两点，∴，解得：，∴抛物线解析式为y＝﹣x2+2x+3；（2）点P作PF⊥x轴于点F，交BC于点E，设BC直线解析式为：y＝kx+b，∵B（3，0），C（0，3），∴，解得，∴y＝﹣x+3，由题意可知P（m，﹣m2+2m+3），E（m，﹣m+3），S＝S△PBE+S△PCE，S＝PE•OB＝（﹣m2+2m+3+m﹣3）×3，，∵，∴当时，S有最大值，此时P点坐标为；（3）存在，M1（1，0），，，M4（1，1），①当AC＝AM时，如图，设对称轴l与AB交于点E，则，∵AM2＝AE2+EM2，∴，解得：，∴M点的坐标为或，②当AC＝MC时，则OC为AM的垂直平分线．因此M与E重合，因此，M点的坐标为（1，0），③当AM＝CM时，如图，设M点的坐标为（1，n），则AM2＝22+n2＝4+n2，CM2＝12+（3﹣n）2，∴4+n2＝12+（3﹣n）2，解得：n＝1，∴M点的坐标为（1，1），综上可知，潢足条件的M点共四个，其坐标为M1（1，0），，，M4（1，1）．13．（2023•三亚一模）如图，抛物线y＝ax2+3x+c（a≠0）与x轴交于点A（﹣2，0）和点B，与y轴交于点C（0，8），顶点为D，连接AC，CD，DB，直线BC 与抛物线的对称轴l交于点E．（1）求抛物线的解析式和直线BC的解析式；（2）求四边形ABDC的面积；（3）P是第一象限内抛物线上的动点，连接PB，PC，当S△PBC ＝S△ABC时，求点P的坐标；（4）在抛物线的对称轴l上是否存在点M，使得△BEM为等腰三角形？若存在，请直接写出点M的坐标；若不存在，请说明理由．【解答】解：（1）∵抛物线y＝ax2+3x+c（a≠0）过点A（﹣2，0）和C（0，8），∴，解得，∴抛物线的解析式为y＝﹣x2+3x+8．令y＝0，得．解得x1＝﹣2，x2＝8．∴点B的坐标为（8，0）．设直线BC的解析式为y＝kx+b．把点B（8，0），C（0，8）分别代入y＝kx+b，得，解得，∴直线BC的解析式为y＝﹣x+8．（2）如图1，设抛物线的对称轴l与x轴交于点H．∵抛物线的解析式为，∴顶点D的坐标为．∴S四边形ABDC ＝S△AOC+S梯形OCDH+S△BDH＝＝＝70．（3）∵．∴．如图2，过点P作PG⊥x轴，交x轴于点G，交BC于点F．设点．∵点F在直线BC上，∴F（t，﹣t+8）．∴．∴．∴．解得t1＝2，t2＝6．∴点P的坐标为（2，12）或P（6，8）．（4）存在．∵△BEM为等腰三角形，∴BM＝EM或BE＝BM或BE＝EM，设M（3，m），∵B（8，0），E（3，5），∴BE＝＝5，EM＝|m﹣5|，BM＝＝，当BM＝EM时，＝|m﹣5|，∴m2+25＝（m﹣5）2，解得：m＝0，∴M（3，0）；当BE＝BM时，5＝，∴m2+25＝50，解得：m＝﹣5或m＝5（舍去），∴M（3，﹣5）；当BE＝EM时，5＝|m﹣5|，解得：m＝5+5或m＝5﹣5，∴M（3，5+5）或（3，5﹣5），综上所述，点M的坐标为（3，0）或（3，﹣5）或（3，5+5）或（3，5﹣5）．14．（2023•南海区一模）如图，在平面直角坐标系中，抛物线y＝ax2+bx﹣3（a ＞0）与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）点P为直线BC下方抛物线上的一动点，PM⊥BC于点M，PN∥y轴交BC 于点N．求线段PM的最大值和此时点P的坐标；（3）点E为x轴上一动点，点Q为抛物线上一动点，是否存在以CQ为斜边的等腰直角三角形CEQ？若存在，请直接写出点E的坐标；若不存在，请说明理由．【解答】解：（1）将A（﹣1，0），B（3，0）代入函数y＝ax2+bx﹣3（a＞0）中，得，解得，∴解析式为y＝x2﹣2x﹣3，故抛物线解析式为y＝x2﹣2x﹣3；（2）当x＝0时，y＝3，∴C（0，﹣3），∵B（3，0），∴∠OCB＝∠OBC＝45°，∵PN∥y轴，∴∠MNP＝45°，∵PM⊥BC，∴PM＝PN，则当PN最大时，PM也最大，设BC的解析式为y＝mx+n，∴，解得，∴BC解析式为y＝x﹣3，设P（x，x2﹣2x﹣3），N（x，x﹣3），∴PN＝x﹣3﹣（x2﹣2x﹣3）＝﹣（x﹣）2+，当x＝时，PN最大，则PM＝PN＝×＝，∴P（，），故PM最大值为，P点坐标为（，﹣）；（3）存在，点E的坐标为（﹣5，0），（，0），（0，0），（，0）．∵CEQ是以CQ为斜边的等腰直角三角形，∴设Q（x，x2﹣2x﹣3），①如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，∵∠CEQ＝90°，∴∠QEM+∠CEN＝90°，∵∠QEM+∠MQE＝90°，∴∠EQM＝∠CEN，∵∠CNE＝∠QME＝90°，EC＝EQ，∴△EMQ≌△CNE（AAS），∴CN＝EM＝x2﹣2x﹣3，MQ＝EN＝3，∴|x Q|+MQ＝CN，﹣x+3＝x2﹣2x﹣3，解得x＝﹣2，x＝3（舍去），∴OE＝CM＝2+3＝5，E（﹣5，0），②如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，同理：△EMC≌△QNE（AAS），CM＝EN＝x2﹣2x﹣3，NQ＝EM＝3，∴﹣x+x2﹣2x﹣3＝3，解得x＝，x＝（舍去），∴OE＝CM＝，E（，0），③如图，点E和点O重合，点Q和点B重合，此时E（0，0），④如图，过点E作x轴的垂线l，再分别过点C和点Q作垂线l的垂线，分别交于点M和点N，同理：△EMC≌△QNE（AAS），CM＝EN＝x2﹣2x﹣3，NQ＝EM＝3，∴x+3＝x2﹣2x﹣3，解得x＝，x＝（舍去），∴OE＝CM＝，E（，0），综上所述，点E的坐标为（﹣5，0），（，0），（0，0），（，0）41。

初二三角形所有知识点总结和常考题知识点：1.三角形：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形.2.三边关系：三角形任意两边的和大于第三边，任意两边的差小于第三边.3.高：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足间的线段叫做三角形的高.4.中线：在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线.5.角平分线：三角形的一个内角的平分线与这个角的对边相交，这个角的顶点和交点之间的线段叫做三角形的角平分线.6.三角形的稳定性：三角形的形状是固定的，三角形的这个性质叫三角形的稳定性.7.多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形.8.多边形的内角：多边形相邻两边组成的角叫做它的内角.9.多边形的外角：多边形的一边与它的邻边的延长线组成的角叫做多边形的外角.10.多边形的对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.11.正多边形：在平面内，各个角都相等，各条边都相等的多边形叫正多边形.12.平面镶嵌：用一些不重叠摆放的多边形把平面的一部分完全覆盖，叫做用多边形覆盖平面，13.公式与性质：⑴三角形的内角和：三角形的内角和为180°⑵三角形外角的性质：性质1：三角形的一个外角等于和它不相邻的两个内角的和.性质2：三角形的一个外角大于任何一个和它不相邻的内角.⑶多边形内角和公式：n边形的内角和等于(2)n-·180°⑷多边形的外角和：多边形的外角和为360°.⑸多边形对角线的条数：①从n边形的一个顶点出发可以引(3)n-条对角线，把多边形分成(2)n-个三角形.②n边形共有(3)2n n-条对角线.常考题：一．选择题（共13小题）1．已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是（）A．13cm B．6cm C．5cm D．4cm2．一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（）A．90°B．100°C．130° D．180°3．已知如图，△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）A．315°B．270° C．180° D．135°4．如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．5．如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD的平分线交于点P，则∠P=（）A．90°﹣αB．90°+αC．D．360°﹣α6．如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A落在边CB上A′处，折痕为CD，则∠A′DB=（）A．40°B．30°C．20°D．10°7．如图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE相交于一点P，若∠A=50°，则∠BPC=（）A．150°B．130°C．120° D．100°8．如图，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA=15米，OB=10米，A、B间的距离不可能是（）A．20米B．15米C．10米D．5米9．将一个n边形变成n+1边形，内角和将（）A．减少180°B．增加90°C．增加180°D．增加360°10．一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（）A．27 B．35 C．44 D．5411．一个多边形的边数每增加一条，这个多边形的（）A．内角和增加360°B．外角和增加360°C．对角线增加一条 D．内角和增加180°12．一个三角形三个内角的度数之比为2：3：7，这个三角形一定是（）A．等腰三角形B．直角三角形C．锐角三角形D．钝角三角形13．如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（）A．13 B．14 C．15 D．16二．填空题（共13小题）14．若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是．15．如图，小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，…，照这样走下去，他第一次回到出发地A点时，一共走了米．16．将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为度．17．当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为．18．若一个多边形内角和等于1260°，则该多边形边数是．19．如图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1+∠2+∠3+∠4+∠5=．20．一个多边形的内角和比外角和的3倍多180°，则它的边数是．21．若正多边形的一个内角等于140°，则这个正多边形的边数是．22．在△ABC中，三个内角∠A、∠B、∠C满足∠B﹣∠A=∠C﹣∠B，则∠B=度．23．如图，在△ABC中，∠A=m°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…∠A2012BC和∠A2012CD的平分线交于点A2013，则∠A2013=度．24．如图，△ABC中，∠A=40°，∠B=72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF=度．25．用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE，其中∠BAC=度．26．平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2=．三．解答题（共14小题）27．如图，直线DE交△ABC的边AB、AC于D、E，交BC延长线于F，若∠B=67°，∠ACB=74°，∠AED=48°，求∠BDF的度数．28．如图，已知D为△ABC边BC延长线上一点，DF⊥AB于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．29．已知△ABC中，∠ACB=90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE=∠CEF．30．如图，AD为△ABC的中线，BE为△ABD的中线，（1）若∠ABE=25°，∠BAD=50°，则∠BED的度数是度．（2）在△ADC中过点C作AD边上的高CH．（3）若△ABC的面积为60，BD=5，求点E到BC边的距离．31．如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．（1）若∠B=35°，∠ACB=85°，求∠E的度数；（2）当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系，写出结论无需证明．32．如图所示，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E，∠AFD=158°，求∠EDF的度数．33．如图，AD平分∠BAC，∠EAD=∠EDA．（1）∠EAC与∠B相等吗？为什么？（2）若∠B=50°，∠CAD：∠E=1：3，求∠E的度数．34．（1）如图1，有一块直角三角板XYZ放置在△ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C．△ABC中，∠A=30°，则∠ABC+∠ACB=，∠XBC+∠XCB=．（2）如图2，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ 仍然分别经过B、C，那么∠ABX+∠ACX的大小是否变化？若变化，请举例说明；若不变化，请求出∠ABX+∠ACX的大小．35．已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON 上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．（1）如图1，若AB∥ON，则①∠ABO的度数是；②当∠BAD=∠ABD时，x=；当∠BAD=∠BDA时，x=．（2）如图2，若AB⊥OM，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．36．平面内的两条直线有相交和平行两种位置关系（1）如图a，若AB∥CD，点P在AB、CD外部，则有∠B=∠BOD，又因∠BOD 是△POD的外角，故∠BOD=∠BPD+∠D，得∠BPD=∠B﹣∠D．将点P移到AB、CD内部，如图b，以上结论是否成立？若成立，说明理由；若不成立，则∠BPD、∠B、∠D之间有何数量关系？请证明你的结论；（2）在图b中，将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q，如图c，则∠BPD﹑∠B﹑∠D﹑∠BQD之间有何数量关系？（不需证明）（3）根据（2）的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数．37．如下几个图形是五角星和它的变形．（1）图（1）中是一个五角星，求∠A+∠B+∠C+∠D+∠E．（2）图（2）中的点A向下移到BE上时，五个角的和（即∠CAD+∠B+∠C+∠D+∠E）有无变化说明你的结论的正确性．（3）把图（2）中的点C向上移到BD上时（1）如图（3）所示，五个角的和（即∠CAD+∠B+∠ACE+∠D+∠E）有无变化说明你的结论的正确性．38．Rt△ABC中，∠C=90°，点D、E分别是△ABC边AC、BC上的点，点P是一动点．令∠PDA=∠1，∠PEB=∠2，∠DPE=∠α．（1）若点P在线段AB上，如图（1）所示，且∠α=50°，则∠1+∠2=°；（2）若点P在边AB上运动，如图（2）所示，则∠α、∠1、∠2之间的关系为：；（3）若点P运动到边AB的延长线上，如图（3）所示，则∠α、∠1、∠2之间有何关系？猜想并说明理由．（4）若点P运动到△ABC形外，如图（4）所示，则∠α、∠1、∠2之间的关系为：．39．如图所示，求∠A+∠B+∠C+∠D+∠E+∠F的度数．40．将纸片△ABC沿DE折叠使点A落在A′处的位置．（1）如果A′落在四边形BCDE的内部（如图1），∠A′与∠1+∠2之间存在怎样的数量关系？并说明理由．（2）如果A′落在四边形BCDE的BE边上，这时图1中的∠1变为0°角，则∠A′与∠2之间的关系是．（3）如果A′落在四边形BCDE的外部（如图2），这时∠A′与∠1、∠2之间又存在怎样的数量关系？并说明理由．初二三角形所有知识点总结和常考题提高难题压轴题练习(含答案解析)参考答案与试题解析一．选择题（共13小题）1．（2008•福州）已知三角形的两边长分别为4cm和9cm，则下列长度的四条线段中能作为第三边的是（）A．13cm B．6cm C．5cm D．4cm【分析】此题首先根据三角形的三边关系，求得第三边的取值范围，再进一步找到符合条件的数值．【解答】解：根据三角形的三边关系，得：第三边应大于两边之差，且小于两边之和，即9﹣4=5，9+4=13．∴第三边取值范围应该为：5＜第三边长度＜13，故只有B选项符合条件．故选：B．【点评】本题考查了三角形三边关系，一定要注意构成三角形的条件：两边之和＞第三边，两边之差＜第三边．2．（2013•河北）一个正方形和两个等边三角形的位置如图所示，若∠3=50°，则∠1+∠2=（）A．90°B．100°C．130° D．180°【分析】设围成的小三角形为△ABC，分别用∠1、∠2、∠3表示出△ABC的三个内角，再利用三角形的内角和等于180°列式整理即可得解．【解答】解：如图，∠BAC=180°﹣90°﹣∠1=90°﹣∠1，∠ABC=180°﹣60°﹣∠3=120°﹣∠3，∠ACB=180°﹣60°﹣∠2=120°﹣∠2，在△ABC中，∠BAC+∠ABC+∠ACB=180°，∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°，∴∠1+∠2=150°﹣∠3，∵∠3=50°，∴∠1+∠2=150°﹣50°=100°．故选：B．【点评】本题考查了三角形的内角和定理，用∠1、∠2、∠3表示出△ABC的三个内角是解题的关键，也是本题的难点．3．（2010•西藏）已知如图，△ABC为直角三角形，∠C=90°，若沿图中虚线剪去∠C，则∠1+∠2等于（）A．315°B．270° C．180° D．135°【分析】利用三角形内角与外角的关系：三角形的任一外角等于和它不相邻的两个内角之和解答．【解答】解：∵∠1、∠2是△CDE的外角，∴∠1=∠4+∠C，∠2=∠3+∠C，即∠1+∠2=2∠C+（∠3+∠4），∵∠3+∠4=180°﹣∠C=90°，∴∠1+∠2=2×90°+90°=270°．故选：B．【点评】此题主要考查了三角形内角与外角的关系：三角形的任一外角等于和它不相邻的两个内角之和．4．（2015•长沙）如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（）A．B．C．D．【分析】根据三角形高线的定义：过三角形的顶点向对边引垂线，顶点和垂足之间的线段叫做三角形的高线解答．【解答】解：为△ABC中BC边上的高的是A选项．故选A．【点评】本题考查了三角形的角平分线、中线、高线，熟记高线的定义是解题的关键．5．（2014•达州）如图，在四边形ABCD中，∠A+∠D=α，∠ABC的平分线与∠BCD 的平分线交于点P，则∠P=（）A．90°﹣αB．90°+αC．D．360°﹣α【分析】先求出∠ABC+∠BCD的度数，然后根据角平分线的性质以及三角形的内角和定理求解∠P的度数．【解答】解：∵四边形ABCD中，∠ABC+∠BCD=360°﹣（∠A+∠D）=360°﹣α，∵PB和PC分别为∠ABC、∠BCD的平分线，∴∠PBC+∠PCB=（∠ABC+∠BCD）=（360°﹣α）=180°﹣α，则∠P=180°﹣（∠PBC+∠PCB）=180°﹣（180°﹣α）=α．故选：C．【点评】本题考查了多边形的内角和外角以及三角形的内角和定理，属于基础题．6．（2009•荆门）如图，Rt△ABC中，∠ACB=90°，∠A=50°，将其折叠，使点A 落在边CB上A′处，折痕为CD，则∠A′DB=（）A．40°B．30°C．20°D．10°【分析】由三角形的一个外角等于与它不相邻的两个内角的和，得∠A′DB=∠CA'D ﹣∠B，又折叠前后图形的形状和大小不变，∠CA'D=∠A=50°，易求∠B=90°﹣∠A=40°，从而求出∠A′DB的度数．【解答】解：∵Rt△ABC中，∠ACB=90°，∠A=50°，∴∠B=90°﹣50°=40°，∵将其折叠，使点A落在边CB上A′处，折痕为CD，则∠CA'D=∠A，∵∠CA'D是△A'BD的外角，∴∠A′DB=∠CA'D﹣∠B=50°﹣40°=10°．故选：D．【点评】本题考查图形的折叠变化及三角形的外角性质．关键是要理解折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，只是位置变化．解答此题的关键是要明白图形折叠后与折叠前所对应的角相等．7．（2004•陕西）如图，在锐角△ABC中，CD，BE分别是AB，AC边上的高，且CD，BE相交于一点P，若∠A=50°，则∠BPC=（）A．150°B．130°C．120° D．100°【分析】根据垂直的定义和四边形的内角和是360°求得．【解答】解：∵BE⊥AC，CD⊥AB，∴∠ADC=∠AEB=90°，∴∠BPC=∠DPE=180°﹣50°=130°．故选B．【点评】主要考查了垂直的定义以及四边形内角和是360度．注意∠BPC与∠DPE 互为对顶角．8．（2009•黑河）如图，为估计池塘岸边A、B的距离，小方在池塘的一侧选取一点O，测得OA=15米，OB=10米，A、B间的距离不可能是（）A．20米B．15米C．10米D．5米【分析】根据三角形的三边关系，第三边的长一定大于已知的两边的差，而小于两边的和，求得相应范围，看哪个数值不在范围即可．【解答】解：∵15﹣10＜AB＜10+15，∴5＜AB＜25．∴所以不可能是5米．故选：D．【点评】已知三角形的两边，则第三边的范围是：＞已知的两边的差，而＜两边的和．9．（2014•临沂）将一个n边形变成n+1边形，内角和将（）A．减少180°B．增加90°C．增加180°D．增加360°【分析】利用多边形的内角和公式即可求出答案．【解答】解：n边形的内角和是（n﹣2）•180°，n+1边形的内角和是（n﹣1）•180°，因而（n+1）边形的内角和比n边形的内角和大（n﹣1）•180°﹣（n﹣2）•180=180°．故选：C．【点评】本题主要考查了多边形的内角和公式，是需要识记的内容．10．（2015•莱芜）一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（）A．27 B．35 C．44 D．54【分析】设出题中所给的两个未知数，利用内角和公式列出相应等式，根据边数为整数求解即可，再进一步代入多边形的对角线计算方法，即可解答．【解答】解：设这个内角度数为x°，边数为n，∴（n﹣2）×180﹣x=1510，180n=1870+x=1800+（70+x），∵n为正整数，∴n=11，∴=44，故选：C．【点评】此题考查多边形的内角和计算公式以及多边形的对角线条数的计算方法，属于需要识记的知识．11．（2011春•滨城区期末）一个多边形的边数每增加一条，这个多边形的（）A．内角和增加360°B．外角和增加360°C．对角线增加一条 D．内角和增加180°【分析】利用多边形的内角和定理和外角和特征即可解决问题．【解答】解：因为n边形的内角和是（n﹣2）•180°，当边数增加一条就变成n+1，则内角和是（n﹣1）•180°，内角和增加：（n﹣1）•180°﹣（n﹣2）•180°=180°；根据多边形的外角和特征，边数变化外角和不变．故选：D．【点评】本题主要考查了多边形的内角和定理与外角和特征．先设这是一个n 边形是解题的关键．12．（2012•滨州）一个三角形三个内角的度数之比为2：3：7，这个三角形一定是（）A．等腰三角形B．直角三角形C．锐角三角形D．钝角三角形【分析】已知三角形三个内角的度数之比，根据三角形内角和定理，可求得三角的度数，由此判断三角形的类型．【解答】解：三角形的三个角依次为180°×=30°，180°×=45°，180°×=105°，所以这个三角形是钝角三角形．故选：D．【点评】本题考查三角形的分类，这个三角形最大角为180°×＞90°．本题也可以利用方程思想来解答，即2x+3x+7x=180，解得x=15，所以最大角为7×15°=105°．13．（2014•毕节市）如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（）A．13 B．14 C．15 D．16【分析】根据多边形内角和公式，可得新多边形的边数，根据新多边形比原多边形多1条边，可得答案．【解答】解：设新多边形是n边形，由多边形内角和公式得（n﹣2）180°=2340°，解得n=15，原多边形是15﹣1=14，故选：B．【点评】本题考查了多边形内角与外角，多边形的内角和公式是解题关键．二．填空题（共13小题）14．（2015•资阳）若一个多边形的内角和是其外角和的3倍，则这个多边形的边数是8．【分析】任何多边形的外角和是360°，即这个多边形的内角和是3×360°．n边形的内角和是（n﹣2）•180°，如果已知多边形的边数，就可以得到一个关于边数的方程，解方程就可以求出多边形的边数．【解答】解：设多边形的边数为n，根据题意，得（n﹣2）•180=3×360，解得n=8．则这个多边形的边数是8．【点评】已知多边形的内角和求边数，可以转化为方程的问题来解决．15．（2006•镇江）如图，小亮从A点出发，沿直线前进10米后向左转30°，再沿直线前进10米，又向左转30°，…，照这样走下去，他第一次回到出发地A点时，一共走了120米．【分析】由题意可知小亮所走的路线为一个正多边形，根据多边形的外角和即可求出答案．【解答】解：∵360÷30=12，∴他需要走12次才会回到原来的起点，即一共走了12×10=120米．故答案为：120．【点评】本题主要考查了多边形的外角和定理．任何一个多边形的外角和都是360°．16．（2014•随州）将一副直角三角板如图放置，使含30°角的三角板的短直角边和含45°角的三角板的一条直角边重合，则∠1的度数为75度．【分析】根据三角形三内角之和等于180°求解．【解答】解：如图．∵∠3=60°，∠4=45°，∴∠1=∠5=180°﹣∠3﹣∠4=75°．故答案为：75．【点评】考查三角形内角之和等于180°．17．（2013•上海）当三角形中一个内角α是另一个内角β的两倍时，我们称此三角形为“特征三角形”，其中α称为“特征角”．如果一个“特征三角形”的“特征角”为100°，那么这个“特征三角形”的最小内角的度数为30°．【分析】根据已知一个内角α是另一个内角β的两倍得出β的度数，进而求出最小内角即可．【解答】解：由题意得：α=2β，α=100°，则β=50°，180°﹣100°﹣50°=30°，故答案为：30°．【点评】此题主要考查了新定义以及三角形的内角和定理，根据已知得出β的度数是解题关键．18．（2013•遂宁）若一个多边形内角和等于1260°，则该多边形边数是9．【分析】根据多边形内角和定理及其公式，即可解答；【解答】解：∵一个多边形内角和等于1260°，∴（n﹣2）×180°=1260°，解得，n=9．故答案为9．【点评】本题考查了多边形的内角定理及其公式，关键是记住多边形内角和的计算公式．19．（2015•北京）如图是由射线AB，BC，CD，DE，EA组成的平面图形，则∠1+∠2+∠3+∠4+∠5=360°．【分析】首先根据图示，可得∠1=180°﹣∠BAE，∠2=180°﹣∠ABC，∠3=180°﹣∠BCD，∠4=180°﹣∠CDE，∠5=180°﹣∠DEA，然后根据三角形的内角和定理，求出五边形ABCDE的内角和是多少，再用180°×5减去五边形ABCDE的内角和，求出∠1+∠2+∠3+∠4+∠5等于多少即可．【解答】解：∠1+∠2+∠3+∠4+∠5=（180°﹣∠BAE）+（180°﹣∠ABC）+（180°﹣∠BCD）+（180°﹣∠CDE）+（180°﹣∠DEA）=180°×5﹣（∠BAE+∠ABC+∠BCD+∠CDE+∠DEA）=900°﹣（5﹣2）×180°=900°﹣540°=360°．故答案为：360°．【点评】此题主要考查了多边形内角和定理，要熟练掌握，解答此题的关键是要明确：（1）n边形的内角和=（n﹣2）•180 （n≥3）且n为整数）．（2）多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和永远为360°．20．（2014•自贡）一个多边形的内角和比外角和的3倍多180°，则它的边数是9．【分析】多边形的内角和比外角和的3倍多180°，而多边形的外角和是360°，则内角和是3×360°+180°．n边形的内角和可以表示成（n﹣2）•180°，设这个多边形的边数是n，得到方程，从而求出边数．【解答】解：根据题意，得（n﹣2）•180°=3×360°+180°，解得：n=9．则这个多边形的边数是9．故答案为：9．【点评】考查了多边形内角与外角，此题只要结合多边形的内角和公式寻求等量关系，构建方程即可求解．21．（2015•徐州）若正多边形的一个内角等于140°，则这个正多边形的边数是 9 ．【分析】首先根据求出外角度数，再利用外角和定理求出边数．【解答】解：∵正多边形的一个内角是140°，∴它的外角是：180°﹣140°=40°，360°÷40°=9．故答案为：9．【点评】此题主要考查了多边形的外角与内角，做此类题目，首先求出正多边形的外角度数，再利用外角和定理求出求边数．22．（2013•黔东南州）在△ABC 中，三个内角∠A 、∠B 、∠C 满足∠B ﹣∠A=∠C ﹣∠B ，则∠B= 60 度．【分析】先整理得到∠A +∠C=2∠B ，再利用三角形的内角和等于180°列出方程求解即可．【解答】解：∵∠B ﹣∠A=∠C ﹣∠B ，∴∠A +∠C=2∠B ，又∵∠A +∠C +∠B=180°，∴3∠B=180°，∴∠B=60°．故答案为：60．【点评】本题考查了三角形的内角和定理，是基础题，求出∠A +∠C=2∠B 是解题的关键．23．（2013•达州）如图，在△ABC 中，∠A=m°，∠ABC 和∠ACD 的平分线交于点A 1，得∠A 1；∠A 1BC 和∠A 1CD 的平分线交于点A 2，得∠A 2；…∠A 2012BC 和∠A 2012CD的平分线交于点A 2013，则∠A 2013= 度．【分析】利用角平分线的性质、三角形外角性质，易证∠A 1=∠A ，进而可求∠A 1，由于∠A 1=∠A ，∠A 2=∠A 1=∠A ，…，以此类推可知∠A 2013=∠A=°． 【解答】解：∵A 1B 平分∠ABC ，A 1C 平分∠ACD ，∴∠A1BC=∠ABC，∠A1CA=∠ACD，∵∠A1CD=∠A1+∠A1BC，即∠ACD=∠A1+∠ABC，∴∠A1=（∠ACD﹣∠ABC），∵∠A+∠ABC=∠ACD，∴∠A=∠ACD﹣∠ABC，∴∠A1=∠A，∴∠A1=m°，∵∠A1=∠A，∠A2=∠A1=∠A，…以此类推∠A2013=∠A=°．故答案为：．【点评】本题考查了角平分线性质、三角形外角性质，解题的关键是推导出∠A1=∠A，并能找出规律．24．（2012春•金台区期末）如图，△ABC中，∠A=40°，∠B=72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF=74度．【分析】利用三角形的内角和外角之间的关系计算．【解答】解：∵∠A=40°，∠B=72°，∴∠ACB=68°，∵CE平分∠ACB，CD⊥AB于D，∴∠BCE=34°，∠BCD=90﹣72=18°，∵DF⊥CE，∴∠CDF=90°﹣（34°﹣18°）=74°．故答案为：74．【点评】主要考查了三角形的内角和外角之间的关系．（1）三角形的外角等于与它不相邻的两个内角和；（2）三角形的内角和是180度，求角的度数常常要用到“三角形的内角和是180°”这一隐含的条件；（3）三角形的一个外角＞任何一个和它不相邻的内角．注意：垂直和直角总是联系在一起．25．（2006•临安市）用一条宽相等的足够长的纸条，打一个结，如图（1）所示，然后轻轻拉紧、压平就可以得到如图（2）所示的正五边形ABCDE，其中∠BAC= 36度．【分析】利用多边形的内角和定理和等腰三角形的性质即可解决问题．【解答】解：∵∠ABC==108°，△ABC是等腰三角形，∴∠BAC=∠BCA=36度．【点评】本题主要考查了多边形的内角和定理和等腰三角形的性质．n边形的内角和为：180°（n﹣2）．26．（2015•河北）平面上，将边长相等的正三角形、正方形、正五边形、正六边形的一边重合并叠在一起，如图，则∠3+∠1﹣∠2=24°．【分析】首先根据多边形内角和定理，分别求出正三角形、正方形、正五边形、正六边形的每个内角的度数是多少，然后分别求出∠3、∠1、∠2的度数是多少，进而求出∠3+∠1﹣∠2的度数即可．【解答】解：正三角形的每个内角是：180°÷3=60°，正方形的每个内角是：360°÷4=90°，正五边形的每个内角是：（5﹣2）×180°÷5=3×180°÷5=540°÷5=108°，正六边形的每个内角是：（6﹣2）×180°÷6=4×180°÷6=720°÷6=120°，则∠3+∠1﹣∠2=（90°﹣60°）+（120°﹣108°）﹣（108°﹣90°）=30°+12°﹣18°=24°．故答案为：24°．【点评】此题主要考查了多边形内角和定理，要熟练掌握，解答此题的关键是要明确：（1）n边形的内角和=（n﹣2）•180 （n≥3）且n为整数）．（2）多边形的外角和指每个顶点处取一个外角，则n边形取n个外角，无论边数是几，其外角和永远为360°．三．解答题（共14小题）27．（2013春•临清市期末）如图，直线DE交△ABC的边AB、AC于D、E，交BC延长线于F，若∠B=67°，∠ACB=74°，∠AED=48°，求∠BDF的度数．【分析】先根据三角形的内角和定理求出∠A的度数，再根据三角形外角的性质求出∠BDF的度数．【解答】解：因为∠A+∠B+∠ACB=180°，所以∠A=180°﹣67°﹣74°=39°，所以∠BDF=∠A+∠AED=39°+48°=87°．【点评】本题考查三角形外角的性质及三角形的内角和定理，解答的关键是外角和内角的关系．28．（2013•湖州校级模拟）如图，已知D为△ABC边BC延长线上一点，DF⊥AB 于F交AC于E，∠A=35°，∠D=42°，求∠ACD的度数．【分析】根据三角形外角与内角的关系及三角形内角和定理解答．【解答】解：∵∠AFE=90°，∴∠AEF=90°﹣∠A=90°﹣35°=55°，∴∠CED=∠AEF=55°，∴∠ACD=180°﹣∠CED﹣∠D=180°﹣55°﹣42°=83°．答：∠ACD的度数为83°．【点评】三角形外角与内角的关系：三角形的一个外角等于和它不相邻的两个内角的和．三角形内角和定理：三角形的三个内角和为180°．29．（2015秋•全椒县期中）已知△ABC中，∠ACB=90°，CD为AB边上的高，BE 平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE=∠CEF．【分析】题目中有两对直角，可得两对角互余，由角平分线及对顶角可得两对角相等，然后利用等量代换可得答案．【解答】证明：∵∠ACB=90°，∴∠1+∠3=90°，∵CD⊥AB，∴∠2+∠4=90°，又∵BE平分∠ABC，∴∠1=∠2，∴∠3=∠4，∵∠4=∠5，∴∠3=∠5，即∠CFE=∠CEF．【点评】本题考查了三角形角平分线、中线和高的有关知识；正确利用角的等量代换是解答本题的关键．30．（2010春•横峰县校级期末）如图，AD为△ABC的中线，BE为△ABD的中线，（1）若∠ABE=25°，∠BAD=50°，则∠BED的度数是度．（2）在△ADC中过点C作AD边上的高CH．（3）若△ABC的面积为60，BD=5，求点E到BC边的距离．【分析】（1）根据三角形的一个外角等于与它不相邻的两个内角和，∠BED=∠ABE+∠BAE=75°；（2）三角形高的基本作法：用圆规以一边两端点为圆心，任意长为半径作两段弧，交于角的两边，再以交点为圆心，用交轨法作两段弧，找到两段弧的交点，连接两个交点，并过另一端点作所成直线的平行线，叫该边所在直线一点，连接该点和另一端点，则为高线；（3）我们通过证明不难得出三角形中线将三角形分成面积相等的两个三角形，那么可依据D是BC中点，E是AD中点，求出三角形BED的面积．三角形BDE 中，E到BD的距离就是BD边上的高，有了三角形BDE的面积，BD的长也容易求得．那么高就求出来了．【解答】解：（1）∠BED=∠ABE+∠BAE=75°；（2）CH为所求的高．（3）解：如图，过点E作EF⊥BD于点F，∵AD是BC的中线∴BD=CD=S△ACD==×60=30∴S△ABD=S△ABE==×30=15同理S△BED又∵S=BD•EF=×5EF=15△BED∴EF=6即点E到BC边的距离为6．【点评】本题主要考查了基本作图中，三角形高的作法，三角形的内角和外角等知识点．31．（2015春•单县期末）如图，在△ABC中，AD平分∠BAC，P为线段AD上的一个动点，PE⊥AD交直线BC于点E．（1）若∠B=35°，∠ACB=85°，求∠E的度数；（2）当P点在线段AD上运动时，猜想∠E与∠B、∠ACB的数量关系，写出结论无需证明．【分析】（1）中，首先根据三角形的内角和定理求得∠BAC的度数，再根据角平分线的定义求得∠DAC的度数，从而根据三角形的内角和定理即可求出∠ADC的度数，进一步求得∠E的度数；（2）中，根据第（1）小题的思路即可推导这些角之间的关系．【解答】解：（1）∵∠B=35°，∠ACB=85°，∴∠BAC=60°，∵AD平分∠BAC，∴∠DAC=30°，∴∠ADC=65°，∴∠E=25°；（2）．设∠B=n°，∠ACB=m°，∵AD平分∠BAC，∴∠1=∠2=∠BAC，∵∠B+∠ACB+∠BAC=180°，∵∠B=n°，∠ACB=m°，∴∠CAB=（180﹣n﹣m）°，∴∠BAD=（180﹣n﹣m）°，∴∠3=∠B+∠1=n°+（180﹣n﹣m）°=90°+n°﹣m°，∵PE⊥AD，∴∠DPE=90°，∴∠E=90°﹣（90°+n°﹣m°）=（m﹣n）°=（∠ACB﹣∠B）．【点评】运用了三角形的内角和定理以及角平分线的定义．特别注意第（2）小题，由于∠B和∠ACB的大小不确定，故表达式应写为两种情况．32．（2010春•朝阳区期末）如图所示，在△ABC中，∠B=∠C，FD⊥BC，DE⊥AB，垂足分别为D，E，∠AFD=158°，求∠EDF的度数．【分析】要求∠EDF的度数，只需求出∠BDE和∠FDC的度数即可，由FD⊥BC，得∠FDC=90°；而∠BDE在Rt△BDE中，故只需求出∠B的度数．因∠B=∠C，只需求出∠C的度数即可．因∠AFD是△CDF的外角，∠AFD=158°∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°．【解答】解：∵FD⊥BC，所以∠FDC=90°，∵∠AFD=∠C+∠FDC，∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°，∴∠B=∠C=68°．∵DE⊥AB，∵∠DEB=90°，∴∠BDE=90°﹣∠B=22°．又∵∠BDE+∠EDF+∠FDC=180°，∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°．【点评】考查三角形内角和定理，外角性质，垂直定义等知识．33．（2014春•岱岳区期末）如图，AD平分∠BAC，∠EAD=∠EDA．（1）∠EAC与∠B相等吗？为什么？（2）若∠B=50°，∠CAD：∠E=1：3，求∠E的度数．【分析】（1）由于AD平分∠BAC，根据角平分线的概念可得∠BAD=∠CAD，再根据三角形的一个外角等于和它不相邻的两个内角和，结合已知条件可得∠EAC 与∠B相等；（2）若设∠CAD=x°，则∠E=3x°．根据（1）中的结论以及三角形的内角和定理及其推论列方程进行求解即可．【解答】解：（1）相等．理由如下：∵AD平分∠BAC，∴∠BAD=∠CAD．又∠EAD=∠EDA，∴∠EAC=∠EAD﹣∠CAD=∠EDA﹣∠BAD=∠B；。

中考数学压轴题专项练习：特殊三角形问题（10道）及答案题库：二次函数压轴题-特殊三角形问题1.如图，抛物线y ＝－12x 2＋bx ＋c 与x 轴交于A (－1，0)、B 两点，与y 轴交于点C (0，2)，抛物线的对称轴交x 轴于点D.(1)求抛物线的解析式； (2)求sin ∠ABC 的值；(3)在抛物线的对称轴上是否存在点P ，使△PCD 是以CD 为腰的等腰三角形，如果存在，直接写出点P 的坐标；如果不存在，请说明理由．第1题图解：(1)将点A (－1，0)，C (0，2)代入抛物线y ＝－12x 2＋bx ＋c 中得，－12－b ＋c ＝0c ＝2，解得b ＝32c ＝2，∴抛物线的解析式为y ＝－12x 2＋32x ＋2； (2)令y ＝－12x 2＋32x ＋2＝0，解得x 1＝－1，x 2＝4，∴点B 的坐标为(4，0)，在Rt △BOC 中，BC ＝OC 2＋OB 2＝22＋42＝25，∴sin ∠ABC ＝OC BC ＝225＝55；(3)存在，点P 坐标为(32，52)或(32，－52)或(32，4)．【解法提示】由抛物线y ＝－12x 2＋32x ＋2得对称轴为直线x ＝32，∴点D 的坐标为(32，0)．∴CD ＝OC 2＋OD 2＝22＋（32）2＝52.∵点P 在对称轴x ＝32上，且△PCD 是以CD 为腰的等腰三角形，∴当点D 为顶点时，有DP ＝CD ＝52，此时点P 的坐标为(32，52)或(32，－52)；当点C 为顶点时，如解图，连接CP ，则CP ＝CD ，过点C 作CG ⊥DP 于点G ，则DG ＝PG ，第1题解图∵DG ＝2，∴PG ＝2，PD ＝4，∴点P 的坐标为(32，4)．综上，存在点P 使△PCD 是以CD 为腰的等腰三角形，点P 的坐标为(32，52)或(32，－52)或(32，4)．2. 如图，已知抛物线y ＝ax 2＋bx ＋c (a ≠0)的对称轴为直线x ＝－1，且经过A (1，0)，C (0，3)两点，与x 轴的另一个交点为B .(1)若直线y ＝mx ＋n 经过B ，C 两点，求抛物线和直线BC 的解析式； (2)在抛物线的对称轴x ＝－1上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求点M 的坐标；(3)设点P 为抛物线的对称轴x ＝－1上的一个动点，求使△BPC 为直角三角形的点P 的坐标．第2题图解：(1)由题意得－b2a ＝－1a ＋b ＋c ＝0c ＝3，解得a ＝－1b ＝－2c ＝3，∴抛物线的解析式为y ＝－x 2－2x ＋3.∵对称轴为直线x ＝－1，抛物线经过A (1，0)，∴B (－3，0)．设直线BC 的解析式y ＝mx ＋n ，把B (－3，0)，C (0，3)分别代入y ＝mx ＋n 得－3m ＋n ＝0n ＝3，解得m ＝1n ＝3，∴直线BC 的解析式为y ＝x ＋3； (2)如解图，连接MA ，第2题解图∵MA ＝MB ，∴MA ＋MC ＝MB ＋MC .∴使MA ＋MC 最小的点M 应为直线BC 与对称轴x ＝－1的交点．设直线BC 与对称轴x ＝－1的交点为M ，把x ＝－1代入直线y ＝x ＋3，得y ＝2.∴M (－1，2);(3)设P (－1，t )，∵B (－3，0)，C (0，3)，∴BC 2＝18， PB 2＝(－1＋3)2＋t 2＝4＋t 2， PC 2＝(－1)2＋(t －3)2＝t 2－6t ＋10.①若B 为直角顶点，则BC 2＋PB 2＝PC 2，即18＋4＋t 2＝t 2－6t ＋10，解得t＝－2；②若C 为直角顶点，则BC 2＋PC 2＝PB 2，即18＋t 2－6t ＋10＝4＋t 2，解得t ＝4；③若P 为直角顶点，则PB 2＋PC 2＝BC 2，即： 4＋t 2＋t 2－6t ＋10＝18，解得t 1＝3＋172，t 2＝3－172.综上所述，满足条件的点P 共有四个，分别为：P 1(－1，－2)，P 2(－1，4)，P 3(－1，3＋172)，P 4(－1，3－172)．3.如图，在平面直角坐标系中，抛物线y ＝x 2＋bx ＋c 经过点A (0，－6)和点C (6，0)．(1)求抛物线的解析式；(2)若抛物线与x 轴的负半轴交于点B ，试判断△ABC 的形状；(钝角三角形、直角三角形、锐角三角形)(3)在抛物线上是否存在点P ，使得△P AC 是以AC 为底的等腰三角形？若存在，请求出所有点P 的坐标；若不存在，请说明理由．第3题图解：(1)将C 、A 两点坐标代入y ＝x 2＋bx ＋c ，可得36＋6b ＋c ＝0c ＝－6，解得b ＝－5c ＝－6，∴抛物线的解析式为y ＝x 2－5x －6； (2)当y ＝0时，则有：x 2－5x －6＝0，即(x ＋1)(x －6)＝0，∴解得x 1＝－1，x 2＝6(舍)，∴B (－1，0)．由两点之间的距离公式可得： BC 2＝[(－1)－6]2＝49， AC 2＝(6－0)2＋[0－(－6)]2＝72，AB 2＝(－1－0)2＋[0－(－6)]2＝37，∵AB 2＋BC 2>AC 2，∴△ABC 为锐角三角形．(3)存在满足条件的点P ，使得△P AC 是以AC 为底的等腰三角形理由：如解图，过线段AC 的中点M ，作AC 的垂线交抛物线于点P ，第3题解图直线MP 与抛物线必有两个满足条件的交点P ，∵A (0，－6)，C (6，0)，∴点M 的坐标为(3，－3)，且OA =OC ，∴直线MP 过点O ，设直线MP 的解析式为y ＝kx ，将点M (3，－3)代入得，k ＝－1，即直线MP 的解析式为y ＝－x ，联立y ＝－x y ＝x 2－5x －6，解得x 1＝2－10y 1＝10－2或x 2＝2＋10y 2＝－2－10 ，∴点P 的坐标为(2－10，10－2)或(2＋10，－2－10)．4. 如图，在平面直角坐标系中，直线y ＝－2x ＋10与x 轴，y 轴相交于A ，B 两点，点C 的坐标是(8，4)，连接AC ，BC .(1)求过O ，A ，C 三点的抛物线的解析式，并判断△ABC 的形状；(2)动点P 从点O 出发，沿OB 以每秒2个单位长度的速度向点B 运动，同时，动点Q 从点B 出发，沿BC 以每秒1个单位长度的速度向点C 运动，规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t 秒．当t 为何值时，P A ＝QA?(3)在抛物线的对称轴上，是否存在点M ，使以A ，B ，M 为顶点的三角形是等腰三角形？若存在，求出点M 的坐标；若不存在，请说明理由．第4题图解：(1)∵直线y ＝－2x ＋10与x 轴、y 轴相交于A 、B 两点，∴A (5，0)，B (0，10)，设过O 、A 、C 三点的抛物线的解析式为y ＝ax 2＋bx (a ≠0)，把点A (5，0)和C (8，4)代入可得25a ＋5b ＝064a ＋8b ＝4，解得a ＝16b ＝－56，∴抛物线的解析式为y ＝16x 2－56x ；∵A (5，0)，B (0，10)，C (8，4)，∴AB 2＝125，AC 2＝25，BC 2＝100，∵AB 2＝AC 2＋BC 2，∴△ABC 是直角三角形．(2)如解图，连接AP ，AQ ，当P ，Q 运动t 秒，即OP ＝2t ，CQ ＝10－t ，第4题解图在Rt △AOP 和Rt △ACQ 中，AC ＝OAP A ＝QA，∴Rt △AOP ≌Rt △ACQ ，∴OP ＝CQ ，∴2t ＝10－t ，∴t ＝103，∵t <5，∴当运动时间为103秒时，P A ＝QA ； (3)存在．由题可得，抛物线的对称轴直线为x ＝52，设点M 的坐标为( 52，b )，利用点的坐标可求得 AB 2＝102＋52＝125， MB 2＝(52)2＋(b －10)2， MA 2＝(52)2＋b 2，∵△MAB 是等腰三角形，∴可分以下三种情况讨论：①当AB ＝MA 时，即125＝(52)2＋b 2，解得b ＝±5192，即点M 的坐标为(52，5192)或(52，－5192)；②当AB ＝BM 时，即125＝(52)2＋(b －10)2，解得b ＝10±5192，即点M 的坐标为(52，10＋5192)或(52，10－5192)；③当MB ＝MA 时，即(52)2＋(b －10)2＝(52)2＋b 2，解得b ＝5，此时点A 、M 、B 共线，故这样的点M 不存在．综上所述，存在点M ，使以点A 、B 、M 为顶点的三角形是等腰三角形，点M 的坐标为(52，5192)或(52，－5192)或(52，10＋5192)或(52，10－5192)．5. 如图，抛物线y ＝x 2＋bx ＋c 与x 轴交于A 、B 两点，B 点坐标为(3，0)，与y 轴交于点C (0，3)．(1)求抛物线的解析式；(2)点P 在x 轴下方的抛物线上，过点P 的直线y ＝x ＋m 与直线BC 交于点E ，与y 轴交于点F ，求PE ＋EF 的最大值；(3)点D 为抛物线对称轴上一点，当△BCD 是以BC 为直角边的直角三角形时，求点D 的坐标．解：(1)由题意得32＋3b ＋c ＝0c ＝3，解得b ＝－4c ＝3，∴抛物线的解析式为y ＝x 2－4x ＋3；(2)如解图①，过点P 作PG ∥CF 交CB 与点G ，第5题解图①由题可知，直线BC 的解析式为y ＝－x ＋3，OC ＝OB ＝3，∴∠OCB ＝45°. 同理可知∠OFE ＝45°，∴△CEF 为等腰直角三角形，∵PG ∥CF ，∴△GPE 为等腰直角三角形，∵F(0，m)，C(0，3)，∴CF＝3－m，∵△CEF∽△GEP∴EF＝22CF＝22(3－m), PE＝22PG，设P(t，t2－4t＋3)(1<t<="">2PG＝22(－t＋3－t－m)＝22(－m－2t＋3)，∵点P是直线y＝x＋m与抛物线的交点，∴t2－4t＋3＝t＋m，∴PE＋EF＝22(3－m)＋22(－m－2t＋3)＝22(－2t－2m＋6)＝－2(t＋m－3)＝－2(t2－4t)＝－2(t－2)2＋42，∴当t＝2时，PE＋EF最大，最大值为42；(3)由(1)知对称轴x＝2，设点D(2，n)，如解图②.第5题解图②当△BCD是以BC为直角边的直角三角形时，分两种情况讨论：(ⅰ)D在C上方D1位置时，由勾股定理得CD21＋BC2＝BD21，即(2－0)2＋(n －3)2＋(32)2＝(3－2)2＋(0－n)2 ，解得n＝5；(ⅱ)D 在C 下方D 2位置时，由勾股定理得BD 22＋BC 2＝CD 22，即(2－3)2＋(n －0)2＋(32)2＝(2－0)2＋(n －3)2 ，解得n ＝－1，综上所述，当△BCD 是以BC 为直角边的直角三角形时，D 为(2，5)或(2，－1)．6.如图，抛物线y ＝ax 2－2ax ＋c (a ≠0)与y 轴交于点C (0，4)，与x 轴交于点A 、B ，点A 的坐标为(4，0)．(1)求该抛物线的解析式；(2)抛物线的顶点为N ，在x 轴上找一点K ，使CK ＋KN 的值最小，求出此时点K 的坐标；(3)若平行于x 轴的动直线l 与该抛物线交于点P ，与直线AC 交于点F ，点D 的坐标为(2，0)．问：是否存在这样的直线l ，使得△ODF 是等腰三角形？若存在，请求出点P 的坐标；若不存在，请说明理由．第6题图解：(1)∵抛物线经过点C (0，4)，A (4，0)，∴c=a a c=??-+?41680，解得a=c=?-124，∴抛物线的解析式为y ＝－12x 2＋x ＋4；</t。

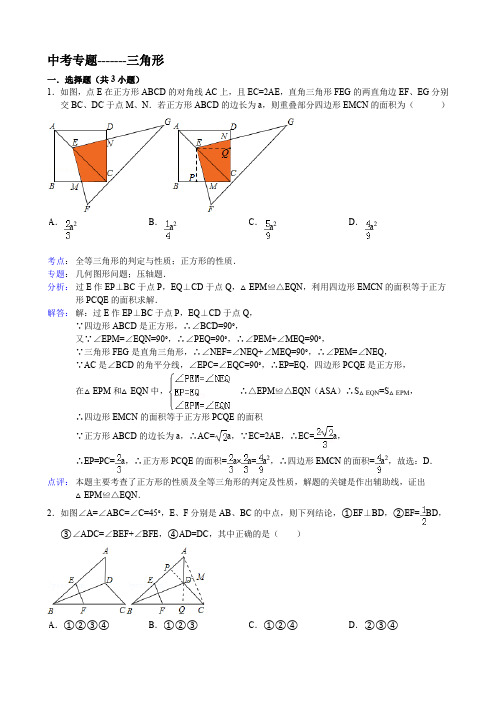
中考专题-------三角形一．选择题（共3小题）1．如图，点E在正方形ABCD的对角线AC上，且EC=2AE，直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N．若正方形ABCD的边长为a，则重叠部分四边形EMCN的面积为（）．a2a2a2a2中，EC=EP=PC=a×a=a a2．如图∠A=∠ABC=∠C=45°，E、F分别是AB、BC的中点，则下列结论，①EF⊥BD，②EF=BD，③∠ADC=∠BEF+∠BFE，④AD=DC，其中正确的是（）EF=ACEF=①AC⊥BD；②BC=DE；③∠DBC=∠DAB；④AB=BE=AE．其中命题一定成立的是（）DAC=4．如图，将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去，结果如下表，则a n=3n+1（用含n的代数式表示）．构成△PAB，△PBC，△PAC均是等腰三角形，则满足上述条件的所有点P的个数为6个．6．如图，△ABC是边长为1的等边三角形，取BC的中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记为S1，取BE的中点E1，作E1D1∥FB，E1F1∥EF．得到四边形E1D1FF1，它的面积记作S2，照此规律，则S2012=．的面积是，求出==×，=×，求出××××，××××××，=×××…××（），∴）=的面积是××=×=，∴=×∴﹣×﹣×××××=×××S××××，×××…××），故答案为：的面积等于．=，即=解得a=．）+，．无需算出算出②．（只填序号）①a2b2+h4=（a2+b2+1）h2；②b4+c2h2=b2c2；③由可以构成三角形；④直角三角形的面积的最大值是．解：根据直角三角形的面积的不同算法，有ch．代入）（（（）+，即（代入）（，∴不能说明（））（ab9．如图，A、B、C分别是线段A1B，B1C，C1A的中点，若△ABC的面积是1，那么△A1B1C1的面积7．10．已知△ABC为等边三角形，点D为直线BC上的一动点（点D不与B、C重合），以AD为边作菱形ADEF（A、D、E、F按逆时针排列），使∠DAF=60°，连接CF．（1）如图1，当点D在边BC上时，求证：①BD=CF；②AC=CF+CD；（2）如图2，当点D在边BC的延长线上且其他条件不变时，结论AC=CF+CD是否成立？若不成立，请写出AC、CF、CD之间存在的数量关系，并说明理由；（3）如图3，当点D在边CB的延长线上且其他条件不变时，补全图形，并直接写出AC、CF、CD之间存在的数量关系．中中11．如图，△ABC中AB=AC，BC=6，，点P从点B出发沿射线BA移动，同时，点Q从点C出发沿线段AC的延长线移动，已知点P、Q移动的速度相同，PQ与直线BC相交于点D．（1）如图①，当点P为AB的中点时，求CD的长；（2）如图②，过点P作直线BC的垂线垂足为E，当点P、Q在移动的过程中，线段BE、DE、CD中是否存在长度保持不变的线段？请说明理由；CFCFFC=CF=右侧作正方形ADEF．（1）如果AB=AC，∠BAC=90°，①当点D在线段BC上时（与点B不重合），如图2，线段CF、BD所在直线的位置关系为垂直，线段CF、BD的数量关系为相等；②当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由；（2）如果AB≠AC，∠BAC是锐角，点D在线段BC上，当∠ACB满足什么条件时，CF⊥BC（点C、F不重合），并说明理由．（1）操作发现如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是DE∥AC；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是S1=S2．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想．（3）拓展探究已知∠ABC=60°，点D是角平分线上一点，BD=CD=4，DE∥AB交BC于点E（如图4）．若在射线BA 上存在点F，使S△DCF=S△BDE，请直接写出相应的BF的长．AC=CD=AC=AB中，∠×，∴△×BE=×÷，∴+的长为．连接MB、ME．（1）如图1，当CB与CE在同一直线上时，求证：MB∥CF；（2）如图1，若CB=a，CE=2a，求BM，ME的长；（3）如图2，当∠BCE=45°时，求证：BM=ME．BM=ME=AG中，AC=CD=BM=DFCG=CF=AG a a AG=DF=×aBM=ME=BE=aDFME=中，中，，∴△BD。

三角形压轴综合问题一、解答题1．（2022·青海·中考真题）两个顶角相等的等腰三角形.如果具有公共的顶角的顶点.并把它们的底角顶点连接起来.则形成一组全等的三角形.把具有这个规律的图形称为“手拉手”图形. (1)问题发现：如图1.若△ABC和△ADE是顶角相等的等腰三角形.BC.DE分别是底边.求证：BD=CE；图1(2)解决问题：如图2.若△ACB和△DCE均为等腰直角三角形.∠ACB=∠DCE=90°.点A.D.E在同一条直线上.CM为△DCE中DE边上的高.连接BE.请判断∠AEB的度数及线段CM.AE.BE之间的数量关系并说明理由.图2【答案】(1)见解析(2)∠DCE=90°；AE=AD+DE=BE+2CM【解析】【分析】（1）先判断出∠BAD=∠CAE.进而利用SAS判断出△BAD∠∠CAE.即可得出结论；（2）同（1）的方法判断出△BAD∠∠CAE.得出AD=BE.∠ADC=∠BEC.最后用角的差.即可得出结论．(1)证明：∠△ABC和△ADE是顶角相等的等腰三角形.∠AB=AC.AD=AE.∠BAC=∠DAE.∠∠BAC−∠CAD=∠DAE−∠CAD.∠∠BAD=∠CAE．在△BAD和△CAE中.{AB=AC∠BAD=∠CAEAD=AE.∠△BAD≌△CAE(SAS).∠BD=CE．(2)解：∠AEB=90°.AE=BE+2CM.理由如下：由（1）的方法得.△ACD≌△BCE.∠AD=BE.∠ADC=∠BEC.∠△CDE是等腰直角三角形.∠∠CDE=∠CED=45°.∠∠ADC=180°−∠CDE=135°.∠∠BEC=∠ADC=135°.∠∠AEB=∠BEC−∠CED=135°−45°=90°．∠CD=CE.CM⊥DE.∠DM=ME．∠∠DCE=90°.∠DM=ME=CM.∠DE=2CM．∠AE=AD+DE=BE+2CM．【点睛】此题是三角形综合题.主要考查了全等三角形的判定和性质.等腰三角形.等边三角形.等腰直角三角形的性质.判断出△ACD∠∠BCE是解本题的关键．2．（2022·辽宁大连·中考真题）综合与实践问题情境：数学活动课上.王老师出示了一个问题：如图1.在△ABC中.D是AB上一点.∠ADC=∠ACB．求证∠ACD=∠ABC．独立思考：（1）请解答王老师提出的问题．实践探究：（2）在原有问题条件不变的情况下.王老师增加下面的条件.并提出新问题.请你解答．“如图2.延长CA至点E.使CE=BD.BE与CD的延长线相交于点F.点G.H分别在BF,BC上.BG=CD.∠BGH=∠BCF．在图中找出与BH相等的线段.并证明．”问题解决：（3）数学活动小组河学时上述问题进行特殊化研究之后发现.当∠BAC=90°时.若给出△ABC 中任意两边长.则图3中所有已经用字母标记的线段长均可求.该小组提出下面的问题.请你解答．“如图3.在（2）的条件下.若∠BAC=90°.AB=4.AC=2.求BH的长．”.【答案】（1）证明见解析；（2）证明见解析；（3）BH=√173【解析】【分析】（1）利用三角形的内角和定理可得答案；（2）如图.在BC上截取BN=CF,证明△CEF≌△BDN,再证明EF=DN,∠EFC=∠DNB,证明△GHB≌△CND,可得BH=DN,从而可得结论；（3）如图.在BC上截取BN=CF,同理可得：BH=DN=EF,利用勾股定理先求解BC=√22+42=2√5,证明△ADC∽△ACB,可得AD=1,CD=√5,可得BG=CD=√5,证明△BGH∽△BCF,可得BF=2BH,而EF=GH,可得BE=3BH,再利用勾股定理求解BE.即可得到答案．【详解】证明：（1）∵∠ADC=∠ACB,∠A=∠A,而∠ACD=180°−∠A−∠ADC,∠ABC=180°−∠A−∠ACB,∴∠ACD=∠ABC,（2）BH=EF,理由如下：如图.在BC上截取BN=CF,∵BD=CE,∠ACD=∠ABC,∴△CEF≌△BDN,∴EF=DN,∠EFC=∠DNB,∵∠BGH=∠BCF.∠GBN=∠FBC,∴∠BHG=∠BFC,∠∠EFC=∠BND,∠∠BFC=∠DNC,∠∠BHG=∠DNC,∠BG=CD,∠△GHB≌△CND,∴BH=DN,∴BH=EF.（3）如图.在BC上截取BN=CF,同理可得：BH=DN=EF,∵AC=2,AB=4,∠BAC=90°,∴BC=√22+42=2√5,∵∠DAC=∠BAC,∠ACD=∠ABC,∴△ADC∽△ACB,∴ADAC =ACAB=CDBC,∴AD2=24=2√5,∴AD=1,CD=√5,∴BG=CD=√5,∵∠GBH=∠FBC,∠BGH=∠BCF,∴△BGH∽△BCF,∴BGBC =GHCF=BHBF=√52√5=12,∴BF=2BH,而EF=GH,∴BE=3BH,∵AB=4,AD=1,BD=CE,∴BD=CE=3,∴AE=3−2=1,而∠BAE=∠BAC=90°,∴BE=√AB2+AE2=√17,∴BH=√17 3.【点睛】本题考查的是三角形的内角和定理的应用.全等三角形的判定与性质.勾股定理的应用.相似三角形的判定与性质.作出适当的辅助线构建全等三角形是解本题的关键．3．（2022·山东青岛·中考真题）【图形定义】有一条高线相等的两个三角形称为等高三角形．例如：如图∠．在△ABC 和△A ′B ′C ′中.AD,A ′D ′分别是BC 和B ′C ′边上的高线.且AD =A ′D ′.则△ABC 和△A ′B ′C ′是等高三角形．【性质探究】如图∠.用S △ABC .S △A ′B ′C ′分别表示△ABC 和△A ′B ′C ′的面积．则S △ABC =12BC ⋅AD,S △A ′B ′C ′=12B ′C ′⋅A ′D ′.∠AD =A ′D ′∠S △ABC :S △A ′B ′C =BC:B ′C ′．【性质应用】(1)如图∠.D 是△ABC 的边BC 上的一点．若BD =3,DC =4.则S △ABD :S △ADC =__________；(2)如图∠.在△ABC 中.D .E 分别是BC 和AB 边上的点．若BE:AB =1:2.CD:BC =1:3.S △ABC =1.则S △BEC =__________.S △CDE =_________；(3)如图∠.在△ABC 中.D .E 分别是BC 和AB 边上的点.若BE:AB =1:m .CD:BC =1:n .S △ABC =a .则S △CDE =__________．【答案】(1)3:4(2)12；16(3)a mn【解析】【分析】（1）由图可知△ABD和△ADC是等高三角形.然后根据等高三角形的性质即可得到答案；（2）根据BE:AB=1:2.S△ABC=1和等高三角形的性质可求得S△BEC.然后根据CD:BC=1:3和等高三角形的性质可求得S△CDE；（3）根据BE:AB=1:m.S△ABC=a和等高三角形的性质可求得S△BEC.然后根据CD:BC=1:n.和等高三角形的性质可求得S△CDE．(1)解：如图.过点A作AE∠BC.则S△ABD=12BD⋅AE.S△ADC=12DC⋅AE∠AE=AE.∠S△ABD:S△ADC=BD:DC=3:4．(2)解：∠△BEC和△ABC是等高三角形.∠S△BEC:S△ABC=BE:AB=1:2.∠S△BEC=12S△ABC=12×1=12；∠△CDE和△BEC是等高三角形.∠S△CDE:S△BEC=CD:BC=1:3.∠S△CDE=13S△BEC=13×12=16．(3)解：∠△BEC和△ABC是等高三角形.∠S△BEC:S△ABC=BE:AB=1:m.∠S△BEC=1m S△ABC=1m×a=am；∠△CDE和△BEC是等高三角形.∠S △CDE :S △BEC =CD:BC =1:n .∠S △CDE =1n S △BEC =1n ×a m =a mn ．【点睛】本题主要考查了等高三角形的定义、性质以及应用性质解题.熟练掌握等高三角形的性质并能灵活运用是解题的关键．4．（2022·山东烟台·中考真题）(1)【问题呈现】如图1.∠ABC 和∠ADE 都是等边三角形.连接BD .CE ．求证：BD ＝CE ．(2)【类比探究】如图2.∠ABC 和∠ADE 都是等腰直角三角形.∠ABC ＝∠ADE ＝90°．连接BD .CE ．请直接写出BD CE 的值．(3)【拓展提升】如图3.∠ABC 和∠ADE 都是直角三角形.∠ABC ＝∠ADE ＝90°.且AB BC ＝AD DE ＝34．连接BD .CE ．∠求BD CE 的值；∠延长CE 交BD 于点F .交AB 于点G ．求sin∠BFC 的值．【答案】(1)见解析(2)√22 (3)∠35；∠45【解析】【分析】（1）证明△BAD ∠∠CAE .从而得出结论；（2）证明△BAD ∠∠CAE .进而得出结果；（3）∠先证明△ABC ∠∠ADE .再证得△CAE ∠∠BAD .进而得出结果；∠在∠的基础上得出∠ACE ＝∠ABD .进而∠BFC ＝∠BAC .进一步得出结果．(1)证明：∠∠ABC和△ADE都是等边三角形.∠AD＝AE.AB＝AC.∠DAE＝∠BAC＝60°.∠∠DAE﹣∠BAE＝∠BAC﹣∠BAE.∠∠BAD＝∠CAE.∠∠BAD∠∠CAE（S A S）.∠BD＝CE；(2)解：∠∠ABC和∠ADE都是等腰直角三角形.∴ABAE =ABAC=√2.∠DAE＝∠BAC＝45°.∠∠DAE﹣∠BAE＝∠BAC﹣∠BAE.∠∠BAD＝∠CAE.∠∠BAD∠∠CAE.∴BDCE =ABAC=√2=√22；(3)解：∠ABAC =ADDE=34.∠ABC＝∠ADE＝90°.∠∠ABC∠∠ADE.∠∠BAC＝∠DAE.ABAC =ADAE=35.∠∠CAE＝∠BAD.∠∠CAE∠∠BAD.∴BDCE =ADAE=35；∠由∠得：∠CAE∠∠BAD.∠∠ACE＝∠ABD.∠∠AGC＝∠BGF.∠∠BFC＝∠BAC.∠sin∠BFC=BCAC =45．【点睛】本题考查了等腰三角形的性质.全等三角形的判定和性质.相似三角形的判定和性质等知识.解决问题的关键是熟练掌握“手拉手”模型及其变形．5．（2022·广西·中考真题）已知∠MON =α.点A .B 分别在射线OM,ON 上运动.AB =6．(1)如图∠.若α=90°.取AB 中点D .点A .B 运动时.点D 也随之运动.点A .B .D 的对应点分别为A′,B′,D′.连接OD,OD′．判断OD 与OD′有什么数量关系?证明你的结论：(2)如图∠.若α=60°.以AB 为斜边在其右侧作等腰直角三角形ABC .求点O 与点C 的最大距离：(3)如图∠.若α=45°.当点A .B 运动到什么位置时.△AOB 的面积最大?请说明理由.并求出△AOB 面积的最大值．【答案】(1)OD =OD ′.证明见解析(2)3√3+3(3)当OA =OB 时.△AOB 的面积最大；理由见解析.△AOB 面积的最大值为9√2+9【解析】【分析】（1）根据“直角三角形斜边中线等于斜边一半”可得OD =12AB .OD ′=12A ′B ′.进而得出结论； （2）作△AOB 的外接圆I .连接CI 并延长.分别交∠I 于O ′和D .当O 运动到O ′时.OC 最大.求出CD 和等边三角形AO ′B 上的高O ′D .进而求得结果；（3）作等腰直角三角形AIB .以I 为圆心.AI 为半径作∠I .取AB 的中点C .连接CI 并延长交∠I 于O .此时△AOB 的面积最大.进一步求得结果．（3）以AB 为斜边在其右侧作等腰直角三角形ABC .连接OC 交AB 于点T .在OT 上取点E .使OE =BE .连接BE .由（2）可知.当OC ⊥AB 时.OC 最大.当OA =OB 时.此时OT 最大.即△AOB 的面积最大.由勾股定理等进行求解即可．(1)解：OD =OD ′.证明如下：∵ ∠AOB =α=90°.AB 中点为D .∴OD =12AB .∵D ′为A ′B ′的中点.∠A ′OB ′=α=90°.∴OD ′=12A ′B ′.∵AB =A ′B ′.∴OD =OD ′；(2)解：如图1.作△AOB 的外接圆I .连接CI 并延长.分别交∠I 于O ′和D .当O 运动到O ′时.OC 最大.此时△AOB 是等边三角形.∠BO ′=AB =6.OC 最大=CO ′=CD +DO ′=12AB +√32BO ′=3+3√3； (3)解：如图2.作等腰直角三角形AIB .以I 为圆心.AI 为半径作∠I .∠AI =√22AB =3√2.∠AOB =12∠AIB ＝45°. 则点O 在∠I 上.取AB 的中点C .连接CI 并延长交∠I 于O .此时△AOB 的面积最大.∠OC =CI +OI =12AB +3√2=3+3√2.∠S△AOB最大=12×6×(3+3√2)=9+9√2．【点睛】本题考查了直角三角形性质.等腰三角形性质.确定圆的条件等知识.解决问题的关键是熟练掌握“定弦对定角”的模型．6．（2022·山东潍坊·中考真题）【情境再现】甲、乙两个含45°角的直角三角尺如图∠放置.甲的直角顶点放在乙斜边上的高的垂足O处.将甲绕点O顺时针旋转一个锐角到图∠位置．小莹用作图软件Geogebra按图∠作出示意图.并连接AG,BH.如图∠所示.AB交HO于E.AC交OG于F.通过证明△OBE≌△OAF.可得OE=OF．请你证明：AG=BH．【迁移应用】延长GA分别交HO,HB所在直线于点P.D.如图∠.猜想并证明DG与BH的位置．．关系．【拓展延伸】小亮将图∠中的甲、乙换成含30°角的直角三角尺如图∠.按图∠作出示意图.并连接HB,AG.如图∠所示.其他条件不变.请你猜想并证明AG与BH的数量．．关系．【答案】证明见解析；垂直；BH=√3AG【解析】【分析】证明△BOH≅△AOG.即可得出结论；通过∠BHO=∠AGO.可以求出∠DGH+∠BHO+∠OHG=90°.得出结论AG⊥BH；证明△BOH∽△AOG.得出AGBH =OAOB=√33.得出结论；【详解】证明：∵AB=AC,AO⊥BC.∴OA=OB,∠AOB=90°.∵∠BOH+∠AOH=90°,∠AOG+∠AOH=90°.∴∠BOH=∠AOG.∵OH=OG.∴△BOH≅△AOG.∴AG=BH；迁移应用：AG⊥BH.证明：∵△BOH≅△AOG.∴∠BHO=∠AGO.∵∠DGH+∠AGO=45°.∴∠DGH+∠BHO=45°.∵∠OHG=45°.∴∠DGH+∠BHO+∠OHG=90°.∴∠HDG=90°.∴AG⊥BH；拓展延伸：BH=√3AG.证明：在Rt△AOB中.tan30°=OAOB =√33.在Rt△HOG中.tan30°=OGOH =√33.∴OAOB =OGOH.由上一问题可知.∠BOH=∠AOG.∴△BOH∽△AOG.∴AGBH =OAOB=√33.∴BH=√3AG．【点睛】本题考查旋转变换.涉及知识点：全等三角形的判定与性质.相似三角形的判定与性质、锐角三角函数、等角的余角相等.解题关键结合图形灵活应用相关的判定与性质．7．（2022·辽宁锦州·中考真题）在△ABC中.AC=BC.点D在线段AB上.连接CD并延长至点E.使DE=CD.过点E作EF⊥AB.交直线AB于点F．(1)如图1.若∠ACB=120°.请用等式表示AC与EF的数量关系：____________．(2)如图2．若∠ACB=90°.完成以下问题：∠当点D.点F位于点A的异侧时.请用等式表示AC,AD,DF之间的数量关系.并说明理由；∠当点D.点F位于点A的同侧时.若DF=1,AD=3.请直接写出AC的长．AC【答案】(1)EF=12(2)∠AD+DF=√2AC；∠4√2或2√2；2【解析】【分析】（1）过点C作CG∠AB于G.先证明∠EDF∠∠CDG.得到EF=CG.然后等腰三角形的性质和含30度直角三角形的性质.即可求出答案；（2）∠过点C作CH∠AB于H.与（1）同理.证明∠EDF∠∠CDH.然后证明△ACH是等腰直角三角形.即可得到结论；∠过点C作CG∠AB于G.与（1）同理.得∠EDF∠∠CDG.然后得到△ACG是等腰直角三角形.利用勾股定理解直角三角形.即可求出答案．(1)解：过点C作CG∠AB于G.如图.∠EF⊥AB.∠∠EFD=∠CGD=90°.∠∠EDF=∠CDG.DE=CD.∠∠EDF∠∠CDG.∠EF=CG；∠在△ABC中.AC=BC.∠ACB=120°.×(180°−120°)=30°.∠∠A=∠B=12AC.∠CG=12AC；∠EF=12AC；故答案为：EF=12(2)解：∠过点C作CH∠AB于H.如图.与（1）同理.可证∠EDF∠∠CDH.∠DF=DH.∠AD+DF=AD+DH=AH.在△ABC中.AC=BC.∠ACB=90°.∠△ABC是等腰直角三角形.∠∠CAH=45°.∠△ACH是等腰直角三角形.∠AH=√2AC.2∠AD+DF=√2AC；2∠如图.过点C作CG∠AB于G.与（1）同理可证.∠EDF∠∠CDG.∠DF=DG=1.∠AD=3.当点F在点A、D之间时.有∠AG=1+3=4.与∠同理.可证△ACG是等腰直角三角形.∠AC=√2AG=4√2；当点D在点A、F之间时.如图：∠AG=AD−DG=3−1=2.与∠同理.可证△ACG是等腰直角三角形.∠AC=√2AG=2√2；综合上述.线段AC的长为4√2或2√2．【点睛】本题考查了等腰直角三角形的判定和性质.全等三角形的判定和性质.勾股定理解直角三角形.三角形的内角和定理.解题的关键是熟练掌握所学的知识.正确的作出辅助线.正确得到三角形全等．8．（2022·北京·中考真题）在△ABC中.∠ACB=90∘.D为△ABC内一点.连接BD.DC.延长DC到点E.使得CE=DC.(1)如图1.延长BC到点F.使得CF=BC.连接AF.EF.若AF⊥EF.求证：BD⊥AF；(2)连接AE.交BD的延长线于点H.连接CH.依题意补全图2.若AB2=AE2+BD2.用等式表示线段CD与CH的数量关系.并证明．【答案】(1)见解析(2)CD=CH；证明见解析【解析】【分析】（1）先利用已知条件证明△FCE≅△BCD(SAS).得出∠CFE=∠CBD.推出EF∥BD.再由AF⊥EF即可证明BD⊥AF；（2）延长BC到点M.使CM＝CB.连接EM.AM.先证△MEC≅△BDC(SAS).推出ME=BD.通过等量代换得到AM2=AE2+ME2.利用平行线的性质得出∠BHE=∠AEM=90°.利用直角三角形斜边中线等于斜边一半即可得到CD=CH．(1)证明：在△FCE和△BCD中.{CE=CD∠FCE=∠BCDCF=CB.∠ △FCE≅△BCD(SAS).∠ ∠CFE=∠CBD.∠ EF∥BD.∠AF⊥EF.∠BD⊥AF．(2)解：补全后的图形如图所示.CD=CH.证明如下：延长BC到点M.使CM＝CB.连接EM.AM.∠∠ACB=90∘.CM＝CB.∠ AC垂直平分BM.∠AB=AM.在△MEC和△BDC中.{CM=CB∠MCE=∠BCDCE=CD.∠ △MEC≅△BDC(SAS).∠ ME=BD.∠CME=∠CBD.∠AB2=AE2+BD2.∠ AM2=AE2+ME2.∠ ∠AEM=90°.∠∠CME=∠CBD.∠ BH∥EM.∠ ∠BHE=∠AEM=90°.即∠DHE=90°.∠CE=CD=12DE.∠ CH=12DE.∠ CD=CH．【点睛】本题考查全等三角形的判定与性质.垂直平分线的性质.平行线的判定与性质.勾股定理的逆用.直角三角形斜边中线的性质等.第二问有一定难度.正确作辅助线.证明∠DHE=90°是解题的关键．9．（2022·福建·中考真题）已知△ABC≌△DEC.AB＝AC.AB＞BC．(1)如图1.CB平分∠ACD.求证：四边形ABDC是菱形；(2)如图2.将（1）中的∠CDE绕点C逆时针旋转（旋转角小于∠BAC）.BC.DE的延长线相交于点F.用等式表示∠ACE与∠EFC之间的数量关系.并证明；(3)如图3.将（1）中的∠CDE绕点C顺时针旋转（旋转角小于∠ABC）.若∠BAD=∠BCD.求∠ADB 的度数．【答案】(1)见解析(2)∠ACE+∠EFC=180°.见解析(3)30°【解析】【分析】（1）先证明四边形ABDC是平行四边形.再根据AB＝AC得出结论；（2）先证出∠ACF=∠CEF.再根据三角形内角和∠CEF+∠ECF+∠EFC=180°.得到∠ACF+∠ECF+∠EFC=180°.等量代换即可得到结论；（3）在AD上取一点M.使得AM＝CB.连接BM.证得△ABM≌△CDB.得到∠MBA=∠BDC.设∠BCD=∠BAD=α.∠BDC=β.则∠ADB=α+β.得到α+β的关系即可．(1)∠△ABC≌△DEC.∠AC＝DC.∠AB＝AC.∠∠ABC＝∠ACB.AB＝DC.∠CB平分∠ACD.∠∠ACB=∠DCB.∠∠ABC=∠DCB.∠AB∥CD.∠四边形ABDC是平行四边形.又∠AB＝AC.∠四边形ABDC是菱形；(2)结论：∠ACE+∠EFC=180°．证明：∠△ABC≌△DEC.∠∠ABC=∠DEC.∠AB＝AC.∠∠ABC=∠ACB.∠∠ACB=∠DEC.∠∠ACB+∠ACF=∠DEC+∠CEF=180°.∠∠ACF=∠CEF.∠∠CEF+∠ECF+∠EFC=180°.∠∠ACF+∠ECF+∠EFC=180°.∠∠ACE+∠EFC=180°；(3)在AD上取一点M.使得AM＝CB.连接BM.∠AB＝CD.∠BAD=∠BCD.∠△ABM≌△CDB.∠BM＝BD.∠MBA=∠BDC.∠∠ADB=∠BMD.∠∠BMD=∠BAD+∠MBA.∠∠ADB=∠BCD+∠BDC.设∠BCD=∠BAD=α.∠BDC=β.则∠ADB=α+β.∠CA＝CD.∠∠CAD=∠CDA=α+2β.∠∠BAC=∠CAD−∠BAD=2β.(180°−∠BAC)=90°−β.∠∠ACB=12∠∠ACD=(90°−β)+α.∠∠ACD+∠CAD+∠CDA=180°.∠(90°−β)+α+2(α+2β)=180°.∠α+β=30°.即∠ADB＝30°．【点睛】本题考查了菱形的判定定理、全等三角形的判定和性质、三角形内角和定理等.灵活运用知识.利用数形结合思想.做出辅助线是解题的关键．10．（2022·山东威海·中考真题）回顾：用数学的思维思考(1)如图1.在∠ABC中.AB＝AC．∠BD.CE是∠ABC的角平分线．求证：BD＝CE．∠点D.E分别是边AC.AB的中点.连接BD.CE．求证：BD＝CE．（从∠∠两题中选择一题加以证明）(2)猜想：用数学的眼光观察经过做题反思.小明同学认为：在∠ABC中.AB＝AC.D为边AC上一动点（不与点A.C重合）．对于点D在边AC上的任意位置.在另一边AB上总能找到一个与其对应的点E.使得BD＝CE．进而提出问题：若点D.E分别运动到边AC.AB的延长线上.BD与CE还相等吗？请解决下面的问题：如图2.在△ABC 中.AB ＝AC .点D .E 分别在边AC .AB 的延长线上.请添加一个条件（不再添加新的字母）.使得BD ＝CE .并证明．(3)探究：用数学的语言表达如图3.在△ABC 中.AB ＝AC ＝2.∠A ＝36°.E 为边AB 上任意一点（不与点A .B 重合）.F 为边AC 延长线上一点．判断BF 与CE 能否相等．若能.求CF 的取值范围；若不能.说明理由．【答案】(1)见解析(2)添加条件CD =BE .见解析(3)能.0＜CF ＜√5−1【解析】【分析】（1）∠利用ASA 证明△ABD ∠∠ACE ．∠利用SAS 证明△ABD ∠∠ACE ．（2）添加条件CD =BE .证明AC +CD =AB +BE .从而利用SAS 证明△ABD ∠∠ACE ．（3）在AC 上取一点D .使得BD =CE .根据BF =CE .得到BD =BF .当BD =BF =BA 时.可证△CBF ∠∠BAF .运用相似性质.求得CF 的长即可．(1)∠如图1.∠AB =AC .∠∠ABC =∠ACB .∠BD .CE 是△ABC 的角平分线.∠∠ABD =12∠ABC .∠ACE =12∠ACB .∠∠ABD=∠ACE.∠AB=AC.∠A=∠A.∠∠ABD∠∠ACE.∠BD=CE．∠如图1.∠AB=AC.点D.E分别是边AC.AB的中点.∠AE=AD.∠AB=AC.∠A=∠A.∠∠ABD∠∠ACE.∠BD=CE．(2)添加条件CD=BE.证明如下：∠AB=AC.CD=BE.∠AC+CD=AB+BE.∠AD=AE.∠AB=AC.∠A=∠A.∠∠ABD∠∠ACE.∠BD=CE．(3)能在AC上取一点D.使得BD=CE.根据BF=CE.得到BD=BF.当BD=BF=BA时.E与A重合.∠∠A＝36°.AB=AC.∠∠ABC=∠ACB=72°.∠A=∠BF A=36°.∠∠ABF=∠BCF=108°.∠BFC=∠AFB.∠△CBF∠∠BAF.∠BF AF =CFBF.∠AB＝AC＝2=BF. 设CF=x.∠2 x+2=x2.整理.得x2+2x−4=0.解得x=√5−1.x=−√5−1（舍去）.故CF= x=√5−1.∠0＜CF＜√5−1．【点睛】本题考查了等腰三角形的性质.三角形全等的判定和性质.三角形相似的判定和性质.一元二次方程的解法.熟练掌握等腰三角形的性质.三角形全等的判定.三角形相似的判定性质是解题的关键．11．（2022·贵州铜仁·中考真题）如图.在四边形ABCD中.对角线AC与BD相交于点O.记△COD的面积为S1.△AOB的面积为S2．（1）问题解决：如图∠.若AB//CD.求证：S1S2=OC⋅ODOA⋅OB（2）探索推广：如图∠.若AB与CD不平行.（1）中的结论是否成立？若成立.请证明；若不成立.请说明理由．（3）拓展应用：如图∠.在OA上取一点E.使OE=OC.过点E作EF∥CD交OD于点F.点H为AB的中点.OH交EF于点G.且OG=2GH.若OEOA =56.求S1S2值．【答案】（1）见解析；（2）（1）中的结论成立.理由见解析：（3）2554【解析】【分析】（1）如图所示.过点D作AE∠AC于E.过点B作BF∠AC于F.求出DE=OD⋅sin∠DOE，BF= OB⋅sin∠BOF.然后根据三角形面积公式求解即可；（2）同（1）求解即可；（3）如图所示.过点A作AM∥EF交OB于M.取BM中点N.连接HN.先证明∠OEF∠∠OCD.得到OD=OF.证明∠OEF∠∠OAM.得到OFOM=OEOA=56.设OE=OC=5m，OF=OD=5n.则OA=6m，OM=6n.证明∠OGF∠∠OHN.推出ON=32OF=15n2.BN=MN=ON−OM=3n2.则OB=ON+BN=9n.由（2）结论求解即可．【详解】解：（1）如图所示.过点D作AE∠AC于E.过点B作BF∠AC于F.∠DE=OD⋅sin∠DOE，BF=OB⋅sin∠BOF.∠S△OCD=S1=12OC⋅DE=12OC⋅OD⋅sin∠DOE.S△AOB=S2=12OA⋅BF=12OA⋅OB⋅sin∠BOF.∠∠DOE=∠BOF.∠sin∠DOE=sin∠BOF；∠S1 S2=12OC⋅OD⋅sin∠DOE12OA⋅OB⋅sin∠BOF=OC⋅ODOA⋅OB；（2）（1）中的结论成立.理由如下：如图所示.过点D作AE∠AC于E.过点B作BF∠AC于F.∠DE=OD⋅sin∠DOE，BF=OB⋅sin∠BOF.∠S△OCD=S1=12OC⋅DE=12OC⋅OD⋅sin∠DOE.S△AOB=S2=12OA⋅BF=12OA⋅OB⋅sin∠BOF.∠∠DOE=∠BOF.∠sin∠DOE=sin∠BOF；∠S1 S2=12OC⋅OD⋅sin∠DOE12OA⋅OB⋅sin∠BOF=OC⋅ODOA⋅OB；（3）如图所示.过点A作AM∥EF交OB于M.取BM中点N.连接HN.∠EF∥CD.∠∠ODC=∠OFE.∠OCD=∠OEF.又∠OE=OC.∠∠OEF∠∠OCD（AAS）.∠OD=OF.∠EF∥AM.∠∠OEF∠∠OAM.∠OF OM=OE OA=56.设OE=OC=5m，OF=OD=5n.则OA=6m，OM=6n.∠H是AB的中点.N是BM的中点.∠HN是∠ABM的中位线.∠HN∥AM∥EF.∠∠OGF∠∠OHN.∠OG OH =OFON.∠OG=2GH.∠OG=23OH.∠OG OH =OF ON=23.∠ON=32OF=15n2.BN=MN=ON−OM=3n2.∠OB=ON+BN=9n.由（2）可知S1S2=OC⋅ODOA⋅OB=5m⋅5n6m⋅9n=2554．【点睛】本题主要考查了解直角三角形.相似三角形的性质与判定.全等三角形的性质与判定.三角形中位线定理.正确作出辅助线是解题的关键．12．（2022·湖北武汉·中考真题）已知CD是△ABC的角平分线.点E.F分别在边AC.BC上.AD= m.BD=n.△ADE与△BDF的面积之和为S．(1)填空：当∠ACB=90°.DE⊥AC.DF⊥BC时.∠如图1.若∠B=45°.m=5√2.则n=_____________.S=_____________；∠如图2.若∠B=60°.m=4√3.则n=_____________.S=_____________；(2)如图3.当∠ACB=∠EDF=90°时.探究S与m、n的数量关系.并说明理由：(3)如图4.当∠ACB=60°.∠EDF=120°.m=6.n=4时.请直接写出S的大小．【答案】(1)∠5√2.25；∠4；8√3(2)S=12mn(3)S=6√3【解析】【分析】（1）∠先证四边形DECF为正方形.再证∠ABC为等腰直角三角形.根据CD平分∠ACB.得出CD∠AB.且AD=BD=m,然后利用三角函数求出BF=BD cos45°=5.DF=BD sin45°=5.AE=AD cos45°=5即可；∠先证四边形DECF为正方形.利用直角三角形两锐角互余求出∠A=90°-∠B=30°.利用30°直角三角形先证求出DE=12AD=12×4√3=2√3.利用三角函数求出AE=ADcos30°=6.DF=DE=2√3.BF=DF tan30°=2.BD=DF÷sin60°=4即可；（2）过点D作DH∠AC于H.DG∠BC于G.在HC上截取HI=BG.连接DI.先证四边形DGCH为正方形.再证∠DFG∠∠DEH（ASA）与∠DBG∠∠DIH（SAS）.然后证明∠IDA=180°-∠A-∠DIH=90°即可；（3）过点D作DP∠AC于P.DQ∠BC于Q.在PC上截取PR=QB.连接DR.过点A作AS∠DR于S.先证明∠DQF∠∠DPE.∠DBQ∠∠DRP.再证∠DBF∠∠DRE.求出∠ADR=∠ADE+∠BDF=180°-∠FDE=60°即可．(1)解：∠∠∠ACB=90°.DE⊥AC.DF⊥BC.CD是△ABC的角平分线.∠四边形DECF为矩形.DE=DF.∠四边形DECF为正方形.∠∠B=45°.∠∠A=90°-∠B=45°=∠B.∠∠ABC为等腰直角三角形.∠CD平分∠ACB.∠CD∠AB.且AD=BD=m,∠m=5√2.∠BD=n=5√2.∠BF=BDcos45°=5.DF=BDsin45°=5.AE=ADcos45°=5.ED=DF=5.∠S= S△ADE+SΔBDF=12×5×5+12×5×5=25；故答案为5√2.25；∠∠∠ACB=90°.DE⊥AC.DF⊥BC.CD是△ABC的角平分线.∠四边形DECF为矩形.DE=DF.∠四边形DECF为正方形.∠∠B=60°.∠∠A=90°-∠B=30°.∠DE=12AD=12×4√3=2√3.AE=AD cos30°=6.DF=DE=2√3.∠∠BDF=90°-∠B=30°.∠BF=DF tan30°=2.∠BD=DF÷sin60°=4.∠BD=n=4.∠S=S△ADE+SΔBDF=12×2√3×6+12×2×2√3=8√3.故答案为：4；8√3；(2)解：过点D作DH∠AC于H.DG∠BC于G.在HC上截取HI=BG.连接DI.∠∠DHC=∠DGC=∠GCH=90°.∠四边形DGCH为矩形.∠CD是△ABC的角平分线.DH∠AC.DG∠BC.∠DG=DH.∠四边形DGCH为正方形.∠∠GDH=90°.∠∠EDF=90°.∠∠FDG+∠GDE=∠GDE+∠EDH=90°.∠∠FDG=∠EDH.在∠DFG和∠DEH中.{∠FDG=∠EDH DG=DH∠DGF=∠DHE.∠∠DFG∠∠DEH（ASA）∠FG=EH.在∠DBG和∠DIH中.{DG=DH∠DGB=∠DHIBG=IH.∠∠DBG∠∠DIH（SAS）.∠∠B=∠DIH.DB=DI=n.∠∠DIH+∠A=∠B+∠A=90°.∠∠IDA=180°-∠A-∠DIH=90°.∠S△ADI=12AD⋅DI=12mn.∠S=S△ADE+SΔBDF=S△ADE+SΔHDI=SΔADI=12mn；(3)过点D作DP∠AC于P.DQ∠BC于Q.在PC上截取PR=QB.连接DR.过点A作AS∠DR于S.∠CD是△ABC的角平分线.DP∠AC.DQ∠BC.∠DP=DQ.∠∠ACB=60°∠∠QDP=120°.∠∠EDF=120°.∠∠FDQ+∠FDP=∠FDP+∠EDP=120°.∠∠FDQ=∠EDP.在∠DFQ和∠DEP中.{∠FDQ=∠EDPDQ=DP∠DQF=∠DPE.∠∠DFQ∠∠DEP（ASA）∠DF=DE.∠QDF=∠PDE.在∠DBQ和∠DRP中.{DQ=DP∠DQB=∠DPRBQ=RP.∠∠DBQ∠∠DRP（SAS）.∠∠BDQ=∠RDP.DB=DR.∠∠BDF=∠BDQ+∠FDQ=∠RDP+∠EDP=∠RDE.∠DB=DE.DB=DR.∠∠DBF∠∠DRE.∠∠ADR=∠ADE+∠BDF=180°-∠FDE=60°.∠S=S△ADR=12AS⋅DR=12ADsin60°×DR=12×6×√32×4=6√3．【点睛】本题考查等腰直角三角形判定与性质.正方形判定与性质.三角形全等判定与性质.直角三角形判定.三角形面积.角平分线性质.解直角三角形.掌握等腰直角三角形判定与性质.正方形判定与性质.三角形全等判定与性质.直角三角形判定.三角形面积.角平分线性质.解直角三角形是解题关键．13．（2022·黑龙江·中考真题）△ABC和△ADE都是等边三角形．(1)将△ADE绕点A旋转到图∠的位置时.连接BD.CE并延长相交于点P（点P与点A重合）.有PA+PB=PC（或PA+PC=PB）成立；请证明．(2)将△ADE绕点A旋转到图∠的位置时.连接BD.CE相交于点P.连接P A.猜想线段P A、PB、PC 之间有怎样的数量关系？并加以证明；(3)将△ADE绕点A旋转到图∠的位置时.连接BD.CE相交于点P.连接P A.猜想线段P A、PB、PC 之间有怎样的数量关系？直接写出结论.不需要证明．【答案】(1)证明见解析(2)图∠结论：PB=PA+PC.证明见解析(3)图∠结论：PA+PB=PC【解析】【分析】（1）由△ABC是等边三角形.得AB=AC.再因为点P与点A重合.所以PB=AB.PC=AC.P A=0.即可得出结论；（2）在BP上截取BF=CP.连接AF.证明△BAD≌△CAE（SAS）.得∠ABD=∠ACE.再证明△CAP≌△BAF（SAS）.得∠CAP=∠BAF.AF=AP.然后证明△AFP是等边三角形.得PF=AP.即可得出结论；（3）在CP上截取CF=BP.连接AF.证明△BAD≌△CAE（SAS）.得∠ABD=∠ACE.再证明△BAP≌△CAF（SAS）.得出∠CAF=∠BAP.AP=AF.然后证明△AFP是等边三角形.得PF=AP.即可得出结论：PA+PB=PF+CF=PC．(1)证明：∠∠ABC是等边三角形.∠AB=AC.∠点P与点A重合.∠PB=AB.PC=AC.P A=0.∠PA+PB=PC或PA+PC=PB；(2)解：图∠结论：PB=PA+PC证明：在BP上截取BF=CP.连接AF.∠△ABC和△ADE都是等边三角形.∠AB=AC.AD=AE.∠BAC=∠DAE=60°∠∠BAC+∠CAD=∠DAE+∠CAD.∠∠BAD=∠CAE.∠△BAD≌△CAE（SAS）.∠∠ABD=∠ACE.∠AC=AB.CP=BF.∠△CAP≌△BAF（SAS）.∠∠CAP=∠BAF.AF=AP.∠∠CAP+∠CAF=∠BAF+∠CAF.∠∠FAP=∠BAC=60°.∠△AFP是等边三角形.∠PF=AP.∠PA+PC=PF+BF=PB；(3)解：图∠结论：PA+PB=PC.理由：在CP上截取CF=BP.连接AF.∠△ABC和△ADE都是等边三角形.∠AB=AC.AD=AE.∠BAC=∠DAE=60°∠∠BAC+∠BAE=∠DAE+∠BAE.∠∠BAD=∠CAE.∠△BAD≌△CAE（SAS）.∠∠ABD=∠ACE.∠AB=AC.BP=CF.∠△BAP≌△CAF（SAS）.∠∠CAF=∠BAP.AP=AF.∠∠BAF+∠BAP=∠BAF+∠CAF.∠∠FAP=∠BAC=60°.∠△AFP是等边三角形.∠PF=AP.∠PA+PB=PF+CF=PC.即PA+PB=PC．【点睛】本题考查等边三角形的判定与性质.全等三角形的判定与性质.熟练掌握等边三角形的判定与性质、全等三角形的判定与性质是解题的关键．14．（2022·陕西·中考真题）问题提出(1)如图1.AD是等边△ABC的中线.点P在AD的延长线上.且AP=AC.则∠APC的度数为__________．问题探究(2)如图2.在△ABC中.CA=CB=6,∠C=120°．过点A作AP∥BC.且AP=BC.过点P作直线l⊥BC.分别交AB、BC于点O、E.求四边形OECA的面积．问题解决(3)如图3.现有一块△ABC型板材.∠ACB为钝角.∠BAC=45°．工人师傅想用这块板材裁出一个△ABP型部件.并要求∠BAP=15°,AP=AC．工人师傅在这块板材上的作法如下：∠以点C为圆心.以CA长为半径画弧.交AB于点D.连接CD；∠作CD的垂直平分线l.与CD于点E；∠以点A为圆心.以AC长为半径画弧.交直线l于点P.连接AP、BP.得△ABP．请问.若按上述作法.裁得的△ABP型部件是否符合要求？请证明你的结论．【答案】(1)75°(2)15√32(3)符合要求.理由见解析【解析】【分析】（1）利用等腰三角形的判定及性质.结合三角形内角和.先求出∠PCD=15°即可；（2）连接BP．先证明出四边形ACBP是菱形．利用菱形的性质得出BP=AC=6.由∠ACB= 120°.得出∠PBE=60°．根据l⊥BC.得BE=PB⋅cos60°=3.PE=PB⋅sin60°=3√3.即可求出S△ABC=1BC⋅PE=9√3.再求出OE=√3.利用S四边形OECA=S△ABC−S△OBE即可求解；2（3）由作法.知AP=AC.根据CD=CA,∠CAB=45°.得出∠ACD=90°．以AC、CD为边.作正方形ACDF.连接PF．得出AF=AC=AP．根据l是CD的垂直平分线.证明出△AFP为等边三角形.即可得出结论．(1)解：∵AC=AP.∴∠ACP=∠APC.∵2(∠ACD+∠PCD)+∠CAP=180°.∴2×(60°+∠PCD)+30°=180°.解得：∠PCD=15°.∴∠ACP=∠ACD+∠PCD=75°.∴∠APC=75°.故答案为：75°；(2)解：如图2.连接BP．图2∠AP∥BC,AP=BC=AC.∠四边形ACBP是菱形．∠BP=AC=6．∠∠ACB=120°.∠∠PBE=60°．∠l⊥BC.∠BE=PB⋅cos60°=3,PE=PB⋅sin60°=3√3．∠S△ABC=12BC⋅PE=9√3．∠∠ABC=30°.∠OE=BE⋅tan30°=√3．∠S△OBE=12BE⋅OE=3√32．∠S四边形OECA =S△ABC−S△OBE=15√32．(3)解：符合要求．由作法.知AP=AC．∠CD=CA,∠CAB=45°.∠∠ACD=90°．如图3.以AC、CD为边.作正方形ACDF.连接PF．图3∠AF=AC=AP．∠l是CD的垂直平分线.∠l是AF的垂直平分线．∠PF=PA．∠△AFP为等边三角形．∠∠FAP=60°.∠∠PAC=30°.∠∠BAP=15°．∠裁得的△ABP型部件符合要求．【点睛】本题考查了等边三角形的性质.等腰三角形的判定及性质、三角形内角和定理、菱形的判定及性质、锐角三角函数、正方形、垂直平分线.解题的关键是要灵活运用以上知识点进行求解.涉及知识点较多.题目较难．15．（2022·湖南岳阳·中考真题）如图.△ABC和△DBE的顶点B重合.∠ABC=∠DBE=90°.∠BAC=∠BDE=30°.BC=3.BE=2．(1)特例发现：如图1.当点D.E分别在AB.BC上时.可以得出结论：ADCE=______.直线AD与直线CE 的位置关系是______；(2)探究证明：如图2.将图1中的△DBE绕点B顺时针旋转.使点D恰好落在线段AC上.连接EC.（1）中的结论是否仍然成立？若成立.请证明；若不成立.请说明理由；(3)拓展运用：如图3.将图1中的△DBE绕点B顺时针旋转α(19°<α<60°).连接AD、EC.它们的延长线交于点F.当DF=BE时.求tan(60°−α)的值．【答案】(1)√3.垂直(2)成立.理由见解析(3)8√5−9√311【解析】【分析】（1）解直角三角形求出EC.AD.可得结论；（2）结论不变.证明△ABD∽△CBE.推出ADEC =ABBC=√3.∠ADB=∠BEC.可得结论；（3）如图3中.过点B作BJ⊥AC于点J.设BD交AK于点K.过点K作KT⊥AC于点K.求出BJ.JK.可得结论．(1)解：在Rt△ABC中.∠B=90°.BC=3.∠A=30°.∠AB=√3BC=3√3.在Rt△BDE中.∠BDE=30°.BE=2.∠BD=√3BE=2√3.∠EC=1.AD=√3.∠ADEC=√3.此时AD⊥EC.故答案为：√3.垂直；(2)结论成立．理由：∠∠ABC=∠DBE=90°.∠∠ABD=∠CBE.∠AB=√3BC.BD=√3BE.∠AC BC =DBEB.∠△ABD∽△CBE.∠AD EC =ABBC=√3.∠ADB=∠BEC.∠∠ADB+∠CDB=180°.∠∠CDB+∠BEC=180°.∠∠DBE+∠DCE=180°.∠∠DBE=90°.∠∠DCE=90°.∠AD⊥EC；(3)如图3中.过点B作BJ⊥AC于点J.设BD交AK于点K.过点K作KT⊥AC于点K．∠∠AJB=90°.∠BAC=30°.∠∠ABJ=60°.∠∠KBJ=60°−α．∠AB=3√3.∠BJ=12AB=3√32.AJ=√3BJ=92.当DF=BE时.四边形BEFD是矩形.∠∠ADB=90°.AD=√AB2−BD2=√(3√3)2−(2√3)2=√15.设KT=m.则AT=√3m.AK=2m.∠∠KTB=∠ADB=90°.∠tanα=KTBT =ADBD.∠m BT =√152√3.∠BT=2√55m.∠√3m+2√55m=3√3.∠m=45−6√1511.∠AK=2m=90−12√1511.∠KJ=AJ−AK=92−90−12√1511=24√15−8122.∠tan(60°−α)=KJBJ =8√5−9√311．【点睛】本题属于三角形综合题.考查了解直角三角形.相似三角形的判定和性质等知识.解题的关键是学会添加常用辅助线.构造直角三角形解决问题.属于中考压轴题．16．（2022·湖北十堰·中考真题）已知∠ABN=90°.在∠ABN内部作等腰△ABC.AB=AC.∠BAC=α(0°<α≤90°)．点D为射线BN上任意一点（与点B不重合）.连接AD.将线段AD绕点A逆时针旋转α得到线段AE.连接EC并延长交射线BN于点F．(1)如图1.当α=90°时.线段BF与CF的数量关系是_________；(2)如图2.当0°<α<90°时.（1）中的结论是否还成立？若成立.请给予证明；若不成立.请说明理由；(3)若α=60°.AB=4√3.BD=m.过点E作EP⊥BN.垂足为P.请直接写出PD的长（用含有m的式子表示）．【答案】(1)BF=CF(2)成立；理由见解析(3)PD=6−m2或PD=0或PD=m2−6【解析】【分析】（1）连接AF.先根据“SAS”证明ΔACE≌ΔABD.得出∠ACE=∠ABD=90°.再证明Rt△ABF≌Rt△ACF.即可得出结论；（2）连接AF.先说明∠EAC=∠BAD.然后根据“SAS”证明ΔACE≌ΔABD.得出∠ACE=∠ABD= 90°.再证明Rt△ABF≌Rt△ACF.即可得出结论；（3）先根据α=60°.AB=AC.得出∠ABC为等边三角形.再按照∠BAD＜60°.∠BAD=60°.∠BAD＞60°三种情况进行讨论.得出结果即可．(1)解：BF=CF；理由如下：连接AF.如图所示：。

2020年中考九年级数学第二轮压轴题复习：解直角三角形1、如图，为测量一座山峰CF的高度，将此山的某侧山坡划分为AB和BC两段，每一段山坡近似是“直”的，测得坡长AB=800米，BC=200米，坡角∠BAF=30°，∠CBE=45°．（1）求AB段山坡的高度EF；（2）求山峰的高度CF．（ 1.414，CF结果精确到米）2、如图，河的两岸l1与l2相互平行，A、B是l1上的两点，C、D是l2上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进20米到达点E （点E在线段AB上），测得∠DEB=60°，求C、D两点间的距离．3、某兴趣小组借助无人飞机航拍校园．如图，无人飞机从A处水平飞行至B处需8秒，在地面C处同一方向上分别测得A处的仰角为75°，B处的仰角为30°．已知无人飞机的飞行速度为4米/秒，求这架无人飞机的飞行高度．（结果保留根号）4、如图，某飞机于空中A处探测到目标C，此时飞行高度AC=1200m，从飞机上看地平面指挥台B的俯角α=43°，求飞机A与指挥台B的距离（结果取整数）（参考数据：sin43°=0.68，cos43°=0.73，tan43°=0.93）5、某中学九年级数学兴趣小组想测量建筑物AB的高度．他们在C处仰望建筑物顶端，测得仰角为48°，再往建筑物的方向前进6米到达D处，测得仰角为64°，求建筑物的高度．（测角器的高度忽略不计，结果精确到0.1米）（参考数据：sin48°≈，tan48°≈，sin64°≈，tan64°≈2）6、在一次课外实践活动中，同学们要测量某公园人工湖两侧A，B两个凉亭之间的距离．如图，现测得∠ABC=30°，∠CBA=15°，AC=200米，请计算A，B两个凉亭之间的距离（结果精确到1米）（参考数据：≈1.414，≈1.732）7、为有效开发海洋资源，保护海洋权益，我国对南海诸岛进行了全面调查，一测量船在A岛测得B岛在北偏西30°，C岛在北偏东15°，航行100海里到达B岛，在B岛测得C岛在北偏东45°，求B，C两岛及A，C两岛的距离（≈2.45，结果保留到整数）8、如图，AB是长为10m，倾斜角为37°的自动扶梯，平台BD与大楼CE垂直，且与扶梯AB的长度相等，在B处测得大楼顶部C的仰角为65°，求大楼CE的高度（结果保留整数）．（参考数据：sin37°≈，tan37°≈，sin65°≈，tan65°≈）9、某市为了打造森林城市，树立城市新地标，实现绿色、共享发展理念，在城南建起了“望月阁”及环阁公园．小亮、小芳等同学想用一些测量工具和所学的几何知识测量“望月阁”的高度，来检验自己掌握知识和运用知识的能力．他们经过观察发现，观测点与“望月阁”底部间的距离不易测得，因此经过研究需要两次测量，于是他们首先用平面镜进行测量．方法如下：如图，小芳在小亮和“望月阁”之间的直线BM上平放一平面镜，在镜面上做了一个标记，这个标记在直线BM上的对应位置为点C，镜子不动，小亮看着镜面上的标记，他来回走动，走到点D时，看到“望月阁”顶端点A在镜面中的像与镜面上的标记重合，这时，测得小亮眼睛与地面的高度ED=1.5米，CD=2米，然后，在阳光下，他们用测影长的方法进行了第二次测量，方法如下：如图，小亮从D点沿DM方向走了16米，到达“望月阁”影子的末端F点处，此时，测得小亮身高FG的影长FH=2.5米，FG=1.65米．如图，已知AB⊥BM，ED⊥BM，GF⊥BM，其中，测量时所使用的平面镜的厚度忽略不计，请你根据题中提供的相关信息，求出“望月阁”的高AB的长度．10、“蘑菇石”是我省著名自然保护区梵净山的标志，小明从山脚B点先乘坐缆车到达观景平台DE观景，然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点，“蘑菇石”A点到水平面BC的垂直距离为1790m．如图，DE∥BC，BD=1700m，∠DBC=80°，求斜坡A E的长度．（结果精确到0.1m）11、为了维护海洋权益，新组建的国家海洋局加大了在南海的巡逻力度。

20XX年复习资料教学复习资料班级：科目：2021年中考数学压轴题专项训练《三角形》1．已知，△ABC是等边三角形，过点C作CD∥AB，且CD＝AB，连接BD交AC于点O．（1）如图1，求证：AC垂直平分BD；（2）如图2，点M在BC的延长线上，点N在线段CO上，且ND＝NM，连接BN．求证：NB ＝NM．（1）证明：∵△ABC是等边三角形，∴∠ABC＝∠ACB＝∠CAB＝60°，∵CD∥AB，且CD＝AB，∴CD＝CA＝BC，∠ACD＝∠ACB＝60°，∴BO＝DO，CO⊥BD，∴AC垂直平分BD；（2）由（1）知AC垂直平分BD，∴NB＝ND，∵ND＝NM，∴NB＝NM．2．等腰Rt△ABC，点D为斜边AB上的中点，点E在线段BD上，连结CD，CE，作AH⊥CE，垂足为H，交CD于点G，AH的延长线交BC于点F．（1）求证：△ADG≌△CDE．（2）若点H恰好为CE的中点，求证：∠CGF＝∠CFG．证明：（1）在等腰Rt△ABC中，∵点D为斜边AB上的中点，∴CD＝AB，CD⊥AB，∵AD＝AB，∴AD＝CD，∵CD⊥AB，∴∠ADG＝∠CDE＝90°，∵AH⊥CE，∴∠CGH+∠GCH＝90°，∵∠AGD+∠GAD＝90°，又∵∠AGD＝∠CGH，∴∠GAD＝∠GCH，在△△ADG和△CDE中∵∠ADG＝∠CDE＝90°，AD＝CD，∠GAD＝∠GCH∴△ADG≌△CDE（ASA），（2）∵AH⊥CE，点H为CE的中点，∴AC＝AE，∴∠CAH＝∠EAH，∵∠CAH+∠AFC＝90°，∠EAH+∠AGD＝90°，∴∠AFC＝∠AGD，∵∠AGD＝∠CGH，∴∠AFC＝∠CGH，即∠CGF＝∠CFG．3．如图，在△ABC中，AD⊥BC且BD＝DE，EF垂直平分AC，交AC于点F，交BC于点E．（1）若∠BAE＝32°，求∠C的度数；（2）若AC＝6cm，DC＝5cm，求△ABC的周长．解：（1）∵AD⊥BC，BD＝DE，EF垂直平分AC∴AB＝AE＝EC∴∠C＝∠CAE，∵∠BAE＝32°∴∠AED＝（180°﹣32°）＝74°；∴∠C＝∠AED＝37°；（2）由（1）知：AE＝EC＝AB，∵BD＝DE，∴AB+BD＝EC+DE＝DC，∴△ABC的周长＝AB+BC+AC，＝AB+BD+DC+AC，＝2DC+AC＝2×5+6＝16（cm）．4．如图，在△ABC中，∠BAC和∠ABC的平分线相交于点O，过点O作EF∥AB交BC于F，交AC于E，过点O作OD⊥BC于D．（1）求证：∠AOB＝90°+∠C；（2）求证：AE+BF＝EF；（3）若OD＝a，CE+CF＝2b，请用含a，b的代数式表示△CEF的面积，S△CEF＝ab（直接写出结果）．证明：（1）∵OA，OB平分∠BAC和∠ABC，∴，，∴∠AOB＝180°﹣∠OAB﹣∠OBA＝＝＝＝（2）∵EF∥AB，∴∠OAB＝∠AOE，∠ABO＝∠BOF又∠OAB＝∠EAO，∠OBA＝∠OBF，∴∠AOE＝∠EAO，∠BOF＝∠OBF，∴AE＝OE，BF＝OF，∴EF＝OE+OF＝AE+BF；（3）∵点O在∠ACB的平分线上，∴点O到AC的距离等于OD，∴S△CEF＝（CE+CF）•OD＝•2b•a＝ab，故答案为：ab．5．如图，在△ABC中，AB＝AC，AD为BC边上的中线，DE⊥AB于点E．（1）求证：BD•AD＝DE•AC．（2）若AB＝13，BC＝10，求线段DE的长．（3）在（2）的条件下，求cos∠BDE的值．证明：（1）∵AB＝AC，BD＝CD，∴AD⊥BC，∠B＝∠C，∵DE⊥AB，∴∠DEB＝∠ADC，∴△BDE∽△CAD．∴，∴BA•AD＝DE•CA；（2）∵AB＝AC，BD＝CD，∴AD⊥BC，在Rt△ADB中，AD＝＝＝12，∵•AD•BD＝•AB•DE，∴DE＝．（3）∵∠ADB＝∠AED＝90°，∴∠BDE＝∠BAD，∴cos∠BDE＝cos∠BAD＝．6．如图，在△ABC中，AB＝AC，以AB为直径作半圆O，交BC于点D，交AC于点E．（1）求证：BD＝CD．（2）若弧DE＝50°，求∠C的度数．（3）过点D作DF⊥AB于点F，若BC＝8，AF＝3BF，求弧BD的长．（1）证明：如图，连接AD．∵AB是圆O的直径，∴AD⊥BD．又∵AB＝AC，∴BD＝CD．（2）解：∵弧DE＝50°，∴∠EOD＝50°．∴∠DAE＝∠DOE＝25°．∵由（1）知，AD⊥BD，则∠ADB＝90°，∴∠ABD＝90°﹣25°＝65°．∵AB＝AC，∴∠C＝∠ABD＝65°．（3）∵BC＝8，BD＝CD，∴BD＝4．设半径OD＝x．则AB＝2x．由AF＝3BF可得AF＝AB＝x，BF＝AB＝x，∵AD⊥BD，DF⊥AB，∴BD2＝BF•AB，即42＝x•2x．解得x＝4．∴OB＝OD＝BD＝4，∴△OBD是等边三角形，∴∠BOD＝60°．∴弧BD的长是：＝．7．阅读下面材料：数学课上，老师给出了如下问题：如图，AD为△ABC中线，点E在AC上，BE交AD于点F，AE＝EF．求证：AC＝BF．经过讨论，同学们得到以下两种思路：思路一如图①，添加辅助线后依据SAS可证得△ADC≌△GDB，再利用AE＝EF可以进一步证得∠G＝∠FAE＝∠AFE＝∠BFG，从而证明结论．思路二如图②，添加辅助线后并利用AE＝EF可证得∠G＝∠BFG＝∠AFE＝∠FAE，再依据AAS可以进一步证得△ADC≌△GDB，从而证明结论．完成下面问题：（1）①思路一的辅助线的作法是：延长AD至点G，使DG＝AD，连接BG；②思路二的辅助线的作法是：作BG＝BF交AD的延长线于点G．（2）请你给出一种不同于以上两种思路的证明方法（要求：只写出辅助线的作法，并画出相应的图形，不需要写出证明过程）．解：（1）①延长AD至点G，使DG＝AD，连接BG，如图①，理由如下：∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，，∴△ADC≌△GDB（SAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EFA，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．故答案为：延长AD至点G，使DG＝AD，连接BG；②作BG＝BF交AD的延长线于点G，如图②．理由如下：∵BG＝BF，∴∠G＝∠BFG，∵AE＝EF，∴∠EAF＝∠EFA，∵∠EFA＝∠BFG，∴∠G＝∠EAF，在△ADC和△GDB中，，∴△A DC≌△GDB（AAS），∴AC＝BG，∴AC＝BF；故答案为：作BG＝BF交AD的延长线于点G；（2）作BG∥AC交AD的延长线于G，如图③所示：则∠G＝∠CAD，∵AD为△ABC中线，∴BD＝CD，在△ADC和△GDB中，，∴△ADC≌△GDB（AAS），∴AC＝BG，∵AE＝EF，∴∠CAD＝∠EFA，∵∠BFG＝∠G，∠G＝∠CAD，∴∠G＝∠BFG，∴BG＝BF，∴AC＝BF．8．如图1，直线AB分别与x轴、y轴交于A、B两点，OC平分∠AOB交AB于点C，点D为线段AB上一点，过点D作DE∥OC交y轴于点E，已知AO＝m，BO＝n，且m、n满足n2﹣8n+16+|n﹣2m|＝0．（1）求A、B两点的坐标；（2）若点D为AB中点，求OE的长；（3）如图2，若点P（x，﹣2x+4）为直线AB在x轴下方的一点，点E是y轴的正半轴上一动点，以E为直角顶点作等腰直角△PEF，使点F在第一象限，且F点的横、纵坐标始终相等，求点P的坐标．解：（1）∵n2﹣8n+16+|n﹣2m|＝0，∴（n﹣4）2+|n﹣2m|＝0，∵（n﹣4）2≥0，|n﹣2m|≥0，∴（n﹣4）2＝0，|n﹣2m|＝0，∴m＝2，n＝4，∴点A为（2，0），点B为（0，4）；（2）延长DE交x轴于点F，延长FD到点G，使得DG＝DF，连接BG，设OE＝x，∵OC平分∠AOB，∴∠BOC＝∠AOC＝45°，∵DE∥OC，∴∠EFO＝∠FEO＝∠BEG＝∠BOC＝∠AOC＝45°，∴OE＝OF＝x，在△ADF和△BDG中，，∴△ADF≌△BDG（SAS），∴BG＝AF＝2+x，∠G＝∠AFE＝45°，∴∠G＝∠BEG＝45°，∴BG＝BE＝4﹣x，∴4﹣x＝2+x，解得：x＝1，∴OE＝1；（3）如图2，分别过点F、P作FM⊥y轴于点M，PN⊥y轴于点N，设点E为（0，m），∵点P的坐标为（x，﹣2x+4），∴PN＝x，EN＝m+2x﹣4，∵∠PEF＝90°，∴∠PEN+∠FEM＝90°，∵FM⊥y轴，∴∠MFE+∠FEM＝90°，∴∠PEN＝∠MFE，在△EFM和△PEN中，，∴△EFM≌△PEN（AAS），∴ME＝NP＝x，FM＝EN＝m+2x﹣4，∴点F为（m+2x﹣4，m+x），∵F点的横坐标与纵坐标相等，∴m+2x﹣4＝m+x，解得：x＝4，∴点P为（4，﹣4）．9．在等边△ABC中，线段AM为BC边上的中线．动点D在直线AM上时，以CD为一边在CD 的下方作等边△CDE，连结BE．（1）若点D在线段AM上时（如图1），则AD＝BE（填“＞”、“＜”或“＝”），∠CAM ＝30 度；（2）设直线BE与直线AM的交点为O．①当动点D在线段AM的延长线上时（如图2），试判断AD与BE的数量关系，并说明理由；②当动点D在直线AM上时，试判断∠AOB是否为定值？若是，请直接写出∠AOB的度数；若不是，请说明理由．解：（1））∵△ABC与△DEC都是等边三角形∴AC＝BC，CD＝CE，∠ACB＝∠DC E＝60°∴∠ACD+∠DCB＝∠DCB+∠BCE∴∠ACD＝∠BCE．在△ADC和△BEC中，∴△ACD≌△BCE（SAS），∴AD＝BE；∵△ABC是等边三角形，∴∠BAC＝60°．∵线段AM为BC边上的中线∴∠CAM＝∠BAC，∴∠CAM＝30°．故答案为：＝，30；（2）①AD＝BE，理由如下：∵△ABC和△CDE都是等边三角形∴AB＝BC，DC＝EC，∠ACB＝∠DCE＝60°，∵∠ACD＝∠ACB﹣∠DCB，∠BCE＝∠DCE﹣∠DCB，∴∠ACD＝∠BCE，∴△ACD≌△BCE（SAS）∴AD＝BE．②∠AOB是定值，∠AOB＝60°，理由如下：当点D在线段AM上时，如图1，由①知△ACD≌△BCE，则∠CBE＝∠CAD＝30°，又∠ABC＝60°，∴∠CBE+∠ABC＝60°+30°＝90°，∵△ABC是等边三角形，线段AM为BC边上的中线∴AM平分∠BAC，即，∴∠BOA＝90°﹣30°＝60°．当点D在线段AM的延长线上时，如图2，∵△ABC与△DEC都是等边三角形∴AC＝BC，CD＝CE，∠ACB＝∠DCE＝60°∴∠ACB+∠DCB＝∠DCB+∠DCE∴∠ACD＝∠BCE在△ACD和△BCE中，∴△ACD≌△BCE（SAS）∴∠CBE＝∠CAD＝30°，同理可得：∠BAM＝30°，∴∠BOA＝90°﹣30°＝60°．10．数学课上，王老师出示了如下框中的题目．小明与同桌小聪讨论后，进行了如下解答：（1）特殊情况•探索结论：在等边三角形ABC中，当点E为AB的中点时，点D在CB点延长线上，且ED＝EC；如图1，确定线段AE与DB的大小关系．请你直接写出结论AE ＝DB；（2）特例启发，解答题目王老师给出的题目中，AE与DB的大小关系是：AE＝DB．理由如下：如图2，过点E作EF∥BC，交AC于点F，（请你完成以下解答过程）（3）拓展结论，设计新题在△ABC中，AB＝BC＝AC＝1；点E在AB的延长线上，AE＝2；点D在CB的延长线上，ED ＝EC，如图3，请直接写CD的长1或3 ．解：（1）如图1，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠AFE＝∠ACB＝∠ABC＝60°，△AEF为等边三角形，∴∠EFC＝∠EBD＝120°，EF＝AE，∵ED＝EC，∴∠EDB＝∠ECB，∠ECB＝∠FEC，∴∠EDB＝∠FEC，在△BDE和△FEC中，，∴△BDE≌△FEC（AAS），∴BD＝EF，∴AE＝BD，故答案为：＝；（2）解答过程如下：如图2，过点E作EF∥BC，交AC于点F，∵△ABC为等边三角形，∴∠AFE＝∠ACB＝∠ABC＝60°，△AEF为等边三角形，∴∠EFC＝∠EBD＝120°，EF＝AE，∵ED＝EC，∴∠EDB＝∠ECB，∠ECB＝∠FEC，∴∠EDB＝∠FEC，在△BDE和△FEC中，∴△BDE≌△FEC（AAS），∴BD＝EF，∴AE＝BD．故答案为：AE＝DB．（3）解：分为四种情况：如图3，∵AB＝AC＝1，AE＝2，∴B是AE的中点，∵△ABC是等边三角形，∴AB＝AC＝BC＝1，△ACE是直角三角形（根据直角三角形斜边的中线等于斜边的一半），∴∠ACE＝90°，∠AEC＝30°，∴∠D＝∠ECB＝∠BEC＝30°，∠DBE＝∠ABC＝60°，∴∠DEB＝180°﹣30°﹣60°＝90°，即△DEB是直角三角形．∴BD＝2BE＝2（30°所对的直角边等于斜边的一半），即CD＝1+2＝3．如图4，过A作AN⊥BC于N，过E作EM⊥CD于M，∵等边三角形ABC，EC＝ED，∴BN＝CN＝BC＝，CM＝MD＝CD，AN∥EM，∴△BAN∽△BEM，∴，∵△ABC边长是1，AE＝2，∴，∴MN＝1，∴CM＝MN﹣CN＝1﹣＝，∴CD＝2CM＝1；如图5，∵∠ECD＞∠EBC（∠EBC＝120°），而∠ECD不能大于120°，否则△EDC不符合三角形内角和定理，∴此时不存在EC＝ED；如图6，∵∠EDC＜∠ABC，∠ECB＞∠ACB，又∵∠ABC＝∠ACB＝60°，∴∠ECD＞∠EDC，即此时ED≠EC，∴此时情况不存在，答：CD的长是3或1．故答案为：1或3．11．定义：如果一个三角形的一个内角等于另一个内角的两倍，则称这样的三角形为“倍角三角形”．（1）如图1，△ABC中，AB＝AC，∠A＝36°，求证：△ABC是倍角三角形；（2）若△ABC是倍角三角形，∠A＞∠B＞∠C，∠B＝30°，AC＝，求△ABC面积；（3）如图2，△ABC的外角平分线AD与CB的延长线相交于点D，延长CA到点E，使得AE＝AB，若AB+AC＝BD，请你找出图中的倍角三角形，并进行证明．（1）证明：∵AB＝AC，∴∠B＝∠C，∵∠A+∠B+∠C＝180°，∠A＝36°，∴∠B＝∠C＝72°，∴∠A＝2∠C，即△ABC是倍角三角形，（2）解：∵∠A＞∠B＞∠C，∠B＝30°，①当∠B＝2∠C，得∠C＝15°，过C作CH⊥直线AB，垂足为H，可得∠CAH＝45°，∴AH＝CH＝AC＝4．∴BH＝，∴AB＝BH﹣AH＝﹣4，∴S＝．②当∠A＝2∠B或∠A＝2∠C时，与∠A＞∠B＞∠C矛盾，故不存在．综上所述，△ABC面积为．（3）∵AD平分∠BAE，∴∠BAD＝∠EAD，∵AB＝AE，AD＝AD，∴△ABD≌△AED（SAS），∴∠ADE＝∠ADB，BD＝DE．又∵AB+AC＝BD，∴AE+AC＝BD，即CE＝BD．∴CE＝DE．∴∠C＝∠BDE＝2∠ADC．∴△ADC是倍角三角形．12．如图，在平面直角坐标系中，OA＝OB，AC＝CD，已知两点A（4，0），C（0，7），点D 在第一象限内，∠DCA＝90°，点B在线段OC上，AB的延长线与DC的延长线交于点M，AC与BD交于点N．（1）点B的坐标为：（0，4）；（2）求点D的坐标；（3）求证：CM＝CN．解：（1）∵A（4，0），∴OA＝OB＝4，∴B（0，4），故答案为：（0，4）．（2）∵C（0，7），∴OC＝7，过点D作DE⊥y轴，垂足为E，∴∠DEC＝∠AOC＝90°，∵∠DCA＝90°，∴∠ECD+∠BCA＝∠ECD+∠EDC＝90°∴∠BCA＝∠EDC，∴△DEC≌△COA（AAS），∴DE＝OC＝7，EC＝OA＝4，∴OE＝OC+EC＝11，∴D（7，11）；（3）证明：∵BE＝OE﹣OB＝11﹣4＝7 ∴BE＝DE，∴△DBE是等腰直角三角形，∴∠DBE＝45°，∵OA＝OB，∴∠OBA＝45°，∴∠DBA＝90°，∴∠BAN+∠ANB＝90°，∵∠DCA＝90°，∴∠CDN+∠DNC＝90°，∵∠DNC＝∠ANB，∴∠CDN＝∠BAN，∵∠DCA＝90°，∴∠ACM＝∠DCN＝90°，∴△DCN≌△ACM（ASA），∴CM＝CN．13．如图，在△ABC中，BD⊥AC，垂足为C，且∠A＜∠C，点E是一动点，其在BC上移动，连接DE，并过点E作EF⊥DE，点F在AB的延长线上，连接DF交BC于点G．（1）请同学们根据以上提示，在上图基础上补全示意图．（2）当△ABD与△FDE全等，且AD＝FE，∠A＝30°，∠AFD＝40°，求∠C的度数．解：（1）补全示意图如图所示，（2）∵DE⊥EF，BD⊥AC，∴∠DEF＝∠ADB＝90°．∵△ABD与△DEF全等，∴AB＝DF，又∵AD＝FE，∴∠ABD＝∠FDE，∴BD＝DE．在Rt△ABD中，∠ABD＝90°﹣∠A＝60°．∴∠FDE＝60°．∵∠ABD＝∠BDF+∠AFD，∵∠AFD＝40°，∴∠BDF＝20°．∴∠BDE＝∠BDF+∠FDE＝20°+60°＝80°．∵BD＝DE，∴∠DBE＝∠BED＝（180°﹣∠BDE）＝50°．在Rt△BDC中，∠C＝90°﹣∠DBE＝90°﹣50°＝40°．14．如图．CP是等边△ABC的外角∠ACE的平分线，点D在边BC上，以D为顶点，DA为一条边作∠ADF＝60°，另一边交射线CP于F．（1）求证．AD＝FD；（2）若AB＝2，BD＝x，DF＝y，求y关于x的函数解析式；（3）联结AF，当△ADF的面积为时，求BD的长．证明：（1）如图1，连接AF，∵∠ACB＝60°，∴∠ACE＝120°，∵CP平分∠ACE，∴∠ACP＝∠PCE＝60°，∴∠ADF＝∠ACP＝60°，∴A、D、C、F四点共圆，∴∠AFD＝∠ACB＝60°，∴∠ADF＝∠AFD＝60°，∴∠DAF＝60°，∴△ADF是等边三角形，∴AD＝FD；（2）如图2，过点A作AH⊥BC，∵△ABC是等边三角形，AH⊥BC，AB＝2，∴BH＝1，AH＝BH＝，∴HD＝BD﹣BH＝x﹣1，∵DF＝＝，∴y＝（3）∵△ADF是等边三角形，且△ADF的面积为，∴DF2＝，∴DF2＝＝x2﹣2x+4∴x＝∴BD＝或15．如图，△ABC是等边三角形，D是BC边的中点，以D为顶点作一个120°的角，角的两边分别交直线AB、直线AC于M、N两点．以点D为中心旋转∠MDN（∠MDN的度数不变），当DM与AB垂直时（如图①所示），易证BM+CN＝BD．（1）如图②，当DM与AB不垂直，点M在边AB上，点N在边AC上时，BM+CN＝BD是否仍然成立？若成立，请给予证明；若不成立，请说明理由；（2）如图③，当DM与AB不垂直，点M在边AB上，点N在边AC的延长线上时，BM+CN ＝BD是否仍然成立？若不成立，请写出BM，CN，BD之间的数量关系，不用证明．解：（1）结论BM+CN＝BD成立，理由如下：如图②，过点D作DE∥AC交AB于E，∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∵DE∥AC，∴∠BED＝∠A＝60°，∠BDE＝∠C＝60°，∴∠B＝∠BED＝∠BDE＝60°，∴△BDE是等边三角形，∠EDC＝120°，∴BD＝BE＝DE，∠EDN+∠CDN＝120°，∵∠EDM+∠EDN＝∠MDN＝120°，∴∠CDN＝∠EDM，∵D是BC边的中点，∴DE＝BD＝CD，在△CDN和△EDM中，，∴△CDN≌△EDM（ASA），∴CN＝EM，∴BD＝BE＝BM+EM＝BM+CN；（2）上述结论不成立，BM，CN，BD之间的数量关系为：BM﹣CN＝BD；理由如下：如图③，过点D作DE∥AC交AB于E，∵△ABC是等边三角形，∴∠A＝∠B＝∠C＝60°，∴∠NCD＝120°，∵DE∥AC，∴∠BED＝∠A＝60°，∠BDE＝∠C＝60°，∴∠B＝∠BED＝∠BDE＝60°，∴△BDE是等边三角形，∠MED＝∠EDC＝120°，∴BD＝BE＝DE，∠NCD＝∠MED，∠EDM+∠CDM＝120°，∵∠CDN+∠CDM＝∠MDN＝120°，∴∠CDN＝∠EDM，∵D是BC边的中点，∴DE＝BD＝CD，在△CDN和△EDM中，，∴△CDN≌△EDM（ASA），∴CN＝EM，∴BD＝BE＝BM﹣EM＝BM﹣CN，∴BM﹣CN＝BD．。

中考数学二轮复习全等三角形压轴几何题知识归纳总结及答案一、全等三角形旋转模型1．ABC △和ADE 都是等腰直角三角形，CE 与BD 相交于点,M BD 交AC 于点,N CE 交AD 于点H .试确定线段BD CE 、的关系.并说明理由.解析：BD CE ⊥且BD CE =【分析】由已知条件可证明BAD CAE ≅△△，再根据全等三角形的性质，得到BD CE ∴= ADB AEC ∠=∠，在AEH △中90AEC AHE ∠+∠=︒，又AHE MHD ∠=∠，可得：90HMD ∠=︒，即可证明BD CE ⊥且BD CE =.【详解】解： ABC 和ADE 是直角三角形BAC DAE ∴∠=∠AB AC =AD AE =则BAC CAD DAE CAD ∠+∠=∠+∠即BAD CAE ∠=∠在BAD 与CAE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩S )AS BAD CAE ∴≅（△△BD CE ∴= ADB AEC ∠=∠在AEH △中90AEC AHE ∠+∠=︒又AHE MHD ∠=∠90ADB MHD ∴∠+∠=︒则MHD 中90HMD ∠=︒，即，BD CE ⊥，综上所述，BD CE ⊥且BD CE =.【点睛】本题主要考查三角形全等的判定方法和性质定理和等腰直角三角形的性质，从复杂的图形中找到全等三角形和“8”字形三角形是解题的关键.2．如图所示，ABC ∆中，1AB BC ==，90ABC ∠=︒，把一块含30角的直角三角板DEF 的直角顶点D 放在AC 的中点上（直角三角板的短直角边为DF ，长直角边为DE ），将三角板DEF 绕D 点按逆时针方向旋转.（1）在如图所见中，DE 交AB 于M ，DF 交BC 于N ，证明DM DN =；（2）继续旋转至如图所见，延长AB 交DE 于M ，延长BC 交DF 于N ，证明DM DN =.答案：B解析：(1)见解析；（2）见解析.【解析】【分析】（1）连接BD ，证明△DMB ≌△DNC ．根据已知，全等条件已具备两个，再证出∠MDB=∠NDC ，用ASA 证明全等，四边形DMBN 的面积不发生变化，因为它的面积始终等于△ABC 面积的一半；（2）同样利用（1）中的证明方法可以证出△DMB ≌△DNC ；（3）方法同（1）．【详解】证明：（1）连接BD,∵AB=BC ，∠ABC=90°，点D 为AC 的中点∴BD ⊥AC ，∠A=∠C=45°∴BD=AD=CD∴∠ABD=∠A=45°∴∠MBD=∠C=45°∵∠MDB+∠BDN=90°∠NDC+∠BDN=90°∴∠MDB=∠NDC在△MDB 和△NDC 中MBD C BD CDMDB NDC ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ∴△MDB ≌△NDC （ASA ）∴DM=DN （5分）（2）DM=DN 仍然成立．理由如下：连接BD ，由（1）知BD ⊥AC ，BD=CD∴∠ABD=∠ACB=45°∵∠ABD+∠MBD=180°∠ACB+∠NCD=180°∴∠MBD=∠NCD∵BD ⊥AC∴∠MDB+∠MDC=90°又∠NDC+∠MDC=90°∴∠MDB=∠NDC在△MDB 和△NDC 中MBD NCD BD CDMDB NDC ∠∠⎧⎪⎨⎪∠∠⎩＝＝＝ ∴△MDB ≌△NDC （ASA ）∴DM=DN.【点睛】本题主要考查学生的推理能力，题目比较典型，利用ASA 求三角形全等（手拉手模型），还运用了全等三角形的性质，等腰直角三角形的性质，及等腰三角形三线合一定理等知识．3．（1）如图1，在OAB 和OCD 中，OA=OB ，OC=OD ，∠AOB=∠COD=40°，连接AC ，BD 交于点M ．求：①AC BD的值； ②∠AMB 的度数． （2）如图2，在OAB 和OCD 中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC 交BD 的延长线于点M ．请判断AC BD的值及∠AMB 的度数，并说明理由； （3）在（2）的条件下，将OCD 点O 在平面内旋转，AC ，BD 所在直线交于点M ，若OD=2，OB=23，请直接写出当点C 与点M 重合时AC 的长．答案：A解析：（1）①1，②40°；（2）AC BD 3∠AMB=90°，见解析；（3）33【分析】（1）①根据已知条件证明△COA ≌△DOB ，即可证明AC=BD ；②根据△COA ≌△DOB 可得∠CAO=∠DBO ，根据已知条件可得∠OAB+∠ABO=140°，然后在△AMB 中，根据等角的转换即可得到答案； （2）根据已知条件证明△AOC ∽△BOD ，可得∠CAO=∠DBO ，进而可得∠MAB=∠OAB+∠DBO ，最后可得∠AMB=180°-（∠OAB+∠ABM+∠DBO ）=90°；（3）分两种情况讨论，根据题（2），同理可得OAC OBD △△，90AMB ∠=︒，3AC BD=，设BD=x ，则3AC x = 用x 表示出AM 、BM 的长，在Rt AMB 中，根据勾股定理222AM BM AB +=列出方程，求解即可．【详解】 解：（1）①如图1，∵∠AOB=∠COD=40°，∴∠COA=∠DOB ，∵OC=OD ，OA=OB ，∴△COA ≌△DOB （SAS ），∴AC=BD ， ∴AC BD =1， ②∵△COA ≌△DOB ，∴∠CAO=∠DBO ，∵∠AOB=40°，∴∠OAB+∠ABO=140°，在△AMB 中，∠AMB=180°﹣（∠CAO+∠OAB+∠ABD ）=180°﹣（∠DBO+∠OAB+∠ABD ）=180°﹣140°=40°，（2）如图2，AC BD=3，∠AMB=90°，理由是：在Rt △COD 中，∠DCO=30°，∠DOC=90°，∴3tan 303OD OC =︒=，同理得：3tan 303OB OA =︒=， ∴OD OB OC OA=， ∵∠AOB=∠COD=90°，∴∠AOC=∠BOD ，∴△AOC ∽△BOD ，∴AC OC BD OD==3，∠CAO=∠DBO ， 在△AMB 中，∠AMB=180°﹣（∠MAB+∠ABM ）=180°﹣（∠OAB+∠ABM+∠DBO ）=90°；（3）AC 的长为23或43．①如图，点C 与点M 重合，同理可得：OAC OBD △△，90AMB ∴∠=︒，3AC BD =设BD=x ，则3AC x =，在Rt ODC 中，30OCD ∠=︒，OD=2，4CD ∴=，在Rt AOB 中，30OAB ∠=︒，33AB ∴=，在Rt AMB 中，222AM BM AB +=，即222(3)(4)(43)x x ++=，解得：x=2或-4(舍)，323x =②如图，点C 与点M 重合，同理可得：90AMB ∠=︒，3AC BD =， 设BD=x ，则AC=3x ，在Rt COD 中， 90OCD ∠=︒，OD=2，4CD ∴=，4BC x =-，在Rt AOB 中，30OAB ∠=︒，23OB =，243AB OB ∴==，在Rt AMB 中，222AM BM AB +=，即222(3)(4)(43)x x +-=，解得：x=4或-2（舍），AC=343x =，综上所述，AC 的长为23或43．【点睛】本题主要考查三角形的综合运用，涉及全等三角形与相似三角形的性质和判定、勾股定理、解一元一次方程、图形旋转证明、特殊角的三角函数值等知识点，难度较大，第（1）题证明△COA ≌△DOB 是关键，第（2）题证明△AOC ∽△BOD 是关键，第（3）题要特别注意分情况讨论．4．如图1，在Rt △ABC 中，∠A ＝90°，AB ＝AC ，点D ，E 分别在边AB ，AC 上，AD ＝AE ，连接DC ，点M ，P ，N 分别为DE ，DC ，BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是 ，位置关系是 ；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连接MN ，BD ，CE ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若AD ＝4，AB ＝10，请直接写出△PMN 面积的最大值．解析：（1）PM ＝PN ，PM ⊥PN ；（2）△PMN 是等腰直角三角形．理由见解析；（3）S △PMN 最大＝492． 【分析】（1）由已知易得BD CE =，利用三角形的中位线得出12PM CE =，12PN BD =，即可得出数量关系，再利用三角形的中位线得出//PM CE 得出DPM DCA ∠=∠，最后用互余即可得出位置关系；（2）先判断出ABD ACE ∆≅∆，得出BD CE =，同（1）的方法得出12PM BD =，12PN BD =，即可得出PM PN =，同（1）的方法由MPN DCE DCB DBC ACB ABC ∠=∠+∠+∠=∠+∠，即可得出结论；（3）方法1：先判断出MN 最大时，PMN ∆的面积最大，进而求出AN ，AM ，即可得出MN 最大AM AN =+，最后用面积公式即可得出结论．方法2：先判断出BD 最大时，PMN ∆的面积最大，而BD 最大是14AB AD +=，即可得出结论．【详解】解：（1）点P ，N 是BC ，CD 的中点，//PN BD ∴，12PN BD =， 点P ，M 是CD ，DE 的中点，//PM CE ∴，12PM CE =， AB AC =，AD AE =，BD CE ∴=，PM PN ∴=，//PN BD ，DPN ADC ∴∠=∠，//PM CE ，DPM DCA ∴∠=∠，90BAC ∠=︒，90ADC ACD ∴∠+∠=︒，90MPN DPM DPN DCA ADC ∴∠=∠+∠=∠+∠=︒，PM PN ∴⊥，故答案为：PM PN =，PM PN ⊥；（2）PMN ∆是等腰直角三角形．由旋转知，BAD CAE ∠=∠，AB AC =，AD AE =，()ABD ACE SAS ∴∆≅∆，ABD ACE ∴∠=∠，BD CE =， 利用三角形的中位线得，12PN BD =，12PM CE =， PM PN ∴=，PMN ∴∆是等腰三角形，同（1）的方法得，//PM CE ，DPM DCE ∴∠=∠，同（1）的方法得，//PN BD ，PNC DBC ∴∠=∠，DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠，MPN DPM DPN DCE DCB DBC ∴∠=∠+∠=∠+∠+∠BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠， 90BAC ∠=︒， 90ACB ABC ∴∠+∠=︒，90MPN ∴∠=︒，PMN ∴∆是等腰直角三角形；（3）方法1：如图2，同（2）的方法得，PMN ∆是等腰直角三角形，MN ∴最大时，PMN ∆的面积最大，//DE BC ∴且DE 在顶点A 上面，MN ∴最大AM AN =+，连接AM ，AN ，在ADE ∆中，4AD AE ==，90DAE ∠=︒，22AM ∴=在Rt ABC ∆中，10AB AC ==，52AN =22522MN ∴=最大，222111149(72)22242PMN S PM MN ∆∴==⨯=⨯=最大． 方法2：由（2）知，PMN ∆是等腰直角三角形，12PM PN BD ==，PM ∴最大时，PMN ∆面积最大，∴点D 在BA 的延长线上，14BD AB AD ∴=+=，7PM ∴=，2211497222PMN S PM ∆∴==⨯=最大． 【点睛】此题属于几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质的综合运用；解（1）的关键是判断出12PM CE =，12PN BD =，解（2）的关键是判断出ABD ACE ∆≅∆，解（3）的关键是判断出MN 最大时，PMN ∆的面积最大．5．如图1，在Rt △ABC 中，AB ＝AC ，∠A ＝90°，点D 、E 分别在边AB 、AC 上，AD ＝AE ，连结DC ，点M 、P 、N 分别为DE 、DC 、BC 的中点．（1）观察猜想：图1中，线段PM 与PN 的数量关系是________，位置关系是__________；（2）探究证明：把△ADE 绕点A 逆时针方向旋转到图2的位置，连结MN ，判断△PMN 的形状，并说明理由；（3）拓展延伸：把△ADE 绕点A 在平面内自由旋转，若DE ＝2，BC ＝4，请直接写出△PMN 面积的最大值．答案：C解析：（1）PM=PN ，PM ⊥PN ，理由见详解；（2）△PMN 是等腰直角三角形，理由见详解；（3）△PMN 面积的最大值是94． 【分析】（1）利用三角形的中位线得出PM=12CE ，PN=12BD ，进而判断出BD=CE ，即可得出结论，再利用三角形的中位线得出PM ∥CE 得出∠DPM=∠DCA ，最后用互余即可得出结论； （2）先判断出△ABD ≌△ACE ，得出BD=CE ，同（1）的方法得出PM=12BD ，PN=12BD ，即可得出PM=PN ，同（1）的方法即可得出结论；（3）先判断出BD 最大时，△PMN 的面积最大，而BD 最大是AB+AD=14，即可得出结论．【详解】解：（1）∵点P，N是BC，CD的中点，∴PN∥BD，PN=12BD，∵点P，M是CD，DE的中点，∴PM∥CE，PM=12CE，∵AB=AC，AD=AE，∴BD=CE，∴PM=PN，∵PN∥BD，∴∠DPN=∠ADC，∵PM∥CE，∴∠DPM=∠DCA，∵∠BAC=90°，∴∠ADC+∠ACD=90°，∴∠MPN=∠DPM+∠DPN=∠DCA+∠ADC=90°，∴PM⊥PN；故答案为：PM=PN，PM⊥PN；（2）△PMN是等腰直角三角形；理由：由旋转知，∠BAD=∠CAE，∵AB=AC，AD=AE，∴△ABD≌△ACE（SAS），∴∠ABD=∠ACE，BD=CE，同（1）的方法，利用三角形的中位线得，PN=12BD，PM=12CE，∴PM=PN，∴△PMN是等腰三角形，同（1）的方法得，PM∥CE，∴∠DPM=∠DCE，同（1）的方法得，PN∥BD，∴∠PNC=∠DBC，∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC，∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC =∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC，∵∠BAC=90°，∴∠ACB+∠ABC=90°，∴∠MPN=90°，∴△PMN是等腰直角三角形；（3）由（2）知，△PMN 是等腰直角三角形，PM=PN=12BD ， ∴PM 最大时，△PMN 面积最大，即：BD 最大时，△PMN 面积最大，∴点D 在BA 的延长线上，∵DE ＝2，BC ＝4，∴2222AD =⨯=，24222AB =⨯= ∴BD=AB+AD=32，∴PM=322， ∴S △PMN 最大=12PM 2=21329()224⨯=； 【点睛】此题是几何变换综合题，主要考查了三角形的中位线定理，等腰直角三角形的判定和性质，全等三角形的判断和性质，直角三角形的性质，解（1）的关键是判断出PM=12CE ，PN=12BD ，解（2）的关键是判断出△ABD ≌△ACE ，解（3）的关键是判断出BD 最大时，△PMN 的面积最大，是一道中考常考题．6．如图，在ABC 中，,AB AC BAC α=∠=，过A 作AD BC ⊥于点D ，点E 为直线AD 上一动点，把线段CE 绕点E 顺时针旋转α，得到线段EF ，连接FC 、FB ，直线AD 与BF 相交于点G ．（1）（发现）如图1，当60α=︒时，填空：①AE BF的值为___________； ②AGB ∠的度数为___________； （2）（探究）如图2，当120α=︒时，请写出AE BF的值及AGB ∠的度数，并就图2的情形给出证明；（3）（应用）如图3，当90α=︒时，若15AB ACE =∠=︒，请直接写出DFG 的面积．答案：G解析：（1）1；60°；（2）AE BF =∠G =30°，理由见解析；（3） 【分析】（1）①根据已知条件可以证明三角形ABC 和三角形EFC 都是等边三角形，然后根据等边三角形的性质证明△AEC ≌△BFC ，即BF =AE 从而得出答案；②根据①中的证明∠ABG =90°，∠BAG =30°，从而计算出∠AGB 的度数；（2）根据题目已知条件可以计算出BC =，同理可以证得CF =，再证ECA FCB ∠=∠即△ACE ∽△BCF ，从而得到比值和角的度数；（3）根据第（2）问的计算结论分E 在AD 上和E 在DA 的延长线上分类讨论求解即可．【详解】解：（1）①∵AB =AC ，CE =EF ，∠BAC =∠FEC =60°∴△ABC 和△EFC 都是等边三角形∴∠ACB =∠ECF =60°，AC =CB ，CE =CF∴∠ACE =∠BCF∴△ACE ≌△BCF∴A E =BF ，即1AE BF= ②∵△ACE ≌△BCF∴∠EAC =∠CBF 由①可知△ABC 是等边三角形∴AD 平分∠BAC ，BD ⊥AD∴∠CAE =∠CBF =30°∴∠AGB =∠180°-∠CBF -∠BDG =60°（2）AE BF = ∵AB =AC ，∠BAC =120°，AD ⊥BC∴∠ABD =30°=∠ACB∴BD AB AC CD === ∴BC =同理∵∠FEC =120°，EF =EC ∴CF =∴BC CF AC CE=，∠ACB =∠ECF =30°∴△ACE ∽△BCF∴∠CAE =∠CBF∴3AE AC BF BC == ∵AD ⊥BC ，∠BAC =120°，∴∠CAE =∠CBF =60°又∵∠BDG =90°∴∠G =30°（3）第一种情况，如图所示，当E 在AD 上时 ∵AB AC ==∠BAC =90°，AD ⊥BC ∴sin 4562BC AD BD CD AB =====∠DAC =45° ∵∠ACE =15° ∴∠CED =∠CAD +∠ACE =60° ∴2tan 60DC DE ==∴AE AD DE =-=BC CF AC CE==，∠ACB =∠ECF =45° 又∵AD ⊥BC ，∠BAC =90°，∴∠CAE =∠CBF =45°∴△ACE ∽△BCF∴BF BC AE AC==∴2BF == ∵∠ADC =∠BDG∴∠G =∠ACB =45°∴BG ==∴2FG BG BF =-=过点D 作DM ⊥BG 交BG 于M ，∵∠G =∠ACB =45°，∠BDG =90°∴=DG BD CD ==∴2DM DG == ∴132DFG S FG DM ==△第二种情况：当E 在DA 的延长线上时过点D 作DM ⊥BG 交BG 于M ， 同上可证2BF BC AE AC ==，6BG BD ==，3DM = ∵∠ACE =15°，∠DAC =45°∴∠DEC =30° ∵AD ⊥CD ，6CD =∴32tan 30DC DE == ∴=6DG BD CD ==326AE DE AD =-=-∴2623FB AE ==-∴6FG BF BG =+=1332DFG S FG DM ==△ 故答案为：3或33．【点睛】本题主要考查了相似三角形的性质与判定，旋转的性质，三角函数等知识点，解题的关键在于能够熟练的掌握相关知识点．7．在ABC 中，,AB AC BAC α=∠=，点P 为线段CA 延长线上一动点，连接PB ，将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ，连接,DB DC ．（1）如图1，当60α=︒时，请直接写出线段PA 与线段CD 的数量关系是__________，DCP ∠为______度；（2）如图2，当120α=︒时，写出线段PA 和线段DC 的数量关系，并说明理由； （3）如图2，在（2）的条件下，当23AB =13BP PC +的最小值． 答案：A解析：（1）PA ＝DC ，60；（2）CD 3PA ．理由见详解；（232【分析】（1）先证明△ABC ，△PBD 是等边三角形，再证明△PBA ≌△DBC ，进而线段PA 与线段CD 的数量关系，利用全等三角形的性质以及三角形内角和等于180°，解决问题即可；（2）证明△CBD ∽△ABP ，可得3CD BC PA AB== （3）过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ， 过点B 作BG ⊥BA 于点G ，当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小，由BGP CNP ∽，得13GP NP BP CP ==，结合勾股定理求出GP ，从而得CP ，进而即可求解． 【详解】（1）①证明： ∵将线段PB 绕点P 逆时针旋转，旋转角为α，得到线段PD ， ∴PB ＝PD ，∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝60°，∴△ABC ，△PBD 是等边三角形，∴∠ABC ＝∠PBD ＝60°，∴∠PBA ＝∠DBC ，∵BP ＝BD ，BA ＝BC ，∴△PBA ≌△DBC （SAS ），∴PA ＝DC ．设BD 交PC 于点O ，如图1，∵△PBA ≌△DBC ，∴∠BPA ＝∠BDC ，∵∠BOP ＝∠COD ，∴∠OBP ＝∠OCD ＝60°，即∠DCP ＝60°．故答案是：PA ＝DC ，60；（2）解：结论：CD 3．理由如下：∵AB ＝AC ，PB ＝PD ，∠BAC ＝∠BPD ＝120°，∴BC ＝2•AB •cos30°3，BD ═2BP •cos30°3， ∴BC BD BA BP=3 ∵∠ABC ＝∠PBD ＝30°，∴∠ABP ＝∠CBD ，∴△CBD ∽△ABP ， ∴3CD BC PA AB== ∴CD 3； （3） 过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ，则PN =13PC ， 过点B 作BG CA ⊥于点G ，则BG =AB ×sin ∠BAG 3=3，AG = AB ×cos ∠BAG 3 当点B 、P 、N 共线时，BP +PN 最小，即13BP PC +最小， ∵∠BGP =∠CNP =90°，∠BPG =∠CPN ， ∴BGP CNP ∽， ∴13GP NP BP CP ==， 设GP =x ，则AP 3-x ，BP =3x ，∴()22233x x +=，解得：x 324∴BP =924，AP =3-324， ∴CP =AC +AP =23+3-324=33-324， ∴13BP PC +最小值=924+13×(33-324)=3+22．【点睛】本题属于几何变换综合题，考查了全等三角形的判定和性质，相似三角形的判定和性质，解直角三角形等知识，第（1）（2）题解题的关键是正确寻找全等三角形或相似三角形解决问题，第（3）题的关键是过点C 作射线CM ，使得sin ∠ACM =13，过点P 作PN ⊥CM 于点N ．8．如图1，在正方形ABCD 中，点,E F 分别在边,AB AD 上，且AE AF =，延长FD 到点G ，使得DG DF =，连接,,EF GE CE ．（特例感知）（1）图1中GE 与CE 的数量关系是______________．（结论探索）（2）图2，将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒，连接FD 并延长到点G ，使得DC DF =，连接,,GE CE BE ，此时GE 与CE 还存在（1）中的数量关系吗？判断并说明理由．（拓展应用）（3）在（2）的条件下，若5,32AB AE ==，当EFG 是以EF 为直角边的直角三角形时，请直接写出GE 的长．答案：G解析：(1) GE =2CE ，(2)存在，证明见解析，（3）258或210或16或4．【分析】(1)连接GC ，证△CDG ≌△CBE ，得出△GCE 为等腰直角三角形即可；(2)类似（1）的方法，先证△AFD ≌△AEB ，再证△CDG ≌△CBE ，得出△GCE 为等腰直角三角形即可；(3)根据E 、F 是直角顶点分类讨论，结合（2）中结论，利用勾股定理求解即可．【详解】解：(1)连接GC ，∵AE =AF ，AD =AB ，∴DF =BE ，∵DG DF =，∴DG = BE ，∵∠GDC =∠B =90°，DC =BC ，∴△CDG ≌△CBE ，∴CE =CG ，∠GCD =∠ECB ，∵∠ECB +∠DCE =90°，∴∠GCE =∠GCD +∠DCE =90°，∴GE =2CE ；故答案为：GE =2CE ；(2) 存在，连接GC ，∵AE =AF ，AD =AB ，∠FAE =∠DAB =90°，∴∠FAD=∠EAB，∴△FAD≌△EAB，∴FD=EB=GD，∠FDA=∠EBA，∵∠GDC+∠FDA=90°，∠EBC+∠EBA=90°，∴∠GDC=∠EBC，∵DC=BD，∴△CDG≌△CBE，与（1）同理，GE=2CE；(3)当∠FEG=90°时，如图1，因为∠FEA=∠GEC=45°，所以，A、E、C在一条直线上，∵AB=5，∴AC=52,CE=52-32=22,GE=2EC=4；如图2，E在CA延长线上，同理可得，EC2，GE =2EC =16；当∠EFG =90°时，如图3，∠AFD =∠EFG +∠AFE =135°，由（2）得，∠AFD =∠AEB =135°，DF =BE ，所以，B 、E 、F 在一条直线上，作AM ⊥EF ，垂足为M ，∵5,32AB AE ==，∴EF =6，AM =ME =MF =3，224BM AB AM =-=，BE =DF =1,FG =2，22210GE FG EF =+=；如图4，同图3，BE =DF =7，FG =14，EF =6，22258GE FG EF =+=，综上，GE的长为258或210或16或4．【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质，解题关键是恰当的连接辅助线，构造全等三角形；会分类讨论，结合题目前后联系，解决问题．9．已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG＝CG；（2）将图①中BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．答案：E解析：（1）见解析；（2）依然成立，见解析；（3）依然成立，EG⊥CG【分析】（1）利用直角三角形斜边上的中线等于斜边的一半，可证出CG＝EG；（2）结论仍然成立，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点；再证明△DAG≌△DCG，得出AG＝CG；再证出△DMG≌△FNG，得到MG＝NG；再证明△AMG≌△ENG，得出AG＝EG；最后证出CG＝EG；（3）结论依然成立，证明方法类似（2）．【详解】（1）证明：∵四边形ABCD是正方形，∴∠DCF＝90°，在Rt△FCD中，∵G为DF的中点，∴CG＝12FD，同理，在Rt△DEF中，EG＝12 FD，∴CG＝EG．（2）解：（1）中结论仍然成立，即EG＝CG．证法：如图，连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点，在△DAG与△DCG中，∵AD＝CD，∠ADG＝∠CDG，DG＝DG，∴△DAG≌△DCG（SAS），∴AG＝CG；在△DMG与△FNG中，∵∠DGM＝∠FGN，FG＝DG，∠MDG＝∠NFG，∴△DMG≌△FNG（ASA），∴MG＝NG；∵∠EAM＝∠AEN＝∠AMN＝90°，∴四边形AENM是矩形，在矩形AENM中，AM＝EN，在△AMG与△ENG中，∵AM＝EN，∠AMG＝∠ENG，MG＝NG，∴△AMG≌△ENG（SAS），∴AG＝EG，∴EG＝CG．（3）解：（1）中的结论仍然成立．理由如下：如图，过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB于N ，∵G 为FD 中点，∴FG =GD ，∵MF ∥CD ，∴∠FMG =∠DCG ，∠GDC =∠GFM ，∴△CDG ≌△MFG ，∴CD ＝FM ，∵NF ∥BC ，∴∠NFH +∠NHF =∠EHB +∠EBH ，又∵∠NHF =∠EBH ，∴∠NFH =∠EBH ，∴∠EFM ＝∠EBC ，又∵BE =EF ，则△EFM ≌△EBC ，∠FEM ＝∠BEC ，EM ＝EC∵∠FEC +∠BEC ＝90°，∴∠FEC +∠FEM ＝90°，即∠MEC ＝90°，∴△MEC 是等腰直角三角形，∵G 为CM 中点，∴EG ＝CG ，EG ⊥CG ．【点睛】本题考查全等三角形的判定和性质、矩形的判定与性质，正方形的性质，旋转的性质，解题的关键是掌握相关性质．10．如图．四边形ABCD 、BEFG 均为正方形．（1）如图1，连接AG 、CE ，请直接写出．．．．．AG 和CE 的数量和位置关系（不必证明）．（2）将正方形BEFG 绕点B 顺时针旋转β角（0180β︒︒＜＜），如图2，直线AG 、CE 相交于点M ．①AG 和CE 是否仍然满足（1）中的结论？如果是，请说明理由：如果不是，请举出反例：②连结MB ，求证：MB 平分AME ∠．（3）在（2）的条件下，过点A 作AN MB ⊥交MB 的延长线于点N ，请直接写出．．．．．线段CM与BN 的数量关系．答案：A解析：（1）AG=EC ，AG ⊥EC ；（2）①满足，理由见解析；②见解析；（3）2．【分析】（1）由正方形BEFG 与正方形ABCD ，利用正方形的性质得到两对边相等，一对直角相等，利用SAS 得出三角形ABG 与三角形CBE 全等，利用全等三角形的对应边相等，对应角相等得到CE=AG ，∠BCE=∠BAG ，再利用同角的余角相等即可得证；（2）①利用SAS 得出△ABG ≌△CEB 即可解决问题；②过B 作BP ⊥EC ，BH ⊥AM ，由全等三角形的面积相等得到两三角形面积相等，而AG=EC ，可得出BP=BH ，利用到角两边距离相等的点在角的平分线上得到BM 为角平分线；（3）在AN 上截取NQ=NB ，可得出三角形BNQ 为等腰直角三角形，利用等腰直角三角形的性质得到2BN ，接下来证明BQ=CM ，即要证明三角形ABQ 与三角形BCM 全等，利用同角的余角相等得到一对角相等，再由三角形ANM 为等腰直角三角形得到NA=NM ，利用等式的性质得到AQ=BM ，利用SAS 可得出全等，根据全等三角形的对应边相等即可得证．【详解】解：（1）AG=EC ，AG ⊥EC ，理由为：∵正方形BEFG ，正方形ABCD ，∴GB=BE ，∠ABG=90°，AB=BC ，∠ABC=90°，在△ABG 和△BEC 中，BG BE ABC EBC BA BC =⎧⎪∠=∠⎨⎪=⎩，∴△ABG ≌△BEC （SAS ），∴CE=AG ，∠BCE=∠BAG ，延长CE 交AG 于点M ，∴∠BEC=∠AEM ，∴∠ABC=∠AME=90°，∴AG=EC ，AG ⊥EC ；（2）①满足，理由是：如图2中，设AM 交BC 于O ．∵∠EBG=∠ABC=90°，∴∠ABG=∠EBC ，在△ABG 和△CEB 中，AB BC ABG CBE BG EB =⎧⎪∠=∠⎨⎪=⎩，∴△ABG ≌△CEB （SAS ），∴AG=EC ，∠BAG=∠BCE ，∵∠BAG+∠AOB=90°，∠AOB=∠COM ，∴∠BCE+∠COM=90°，∴∠OMC=90°，∴AG ⊥EC ．②过B 作BP ⊥EC ，BH ⊥AM ，∵△ABG ≌△CEB ，∴S △ABG =S △EBC ，AG=EC ， ∴12EC•BP=12AG•BH ， ∴BP=BH ，∴MB 平分∠AME ；（3）CM=2BN ，理由为：在NA 上截取NQ=NB ，连接BQ ，∴△BNQ 为等腰直角三角形，即BQ=2BN ，∵∠AMN=45°，∠N=90°，∴△AMN 为等腰直角三角形，即AN=MN ，∴MN-BN=AN-NQ ，即AQ=BM ，∵∠MBC+∠ABN=90°，∠BAN+∠ABN=90°，∴∠MBC=∠BAN ，在△ABQ 和△BCM 中，AQ BM BAN MBC AB BC =⎧⎪∠=∠⎨⎪=⎩，∴△ABQ ≌△BCM （SAS ），∴CM=BQ ，则CM=2BN ．【点睛】此题考查了正方形，全等三角形的判定与性质，等腰直角三角形的判定与性质，角平分线的判定，熟练掌握正方形的性质是解本题的关键．11．在平面直角坐标系中，点A 在y 轴正半轴上，点B 在x 轴负半轴上，BP 平分∠ABO ． （1）如图1，点T 在BA 延长线上，若AP 平分∠TAO ，求∠P 的度数；（2）如图2，点C 为x 轴正半轴上一点，∠ABC ＝2∠ACB ，且P 在AC 的垂直平分线上． ①求证：AP //BC ；②D 是AB 上一点，E 是x 轴正半轴上一点，连接AE 交DP 于H ．当∠DHE 与∠ABE 满足什么数量关系时，DP ＝AE ．给出结论并说明理由．答案：D解析：（1）45°；（2）①见解析；②∠DHE+∠ABE＝180°，理由见解析【分析】（1）由三角形的外角性质和角平分线的性质可得∠AOB＝2∠P＝90°，可求解；（2）①过点P作PE⊥AB交BA延长线于E，过点P作PF⊥BC于F，连接PC，由角平分线的性质可得PE＝PF，由垂直平分线的性质可得PA＝PC，由“HL”可证Rt△APE≌Rt△CPF，可得∠EPA＝∠CPF，由四边形内角和定理可得∠EBF+∠EPF＝180°，由角的数量关系可证∠ACB＝∠PAC，由平行线的判定可证AP∥BC；②如图3，在OE上截取ON＝OB，连接AN，通过证明△ADP≌△NEA，可得DP＝AE．【详解】解：（1）∵BP平分∠ABO，AP平分∠TAO，∴∠PBT＝12∠ABO，∠TAP＝12∠TAO，∵∠TAO＝∠ABO+∠AOB，∠TAP＝∠P+∠ABP，∴∠AOB＝2∠P＝90°，∴∠P＝45°；（2）①如图2，过点P作PE⊥AB交BA延长线于E，过点P作PF⊥BC于F，连接PC，又∵PB平分∠ABC，∴PE＝PF，∵P在AC的垂直平分线上，∴PA＝PC，∴∠PAC＝∠PCA，在Rt△APE和Rt△CPF中，AP PC PE PF =⎧⎨=⎩， ∴Rt △APE ≌Rt △CPF （HL ），∴∠EPA ＝∠CPF ，∴∠EPF ＝∠APC ，在四边形BEPF 中，∠EBF+∠BEP+∠EPF+∠PFB ＝180°，∴∠EBF+∠EPF ＝180°，∴∠ABC+∠APC ＝180°，∵∠APC+∠PAC+∠PCA ＝180°，∴∠ABC ＝∠PAC+∠PCA ＝2∠PAC ，∵∠ABC ＝2∠ACB ，∴∠ACB ＝∠PAC ，∴AP ∥BC ；②当∠DHE+∠ABE ＝180°时，DP ＝AE ，理由如下：如图3，在OE 上截取ON ＝OB ，连接AN ，∵OB ＝ON ，AO ⊥BE ，∴AB ＝AN ，∴∠ABN ＝∠ANB ，∵AP ∥BE ，BP 平分∠ABE ，∴∠APB ＝∠PBE ＝∠ABP ，∠ABN+∠BAP ＝180°，∴AP ＝AB ，∴AP ＝AN ，∵∠ANB+∠ANE ＝180°，∴∠BAP ＝∠ANE ，∵∠DHE+∠ABE ＝180°，∠DHE+∠ABE+∠BDH+∠BEH ＝360°，∴∠BDH+∠BEH ＝180°，∵∠ADP+∠BDP ＝180°，∴∠ADP ＝∠AEN ，在△ADP 和△NEA 中，DAP ANEADP AEN AP AN∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADP ≌△NEA （AAS ），∴DP ＝AE ．【点睛】本题是三角形综合题，考查了全等三角形的判定和性质，角平分线的性质，线段垂直平分线的性质，四边形内角和定理等知识，添加恰当辅助线构造全等三角形是本题的关键． 12．综合与实践实践操作：①如图1，ABC ∆是等边三角形，D 为BC 边上一个动点，将ACD ∆绕点A 逆时针旋转60︒得到AEF ∆，连接CE ．②如图2，在ABC ∆中，AD BC ⊥于点D ，将ABD ∆绕点A 逆时针旋转90︒得到AEF ∆，延长FE 与BC 交于点G ．③如图3，将图2中得到AEF ∆沿AE 再一次折叠得到AME ∆，连接MB ．问题解决：（1）小明在探索图1时发现四边形ABCE 是菱形．小明是这样想的：请根据小明的探索直接写出图1中线段CD ，CF ，AC 之间的数量关系为 ： （2）猜想图2中四边形ADGF 的形状，并说明理由；问题再探：（3）在图3中，若AD=6，BD=2，则MB 的长为 ．答案：C解析：（1）CD+CF=AC ；（2）四边形ADGF 为正方形；理由见解析；（3）13【分析】（1）先证明C 、F 、E 在同一直线上，再证明△BAD ≌△CAF （SAS ），则∠ADB=∠AFC ，BD=CF，可得AC=CF+CD；（2）先根据∠ADC=∠DAF=∠F=90°，证明得四边形ADGF是矩形，由邻边相等可得四边形ADGF是正方形；（3）证明△BAM≌△EAD（SAS），根据BM=DE及勾股定理可得结论．【详解】解：（1）如图：由旋转得：∠DAF=60°=∠BAC，AD=AF，∴∠BAD=∠CAF，∵△ABC是等边三角形，∴AB=AC，∴△BAD≌△CAF（SAS），∴∠ADB=∠AFC，BD=CF，∵∠ADC+∠ADB=∠AFC+∠AFE=180°，∴C、F、E在同一直线上，∴AC=BC=BD+CD=CF+CD，+=；故答案为：CD CF AC（2）四边形ADGF是正方形，理由如下：如图：∵Rt△ABD绕点A逆时针旋转90°得到△AEF，∴AF=AD，∠DAF=90°，∵AD⊥BC，∴∠ADC=∠DAF=∠F=90°，∴四边形ADGF是矩形，∵AF=AD，∴四边形ADGF是正方形；（3）如图3，连接DE，∵四边形ADGF是正方形，DG=FG=AD=AF=6，∵△ABD绕点A逆时针旋转90°，得到△AEF，∴∠BAD=∠EAF，BD=EF=2，∴EG=FG-EF=6-2=4，∵将△AFE沿AE折叠得到△AME，∴∠MAE=∠FAE，AF=AM，∴∠BAD=∠EAM，∴∠BAD+∠DAM=∠EAM+∠DAM，即∠BAM=∠DAE，∵AF=AD，∴AM=AD，在△BAM和△EAD中，∵AM ADBAM DAEAB AE=⎧⎪∠=∠⎨⎪=⎩，∴△BAM≌△EAD（SAS），∴22EG DG+2246213+=故答案为：13【点睛】本题属于四边形综合题，主要考查了旋转的性质、全等三角形的判定与性质、等边三角形的判定与性质、正方形的性质以及勾股定理的综合应用，解决问题的关键是熟练掌握等边三角形和全等三角形的性质，依据图形的性质进行计算求解．13．如图，BC⊥CA，BC＝CA，DC⊥CE，DC＝CE，直线BD与AE交于点F，交AC于点G，连接CF．（1）求证：△ACE≌△BCD；（2）求证：BF⊥AE；（3）请判断∠CFE与∠CAB的大小关系并说明理由．答案：C解析：（1）见解析；（2）见解析；（3）∠CFE ＝∠CAB ，见解析【分析】（1）根据垂直的定义得到∠ACB ＝∠DCE ＝90°，由角的和差得到∠BCD ＝∠ACE ，即可得到结论；（2）根据全等三角形的性质得到∠CBD ＝∠CAE ，根据对顶角的性质得到∠BGC ＝∠AGE ，由三角形的内角和即可得到结论；（3）过C 作CH ⊥AE 于H ，CI ⊥BF 于I ，根据全等三角形的性质得到AE ＝BD ，S △ACE ＝S △BCD ，根据三角形的面积公式得到CH ＝CI ，于是得到CF 平分∠BFH ，推出△ABC 是等腰直角三角形，即可得到结论．【详解】（1）证明：∵BC ⊥CA ，DC ⊥CE ，∴∠ACB ＝∠DCE ＝90°，∴∠BCD ＝∠ACE ，在△BCD 与△ACE 中，BC CA ACD ACE CD CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACE ≌△BCD ；（2）∵△BCD ≌△ACE ，∴∠CBD ＝∠CAE ，∵∠BGC ＝∠AGE ，∴∠AFB ＝∠ACB ＝90°，∴BF ⊥AE ；（3）∠CFE ＝∠CAB ，过C 作CH ⊥AE 于H ，CI ⊥BF 于I ，∵△BCD ≌△ACE ，∴ACE BCD AE BD,S S ∆∆==，∴CH ＝CI ，∴CF 平分∠BFH ，∵BF ⊥AE ，∴∠BFH ＝90°，∠CFE ＝45°，∵BC ⊥CA ，BC ＝CA ，∴△ABC 是等腰直角三角形，∴∠CAB ＝45°，∴∠CFE ＝∠CAB ．【点睛】角的和差、对顶角的性质这些知识点在证明全等和垂直过程中经常会遇到，需要掌握。

中考数学几何压轴题（有关三角形、四边形）的综合专题1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△，可推证△CEF是三角形，从而求得∠DCE＝．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．3、（2019秋•锦江区校级期末）在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．4、（2019•镇平县三模）如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为；∠EFC的度数为；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．5、（2017春•西城区校级期末）如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．7、（1）如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．9、（2018•大东区一模）如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于时，线段BC的长取得最大值，且最大值为（用含b，c的式子表示）（直接填空）.模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线上时，线段PC、PG又有怎样的数量关系，请直接写出你的结论，并画出论证过程中需要添加的辅助线．17、在△ABC中，∠BAC＝60°，点D、E分别在边AC、AB上，AD＝AE，连接CE、BD相交于点F，且∠BEC＝∠ADF，连接AF．（1）如图1，连接ED，求证：∠ABD＝∠CED；（2）如图2，求证：EF+FD＝AF；（3）如图3，取BC的中点G，连接AG交BD于点H，若∠GAC＝3∠ABD，BH＝7，求△ABH的面积．18、点D，E分别在△ABC的边AC，BD上，BD，CE交于点F，连接AF，∠F AE＝∠F AD，FE＝FD．（1）如图1，若∠AEF＝∠ADF，求证：AE＝AD；（2）如图2，若∠AEF≠∠ADF，FB平分∠ABC，求∠BAC的度数；（3）在（2）的条件下，如图3，点G在BE上，∠CFG＝∠AFB若AG＝6，△ABC的周长为20，求BC长．中考数学几何压轴题（有关三角形、四边形）的综合专题参考答案1、如图，在△ABC中，∠ACB＝90°，AC＝BC，E为AC边的一点，F为AB边上一点，连接CF，交BE于点D且∠ACF＝∠CBE，CG平分∠ACB交BD于点G，（1）求证：CF＝BG；（2）延长CG交AB于H，连接AG，过点C作CP∥AG交BE的延长线于点P，求证：PB＝CP+CF；（3）在（2）问的条件下，当∠GAC＝2∠FCH时，若S△AEG＝3，BG＝6，求AC的长．证明：（1）如图1，∵∠ACB＝90°，AC＝BC，∴∠A＝45°，∵CG平分∠ACB，∴∠ACG＝∠BCG＝45°，∴∠A＝∠BCG，在△BCG和△CAF中，∵，∴△BCG≌△CAF（ASA），∴CF＝BG；（2）如图2，∵PC∥AG，∴∠PCA＝∠CAG，∵AC＝BC，∠ACG＝∠BCG，CG＝CG，∴△ACG≌△BCG，∴∠CAG＝∠CBE，∵∠PCG＝∠PCA+∠ACG＝∠CAG+45°＝∠CBE+45°，∠PGC＝∠GCB+∠CBE＝∠CBE+45°，∴∠PCG＝∠PGC，∴PC＝PG，∵PB＝BG+PG，BG＝CF，∴PB＝CF+CP；（3）解法一：如图3，过E作EM⊥AG，交AG于M，∵S△AEG＝AG•EM＝3，由（2）得：△ACG≌△BCG，∴BG＝AG＝6，∴×6×EM＝3，EM＝，设∠FCH＝x°，则∠GAC＝2x°，∴∠ACF＝∠EBC＝∠GAC＝2x°，∵∠ACH＝45°，∴2x+x＝45，x＝15，∴∠ACF＝∠GAC＝30°，在Rt△AEM中，AE＝2EM＝2，AM＝＝3，∴M是AG的中点，∴AE＝EG＝2，∴BE＝BG+EG＝6+2，在Rt△ECB中，∠EBC＝30°，∴CE＝BE＝3+，∴AC＝AE+EC＝2+3+＝3+3．解法二：同理得：∠CAG＝30°，AG＝BG＝6，如图4，过G作GM⊥AC于M，在Rt△AGM中，GM＝3，AM＝＝＝3，∵∠ACG＝45°，∠MGC＝90°，∴GM＝CM＝3，∴AC＝AM+CM＝3+3．2、[问题背景]如图1所示，在△ABC中，AB＝BC，∠ABC＝90°，点D为直线BC上的一个动点（不与B、C重合），连结AD，将线段AD绕点D按顺时针方向旋转90°，使点A旋转到点E，连结EC．[问题初探]如果点D在线段BC上运动，通过观察、交流，小明形成了以下的解题思路：过点E作EF⊥BC 交直线BC于F，如图2所示，通过证明△DEF≌△ADB，可推证△CEF是等腰直角三角形，从而求得∠DCE＝135°．[继续探究]如果点D在线段CB的延长线上运动，如图3所示，求出∠DCE的度数．[拓展延伸]连接BE，当点D在直线BC上运动时，若AB＝，请直接写出BE的最小值．解：[问题初探]如图2，过点E作EF⊥BC交直线BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝135°，故答案为：ADB，等腰直角，135；[继续探究]如图3，过点E作EF⊥BC于F，∴∠DFE＝90°＝∠ABD，∴∠EDF+∠DEF＝90°，由旋转知，AD＝DE，∠ADE＝90°，∴∠ADB+∠EDF＝90°，∴∠ADB＝∠DEF，∴△ABD≌△DFE（AAS），∴BD＝EF，DF＝AB，∵AB＝BC，∴BC＝DF，∴BD＝CF，∴EF＝CF，∴△CEG是等腰直角三角形，∴∠ECF＝45°，∴∠DCE＝45°；[拓展延伸]如图4，在△ABC中，∠ABC＝90°，AB＝BC＝，∴∠ACB＝45°当点D在射线BC上时，由[问题初探]知，∠BCM＝135°，∴∠ACM＝∠BCM﹣∠ACB＝90°，当点D在线段CB的延长线上时，由[继续探究]知，∠BCE＝45°，∴∠ACN＝∠ACB+∠BCM＝90°，∴点E是过点C垂直于AC的直线上的点，∴当BE⊥MN时，BE最小，∵∠BCE＝45°，∴∠CBE＝45°＝∠BCE，∴BE＝CE，∴BE最小＝BC＝，即：BE的最小值为．3、在Rt△ABC中，∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线．（1）如图1，求证：AD＝2DC．（2）如图2，作∠CBD的角平分线交线段CD于点M，若CM＝1，求△DBM的面积；（3）如图3，过点D作DE⊥AB于点E，点N是线段AC上一点（不与C、D重合），以BN为一边，在BN的下方作∠BNG＝60°，NG交DE延长线于点G，试探究线段ND，DG与AD之间的数量关系，并说明理由．证明：（1）如图1，过点D作DE⊥AB，∵BD是△ABC的角平分线，DE⊥AB，∠ACB＝90°，∴DC＝DE，∵∠A＝30°，DE⊥AB，∴AD＝2DE，∴AD＝2DC；（2）如图2，过点M作ME∥BD，∵∠ACB＝90°，∠A＝30°，∴∠ABC＝60°，∵BD是△ABC的角平分线，∴∠ABD＝∠DBC＝30°，∵BM平分∠CBD，∴∠CBM＝15°＝∠DBM，∵ME∥BD，∴∠MEC＝∠CBD＝30°，∠EMB＝∠DBM＝∠MBE，∴ME＝BE，∵∠MEC＝30°，∠C＝90°∴CE＝MC＝，ME＝2MC＝2＝BE，∴BC＝+2，∵∠CBD＝30°，∠C＝90°，∴BC＝CD，∴CD＝1+，∴DM＝，∴△DBM的面积＝××（+2）＝1+；（3）若点N在CD上时，AD＝DG+DN，理由如下：如图3所示：延长ED使得DW＝DN，连接NW，∵∠ACB＝90°，∠A＝30°，BD是△ABC的角平分线，DE⊥AB于点E，∴∠ADE＝∠BDE＝60°，AD＝BD，∵DN＝DW，且∠WDN＝60°∴△WDN是等边三角形，∴NW＝DN，∠W＝∠WND＝∠BNG＝∠BDN＝60°，∴∠WNG＝∠BND，在△WGN和△DBN中，∴△WGN≌△DBN（SAS），∴BD＝WG＝DG+DN，∴AD＝DG+DN．（3）若点N在AD上时，AD＝DG﹣DN，理由如下：如图4，延长BD至H，使得DH＝DN，连接HN，由（1）得DA＝DB，∠A＝30°．∵DE⊥AB于点E．∴∠2＝∠3＝60°．∴∠4＝∠5＝60°．∴△NDH是等边三角形．∴NH＝ND，∠H＝∠6＝60°．∴∠H＝∠2．∵∠BNG＝60°，∴∠BNG+∠7＝∠6+∠7．即∠DNG＝∠HNB．在△DNG和△HNB中，∴△DNG≌△HNB（ASA）．∴DG＝HB．∵HB＝HD+DB＝ND+AD，∴DG＝ND+AD．∴AD＝DG﹣ND．4、如图1，已知直角三角形ABC，∠ACB＝90°，∠BAC＝30°，点D是AC边上一点，过D作DE⊥AB于点E，连接BD，点F是BD中点，连接EF，CF．（1）发现问题：线段EF，CF之间的数量关系为EF＝CF；∠EFC的度数为120°；（2）拓展与探究：若将△AED绕点A按顺时针方向旋转α角（0°＜α＜30°），如图2所示，（1）中的结论还成立吗？请说明理由；（3）拓展与运用：如图3所示，若△AED绕点A旋转的过程中，当点D落到AB边上时，AB边上另有一点G，AD＝DG＝GB，BC＝3，连接EG，请直接写出EG的长度．解：（1）如图1中，∵DE⊥AB，∴∠BED＝90°，∵∠BCD＝90°，BF＝DF，∴FE＝FB＝FD＝CF，∴∠FBE＝∠FEB，∠FBC＝∠FCB，∴∠EFC＝∠EFD+∠CFD＝∠FBE+∠FEB+∠FBC+∠FCB＝2（∠FBE+∠FBC）＝2∠ABC＝120°，故答案为：EF＝CF，120°．（2）结论成立．理由：如图2中，取AB的中点M，AD的中点N，连接MC，MF，ED，EN，FN．∵BM＝MA，BF＝FD，∴MF∥AD，MF＝AD，∵AN＝ND，∴MF＝AN，MF∥AN，∴四边形MFNA是平行四边形，∴NF＝AM，∠FMA＝∠ANF，在Rt△ADE中，∵AN＝ND，∠AED＝90°，∴EN＝AD＝AN＝ND，同理CM＝AB＝AM＝MB，在△AEN和△ACM中，∠AEN＝∠EAN，∠MCA＝∠MAC，∵∠MAC＝∠EAN，∴∠AMC＝∠ANE，又∵∠FMA＝∠ANF，∴∠ENF＝∠FMC，在△MFC和△NEF中，，∴△MFC≌△NEF（SAS），∴FE＝FC，∠NFE＝∠MCF，∵NF∥AB，∴∠NFD＝∠ABD，∵∠ACB＝90°，∠BAC＝30°，∴∠ABC＝60°，△BMC是等边三角形，∠MCB＝60°∴∠EFC＝∠EFN+∠NFD+∠DFC＝∠MCF+∠ABD+∠FBC+∠FCB＝∠ABC+∠MCB＝60°+60°＝120°．（3）如图3中，作EH⊥AB于H．在Rt△ABC中，∵∠BAC＝30°，BC＝3，∴AB＝2BC＝6，在Rt△AED中，∠DAE＝30°，AD＝2，∴DE＝AD＝1，在Rt△DEH中，∵∠EDH＝60°，DE＝1，∴EH＝ED•sin60°＝，DH＝ED•cos60°＝，在Rt△EHG中，EG＝＝．5、如图1，在等腰△ABC中，AB＝AC，∠BAC＝a，点P是线段AB的中点，点E是线段CB延长线上一点，且PE＝PC，将线段PC绕点P顺时针旋转α得到PD，连接BD．（1）如图2，若α＝60°，其他条件不变，先补全图形，然后探究线段BD和BC之间的数量关系，并说明理由．（2）如图3，若α＝90°，其他条件不变，探究线段BP、BD和BC之间的等量关系，并说明理由．解：（1）BC＝2BD，理由：如图2，连接CD，由旋转可得，CP＝DP，∠CPD＝60°，∴△CDP是等边三角形，∴∠CDP＝60°＝∠PCD，又∵P是AB的中点，AB＝AC，∠A＝60°，∴等边三角形ABC中，∠PCB＝30°，CP⊥AB，∴∠BCD＝30°，即BC平分∠PCD，∴BC垂直平分PD，∴∠BDC＝∠BPC＝90°，∴Rt△BCD中，BC＝2BD．（2）如图3，取BC中点F，连接PF，∵∠A＝90°，AB＝AC，∴△ABC是等腰直角三角形，∵P是AB的中点，F是BC的中点，∴PF是△ABC的中位线，∴PF∥AC，∴∠PFB＝∠ACB＝45°，∠BPF＝∠A＝90°，∴△BPF是等腰直角三角形，∴BF＝BP，BP＝PF，∵∠DPC＝∠BPF＝90°，∴∠BPD＝∠FPC，又∵PD＝PC，∴△BDP≌△FCP，∴BD＝CF，∵BC＝BF+FC，∴BC＝BD+BP．6、【发现问题】如图1，已知△ABC，以点A为直角顶点、AB为腰向△ABC外作等腰直角△ABE．请你以A为直角顶点、AC为腰，向△ABC外作等腰直角△ACD（不写作法，保留作图痕迹）．连接BD、CE．那么BD与CE的数量关系是BD＝CE．【拓展探究】如图2，已知△ABC，以AB、AC为边向外作正方形AEFB和正方形ACGD，连接BD、CE，试判断BD与CE之间的数量关系，并说明理由．【解决问题】如图3，有一个四边形场地ABCD，∠ADC＝60°，BC＝15，AB＝8，AD＝CD，求BD的最大值．【发现问题】解：延长CA到M，作∠MAC的平分线AN，在AN上截取AD＝AC，连接CD，即可得到等腰直角△ACD；连接BD、CE，如图1所示：∵△ABE与△ACD都是等腰直角三角形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE，【拓展探究】解：BD＝CE；理由如下：∵四边形AEFB与四边形ACGD都是正方形，∴AB＝AE，AD＝AC，∠BAE＝∠CAD＝90°，∴∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；【解决问题】解：以AB为边向外作等边三角形ABE，连接CE，如图3所示：则∠BAE＝60°，BE＝AB＝AE＝8，∵AD＝CD，∠ADC＝60°，∴△ACD是等边三角形，∴∠CAD＝60°，AC＝AD，∴∠CAD+∠BAC＝∠BAE+∠BAC，即∠BAD＝∠EAC，在△BAD和△EAC中，，∴△BAD≌△EAC（SAS），∴BD＝CE；当C、B、E三点共线时，CE最大＝BC+BE＝15+8＝23，∴BD的最大值为23．7、如图1，点C为线段AB外一个动点，已知AB＝a，AC＝b．当点C位于BA的延长线上时，线段BC取得最大值，则最大值为a+b（用含a，b的式子表示）；（2）如图2，点C为线段AB外一个动点，若AB＝10，AC＝3，分别以AC，BC为边，作等边三角形ACD和等边三角形BCE，连接AE，DB．①求证：AE＝DB；②请直接写出线段AE的最大值；（3）如图3，AB＝6，点M为线段AB外一个动点，且AM＝2，MB＝MN，∠BMN＝90°，请直接写出线段AN的最大值．（1）解：∵点C为线段AB外一动点，且AC＝b，AB＝a，∴当点C位于BA的延长线上时，线段BC的长取得最大值，且最大值为AC+AB＝a+b，（2）①证明：如图2中，∵△ACD与△BCE是等边三角形，∴CD＝AC，CB＝CE，∠ACD＝∠BCE＝60°，∴∠DCB＝∠ACE，在△CAD与△EAB中，，∴△CAD≌△EAB（SAS），∴AE＝BD．②∵线段AE长的最大值＝线段BD的最大值，由（1）知，当线段BD的长取得最大值时，点D在BA的延长线上，∴最大值为AD+AB＝3+10＝13；（3）如图3中，连接BN，∵将△AMN绕着点M顺时针旋转90°得到△PBM，连接AP，则△APM是等腰直角三角形，∴MA＝MP＝2，BP＝AN，∴P A＝2，∵AB＝6，∴线段AN长的最大值＝线段BP长的最大值，∴当P在线段BA的延长线时，线段BP取得最大值最大值＝AB+AP＝6+2．8、【初步探索】（1）如图1：在四边形ABC中，AB＝AD，∠B＝∠ADC＝90°，E、F分别是BC、CD上的点，且EF ＝BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG＝BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是∠BAE+∠F AD＝∠EAF；【灵活运用】（2）如图2，若在四边形ABCD中，AB＝AD，∠B+∠D＝180°．E、F分别是BC、CD上的点，且EF＝BE+FD，上述结论是否仍然成立，并说明理由；【拓展延伸】（3）如图3，已知在四边形ABCD中，∠ABC+∠ADC＝180°AB＝AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF＝BE+FD，请写出∠EAF与∠DAB的数量关系，并给出证明过程．解：（1）∠BAE+∠F AD＝∠EAF．理由：如图1，延长FD到点G，使DG＝BE，连接AG，根据SAS可判定△ABE≌△ADG，进而得出∠BAE＝∠DAG，AE＝AG，再根据SSS可判定△AEF≌△AGF，可得出∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF．故答案为：∠BAE+∠F AD＝∠EAF；（2）仍成立，理由：如图2，延长FD到点G，使DG＝BE，连接AG，∵∠B+∠ADF＝180°，∠ADG+∠ADF＝180°，∴∠B＝∠ADG，又∵AB＝AD，∴△ABE≌△ADG（SAS），∴∠BAE＝∠DAG，AE＝AG，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠EAF＝∠GAF＝∠DAG+∠DAF＝∠BAE+∠DAF；（3）∠EAF＝180°﹣∠DAB．证明：如图3，在DC延长线上取一点G，使得DG＝BE，连接AG，∵∠ABC+∠ADC＝180°，∠ABC+∠ABE＝180°，∴∠ADC＝∠ABE，又∵AB＝AD，∴△ADG≌△ABE（SAS），∴AG＝AE，∠DAG＝∠BAE，∵EF＝BE+FD＝DG+FD＝GF，AF＝AF，∴△AEF≌△AGF（SSS），∴∠F AE＝∠F AG，∵∠F AE+∠F AG+∠GAE＝360°，∴2∠F AE+（∠GAB+∠BAE）＝360°，∴2∠F AE+（∠GAB+∠DAG）＝360°，即2∠F AE+∠DAB＝360°，∴∠EAF＝180°﹣∠DAB．9、如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点O为AB中点，点P为直线BC上的动点（不与点B、点C重合），连接OC、OP，将线段OP绕点P逆时针旋转60°，得到线段PQ，连接BQ．（1）如图1，当点P在线段BC上时，请直接写出线段BQ与CP的数量关系．（2）如图2，当点P在CB延长线上时，（1）中结论是否成立？若成立，请加以证明；若不成立，请说明理由；（3）如图3，当点P在BC延长线上时，若∠BPO＝45°，AC＝，请直接写出BQ的长．解：（1）CP＝BQ，理由：如图1，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°⊅∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（2）CP＝BQ，理由：如图2，连接OQ，由旋转知，PQ＝OP，∠OPQ＝60°∴△POQ是等边三角形，∴OP＝OQ，∠POQ＝60°，在Rt△ABC中，O是AB中点，∴OC＝OA＝OB，∴∠BOC＝2∠A＝60°＝∠POQ，∴∠COP＝∠BOQ，在△COP和△BOQ中，，∴△COP≌△BOQ（SAS），∴CP＝BQ，（3）如图3，在Rt△ABC中，∠A＝30°，AC＝，∴BC＝AC•tan∠A＝，过点O作OH⊥BC，∴∠OHB＝90°＝∠BCA，∴OH∥AB，∵O是AB中点，∴CH＝BC＝，OH＝AC＝，∵∠BPQ＝45°，∠OHP＝90°，∴∠BPQ＝∠PQH，∴PH＝OH＝，∴CP＝PH﹣CH＝﹣＝，连接BQ，同（1）的方法得，BQ＝CP＝．10、模型发现：同学们知道，三角形的两边之和大于第三边，即如图1，在△ABC中，AB+AC＞BC．对于图1，若把点C看作是线段AB外一动点，且AB＝c，AC＝b，则线段BC的长会因为点C的位置的不同而发生变化．因为AB、AC的长度固定，所以当∠BAC越大时，BC边越长．特别的，当点C位于线段BA的延长线上时，线段BC的长取得最大值，且最大值为b+c（用含b，c的式子表示）（直接填空）模型应用：点C为线段AB外一动点，且AB＝3，AC＝2，如图2所示，分别以AC，BC为边，作等边三角形ACD 和等边三角形BCE，连接BD，AE．（1）求证：BD＝AE．（2）线段AE长的最大值为5．模型拓展：如图3，在平面直角坐标系中，点A是y轴正半轴上的一动点，点B是x轴正半轴上的一动点，且AB ＝8．若AC⊥AB，AC＝3，试求OC长的最大值．解：当点C位于线段BA的延长线上时，线段BC的长取得最大值，最大值为b+c，故答案为：线段BA的延长线上；b+c；模型应用：（1）证明：∵△ACD、△BCE都是等边三角形，∴CD＝CA＝AD，CB＝CE，∠ACD＝60°，∠BCE＝60°，∴∠DCB＝∠ACE，在△DCB和△ACE中，，∴△DCB≌△ACE（SAS）∴BD＝AE；（2）当点D位于线段BA的延长线上时，线段BD的长取得最大值，最大值为AB+AD＝AB+AC＝3+2＝5，∵AE＝BD，∴线段AE长的最大值为5，模型拓展：取AB的中点G，连接OG、CG，在Rt△AOB中，G为AB的中点，∴OG＝AB＝4，在Rt△CAG中，CG＝＝＝5，当点O、G、C在同一条直线上时，OC最大，最大值为4+5＝9．11、已知：△ABC中，∠ACB＝90°，AC＝BC．（1）如图1，点D在BC的延长线上，连AD，过B作BE⊥AD于E，交AC于点F．求证：AD＝BF；（2）如图2，点D在线段BC上，连AD，过A作AE⊥AD，且AE＝AD，连BE交AC于F，连DE，问BD与CF有何数量关系，并加以证明；（3）如图3，点D在CB延长线上，AE＝AD且AE⊥AD，连接BE、AC的延长线交BE于点M，若AC ＝3MC，请直接写出的值．（1）证明：如图1中，∵BE⊥AD于E，∴∠AEF＝∠BCF＝90°，∵∠AFE＝∠CFB，∴∠DAC＝∠CBF，∵BC＝CA，∴△BCF≌△ACD，∴BF＝AD．（2）结论：BD＝2CF．理由：如图2中，作EH⊥AC于H．∵∠AHE＝∠ACD＝∠DAE＝90°，∴∠DAC+∠ADC＝90°，∠DAC+∠EAH＝90°，∴∠DAC＝∠AEH，∵AD＝AE，∴△ACD≌△EHA，∴CD＝AH，EH＝AC＝BC，∵CB＝CA，∴BD＝CH，∵∠EHF＝∠BCF＝90°，∠EFH＝∠BFC，EH＝BC，∴△EHF≌△BCF，∴FH＝CF，∴BD＝CH＝2CF．（3）如图3中，同法可证BD＝2CM．∵AC＝3CM，设CM＝a，则AC＝CB＝3a，BD＝2a，∴＝＝．12、已知在△ABC中，AB＝AC，射线BM、BN在∠ABC内部，分别交线段AC于点G、H．（1）如图1，若∠ABC＝60°，∠MBN＝30°，作AE⊥BN于点D，分别交BC、BM于点E、F．①求证：∠1＝∠2；②如图2，若BF＝2AF，连接CF，求证：BF⊥CF；（2）如图3，点E为BC上一点，AE交BM于点F，连接CF，若∠BFE＝∠BAC＝2∠CFE，求的值．（1）①证明：如图1中，∵AB＝AC，∠ABC＝60°∴△ABC是等边三角形，∴∠BAC＝60°，∵AD⊥BN，∴∠ADB＝90°，∵∠MBN＝30°，∠BFD＝60°＝∠1+∠BAF＝∠2+∠BAF，∴∠1＝∠2②证明：如图2中，在Rt△BFD中，∵∠FBD＝30°，∴BF＝2DF，∵BF＝2AF，∴BF＝AD，∵∠BAE＝∠FBC，AB＝BC，∴△BFC≌△ADB，∴∠BFC＝∠ADB＝90°，∴BF⊥CF（2）在BF上截取BK＝AF，连接AK．∵∠BFE＝∠2+∠BAF，∠CFE＝∠4+∠1，∴∠CFB＝∠2+∠4+∠BAC，∵∠BFE＝∠BAC＝2∠EFC，∴∠1+∠4＝∠2+∠4∴∠1＝∠2，∵AB＝AC，∴△ABK≌CAF，∴∠3＝∠4，S△ABK＝S△AFC，∵∠1+∠3＝∠2+∠3＝∠CFE＝∠AKB，∠BAC＝2∠CEF，∴∠KAF＝∠1+∠3＝∠AKF，∴AF＝FK＝BK，∴S△ABK＝S△AFK，∴＝2．13、已知，△ABC中，AB＝AC，∠BAC＝90°，E为边AC任意一点，连接BE．（1）如图1，若∠ABE＝15°，O为BE中点，连接AO，且AO＝1，求BC的长；（2）如图2，F也为AC上一点，且满足AE＝CF，过A作AD⊥BE交BE于点H，交BC于点D，连接DF交BE于点G，连接AG；①若AG平分∠CAD，求证：AH＝AC；②如图3，当G落在△ABC外时，若将△EFG沿EF边翻折，点G刚好落在AB边上点P，直接写出AG与EF的数量关系．（1）解：如图1中，在AB上取一点M，使得BM＝ME，连接ME．在Rt△ABE中，∵OB＝OE，∴BE＝2OA＝2，∵MB＝ME，∴∠MBE＝∠MEB＝15°，∴∠AME＝∠MBE+∠MEB＝30°，设AE＝x，则ME＝BM＝2x，AM＝x，∵AB2+AE2＝BE2，∴（2x+x）2+x2＝22，∴x＝（负根已经舍弃），∴AB＝AC＝（2+）•，∴BC＝AB＝+1．方法二：作EH⊥BC于H，求出BH，CH即可解决问题．（2）证明：如图2中，作CP⊥AC，交AD的延长线于P，GM⊥AC于M．∵BE⊥AP，∴∠AHB＝90°，∴∠ABH+∠BAH＝90°，∵∠BAH+∠P AC＝90°，∴∠ABE＝∠P AC，在△ABE和△CAP中，，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，，∴△AGH≌△AGM，∴AH＝AM＝CM＝AC（3）解：结论：AG＝EF．理由：如图3中，作CM⊥AC交AD的延长线于M，连接PG交AC于点O．由（2）可知△ACM≌△BAE，△CDF≌△CDM，∴∠AEB＝∠M＝∠GEF，∠M＝∠CFD＝∠GFE，AE＝CM＝CF，∴∠GEF＝∠GFE，∴GE＝GF，∵△EFP是由△EFG翻折得到，∴EG＝EP＝GF＝PF，∴四边形EGFP是菱形，∴PG⊥AC，OE＝OF，∵AE＝CF，∴AO＝OC，∵AB∥OP，∴BP＝PC，∵PF∥BE，∴EF＝CF＝AE，∵PB＝PC，AO＝OC，∴PO＝OG＝AB，∴AB＝PG，AB∥PG，∴四边形ABPG是平行四边形，∴AG∥BC，∴∠GAO＝∠ACB＝45°，设EO＝OF＝a，则OA＝OG＝3a，AG＝3a，∴＝＝，∴AG＝EF14、如图所示，Rt△ABC中，∠ACB＝90°，E为AC中点，作ED⊥AC交AB于D，连接CD；（1）如图1，求证：AB＝2CD；（2）如图2，作CF⊥AB交AB于F，点G为CF上一点，点H为DE延长线上一点，分别连接AH、GH，若∠AHG＝2∠B，求证：AH＝GH；（3）如图3，在（2）的条件下，连接DG，且有DE＝BF，∠EDG＝90°，若AC＝6，求AH的长度．解：（1）∵E为AC中点，作ED⊥AC交AB于D，∴AD＝CD，∵∠ACB＝90°，∴BC∥DE，∴AD＝BD，∴CD＝BD，∴AB＝2CD；（2）如图2，连接CH，∵点E是AC的中点，∴AE＝CE，∵DE⊥AC，∴CH＝AH，∴∠ACH＝∠CAH，∵∠ACB＝90°，∴∠B+∠BAC＝90°，∵CF⊥AB，∴∠BAC+∠ACF＝90°，∴∠ACF＝∠B，∴∠HCG＝∠ACH+∠ACF＝∠CAH+∠B，∠AHG＝2∠B∴在四边形AHGF中，∠AFG+∠FGH+∠AHG+∠F AH＝360°，∴∠FGH＝360°﹣（∠AFG+∠AHG+∠F AH）＝360°﹣（90°+2∠B+∠CAH+∠BAC）＝360°﹣（90°+2∠B+∠CAH+90°﹣∠B）＝360°﹣（180°+∠B+∠CAH）＝180°﹣（∠B+∠CAH），∵∠CGH＝180°﹣∠FGH＝∠B+∠CAH＝∠HCG，∴CH＝GH，∵CH＝AH，∴AH＝GH；（3）如图3，由（1）知，DE∥BC，∴∠B＝∠ADE，在△BFC和△DEA中，，∴△BFC≌△DEA，∴BC＝AD，∵AD＝BD＝CD，∴BC＝BD＝CD，∴△BCD是等边三角形，∴∠B＝60°，在Rt△ABC中，AC＝6，∴BC＝2，AB＝4，∵CF⊥BD，∴DF＝，CF＝3，∵∠BAC＝30°，∴∠ADE＝60°，∵∠EDG＝90°，∠FDG＝30°，在Rt△DFG中，DF＝，∴FG＝1，DG＝2，∴CG＝CF﹣FG＝2过点H作HN⊥CF，由（2）知，CH＝GH，∴NG＝CG＝1，∴FN＝NG+FG＝2，过点H作HM⊥AB，∴∠FMH＝∠NFM＝∠HNF＝90°，∴四边形NFMH是矩形，∴HM＝FN＝2，在Rt△DMH中，∠ADE＝60°，HM＝2，∴DH＝，在Rt△HDG中，根据勾股定理得，HG＝＝．15、【问题情境】一节数学课后，老师布置了一道课后练习题：如图：已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，点E、F分别在A和BC上，∠1＝∠2，FG⊥AB于点G，求证：△CDE≌△EGF．（1）阅读理解，完成解答本题证明的思路可用下列框图表示：根据上述思路，请你完整地书写这道练习题的证明过程；（2）特殊位置，证明结论若CE平分∠ACD，其余条件不变，求证：AE＝BF；（3）知识迁移，探究发现如图，已知在Rt△ABC中，AC＝BC，∠ACB＝90°，CD⊥AB于点D，若点E是DB的中点，点F在直线CB上且满足EC＝EF，请直接写出AE与BF的数量关系．（不必写解答过程）（1）证明：∵AC＝BC，∠ACB＝90°，∴∠A＝∠B＝45°，∵CD⊥AB，∴∠CDB＝90°，∴∠DCB＝45°，∵∠ECF＝∠DCB+∠1＝45°+∠1，∠EFC＝∠B+∠2＝45°+∠2，∠1＝∠2，∴∠ECF＝∠EFC，∴CE＝EF，∵CD⊥AB，FG⊥AB，∴∠CDE＝∠EGF＝90°，在△CDE和△EGF中，，∴△CDE≌△EGF（AAS）；（2）证明：由（1）得：CE＝EF，∠A＝∠B，∵CE平分∠ACD，∴∠ACE＝∠1，∵∠1＝∠2，∴∠ACE＝∠2，在△ACE和△BEF中，，∴△ACE≌△BEF（AAS），∴AE＝BF；（3）AE＝BF，作EH⊥BC与H，如图3所示：设DE＝x，根据题意得：BE＝DE＝x，AD＝BD＝2x，CD＝AD＝2x，AE＝3x，根据勾股定理得：BC＝AC＝2x，∵∠ABC＝45°，EH⊥BC，∴BH＝x，∴CH＝BC﹣BH＝x，∵EC＝EF，∴FH＝CH＝x，∴BF＝x﹣x＝x，∴＝，∴AE＝．16、在正方形ABCD和等腰直角△BGF中，∠BGF＝90°，P是DF的中点，连接PG、PC．（1）如图1，当点G在BC边上时，延长GP交DC于点E．求证：PG＝PC；（2）如图2，当点F在AB的延长线上时，（1）中的结论是否成立？请证明你的结论；（3）如图3，若四边形ABCD为菱形，且∠ABC＝60°，△BGF为等边三角形，点F在CB的延长线。