初一整式加减与方程测试题9

初一数学整式的加减试题答案及解析1.因式分解：(1)x3-4x； (2)(3a-b)(x-y)＋(a＋3b)(y-x)．【答案】(1) x(x+2)(x-2)；(2) 2(x-y)(a-2b).【解析】（1）先提出公因式x，剩下的因式用平方差公式分解即可；（2）两次提取公因式即可得解.试题解析：（1）原式=x(x2-4)=x(x+2)(x-2)；（2）原式=(3a-b)(x-y)-(a＋3b)(x-y)=(x-y)(2a-4b)=2(x-y)(a-2b).【考点】1.因式分解——提公因式法；2.因式分解——公式法.2.已知代数式的值为，求代数式的值.【答案】-6【解析】解：.因为3，故上式.3.先化简，后求值：已知，求代数式的值.【答案】【解析】解：由得，，解得，.将代数式化简得.将，代入得原式.4.多项式3a2b2-5ab2+a2-6是___次项式，常数项是 .【答案】四次四项式、-6【解析】本题中未知数的最高次是4次，所以是四次，未知数有a，b两个，故是四次二项式；常数项是-6【考点】多项式点评：本题属于对多项式的基本常识的考查，需要考生在对多项式基本次数的基础上熟练把握5.下列计算正确的是（）A．2x＋3y＝5xy B．－3x－x＝－xC．－xy＋6x y＝5x y D．5ab－b a＝ab【答案】D【解析】根据合并同类项的法则依次分析各选项即可作出判断.A、2x与3y不是同类项，无法合并，B、－3x－x＝－x，C、－xy与6x y不是同类项，无法合并，故错误；D、5ab－b a＝ab，本选项正确.【考点】合并同类项点评：解题的关键是熟练掌握合并同类项的法则：把同类项的系数相加，字母和字母的指数不变.6.若2x y与－3x y是同类项，则－m=【答案】3【解析】先根据同类项的定义求得m、n的值，再根据有理数的乘方法则计算即可.由题意得，解得，则－m【考点】同类项，有理数的乘方点评：解题的关键是熟记同类项的定义：所含字母相同，并且相同字母的指数也分别相同的项是同类项.7.已知：A=x＋xy＋y，B=－3xy－x求（1）B－A；（2）2A－3B；（3）若A－B－C=0，则C如何用含x，y的代数式表示？【答案】（1）－2x－4xy－y；（2）5x＋11xy＋2y；（3）2x＋4xy＋y【解析】先根据题意分别列出代数式，再去括号、合并同类项即可.（1）B－A=（－3xy－x）－（x＋xy＋y）=－3xy－x－x－xy－y=－2x－4xy－y；（2）2A－3B=2（x＋xy＋y）－3（－3xy－x）=2x＋2xy＋2y+9xy+3x=5x＋11xy＋2y ；（3）∵A－B－C=0∴C= A－B=（x＋xy＋y）－（－3xy－x）=x＋xy＋y+3xy+x= 2x＋4xy＋y.【考点】整式的加减点评：解题的关键是熟练掌握在去括号时，若括号前是“-”号，把括号和括号前的“-”号去掉后，括号里各项的符号均要改变.8.化简或求值：（1）化简：（2）已知，求的值。

整式的加减及一元一次方程测试题（考试60分钟，满分120分）一、选择题（每小题3分，共30分）1、下列各题去括号错误的是（ ）A 、213)213(+-=--y x y x B 、b a n m b a n m -+-=-+-+)( C 、332)364(21++-=+--y x y x D 、723121)7231()21(-++=+--+c b a c b a 2、下列说法正确的是（ ） A 、xyz 32与xy 32是同类项 B 、x 1和x 21是同类项 C 、235.0y x 与327y x 是同类项 D 、n m 25与24nm -是同类项 3、下列方程是一元一次方程的是( )A x +2y =9B x 2－3x =1 C11=x D x x 3121=- 4、计算：3562+-a a 与1252-+a a 的差，结果正确的是（ ）A 、432+-a aB 、232+-a aC 、272+-a aD 、472+-a a5、下列变形正确的是( )A 4x －5＝3x ＋2变形得4x －3x ＝－2＋5B 23 x －1＝12x+3变形得4x －6＝3x ＋18 C 3(x －1)＝2(x ＋3)变形得3x －1＝2x ＋6 D 6x ＝2变形得x ＝36、解方程3112-=-x x 时，去分母正确的是( ) A ．2233-=-x x B ．2263-=-x x C ．1263-=-x x D ．1233-=-x x7、方程x x -=-22的解是( )A ．1=xB ．1-=xC ．2＝xD ．0=x8、下列两个方程的解相同的是( )A ．方程635=+x 与方程42=xB ．方程13+=x x 与方程142-=x xC ．方程021=+x 与方程021=+x D ．方程5)25(36=--x x 与3156=-x x 9、如果x =y ，那么下列等式不一定成立的是（ ） A x －5=y －5 B 33y x -=- C 33+=+a y a x D 1122+=+a y a x 10、某种品的标价为120元，若以九折降价出售，相对于进货价仍获利20%，该商品的进货价为（ ）A ．80元B ．85元C ．90元D ．95元二、填空题（每小题3分，共24分）11、一个三位数，十位数字为x ，个位数字比十位数字少3，百位数字是十位数字的3倍，则这个三位数可表示为________________________。

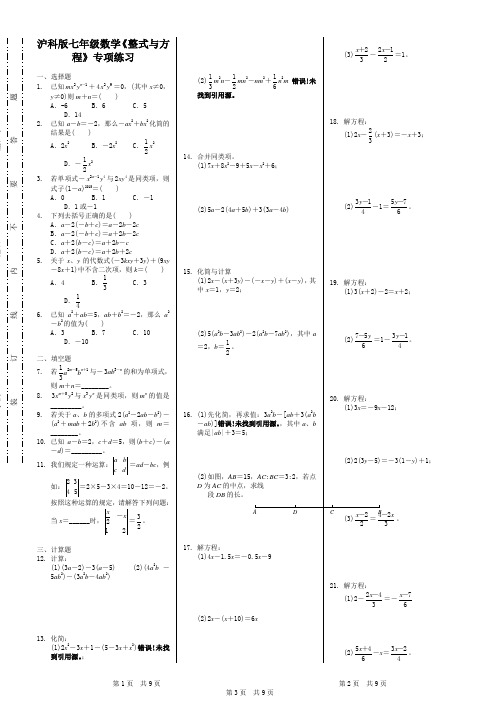
装订线内不要答题沪科版七年级数学《整式与方程》专项练习一、选择题1. 已知n mx y 2－1＋x y 294＝0，(其中x ≠0，y ≠0)则m ＋n ＝( )A ．-6B ．6C ．5D ．142. 已知a －b ＝－2，那么－ax 2＋bx 2化简的结果是( )A ．2x 2B ．－2x 2C ．12x 2D ．－12x 23. 若单项式－a x y 2－14与xy 42是同类项，则式子(1－a )2015＝( )A ．0B ．1C ．－1D ．1或－14. 下列去括号正确的是( )A ．a －2(－b ＋c )＝a －2b －2cB ．a －2(－b ＋c )＝a ＋2b －2cC ．a ＋2(b －c )＝a ＋2b －cD ．a ＋2(b －c )＝a ＋2b ＋2c5. 关于x 、y 的代数式(－3kxy ＋3y )＋(9xy－8x ＋1)中不含二次项，则k ＝( )A ．4B ．13C ．3D ．146. 已知a 2＋ab ＝5，ab ＋b 2＝－2，那么a2－b 2的值为( )A ．3B ．7C ．10D ．－10二、填空题7. 若m n a b 2－5＋113与－n ab 3－3的和为单项式，则m ＋n ＝________。

8. m x y ＋523与n x y 3是同类项，则n m 的值是_________。

9. 若关于a 、b 的多项式2(a 2－2ab －b 2)－(a 2＋mab ＋2b 2)不含ab 项，则m ＝________。

10. 已知a －b ＝2，c ＋d ＝5，则(b ＋c )－(a－d )＝_________。

11. 我们规定一种运算： a bc d＝ad －bc ，例如：2345＝2×5－3×4＝10－12＝－2。

按照这种运算的规定，请解答下列问题：当x ＝______时， xx －212＝32。

三、计算题 12. 计算：(1)(3a －2)－3(a －5) (2)(4a 2b －5ab 2)－(3a 2b －4ab 2)13. 化简：(1)2x 2－3x ＋1－(5－3x ＋x 2)错误！未找到引用源。

整式的加减练习100题有答案整式的加减是初中数学中的重要基础知识，通过大量的练习可以帮助我们更好地掌握这部分内容。

以下是 100 道整式加减的练习题及答案，希望能对您有所帮助。

一、选择题1、下列式子中，是单项式的是（）A ＼（x ＋ y\）B ＼（3x^｛2}y\）C ＼（＼dfrac{1}｛x} ＼）D ＼（x^｛2} ＋ 1\）答案：B解析：由数与字母的积组成的代数式叫做单项式，单独的一个数或一个字母也叫做单项式。

选项 A 是多项式，选项 C 是分式，选项 D 是多项式，只有选项 B 是单项式。

2、下列计算正确的是（）A ＼（3a ＋ 2b ＝ 5ab\）B ＼（5y^｛2} 3y^｛2} ＝ 2\）C ＼（7a ＋ a ＝ 7a^｛2}＼）D ＼（3x^｛2}y 2yx^｛2} ＝ x^｛2}y\）答案：D解析：选项 A 中，3a 与 2b 不是同类项，不能合并；选项 B 中，＼（5y^｛2} 3y^｛2} ＝ 2y^｛2}＼）；选项 C 中，＼（7a ＋ a ＝ 8a\）；选项 D 计算正确。

3、化简\（（a b)＼）的结果是（）A ＼（ a ＋ b\）B ＼（ a b\）C ＼（a b\）D ＼（a ＋ b\）答案：C解析：＼（（a b) ＝ a b\）4、一个多项式加上\（3x^｛2}y 3xy^｛2}＼）得\（x^｛3} 3x^｛2}y\），则这个多项式是（）A ＼（x^｛3} ＋ 3xy^｛2}＼）B ＼（x^｛3} 3xy^｛2}＼）C ＼（x^｛3} 6x^｛2}y ＋ 3xy^｛2}＼） D ＼（ x^｛3} ＋ 6x^｛2}y 3xy^｛2}＼）答案：C解析：这个多项式为：＼（（x^｛3} 3x^｛2}y) （3x^｛2}y 3xy^｛2}）＝ x^｛3} 3x^｛2}y 3x^｛2}y ＋ 3xy^｛2} ＝ x^｛3} 6x^｛2}y ＋ 3xy^｛2}＼）5、化简\（5(2x 3) ＋ 4(3 2x)＼）的结果为（）A ＼（2x 3\）B ＼（2x ＋ 9\）C ＼（8x 3\）D ＼（18x 3\）答案：A解析：＼＼begin{align}＆5(2x 3) ＋ 4(3 2x)＼＼＝＆10x 15 ＋ 12 8x\＼＝＆（10x 8x) ＋（12 15)＼＼＝＆2x 3＼end{align}＼6、若\（A ＝ x^｛2} 2xy ＋ y^｛2}＼），＼（B ＝ x^｛2} ＋ 2xy ＋ y^｛2}＼），则\（A B ＝＼）（）A ＼（4xy\）B ＼（ 4xy\）C ＼（0\）D ＼（2y^｛2}＼）答案：B解析：＼（A B ＝（x^｛2} 2xy ＋ y^｛2}）（x^｛2} ＋ 2xy ＋y^｛2}）＝ x^｛2} 2xy ＋ y^｛2} x^｛2} 2xy y^｛2} ＝ 4xy\）7、下列去括号正确的是（）A ＼（a ＋（b c) ＝ a ＋ b ＋ c\）B ＼（a （b c) ＝ a b c\）C ＼（a （ b ＋ c) ＝ a ＋ b c\）D ＼（a （ b c) ＝ a ＋ b c\）答案：C解析：选项 A，＼（a ＋（b c) ＝ a ＋ b c\）；选项 B，＼（a （bc) ＝ a b ＋ c\）；选项 C 正确；选项 D，＼（a （ b c) ＝ a ＋ b ＋ c\）8、化简\（（a b) （a ＋ b)＼）的结果是（）A ＼（ 2b\）B ＼（2b\）C ＼（ 2a\）D ＼（2a\）答案：C解析：＼＼begin{align}＆（a b) （a ＋ b)＼＼＝＆a b a b\＼＝＆（a a) ＋（ b b)＼＼＝＆ 2b＼end{align}＼9、若单项式\（ 3a^｛m}b^｛3}＼）与\（4a^｛2}b^｛n}＼）是同类项，则\（m ＋ n ＝＼）（）A ＼（5\）B ＼（6\）C ＼（8\）D ＼（9\）答案：B解析：因为单项式\（ 3a^｛m}b^｛3}＼）与\（4a^｛2}b^｛n}＼）是同类项，所以\（m ＝ 2\），＼（n ＝ 3\），则\（m ＋ n ＝ 2 ＋ 3 ＝5\）10、下列式子中，正确的是（）A ＼（3x ＋ 5y ＝ 8xy\）B ＼（3y^｛2} y^｛2} ＝ 3\）C ＼（15ab 15ba ＝ 0\） D ＼（29x^｛3} 28x^｛3} ＝ x\）答案：C解析：选项 A 中，＼（3x\）与\（5y\）不是同类项，不能合并；选项 B 中，＼（3y^｛2} y^｛2} ＝ 2y^｛2}＼）；选项 C 正确；选项 D 中，＼（29x^｛3} 28x^｛3} ＝ x^｛3}＼）二、填空题11、单项式\（＼dfrac{2\pi ab^｛2}｝｛5}＼）的系数是_____，次数是_____。

(9)初一整式加减与方程测试题一、填空题：1．已知A=3x 2＋2x －3，B=2x 2－3x ＋3，则A ＋B= ，A －2B= 。

2．已知(a ＋b)2＋12-b =0，则 6ab －2ab －3(ab －1)= 。

3．如果x ＋y=5，则3－x －y= ；如果x －y=43，则4(y －x)= 。

4．若 53x a+1y 5 与 4x 2y b-1 是同类项，则a= ，b= 。

5．若(3＋m)x n+1y 是关于x ，y 的五次单项式，则n 。

6．若x p ＋4x 3－qx 2－2x ＋5是关于x 的五次五项式，则－p= 。

7．若方程2mx －5=x －4m 的解是x =1的解，则m= 。

8．若方程(m ＋1)x=2的解是 x = 1，则m= 。

9．方程x -1=1的解是x= 。

10．一种商品的进价是150元，销售价是180元，这种商品的利润率为 。

二、选择题:1．设－m 2为A ，1－n 2为B ，那么A －3B 为 （ ）（A ） －m 2－n 2＋3 （B ）m 2－n 2－3（C ）－m 2＋3n 2－3 （D ）5m 2＋n 2－32．已知y=bx 3＋2，当x=－1时，y=0，那么当x=2时，y 的值是 （ ）（A ）17 （B ）－17 （C ）18 （D ）－183．使ax 2－2xy ＋y 2 = 6x 2 + bxy ＋cy 2成立的a ，b ，c 依次是（ ）（A ）6，－2，－1 （B ）－3，7，－1（C ）6，2，1 （D ）6，－2，14．一个数增加2倍后再加上22，和为55，这个数是 （ ）（A ）22 （B ）33 （C ）11 （D ）445．如果三个连续偶数的和为72，那么其中最大数为 （ ）（A ）26 （B ）27 （C ）28 （D ）30三、计算题 :1．(－3x 2－5xy ＋3y 2)－(－21x 2－37xy ＋3y 2)2．(4x 2－2x －1)－{5x 2－[8x －2－3(x 2＋x)]－x 2}四、解下列方程:1． 2x －31x - － 232-x = 6x ＋12．2145+x ＋3=6五、解答题 ：1．一队学生从学校出发去部队军训，行进速度是5千米/ 时，走了4.5千米时，一名通讯员按原路返回学校报信，然后他随即追赶队伍，通讯员的速度是14千米/ 时，他在距部队6千米处追上队伍。

整式的加减练习100题有答案整式的加减是初中数学中的重要基础知识，对于后续学习方程、函数等内容起着关键作用。

为了帮助大家更好地掌握整式的加减运算，以下为大家准备了 100 道练习题，并附上详细的答案及解析。

一、选择题（共 30 题）1、下列式子中，属于整式的是（）A x ＋ 1B 1/xC x²＋1D √x答案：C解析：整式为单项式和多项式的统称，单项式是数或字母的乘积，单独的一个数或字母也是单项式；几个单项式的和叫做多项式。

选项A 是多项式；选项 B 是分式；选项 C 是多项式；选项 D 是根式，不是整式。

所以属于整式的是 C。

2、下列整式中，次数为 2 的是（）A x²B x³ 2xC x ＋ y²D 2x²y答案：A解析：单项式的次数是指单项式中所有字母的指数和。

选项 A 次数为 2；选项 B 次数为 3；选项 C 次数为 2，但它是多项式；选项 D 次数为 3。

所以次数为 2 的是 A。

3、化简－3(x 2y) ＋ 4(x 2y)的结果是（）A x 2yB x ＋ 2yC x 2yD x ＋ 2y答案：A解析：－3(x 2y) ＋ 4(x 2y) ＝－3x ＋ 6y ＋ 4x 8y ＝ x 2y4、下列式子中，与 2a 是同类项的是（）A 3a²B 2abC －3aD a²b答案：C解析：同类项是指所含字母相同，并且相同字母的指数也相同的项。

选项 A 字母指数不同；选项 B 字母不同；选项 C 与 2a 是同类项；选项 D 字母不同。

所以与 2a 是同类项的是 C。

5、化简 5(2x 3) ＋ 4(3 2x)的结果为（）A 2x 3B 2x ＋ 3C 18x 27D 18x ＋ 27答案：A解析：5(2x 3) ＋ 4(3 2x) ＝ 10x 15 ＋ 12 8x ＝ 2x 3二、填空题（共 30 题）1、单项式－2xy³的系数是_____，次数是_____。

整式的加减测试题含有绝对值的方程的加减运算整式的加减是数学中常见的基础运算，而含有绝对值的方程则是一类稍微复杂的方程。

本文将结合这两个概念，介绍整式的加减测试题以及含有绝对值的方程的加减运算方法。

一、整式的加减测试题整式是由常数和变量以及它们的乘积、积和幂作基本运算，按照运算法则排列而成的代数式。

整式的加减即将同类项相加或相减。

1. 例题1：将4x² + 3x - 5和2x² - 2x + 7进行相加。

解：首先将相同次数的项进行相加，得到：(4x² + 2x²) + (3x - 2x) + (-5 + 7)。

计算得到结果为6x² + x + 2。

2. 例题2：将6x³ - 4x² + 3x + 2和3x³ + 2x² - 5x + 1进行相减。

解：首先将相同次数的项进行相减，得到：(6x³ - 3x³) + (-4x² - 2x²) + (3x + 5x) + (2 - 1)。

计算得到结果为3x³ - 6x² + 8x + 1。

二、含有绝对值的方程的加减运算含有绝对值的方程是常见的一类方程，其特点是方程中含有绝对值符号。

在解这类方程时，需要分情况讨论。

1. 例题3：解方程|2x + 1| + |x - 3| = 7解：首先将绝对值展开，得到以下四种情况：当2x + 1 ≥ 0 且 x - 3 ≥ 0时，原方程变为(2x + 1) + (x - 3) = 7，解得x = 2；当2x + 1 ≥ 0 且 x - 3 < 0时，原方程变为(2x + 1) - (x - 3) = 7，解得x = 2；当2x + 1 < 0 且 x - 3 ≥ 0时，原方程变为-(2x + 1) + (x - 3) = 7，解得x = 5；当2x + 1 < 0 且 x - 3 < 0时，原方程变为-(2x + 1) - (x - 3) = 7，解得x = 5。

初一整式的加减试题及答案一、选择题（每题2分，共10分）1. 下列哪个选项不是同类项？A. 3x²B. -2x²C. 5xD. 4x²2. 计算下列整式相加的结果：(3x - 2y) + (4x + y) =A. 7x - yB. 7x + 3yC. 6x - yD. 6x + y3. 合并同类项后，下列整式的结果是多少？5x² + 3x - 2x² - 4x + 1A. 3x² + x + 1B. 3x² - x + 1C. x² - x + 1D. x² + 4x + 14. 如果a + b = 10，那么下列哪个表达式的结果不是10？A. a + bB. a - b + 2bC. a + 2b - bD. 2a + 2b - a5. 根据题目条件，下列哪个选项是正确的？已知2x + 3 = 11，求x的值。

A. x = 4B. x = 5C. x = 6D. x = 7二、填空题（每题2分，共10分）6. 计算下列整式的差：(5x² - 3x + 1) - (3x² + 2x - 4) =__________。

7. 如果3x + 4 = 16，那么3x = __________。

8. 合并同类项：4y + 2 - 3y - 5 = __________。

9. 已知a = 3，b = 5，求下列整式的值：a² - b = __________。

10. 计算下列整式的和：(2x - 3) + (3x + 2) = __________。

三、解答题（每题5分，共10分）11. 已知x + y = 7，x - y = 5，求2x的值。

12. 计算下列整式的值，其中a = 2，b = 3：3a² b - 2ab² + 4ab - 5b²。

答案1. 答案：C2. 答案：A3. 答案：C4. 答案：B5. 答案：A6. 答案：2x² - 5x + 57. 答案：128. 答案：y - 39. 答案：410. 答案：5x - 111. 解答：由x + y = 7和x - y = 5，相加得2x = 12，所以2x = 12。

初一数学整式的加减试题答案及解析1.某城市一年漏掉的水，相当于建一个自来水厂，据不完全统计，全市至少有个水龙头，个抽水马桶漏水。

如果一个关不紧的水龙头一个月漏掉a立方米水，一个抽水马桶一个月漏掉b立方米水，那么一个月造成的水流失量至少是( )立方米.A．6a+2b B．C．D．【答案】C.【解析】因为全市至少有个水龙头，一个关不紧的水龙头一个月漏掉a立方米水，所以全市水龙头一个月造成的水流失量至少是：立方米，全市至少有个抽水马桶漏水，个抽水马桶一个月漏掉b立方米水，所以全市马桶一个月造成的水流失量至少是：立方米，所以一个月造成的水流失量至少是：立方米，所以C正确.【考点】整式的加减.2.先化简，后求值：已知，求代数式的值.【答案】【解析】解：由得，，解得，.将代数式化简得.将，代入得原式.3.在排成每行七天的日历表中取下一个方块（如图）.若所有日期数之和为189，则的值为（）A．21B．11C．15D．9【答案】A【解析】日历的排列是有一定规律的，在日历表中取下一个3×3方块，当中间的数是的话，它上面的数是，下面的数是，左边的数是，右边的数是，左边最上面的数是，最下面的数是，右边最上面的数是，最下面的数是.若所有日期数之和为189，则，即，解得：，故选A．4.化简关于的代数式.当为何值时，代数式的值是常数？【答案】【解析】解：将去括号，得，合并同类项，得.若代数式的值是常数，则，解得.故当时，代数式的值是常数.5.已知实数,满足，则等于（）A．3B．-3C．D．-1【答案】A【解析】根据根号下为非负数及任何数的平方为非负数可判断：x-2=0，y+1=0.x=2，y=-1。

所以x-y=3.选A【考点】整式运算点评：本题难度较低，主要考查学生对实数与整式运算知识点的掌握。

为中考常考题型，要求学生牢固掌握。

6.将n张长度为10厘米的纸条，一张接一张地粘成长纸条，粘合部分的长度都是3厘米，则这张粘合后的长纸条总长是______________厘米．(用含n的代数式表示)【答案】7n+3【解析】由题意可知10n-3（n-0）=7n-3.根据题意显然粘和部分共有（n-1）个，所以10n-3（n-1）=7n+3【考点】代数式的求法点评：本题属于利用代数式的基本形式进行找规律推导分析进而利用基本知识运算7.下列各式计算正确的是 ( )A．B．C．D．【答案】D【解析】A ；B．已经为最简式。