四川省渠县崇德实验学校2020年中考数学第三轮总复习：三角形的内角和与外角和(含答案)

四川省渠县崇德实验学校2020年中考第二轮九年级数学三角形、四边形压轴题专题复习一、选择题1、如图，矩形ABCD中，AB＝4，AD＝2，E为AB的中点，F为EC上一动点，P为DF中点，连接PB，则PB的最小值是（）A．2B．4C D．2、如图，在Rt△ABO中，∠OBA＝90°，A(4，4)，点C在边AB上，且ACBC＝13，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P的坐标为（）A．(2，2) B．(52，52) C．(83，83) D．(3，3)3、如图，正方形ABCD，点F在边AB上，且AF：FB＝1：2，CE⊥DF，垂足为M，且交AD于点E，AC与DF交于点N，延长CB至G，使BG＝12BC，连接GM．有如下结论：①DE＝AF；②AN＝4AB；③∠ADF＝∠GMF；④S△ANF：S四边形CNFB＝1：8．上述结论中，所有正确结论的序号是（）A．①②B．①③C．①②③D．②③④二、填空题4、在矩形ABCD中，M，N，P，Q分别为边AB，BC，CD，DA上的点（不与端点重合）．对于任意矩形ABCD，下面四个结论中，①存在无数个四边形MNPQ是平行四边形；②存在无数个四边形MNPQ是矩形；③存在无数个四边形MNPQ是菱形；④至少存在一个四边形MNPQ是正方形．所有正确结论的序号是______5、如图，一个正方体由27个大小相同的小立方块搭成，现从中取走若干个小立方块，得到一个新的几何体．若新几何体与原正方体的表面积相等，则最多可以取走个小立方块．6、如图，▱ABCD的对角线AC，BD交于点O，CE平分∠BCD交AB于点E，交BD于点F，且∠ABC＝60°，AB＝2BC，连接OE．下列结论：①EO⊥AC；②S△AOD＝4S△OCF；③AC：BD＝：7；④FB2＝OF•DF．其中正确的结论有（填写所有正确结论的序号）7、如图，在以A为直角顶点的等腰直角三角形纸片ABC中，将B角折起，使点B落在AC 边上的点D（不与点A，C重合）处，折痕是EF．如图1，当CD＝12AC时，tanα1＝34；如图2，当CD＝13AC时，tanα2＝512；如图3，当CD＝14AC时，tanα3＝724；…依此类推，当CD＝1n1＋AC（n为正整数）时，tanαn＝．8、在平面直角坐标系中，直线l：y＝x+1与y轴交于点A1，如图所示，依次作正方形OA1B1C1，正方形C1A2B2C2，正方形C2A3B3C3，正方形C3A4B4C4，……，点A1，A2，A3，A4，……在直线l上，点C1，C2，C3，C4，……在x轴正半轴上，则前n个正方形对角线长的和是．三、解答题9、如图1，正方形ABDE和BCFG的边AB，BC在同一条直线上，且AB＝2BC，取EF的中点M，连接MD，MG，MB．（1）试证明DM⊥MG，并求MBMG的值．（2）如图2，将图1中的正方形变为菱形，设∠EAB＝2α（0＜α＜90°），其它条件不变，问（1）中MBMG的值有变化吗？若有变化，求出该值（用含α的式子表示）；若无变化，说明理由．10、【问题探究】（1）如图1，△ABC和△DEC均为等腰直角三角形，∠ACB＝∠DCE＝90°，点B，D，E在同一直线上，连接AD，BD．①请探究AD与BD之间的位置关系：；②若AC＝BC＝，DC＝CE＝，则线段AD的长为；【拓展延伸】（2）如图2，△ABC和△DEC均为直角三角形，∠ACB＝∠DCE＝90°，AC＝，BC＝，CD＝，CE＝1．将△DCE绕点C在平面内顺时针旋转，设旋转角∠BCD为α（0°≤α＜360°），作直线BD，连接AD，当点B，D，E在同一直线上时，画出图形，并求线段AD的长．11、如图，在正方形ABCD中，AB＝10cm，E为对角线BD上一动点，连接AE，CE，过E点作EF⊥AE，交直线BC于点F．E点从B点出发，沿着BD方向以每秒2cm的速度运动，当点E与点D重合时，运动停止．设△BEF的面积为ycm2，E点的运动时间为x秒．（1）求证：CE＝EF；（2）求y与x之间关系的函数表达式，并写出自变量x的取值范围；（3）求△BEF面积的最大值．12、在△ABC中，∠BAC＝90°，AB＝AC，AD⊥BC于点D．（1）如图1，点M，N分别在AD，AB上，且∠BMN＝90°，当∠AMN＝30°，AB＝2时，求线段AM的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+AN＝AM．13、如图，四边形ABCD是正方形，△EFC是等腰直角三角形，点E在AB上，且∠CEF＝90°，FG⊥AD，垂足为点C．（1）试判断AG与FG是否相等？并给出证明；（2）若点H为CF的中点，GH与DH垂直吗？若垂直，给出证明；若不垂直，说明理由．14、已知：如图，在四边形ABCD中，AB∥CD，∠ACB＝90°，AB＝10cm，BC＝8cm，OD 垂直平分A C．点P从点B出发，沿BA方向匀速运动，速度为1cm/s；同时，点Q从点D 出发，沿DC方向匀速运动，速度为1cm/s；当一个点停止运动，另一个点也停止运动．过点P作PE⊥AB，交BC于点E，过点Q作QF∥AC，分别交AD，OD于点F，G．连接OP，EG．设运动时间为t（s）（0＜t＜5），解答下列问题：（1）当t为何值时，点E在∠BAC的平分线上？（2）设四边形PEGO的面积为S（cm2），求S与t的函数关系式；（3）在运动过程中，是否存在某一时刻t，使四边形PEGO的面积最大？若存在，求出t的值；若不存在，请说明理由；（4）连接OE，OQ，在运动过程中，是否存在某一时刻t，使OE⊥OQ？若存在，求出t的值；若不存在，请说明理由．15、如图1，在矩形ABCD中，AB＝8，AD＝10，E是CD边上一点，连接AE，将矩形ABCD 沿AE折叠，顶点D恰好落在BC边上点F处，延长AE交BC的延长线于点G．（1）求线段CE的长；（2）如图2，M，N分别是线段AG，DG上的动点（与端点不重合），且∠DMN＝∠DAM，设AM＝x，DN＝y．①写出y关于x的函数解析式，并求出y的最小值；②是否存在这样的点M，使△DMN是等腰三角形？若存在，请求出x的值；若不存在，请说明理由．16、如图，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC＝∠DAE＝90°．（1）如图1，连接BE，CD，BE的廷长线交AC于点F，交CD于点P，求证：BP⊥CD；（2）如图2，把△ADE绕点A顺时针旋转，当点D落在AB上时，连接BE，CD，CD的延长线交BE于点P，若BC＝6，AD＝3，求△PDE的面积．17、如图1，菱形AEGH的顶点E、H在菱形ABCD的边上，且∠BAD＝60°，请直接写出HD：GC：EB的结果（不必写计算过程）（2）将图1中的菱形AEGH绕点A旋转一定角度，如图2，求HD：GC：EB；（3）把图2中的菱形都换成矩形，如图3，且AD：AB＝AH：AE＝1：2，此时HD：GC：EB 的结果与（2）小题的结果相比有变化吗？如果有变化，直接写出变化后的结果（不必写计算过程）；若无变化，请说明理由．18、问题提出：如图，图①是一张由三个边长为1的小正方形组成的“L”形纸片，图②是一张a×b的方格纸（a×b的方格纸指边长分别为a，b的矩形，被分成a×b个边长为1的小正方形，其中a≥2，b≥2，且a，b为正整数）．把图①放置在图②中，使它恰好盖住图②中的三个小正方形，共有多少种不同的放置方法？问题探究：为探究规律，我们采用一般问题特殊化的策略，先从最简单的情形入手，再逐次递进，最后得出一般性的结论．探究一：把图①放置在2×2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图③，对于2×2的方格纸，要用图①盖住其中的三个小正方形，显然有4种不同的放置方法．探究二：把图①放置在3×2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图④，在3×2的方格纸中，共可以找到2个位置不同的2 2×方格，依据探究一的结论可知，把图①放置在3×2的方格纸中，使它恰好盖住其中的三个小正方形，共有2×4＝8种不同的放置方法．探究三：把图①放置在a×2的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图⑤，在a×2的方格纸中，共可以找到个位置不同的2×2方格，依据探究一的结论可知，把图①放置在a×2的方格纸中，使它恰好盖住其中的三个小正方形，共有种不同的放置方法．探究四：把图①放置在a×3的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？如图⑥，在a×3的方格纸中，共可以找到个位置不同的2×2方格，依据探究一的结论可知，把图①放置在a×3的方格纸中，使它恰好盖住其中的三个小正方形，共有种不同的放置方法．……问题解决：把图①放置在a×b的方格纸中，使它恰好盖住其中的三个小正方形，共有多少种不同的放置方法？（仿照前面的探究方法，写出解答过程，不需画图．）问题拓展：如图，图⑦是一个由4个棱长为1的小立方体构成的几何体，图⑧是一个长、宽、高分别为a，b，c（a≥2，b≥2，c≥2，且a，b，c是正整数）的长方体，被分成了a×b×c个棱长为1的小立方体．在图⑧的不同位置共可以找到个图⑦这样的几何体．19、如图1，菱形ABCD的顶点A，D在直线上，∠BAD＝60°，以点A为旋转中心将菱形ABCD顺时针旋转α（0°＜α＜30°），得到菱形AB′C′D′，B′C′交对角线AC于点M，C′D′交直线l于点N，连接MN．（1）当MN∥B′D′时，求α的大小．（2）如图2，对角线B′D′交AC于点H，交直线l与点G，延长C′B′交AB于点E，连接EH．当△HEB′的周长为2时，求菱形ABCD的周长．20、如图，在正方形ABCD中，边长为4，∠MDN＝90°，将∠MDN绕点D旋转，其中DM边分别与射线BA、直线AC交于E、Q两点，DN边与射线BC交于点F；连接EF，且EF与直线AC交于点P．（1）如图1，点E在线段AB上时，①求证：AE＝CF；②求证：DP垂直平分EF；（2）当AE＝1时，求PQ的长．。

四川省渠县崇德实验学校2020年中考九年级数学：全等三角形复习测试卷（测试时间120分钟，满分100分）一、选择题（每小题3分，共24分）1.有下列说法：①形状相同的三角形是全等三角形；②面积相等的三角形是全等三角形；③全等三角形的周长相等；④经过平移、翻折或旋转得到的三角形与原三角形是全等三角形.其中正确的有(B)A.1个B.2个C.3个D.4个2.如图，已知∠ABC＝∠DCB，添加以下条件，不能判定△ABC≌△DCB的是(C)A.∠A＝∠DB.∠ACB＝∠DBCC.AC＝DBD.AB ＝DC3.如图，点E，F在线段BC上，△ABF与△DCE全等，点A与点D，点B与点C 是对应点，AF与DE相交于点M，则∠DCE＝(A)A.∠BB.∠AC.∠EMFD.∠AFB4.在下列各图中，a，b，c为三角形的边长，则甲、乙、丙三个三角形和左侧△ABC全等的是(B)A.甲和乙B.乙和丙C.甲和丙D.只有丙5.如图，在△ABC和△DEC中，已知AB＝DE，还须添加两个条件才能使△ABC≌△DEC，不能添加的一组条件是(B)A.BC＝EC，∠B＝∠EB.BC＝DC，∠A＝∠DC.BC＝EC，AC＝DCD.∠B＝∠E，∠A＝∠D6.如图，在等边△ABC中，M，N分别在BC，AC上移动，且BM＝CN，AM与BN相交于点Q，则∠BAM＋∠ABN的度数是(A)A.60°B.55°C.45°D.不能确定7.如图，△ACB和△ECD都是等腰直角三角形，CA＝CB，CE＝CD，△ACB的顶点A 在△ECD的斜边DE上.若AE＝2，AD＝6，则两个三角形重叠部分的面积为(D)A. 2B.3－ 2C.3－1D.3－ 38.如图，在△OAB和△OCD中，OA＝OB，OC＝OD，OA＞OC，∠AOB＝∠COD＝40°，连接AC，BD交于点M，连接OM.下列结论：①AC＝BD；②∠AMB＝40°；③OM平分∠BOC；④MO平分∠BMC.其中正确的个数为(B)A.4B.3C.2D.1二、填空题（每小题3分，共15分）9.如图，已知AD＝AE，请你添加一个条件，使得△ADC≌△AEB，你添加的条件是答案不唯一，如：AB＝AC，∠ADC＝∠AEB或∠ABE＝∠ACD.(不添加任何字母和辅助线)10.如图，在△ABC中，AB＝AC，点D，E都在边BC上，∠BAD＝∠CAE.若BD＝9，则CE的长为9.11.如图，把△ABC沿直线AB翻折至△ABD.(1)△ABC≌△ABD；(2)若CB＝5，则DB＝5；(3)若△ABC的面积为10，则△ABD的面积为10.12.如图，正方形ABCD的边长为5，点E，F分别在AD，CD上，AE＝DF＝2，BE与AF相交于点G，点H为BF的中点，连接GH，则GH213.如图，正方形ABCD的边长为a，点E在边AB上运动(不与点A，B重合)，∠DAM＝45°，点F在射线AM上，且AF＝2BE，CF与AD相交于点G，连接EC，EF，EG，则下列结论：①∠ECF＝45°；②△AEG的周长为(1＋22)a；③BE2＋DG2＝EG2；④△EAF的面积的最大值18a2.其中正确的结论是①④.(填写所有正确结论的序号)三、解答题（共61分）14.已知：如图，AB＝AE，AB∥DE，∠ECB＝70°，∠D＝110°，求证：△ABC≌△EAD.证明：∵∠ECB＝70°，∴∠ACB＝110°.又∵∠D ＝110°， ∴∠ACB ＝∠D.∵AB ∥DE ，∴∠CAB ＝∠E. 在△ABC 和△EAD 中，⎩⎨⎧∠ACB ＝∠D ，∠CAB ＝∠E ，AB ＝EA ，∴△ABC ≌△EAD(AAS).15.如图，点O 是线段AB 的中点，OD ∥BC ，且OD ＝BC.(1)求证：△AOD ≌△OBC ；(2)若∠ADO ＝35°，求∠DOC 的度数.解：(1)证明：∵点O 是线段AB 的中点，∴AO ＝OB. ∵OD ∥BC ，∴∠AOD ＝∠OBC.在△AOD 和△OBC 中，⎩⎨⎧AO ＝OB ，∠AOD ＝∠OBC ，OD ＝BC ，∴△AOD ≌△OBC(SAS).(2)∵△AOD ≌△OBC ，∴∠ADO ＝∠OCB ＝35°. ∵OD ∥BC ，∴∠DOC ＝∠OCB ＝35°.16.如图，点D 是AB 上一点，DF 交AC 于点E ，DE ＝FE ，FC ∥AB.求证：AE ＝CE.证明：∵FC ∥AB ，∴∠DAE ＝∠FCE ，∠ADE ＝∠CFE. 在△ADE 和△CFE 中，⎩⎨⎧∠DAE ＝∠FCE ，∠ADE ＝∠CFE ，DE ＝FE ，∴△ADE ≌△CFE(AAS). ∴AE ＝CE.17.如图，在四边形ABCD 中，AB ∥DC ，点E 是CD 的中点，AE ＝BE.求证：∠D ＝∠C.证明：∵AE ＝BE ， ∴∠EAB ＝∠EBA. ∵AB ∥DC ，∴∠DEA ＝∠EAB ，∠CEB ＝∠EBA. ∴∠DEA ＝∠CEB. ∵点E 是CD 的中点， ∴DE ＝CE.在△ADE 和△BCE 中，⎩⎨⎧DE ＝CE ，∠DEA ＝∠CEB ，AE ＝BE.∴△ADE ≌△BCE(SAS). ∴∠D ＝∠C.7.如图，DE ⊥AB ，CF ⊥AB ，垂足分别是E ，F ，DE ＝CF ，AE ＝BF ，求证：AC ∥BD.证明：∵AE ＝BF ，∴AE ＋EF ＝BF ＋EF ，即AF ＝BE. ∵CF ⊥AB ，DE ⊥AB ， ∴∠AFC ＝∠BED ＝90°.在△AFC 和△BED 中，⎩⎨⎧AF ＝BE ，∠AFC ＝∠BED ，CF ＝DE ，∴△AFC ≌△BED(SAS). ∴∠A ＝∠B.∴AC ∥BD.18.如图，点M ，N 分别是正五边形ABCDE 的边BC ，CD 上的点，且BM ＝CN ，AM 交BN 于点P.(1)求证：△ABM ≌△BCN ； (2)求∠APN 的度数.解：(1)证明：∵五边形ABCDE 为正五边形， ∴AB ＝BC ，∠ABM ＝∠C. ∴在△ABM 和△BCN 中，⎩⎨⎧AB ＝BC ，∠ABM ＝∠C ，BM ＝CN ，∴△ABM ≌△BCN(SAS). (2)∵△ABM ≌△BCN ， ∴∠BAM ＝∠CBN.∵∠APN ＝∠BAM ＋∠ABP ，∴∠APN ＝∠CBN ＋∠ABP ＝∠ABC ＝（5－2）×180°5＝108°，即∠APN 的度数为108°.19.如图，在四边形ABCD 中，∠A ＝∠BCD ＝90°，BC ＝CD ，CE ∥AD 与AB 交于点E.求证：AE ＝CE.证明：过点D 作DF ⊥CE 于点F ， ∵CE ∥AD ，∴∠1＝∠A ＝90°.∴四边形AEFD是矩形.∴DF＝AE.∵∠BCD＝90°，∴∠2＋∠3＝90°.∵∠B＋∠2＝90°，∴∠B＝∠3.∵∠1＝∠DFC＝90°，BC＝CD，∴△BCE≌△CDF(AAS).∴CE＝DF.∴AE＝CE.20.如图1，在锐角△ABC中，∠ABC＝45°，高AD，BE相交于点F.(1)判断BF与AC的数量关系，并说明理由；(2)如图2，将△ACD沿线段AD对折，点C落在BD上的点M，AM与BE相交于点N，当DE∥AM时，判断NE与AC的数量关系，并说明理由.解：(1)BF＝AC，理由如下：∵AD⊥BC，BE⊥AC，∴∠ADB＝∠ADC＝∠AEB＝90°.∵∠ABC＝45°，∴△ABD是等腰直角三角形.∴AD＝BD.∵∠AFE ＝∠BFD ，∴∠DAC ＝∠DBF. 在△ADC 和△BDF 中，⎩⎨⎧∠DAC ＝∠DBF ，AD ＝BD ，∠ADC ＝∠BDF ，∴△ADC ≌△BDF(ASA).∴BF ＝AC. (2)NE ＝12AC.理由如下：由折叠得：MD ＝DC ，∵DE ∥AM ，∴AE ＝EC.∵BE ⊥AC ，∴AB ＝BC. ∴∠ABE ＝∠CBE.由(1)得：△ADC ≌△BDF ， ∵△ADC ≌△ADM ，∴△BDF ≌△ADM. ∴∠DBF ＝∠MAD.∵∠DBA ＝∠BAD ＝45°.∴∠DBA －∠DBF ＝∠BAD －∠MAD ，即∠ABN ＝∠BAN.∵∠ANE ＝∠ABN ＋∠BAN ＝2∠ABE ，∠NAE ＝2∠NAD ＝2∠CBE ， ∴∠ANE ＝∠NAE ＝45°.∴AE ＝NE. ∴NE ＝12AC.。

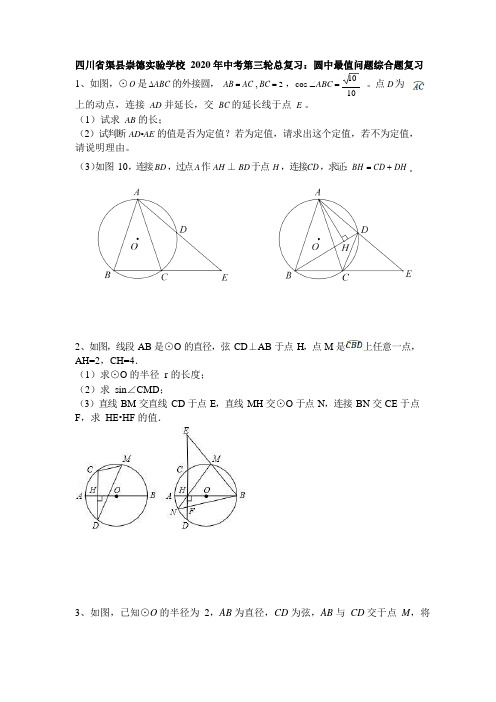
四川省渠县崇德实验学校2020 年中考第三轮总复习：圆中最值问题综合题复习1、如图，⊙O 是∆ABC 的外接圆，AB =AC , BC = 2 ，cos ∠ABC=1010上的动点，连接AD 并延长，交BC 的延长线于点 E 。

（1）试求AB 的长；。

点D为（2）试判断AD▪AE 的值是否为定值？若为定值，请求出这个定值，若不为定值，请说明理由。

（3）如图10，连接BD，过点A作AH⊥BD于点H，连接CD ，求证：BH =CD +DH 。

2、如图，线段AB 是⊙O 的直径，弦CD⊥AB 于点H，点M 是上任意一点，AH=2，CH=4．（1）求⊙O 的半径r 的长度；（2）求sin∠CMD；（3）直线BM 交直线CD 于点E，直线MH 交⊙O 于点N，连接BN 交CE 于点F，求HE•HF 的值．3、如图，已知⊙O 的半径为2，AB 为直径，CD 为弦，AB 与CD 交于点M，将弧CD 沿着CD 翻折后，点A 与圆心O 重合，延长OA 至P，使AP=OA，连接PC。

（1）求CD 的长；（2）求证：PC 是⊙O 的切线；（3）点G 为弧ADB 的中点，在PC 延长线上有一动点Q，连接QG 交AB 于点E，交弧BC 于点F（F 与B、C 不重合）。

问GE▪GF 是否为定值？如果是，求出该定值；如果不是，请说明理由。

4、如图，在平面直角坐标系xoy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A、B 两点，交 y 轴于C、D 两点，且C 为的中点，AE 交 y 轴于G 点，若点 A 的坐标为（－2，0），AE 8（1）求点C 的坐标.（2）连结MG、BC ，求证：MG ∥BC（3）如图10－2，过点D 作⊙M 的切线，交x 轴于点P .动点F 在⊙M 的圆周上运动时，的比值是否发生变化，若不变，求出比值：若变化，说明变化规律。

5、如图1，以点M（－1,0）为圆心的圆与y 轴、x 轴分别交于点A、B、C、D，3 3 直 线与⊙M 相切于点 H ，交 x 轴于点 E ，交 y 轴于点 F ．（1）请直接写出 OE 、⊙M 的半径 r 、CH 的长；（2）如图 2，弦 HQ 交 x 轴于点 P ，且 DP :PH ＝3:2，求 cos ∠QHC 的值； （3）如图 3，点 K 为线段 EC 上一动点（不与 E 、C 重合），连接 BK 交⊙M 于点 T ，弦 AT 交 x 轴于点 N ．是否存在一个常数 a ，始终满足 MN ·MK ＝a ，如果存在，请求出 a 的值；如果不存在，请说明理由．图 1图 2图 36、如图，在平面直角坐标系 xoy 中，点 A （ - ，0）、B （ 3为直径的⊙G 交 y 轴于 C 、D 两点。

四川省渠县崇德实验学校2020年中考九年级数学：相似三角形复习测试题一、选择题（每小题3分，共36分）1.下列说法正确的是( )A.两个直角三角形一定相似B.两个相似图形一定是位似图形C.两个菱形一定相似D.两个正三角形一定相似 2.如图，点C 把线段AB 分成两条线段AC 和BC ，如果AC AB ＝BCAC，那么称线段AB 被点C 黄金分割，AC 与AB 的比叫做黄金比，其比值是( )A.5－12B.3－52C.5＋12D.3＋523.下列命题是真命题的是( )A.如果两个三角形相似，相似比为4∶9，那么这两个三角形的周长比为2∶3B.如果两个三角形相似，相似比为4∶9，那么这两个三角形的周长比为4∶9C.如果两个三角形相似，相似比为4∶9，那么这两个三角形的面积比为2∶3D.如果两个三角形相似，相似比为4∶9，那么这两个三角形的面积比为4∶9 4.如图，在△ABC 中，点D ，E ，F 分别在边AB ，AC ，BC 上，且DE∥BC，EF∥AB.若AD ＝2BD ，则CFBF的值为( )A.12B.13C.14D.235.要制作两个形状相同的三角形框架，其中一个三角形的三边长分别为5 cm ，6 cm 和9 cm ，另一个三角形的最短边长为2.5 cm ，则它的最长边为( ) A.3 cm B.4 cm C.4.5 cm D.5 cm6.如图，在△ABC 中，点D 是边AB 上的一点，∠ADC＝∠ACB，AD ＝2，BD ＝6，则边AC 的长为( )A.2B.4C.6D.87.学校门口的栏杆如图所示，栏杆从水平位置BD 绕O 点旋转到AC 位置，已知AB⊥BD，CD⊥BD.垂足分别为B ，D ，AO ＝4 m ，AB ＝1.6 m ，CO ＝1 m ，则栏杆C 端应下降的垂直距离CD 为( )A.0.2 mB.0.3 mC.0.4 mD.0.5 m 8.如图，在△ABC 中，点D ，E 分别在AB 和AC 上，DE∥BC，M 为BC 边上一点(不与点B ，C 重合)，连接AM 交DE 于点N ，则( )A.AD AN ＝AN AEB.BD MN ＝MN CEC.DN BM ＝NE MCD.DN MC ＝NE BM9.如图，⊙O 是△ABC 的外接圆，已知AD 平分∠BAC 交⊙O 于点D ，交BC 边于点E ，AD ＝5，BD ＝2，则DE 的长为( )A.35B.425C.225D.4510.如图，在△ABC 中，点D ，E 分别在AB ，AC 边上，DE∥BC，∠ACD＝∠B.若AD ＝2BD ，BC ＝6，则线段CD 的长为( )A.2 3B.3 2C.2 6D.511.如图，在正方形ABCD 中，E ，F 分别在边AD ，CD 上，AF ，BE 相交于点G.若AE ＝3ED ，DF ＝CF ，则AGGF的值是( )A.43B.54C.65D.7612.如图所示，若△ABC 内一点P 满足∠PAC＝∠PBA＝∠PCB，则点P 为△ABC 的布洛卡点.三角形的布洛卡点(Brocard point)是法国数学家和数学教育家克洛尔(A.L.Crelle 1780－1855)于1816年首次发现，但他的发现并未被当时的人们所注意，1875年，布洛卡点被一个数学爱好者法国军官布洛卡(Brocard 1845－1922)重新发现，并用他的名字命名.问题：已知在等腰Rt△DEF 中，∠EDF＝90°.若点Q 为Rt△DEF 的布洛卡点，DQ ＝1，则EQ ＋FQ ＝( )A.5B.4C.3＋ 2D.2＋ 2 二、填空题（每小题3分，共18分） 13.若x y ＝23，则x －2y y＝.14.如图，在▱ABCD 中，点E 是边AD 的中点，EC 交对角线BD 于点F ，则EF∶FC 等于.15.如图，一组平行横格线，其相邻横格线间的距离都相等，已知点A ，B ，C ，D ，O 都在横格线上，且线段AD ，BC 交于点O ，则AB∶CD 等于.16.如图，点E 是▱ABCD 的边BC 延长线上一点，连接AE ，交CD 于点F ，连接BF.写出图中任意一对相似三角形：17.在▱ABCD 中，E 是AD 上一点，且点E 将AD 分为2∶3的两部分，连接BE ，AC 相交于F ，则S △AEF ∶S △CBF 是18.如图，在Rt△ABC中，∠ACB＝90°，AB＝10，BC＝6，CD∥AB，∠ABC的平分线BD交AC于E，DE＝三、解答题（共66分）19.如图，在▱ABCD中，连接对角线AC，延长AB至点E，使BE＝AB，连接DE，分别交BC，AC交于点F，G.(1)求证：BF＝CF；(2)若BC＝6，DG＝4，求FG的长.20.如图，在正方形ABCD中，点E，F分别在边AB，AD上，EF⊥CE于点E. (1)求证：△AEF∽△BCE；(2)若BEAE＝12，求EFCE的值.21.如图，∠ABD＝∠BCD＝90°，DB平分∠ADC，过点B作BM∥CD交AD于点M，连接CM交DB于点N.(1)求证：BD2＝AD·CD；(2)若CD＝6，AD＝8，求MN的长.22.如图，Rt△ABC中，∠ACB＝90°，AC＝BC，P为△ABC内部一点，且∠APB＝∠BPC＝135°.(1)求证：△PAB∽△PBC；(2)求证：PA＝2PC；(3)若点P到三角形的边AB，BC，CA的距离分别为h1，h2，h3，求证：h21＝h2h3.参考答案：一、选择题1-12 DABACBCCDCCD二、填空题13、－43 14、1∶2 15、2∶3 16、答案不唯一，如△EFC∽△AFD，△EAB∽△AFD，△EFC∽△EAB. 17、4∶25或9∶25. 18、955. 三、解答题19、解：(1)证明：∵四边形ABCD 是平行四边形， ∴AD∥BC，AD ＝BC. ∴△EBF∽△EAD. ∴BF AD ＝EB EA ＝12. ∴BF＝12AD ＝12BC.∴BF＝CF.(2)∵四边形ABCD 是平行四边形， ∴AD∥BC.∴△FGC∽△DGA. ∴FG DG ＝FC AD ，即FG 4＝12. 解得FG ＝2.20、解：(1)∵∠A＝∠B＝90°，∠FEC＝90°， ∴∠AEF＋∠AFE＝90°，∠AEF＋∠BEC＝90°. ∴∠AFE＝∠BEC. ∴△AEF∽△BCE. (2)由BE AE ＝12，设BE ＝x ，则AE ＝2x ，AB ＝3x ＝BC. ∵△AEF∽△BCE，∴EF CE ＝AE BC ＝23. 21解：(1)证明：∵BD 平分∠ADC， ∴∠ADB＝∠BDC.又∵∠ABD＝∠BCD＝90°， ∴△DAB∽△DBC.∴BD CD ＝ADBD，即BD 2＝AD·CD. (2)由(1)可知：BD 2＝AD·CD. ∵CD＝6，AD ＝8，∴BD 2＝6×8＝48. ∴BC 2＝BD 2－CD 2＝48－36＝12.∵BM∥CD，∴∠MBD＝∠BDC＝∠ADB，∠MBC＝180°－∠BCD＝90°. ∴DM＝BM.∵∠ADB＋∠A＝∠MBD＋∠MBA＝90°， ∴∠A＝∠MBA.∴AM＝BM ＝DM ＝12AD ＝4.∴CM＝BM 2＋BC 2＝16＋12＝27. ∵BM∥CD，∴△BMN∽△DCN.∴MN CN ＝BMCD.设MN ＝x ，则CN ＝27－x. 则x 27－x ＝46.解得x ＝475.经检验，x ＝475是原分式方程的解.∴MN＝475. 22、证明：(1)∵∠ACB＝90°，AC ＝BC ， ∴∠ABC＝∠PBA＋∠PBC＝45°. 又∵∠APB＝135°，∴∠PAB＋∠PBA＝45°.∴∠PBC＝∠PAB. 又∵∠APB＝∠BPC＝135°，∴△PAB∽△PBC. (2)∵△PAB∽△PBC，∴PA PB ＝PB PC ＝ABBC . 在Rt△ABC 中，BC ＝AC ，∴ABBC＝ 2. ∴PB＝2PC ，PA ＝2PB.∴PA＝2PC.(3)过点P 作PD⊥BC 于点D ，PE⊥A C 于点E ，PF⊥AB 于点F. ∴PF＝h 1，PD ＝h 2，PE ＝h 3.∵∠CPB＋∠APB＝135°＋135°＝270°， ∴∠APC＝90°.∴∠EAP＋∠ACP＝90°. 又∵∠ACB＝∠ACP＋∠PCD＝90°， ∴∠EAP＝∠PCD.∴Rt△AEP∽Rt△CDP. ∴PE DP ＝AP PC ＝2，即h 3h 2＝2.∴h 3＝2h 2.∵△PAB∽△PBC，∴h1h2＝ABBC＝2.∴h1＝2h2.∴h21＝2h22＝2h2·h2＝h2h3，即h21＝h2h3.。

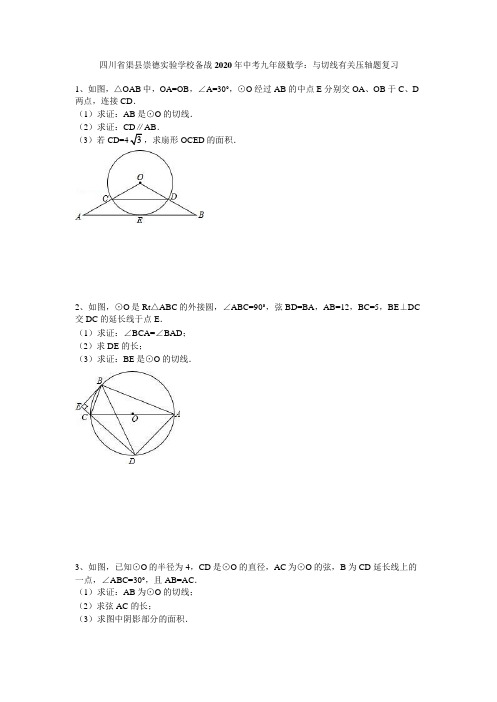
四川省渠县崇德实验学校备战2020 年中考九年级数学：与切线有关压轴题复习1、如图，△OAB 中，OA=OB，∠A=30°，⊙O 经过AB 的中点E 分别交OA、OB 于C、D 两点，连接CD．（1）求证：AB 是⊙O 的切线．（2）求证：CD∥AB．（3）若CD=4，求扇形OCED 的面积．2、如图，⊙O 是Rt△ABC 的外接圆，∠ABC=90°，弦BD=BA，AB=12，BC=5，BE⊥DC 交DC 的延长线于点E．（1）求证：∠BCA=∠BAD；（2）求DE 的长；（3）求证：BE 是⊙O 的切线．3、如图，已知⊙O 的半径为4，CD 是⊙O 的直径，AC 为⊙O 的弦，B 为CD 延长线上的一点，∠ABC=30°，且AB=AC．（1）求证：AB 为⊙O 的切线；（2）求弦AC 的长；（3）求图中阴影部分的面积．4、如图，已知⊙O 是等腰直角三角形ADE 的外接圆，∠ADE=90°，延长ED 到C 使DC=AD，以AD，DC 为邻边作正方形ABCD，连接AC，连接BE 交AC 于点H．求证：（1）AC 是⊙O 的切线．（2）HC=2AH．5、如图，在△ABC 中，AB=AC，以AB 为直径的圆O 交BC 于点D，交AC 于点E，过点D 作DF⊥AC，垂足为F．（1）求证：DF 为⊙O 的切线；（2）若过A 点且与BC 平行的直线交BE 的延长线于G 点，连接CG．当△ABC 是等边三角形时，求∠AGC 的度数．6、如图，⊙O 是△ABC 的外接圆，AC 是直径，过点O 作OD⊥AB 于点D，延长DO 交⊙O 于点P，过点P 作PE⊥AC 于点E，作射线DE 交BC 的延长线于F 点，连接PF．（1）若∠POC=60°，AC=12，求劣弧PC 的长；（结果保留π）（2）求证：OD=OE；（3）求证：PF 是⊙O 的切线．7、如图，AB、AC 分别是⊙O 的直径和弦，点D 为劣弧AC 上一点，弦DE⊥AB 分别交⊙O 于E，交AB 于H，交AC 于F．P 是ED 延长线上一点且PC=PF．（1）求证：PC 是⊙O 的切线；（2）点D 在劣弧AC 什么位置时，才能使AD2=DE•DF，为什么？（3）在（2）的条件下，若OH=1，AH=2，求弦AC 的长．8、如图所示，AB 是⊙O 的直径，AE 是弦，C 是劣弧AE 的中点，过C 作CD⊥AB 于点D，CD 交AE 于点F，过C 作CG∥AE 交BA 的延长线于点G．（1）求证：CG 是⊙O 的切线．（2）求证：AF=CF．（3）若∠EAB=30°，CF=2，求GA 的长．9、如图，⊙O 是△ABC 的外接圆，BD 为圆O 的直径，AB=AC，AD 交BC 于E，ED=2AE．（1）求证：AB2=AD•AE；（2）求∠ADB 的度数；（3）延长DB 到F，使BF=BO，连接FA．求证：直线FA 为⊙O 的切线．10、如图，直线AB 经过⊙O 上的点C，并且OA=OB，CA=CB，⊙O 交直线OB 于E，D，连接EC，CD．（1）求证：直线AB 是⊙O 的切线；（2）试猜想BC，BD，BE 三者之间的等量关系，并加以证明；（3）若tan∠CED=12，⊙O 的半径为3，求OA 的长．11、已知△ABC 内接于⊙O，过点A 作直线EF．（1）如图①所示，若AB 为⊙O 的直径，要使EF 成为⊙O 的切线，还需要添加的一个条件是（至少说出两种）：或者．（2）如图②所示，如果AB 是不过圆心O 的弦，且∠CAE=∠B，那么EF 是⊙O 的切线吗？试证明你的判断．12、如图，在△ABC 中，∠BAC=90°，AB=AC，AB 是⊙O 的直径，⊙O 交BC 于点D，DE⊥AC 于点E，BE 交⊙O 于点F，连接AF，AF 的延长线交DE 于点P．（1）求证：DE 是⊙O 的切线；（2）求tan∠ABE 的值；（3）若OA=2，求线段AP 的长．13、如图，在△ABC 中，∠ABC=90°，D 是边AC 上的一点，连接BD，使∠A=2∠1，E 是BC 上的一点，以BE 为直径的⊙O 经过点D．（1）求证：AC 是⊙O 的切线；（2）若∠A=60°，⊙O 的半径为2，求阴影部分的面积．（结果保留根号和π）14、如图，在△ABC 中，∠ABC=90°，以AB 的中点O 为圆心、OA 为半径的圆交AC 于点D，E 是BC 的中点，连接DE，OE．（1）判断DE 与⊙O 的位置关系，并说明理由；（2）求证：BC2=CD•2OE；（3）若cos∠BAD=35，BE=6，求OE 的长．15、如图，在平面直角坐标系，A，B 两点的坐标分别为（0，﹣2），（0，8），以AB 为一边作正方形ABCD，再以CD 为直径的半圆P．设x 轴交半圆P 于点E，交边CD 于点F．（1）求线段EF 的长；（2）连接BE，试判断直线B 与⊙P 的位置关系，并说明你的理由；（3）直线BE 上是否存在着点Q，使得以Q 为圆心、r 为半径的圆，既与y 轴相切又与⊙P 外切？若存在，试求r 的值；若不存在，请说明理由．16、如图，△ABC 内接于半圆，AB 为直径，过点A 作直线MN，若∠MAC=∠ABC．（1）求证：MN 是半圆的切线．（2）设D 是弧AC 的中点，连接BD 交AC 于G，过D 作DE⊥AB 于E，交AC 于F，求证：FD=FG．（3）在（2）的条件下，若△DFG 的面积为4.5，且DG=3，GC=4，试求△BCG 的面积．17、如图，在平面直角坐标系中，直线l：y=﹣2x﹣8 分别与x 轴，y 轴相交于A，B 两点，点P（0，k）是y 轴的负半轴上的一个动点，以P 为圆心，3 为半径作⊙P．（1）连接PA，若PA=PB，试判断⊙P 与x 轴的位置关系，并说明理由；（2）当k 为何值时，以⊙P 与直线l 的两个交点和圆心P 为顶点的三角形是正三角形．18、如图所示，扇形OAB 的半径OA=r，圆心角∠AOB=90°，点C 是上异于A、B 的动点，过点C 作CD⊥OA 于点D，作CE⊥OB 于点E，点M 在DE 上，DM=2EM，过点C 的直线PC 交OA 的延长线于点P，且∠CPD=∠CDE．（1）求证：DM=23r；（2）求证：直线PC 是扇形OAB 所在圆的切线；（3）设y=CD2+3CM2，当∠CPO=60°时，请求出y 关于r 的函数关系式．19、已知四边形ABCD 内接于⊙O，∠ADC=90°，∠DCB＜90°，对角线AC 平分∠DCB，延长DA，CB 相交于点E．（1）如图1，EB=AD，求证：△ABE 是等腰直角三角形；（2）如图2，连接OE，过点E 作直线EF，使得∠OEF=30°，当∠ACE≥30°时，判断直线EF 与⊙O 的位置关系，并说明理由．20、如图，在直角坐标系xoy 中，O 是坐标原点，点A 在x 正半轴上，，点B在y 轴的正半轴上，OB=12cm，动点P 从点O 开始沿OA 以cm/s 的速度向点A 移动，动点Q 从点A 开始沿AB 以4cm/s 的速度向点B 移动，动点R 从点B 开始沿BO 以2cm/s 的速度向点O 移动．如果P、Q、R 分别从O、A、B 同时移动，移动时间为t（0＜t＜6）s．（1）求∠OAB 的度数．（2）以OB 为直径的⊙O′与AB 交于点M，当t 为何值时，PM 与⊙O′相切？（3）写出△PQR 的面积S 随动点移动时间t 的函数关系式，并求s 的最小值及相应的t 值．（4）是否存在△APQ 为等腰三角形？若存在，求出相应的t 值；若不存在请说明理由．。

四川省渠县崇德实验学校2020年中考第三轮总复习：几何三角形 压轴题综合题练习1．如图乙，ABC ∆和ADE ∆是有公共顶点的等腰直角三角形，90BAC DAE ∠=∠=︒，点P 为射线BD ，CE 的交点．（1）如图甲，将ADE ∆绕点A 旋转，当C 、D 、E 在同一条直线上时，连接BD 、BE ，则下列给出的四个结论中，其中正确的是________ ．①BD CE =②BD CE ⊥③45ACE DBC ∠+∠=︒④2222()BE AD AB =+（2）若4AB =，2AD =，把ADE ∆绕点A 旋转，①当90EAC ∠=︒时，求PB 的长；②求旋转过程中线段PB 长的最大值．2．在平面直角坐标系中，O 为原点，点(4,0)A ，点(0,3)B ，把ABO ∆绕点B 逆时针旋转，得△A BO ''，点A ，O 旋转后的对应点为A '，O '，记旋转角为α．（Ⅰ）如图①，若90α=︒，求AA '的长；（Ⅱ）如图②，若120α=︒，求点O '的坐标； （Ⅲ）在（Ⅱ）的条件下，边OA 上 的一点P 旋转后的对应点为P '，当O P BP '+'取得最小值时，求点P '的坐标（直接写出结果即可）3．观察猜想（1）如图①，在Rt ABCAB AC∠=︒，3==，点D与点A重合，点E在边BC ∆中，90BAC上，连接DE，将线段DE绕点D顺时针旋转90︒得到线段DF，连接BF，BE与BF的位置关系是BF BE+=；⊥，BE BF探究证明（2）在（1）中，如果将点D沿AB方向移动，使1AD=，其余条件不变，如图②，判断BE 与BF的位置关系，并求BE BF+的值，请写出你的理由或计算过程；拓展延伸（3）如图③，在ABC=，∠=，点D在边BA的延长线上，BD n=，BACα∆中，AB AC连接DE，将线段DE绕着点D顺时针旋转，旋转角EDFα+的∠=，连接BF，则BE BF值是多少？请用含有n，α的式子直接写出结论．4．数学活动课上，某学习小组对有一内角为120︒的平行四边形(120)∠=︒进行探ABCD BAD 究：将一块含60︒的直角三角板如图放置在平行四边形ABCD所在平面内旋转，且60︒角的顶点始终与点C重合，较短的直角边和斜边所在的两直线分别交线段AB，AD于点E，F （不包括线段的端点）． （1）初步尝试如图1，若AD AB =，求证：①BCE ACF ∆≅∆，②AE AF AC +=；（2）类比发现如图2，若2AD AB =，过点C 作CH AD ⊥于点H ，求证：2AE FH =；（3）深入探究如图3，若3AD AB =，探究得：3AE AF AC+的值为常数t ，则t = ．5．如图，Rt ABC ∆中，90C ∠=︒，15AB =，9BC =，点P ，Q 分别在BC ，AC 上，3CP x =，4(03)CQ x x =<<．把PCQ ∆绕点P 旋转，得到PDE ∆，点D 落在线段PQ 上．（1）求证：//PQ AB ；（2）若点D 在BAC ∠的平分线上，求CP 的长；（3）若PDE ∆与ABC ∆重叠部分图形的周长为T ，且1216T 剟，求x 的取值范围．6．如图1，已知线段2BC =，点B 关于直线AC 的对称点是点D ，点E 为射线CA 上一点，且ED BD =，连接DE ，BE ．（1）依题意补全图1，并证明：BDE ∆为等边三角形；（2）若45ACB ∠=︒，点C 关于直线BD 的对称点为点F ，连接FD 、FB ．将CDE ∆绕点D 顺时针旋转α度(0360)α︒<<︒得到△C DE ''，点E 的对应点为E '，点C 的对应点为点C '． ①如图2，当30α=︒时，连接BC '．证明：EF BC ='；②如图3，点M 为DC 中点，点P 为线段C E ''上的任意一点，试探究：在此旋转过程中，线段PM 长度的取值范围？7．已知Rt OAB ∆，90OAB ∠=︒，30ABO ∠=︒，斜边4OB =，将Rt OAB ∆绕点O 顺时针旋转60︒，如图1，连接BC ．（1）填空：OBC ∠= ︒；（2）如图1，连接AC ，作OP AC ⊥，垂足为P ，求OP 的长度；（3）如图2，点M ，N 同时从点O 出发，在OCB ∆边上运动，M 沿O C B →→路径匀速运动，N 沿O B C →→路径匀速运动，当两点相遇时运动停止，已知点M 的运动速度为1.5单位t 秒，点N 的运动速度为1单位t 秒，设运动时间为x 秒，OMN ∆的面积为y ，求当x 为何值时y 取得最大值？最大值为多少？8．【问题提出】如图①，已知ABC∆是等腰三角形，点E在线段AB上，点D在直线BC上，且ED EC=，将BCE∆连接EF∆绕点C顺时针旋转60︒至ACF试证明：AB DB AF=+【类比探究】（1）如图②，如果点E在线段AB的延长线上，其他条件不变，线段AB，DB，AF之间又有怎样的数量关系？请说明理由（2）如果点E在线段BA的延长线上，其他条件不变，请在图③的基础上将图形补充完整，并写出AB，DB，AF之间的数量关系，不必说明理由．9．已知135∠=︒，正方形ABCD绕点A旋转．MAN（1）当正方形ABCD旋转到MAN∠的外部（顶点A除外）时，AM，AN分别与正方形ABCD 的边CB，CD的延长线交于点M，N，连接MN．①如图1，若BM DN=+；=，则线段MN与BM DN+之间的数量关系是MN BM DN②如图2，若BM DN≠，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，当正方形ABCD旋转到MAN∠的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．10．如图1，在ABCEAC∠=︒，点M为射线AE上任意=，90ACB∠=︒，AC BC∆中，90一点（不与A重合），连接CM，将线段CM绕点C按顺时针方向旋转90︒得到线段CN，直线NB分别交直线CM、射线AE于点F、D．（1）直接写出NDE∠的度数；（2）如图2、图3，当EAC∠为锐角或钝角时，其他条件不变，（1）中的结论是否发生变化？如果不变，选取其中一种情况加以证明；如果变化，请说明理由；（3）如图4，若15∠=︒，直线CM与AB交于G，BD=，其ACMEAC∠=︒，60他条件不变，求线段AM的长．11．在图1，2，3中，已知▱ABCD，∠ABC＝120°，点E为线段BC上的动点，连接AE，以AE为边向上作菱形AEFG，且∠EAG＝120°．（1）如图1，当点E与点B重合时，∠CEF＝°；（2）如图2，连接AF．①填空：∠F AD∠EAB（填“＞”，“＜“，“＝”）；②求证：点F在∠ABC的平分线上；（3）如图3，连接EG，DG，并延长DG交BA的延长线于点H，当四边形AEGH是平行四边形时，求的值．12．如图，等边△ABC中，AB＝6，点D在BC上，BD＝4，点E为边AC上一动点（不与点C重合），△CDE关于DE的轴对称图形为△FDE．（1）当点F在AC上时，求证：DF∥AB；（2）设△ACD的面积为S1，△ABF的面积为S2，记S＝S1﹣S2，S是否存在最大值？若存在，求出S的最大值；若不存在，请说明理由；（3）当B，F，E三点共线时．求AE的长．13．如图，△ABC是等腰直角三角形，∠ACB＝90°，D是射线CB上一点（点D不与点B 重合），以AD为斜边作等腰直角三角形ADE（点E和点C在AB的同侧），连接CE．（1）如图①，当点D与点C重合时，直接写出CE与AB的位置关系；（2）如图②，当点D与点C不重合时，（1）的结论是否仍然成立？若成立，请写出证明过程；若不成立，请说明理由；（3）当∠EAC＝15°时，请直接写出的值．14．（1）问题发现，如图1，在Rt△ABC中，∠A＝90°，ABBC＝1，点P是边BC上一动点（不与点B重合），∠P AD＝90°，∠APD＝∠B，连接CD．填空：①PBCD＝；②∠ACD的度数为．（2）拓展探究如图2，在Rt△ABC中，∠A＝90°，ABBC＝k．点P是边BC上一动点（不与点B重合），∠P AD＝90°，∠APD＝∠B，连接CD，请判断∠ACD与∠B的数量关系以及PB与CD 之间的数量关系，并说明理由．（3）解决问题如图3，在△ABC中，∠B＝45°，AB＝，BC＝12，P是边BC上一动点（不与点B 重合），∠P AD＝∠BAC，∠APD＝∠B，连接CD．若P A＝5，请直接写出CD的长．15．定义：若实数x，y满足x2＝2y+t，y2＝2x+t，且x≠y，t为常数，则称点M（x，y）为“线点”．例如，点（0，﹣2）和（﹣2，0）是“线点”．已知：在直角坐标系xOy中，点P（m，n）．（1）P1（3，1）和P2（﹣3，1）两点中，点是“线点”；（2）若点P是“线点”，用含t的代数式表示mn，并求t的取值范围；（3）若点Q（n，m）是“线点”，直线PQ分别交x轴、y轴于点A，B，当|∠POQ﹣∠AOB|＝30°时，直接写出t的值．16．如图，已知一个直角三角形纸片ACB，其中∠ACB＝90°，AC＝4，BC＝3，E、F分别是AC、AB边上点，连接EF．（1）图①，若将纸片ACB的一角沿EF折叠，折叠后点A落在AB边上的点D处，且使S四边形ECBF＝3S△EDF，求AE的长；（2）如图②，若将纸片ACB的一角沿EF折叠，折叠后点A落在BC边上的点M处，且使MF∥CA．①试判断四边形AEMF的形状，并证明你的结论；②求EF的长；（3）如图③，若FE的延长线与BC的延长线交于点N，CN＝1，CE＝47，求AFBF的值．17．如图，△ABC中，AB＝AC，DE垂直平分AB，交线段BC于点E（点E与点C不重合），点F为AC上一点，点G为AB上一点（点G与点A不重合），且∠GEF+∠BAC＝180°．（1）如图1，当∠B＝45°时，线段AG和CF的数量关系是．（2）如图2，当∠B＝30°时，猜想线段AG和CF的数量关系，并加以证明．（3）若AB＝6，DG＝1，cos B＝34，请直接写出CF的长．18．在△ABC和△ADE中，BA＝BC，DA＝DE．且∠ABC＝∠ADE＝α，点E在△ABC的内部，连接EC，EB和BD，并且∠ACE+∠ABE＝90°．（1）如图①，当α＝60°时，线段BD与CE的数量关系为，线段EA，EB，EC的数量关系为；（2）如图②，当α＝90°时，请写出线段EA，EB，EC的数量关系，并说明理由；（3）在（2）的条件下，当点E在线段CD上时，若BC＝BDE的面积．19．已知Rt△ABC中，∠ACB＝90°，点D、E分别在BC、AC边上，连结BE、AD交于点P，设AC＝kBD，CD＝kAE，k为常数，试探究∠APE的度数：（1）如图1，若k＝1，则∠APE的度数为；（2）如图2，若k1）中的结论是否成立？若成立，请说明理由；若不成立，求出∠APE的度数．（3）如图3，若k且D、E分别在CB、CA的延长线上，（2）中的结论是否成立，请说明理由．20．思维启迪：（1）如图1，A，B两点分别位于一个池塘的两端，小亮想用绳子测量A，B 间的距离，但绳子不够长，聪明的小亮想出一个办法：先在地上取一个可以直接到达B 点的点C，连接BC，取BC的中点P（点P可以直接到达A点），利用工具过点C作CD ∥AB交AP的延长线于点D，此时测得CD＝200米，那么A，B间的距离是米．思维探索：（2）在△ABC和△ADE中，AC＝BC，AE＝DE，且AE＜AC，∠ACB＝∠AED＝90°，将△ADE绕点A顺时针方向旋转，把点E在AC边上时△ADE的位置作为起始位置（此时点B和点D位于AC的两侧），设旋转角为α，连接BD，点P是线段BD的中点，连接PC，PE．①如图2，当△ADE 在起始位置时，猜想：PC 与PE 的数量关系和位置关系分别是 ； ②如图3，当α＝90°时，点D 落在AB 边上，请判断PC 与PE 的数量关系和位置关系，并证明你的结论；③当α＝150°时，若BC ＝3，DE ＝1，请直接写出PC 2的值．参考答案1、【解答】（1）解：如图甲：①90BAC DAE ∠=∠=︒Q ，BAC DAC DAE DAC ∴∠+∠=∠+∠，即BAD CAE ∠=∠．在ABD ∆和ACE ∆中，AD AE BAD CAE AB AC =⎧⎪∠=∠⎨⎪=⎩，()ABD ACE SAS ∴∆≅∆，BD CE ∴=，∴①正确；②ABD ACE ∆≅∆Q ，ABD ACE ∴∠=∠．90CAB ∠=︒Q ，90ABD AFB ∴∠+∠=︒，90ACE AFB ∴∠+∠=︒．DFC AFB ∠=∠Q ，90ACE DFC ∴∠+∠=︒，90FDC ∴∠=︒．BD CE ∴⊥，∴②正确；③90BAC ∠=︒Q ，AB AC =，45ABC ∴∠=︒，45ABD DBC ∴∠+∠=︒．45ACE DBC ∴∠+∠=︒，∴③正确；④BD CE ⊥Q ，222BE BD DE ∴=+，90BAC DAE ∠=∠=︒Q ，AB AC =，AD AE =， 222DE AD ∴=，222BC AB =，2222BC BD CD BD =+≠Q ，22222AB BD CD BD ∴=+≠，2222()BE AD AB ∴≠+，∴④错误．故答案为：①②③．（2）①解：a 、如图乙1-中，当点E 在AB 上时，2BE AB AE =-=．90EAC ∠=︒Q ，CE ∴==，同（1）可证ADB AEC ∆≅∆．DBA ECA ∴∠=∠．PEB AEC ∠=∠Q ，PEB AEC ∴∆∆∽． ∴PB BE AC CE=， ∴4PB =PB ∴=．b 、如图乙2-中，当点E 在BA 延长线上时，6BE =．90EAC ∠=︒Q ，CE ∴==，同（1）可证ADB AEC ∆≅∆．DBA ECA ∴∠=∠．BEP CEA ∠=∠Q ，PEB AEC ∴∆∆∽， ∴PB BE AC CE=， ∴4PB =，PB ∴=综上，PB =． ②解：如图乙3-中，以A 为圆心AD 为半径画圆，当CE 在A e 上方与A e 相切时，PB 的值最大．理由：此时BCE ∠最大，因此PB 最大，(PBC ∆是直角三角形，斜边BC 为定值，BCE ∠最大，因此PB 最大）AE EC ⊥Q ，EC ∴==，由（1）可知，ABD ACE ∆≅∆，90ADB AEC ∴∠=∠=︒，BD CE ==90ADP DAE AEP ∴∠=∠=∠=︒，∴四边形AEPD 是矩形，2PD AE ∴==，2PB BD PD ∴=+=．综上所述，PB 长的最大值是2+．2、【解答】解：（1）如图①，Q 点(4,0)A ，点(0,3)B ，4OA ∴=，3OB =，5AB ∴==，ABO ∆Q 绕点B 逆时针旋转90︒，得△A BO ''， BA BA ∴='，90ABA ∠'=︒，ABA ∴∆'为等腰直角三角形，AA ∴'==（2）作O H y '⊥轴于H ，如图②，ABO ∆Q 绕点B 逆时针旋转120︒，得△A BO ''， 3BO BO ∴='=，120OBO ∠'=︒，60HBO ∴∠'=︒，在Rt BHO ∆'中，9030BO H HBO ∠'=︒-∠'=︒Q ， 1322BH BO ∴='=，O H '=， 39322OH OB BH ∴=+=+=， O ∴'点的坐标为9)2； （3）ABO ∆Q 绕点B 逆时针旋转120︒，得△A BO ''，点P 的对应点为P '， BP BP ∴='，O P BP O P BP ∴'+'='+，作B 点关于x 轴的对称点C ，连接O C '交x 轴于P 点，如图②， 则O P BP O P PC O C '+='+='，此时O P BP '+的值最小， Q 点C 与点B 关于x 轴对称，(0,3)C ∴-，设直线O C '的解析式为y kx b =+，把O '9)2，(0,3)C -代入得923b b +=⎪=-⎩，解得3k b ⎧=⎪⎨⎪=-⎩， ∴直线O C '的解析式为3y x =-， 当0y =30-=，解得x =，则P 0)，OP ∴=，O P OP ∴''== 作P D O H '⊥'于D ，90BO A BOA ∠''=∠=︒Q ，30BO H ∠'=︒，30DP O ∴∠''=︒，12O D O P ∴'=''=910P D D '='=，DH O H O D ∴='-'=-=，P ∴'点的坐标为，27)5．3、【解答】解：（1）如图①中，90EAF BAC ∠=∠=︒Q ，BAF CAE ∴∠=∠，AF AE =Q ，AB AC =，BAF CAE ∴∆≅∆，ABF C ∴∠=∠，BF CE =，AB AC =Q ，90BAC ∠=︒，45ABC C ∴∠=∠=︒，90FBE ABF ABC ∴∠=∠+∠=︒，BC BE EC BE BF =+=+， 故答案为：BF BE ⊥，BC ．（2）如图②中，作//DH AC 交BC 于H ．//DH AC Q ，90BDH A ∴∠=∠=︒，DBH ∆是等腰直角三角形， 由（1）可知，BF BE ⊥，BF BE BH +=，3AB AC ==Q ，1AD =，2BD DH ∴==，BH ∴=BF BE BH ∴+==；（3）如图③中，作//DH AC 交BC 的延长线于H ，作DM BC ⊥于M ．//AC DH Q ，ACB H ∴∠=∠，BDH BAC α∠=∠=， AB AC =Q ，ABC ACB ∴∠=∠DBH H ∴∠=∠，DB DH ∴=，EDF BDH α∠=∠=Q ， BDF HDE ∴∠=∠，DF DE =Q ，DB DH =， BDF HDE ∴∆≅∆，BF EH ∴=，BF BE EH BE BH ∴+=+=， DB DH =Q ，DM BH ⊥， BM MH ∴=，BDM HDM ∠=∠， sin 2BM MH BD α∴==g ．2sin 2BF BE BH n α∴+==g ．4、【解答】解；（1）①Q 四边形ABCD 是平行四边形，120BAD ∠=︒，AD AB =Q ，ABC ∴∆，ACD ∆都是等边三角形，60B CAD ∴∠=∠=︒，60ACB ∠=︒，BC AC =，60ECF ∠=︒Q ，60BCE ACE ACF ACE ∴∠+∠=∠+∠=︒，BCE ACF ∴∠=∠，在BCE ∆和ACF ∆中，B CAF BC ACBCE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩BCE ACF ∴∆≅∆．②BCE ACF ∆≅∆Q ，BE AF ∴=，AE AF AE BE AB AC ∴+=+==．（2）设DH x =，由题意，2CD x =，CH =，24AD AB x ∴==，3AH AD DH x ∴=-=，CH AD ⊥Q ，AC ∴==，222AC CD AD ∴+=，90BAC ACD ∴∠=∠=︒，30CAD ∴∠=︒，60ACH ∴∠=︒，60ECF ∠=︒Q ，HCF ACE ∴∠=∠，ACE HCF ∴∆∆∽， ∴2AE AC FH CH==， 2AE FH ∴=．（3）如图3中，作CN AD ⊥于N ，CM BA ⊥于M ，CM 与AD 交于点H ． 180ECF EAF ∠+∠=︒Q ，180AEC AFC ∴∠+∠=︒，180AFC CFN ∠+∠=︒Q ，CFN AEC ∴∠=∠，90M CNF ∠=∠=︒Q ，CFN CEM ∴∆∆∽， ∴CN FN CM EM=， AB CM AD CN =Q g g ，3AD AB =，3CM CN ∴=， ∴13CN FN CM EM ==，设CN a =，FN b =，则3CM a =，3EM b =， 60MAH ∠=︒Q ，90M ∠=︒，30AHM CHN∴∠=∠=︒，2HC a∴=，HM a=，HN=，AM ∴=，AH=，AC∴==，3()3()33333AE AF EM AM AH HN FN EM AM AH HN FN AH HN AM +=-++-=-++-=+-=∴3AE AFAC+==．．5、【解答】（1）证明：Q在Rt ABC∆中，15AB=，9BC=，12AC∴===．Q393PC x xBC==，4123QC x xAC==，∴PC QCBC AC=．C C∠=∠Q，PQC BAC ∴∆∆∽，CPQ B ∴∠=∠，//PQ AB ∴；（2）解：连接AD ，//PQ AB Q ，ADQ DAB ∴∠=∠．Q 点D 在BAC ∠的平分线上，DAQ DAB ∴∠=∠，ADQ DAQ ∴∠=∠，AQ DQ ∴=．在Rt CPQ ∆中，5PQ x =，3PD PC x ==Q ，2DQ x ∴=．124AQ x =-Q ，1242x x ∴-=，解得2x =，36CP x ∴==．（3）解：当点E 在AB 上时，//PQ AB Q ，DPE PGB ∴∠=∠．CPQ DPE ∠=∠Q ，CPQ B ∠=∠，B PGB ∴∠=∠，5PB PG x ∴==，359x x ∴+=，解得98x =． ①当908x <„时，34512T PD DE PE x x x x =++=++=，此时2702T <„； ②当938x <<时，设PE 交AB 于点G ，DE 交AB 于F ，作GH PQ ⊥，垂足为H ， HG DF ∴=，FG DH =，Rt PHG Rt PDE ∆∆∽， ∴GH PG PH ED PE PD==． 93PG PB x ==-Q ， ∴93453GH x PH x x x-==， 4(93)5GH x ∴=-，3(93)5PH x =-， 33(93)5FG DH x x ∴==--， 43(93)3(93)[3(93)]55T PG PD DF FG x x x x x ∴=+++=-++-+-- 125455x =+， 此时，27182T <<． ∴当03x <<时，T 随x 的增大而增大，12T ∴=时，即1212x =，解得1x =；16T =时，即12541655x +=，解得136x =． 1216T Q 剟，x ∴的取值范围是1316x 剟．6、【解答】解：（1）补全图形，如图1所示；证明：由题意可知：射线CA 垂直平分BD ，EB ED ∴=，又ED BD =Q ，EB ED BD ∴==，EBD ∴∆是等边三角形；（2）①证明：如图2：由题意可知90BCD ∠=︒，BC DC = 又Q 点C 与点F 关于BD 对称，∴四边形BCDF 为正方形，90FDC ∴∠=︒，CD FD =，30CDC α∠'==︒Q ，60FDC ∴∠'=︒，由（1）BDE ∆为等边三角形，60EDB FDC ∴∠=∠'=︒，ED BD =，EDF BDC ∴∠=∠'，又Q △E DC ''是由EDC ∆旋转得到的，C D CD FD ∴'==，()EDF DBC SAS ∴∆≅∆'，EF BC ∴='；②线段PM 11PM -+剟． 设射线CA 交BD 于点O ，I ：如图3（1）当E C DC ''⊥，MP E C ⊥''，D 、M 、P 、C 共线时，PM 有最小值．此时DP DO ==1DM =，1PM DP DM ∴=-=-，II ：如图3（2）， 当点P 与点E '重合，且P 、D 、M 、C 共线时，PM 有最大值．此时DP DE DE DB ='===，1DM =，1PM DP DM ∴=+=+，∴线段PM 11PM +剟．7、【解答】解：（1）由旋转性质可知：OB OC =，60BOC ∠=︒，OBC ∴∆是等边三角形，60OBC ∴∠=︒．故答案为：60．（2）如图1中，4OB =Q ，30ABO ∠=︒，122OA OB ∴==，AB == 11222AOC S OA AB ∆∴==⨯⨯=g g ， BOC ∆Q 是等边三角形，60OBC ∴∠=︒，90ABC ABO OBC ∠=∠+∠=︒，AC ∴==2AOC S OP AC ∆∴=== （3）①当803x <…时，M 在OC 上运动，N 在OB 上运动，此时过点N 作NE OC ⊥且交OC 于点E ．则sin 60NE ON =︒=g ，11 1.522OMN S OM NE x ∆∴==⨯g g ，2y x ∴=．83x ∴=时，y 有最大值，最大值=． ②当843x <„时，M 在BC 上运动，N 在OB 上运动．作MH OB ⊥于H ．则8 1.5BM x =-，sin 60 1.5)MH BM x =︒=-g ，212y ON MH x ∴=⨯⨯=+．当83x =时，y 取最大值，y <，③当4 4.8x <„时，M 、N 都在BC 上运动，作OG BC ⊥于G ．12 2.5MN x =-，OG AB ==12y MN OG ∴==g g ， 当4x =时，y 有最大值，4x >Q ，y ∴最大值<，综上所述，y ． 8、【解答】证明：ED EC CF ==，BCE ∆Q 绕点C 顺时针旋转60︒至ACF ∆，60ECF ∴∠=︒，60BCA ∠=︒，BE AF =，EC CF =， CEF ∴∆是等边三角形，EF EC ∴=，60CEF ∠=︒，又ED EC =Q ，ED EF ∴=，ABC ∆Q 是等腰三角形，60BCA ∠=︒，ABC ∴∆是等边三角形，60CAF CBA ∴∠=∠=︒，120EAF BAC CAF ∴∠=∠+∠=︒，120DBE ∠=︒，EAF DBE ∠=∠， 60CAF CEF ∠=∠=︒Q ，A ∴、E 、C 、F 四点共圆，AEF ACF ∴∠=∠，又ED EC =Q ，D BCE ∴∠=∠，BCE ACF ∠=∠，D AEF ∴∠=∠，在EDB ∆和FEA ∆中，DBE EAF D AEFED EF ∠=∠⎧⎪∠=∠⎨⎪=⎩()EDB FEA AAS ∴∆≅∆，DB AE ∴=，BE AF =，AB AE BE =+Q ，AB DB AF ∴=+．（1）AB BD AF =-；延长EF 、CA 交于点G ，BCE ∆Q 绕点C 顺时针旋转60︒至ACF ∆，60ECF ∴∠=︒，BE AF =，EC CF =，CEF ∴∆是等边三角形，EF EC ∴=，又ED EC =Q ，ED EF ∴=，60EFC BAC ∠=∠=︒，EFC FGC FCG ∠=∠+∠Q ，BAC FGC FEA ∠=∠+∠，FCG FEA ∴∠=∠，又FCG ECD ∠=∠Q ，D ECD ∠=∠，D FEA ∴∠=∠，由旋转的性质，可得120CBE CAF ∠=∠=︒，60DBE FAE ∴∠=∠=︒，在EDB ∆和FEA ∆中，DBE EAF D AEFED EF ∠=∠⎧⎪∠=∠⎨⎪=⎩， ()EDB FEA AAS ∴∆≅∆，BD AE ∴=，EB AF =，BD FA AB ∴=+，即AB BD AF =-．（2）如图③，，BCE ∆Q 绕点C 顺时针旋转60︒至ACF ∆，60ECF ∴∠=︒，BE AF =，EC CF =，BC AC =，CEF ∴∆是等边三角形，EF EC ∴=，又ED EC =Q ，ED EF ∴=，AB AC =Q ，BC AC =，ABC ∴∆是等边三角形，60ABC ∴∠=︒，又CBE CAF ∠=∠Q ，60CAF ∴∠=︒，180EAF CAF BAC ∴∠=︒-∠-∠1806060=︒-︒-︒60=︒DBE EAF ∴∠=∠；ED EC =Q ，ECD EDC ∴∠=∠，BDE ECD DEC EDC DEC ∴∠=∠+∠=∠+∠，又EDC EBC BED ∠=∠+∠Q ，60BDE EBC BED DEC BEC ∴∠=∠+∠+∠=︒+∠，60AEF CEF BEC BEC ∠=∠+∠=︒+∠Q ，BDE AEF ∴∠=∠，在EDB ∆和FEA ∆中，()DBE EAF BDE AEF AAS ED EF ∠=∠⎧⎪∠=∠⎨⎪=⎩EDB FEA ∴∆≅∆，BD AE ∴=，EB AF =，BE AB AE =+Q ，AF AB BD ∴=+，即AB ，DB ，AF 之间的数量关系是：AF AB BD =+．9、【解答】解：（1）①如图1，若BM DN =，则线段MN 与BM DN +之间的数量关系是MN BM DN =+．理由如下：在ADN ∆与ABM ∆中，90AD AB ADN ABM DN BM =⎧⎪∠=∠=︒⎨⎪=⎩，()ADN ABM SAS ∴∆≅∆，AN AM ∴=，NAD MAB ∠=∠，135MAN ∠=︒Q ，90BAD ∠=︒，1(36013590)67.52NAD MAB ∴∠=∠=︒-︒-︒=︒， 作AE MN ⊥于E ，则2MN NE =，167.52NAE MAN ∠=∠=︒．在ADN ∆与AEN ∆中，9067.5ADN AEN NAD NAE AN AN ∠=∠=︒⎧⎪∠=∠=︒⎨⎪=⎩，()ADN AEN AAS ∴∆≅∆，DN EN ∴=，BM DN =Q ，2MN EN =，MN BM DN ∴=+．故答案为：MN BM DN =+；②如图2，若BM DN ≠，①中的数量关系仍成立．理由如下：延长NC 到点P ，使DP BM =，连结AP ．Q 四边形ABCD 是正方形，AB AD ∴=，90ABM ADC ∠=∠=︒．在ABM ∆与ADP ∆中，90AB AD ABM ADP BM DP =⎧⎪∠=∠=︒⎨⎪=⎩，()ABM ADP SAS ∴∆≅∆，AM AP ∴=，123∠=∠=∠，1490∠+∠=︒Q ，3490∴∠+∠=︒，135MAN ∠=︒Q ，360(34)36013590135PAN MAN ∴∠=︒-∠-∠+∠=︒-︒-︒=︒．在ANM ∆与ANP ∆中，135AM AP MAN PAN AN AN =⎧⎪∠=∠=︒⎨⎪=⎩，()ANM ANP SAS ∴∆≅∆，MN PN ∴=，PN DP DN BM DN =+=+Q ，MN BM DN ∴=+；（2）如图3，以线段BM ，MN ，DN 的长度为三边长的三角形是直角三角形．理由如下： Q 四边形ABCD 是正方形，45BDA DBA ∴∠=∠=︒，135MDA NBA ∴∠=∠=︒．1245∠+∠=︒Q ，2345∠+∠=︒，13∴∠=∠．在ANB ∆与MAD ∆中，13513ABN MDA ∠=∠=︒⎧⎨∠=∠⎩，ANB MAD ∴∆∆∽， ∴BN AB AD MD=， 2AB BN MD ∴=g ，AB =Q ，221)2BN MD BD ∴==g ， 22BD BN MD ∴=g ，222222222222MD MD BD BD BD BD BN BN MD BD BN MD BD BD BN BN MD ∴+++++=+++++g g g g g 222()()()MD BD BD BN DM BD BN ∴+++=++，即222MB DN MN +=，∴以线段BM ，MN ，DN 的长度为三边长的三角形是直角三角形．10、【解答】解：（1）90ACB ∠=︒Q ，90MCN ∠=︒，ACM BCN ∴∠=∠，在MAC ∆和NBC ∆中，AC BC ACM BCN MC NC =⎧⎪∠=∠⎨⎪=⎩，MAC NBC ∴∆≅∆，90NBC MAC ∴∠=∠=︒，又90ACB ∠=︒Q ，90EAC ∠=︒，90NDE ∴∠=︒；（2）不变，在MAC NBC ∆≅∆中，AC BC ACM BCN MC NC =⎧⎪∠=∠⎨⎪=⎩，MAC NBC ∴∆≅∆，N AMC ∴∠=∠，又MFD NFC ∠=∠Q ，90MDF FCN ∠=∠=︒，即90NDE ∠=︒；（3）作GK BC ⊥于K ，15EAC ∠=︒Q ，30BAD ∴∠=︒，60ACM ∠=︒Q ，30GCB ∴∠=︒，75AGC ABC GCB ∴∠=∠+∠=︒，75AMG ∠=︒，AM AG ∴=，MAC NBC ∆≅∆Q ，MAC NBC ∴∠=∠，A ∴、C 、D 、B 四点共圆，90BDA BCA ∴∠=∠=︒，BD =Q ，∴=，AB==，1AC BC设BK a=，CK=，=，则GK a∴+=，a1∴=，1aKB KG∴==，BG1AG=，∴=AM11、【解答】解：（1）∵四边形AEFG是菱形，∴∠AEF＝180°﹣∠EAG＝60°，∴∠CEF＝∠AEC﹣∠AEF＝60°，故答案为：60°；（2）①∵四边形ABCD是平行四边形，∴∠DAB＝180°﹣∠ABC＝60°，∵四边形AEFG是菱形，∠EAG＝120°，∴∠F AE＝60°，∴∠F AD＝∠EAB，故答案为：＝；②当BA＜BE时，如图，作FN⊥BC于N，FM⊥BA交BA的延长线于M，则∠FMB＝∠FNB＝90°，∴∠MFN＝60°，又∠AFE＝60°，∴∠AFM＝∠EFN，∵EF＝EA，∠F AE＝60°，∴△AEF为等边三角形，∴F A＝FE，在△AFN和△EFM中，∠AFN=∠EFM,∠FNA=∠FME.FA=FE，∴△AFM≌△EFN（AAS）∴FM＝FN，又FN⊥BC，FM⊥BA，∴点F在∠ABC的平分线上，当BA＝BE时，如图4，∵BA＝BE，∠ABC＝120°，∴∠BAE＝∠BEA＝30°，∵∠EAG＝120°，四边形AEFG为菱形，∴∠EAF＝60°，又EA＝EF，∴△AEF为等边三角形，∴∠FEA＝60°，F A＝FE，则∠F AB＝∠FEB＝90°，又F A＝FE，∴点F在∠ABC的平分线上，当BA＞BE时，同理可证，点F在∠ABC的平分线上，综上所述，点F在∠ABC的平分线上；（3）∵四边形AEFG是菱形，∠EAG＝120°，∴∠AGF＝60°，∴∠FGE＝∠AGE＝30°，∵四边形AEGH为平行四边形，∴GE∥AH，∴∠GAH＝∠AGE＝30°，∠H＝∠FGE＝30°，∴∠GAN＝90°，又∠AGE＝30°，∴GN＝2AN，∵∠DAB＝60°，∠H＝30°，∴∠ADH＝30°，∴AD＝AH＝GE，∵四边形ABCD为平行四边形，∴BC＝AD，∴BC＝GE，∵∠HAE＝∠EAB＝30°，∴平行四边形ABEN为菱形，∴AB＝AN＝NE，∴GE＝3AB，∴BCAB＝3．12【解答】解：（1）∵△ABC是等边三角形∴∠A＝∠B＝∠C＝60°由折叠可知：DF＝DC，且点F在AC上∴∠DFC＝∠C＝60°∴∠DFC＝∠A∴DF∥AB；（2）存在，过点D 作DM ⊥AB 交AB 于点M ，∵AB ＝BC ＝6，BD ＝4，∴CD ＝2∴DF ＝2，∴点F 在以D 为圆心，DF 为半径的圆上，∴当点F 在DM 上时，S △ABF 最小，∵BD ＝4，DM ⊥AB ，∠ABC ＝60°∴MD ＝∴S △ABF 的最小值＝12×6×（2）＝6∴S 最大值＝12×2×﹣（6）＝﹣+6 （3）如图，过点D 作DG ⊥EF 于点G ，过点E 作EH ⊥CD 于点H ，∵△CDE 关于DE 的轴对称图形为△FDE∴DF ＝DC ＝2，∠EFD ＝∠C ＝60°∵GD ⊥EF ，∠EFD ＝60°∴FG ＝1，DG FG ∵BD 2＝BG 2+DG 2，∴16＝3+（BF +1）2，∴BF1∴BG∵EH ⊥BC ，∠C ＝60°∴CH ＝2EC ，EHHCEC ∵∠GBD ＝∠EBH ，∠BGD ＝∠BHE ＝90°∴△BGD ∽△BHE ∴=DG EH BG BH26-2EC EC ∴EC1∴AE ＝AC ﹣EC ＝713、【解答】解：（1）当点D 与点C 重合时，CE ∥AB ， 理由如下：∵△ABC 是等腰直角三角形，∴∠CAB ＝45°，∵△ADE 是等腰直角三角形，∴∠ADE ＝45°，∴∠CAB ＝∠ADE ，∴CE ∥AB ；（2）当点D 与点C 不重合时，（1）的结论仍然成立， 理由如下：在AC 上截取AF ＝CD ，连接EF ，∵∠AED ＝∠ACB ＝90°，∴∠EAF ＝∠EDC ，在△EAF 和△EDC 中，AE=ED,∠EAF=∠EDC,AF=DC ， ∴△EAF ≌△EDC （SAS ），∴EF ＝EC ，∠AEF ＝∠DEC ，∵∠AED ＝90°，∴∠FEC ＝90°，∴∠ECA ＝45°，∴∠ECA ＝∠CAB ，∴CE ∥AB ；（3）如图②，∠EAC ＝15°，∴∠CAD ＝30°，∴AD ＝2CD ，AC ，∴FC 1）CD ，∵△CEF 为等腰直角三角形，∴EC ＝2FC ＝2CD ， ∵△ABC 是等腰直角三角形，∴ABACCD ， ∴CE AB如图③，∠EAC ＝15°，由（2）得，∠EDC ＝∠EAC ＝15°，∴∠ADC ＝30°，∴CD＝3AC ，AB ＝AC ，延长AC 至G ，使AG ＝CD ，∴CG ＝AG ﹣AC ＝DC ﹣AC AC ﹣AC ，在△EAG 和△EDC 中，AG=DC,∠EAG=∠EDC,AE=DE ， ∴△EAG ≌△EDC （SAS ），∴EG ＝EC ，∠AEG ＝∠DEC ，∴∠CEG ＝90°，∴△CEG 为等腰直角三角形，∴EC CG AC ， ∴CE AB＝2， 综上所述，当∠EAC ＝15°时，CE AB14、【解答】解：（1）∵∠A＝90°，ABBC＝1，∴AB＝AC，∴∠B＝45°，∵∠P AD＝90°，∠APD＝∠B＝45°，∴AP＝AD，∴∠BAP＝∠CAD，在△ABP与△ACD中，AB=AC,∠BAP=∠CAD,AP=AD，∴△ABP≌△ACD，∴PB＝CD，∠ACD＝∠B＝45°，∴PBCD＝1，故答案为：1，45°；（2）∠ACD＝∠B，PBCD＝ABBC＝k；理由是：∵∠BAC＝∠P AD＝90°，∠B＝∠APD，∴△ABC∽△APD，∴PBCD＝ABBC＝k∵∠BAP+∠P AC＝∠P AC+∠CAD＝90°，∴∠BAP＝∠CAD，∴△ABP∽△ACD，∴∠ACD＝∠B，PBCD＝ABBC＝k（3）过A作AH⊥BC于H，∵∠B＝45°，∴△ABH是等腰直角三角形，∵AB＝，∴AH＝BH＝4，∵BC＝12，∴CH＝8，∴AC＝＝∴PH＝＝3，∴PB＝1，∵∠BAC＝∠P AD＝，∠B＝∠APD，∴△ABC∽△APD，∴APAD＝ABBC，∴∠BAP ＝∠CAD ，∴△ABP ∽△ACD ，∴AB BC ＝PB CD 1=CD∴CD ＝2． 过A 作AH ⊥BC 于H ，∵∠B ＝45°，∴△ABH 是等腰直角三角形，∵AB ＝，∴AH ＝BH ＝4，∵BC ＝12，∴CH ＝8，∴AC ＝＝∴PH ＝＝3，∴PB ＝7，∵∠BAC ＝∠P AD ＝，∠B ＝∠APD ，∴△ABC ∽△APD ， ∴AP AD ＝AB BC ，∴∠BAP ＝∠CAD ，∴△ABP ∽△ACD ，∴AB BC ＝PB CD 7=CD，∴CD ＝2．15、【解答】解：（1）∵当M 点（x ，y ），若x ，y 满足x 2﹣2y ＝t ，y 2﹣2x ＝t 且x ≠y ，t 为常数，则称点M 为“线点”，又∵P 1（3，1），则32﹣2×1＝7，（1）2﹣2×3＝﹣5，7≠﹣5， ∴点P 1不是线点；∵P 2（﹣3，1），则（﹣3）2﹣2×1＝7，12﹣2×（﹣3）＝7，7＝7， ∴点P 2是线点，故答案为：P 2；（2）∵点P （m ，n ）为“线点”，则m 2﹣2n ＝t ，n 2﹣2m ＝t ，∴m 2﹣2n ﹣n 2+2m ＝0，m 2﹣2n +n 2﹣2m ＝2t ，。

四川省渠县崇德实验学校2020年中考九年级数学：直角三角形专题复习测试题一、选择题（每小题3分，共30分） 1.如图，图中直角三角形有(C)A.1个B.2个C.3个D.4个2.如图，点E 在正方形ABCD 的边AB 上.若EB ＝1，EC ＝2，则正方形ABCD 的面积为(B)A. 3B.3C. 5D.5 3.满足下列条件时，△ABC 不是直角三角形的为(C)A.AB ＝41，BC ＝4，AC ＝5B.AB∶BC∶AC＝3∶4∶5C.∠A∶∠B∶∠C＝3∶4∶5D.|cosA －12|＋(tanB －33)2＝04.已知M ，N 是线段AB 上两点，AM ＝MN ＝2，NB ＝1，以点A 为圆心，AN 长为半径画弧；再以点B 为圆心，BM 长为半径画弧，两弧交于点C ，连接AC ，BC ，则△ABC 一定是(B)A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形5.如图，点D 在BC 的延长线上，DE⊥AB 于点E ，交AC 于点F.若∠A＝35°，∠D＝15°，则∠ACB 的度数为(B)A.65°B.70°C.75°D.85°6.如图，数轴上点A 表示的数是－1，原点O 是线段AB 的中点，∠BAC ＝30°，∠ABC＝90°，以点A 为圆心，AC 为半径画弧，交数轴于点D ，则点D 表示的数是(D)A.233－1 B.233 C.433 D.433－1 7.如图，在△ABC 中，AC ＝8，∠ABC＝60°，∠C＝45°，AD⊥BC，垂足为D ，∠ABC 的平分线交AD 于点E ，则AE 的长为(C)A.433 B.2 2 C.832 D.3 28.如图，在矩形ABCD中，AB＝5，BC＝7，点E为BC上一动点，把△ABE沿AE折叠，当点B的对应点B′落在∠ADC 的角平分线上时，则点B′到BC的距离为(A)A.1或2B.2或3C.3或4D.4或59.“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a，较短直角边长为b.若ab ＝8，大正方形的面积为25，则小正方形的边长为(D)A.9B.6C.4D.310.勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载.如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出(C)A.直角三角形的面积B.最大正方形的面积C.较小两个正方形重叠部分的面积D.最大正方形与直角三角形的面积和二、填空题（每小题3分，共30分）11.如图所示，在Rt△ABC中，∠ACB＝90°，CM是斜边AB上的中线，E，F分别为MB，BC的中点.若EF＝1，则AB ＝4.12.如图，在△ABC中，CD⊥AB于点D，E是AC的中点.若AD＝6，DE＝5，则CD的长等于8.13.无盖圆柱形杯子的展开图如图所示.将一根长为20 cm的细木筷斜放在该杯子内，木筷露在杯子外面的部分至少有5cm.14.若实数m，n满足|m－3|＋n－4＝0，且m，n恰好是直角三角形的两条边的长，则该直角三角形的斜边长为5或4.15.如图，我国古代数学家得出的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形与大正方形的面积之比为1∶13，则直角三角形较短的直角边a与较长的直角边b的比值为2∶3.16.把两个同样大小的含45°角的三角尺按如图所示的方式放置，其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A ，且另外三个锐角顶点B ，C ，D 在同一直线上.若AB ＝2，则CD ＝6－ 2.17.如图所示的网格是正方形网格，则∠PAB ＋∠PBA＝45°(点A ，B ，P 是网格线交点).18.如图，在扇形OAB 中，∠AOB＝90°.P 为AB ︵上的一点，过点P 作PC⊥OA，垂足为C ，PC 与AB 交于点D.若PD ＝2，CD ＝1，则该扇形的半径长为5.19.如图，在△ABC 中，AC ＝3，BC ＝4，若AC ，BC 边上的中线BE ，AD 垂直相交于点O ，则AB ＝ 5.20.如图，已知线段AB ＝4，O 是AB 的中点，直线l 经过点O ，∠1＝60°，P 点是直线l 上一点，当△APB 为直角三角形时，则BP ＝2或23或27.三、解答题（共60分）21.如图，在△ABC 中，内角∠A，∠B，∠C 所对的边分别为a ，b ，c.若aa －b ＋c ＝12（a ＋b ＋c ）c ，求证：△ABC 是直角三角形.证明：∵aa －b ＋c ＝12（a ＋b ＋c ）c ， ∴ac＝12(a ＋b ＋c)(a －b ＋c).∴2ac＝(a ＋c)2－b 2. ∴b 2＝a 2＋c 2.∴△ABC 是直角三角形.22.如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离BC 为0.7米，梯子顶端到地面的距离AC 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离A′D 为1.5米，求小巷有多宽？解：在Rt△ACB 中，∵∠ACB＝90°，BC ＝0.7米，AC ＝2.4米， ∴AB 2＝0.72＋2.42＝6.25. 在Rt△A′BD 中，∵∠A′DB＝90°，A′D＝1.5米， BD 2＋A′D 2＝A′B′2， ∴BD 2＋1.52＝6.25. ∴BD 2＝4.∵BD＞0，∴BD＝2米.∴CD＝BC ＋BD ＝0.7＋2＝2.7(米). 答：小巷的宽度CD 为2.7米.23.如图，等腰直角三角板如图放置，直角顶点C 在直线m 上，分别过点A ，B 作AE⊥m 于点E ，BD⊥m 于点D. (1)求证：EC ＝BD ；(2)若设△AEC 三边长分别为a ，b ，c ，利用此图证明勾股定理.证明：(1)∵∠ACB＝90°，∴∠ACE＋∠BCD＝90°. ∵BD⊥m，AE⊥m，∴∠CDB＝90°，∠AEC＝90°. ∴∠ACE＋∠CAE＝90°.∴∠CAE＝∠BCD. 在△AEC 和△CDB 中，⎩⎪⎨⎪⎧∠AEC＝∠CDB，∠CAE＝∠BCD ，AC ＝CB ，∴△AEC≌△CDB(AAS).∴EC＝BD.(2)由(1)知BD ＝CE ＝a ，CD ＝AE ＝b ，∴S 梯形ABDE ＝12(a ＋b)(a ＋b)＝12a 2＋ab ＋12b 2.又∵S 梯形ABDE ＝S △AEC ＋S △BCD ＋S △ABC ＝12ab ＋12ab ＋12c 2＝ab ＋12c 2，∴12a 2＋ab ＋12b 2＝ab ＋12c 2.∴a 2＋b 2＝c 2. ∴直角三角形两条直角边的平方和等于斜边的平方.24.如图，在△ABC 中，AB ＝5，AC ＝13，BC 上的中线AD ＝6，求BC 的长.解：延长AD 至点E ，使DE ＝AD ，连接BE. 在△ADC 和△EDB 中， ⎩⎪⎨⎪⎧AD ＝ED ，∠ADC＝∠EDB，CD ＝BD ，∴△ADC≌△EDB(SAS).∴AC＝BE ＝13. ∵在△ABE 中，AB ＝5，AE ＝12，BE ＝13， ∴AB 2＋AE 2＝BE 2. ∴∠BAE＝90°.∵在△ABD 中，∠BAD＝90°，AB ＝5，AD ＝6， ∴BD＝AB 2＋AD 2＝61. ∴BC＝261.25.如图，一艘船由A 港沿北偏东60°方向航行10km 至B 港，然后再沿北偏西30°方向航行10 km 至C 港. (1)求A ，C 两港之间的距离(结果精确到0.1 km ，参考数据：2≈1.414，3≈1.732)； (2)确定C 港在A 港的什么方向？解：(1)由题意可得，∠PBC＝30°，∠MAB＝60°， ∴∠CBQ＝60°，∠BAN＝30°. ∴∠ABQ＝30°.∴∠ABC＝90°.∵AB＝BC＝10 km，∴AC＝AB2＋BC2＝102≈14.1(km).答：A，C两港之间的距离约为14.1 km.(2)由(1)知，△ABC为等腰直角三角形，∴∠BAC＝45°.∴∠CAM＝15°.∴C港在A港北偏东15°的方向上.。

CDOBA5030y (米)62x (时)O四川省渠县崇德实验学校2020年中考九年级数学基础复习综合测试卷三一、选择题(本大题每小题4分，满分24分)1. ﹣2的相反数是( ) A.﹣2B.2C.12D.－122. 下列根式中，与√3是同类二次根式的是( ) A.√8B.√6C.√12D.√123. 小伟五次数学考试成绩分别为：86分，80分，85分，92分，李老师想了解小伟数学学习的稳定情况，则李老师最关注小伟数学成绩的( ) A.平均数B.众数C.中位数D.方差4. 下列图形中，旋转60°后可以和原图形重合的是( ) A.正六边形B.正五边形C.正方形D.正三角形5. 如图，平行四边形ABCD 中，对角线AC 、BD 交于点O ，下列等式成立的是( )A.AB CD =u u u r u u u rB.2BD OB =u u u r u u u rC.AB AD AC +=u u u r u u u r u u u rD.AC AB CB -=u u u r u u u r u u u r6. 如图是反映某工程队所挖河渠长度y(米)与挖掘时间x (时)之间关系的部分图像。

下列说法正确的是( ) A.该工程队每小时挖河渠253米； B.该河渠总长为50米；C.该工程队挖了30米之后加快了挖掘速度；D.开挖到30米时，用了2小时。

二、填空题(本大题每小题4分，满分48分)7. 当m<3时，3m -= .8.在函数y =x 的取值范围是9. 若关于x 的一元二次方程230x x m -+=有实数根，则m 的取值范围是10. 在平面直角坐标系中，若点P(x -2,x )在第二象限，则x 的取值范围为卖房的套数(套)(m 2)第15题图EDCHGFB ABCDEA第16题图A(-3,0)B(0,2)yxO11. 今年市场上荔枝的价格比去年便宜了5%，去年的价格是每千克m 元，则今年的价格是每千克 元。

四川省渠县崇德实验学校2020年中考九年级数学专题复习：等腰三角形测试题一、选择题（每小题3分，共24分）1．在△ABC中，其两个内角的度数如下，则能判定△ABC为等腰三角形的是(C)A．∠A＝40°，∠B＝50° B．∠A＝40°，∠B＝60°C．∠A＝20°，∠B＝80° D．∠A＝40°，∠B＝80°2．如图，AB∥CD，AD＝CD，∠1＝50°，则∠2的度数是(C)A．55° B．60° C．65° D．70°3．如图，在△ABC中，AC＝BC，∠A＝40°，观察图中尺规作图的痕迹，可知∠BCG 的度数为(C)A．40° B．45° C．50° D．60°4．如图，在△ABC中，AB＝AC，AD是△ABC的角平分线．若AB＝13，AD＝12，则BC的长为(B)A．5 B．10 C．20 D．245．如图，在等边△ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC＝45°，则∠ACE等于(A)A．15° B．30° C．45° D．60°6．如图，在△ABC中，AC＝BC，点D和E分别在AB和AC上，且AD＝AE.连接DE，过点A的直线GH与DE平行．若∠C＝40°，则∠GAD的度数为(C)A．40° B．45° C．55° D．70°7．如图，在△ABC中，∠B＝50°，CD⊥AB于点D，∠BCD和∠BDC的平分线相交于点E，F为边AC的中点，CD＝CF，则∠ACD＋∠CED＝(C)A．125° B．145° C．175° D．190°8．“三等分角”大约是在公元前五世纪由古希腊人提出来的，借助如图所示的“三等分角仪”能三等分任一角．这个三等分角仪由两根有槽的棒OA，OB组成，两根棒在O点相连并可绕O转动，C点固定，OC＝CD＝DE，点D，E可在槽中滑动．若∠BDE＝75°，则∠CDE的度数是(D)A．60° B．65° C．75° D．80°二、填空题（每小题3分，共27分）9．如图，在△ABC中，∠A＝36°，AB＝AC，BD平分∠ABC，则图中等腰三角形的个数是3.10．等腰三角形的两边长分别为6 cm，13 cm，其周长为32cm.11．如图，直线a∥b，△ABC的顶点C在直线b上，边AB与直线b相交于点D.若△BCD 是等边三角形，∠A＝20°，则∠1＝40°.12．在△ABC 中，AB ＝AC ，∠A ＝40°，则∠B ＝70°．13．如图，以△ABC 的顶点B 为圆心，BA 长为半径画弧，交BC 边于点D ，连接AD.若∠B ＝40°，∠C ＝36°，则∠DAC 的大小为34°．14．定义：等腰三角形的顶角与其一个底角的度数的比值k 称为这个等腰三角形的“特征值”．若在等腰△ABC 中，∠A ＝80°，则它的特征值k ＝85或14.15．如图，在△ABC 中，AB ＝AC ，点D 在AC 上，且BD ＝BC ＝AD ，则∠A ＝36°．16．在等腰△ABC 中，BD ⊥AC ，垂足为D ，且BD ＝12AC ，则等腰△ABC 底角的度数为45°，75°或15°．17．如图，在四边形ABCD 中，AB ＝AD ，BC ＝DC ，∠A ＝60°，点E 为AD 边上一点，连接BD ，CE ，CE 与BD 交于点F ，且CE ∥AB.若AB ＝8，CE ＝6，则BC 的长为三、解答题（共49分）18．如图，在△ABC 中，AB ＝AC ，D 是BC 边上的中点，连接AD ，BE 平分∠ABC 交AC 于点E ，过点E 作EF ∥BC 交AB 于点F.(1)若∠C ＝36°，求∠BAD 的度数； (2)求证：FB ＝FE.解：(1)∵AB＝AC，∴∠C＝∠ABC.∵∠C＝36°，∴∠ABC＝36°.∵BD＝CD，AB＝AC，∴AD⊥BC.∴∠ADB＝90°.∴∠BAD＝90°－36°＝54°.(2)证明：∵BE平分∠ABC，∴∠ABE＝∠CBE.∵EF∥BC，∴∠FEB＝∠CBE.∴∠FBE＝∠FEB.∴FB＝FE.19.如图，在△ABC中，∠C＝∠ABC，BE⊥AC，△BDE是等边三角形．求∠C的度数．解：∵△BDE是等边三角形，∴∠DBE＝60°.∵BE⊥AC，∴∠BEC＝90°.∵∠C＝∠ABC＝∠ABE＋∠EBC，∴∠EBC＝∠C－60°.∵∠EBC＋∠C＝90°，即∠C－60°＋∠C＝90°，∴∠C＝75°.20．如图，AB＝AC，∠BAC＝120°，AD⊥AC，AE⊥AB.(1)求∠C 的度数；(2)求证：△ADE 是等边三角形．解：(1)∵AB ＝AC ，∠BAC ＝120°， ∴∠B ＝∠C ＝30°.(2)证明：∵∠B ＝∠C ＝30°，AD ⊥AC ，AE ⊥AB ， ∴∠DAC ＝∠EAB ＝90°. ∴∠ADC ＝∠AEB ＝60°.∴∠ADC ＝∠AEB ＝∠EAD ＝60°. ∴△ADE 是等边三角形．21．在等边△ABC 中，点E 在AB 上，点D 在CB 的延长线上，且AE ＝BD. (1)当点E 为AB 的中点时，如图1，求证：EC ＝ED ；(2)当点E 不是AB 的中点时，如图2，过点E 作EF ∥BC ，求证：△AEF 是等边三角形； (3)在(2)的条件下，EC 与ED 还相等吗？请说明理由．解：(1)证明：∵△ABC 为等边三角形， ∴∠ABC ＝∠ACB ＝∠A ＝60°. ∵点E 为AB 的中点，∴AE ＝EB ＝BD ，∠ECB ＝12∠ACB ＝30°.∴∠EDB ＝∠DEB ＝12∠ABC ＝30°.∴∠EDB ＝∠ECB.∴EC ＝ED.(2)证明：∵EF ∥BC ，∴∠AEF ＝∠ABC ＝60°，∠AFE ＝∠ACB ＝60°. ∴∠A ＝∠AEF ＝∠AFE ＝60°. ∴△AEF 为等边三角形． (3)EC ＝ED.理由：∵△AEF 为等边三角形， ∴AE ＝AF ＝EF ＝BD. ∵∠AFE ＝∠ABC ＝60°， ∴∠EFC ＝∠DBE ＝120°. ∵AB ＝AC ，AE ＝AF ，∴AB －AE ＝AC －AF ，即BE ＝FC. 在△DBE 和△EFC 中，⎩⎪⎨⎪⎧DB ＝EF ，∠DBE ＝∠EFC ，BE ＝FC ，∴△DBE ≌△EFC(SAS)． ∴ED ＝CE.。

四川省渠县崇德实验学校2020年中考九年级数学：等腰三角形专题复习测试题 一、选择题（每小题3分，共30分）1、如图，在中，，观察图中尺规作图的痕迹，可知的度数为( )A ．B ．C ．D ．2、在Rt △ABC 中，∠ACB=90°，CD ⊥AB 于D ，CE 平分∠ACD 交AB 于E ，则下列结论一定成立的是（ ）A ．BC=ECB ．EC=BEC ．BC=BED ．AE=EC3、如图，∠AOB=60°，点P 是∠AOB 内的定点且OP=，若点M 、N 分别是射线OA 、OB 上异于点O 的动点，则△PMN 周长的最小值是（ ） A ．B ．C ．6D ．34、如图，在菱形ABCD 中，AC=6，BD=6，E 是BC 边的中点，P ，M 分别是AC ，AB 上的动点，连接PE ，PM ，则PE+PM 的最小值是（ ） A ．6 B ．3C ．2D ．4.5ABC ∆,40AC BC A =∠=︒BCG∠40︒45︒50︒60︒5、如图，在△OAB 和△OCD 中，OA ＝OB ，OC ＝OD ，OA ＞OC ，∠AOB ＝∠COD ＝40°，连接AC ，BD 交于点M ，连接OM ．下列结论：①AC ＝BD ；②∠AMB ＝40°；③OM 平分∠BOC ；④MO 平分∠BMC ．其中正确的个数为（ ） A ．4B ．3C ．2D ．16、如图，点P 是边长为1的菱形ABCD 对角线AC 上的一个动点，点M ，N 分别是AB ，BC 边上的中点，则MP+PN 的最小值是（ ） A ． B ．1C ．D ．27、如图，在中，点是上的点，，将沿着翻折得到，则（ ）A ．20°B ．25°C ．30°D ．40°8、若实数m 、n 满足等式|m ﹣2|+=0，且m 、n 恰好是等腰△ABC的两条边的ABC △D BC 40BAD ABC ∠=∠=︒ABD △AD AED △CDE ∠=边长，则△ABC的周长是（）A．12 B．10 C．8 D．69、如图，△ABC中，AB=AC，AD⊥BC于D点，DE⊥AB于点E，BF⊥AC于点F，DE=3cm，则BF= cm．A．5 B．6 C．7 D．810、如图，在等腰直角三角形ABC中，∠BAC＝90°，一个三角尺的直角顶点与BC边的中点O重合，且两条直角边分别经过点A和点B，将三角尺绕点O按顺时针方向旋转任意一个锐角，当三角尺的两直角边与AB，AC分别交于点E，F时，下列结论中错误的是（）A．AE+AF＝AC B．∠BEO+∠OFC＝180°C．OE+OF＝BC D．S四边形AEOF＝S△ABC二、填空题（每小题3分，共24分）11、如图，AD，CE分别是△ABC的中线和角平分线．若AB=AC，∠CAD=20°，则∠ACE的度数是．12、如图，在边长为4的等边△ABC中，D，E分别为AB，BC的中点，EF⊥AC于点F，G为EF的中点，连接DG，则DG的长为．13、如图，在Rt △ABC 中，CM 平分∠ACB 交AB 于点M ，过点M 作MN ∥BC 交AC 于点N ，且MN 平分∠AMC ，若AN=1，则BC 的长为 ．14、如图，△ABC 中，AB =BC ，∠ABC =90°，F 为AB 延长线上一点，点E 在BC 上，且AE =CF ，若∠BAE =25°，则∠ACF =__________度．15、如图，等边的边长为2，则点的坐标为 ．16、如图，在△ABC 中，BC 的垂直平分线MN 交AB 于点D ，CD 平分∠ACB ．若AD =2，BD =3，则AC 的长为__________．17、如图，在△ABC 中，AC=BC=2，AB=1，将它沿AB 翻折得到△ABD ，则四边形ADBC 的形状是 形，点P 、E 、F 分别为线段AB 、AD 、DB 的任意点，则PE+PF 的最小值是 ．OAB △B18、如图，已知等边△ABC的边长是2，以BC边上的高AB1为边作等边三角形，得到第一个等边△AB1C1；再以等边△AB1C1的B1C1边上的高AB2为边作等边三角形，得到第二个等边△AB2C2；再以等边△AB2C2的B2C2边上的高AB3为边作等边三角形，得到第三个等边△AB3C3；…，记△B1CB2的面积为S1，△B2C1B3的面积为S2，△B3C2B4的面积为S3，如此下去，则Sn= ．三、解答题（共66分）19、如图，AB=AD，BC=DC，点E在AC上．（1）求证：AC平分∠BAD；（2）求证：BE=DE．20、如图，在△ABC中，AB=AC，点D、E分别在AB、AC上，BD=CE，BE、CD相交于点O．求证：（1）；（2）．DBC ECB△≌△OB OC21、如图，在△ABC中，AB=AC，AD⊥BC于点D．（1）若∠C=42°，求∠BAD的度数；（2）若点E在边AB上，EF∥AC交AD的延长线于点F．求证：AE=FE．22、．如图，在△ABC中，AB=AC，D是BC边上的中点，连结AD，BE平分∠ABC 交AC于点E，过点E作EF∥BC交AB于点F．（1）若∠C=36°，求∠BAD的度数．（2）若点E在边AB上，EF∥AC叫AD的延长线于点F．求证：FB=FE．23、如图，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC＝∠DAE＝90°．（1）如图1，连接BE，CD，BE的廷长线交AC于点F，交CD于点P，求证：BP ⊥CD ；（2）如图2，把△ADE 绕点A 顺时针旋转，当点D 落在AB 上时，连接BE ，CD ，CD 的延长线交BE 于点P ，若BC ＝，AD ＝3，求△PDE 的面积．24、如图，在Rt △ABC 中，（M 2，N 2），∠BAC=30°，E 为AB 边的中点，以BE 为边作等边△BDE ，连接AD ，CD ． （1）求证：△ADE ≌△CDB ； （2）若BC=，在AC 边上找一点H ，使得BH+EH 最小，并求出这个最小值．25、在△ABC 中，∠BAC ＝90°，AB ＝AC ，AD ⊥BC 于点D ．（1）如图1，点M ，N 分别在AD ，AB 上，且∠BMN ＝90°，当∠AMN ＝30°，AB ＝2时，求线段AM 的长；（2）如图2，点E，F分别在AB，AC上，且∠EDF＝90°，求证：BE＝AF；（3）如图3，点M在AD的延长线上，点N在AC上，且∠BMN＝90°，求证：AB+ANAM．。