当前位置：文档之家 › 结构动力学4 PPT课件

结构动力学4 PPT课件

  • 格式：ppt
  • 大小：3.22 MB
  • 文档页数：43

下载文档原格式

  / 43

合集下载

结构动力学完整ppt课件

结构动力学完整ppt课件

输出 （动力反应）
.
第四类问题：控制问题
输入 （动力荷载）
结构 （系统）
输出 （动力反应）
控制系统 （装置、能量）
本课程主要介绍结构的反应分析
任务 讨论结构在动力荷载作用下反应的分析的方法。寻找
结构固有动力特性、动力荷载和结构反应三者间的相互关 系，即结构在动力荷载作用下的反应规律，为结构的动力 可靠性（安全、舒适）设计提供依据。
结构动力学是研究结构、动荷载、结构反应三者关 系的学科。
.
当前结构动力学的研究内容为:
第一类问题：反应分析（结构动力计算）
输入 （动力荷载）
结构 （系统）
输出 （动力反应）
第二类问题：参数（或称系统）识别
输入 （动力荷载）
结构 （系统）
第三类问题：荷载识别。
输出 （动力反应）
输入 （动力荷载）
结构 （系统）
11
l3 3 EI
柔度系数
m y (t)3lE3 Iy(t)P(t)
柔度法步骤： 1.在质量上沿位移正向加惯性力； 2.求外力和惯性力引起的位移； 3.令该位移等于体系位移。
.
二、刚度法
P(t)
m
1
m y(t)
y(t)
l EI
y
k11
k11y(t)
k 1y 1 (t)P (t) m y (t)
EI
m
l/2
l/2
W
m y(t)
1
11
st y(t)
Y(t)y(t)st
加速度为
Y(t) y(t)
y (t) s t 1[P 1 (t) W m y (t)]
st W11
结构动力学

结构动力学课件PPT

结构动力学课件PPT

my cy ky FP (t)
§2-5 广义单自由度体系：刚体集合
➢刚体的集合（弹性变形局限于局部弹性 元件中）
➢分布弹性（弹性变形在整个结构或某些 元件上连续形成）
➢只要可假定只有单一形式的位移，使得 结构按照单自由度体系运动，就可以按 照单自由度体系进行分析。
E2-1
x
p( x,t
)
=p
)
3
B'
M I1
E'
D'
F' G'
A
D
E
B
F
G
C
fD1
fI1
fS1
f D2
f I2
f S2
a
2a
a aa a
Z(t )
f S1
k1(EE')
3 4
k1Z (t )
f D1
d c1( dt
DD')
1 4
c1Z (t )
fS2
k1(GG')
1 3
k2
Z
(t
)
fD2 c2Z (t)
f
I1
m1
1 2
Z(t)
3. 有限单元法
—— 将有限元法的思想用于解决结构的动力计算问题。
要点：
▪ 先把结构划分成适当（任意）数量的单元；
▪ 对每个单元施行广义坐标法，通常取单元的节点位移作 为广义坐标；
▪ 对每个广义坐标取相应的位移函数 （插值函数）；
▪ 由此提供了一种有效的、标准 化的、用一系列离散坐标 表示无限自由度的结构体系。
建立体系运动方程的方法
▪ 直接平衡法，又称动静法，将动力学问题转化为任一时刻 的静力学问题：根据达朗贝尔原理，把惯性力作为附加的 虚拟力，并考虑阻尼力、弹性力和作用在结构上的外荷载， 使体系处于动力平衡条件，按照静力学中建立平衡方程的 思路，直接写出运动方程。

哈工大结构动力学张金生老师讲稿-4

哈工大结构动力学张金生老师讲稿-4

& v 0 = y ( t1 ) = 0
y ( t ) = y 0 cos ω t =
π
2
y st cos ω t
最大位移反应
T t 1 > ( β < 1) 2
最大位移反应发生于第一阶段； 最大位移反应发生于第一阶段；
T t 1 < ( β > 1) 2
最大位移反应发生于第二阶段； 最大位移反应发生于第二阶段；
一. 矩形脉冲 1. 位移反应
P(t )
m
y (t )
P(t )
荷载离开前 ( 0 ≤ t ≤ t1 ) t P y (t ) = ∫ sin ω ( t − τ ) d τ 0 mω = y st (1 − cos ω t )
= y st µ 1 ( t )
k
P
t
t1
2
µ 1 ( t ) = 1 − cos ω t = 2 sin
y(t) = Ae
−ξωt
P(τ ) −ξω (t −τ ) sin( ωDt +ϕ) + ∫ e sinωD (t −τ )dτ 0m ωD
t
§2.6 冲击荷载的动力反应
冲击荷载的特点---作用时间短。 冲击荷载的特点---作用时间短。 ---作用时间短 结构动力反应的特点---最大反应出现快、荷载消失前 结构动力反应的特点---最大反应出现快、 ---最大反应出现快 后反应不同。 后反应不同。 计算特点： 计算特点： 不计阻尼； 1. 不计阻尼； 要考虑瞬态振动； 2. 要考虑瞬态振动； 3. 要分析荷载消失前后两种状态
f = 1/ k
---柔度系数 ---柔度系数
PE = Pt 1ω
---冲量等效荷载 ---冲量等效荷载

结构动力学(5)-第四章 结构动力学的求解

结构动力学(5)-第四章 结构动力学的求解

H ( ) Z 1 ( ) ( K 2 M )1 , r
def
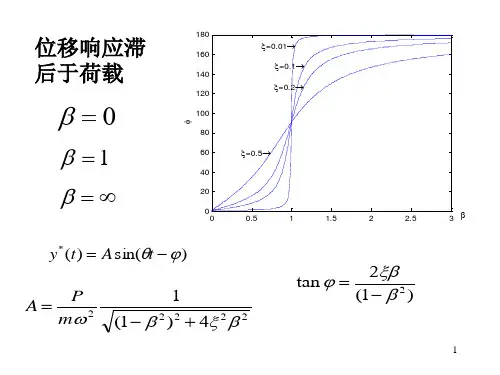
u H ( ) f
其中 H ( ) 正是系统的位移频响函数矩阵，它的元素 H ij ( ) 具有柔度系数的量纲， 反映了在系统第j个自由度上施加单位正弦激励后第i个自由度的稳态位移响应幅值。
（2）频响函数矩阵的模态展开式 利用固有振型关于质量矩阵和刚度矩阵的加权正交性，对式动刚度矩阵左乘 和右乘
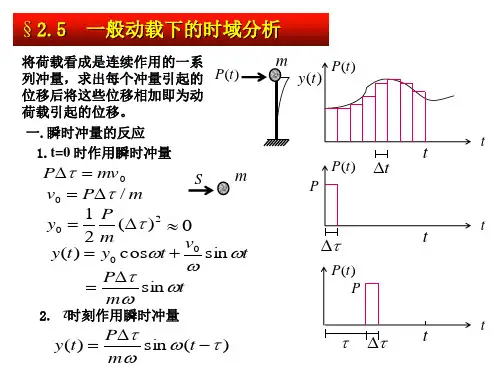
4．1 无阻尼自由振动
Mu(t ) Ku(t ) 0 u(0) u0 , u(0) u0
特性： 质量矩阵 1）反映系统的动能
T
1 T u Mu 0 2
1 T u Mu 0 2
2）正定 但也有例外：存在纯静态模态
u ，使
（针对两种情况：当采用集中质量矩阵时和当离散系统中设有无质量点的自由度时）
根据前面的分析，线性系统的响应可分为零初始状态下激励引起的响应及零 激励条件下初始条件引起的响应，即零状态响应及零输入响应。系统的响应可以 是其中某一种或两种之线性组合。研究下述微分方程的求解问题
Mu(t ) Ku(t ) f (t ) u(0) 0 u(0) 0,
Φ{diag [cos r t ]a diag [sin
1 r N
1 r N
r
t ]b}
其中
a [a1 aN ] ,
T def
b [b1 bN ]T
def
对于给定的初始条件
u0
和
u0
，可得到
u0 Φa ,
解出参数向量
u0 Φ diag[ r ]b
0 0
t
t
当考虑进系统初始状态对响应的贡献时，系统的响应为

第12章结构动力学 ppt课件

第12章结构动力学 ppt课件

§14-1 概 述
一、结构动力计算的特点 动力荷载作用下，结构将发生振动，各种量值均随时间而变化。
1、内容： （1）研究动力荷载作用下，结构的内力、位移等计算原理和计算方法。 求出它们的最大值并作为结构设计的依据。
（2）研究单自由度及多自由度的自由振动、强迫振动。 2、静荷载和动荷载 （1）静荷载：荷载的大小和方向不随时间变化（如梁板自重）。 （2）动荷载：荷载的大小和方向随时间变化，需要考虑惯性力。 3、特点 (1)必须考虑惯性力。 （2）内力与荷载不能构成静平衡。必须考据惯性力。依达朗伯原理， 加惯性力后，将动力问题转化为静力问题。
动力自由度的确定方法：加附加链杆约束质点位移，最少链杆数即为自 由度
图刚架上有四个集中质点，但只需要加三根链杆 便可限制全部质点的位置。如图e。
自由度=3 或
图示梁，其分布质量集度为m，可看作有无穷多 个mdx的集中质量，是无限自由度结构。
自由度的数目与结构是否静定或超静定无关
§14-2 结构振动的自由度
2、运动方程的解：
方程
y2y0
为一常系数线性齐次微分方程，其通解为
y (t) A 1 co t s A 2sitn
A1和A2为任意常数，可有初始条件来确定。
振动的初始条件为 t 0 时 y y ， 0 ， y y 0
式中y0—初位移， y0—初速度。则有Fra bibliotekA1y0，A2
y0
可得
yy0cots y0si nt
第十四章 结构动力学
§14-1 概 述 §14-2 结构振动的自由度 §14-3 单自由度结构的自由振动 §14-4 单自由度结构在简谐荷载作用下的强迫振动 §14-5 单自由度结构在任意荷载作用下的强迫振动 §14-6 多自由度结构的自由振动 §14-7 多自由度结构在简谐荷载作用下的强迫振动 §14-8 振型分解法 §14-9 无限自由度结构的振动 §14-10 计算频率的近似法

结构力学课件-15动力学4

结构力学课件-15动力学4

-3.0
当 0.618 k m 1 和 1.618 k m 2时,Y1和Y2 趋于无穷大。 可见在两个自由度体系中，在两种情况下可能出现共振。
7
也有例外情况
如图示对称结构在对称荷载作用下。
k11 k22 , k12 k21
l/3
与ω2相应的振型是
Psinθt m
l/3
Psinθt m
l/3
Y12 k12
为了使假设的振型尽可能的接近真实振型，尽可能减小假设振型对体系所附 加的约束， Ritz 提出了改进方法：
1、假设多个近似振型 2、将它们进行线性组合
1,2 n 都满足前述两个条件。 Y (x) a1 1 a2 2 an n
（a1、a2、·········、an是待定常数）
3、确定待定常数的准则是：获得最佳的线性组合，这样的Y（x）代入频率
k
P
yst1
θ2mY1
Y1 P
k
(1
1mk 2
2 12 )(1
2
2 2
)
1
Y2 P
k
(1
2
1 12 )(1
) 2
2 2
2
Q1
1
2m k
(1
2
)
k
层间动剪力:
Q1 P 2m(Y1 Y2 )
P(1
2m k
(
1
2
))
由此可见，在多自由度体系中，没有一个统一的动力系数。
9
例15-9：质量集中在楼层上m1、m2 ，层间侧移刚度为k1、k2
(
x)dx
2
0l q(x)Y (x)dx
0l m[Y (x)]2 dxmiYi2 13
例12 试求等截面简支梁的第一频率。

结构动力学有限元法


100%
动力响应分析
研究车辆、风、地震等外部激励 下桥梁的动力响应，评估其安全 性能。
80%
稳定性分析
分析桥梁在极端载荷下的稳定性 ，确保其正常工作。
建筑结构的抗震分析
地震作用下的结构响应
通过有限元法模拟地震对建筑 结构的作用，计算结构的位移 、加速度等响应。
结构抗震性能评估
根据计算结果评估建筑结构的 抗震性能，优化设计以提高其 抗震能力。
局限性
由于结构动力学有限元法需要进行大量的数值计算和存储，因此 对于大规模复杂结构的分析可能会面临计算效率和精度方面的问 题。此外，对于一些特殊结构和复杂工况，可能需要采用特殊的 建模和分析方法。
04
结构动力学有限元法的应用实例
桥梁结构的动力学分析
80%
桥梁结构的模态分析
通过有限元法计算桥梁的固有频 率和振型，了解其自振特性。
结构减震设计
利用有限元法进行减震设计， 如设置隔震支座、阻尼器等， 降低地震对结构的影响。
机械设备的动态特性分析
01
设备模态分析
02
设备振动分析
03
设备优化设计
通过有限元法分析机械设备的固 有频率和振型，了解其动态特性。
研究机械设备在工作过程中的振 动情况，分析其振动原因和影响。
根据动态特性分析结果，优化机 械设备的设计，降低振动和噪声。
用于分析电磁场的分布和变化规律，如电机、变 压器、天线等。
流体动力学
用于模拟流体在各种条件下的流动特性，如航空 、航海、管道流动等。
热传导分析
用于分析温度场的变化和热量传递规律，如热力 管道、电子设备等。
有限元法的研究意义
提高工程设计的可靠性和安全性

《结构动力学》PPT课件


重物落在结构上（突然加载和突然卸载）
④快速移动荷载——高速通过桥梁的火车、汽车
⑤随机荷载——地震的激振、风力脉动作用
荷载变化极不规律，只能用概率方法求其统计规律
a
2
周期荷载（简谐）
周期荷载（非简谐）
冲击荷载（急剧增大、急剧减少）
a
3
随机荷载
a
4
内容：自由振动
无阻尼 单、多自由度
强迫振动
有阻尼 无限多自由度
myky0 达朗伯尔原理 隔离体平衡方程
微分方程
y 2y 0
k 1
m m
a
11
（2）柔度法——列位移方程 ——弹性体系（非隔离体）（图14 – 5c）
运动过程，质量只受惯性力——按静力荷载考虑， I my
m在时刻 t 的位移等于惯性力作用下的静力位移
即 y my
单自由度体系 myy0 1 k
周期运动 y( t + T ) = y( t )
y(t)asint2
asint2y(tT)
自振周期 频率
T＝ 2
每隔一段时间就重复原来运动 单位：秒（S）
f 1 T 2
单位时间内的振动次数 ， 单位： 1／秒（1/S）
园频率（频率）＝2 ＝2f
Ta
2π秒内完成的 振动次数
16
＝k 1 g g m m W st
②动力反应 动内力/位移随时间变化的规律 ——最大值——设计依据
a
5
§14－2 结构振动的自由度
振动自由度
——为了确定全部质量位置所需的独立几何参数的数目
集中质量法：突出主要质量——静力等效
单自由度结构
多自由度结构
a

有限元课件ch9 结构动力学

n
K
(n)
K 1 0 0
n i

0 0 K n
令
y 1 Y
Y Y Y
2 i 1
可 以 得 到 ： i
Y M y
(i) T
(1 )
Y Y Y Y { }
(2) 2
y 称为几何坐标， 称为正则坐标 M Y K Y P (t )
Y M K P ( t ) ， P ( t ) 广义荷载列阵
(i) T ( j) 2
j
(i) T
( j)
又已知：
M M ， K K
T
T
Y M Y 0 Y K Y 0
(i) T ( j) (i) T ( j)
振型关于质量正交 振型也关于刚度正交
Y M Y M
(i) T (i)
M
i
， i (0)
Y M y ( 0 )
(i) T
M
i
i ( t ) i ( 0 ) cos i t
i (0)

sin
i
t
1 M i
i

t
0
ቤተ መጻሕፍቲ ባይዱ
Pi (τ ) sin
i
( t τ ) dτ
i
1、主要问题：确定自振频率和相应振型；
m2
Y1 2
2、自振频率和自由度个数相等，由特征方程求出； 3、每个频率都对应自己的主振型； 4、主振型是结构的固有性质。
m1
第2振型

结构动力学之多自由度体系的振动问题ppt课件

1 536EI
448 (1 536)2
m1m2l 6 (EI )2
0
解得
21
23l3 (m1 m2 2 1 536EI
)
529(m1 m2 )2l6 41 5362 (EI )2
448m1m2l 6 1 5362 (EI )2
从而得第一和第二阶自振频率
1
1
1
2
1
2
为了确定第一阶振型，可将1代入平衡方程。
其展开式是关于λ的n次代数方程,先求出λi再求 出频率ωi
柔度法
(11m1 )
12m2
...
21m1 ( 22m2 ) ...
...
...
...
1n mn 2nmn 0
...
n1m1
n2m2 ... ( nnmn )
将λi代入 ( [δ] [M] － λi [I ] ){Y(i)}={0} 可求出n个主振型。
多个自由度体系的自由振动
结构在受迫振动时的动力响应与结构的动力特性 密切相关；另外，当用振型叠加法计算任意干扰力 作用下结构的动力响应时，往往要用到自由振动的 频率(frequency)和振型(mode)。
为此，要需要首先分析自由振动。
自振频率和振型的计算
m1
m2
mi
mn
y1(t) y2(t)
yi(t)
刚度法
其中最小的频率1 称为最低自振频率，或称
基本频率。 通常将上述每一个频率所对应的振动都称为
主振动，对应于每一个主振动的形状称为主振 型。
1）如果各质体的初速度为零，而初位移和某 一振型成比例，然后任其自然，则系统就按 这个振型作简谐自由振动，此解答就相应于 该振动的一组特解；
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

泛美大厦，60层钢结 构，南北方向的基本固 有周期为2.90秒，
大坝，400英尺高的混凝土重力 坝的基本固有周期由强迫振动试验 测得在蓄水为310英尺和345英尺 十分别为0.288秒和0.306秒，
金门大桥，金门大桥桥墩跨距 1280.2米全桥总长2737.4米的悬索 桥，其横向振动的基本基本固有周期 为18.20秒，竖向振动的基本基本固 有周期为10.90秒，纵向振动的基本 基本固有周期为3.81秒，扭转振动 的基本基本固有周期为4.43秒
[例13.2] 图示机器与基础总重量W=60kN，基础下
土壤的抗压刚度系数为 cz=0.6N/cm3，基础底面积 A=20m2。试求机器连同基础作竖向振动时振频率。
解: 让振动质量向下单位位移 需施加的力为：
k = cz A= 0.6×103×20
W
=12×103 kN/m
自振频率为：
k kg 12103 9.8 44.27s1
用 f表示频率：每秒钟内的振动次数 用表示圆频率： 2 秒内的振动次数
f1 T 2
1)自振周期计算公式： 2)自振频率计算公式：
T 2 m 2 m
k
2 W 2 st
g
g
k 1 g g m m W st
13.2.3 结构的自振周期和自振频率
3)自振周期和频率的讨论
T 2
m 2
k
设特解为：y Cet
1.振动方程
建立动平衡方程
my cy ky 0
标准化得:
y c y k y0 mm
特征方程为：2 2 2 0
根为 1、2＝ － 2－1
微分方程的解与相应 特征方程的根有关
2.讨论根的三种情况 1、 1、 1
—— 称为阻尼比,是体系的一种特性，它取 决于体系的质量和刚度
13.2.4 阻尼对自由振动的影响
y m
y=0 阻尼是客观存在的
m
（1）产生阻尼的原因
1)结构与支承之间的外摩擦
2)材料之间的内摩擦
k
kc
3)周围介质的阻力
（2）阻尼力的确定
1) 不考虑阻尼
y(t)
a
2) 考虑阻尼
1)与质点速度成正比 2)与质点速度平方成正比 3)与质点速度无关
0 振幅随时间减小，这表明在振动过
振幅：A
y02
v02
2
初始相位角： tan1 y0
v0
y0 yst 初始条件： y0 2gh
13.2.3 结构的自振周期和自振频率
具体例子比较:
1.例如设:yst 0.4cm, h 则10cm
g 980 49.5rad / s
h
yst
0.4
A 0.42 2100.4 2.86cm
y A
（位移幅值）
y A2
（加速度幅值）
I mA2
（惯性力幅值）
在运动的任一瞬时质体都处于平衡状态，在幅值出现时刻也一
样，于是可在幅值处建立运动方程，此时方程中将不含时间t，
结果把微分方程转化为代数方程了，使计算得以简化。
13.2.3 结构的自振周期和自振频率
[例13.1] 求图示梁结构的自振周期和自振频率。
y
et [
y0
cos r t
0
r
y0
sin rt]
初始条件
也可: y eta sin(rt )，a
y
y aet
y02
(v0
y0 )2 r2
,
tg
v0
y0r y0
▲特点：
yk yk+1
1)振幅逐渐衰减；
t
2)振幅呈等比级数递减
tk
T
讨论: 1)阻尼振幅对的影响
阻尼对自由振动的影响
2
则振动规律为：
g 980 49.5rad / s
yst
0.4
y 0.4sin(49.5t )
2
y 2.86sin(49.5t 0.14)
比较结果可知，h＝10cm时的振幅位移是h＝0的7倍
作业
[1] 求结构的自振频率。
EI
k
L
L/2
[3] 求结构的自振频率。
m
[2]列出图示结构的运动方程并求图示
a 程中要产生能量的损耗，称为阻尼。
粘滞阻尼
t
FR t cy
C —— 称为阻尼系数
13.2.4 阻尼对自由振动的影响
y(t) c km
有阻尼模型
其中: k称为阻尼比
cr —— 临界阻尼系数
y
二阶常微分方程可变为：
ky m
my
cy
y 2 y 2 y 0
一、有阻尼的自由振动
m EI
解：为求柔度系数，在质点 上加单位力1（图乘法）
l/2
l/2
P 1
l3
48EI
48EI
l3m
T 2
l/4
[思考] 比较图示结构的自振频率
m
m
m 2 ml3
48EI
(a)<(b)<(c) m
l/2
l/2
l/2
l/2
l/2
l/2
(a)
(b)
(c)
13.2.3 结构的自振周期和自振频率
[13-7] 为了计算自由振动是质点在任意时刻的位移，除了 要知道质点的初始速度之外，它还需要知道些什么？
13.2.3 结构的自振周期和自振频率
[1] 求图示结构的自振频率。
EI
L/2 P=1
k
L
L/2
k
M1图
3/2
解： 画M1图；由M1图求得 ；由 求得 。
1 (LL L 3 L L L 1 3 L) 3 3
EI
结构的自振频率。
EI
EI
2m
k
m
L/2
L/2
L/3
L
m EI L
作业
思考题P286页 13-1，13-2，13-4，13-5，13-6，13-7 [13-1] 结构静力计算和动力计算的主要区别是什么？
[13-2] 结构静力自由度和动力自由度的概念有何异同？ [13-4] 在建立振动方程时，如考虑重力的影响，动位移的 方程有无改变？ [13-6] 为什么说自振周期是结构的固有性质？它与结构那 些固有量有关？
阻尼对固有振动蘋率的影响
3）阻尼对自由振动 衰减速率的影响 如图右
具有四种阻尼水平体系的自由振动
13.2.4 阻尼对自由振动的影响
3 两个连续峰值之比与阻尼比之间的关系
振幅为 ae随时t 间衰减相邻两个振幅的比。
yk 1 yk
ae(tk T ) aetk
eT
常数
ln yk T 2
yk 1
arctg( 0.4 ) arctg0.141 0.14rad
2 10
则振动规律为：
y 2.86sin(49.5t 0.14)
13.2.3 结构的自振周期和自振频率
2. 如图所示简支梁，将一重为W的物体将物体无初速地 放置在梁中点，求该系统的振动规律。
st yst W
A yst 0.4cm arctg()
r
对数递减率：
ln yk 2
yk 1
13.2.4 阻尼对自由振动的影响
4 阻尼比的测定 对数递减率：
ln yk 2 yk1 1 2
当 0.2，则 1 r
1 r ln yk 1 ln yk 2 yk1 2 yk1
2
对数衰减率与阻尼比之间 的精确和近似关系
13.2.4 阻尼对自由振动的影响
1 ( L L 1 2 L L L 1 2 L) 2 L3
EI 2 2 2 3 2 2 2 3 2
4EI
4EI 2mL3
13.2.3 结构的自振周期和自振频率
[2] 列出图示结构的运动方程。
EI
2m
k
m
L/2
L/2
L/3
(t )
2my1 1 k
2 my2
解：是单自由度体系。 以 建(t立) 位移方程。
令为r
令： r 1 2 (低阻尼体系的自振圆频率)
一般建筑物ξ很小，约0.01～0.1 。像我们感兴趣的房屋、 桥梁、水坝、核电站、海洋结构等都属这一类；
r
汽车减震系统，阻尼通常小于临界阻尼的一半ξ＜0.5
13.2.4 阻尼对自由振动的影响
则微分方程通解为：
实部
虚部
y et C1 cosrt C2 sinrt
mW
60
13.2.3 结构的自振周期和自振频率
[例13.3] 如图所示简支梁，将一重为W的物体从高 h处自由释放，落到梁的中点处，求该系统的振动规律。
W
设： y Asin(t )
yst
y
h
其中： g
yst
y
解:自由落体后，梁以一定的
初速度上下作自由振动， 其振动平衡位置为 yst 。
st yst W
13.2.2 单自由度体系自由振动微分方程解答
原方程： my ky 0 y k 2 y 0 (令： k )
m
m
通解为： y(t) C1 sin t C2 cost
由初始条件： y(0) y0 C2 y0
解为：
y(t)
y0
cos t
v0
sin t
y(0)
v0
C1
v0
y(t)
T
y0
m 2
W
g
2
st g
k 1 g g m m W st
① ω和T只与结构的质量与刚度有关，与外界干扰无关；
② T与质量成正比，质量越大，周期越大；与刚度成反比， 刚度越大，周期越小。要改变ω和T，只能改变质量和刚度。