蒙特卡洛方法 (MC) 方法

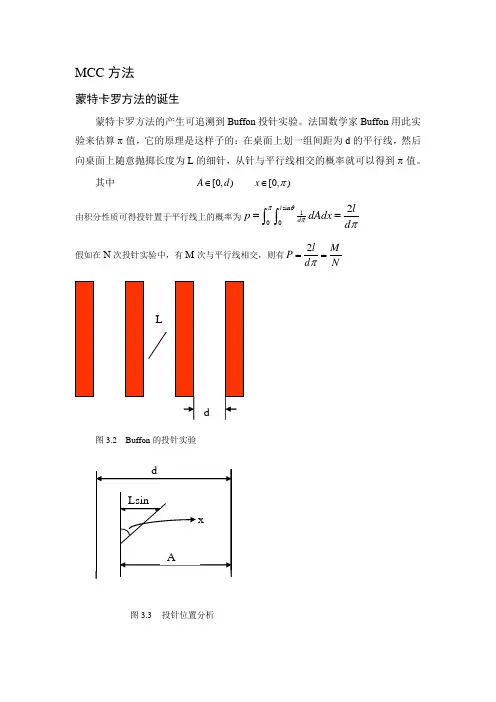
MCC 方法蒙特卡罗方法的诞生蒙特卡罗方法的产生可追溯到Buffon 投针实验。

法国数学家Buffon 用此实验来估算π值，它的原理是这样子的：在桌面上划一组间距为d 的平行线，然后向桌面上随意抛掷长度为L 的细针，从针与平行线相交的概率就可以得到π值。

其中 [0,)A d ∈ [0,)x π∈ 由积分性质可得投针置于平行线上的概率为sin 12l d l p dAdx d πθππ==⎰⎰假如在N 次投针实验中，有M 次与平行线相交，则有2l M P d Nπ==图3.2Buffon 的投针实验图3.3 投针位置分析1930年，费米利用蒙特卡罗方法研究了中子的扩散，并设计了一个蒙特卡罗机械装置，用于计算核反应堆的临界状态。

冯.诺依曼是蒙特卡罗方法的正式奠基者,他与Stanislaw Ulam 合作建立了概率密度函数、反累积分布函数的数学基础，以及伪随机数产生器，从而使得蒙特卡罗方法得以推广，成为科学领域一种常用的模拟方法。

蒙特卡罗方法的基本思想对某一个待解决的物理问题（当这个物理问题可以抽象为数学问题时）建立一个概率模型，即确定某个随机事件X ，使得待求问题的解等于随机事件X 出现的概率或随机变量的数学期望值。

然后进行模拟实验，重复多次地模拟随机事件X 。

最后对随机实验结果进行统计平均，求出X 出现的频数作为问题的近似解。

这就是蒙特卡罗方法的基本思想。

具体来说：假设所要求的量x 是随机变量的数学期望，那么近似确定x 的方法是对进行N次重复抽样，产生相互独立的值的序列、、……、，并计算其算术平均值：11NNnn Nξξ==∑根据大数定理有P (l i m )N N x ξ→∞==因此，当N 充分大时，下式 ()N E x ξξ≈=成立的概率为1,亦即可以用作为所求量x 的估计值。

用蒙特卡罗方法求解时，最简单的情况是模拟一个发生概率为P 的随机事件A 。

考虑一个随机变量，若在一次试验中事件A 出现，则取值为1；若事件A 不出现，则取值为0。

蒙特卡洛方法1、蒙特卡洛方法的由来蒙特卡罗分析法（Monte Carlo method），又称为统计模拟法，是一种采用随机抽样（Random Sampling）统计来估算结果的计算方法。

由于计算结果的精确度很大程度上取决于抽取样本的数量，一般需要大量的样本数据，因此在没有计算机的时代并没有受到重视。

第二次世界大战时期，美国曼哈顿原子弹计划的主要科学家之一，匈牙利美藉数学家约翰·冯·诺伊曼（现代电子计算机创始人之一）在研究物质裂变时中子扩散的实验中采用了随机抽样统计的手法，因为当时随机数的想法来自掷色子及轮盘等赌博用具，因此他采用摩洛哥著名赌城蒙特卡罗来命名这种计算方法，为这种算法增加了一层神秘色彩。

蒙特卡罗方法提出的初衷是用于物理数值模拟问题, 后来随着计算机的快速发展, 这一方法很快在函数值极小化、计算几何、组合计数等方面得到应用, 于是它作为一种独立的方法被提出来, 并发展成为一门新兴的计算科学, 属于计算数学的一个分支。

如今MC 方法已是求解科学、工程和科学技术领域大量应用问题的常用数值方法。

2、蒙特卡洛方法的核心—随机数蒙特卡洛方法的基本理论就是通过对大量的随机数样本进行统计分析，从而得到我们所需要的变量。

因此蒙特卡洛方法的核心就是随机数，只有样本中的随机数具有随机性，所得到的变量值才具有可信性和科学性。

在连续型随机变量的分布中, 最基本的分布是[0, 1]区间上的均匀分布, 也称单位均匀分布。

由该分布抽取的简单子样ξ1，ξ2ξ3 ……称为随机数序列, 其中每一个体称为随机数, 有时称为标准随机数或真随机数, 独立性和均匀性是其必备的两个特点。

真随机数是数学上的抽象, 真随机数序列是不可预计的, 因而也不可能重复产生两个相同的真随机数序列。

真随机数只能用某些随机物理过程来产生, 如放射性衰变、电子设备的热噪音、宇宙射线的触发时间等。

实际使用的随机数通常都是采用某些数学公式产生的，称为伪随机数。

蒙特卡罗方法（MC）蒙特卡罗（Monte Carlo）方法：蒙特卡罗（Monte Carlo）方法，又称随机抽样或统计试验方法，属于计算数学的一个分支，它是在本世纪四十年代中期为了适应当时原子能事业的发展而发展起来的。

传统的经验方法由于不能逼近真实的物理过程，很难得到满意的结果，而蒙特卡罗方法由于能够真实地模拟实际物理过程，故解决问题与实际非常符合，可以得到很圆满的结果。

这也是我们采用该方法的原因。

蒙特卡罗方法的基本原理及思想如下：当所要求解的问题是某种事件出现的概率，或者是某个随机变量的期望值时，它们可以通过某种“试验”的方法，得到这种事件出现的频率，或者这个随机变数的平均值，并用它们作为问题的解。

这就是蒙特卡罗方法的基本思想。

蒙特卡罗方法通过抓住事物运动的几何数量和几何特征，利用数学方法来加以模拟，即进行一种数字模拟实验。

它是以一个概率模型为基础，按照这个模型所描绘的过程，通过模拟实验的结果，作为问题的近似解。

可以把蒙特卡罗解题归结为三个主要步骤：构造或描述概率过程；实现从已知概率分布抽样；建立各种估计量。

蒙特卡罗解题三个主要步骤：构造或描述概率过程：对于本身就具有随机性质的问题，如粒子输运问题，主要是正确描述和模拟这个概率过程，对于本来不是随机性质的确定性问题，比如计算定积分，就必须事先构造一个人为的概率过程，它的某些参量正好是所要求问题的解。

即要将不具有随机性质的问题转化为随机性质的问题。

实现从已知概率分布抽样：构造了概率模型以后，由于各种概率模型都可以看作是由各种各样的概率分布构成的，因此产生已知概率分布的随机变量（或随机向量），就成为实现蒙特卡罗方法模拟实验的基本手段，这也是蒙特卡罗方法被称为随机抽样的原因。

最简单、最基本、最重要的一个概率分布是(0,1)上的均匀分布（或称矩形分布）。

随机数就是具有这种均匀分布的随机变量。

随机数序列就是具有这种分布的总体的一个简单子样，也就是一个具有这种分布的相互独立的随机变数序列。

第三章 随机性模拟方法—蒙特卡罗方法（MC ）§ 3.1 预备知识例：一个粒子在一个二维正方格点上跳跃运动随机行走：每一时间步上，粒子可选择跳到四个最近邻格点上的任何一个，而记不得自己来自何方；自回避行走：粒子记得自己来自什么地方，而回避同它自己的路径交叉。

随机行走的每一步的结果就是系统的一个状态，从一个状态到另一个状态的跃迁只依赖于出发的状态，这些状态形成一个序列，这就是一个马尔可夫链。

状态序列：x 0, x 1, …, x n , …已给出状态x 0, x 1, …, x n+1 的确定值，x n 出现的概率叫做条件概率 ()01,x x x -n n P 马尔可夫链的定义：如果序列x 0, x 1, …, x n , …对任何n 都有 ()()101,--=n n n n P P x x x x x 则此序列为一个马尔可夫链（或过程）。

§ 3.2 布朗动力学（BD ） 1．郎之万方程 v t R dtdvmβ-=)( 方程右边第一项为随机力，对粒子起加热作用；第二项为摩擦力，避免粒子过热。

将方程变形为：dt mvt R dt m v dv )(+-=β 于是，解可写为：])0()(11[)0( )0()(0)()(10⎰+≈⎰=---tt mt md v R m tm d ev R m ev eev t v tττββτττβ⎰+≈---t m t t md Re m ev 0)()(1)0( ττβτβ当随机力R(t)服从高斯分布时，上述方程的解描述的即为布朗运动，于是，布朗运动问题就化为在一些补充条件下求解郎之万方程，即⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧><=>=<>=<=+><--)( 2)()(2)0()(,0)()(222/2/12高斯分布R R B e R R P t T k R t R t R m t R m v dt dv πδββ 注：)()()(t t q t R t R '->='<δ 表示随机力R 在t 和t ’时刻没有关联, q 为噪声强度。

微观流体力学中的数值模拟技术微观流体力学是研究微米尺度下流体运动行为的一个分支学科。

在这个领域，微观粒子的运动和作用起着至关重要的作用。

但是，由于经验和理论模型的限制，微观粒子的解析解通常难以获得。

这时，数值模拟技术便成为了一种解决微观流体力学问题的有效手段。

本文将介绍微观流体力学中的数值模拟技术及其应用。

第一部分：微观流体力学中的数值模拟方法微观流体力学中的数值模拟方法通常分为分子动力学和蒙特卡罗方法两类。

下面将逐一介绍。

1.分子动力学方法分子动力学（Molecular Dynamics，MD）方法是将流体视为大量分子集合，并以牛顿运动方程为基础，通过计算每个分子的运动轨迹得出整个流体的运动状态。

常见的MD算法包括Verlet算法、Leapfrog算法、Velocity-Verlet算法等。

分子动力学方法的优点是可以考虑分子间的相互作用，能够获得各个方向的流体速度分布和物理量的统计分布，但是对于大规模系统计算量较大，难以处理相变等多相系统。

2.蒙特卡罗方法蒙特卡罗（Monte Carlo，MC）方法是基于概率统计原理的一种数值计算方法，可获得宏观物理量的统计分布。

常用的MC算法有Metropolis算法、Kawasaki动力学算法等。

蒙特卡罗方法的优点是能够处理相变和相界面情况，适合处理多相系统，且计算量相对MD方法较小。

但是这种方法难以处理如空气动力学等宏观问题。

第二部分：微观流体力学数值模拟方法的应用微观流体力学数值模拟方法的应用十分广泛，下面将以三个案例进行介绍。

1.纳米流体管道的模拟纳米流体管道在微流控和纳流体力学研究中具有重要意义。

使用分子动力学方法对管道中的交付和转移过程进行探究，对了解纳米流体环境下的分子传输，以及微型流动和传质机理有重要意义。

在这种情况下，分子动力学中的非平衡分子动力学方法得到了广泛应用。

2.多组分流体的模拟在工程实际应用中，多组分流体在润滑油、生物学和食品加工等各领域中都有着广泛的应用。

mc算法原理
MC算法原理是蒙特卡洛算法的简称。

蒙特卡洛算法是一种基于统计模拟的随机算法，可以用于解决复杂的计算问题。

MC算法原理的基本思想是通过随机取样来近似计算问题的解。

具体而言，MC算法通过生成大量的随机样本来模拟问题的概率分布或者数值分布，然后利用这些样本数据进行统计分析，得出问题的解或者近似解。

MC算法的主要步骤包括样本生成、统计分析和结果输出。

首先，根据问题的特点，设计合适的抽样方法生成具有代表性的随机样本。

其次，对生成的样本数据进行统计分析，比如计算样本均值、方差等参数，或者通过统计直方图、密度估计等方式得到问题的概率或者数值分布。

最后，根据统计分析的结果，输出问题的解或者近似解。

MC算法在众多领域中得到广泛应用。

在金融学中，可以用MC算法进行期权定价；在物理学中，可以用MC算法模拟粒子运动；在生物学中，可以用MC算法预测蛋白质的结构等等。

总之，MC算法原理是一种基于统计模拟的随机算法，通过生成大量的随机样本进行统计分析来近似计算问题的解。

它在各个领域都发挥着重要的作用，是一种强大而灵活的计算工具。

第七章蒙特卡洛方法1蒙特卡洛方法蒙特卡洛方法(M-C)又称之为随机取样法,统计模拟法,是利用随机数的统计规律来进行计算和模拟的方法.它可用于数值计算,也可用于数值仿真。

例计算园周率。

单位圆的面积是π,它在第一象限的面积为π/4,因此有π=41dx11dx2θ(1−x21−x22)其中θ是单位阶跃函数。

计算时，生成二维的等几率分布的随机数(x,y)，统计所有满足x2+y2<1的点数，计算它们与总点数之比，就是所求。

用M-C计算这个二维积分的指令是p=4/1000000*length(find(sum(rand(2,1000000).^2)<1))这里取N=106。

例氢原子电子云的模拟。

氢原子的基态（n=1,l=0,m=0）的电子分布几率密度函数是D=4r2 a31e−2r/a1,a1=5.29×10−2nm,D的最大值D max=1.1,r0=0.25nm是D的收敛点。

模拟是用点的密度来表示电子的几率分布密度。

模拟时先产生一个随机的电子轨道半径r=r0rand(1),显然有0≤r≤r0,由r计算出D(r)。

再产生一个随机的概率判据D0=D max rand(1),显然有0≤D0≤D max,然后进行判断，如果D(r)<D0,则舍弃它，反之就计算一个随机的角度值，θ=2πrand(1),最后得到的点的坐标是x=r cosθ,y=r sinθ。

在程序中使用矢量化编程以提高计算速度。

clear allN=600000;r0=25;a=0.529;r=r0*rand(1,N);Dr=4/a^3*r.^2.*exp(-2/a*r);D0=1.1*rand(1,N);DD=Dr-D0;r=r(find(DD>0));n=length(r);Q=2*pi*rand(1,n);[X,Y]=pol2cart(Q,r);plot(X,Y,’r.’,’marker’,’.’,’markersize’,1)r=0:0.01:20;Dr=4/a^3*r.^2.*exp(-2/a*r);figureplot(r,Dr)2等几率随机数的生成生成等一维几率随机数的指令是rand,可以用指令hist来检验它所生成的数。

mc法模拟计算x射线质量衰减系数MC法模拟计算X射线质量衰减系数是一种常用于医学、工业、科研等领域的辐射学计算方法。

本文将详细介绍MC法的原理、应用以及计算步骤，以期为读者提供指导意义。

MC法，即蒙特卡洛模拟方法（Monte Carlo Simulation），是一种基于随机数的数值计算方法，模拟粒子的运动轨迹并统计其与介质相互作用的过程。

在X射线质量衰减系数的计算中，MC法可以模拟X 射线与物质相互作用的过程，从而得到X射线在不同介质中的衰减情况。

MC法的应用广泛。

在医学领域，MC法可以用于计算放射治疗过程中X射线的剂量分布，以优化放疗方案并保护患者的安全；在工业领域，MC法可以用于计算射线照射设备的剂量分布，以保证工作人员的安全；在科研领域，MC法可以用于模拟X射线与材料、生物组织等相互作用的过程，研究射线对物质的影响。

下面我们将介绍MC法计算X射线质量衰减系数的具体步骤：1. 确定模型：根据实际需求，确定X射线的能量范围和材料的性质，并建立相应的模型。

2. 生成射线：使用随机数生成器产生大量符合X射线能谱要求的射线。

3. 轨迹模拟：根据射线的起始位置和方向，并结合介质的性质，模拟射线在介质中的运动轨迹。

4. 相互作用模拟：根据不同介质的性质，模拟射线与介质相互作用的过程，如光电效应、康普顿散射等。

5. 计算剂量：根据射线与介质相互作用的结果，统计射线在介质中的剂量分布。

6. 衰减系数计算：根据统计得到的剂量数据，计算出X射线在不同介质中的质量衰减系数。

7. 结果分析：对计算得到的质量衰减系数进行分析，并与实验结果进行对比，评估模拟的准确性和可靠性。

MC法模拟计算X射线质量衰减系数具有一定的优势，如可以考虑到X射线与介质之间的相互作用的随机性，能够更真实地模拟实际情况。

但也存在一些挑战，如计算时间较长、计算结果受到随机数生成器的影响等。

总之，MC法模拟计算X射线质量衰减系数是一种有效的方法，可广泛应用于医学、工业、科研等领域。