复变函数 留数和留数定理

复变函数与留数定理复变函数在数学中有着重要的地位，它是实变函数的推广和扩展。

复变函数的研究依赖于留数定理，这是复分析中的重要概念。

本文将介绍复变函数以及留数定理的基本概念和应用。

一、复变函数的定义与性质复变函数是定义在复数域上的函数，其定义域和值域都是复数集合。

复变函数可以表示为f(z)=u(x,y)+iv(x,y)，其中z=x+iy，u和v是实变函数。

复变函数和实变函数的性质有相似之处，如连续性、可微性和可导性等。

但复变函数的导数是一个复数，具有方向和模的概念。

二、留数定理的基本概念留数是复变函数在孤立奇点处的特殊性质。

留数定理是复变函数理论中的核心内容之一。

对于函数f(z)，若z=a是它的孤立奇点，可以通过留数计算沿闭合曲线的积分。

留数定理包括留数定理、柯西公式和狄利克雷问题等。

1. 留数定理留数定理是针对有限孤立奇点的情况。

当f(z)在区域D内有孤立奇点a1,a2,...,an时，针对闭合曲线C内的函数f(z)，可以通过求解a1,a2,...,an处的留数来计算C上的积分。

这个定理在复积分计算、曲线积分和求和等问题中有广泛的应用。

2. 柯西公式柯西公式是留数定理的一个重要推论。

柯西公式表明，如果函数f(z)在区域D内解析（即可导），则它在D内的任何闭合曲线C上的积分为零。

这个结论为复变函数的求解和计算提供了方便。

3. 狄利克雷问题狄利克雷问题是留数定理与边值问题相结合的应用，它在电磁学和热传导等领域中起着重要作用。

狄利克雷问题可以通过留数定理求解，将定义在一条封闭曲线上的边值问题转化为计算特定点上的积分问题。

三、复变函数与实变函数的关系复变函数理论是实变函数理论的扩展和推广，两者之间有着密切的联系。

复分析的基本定理和方法可以归结为实分析的特殊情况，同时复分析也为实分析提供了新的解题思路和工具。

1. 复变函数的导数与实变函数的导数复变函数的导数是一个复数，可以表示为f'(z)=u_x+iv_x，其中u_x和v_x是u和v相对于x的偏导数。

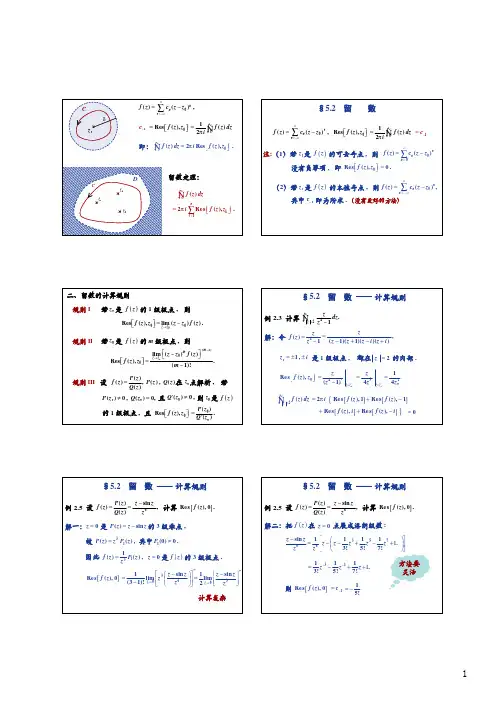
第六章留数理论及其应用§1.留数1.（定理6.1 柯西留数定理）：∫f(z)dz=2πi∑Res(f(z),a k)nk=1C2.（定理6.2）：设a为f(z)的m阶极点，f(z)=φ(z) (z−a)n,其中φ(z)在点a解析，φ(a)≠0，则Res(f(z),a)=φ(n−1)(a) (n−1)!3.（推论6.3）：设a为f(z)的一阶极点，φ(z)=(z−a)f(z),则Res(f(z),a)=φ(a) 4.（推论6.4）：设a为f(z)的二阶极点φ(z)=(z−a)2f(z)则Res(f(z),a)=φ′(a)5.本质奇点处的留数：可以利用洛朗展式6.无穷远点的留数：Res(f(z),∞)=12πi∫f(z)dzΓ−=−c−1即，Res(f(z),∞)等于f(z)在点∞的洛朗展式中1z这一项系数的反号7.（定理6.6）如果函数f(z)在扩充z平面上只有有限个孤立奇点（包括无穷远点在内），设为a1,a2,…,a n,∞,则f(z)在各点的留数总和为零。

注：虽然f(z)在有限可去奇点a处，必有Res(f(z),∞)=0，但是，如果点∞为f(z)的可去奇点（或解析点），则Res(f(z),∞)可以不为零。

8.计算留数的另一公式：Res (f (z ),∞)=−Res (f (1t )1t 2,0)§2.用留数定理计算实积分一.∫R (cosθ,sinθ)dθ2π0型积分 → 引入z =e iθ注：注意偶函数二.∫P(x)Q(x)dx +∞−∞型积分1.（引理6.1 大弧引理）：S R 上lim R→+∞zf (z )=λ则lim R→+∞∫f(z)dz S R=i(θ2−θ1)λ 2.（定理6.7）设f (z )=P (z )Q (z )为有理分式，其中P (z )=c 0z m +c 1z m−1+⋯+c m (c 0≠0)Q (z )=b 0z n +b 1z n−1+⋯+b n (b 0≠0)为互质多项式，且符合条件：（1）n-m ≥2;（2）Q(z)没有实零点于是有∫f (x )dx =2πi ∑Res(f (z ),a k )Ima k >0+∞−∞注：lim R→R+∞∫f(x)dx +R −R 可记为P.V.∫f(x)dx +∞−∞ 三. ∫P(x)Q(x)e imx dx +∞−∞型积分 3.（引理6.2 若尔当引理）：设函数g(z)沿半圆周ΓR :z =Re iθ(0≤θ≤π，R 充分大)上连续，且lim R→+∞g (z )=0在ΓR 上一致成立。

复变函数留数定理复变函数留数定理（Residue Theorem）是复分析中的重要概念，用于计算对应于奇异点（singular point）的留数（residue）。

留数定理提供了计算复变函数沿闭曲线的积分的一种有效方法，它与复分析中其他重要的定理和方法相辅相成，对于解决实际问题具有重要意义。

一、留数的定义设函数f(z)在点z=a附近解析且具有洛朗展开式f(z)=∑(n=-∞)^∞ a(n)(z-a)^n其中a(n)是复数，令C为以a为圆心的半径为R的圆周，且其方向与实轴正方向一致。

如果函数f(z)在圆盘界上的点（除去a点）上解析，则称a点是函数f(z)的奇异点。

奇异点主要有三种形式：可去奇点、极点和本性奇点。

对于函数f(z)一个奇异点a，定义留数Res[f(z), a]为Res[f(z), a] = a(-1)即留数等于洛朗展开式的一次项系数a(-1)。

二、留数的求解方法1. 求可去奇点的留数当a点是函数f(z)的可去奇点时，即a点是f(z)的解析点，那么留数等于0。

2. 求一阶极点的留数当a点是函数f(z)的一阶极点时，即a点是f(z)的奇异点且它的最低零次是-1次，要求a(-1)≠0。

此时留数可以通过以下方法求解：Res[f(z), a] = lim(z→a) (z-a)f(z)3. 求高阶极点的留数当a点是函数f(z)的高阶极点时，即a点是f(z)的奇异点且它的最低零次大于等于-1次。

此时留数可以通过以下公式计算：Res[f(z), a] = a(-1) = 1/(n-1)! * d^(n-1)/dz^(n-1) [(z-a)^n * f(z)]其中，n为a点的零次。

三、留数定理的表述留数定理的基本表述为：设函数f(z)在闭合曲线C的内部除有限个奇异点外是全纯的，则有积分公式成立：∮[C] f(z)dz = 2πi * ∑ Res[f(z), a]其中，[C]代表C内部的积分，∑代表对所有奇异点求和。

复变函数中的留数定理
复变函数是指既定义在复数域上又取复数值的函数。

复变函数具有许多特殊的性质和定理，其中留数定理是其中一个重要的定理。

本文将介绍复变函数中的留数定理以及其应用。

一、留数的定义和计算方法
在复变函数中，留数(residue)是指当函数在某个点存在奇点时，即函数在该点不解析的情况下，奇点点内仍然具有一定的数值。

留数的计算方法可以通过洛朗级数展开或者柯西积分公式来实现。

对于一个圆心在奇点上的积分路径，留数的计算公式可以表示为：Res[f;z_0] = (1 / (2πi)) ∮ f(z)dz
二、留数定理的表述
留数定理是指当一个函数在一个环形区域上解析且没有奇点时，该函数的积分沿该闭合曲线的环形轮廓，等于沿环形区域内部孤立奇点的留数之和。

数学表述如下：
∮ f(z)dz = 2πi ∑Res[f;z_i]
三、留数定理的应用
1. 计算积分：留数定理是计算复变函数的积分的重要工具。

通过计算函数在奇点处的留数，可以将积分转化为留数之和的形式，从而简化计算过程。

2. 求解无穷级数：通过留数定理，可以将一个函数展开为洛朗级数，从而求解一些复杂的无穷级数。

3. 解析函数的奇点：留数定理可以帮助我们分析函数在复平面上的
奇点，并研究奇点的类型和性质。

总结：
复变函数中的留数定理是一个重要的工具，可以在计算积分、求解
无穷级数和分析奇点等方面发挥关键作用。

留数定理的应用不仅仅局
限于数学领域，而且在物理学、工程学和经济学等学科中也具有重要
的意义。

通过掌握留数定理的原理和计算方法，我们可以更好地理解
和应用复变函数的知识。