(重点)平面向量数量积公式的应用(可编辑修改word版)

突破6.4 平面向量的应用一、学情分析高考对本部分的考查主要涉及平面向量的数量积和向量的线性运算，以运算求解和数形结合为主，重点掌握数量积的坐标表达式，会进行平面向量数量积的运算，能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系，掌握向量加法、减法、数乘的运算及其几何意义等，注重转化与化归思想的应用.1．平面向量的数量积一直是高考的一个热点，尤其是平面向量的数量积，主要考查平面向量的数量积的 运算、向量的几何意义、模与夹角、两向量的垂直等问题．题型一般以选择题、填空题为主.2．平面向量的基本定理及坐标表示是高考中的一个热点内容，尤其是用坐标表示的向量共线的条件是高 考考查的重点内容，一般是通过向量的坐标表示，将几何问题转化为代数问题来解决，多以选择题或填空题的形式呈现，有时也作为解答题中的条件，应用向量的平行或垂直关系进行转换．二、学法指导与考点梳理考点一 向量在平面几何中的应用 (1)用向量解决常见平面几何问题的技巧： 问题类型 所用知识 公式表示线平行、点共线等问题共线向量定理a ∥b ⇔a ＝λb ⇔x 1y 2－x 2y 1＝0， 其中a ＝(x 1，y 1)，b ＝(x 2，y 2)，b ≠0 垂直问题数量积的运算性质a ⊥b ⇔a ·b ＝0⇔x 1x 2＋y 1y 2＝0，其中a ＝(x 1，y 1)，b ＝(x 2，y 2)，且a ，b 为非零向量夹角问题数量积的定义cos θ＝a ·b|a ||b |(θ为向量a ，b 的夹角)，其中a ，b 为非零向量长度问题数量积的定义|a |＝a 2＝x 2＋y 2，其中a ＝(x ，y )，a 为非零向量平面几何问题――→设向量向量问题――→运算解决向量问题――→还原解决几何问题。

考点二 正弦定理和余弦定理1.在△ABC 中，若角A ，B ，C 所对的边分别是a ，b ，c ，R 为△ABC 外接圆半径，则 定理 正弦定理余弦定理公式a sin A ＝b sin B ＝c sin C＝2R a 2＝b 2＋c 2－2bc cos A ；b 2＝c 2＋a 2－2ca cos B ；c 2＝a 2＋b 2－2ab cos C常见 变形(1)a ＝2R sin A ，b ＝2R sin B ，c ＝2R sin C ；(2)sin A ＝a 2R ，sin B ＝b 2R ，sin C ＝c2R ；(3)a ∶b ∶c ＝sin A ∶sin B ∶sin C ；(4)a sin B ＝b sin A ，b sin C ＝c sin B ，a sin C ＝c sin Acos A ＝b 2＋c 2－a 22bc ；cos B ＝c 2＋a 2－b 22ac ；cos C ＝a 2＋b 2－c 22ab2.S △ABC ＝12ab sin C ＝12bc sin A ＝12ac sin B ＝abc 4R ＝12(a ＋b ＋c )·r (r 是三角形内切圆的半径)，并可由此计算R ，r .3.在△ABC 中，已知a ，b 和A 时，解的情况如下：A 为锐角A 为钝角或直角图形关系式 a ＝b sin A b sin A <a <b a ≥b a >b a ≤b 解的个数一解两解一解一解无解重难点题型突破1 平面向量在平面几何中的应用（奔驰定理）例1、（1）．（2022·四川西昌·高二期末（理））在平面上有ABC 及内一点O 满足关系式：0OBC OAC OAB S OA S OB S OC ⋅+⋅+⋅=△△△即称为经典的“奔驰定理”，若ABC 的三边为a ，b ，c ，现有0a OA b OB c OC ⋅+⋅+⋅=则O 为ABC 的（ ）A ．外心B ．内心C ．重心D ．垂心【答案】B 【解析】 【分析】利用三角形面积公式，推出点O 到三边距离相等。

平面向量的数量积平面向量的数量积，也叫点积或内积，是向量运算中的一种重要操作。

它与向量的夹角以及向量的长度有着密切的关系。

在本文中，我们将详细介绍平面向量的数量积的概念、计算方法以及一些应用。

一、概念平面向量的数量积是指将两个向量的对应分量相乘，并将所得乘积相加而得到的数值。

设有两个平面向量A和A，它们的数量积记作A·A，计算公式为：A·A = AAAA + AAAA其中，AA和AA分别是向量A在A轴和A轴上的分量，AA和AA分别是向量A在A轴和A轴上的分量。

二、计算方法要计算平面向量的数量积，需要先求出两个向量在A轴和A轴上的分量，然后按照数量积的计算公式进行计算。

假设有两个向量A = (A, A)和A = (A, A)，它们的数量积为A·A，计算步骤如下：1. 计算A和A在A轴上的分量AA和AA，分别为A和A；2. 计算A和A在A轴上的分量AA和AA，分别为A和A；3. 将AA和AA、AA和AA进行相乘得到AA和AA；4. 将AA和AA相加，得到平面向量的数量积A·A。

三、性质平面向量的数量积具有以下性质：1. 交换律：A·A = A·A2. 数乘结合律：(AA)·A = A(A·A) = A·(AA)3. 分配律：(A + A)·A = A·A + A·A其中，A为任意实数，A、A和A为任意向量。

四、夹角与数量积的关系两个非零向量A和A的数量积A·A与它们夹角A的余弦函数之间存在着如下关系：A·A = ‖A‖‖A‖cosA其中，‖A‖和‖A‖分别为向量A和A的长度。

五、应用平面向量的数量积在几何和物理学中有着广泛的应用。

以下是一些常见的应用：1. 判断两个向量是否垂直：如果两个向量的数量积为零，即A·A = 0，那么它们是垂直的。

2. 计算向量的模：根据数量积的性质，向量的模可以通过向量与自身的数量积来计算。

专题5.3 平面向量的数量积一、考情分析1.理解平面向量数量积的含义及其物理意义；2.了解平面向量的数量积与向量投影的关系；3.掌握数量积的坐标表达式，会进行平面向量数量积的运算；4.能运用数量积表示两个向量的夹角，会用数量积判断两个平面向量的垂直关系；5.会用向量的方法解决某些简单的平面几何问题；6.会用向量方法解决简单的力学问题与其他一些实际问题。

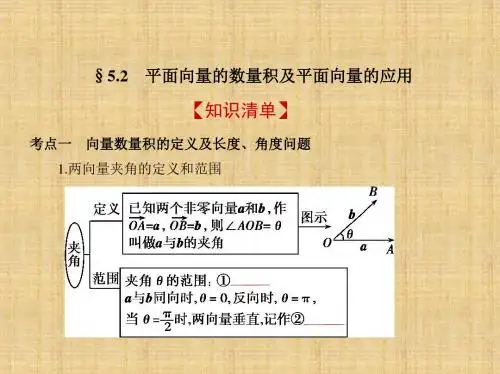
二、经验分享考点一 向量的夹角定义图示范围共线与垂直 已知两个非零向量a 和b ，作OA ―→＝a ，OB ―→＝b ，则∠AOB 就是a 与b 的夹角设θ是a 与b 的夹角，则θ的取值范围是0°≤θ≤180°θ＝0°或θ＝180°⇔a ∥b ，θ＝90°⇔a ⊥b考点二 平面向量的数量积定义设两个非零向量a ，b 的夹角为θ，则数量|a||b|cos θ叫做a 与b 的数量积，记作a·b投影 |a|cos θ叫做向量a 在b 方向上的投影， |b|cos θ叫做向量b 在a 方向上的投影几何意义数量积a·b 等于a 的长度|a|与b 在a 的方向上的投影|b|cos θ的乘积考点三 向量数量积的运算律 交换律 a ·b ＝b ·a 分配律 (a ＋b)·c ＝a ·c ＋b ·c 数乘结合律(λa)·b ＝λ(a ·b)＝a ·(λb)考点四 平面向量数量积的有关结论已知非零向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，a 与b 的夹角为θ.结论 几何表示 坐标表示模 |a|＝a·a |a|＝x 21＋y 21夹角cos θ＝a·b |a||b|cos θ＝x 1x 2＋y 1y 2x 21＋y 21·x 22＋y 22|x1x2＋y1y2|≤ x21＋y21x22＋y22考点五必备结论1．平面向量数量积运算的常用公式：(1)(a＋b)·(a－b)＝a2－b2；(2) (a±b)2＝a2±2a·b＋b2.2．有关向量夹角的两个结论：(1)两个向量a与b的夹角为锐角，则有a·b＞0，反之不成立(因为a与b夹角为0时不成立)．(2)两个向量a与b的夹角为钝角，则有a·b＜0，反之不成立(因为a与b夹角为π时不成立)．三、题型分析重难点题型突破1 平面向量数量积的运算例1、(2020·西安调研)在梯形ABCD 中，AB ∥CD ，AB ＝4，BC ＝CD ＝DA ＝2，若E 为BC 的中点，则AC →·AE →＝( ) A. 3 B ．3 C ．2 3 D ．12【答案】D【解析】解法一：如图过点D 作DM ⊥AB ，交AB 于点M ，过点C 作CN ⊥AB ，交AB 于点N ，则MN ＝DC ＝2.在Rt △ADM 中，AD ＝2，AM ＝AB －MN 2＝4－22＝1，所以∠DAM ＝60°.因为AC →＝AD →＋DC →＝AD →＋12AB →，AE →＝AD →＋DC →＋CE →＝AD →＋12AB →＋12CB →＝AD →＋12AB →＋12(CD →＋DA →＋AB →)＝12AD →＋34AB →，所以AC →·AE →＝⎝⎛⎭⎫AD →＋12AB →·⎝⎛⎭⎫12AD →＋34AB →＝12AD →2＋AD →·AB →＋38AB →2＝12×22＋2×4×cos60°＋38×42＝12.故选D.解法二：如图以A 为坐标原点，AB 所在直线为x 轴建立直角坐标系，则A (0,0)，B (4,0)． 设D (m ，n )(n >0)，则C (m ＋2，n )，因此BC 边的中点E ⎝⎛⎭⎫m ＋62，n 2.则AC →＝(m ＋2，n )，AE →＝⎝⎛⎭⎫m ＋62，n 2.又由BC ＝DA ＝2，得⎩⎨⎧(m ＋2－4)2＋n 2＝2，m 2＋n 2＝2，所以m ＝1，n 2＝3.则AC →·AE →＝(m ＋2)·m ＋62＋n 22＝3×72＋32＝12.故选D.【变式训练1-1】、(2020·河南安阳二模)如图所示，直角梯形ABCD 中，AB ∥CD ，AB ⊥AD ，AB ＝AD ＝4，CD ＝8.若CE →＝－7DE →，3BF →＝FC →，则AF →·BE →＝( )A ．11B ．10C ．－10D ．－11【答案】D 【解析】：.以A 为坐标原点，建立直角坐标系如图所示．则A (0，0)，B (4，0)，E (1，4)，F (5，1)，所以AF →＝(5，1)，BE →＝(－3，4)，则AF →·BE →＝－15＋4＝－11.故选D.【变式训练1-2】、(2020·黑龙江大庆实验中学高考模拟)在矩形ABCD 中，AB ＝2，BC ＝2，点E 为BC 的中点，点F 在CD 上，若AB →·AF →＝2，则AE →·BF →的值为( )A. 2 B ．2 C ．0 D ．1【答案】A【解析】建立如图所示的坐标系可得A (0,0)，B (2，0)，E (2，1)，F (x,2)，∴AB →＝(2，0)，AF →＝(x,2)，∴AB →·AF →＝2x ＝2，解得x ＝1，∴F (1,2)， ∴AE →＝(2，1)，BF →＝(1－2，2)，重难点题型突破2平面向量数量积的性质例2、已知|a |＝2，|b |＝3，a 与b 的夹角为2π3，且a ＋b ＋c ＝0，则|c |＝________.【答案】7【解析】因为a ＋b ＋c ＝0，所以c ＝－a －b ，所以c 2＝a 2＋b 2＋2a ·b ＝22＋32＋2×2×3×cos 2π3＝4＋9－6＝7.所以|c |＝7.【变式训练2-1】、已知非零向量a ，b 满足|a |＝2|b |，且(a －b )⊥b ，则a 与b 的夹角为( ) A.π6 B ．π3C.2π3 D ．5π6【答案】B.【解析】：设a 与b 的夹角为α， 因为(a －b )⊥b ， 所以(a －b )·b ＝0， 所以a ·b ＝b 2，所以|a |·|b |cos α＝|b |2，又|a |＝2|b |，所以cos α＝12，因为α∈(0，π)，所以α＝π3.故选B.重难点题型突破3 向量数量积的综合应用例3、(2020·华南师大附中一模)已知向量|OA →|＝3，|OB →|＝2，BC →＝(m －n )OA →＋(2n －m －1)OB →，若OA →与OB →的夹角为60°，且OC →⊥AB →，则实数m n 的值为( )A.87B.43C.65D.16【答案】A【解析】由题意得，OC →＝OB →＋BC →＝(m －n )OA →＋(2n －m )OB →，AB →＝OB →－OA →，OA →·OB →＝3×2×cos60°＝3.又因为OC →⊥AB →，所以OC →·AB →＝[(m －n )OA →＋(2n －m )OB →]·(OB →－OA →)＝－(m －n )OA →2＋(2m －3n )OA →·OB →＋(2n －m )·OB →2＝－9(m －n )＋3(2m －3n )＋4(2n －m )＝0， 整理得7m －8n ＝0，故m n ＝87.【变式训练3-1】、(2020·天津市宁河区芦台第一中学高考模拟)如图所示，等边△ABC 的边长为2，D 为边AC 上的一点，且AD →＝λAC →，△ADE 也是等边三角形，若BE →·BD →＝449，则λ的值是( )A.23B.33C.34D.13【答案】A【解析】 BE →·BD →＝(BA →＋AE →)·(BA →＋AE →＋ED →)＝BA →2＋BA →·AE →＋BA →·ED →＋AE →·BA →＋AE →2＋AE →·ED →＝22＋2·2λcosπ3－2·2λ＋2·2λcos π3＋4λ2＋4λ2cos 2π3＝2λ2＋4＝449⇒λ2＝49，因为λ>0，所以λ＝23，选A.【变式训练3-2】、(2020·石家庄质量检测(一))已知AB →与AC →的夹角为90°，|AB →|＝2，|AC →|＝1，AM →＝λAB →＋μAC →(λ，μ∈R )，且AM →·BC →＝0，则λμ的值为________．【答案】：14【解析】：根据题意，建立如图所示的平面直角坐标系则A (0，0)，B (0，2)，C (1，0)，所以AB →＝(0，2)，AC →＝(1，0)，BC →＝(1，－2)．设M (x ，y )，则AM →＝(x ，y )，所以AM →·BC →＝(x ，y )·(1，－2)＝x －2y ＝0，所以x ＝2y ，又AM →＝λAB →＋μAC →，即(x ，y )＝λ(0，2)＋μ(1，0)＝(μ，2λ)，所以x ＝μ，y ＝2λ，所以λμ＝12y x ＝14.重难点题型突破4 平面向量与三角函数例4、(2020·开封模拟)已知AB →，AC →是非零向量，且满足(AB →－2AC →)⊥AB →，(AC →－2AB →)⊥AC →，则△ABC 的形状为( ) A ．等腰三角形 B ．直角三角形 C ．等边三角形 D ．等腰直角三角形【答案】C【解析】∵(AB →－2AC →)⊥AB →⇒(AB →－2AC →)·AB →＝0，即AB →·AB →－2AC →·AB →＝0，(AC →－2AB →)⊥AC →⇒(AC →－2AB →)·AC →＝0，即AC →·AC →－2AB →·AC →＝0，∴AB →·AB →＝AC →·AC →＝2AB →·AC →，即|AB →|＝|AC →|，则cos A ＝AB →·AC →|AB →||AC →|＝12，∴∠A ＝60°，∴△ABC 为等边三角形．【变式训练4-1】、在△ABC 中，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，已知向量m ＝(cos B ，2cos 2 C2－1)，n ＝(c ，b －2a )，且m·n ＝0. (1)求∠C 的大小；(2)若点D 为边AB 上一点，且满足AD →＝DB →，|CD →|＝7，c ＝23，求△ABC 的面积． 【答案】见解析【解析】：(1)因为m ＝(cos B ，cos C )，n ＝(c ，b －2a )，m ·n ＝0，所以c cos B ＋(b －2a )cos C ＝0，在△ABC 中，由正弦定理得sin C cos B ＋(sin B －2sin A )cos C ＝0， sin A ＝2sin A cos C ，又sin A ≠0，所以cos C ＝12，而C ∈(0，π)，所以∠C ＝π3.(2)由AD →＝DB →知，CD →－CA →＝CB →－CD →， 所以2CD →＝CA →＋CB →，两边平方得4|CD →|2＝b 2＋a 2＋2ba cos ∠ACB ＝b 2＋a 2＋ba ＝28.① 又c 2＝a 2＋b 2－2ab cos ∠ACB ， 所以a 2＋b 2－ab ＝12.② 由①②得ab ＝8，所以S △ABC ＝12ab sin ∠ACB ＝23四、迁移应用1．已知AB →＝(2，3)，AC →＝(3，t )，|BC →|＝1，则AB →·BC →＝( ) A ．－3 B ．－2 C ．2 D ．3【答案】C.【解析】：因为BC →＝AC →－AB →＝(1，t －3)，所以|BC →|＝1＋（t －3）2＝1，解得t ＝3，所以BC →＝(1，0)，所以AB →·BC →＝2×1＋3×0＝2，故选C.2．已知向量|OA →|＝3，|OB →|＝2，OC →＝mOA →＋nOB →，若OA →与OB →的夹角为60°，且OC →⊥AB →，则实数m n 的值为( )A.16 B ．14C ．6D ．4 【答案】A.【解析】：因为向量|OA →|＝3，|OB →|＝2，OC →＝mOA →＋nOB →，OA →与OB →夹角为60°，所以OA →·OB →＝3×2×cos 60°＝3，所以AB →·OC →＝(OB →－OA →)·(mOA →＋nOB →)＝(m －n )OA →·OB →－m |OA →|2＋n |OB →|2＝3(m －n )－9m ＋4n ＝－6m ＋n ＝0，所以m n ＝16，故选A.3.已知向量a ＝(－2，m )，b ＝(1,2)，若向量a 在向量b 方向上的投影为2，则实数m ＝( ) A ．－4 B ．－6 C ．4 D.5＋1【答案】D【解析】 ∵a ·b ＝－2＋2m ，∴|a |cos θ＝a ·b |b |＝－2＋2m1＋4＝2.解得m ＝5＋1. 4．已知e 1，e 2为单位向量且夹角为2π3，设a ＝3e 1＋2e 2，b ＝3e 2，则a 在b 方向上的投影为________．【答案】：12【解析】：根据题意得，a ·b ＝9e 1·e 2＋6e 22＝9×1×1×⎪⎭⎫⎝⎛21-＋6＝－92＋6＝32，又因为|b |＝3，所以a 在b 方向上的投影为a ·b |b |＝323＝12.5.已知向量a ＝(sin θ，cos θ－2sin θ)，b ＝(1,2)． (1)若a ∥b ，求sin θ·cos θ1＋3cos 2θ的值；(2)若|a |＝|b |,0<θ<π，求θ的值．【答案】见解析【解析】(1)因为a ∥b ，所以2sin θ＝cos θ－2sin θ，于是4sin θ＝cos θ； 当cos θ＝0时，sin θ＝0，与sin 2θ＋cos 2θ＝1矛盾， 所以cos θ≠0，故tan θ＝14，所以sin θ·cos θ1＋3cos 2θ＝sin θ·cos θsin 2θ＋4cos 2θ＝tan θtan 2θ＋4＝465. (2)由|a |＝|b |知，sin 2θ＋(cos θ－2sin θ)2＝5， 即1－4sin θcos θ＋4sin 2θ＝5， 从而－2sin2θ＋2(1－cos2θ)＝4， 即sin2θ＋cos2θ＝－1， 于是sin ⎪⎭⎫⎝⎛+42πθ＝－22， 又由0<θ<π知，π4<2θ＋π4<9π4，所以2θ＋π4＝5π4或2θ＋π4＝7π4，因此θ＝π2或θ＝3π4.。

江苏省高邮职业教育中心校教案纸首页江苏省高邮职业教育中心校教案纸续页一、复习引入：1． 向量共线定理 向量b 与非零向量a共线的充要条件是：有且只有一个非零实数λ，使b =λa2．平面向量基本定理：如果1e ，2e 是同一平面内的两个不共线向量，那么对于这一平面内的任一向量a ，有且只有一对实数λ1，λ2使a=λ11e +λ22e 3．平面向量的坐标表示分别取与x 轴、y 轴方向相同的两个单位向量i 、j 作为基底任作一个向量a ，由平面向量基本定理知，有且只有一对实数x 、y ，使得yj xi a +=把),(y x 叫做向量a 的（直角）坐标，记作),(y x a = 4．平面向量的坐标运算 若),(11y x a =，),(22y x b =，则b a +),(2121y y x x ++=，b a -),(2121y y x x --=，),(y x a λλλ=若),(11y x A ，),(22y x B ，则()1212,y y x x AB --=5．a ∥b (b0)的充要条件是x 1y 2-x 2y 1=06．线段的定比分点及λP 1, P 2是直线l 上的两点，P 是l 上不同于P 1, P 2的任一点，存在实数λ，使 P P 1=λ2PP ，λ叫做点P 分21P P 所成的比，有三种情况：λ>0(内分) (外分) λ<0 (λ<-1) ( 外分)λ<0 (-1<λ<0)7定比分点坐标公式：若点P １(x 1,y 1) ，Ｐ２(x 2,y 2)，λ为实数，且P P 1＝λ2PP ，则点P 的坐标为（λλλλ++++1,12121y y x x ），我们称λ为点P 分21P P 所成的比 8点P 的位置与λ的范围的关系：①当λ＞０时，P P 1与2PP 同向共线，这时称点P 为21P P 的内分点②当λ＜０(1-≠λ)时，P P 1与2PP 反向共线，这时称点P 为21P P 的外分点9线段定比分点坐标公式的向量形式：在平面内任取一点O ，设1OP ＝ａ，2OP ＝ｂ，可得OP =b a b a λλλλλ+++=++111110．力做的功：W = |F |⋅|s |cos ，是F 与s 的夹角二、讲解新课：1．两个非零向量夹角的概念已知非零向量ａ与ｂ，作OA ＝ａ，OB ＝ｂ，则∠ＡＯＢ＝θ（０≤θ≤π）叫ａ与ｂ的夹角说明：（1）当θ＝０时，ａ与ｂ同向；（2）当θ＝π时，ａ与ｂ反向； （3）当θ＝2π时，ａ与ｂ垂直，记ａ⊥ｂ； （4）注意在两向量的夹角定义，两向量必须是同起点的范围0≤≤1802．平面向量数量积（内积）的定义：已知两个非零向量ａ与ｂ，它们的夹角是θ，则数量|a ||b |cos 叫ａ与ｂ的数量积，记作a ⋅b ，即有a ⋅b = |a ||b |cos ，（０≤θ≤π）并规定0与任何向量的数量积为0⋅探究：两个向量的数量积与向量同实数积有很大区别 （1）两个向量的数量积是一个实数，不是向量，符号由cos的符号所决定（2）两个向量的数量积称为内积，写成a ⋅b ；今后要学到两个向量的外积a ×b ，而a ⋅b 是两个向量的数量的积，书写时要严格区分符号“· ”在向量运算中不是乘号，既不能省略，也不能用“×”代替（3）在实数中，若a 0，且a ⋅b =0，则b =0；但是在数量积中，若a 0，且a ⋅b =0，不能推出b =0因为其中cos有可能为0（4）已知实数a 、b 、c (b 0)，则ab=bc ⇒ a=c 但是a ⋅b = b ⋅ca = c如右图：a ⋅b = |a ||b |cos= |b ||OA|，b ⋅c = |b ||c |cos = |b ||OA|⇒ a ⋅b = b ⋅c 但ac(5)在实数中，有(a ⋅b )c = a (b ⋅c )，但是(a ⋅b )ca (b ⋅c )显然，这是因为左端是与c 共线的向量，而右端是与a 共线的向量，而一般a 与c 不共线3．“投影”的概念：作图定义：|b |cos叫做向量b 在a 方向上的投影投影也是一个数量，不是向量；当为锐角时投影为正值；当为钝角时投影为负值；当为直角时投影为0；当 = 0时投影为 |b |；当 = 180时投影为 |b |4．向量的数量积的几何意义：数量积a ⋅b 等于a 的长度与b 在a 方向上投影|b |cos 的乘积5．两个向量的数量积的性质：设a 、b 为两个非零向量，e 是与b 同向的单位向量1e ⋅a = a ⋅e =|a |cos2aba ⋅b = 0C3当a 与b 同向时，a ⋅b = |a ||b |；当a 与b 反向时，a ⋅b = |a ||b |特别的a ⋅a = |a |2或a a a ⋅=||4cos=||||b a ba ⋅5|a ⋅b | ≤ |a ||b |三、讲解范例：例1 判断正误，并简要说明理由①ａ·0＝0；②0·ａ＝０；③0－AB ＝BA ；④｜ａ·ｂ｜＝｜ａ｜｜ｂ｜；⑤若ａ≠0，则对任一非零ｂ有ａ·ｂ≠０；⑥ａ·ｂ＝０，则ａ与ｂ中至少有一个为0；⑦对任意向量ａ，ｂ，с都有（ａ·ｂ）с＝ａ（ｂ·с）；⑧ａ与ｂ是两个单位向量，则ａ２＝ｂ２解：上述8个命题中只有③⑧正确；对于①：两个向量的数量积是一个实数，应有0·ａ＝０； 对于②：应有０·ａ＝0；对于④：由数量积定义有｜ａ·ｂ｜＝｜ａ｜·｜ｂ｜·｜cos θ｜≤｜ａ｜｜ｂ｜，这里θ是ａ与ｂ的夹角，只有θ＝０或θ＝π时，才有｜ａ·ｂ｜＝｜ａ｜·｜ｂ｜；对于⑤：若非零向量ａ、ｂ垂直，有ａ·ｂ＝０； 对于⑥：由ａ·ｂ＝０可知ａ⊥ｂ可以都非零； 对于⑦：若ａ与с共线，记ａ＝λс则ａ·ｂ＝（λс）·ｂ＝λ（с·ｂ）＝λ（ｂ·с），∴（ａ·ｂ）·с＝λ（ｂ·с）с＝（ｂ·с）λс＝（ｂ·с）ａ 若ａ与с不共线，则(ａ·ｂ)с≠（ｂ·с）ａ评述：这一类型题，要求学生确实把握好数量积的定义、性质、运算律例2 已知｜ａ｜＝３，｜ｂ｜＝６，当①ａ∥ｂ，②ａ⊥ｂ，③ａ与ｂ的夹角是60°时，分别求ａ·ｂ解：①当ａ∥ｂ时，若ａ与ｂ同向，则它们的夹角θ＝０°，∴ａ·ｂ＝｜ａ｜·｜ｂ｜cos0°＝3×6×1＝18； 若ａ与ｂ反向，则它们的夹角θ＝180°，∴ａ·ｂ＝｜ａ｜｜ｂ｜cos180°＝3×6×（-1）＝－18； ②当ａ⊥ｂ时，它们的夹角θ＝90°， ∴ａ·ｂ＝０；③当ａ与ｂ的夹角是60°时，有ａ·ｂ＝｜ａ｜｜ｂ｜cos60°＝3×6×21＝9 评述：两个向量的数量积与它们的夹角有关，其范围是［0°，180°］，因此，当ａ∥ｂ时，有0°或180°两种可能四、课堂练习：五、小结 通过本节学习，要求大家掌握平面向量的数量积的定义、重要性质、运算律，并能运用它们解决相关的问题。

第3节 平面向量的数量积及平面向量的应用知识梳理1.平面向量数量积的有关概念(1)向量的夹角：已知两个非零向量a 和b ，作OA →＝a ，OB →＝b ，则∠AOB ＝θ(0°≤θ≤180°)叫做向量a 与b 的夹角.(2)数量积的定义：已知两个非零向量a 与b ，它们的夹角为θ，则a 与b 的数量积(或内积)a ·b ＝|a ||b |cos__θ.规定：零向量与任一向量的数量积为0，即0·a ＝0. (3)数量积的几何意义：数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影|b |cos__θ的乘积.2.平面向量数量积的性质及其坐标表示设向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，θ为向量a ，b 的夹角. (1)数量积：a ·b ＝|a ||b |cos θ＝x 1x 2＋y 1y 2.(2)模：|a |＝a ·a ＝x 21＋y 21.(3)夹角：cos θ＝a ·b |a ||b |＝x 1x 2＋y 1y 2x 21＋y 21·x 22＋y 22. (4)两非零向量a ⊥b 的充要条件：a ·b ＝0⇔x 1x 2＋y 1y 2＝0.(5)|a ·b |≤|a ||b |(当且仅当a ∥b 时等号成立)⇔|x 1x 2＋y 1y 2|≤x 21＋y 21·x 22＋y 22.3.平面向量数量积的运算律 (1)a ·b ＝b ·a (交换律).(2)λa ·b ＝λ(a ·b )＝a ·(λb )(结合律). (3)(a ＋b )·c ＝a ·c ＋b ·c (分配律). 4.平面几何中的向量方法三步曲：(1)用向量表示问题中的几何元素，将几何问题转化为向量问题； (2)通过向量运算，研究几何元素之间的关系； (3)把运算结果“翻译”成几何关系.1.两个向量a ，b 的夹角为锐角⇔a ·b >0且a ，b 不共线；两个向量a ，b 的夹角为钝角⇔a ·b <0且a ，b 不共线. 2.平面向量数量积运算的常用公式 (1)(a ＋b )·(a －b )＝a 2－b 2； (2)(a ＋b )2＝a 2＋2a ·b ＋b 2. (3)(a －b )2＝a 2－2a ·b ＋b 2.3.数量积运算律要准确理解、应用，例如，a ·b ＝a ·c (a ≠0)，不能得出b ＝c ，两边不能约去同一个向量.诊断自测1.判断下列结论正误(在括号内打“√”或“×”) (1)两个向量的夹角的范围是⎣⎢⎡⎦⎥⎤0，π2.( )(2)向量在另一个向量方向上的投影为数量，而不是向量.( )(3)两个向量的数量积是一个实数，向量的加、减、数乘运算的运算结果是向量.( )(4)若a ·b ＝a ·c (a ≠0)，则b ＝c .( ) 答案 (1)× (2)√ (3)√ (4)× 解析 (1)两个向量夹角的范围是[0，π].(4)由a ·b ＝a ·c (a ≠0)得|a ||b |·cos 〈a ，b 〉＝|a ||c |·cos 〈a ，c 〉，所以向量b 和c 不一定相等.2.已知向量a ＝(1，1)，b ＝(2，4)，则(a －b )·a ＝( ) A.－14 B.－4C.4D.14答案 B解析 由题意得a －b ＝(－1，－3)，则(a －b )·a ＝－1－3＝－4. 3.设a ，b 是非零向量，则“a ·b ＝|a ||b |”是“a ∥b ”的( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件答案 A解析 设a 与b 的夹角为θ.因为a ·b ＝|a |·|b |cos θ＝|a |·|b |，所以cos θ＝1，即a 与b 的夹角为0°，故a ∥b .当a ∥b 时，a 与b 的夹角为0°或180°， 所以a ·b ＝|a |·|b |cos θ＝±|a |·|b |，所以“a ·b ＝|a |·|b |”是“a ∥b ”的充分而不必要条件.4.(2020·湘潭模拟)已知平面向量a ，b ，满足|a |＝|b |＝1，若(2a －b )·b ＝0，则向量a ，b 的夹角为( ) A.π6 B.π4C.π3D.2π3答案 C解析 由(2a －b )·b ＝0，可得a ·b ＝12b 2＝12，设向量a 、b 的夹角为θ， 则cos θ＝a ·b |a ||b |＝12，又θ∈[0，π]，所以向量a 、b 的夹角为π3.5.(多选题)(2021·青岛统检)已知向量a ＋b ＝(1，1)，a －b ＝(－3，1)，c ＝(1，1)，设a ，b 的夹角为θ，则( ) A.|a |＝|b | B.a ⊥c C.b ∥cD.θ＝135°答案 BD解析 由a ＋b ＝(1，1)，a －b ＝(－3，1)，得a ＝(－1，1)，b ＝(2，0)，则|a |＝2，|b |＝2，故A 不正确；a ·c ＝－1×1＋1×1＝0，故B 正确； 不存在λ∈R ，使b ＝λc 成立，故C 不正确；cos θ＝a ·b |a |·|b |＝－22×2＝－22，所以θ＝135°，故D 正确.综上知选BD.6.(2020·全国Ⅱ卷)已知单位向量a ，b 的夹角为45°，k a －b 与a 垂直，则k ＝________. 答案 22解析 由题意知(k a －b )·a ＝0，即k a 2－b ·a ＝0. 因为a ，b 为单位向量，且夹角为45°，所以k ×12－1×1×22＝0，解得k ＝22.考点一 平面向量的数量积运算1.已知向量a ，b 满足|a |＝1，a ·b ＝－1，则a ·(2a －b )＝( ) A.4 B.3C.2D.0答案 B解析 a ·(2a －b )＝2|a |2－a ·b ＝2×12－(－1)＝3.2.(2020·北京卷)已知正方形ABCD 的边长为2，点P 满足AP →＝12()AB →＋AC →，则|PD→|＝__________；PB →·PD →＝__________. 答案5 －1解析 法一 ∵AP→＝12(AB →＋AC →)，∴P 为BC 的中点.以A 为原点，建立如图所示的平面直角坐标系，由题意知A (0，0)，B (2，0)，C (2，2)，D (0，2)，P (2，1)，∴|PD →|＝（2－0）2＋（1－2）2＝ 5. 易得PB→＝(0，－1)，PD →＝(－2，1). ∴PB→·PD →＝(0，－1)·(－2，1)＝－1.法二 如图，在正方形ABCD 中，由AP→＝12(AB →＋AC →)得点P 为BC的中点，∴|PD→|＝12＋22＝ 5. PB→·PD →＝PB →·(PC →＋CD →)＝PB →·PC →＋PB →·CD → ＝－PB→2＋0＝－1. 3.在四边形ABCD 中，AD ∥BC ，AB ＝23，AD ＝5，∠A ＝30°，点E 在线段CB的延长线上，且AE ＝BE ，则BD →·AE →＝________. 答案 －1解析 如图，在等腰△ABE 中， 易得∠BAE ＝∠ABE ＝30°，故BE ＝2. 则BD→·AE →＝(AD →－AB →)·(AB →＋BE →) ＝AD→·AB →＋AD →·BE →－AB →2－AB →·BE → ＝5×23×cos 30°＋5×2×cos 180°－12－23×2×cos 150° ＝15－10－12＋6＝－1.4.(2020·新高考山东卷)已知P 是边长为2的正六边形ABCDEF 内的一点，则AP→·AB →的取值范围是( ) A.(－2，6) B.(－6，2)C.(－2，4)D.(－4，6)答案 A解析 法一 如图，取A 为坐标原点，AB 所在直线为x 轴建立平面直角坐标系，则A (0，0)，B (2，0)，C (3，3)，F (－1，3).设P (x ，y )，则AP→＝(x ，y )，AB →＝(2，0)，且－1＜x ＜3.所以AP →·AB →＝(x ，y )·(2，0)＝2x ∈(－2，6). 故选A.法二 AP→·AB →＝|AP →|·|AB →|·cos ∠P AB ＝2|AP →|·cos ∠P AB ，又|AP→|cos ∠P AB 表示AP →在AB →方向上的投影. 结合几何图形，当点P 与F 重合时投影最小，当P 与点C 重合时，投影最大， 又AC→·AB →＝23×2×cos 30°＝6，AF →·AB →＝2×2cos 120°＝－2， 故当点P 在正六边形ABCDEF 内时，－2<AP →·AB →<6.感悟升华 1.计算平面向量的数量积主要方法： (1)利用定义：a ·b ＝|a ||b |cos 〈a ，b 〉.(2)利用坐标运算，若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ·b ＝x 1x 2＋y 1y 2. (3)活用平面向量数量积的几何意义.2.解决涉及几何图形的向量的数量积运算问题时，可先利用向量的加、减运算或数量积的运算律化简后再运算.但一定要注意向量的夹角与已知平面几何图形中的角的关系是相等还是互补.考点二向量数量积的性质及应用角度1夹角与垂直【例1】(1)(2020·全国Ⅱ卷)已知单位向量a，b的夹角为60°，则在下列向量中，与b垂直的是()A.a＋2bB.2a＋bC.a－2bD.2a－b(2)(2021·新高考8省联考)已知单位向量a，b满足a·b＝0，若向量c＝7a＋2b，则sin〈a，c〉等于()A.73 B.23 C.79 D.29答案(1)D(2) B解析(1)易知a·b＝|a||b|cos 60°＝1 2，则b·(a＋2b)＝52≠0，b·(2a＋b)＝2≠0，b·(a－2b)＝a·b－2b2＝－32≠0，b·(2a－b)＝0.因此b⊥(2a－b).(2)法一设a＝(1，0)，b＝(0，1)，则c＝(7，2)，∴sin〈a，c〉＝2 3.法二a·c＝a·(7a＋2b)＝7a2＋2a·b＝7，|c|＝（7a＋2b）2＝7a2＋2b2＋214a·b＝7＋2＝3，∴cos〈a，c〉＝a·c|a||c|＝71×3＝73，∴sin〈a，c〉＝2 3.角度2平面向量的模【例2】(1)(2020·南昌模拟)设x，y∈R，a＝(x，1)，b＝(2，y)，c＝(－2，2)，且a⊥c，b∥c，则|2a＋3b－c|＝()A.234B.26C.12D.210(2)已知a ，b 是单位向量，a ·b ＝0.若向量c 满足|c －a －b |＝1，则|c |的最大值是________.答案 (1)A (2)2＋1解析 (1)因为a ⊥c ，所以a ·c ＝－2x ＋2＝0，解得x ＝1，则a ＝(1，1)， 因为b ∥c ，所以4＋2y ＝0，解得y ＝－2，则b ＝(2，－2). 所以2a ＋3b －c ＝(10，－6)，则|2a ＋3b －c |＝234. (2)法一 由a ·b ＝0，得a ⊥b .如图所示，分别作OA→＝a ，OB →＝b ，作OC →＝a ＋b ，则四边形OACB 是边长为1的正方形，所以|OC →|＝ 2.作OP→＝c ，则|c －a －b |＝|OP →－OC →|＝|CP →|＝1. 所以点P 在以C 为圆心，1为半径的圆上.由图可知，当点O ，C ，P 三点共线且点P 在点P 1处时，|OP →|取得最大值2＋1.故|c |的最大值是2＋1. 法二 由a ·b ＝0，得a ⊥b .建立如图所示的平面直角坐标系，则OA →＝a ＝(1，0)，OB →＝b＝(0，1).设c ＝OC →＝(x ，y )， 由|c －a －b |＝1， 得(x －1)2＋(y －1)2＝1，所以点C 在以(1，1)为圆心，1为半径的圆上. 所以|c |max ＝2＋1.法三 易知|a ＋b |＝2，|c －a －b |＝|c －(a ＋b )| ≥||c |－|a ＋b ||＝||c |－2|， 由已知得||c |－2|≤1，所以|c |≤1＋2，故|c |max ＝2＋1.感悟升华 1.两个向量垂直的充要条件是两向量的数量积为0，若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ⊥b ⇔a ·b ＝0⇔x 1x 2＋y 1y 2＝0.2.若题目给出向量的坐标，可直接运用公式cos θ＝x1x2＋y1y2x21＋y21·x22＋y22求解.没有坐标时可用公式cos θ＝a·b|a||b|.研究向量夹角应注意“共起点”，注意取值范围是[0，π].3.向量模的计算主要利用a2＝|a|2，把向量模的运算转化为数量积运算，有时借助几何图形的直观性，数形结合，提高解题效率.【训练1】(1)(多选题)(2021·湖南三校联考)已知a，b是单位向量，且a＋b＝(1，－1)，则()A.|a＋b|＝2B.a与b垂直C.a与a－b的夹角为π4 D.|a－b|＝1(2)已知单位向量a，b的夹角为θ，且tan θ＝12，若向量m＝5a－3b，则|m|＝()A.2B.3C.26D.2或26答案(1)BC(2)A解析(1)|a＋b|＝12＋（－1）2＝2，故A错误；因为a，b是单位向量，所以|a|2＋|b|2＋2a·b＝1＋1＋2a·b＝2，得a·b＝0，a与b 垂直，故B正确；|a－b|2＝a2＋b2－2a·b＝2，|a－b|＝2，故D错误；cos〈a，a－b〉＝a·（a－b）|a||a－b|＝a2－a·b1×2＝22，所以a与a－b的夹角为π4，故C正确.故选BC.(2)依题意|a|＝|b|＝1，又θ为a，b的夹角，且tan θ＝1 2，∴θ为锐角，且cos θ＝2sin θ，又sin2θ＋cos2θ＝1，从而cos θ＝25 5.由m＝5a－3b，∴m2＝(5a－3b)2＝5a2＋9b2－65a·b＝2，因此|m|＝ 2.考点三 平面向量的综合应用【例3】 (1)(2020·天津卷)如图，在四边形ABCD 中，∠B ＝60°，AB ＝3，BC ＝6，且AD→＝λBC →，AD →·AB →＝－32，则实数λ的值为__________；若M ，N 是线段BC 上的动点，且|MN→|＝1，则DM →·DN →的最小值为__________.答案 16 132解析 因为AD→＝λBC →，所以AD ∥BC ，则∠BAD ＝120°，所以AD→·AB →＝|AD →|·|AB →|·cos 120°＝－32， 解得|AD→|＝1. 因为AD→，BC →同向，且BC ＝6， 所以AD→＝16BC →，即λ＝16. 在四边形ABCD 中，作AO ⊥BC 于点O ，则BO ＝AB ·cos 60°＝32，AO ＝AB ·sin 60°＝332.以O 为坐标原点，以BC 和AO 所在直线分别为x ，y 轴建立平面直角坐标系. 如图，设M (a ，0)，不妨设点N 在点M 右侧， 则N (a ＋1，0)，且－32≤a ≤72.又D ⎝ ⎛⎭⎪⎫1，332，所以DM →＝⎝ ⎛⎭⎪⎫a －1，－332， DN→＝⎝⎛⎭⎪⎫a ，－332， 所以DM→·DN →＝a 2－a ＋274＝⎝ ⎛⎭⎪⎫a －122＋132. 所以当a ＝12时，DM→·DN →取得最小值132.(2)已知在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，向量m ＝(sin A ，sin B )，n ＝(cos B ，cos A )，m ·n ＝sin 2C . ①求角C 的大小；②若sin A ，sin C ，sin B 成等差数列，且CA →·(AB →－AC →)＝18，求c .解 ①m ·n ＝sin A ·cos B ＋sin B ·cos A ＝sin(A ＋B )，在△ABC 中，A ＋B ＝π－C ，0<C <π， 所以sin(A ＋B )＝sin C ，所以m ·n ＝sin C ，又m ·n ＝sin 2C ， 所以sin 2C ＝sin C ，cos C ＝12. 又因为C ∈(0，π)，故C ＝π3.②由sin A ，sin C ，sin B 成等差数列，可得2sin C ＝sin A ＋sin B ，由正弦定理得2c ＝a ＋b .因为CA→·(AB →－AC →)＝18，所以CA →·CB →＝18， 即ab cos C ＝18，ab ＝36. 由余弦定理得c 2＝a 2＋b 2－2ab cos C ＝(a ＋b )2－3ab ， 所以c 2＝4c 2－3×36，c 2＝36，所以c ＝6.感悟升华 1.以平面几何为载体的向量问题有两种基本解法：(1)基向量法：恰当选择基底，结合共线定理、平面向量的基本定理进行向量运算.(2)坐标法：如果图形比较规则，可建立平面坐标系，把有关点与向量用坐标表示，从而使问题得到解决.2.解决平面向量与三角函数的交汇问题，关键是准确利用向量的坐标运算化简已知条件，将其转化为三角函数中的有关问题.【训练2】 (1)(2020·全国Ⅲ卷)在平面内，A ，B 是两个定点，C 是动点.若AC →·BC →＝1，则点C 的轨迹为( ) A.圆B.椭圆C.抛物线D.直线(2)如图，在△ABC 中，D 是BC 的中点，E 在边AB 上，BE ＝2EA ，AD 与CE 交于点O .若AB →·AC →＝6AO →·EC →，则AB AC 的值是________. 答案 (1)A (2)3解析 (1)以AB 所在直线为x 轴，线段AB 的垂直平分线为y 轴建立平面直角坐标系，设点A ，B 分别为(－a ，0)，(a ，0)(a >0)，点C 为(x ，y )，则AC→＝(x ＋a ，y )，BC→＝(x －a ，y )，所以AC →·BC →＝(x －a )(x ＋a )＋y ·y ＝x 2＋y 2－a 2＝1，整理得x 2＋y 2＝a 2＋1.因此点C 的轨迹为圆.故选A.(2)法一 如图，过点D 作DF ∥CE 交AB 于点F ，由D 是BC 的中点，可知F 为BE 的中点.又BE ＝2EA ，则知EF ＝EA ，从而可得AO ＝OD ，则有AO→＝12AD →＝14(AB →＋AC →)，EC →＝AC →－AE →＝AC →－13AB →，所以6AO →·EC →＝32(AB →＋AC →)·⎝ ⎛⎭⎪⎫AC →－13AB →＝32AC →2－12AB →2＋AB →·AC →＝AB→·AC →，整理可得AB →2＝3AC →2，所以AB AC＝ 3.法二 以点A 为坐标原点，AB 所在直线为x 轴建立平面直角坐标系，如图所示.设E (1，0)，C (a ，b )，则B (3，0)，D ⎝ ⎛⎭⎪⎫a ＋32，b 2.⎭⎪⎬⎪⎫l AD ：y ＝ba ＋3x ，l CE ：y ＝ba －1（x －1）⇒O ⎝ ⎛⎭⎪⎫a ＋34，b 4. ∵AB→·AC →＝6AO →·EC →， ∴(3，0)·(a ，b )＝6⎝ ⎛⎭⎪⎫a ＋34，b 4·(a －1，b )，即3a ＝6⎣⎢⎡⎦⎥⎤（a ＋3）（a －1）4＋b 24，∴a 2＋b 2＝3，∴AC ＝ 3.∴AB AC ＝33＝ 3.平面向量与三角形的“四心”向量具有数形二重性，借助几何直观研究向量，优化解题过程，进而提高解题效率.设O 为△ABC 所在平面上一点，内角A ，B ，C 所对的边分别为a ，b ，c ，则 (1)O 为△ABC 的外心⇔|OA→|＝|OB →|＝|OC →|＝a 2sin A .(2)O 为△ABC 的重心⇔OA→＋OB →＋OC →＝0.(3)O 为△ABC 的垂心⇔OA→·OB →＝OB →·OC →＝OC →·OA →.(4)O 为△ABC 的内心⇔aOA →＋bOB →＋cOC →＝0.一、平面向量与三角形的“重心”【例1】已知A ，B ，C 是平面上不共线的三点，O 为坐标原点，动点P 满足OP →＝13[(1－λ)OA →＋(1－λ)OB →＋(1＋2λ)·OC →]，λ∈R ，则点P 的轨迹一定经过( ) A.△ABC 的内心B.△ABC 的垂心C.△ABC 的重心D.AB 边的中点答案 C解析 取AB 的中点D ，则2OD→＝OA →＋OB →，∵OP→＝13[(1－λ)OA →＋(1－λ)OB →＋(1＋2λ)OC →]， ∴OP→＝13[2(1－λ)OD →＋(1＋2λ)OC →] ＝2（1－λ）3OD →＋1＋2λ3OC →，而2（1－λ）3＋1＋2λ3＝1，∴P ，C ，D 三点共线，∴点P 的轨迹一定经过△ABC 的重心. 二、平面向量与三角形的“内心”问题【例2】在△ABC 中，AB ＝5，AC ＝6，cos A ＝15，O 是△ABC 的内心，若OP→＝xOB →＋yOC →，其中x ，y ∈[0，1]，则动点P 的轨迹所覆盖图形的面积为( ) A.1063 B.1463 C.43D.62答案 B解析 根据向量加法的平行四边形法则可知，动点P 的轨迹是以OB ，OC 为邻边的平行四边形及其内部，其面积为△BOC 的面积的2倍.在△ABC 中，设内角A ，B ，C 所对的边分别为a ，b ，c ，由余弦定理a 2＝b 2＋c 2－2bc cos A ，得a ＝7.设△ABC 的内切圆的半径为r ，则 12bc sin A ＝12(a ＋b ＋c )r ，解得r ＝263， 所以S △BOC ＝12×a ×r ＝12×7×263＝763.故动点P 的轨迹所覆盖图形的面积为2S △BOC ＝1463. 三、平面向量与三角形的“外心”问题【例3】(2020·安庆质检)在△ABC 中，O 为其外心，OA →·OC →＝3，且3OA →＋7OB →＋OC →＝0，则边AC 的长是________. 答案3－1解析 设△ABC 外接圆的半径为R ， ∵O 为△ABC 的外心， ∴|OA→|＝|OB →|＝|OC →|＝R ， 又3OA→＋7OB →＋OC →＝0， 则3OA→＋OC →＝－7OB →， ∴3OA→2＋OC →2＋23OA →·OC →＝7OB →2， 从而OA→·OC →＝32R 2， 又OA→·OC →＝3，所以R 2＝2， 又OA→·OC →＝|OA →||OC →|cos ∠AOC ＝R 2cos ∠AOC ＝3， ∴cos ∠AOC ＝32，∴∠AOC ＝π6， 在△AOC 中，由余弦定理得 AC 2＝OA 2＋OC 2－2OA ·OC ·cos ∠AOC ＝R 2＋R 2－2R 2×32＝(2－3)R 2＝4－2 3. 所以AC ＝3－1.四、平面向量与三角形的“垂心”问题【例4】已知O 是平面上的一个定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP →＝OA →＋λ(AB →|AB →|cos B ＋AC →|AC →|cos C )，λ∈(0，＋∞)，则动点P 的轨迹一定通过△ABC 的( ) A.重心 B.垂心C.外心D.内心答案 B解析 因为OP→＝OA →＋λ(AB →|AB →|cos B ＋AC→|AC →|cos C)，所以AP →＝OP →－OA →＝λ(AB →|AB →|cos B ＋AC →|AC →|cos C )，所以BC→·AP →＝BC →·λ(AB →|AB →|cos B ＋AC→|AC →|cos C)＝λ(－|BC→|＋|BC →|)＝0，所以BC →⊥AP →，所以点P 在BC 的高线上，即动点P 的轨迹一定通过△ABC 的垂心.A 级 基础巩固一、选择题1.已知向量a ＝(k ，3)，b ＝(1，4)，c ＝(2，1)，且(2a －3b )⊥c ，则实数k ＝( ) A.－92 B.0C.3D.152答案 C解析 因为2a －3b ＝(2k －3，－6)，(2a －3b )⊥c ，所以(2a －3b )·c ＝2(2k －3)－6＝0，解得k ＝3，选C.2.(2020·新乡质检)已知向量a ＝(0，2)，b ＝(23，x )，且a 与b 的夹角为π3，则x ＝( ) A.－2B.2C.1D.－1答案 B解析 由题意得a ·b |a ||b |＝2x 2·12＋x 2＝12， 则2x ＝12＋x 2，解之得x ＝2，x ＝－2(舍去).3.(2021·长沙调研)如图所示，直角梯形ABCD 中，AB ∥CD ，AB ⊥AD ，AB ＝AD ＝4，CD ＝8.若CE→＝－7DE →，3BF →＝FC →，则AF →·BE →＝( )A.11B.10C.－10D.－11答案 D解析 以A 为坐标原点，建立直角坐标系如图.则A (0，0)，B (4，0)，E (1，4)，F (5，1)，所以AF →＝(5，1)，BE→＝(－3，4)，则AF →·BE →＝－15＋4＝－11. 4.若两个非零向量a ，b 满足|a ＋b |＝|a －b |＝2|b |，则向量a ＋b 与a 的夹角为( ) A.π3 B.2π3C.5π6D.π6答案 D解析 设|b |＝1，则|a ＋b |＝|a －b |＝2. 由|a ＋b |＝|a －b |，得a ·b ＝0，故以a 、b 为邻边的平行四边形是矩形，且|a |＝3， 设向量a ＋b 与a 的夹角为θ，则cos θ＝a ·（a ＋b ）|a |·|a ＋b |＝a 2＋a ·b |a |·|a ＋b |＝|a ||a ＋b |＝32，又0≤θ≤π，所以θ＝π6.5.(多选题)(2021·武汉调研)如图，点A ，B 在圆C 上，则AB →·AC →的值( )A.与圆C 的半径有关B.与圆C 的半径无关C.与弦AB 的长度有关D.与点A ，B 的位置有关 答案 BC解析 如图，连接AB ，过C 作CD ⊥AB 交AB 于D ，则D 是AB 的中点，故AB →·AC →＝|AB →|·|AC →|·cos ∠CAD ＝|AB →|·|AC →|·12|AB →||AC →|＝12|AB →|2，故AB→·AC →的值与圆C 的半径无关，只与弦AB 的长度有关，故选BC. 6.(多选题)(2020·青岛调研)在Rt △ABC 中，CD 是斜边AB 上的高，如图，则下列等式成立的是( ) A.|AC→|2＝AC →·AB → B.|BC→|2＝BA →·BC → C.|AB→|2＝AC →·CD → D.|CD →|2＝（AC →·AB →）×（BA →·BC →）|AB →|2答案 ABD解析 因为AC→·AB →＝|AC →||AB →|cos A ＝|AC →||AC →|＝|AC →|2，选项A 正确；因为BA→·BC →＝|BA →||BC →|cos B ＝|BC →||BC →|＝|BC →|2，选项B 正确； 由AC→·CD →＝|AC →||CD →|·cos(π－∠ACD )＜0，|AB →|2＞0，知选项C 错误； 由题图可知Rt △ACD ∽Rt △ABC ，所以|AC→||BC →|＝|AB →||CD →|，结合选项A ，B 可得|CD →|2＝（AC →·AB →）×（BA →·BC →）|AB →|2，选项D 正确.故选ABD.二、填空题7.已知a ，b 为单位向量，且a ·b ＝0，若c ＝2a －5b ，则cos 〈a ，c 〉＝________. 答案 23解析 由题意，得cos 〈a ，c 〉＝a ·（2a －5b ）|a |·|2a －5b |＝2a 2－5a ·b|a |·|2a －5b |2＝21×4＋5＝23.8.(2020·全国Ⅰ卷)设a ，b 为单位向量，且|a ＋b |＝1，则|a －b |＝________. 答案3解析 如图，设OA →＝a ，OB →＝b ，利用平行四边形法则得OC →＝a ＋b ，∵|a |＝|b |＝|a ＋b |＝1，∴△OAC 为正三角形，∴|BA →|＝|a －b |＝2×32×|a |＝ 3.9.已知四边形ABCD 中，AD ∥BC ，∠BAD ＝90°，AD ＝1，BC ＝2，M 是AB 边上的动点，则|MC →＋MD →|的最小值为________.答案 3解析 以BC 所在直线为x 轴，BA 所在直线为y 轴建立如图所示的平面直角坐标系，设A (0，a )，M (0，b )，且0≤b ≤a ，由于BC ＝2，AD ＝1. ∴C (2，0)，D (1，a ).则MC →＝(2，－b )，MD →＝(1，a －b )， ∴MC→＋MD →＝(3，a －2b ). 因此|MC→＋MD →|＝9＋（a －2b ）2， ∴当且仅当a ＝2b 时，|MC →＋MD →|取得最小值3.三、解答题10.已知向量a ＝(cos x ，sin x )，b ＝(3，－3)，x ∈[0，π]. (1)若a ∥b ，求x 的值；(2)记f (x )＝a ·b ，求f (x )的最大值和最小值以及对应的x 的值. 解 (1)因为a ＝(cos x ，sin x )，b ＝(3，－3)，a ∥b ， 所以－3cos x ＝3sin x .若cos x ＝0，则sin x ＝0，与sin 2x ＋cos 2x ＝1矛盾， 故cos x ≠0，于是tan x ＝－33.又x ∈[0，π]，所以x ＝5π6.(2)f (x )＝a ·b ＝(cos x ，sin x )·(3，－3) ＝3cos x －3sin x ＝23cos ⎝ ⎛⎭⎪⎫x ＋π6.因为x ∈[0，π]，所以x ＋π6∈⎣⎢⎡⎦⎥⎤π6，7π6，从而－1≤cos ⎝ ⎛⎭⎪⎫x ＋π6≤32.于是，当x ＋π6＝π6，即x ＝0时，f (x )取到最大值3；当x ＋π6＝π，即x ＝5π6时，f (x )取到最小值－2 3.B 级 能力提升11.(2021·石家庄调研)已知向量a ，b 满足|a |＝1，(a －b )⊥(3a －b )，则a 与b 的夹角的最大值为( ) A.π6 B.π3C.2π3D.5π6答案 A解析 设a 与b 的夹角为θ，θ∈[0，π]. 因为(a －b )⊥(3a －b )，所以(a －b )·(3a －b )＝0. 整理可得3a 2－4a ·b ＋b 2＝0， 即3|a |2－4a ·b ＋|b |2＝0.将|a |＝1代入3|a |2－4a ·b ＋|b |2＝0， 可得3－4|b |cos θ＋|b |2＝0， 整理可得cos θ＝34|b |＋|b |4≥234|b |×|b |4＝32，当且仅当34|b |＝|b |4，即|b |＝3时取等号， 故cos θ≥32，结合θ∈[0，π]， 可知θ的最大值为π6.12.(2021·重庆联考)已知点O 为坐标原点，向量OA →＝(1，2)，OB →＝(x ，y )，且OA→·OB →＝10，则|OB →|的最小值为________. 答案 25解析 由题意知|OB→|＝x 2＋y 2，x ＋2y ＝10，∴点B 在直线x ＋2y －10＝0上，∴|OB→|的最小值为点O 到直线x ＋2y －10＝0的距离. 则|OB →|min＝|0＋0－10|12＋22＝105＝2 5. 13.(2020·浙江卷)已知平面单位向量e 1，e 2满足|2e 1－e 2|≤ 2.设a ＝e 1＋e 2，b ＝3e 1＋e 2，向量a ，b 的夹角为θ，则cos 2θ的最小值是__________. 答案 2829解析 因为单位向量e 1，e 2满足|2e 1－e 2|≤2， 所以|2e 1－e 2|2＝5－4e 1·e 2≤2，即e 1·e 2≥34. 因为a ＝e 1＋e 2，b ＝3e 1＋e 2，a ，b 的夹角为θ，所以cos 2θ＝（a ·b ）2|a |2|b |2＝[（e 1＋e 2）·（3e 1＋e 2）]2|e 1＋e 2|2·|3e 1＋e 2|2＝（4＋4e 1·e 2）2（2＋2e 1·e 2）（10＋6e 1·e 2）＝4＋4e 1·e 25＋3e 1·e 2. 不妨设t ＝e 1·e 2，则t ≥34，cos 2θ＝4＋4t 5＋3t ，又y ＝4＋4t 5＋3t 在⎣⎢⎡⎭⎪⎫34，＋∞上单调递增，所以cos 2θ≥4＋35＋94＝2829， 所以cos 2θ的最小值为2829.14.在△ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，向量m ＝(cos(A －B )， sin(A －B ))，n ＝(cos B ，－sin B )，且m ·n ＝－35. (1)求sin A 的值；(2)若a ＝42，b ＝5，求角B 的大小及向量BA →在BC →方向上的投影. 解 (1)由m ·n ＝－35，得cos(A －B )cos B －sin(A －B )sin B ＝－35， 所以cos A ＝－35.因为0<A <π， 所以sin A ＝1－cos 2A ＝1－⎝ ⎛⎭⎪⎫－352＝45. (2)由正弦定理，得a sin A ＝bsin B ，则sin B ＝b sin A a ＝5×4542＝22， 因为a >b ，所以A >B ，且B 是△ABC 一内角，则B ＝π4.由余弦定理得(42)2＝52＋c 2－2·5c ·⎝ ⎛⎭⎪⎫－35，解得c ＝1，c ＝－7(舍去)，故向量BA→在BC →方向上的投影为|BA →|cos B ＝c cos B ＝1×22＝22.。