复合材料结构力学试题
- 格式:doc
- 大小:114.00 KB
- 文档页数:3
1.已知铝的工程弹性常数E=69Gpa,G=26.54Gpa,υ=0.3,试求铝的柔量分量和模量分量。
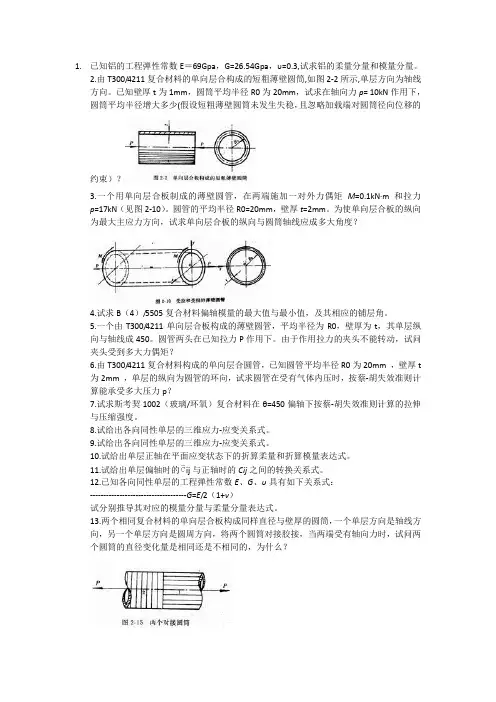
2.由T300/4211复合材料的单向层合构成的短粗薄壁圆筒,如图2-2所示,单层方向为轴线方向。
已知壁厚t为1mm,圆筒平均半径R0为20mm,试求在轴向力p= 10kN作用下,圆筒平均半径增大多少(假设短粗薄壁圆筒未发生失稳,且忽略加载端对圆筒径向位移的约束)?3.一个用单向层合板制成的薄壁圆管,在两端施加一对外力偶矩M=0.1kN·m和拉力p=17kN(见图2-10)。
圆管的平均半径R0=20mm,壁厚t=2mm。
为使单向层合板的纵向为最大主应力方向,试求单向层合板的纵向与圆筒轴线应成多大角度?4.试求B(4)/5505复合材料偏轴模量的最大值与最小值,及其相应的铺层角。
5.一个由T300/4211单向层合板构成的薄壁圆管,平均半径为R0,壁厚为t,其单层纵向与轴线成450。
圆管两头在已知拉力P作用下。
由于作用拉力的夹头不能转动,试问夹头受到多大力偶矩?6.由T300/4211复合材料构成的单向层合圆管,已知圆管平均半径R0为20mm ,壁厚t为2mm ,单层的纵向为圆管的环向,试求圆管在受有气体内压时,按蔡-胡失效准则计算能承受多大压力p?7.试求斯考契1002(玻璃/环氧)复合材料在θ=450偏轴下按蔡-胡失效准则计算的拉伸与压缩强度。
8.试给出各向同性单层的三维应力-应变关系式。
9.试给出各向同性单层的三维应力-应变关系式。
10.试给出单层正轴在平面应变状态下的折算柔量和折算模量表达式。
11.试给出单层偏轴时的ij与正轴时的Cij之间的转换关系式。
12.已知各向同性单层的工程弹性常数E、G、υ具有如下关系式:------------------------------------G=E/2(1+v)试分别推导其对应的模量分量与柔量分量表达式。
13.两个相同复合材料的单向层合板构成同样直径与壁厚的圆筒,一个单层方向是轴线方向,另一个单层方向是圆周方向,将两个圆筒对接胶接,当两端受有轴向力时,试问两个圆筒的直径变化量是相同还是不相同的,为什么?2.14. 在正轴下,一点处的正应变ε1、、ε2只与该处的正应力σ1、、、σ2有关,而与剪应力τ12无关,为什么?15.一块边长为a的正方形单向层合板,材料为T300/4211,厚度为h=4mm,紧密地夹在两块刚度无限大的刚性板之间(见图2-16),在压力p=2kN作用下,试分别计算在(a)、(b)两种情况下,单向层合板在压力p方向的变量△a,哪一种情况的变形较小?16.试用应力转换和应变转换关系式,证明各向同性材料的工程弹性常数存在如下关系式:--------------------------------G=E/2(1+v)。

矩阵位移法答案1、 计算连续梁的转角和杆端弯矩,并画出弯矩图。
解: 1)、编码2)、求单元刚度矩阵[][]⎥⎦⎤⎢⎣⎡i i i i k k 4224==②①3)、求整体刚度矩阵⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧2110==②①λλ[]⎥⎦⎤⎢⎣⎡i i i i K 4228=4)、求单元等效结点荷载{}P e{}{}m KN q q P P l l F F ⋅⎭⎬⎫⎩⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎭⎬⎫⎩⎨⎧=30301211210022②①{}{}{}F P P P eee-=={}{}m KN P P ⋅⎭⎬⎫⎩⎨⎧-⎭⎬⎫⎩⎨⎧303000==②①5)、集成结构等效结点荷载向量{}P{}m KN P ⋅⎭⎬⎫⎩⎨⎧-=30306)、解方程[]{}{}P K =∆ii i i i 717545303042282121⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎥⎦⎤⎢⎣⎡ 7)、求各杆的杆端内力{}F e{}[]{}{}F k F P e e e e +∆=单元① {}m KN i i i i i F ⋅⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=71.2586.120074504224①单元② {}m KN i i i i i i F ⋅⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=071.2530307757454224-②8)、做M 图2、 求图示刚架的M 、Q 、N 图。
解:1)、整理原始数据及编码2)、求局部坐标系中的单元刚度矩阵{}K e2442101.2,300,20,100cm KN E cm I cm A cm L ⨯====mKN LEI m KN L EI KN L EI m KN LEI m KN L EA ⋅⨯=⨯=⨯=⋅⨯=⨯=2232222106.122106.7512108.376102.2541042003)、计算整体坐标系中的单元刚度矩阵{}k e单元①和单元③单元②{}{}{}2102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200⨯===⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------k k k ③②①[][]I T =,= 0α[][][][]②②①①=,=kk k k90=α[]⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--=100000001000010000000100000001000010T [][][][]2102.2508.376.1208.370420000420008.3716.758.3706.756.1208.372.2508.370420*********.3706.758.3706.75⨯==⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------T k T k T ②②4)、用单元集成法形成整体刚度矩阵{}K⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧000321000321321000===③②①λλλ {}2106.7508.3702.435108.3706.8475⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=K5)、求单元等效结点荷载{}P e{}{}[]833.050833.050-=-=TF P P①①{}{}[]833.050833.050-=TP P ①①=6)、用单元集成法形成整体结构的等效结点荷载{}P{}[]TP 833.050-=7)、形成整体结构的综合结点荷载{}[]TF 402000={}{}[]TP F 167.392500=+8)、解方程[]{}{}{}0F P K +=∆[][]I T =,= 0α⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--167.39250106.7508.3702.435108.3706.84753212 432110924.51575.0232.0-⨯⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆ 9)、求各杆的杆端内力{}F e{}[][]{}{}F T k F P e e e e +∆=单元①{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧----+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=700.13193.24744.9492.5193.14744.9833.050833.05010924.51575.0232.000010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=①①①①F T k F P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=455.6452.19150.24997.12452.19150.2400000010000924.51575.0232.010421000010000100000001000000010000102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=②②②②F T kF P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=760.6062.20744.9302.13062.20744.900000010000924.51575.0232.010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=③③③③F T k F P结构动力学作业答案1、求图示结构的自振频率。

结构力学考试题及答案一、选择题1. 结构力学中,下列哪项不是结构的基本概念?A. 结构的刚度B. 结构的稳定性C. 结构的强度D. 结构的美观性答案:D2. 简支梁受均布荷载作用时,最大弯矩出现在:A. 跨中B. 支点处C. 任意截面D. 四分之三跨长处答案:A3. 在结构力学中,剪力和弯矩的方向约定为:A. 剪力向上为正,弯矩顺时针为正B. 剪力向下为正,弯矩逆时针为正C. 剪力向上为正,弯矩逆时针为正D. 剪力向下为正,弯矩顺时针为正答案:B4. 确定结构的内力分布情况通常采用的方法是:A. 能量法B. 虚功原理C. 弯矩分配法D. 刚度法答案:D5. 连续梁与简支梁相比,其特点是:A. 刚度更高B. 跨越能力更强C. 造价更低D. 所有上述选项答案:D二、填空题1. 结构力学中的__________是指结构在荷载作用下不发生位移的能力。
答案:刚度2. 结构的__________是指结构在荷载作用下不发生翻转的能力。
答案:稳定性3. 在进行结构分析时,通常首先需要确定结构的__________和反力。
答案:内力4. 结构力学中,__________是指构件截面上所有外力的集合效果。
答案:截面剪力5. 对于简支梁,当荷载作用在离支点一定距离处时,该点处的弯矩可以通过__________计算得出。
答案:剪力乘以距离三、简答题1. 请简述结构力学中的虚功原理及其应用。
答:虚功原理是指在一个平衡系统中,任何微小的位移或变形所对应的虚功等于该系统内力对该变形所做的功。
这个原理在结构力学中用于分析静不定结构,通过假设结构的位移或变形,计算出相应的虚功,然后根据虚功原理建立平衡方程,求解未知的反力或内力。
2. 描述简支梁受集中荷载作用时的弯矩图和剪力图。
答:简支梁受集中荷载作用时,弯矩图在荷载作用点会出现一个突变,即弯矩值突然增大到最大值,然后随着距离的增加逐渐减小回到零。
剪力图则显示在荷载作用点两侧的剪力值相反,一边为正值,另一边为负值,且随着距离的增加,剪力值逐渐减小到零。

复合材料力学试题答案判断题(正确的在括弧内划√,错误的在括弧内划×)。
1.“宏观力学”是在研究复合材料力学性能时,假定材料是均质的。
(√)2.单层是层合板的基本单元,在复合材料结构设计中又叫做三次结构。
(×)3.层合板由若干具体不同纤维方向的单层叠合而成,在复合材料机构设计中又叫二次结构。
(√)4.复合材料力学中,1为纵向,2为横向,应力规定拉为负,压为正。
(×)5.在单层板(正交各向异性)材料中,τ12不仅形成剪切变形,还存在剪拉耦合效应。
(×)6.在单层正交各向异性板中,11)1(11σεE =。
(√) 7.在单层正交各向异性板中,11122)1(2)2(221συσεεεE E -=+=。
(√) 8.单层板的工程弹性常数有5个,且相互独立。
(×)9.柔量矩阵{S}是对称矩阵,而模量举证{Q}不是对称矩阵。
(×)10.在正交单层板中,Q16=Q26=0,Q61=Q62,但其值不为零。
(×)11.在复合材料力学中,对于工程弹性常数存在如下关系:2121υυ=E E 。
(√) 12.在单层板偏轴刚度中,应力转换和应变转换关系式中,m=sin θ,n=cos θ。
(×)13. 在单层板偏轴刚度中,应力转换和应变转换关系式中存在如下关系:[][][]T T T 1-=σε。
(√)14.在ij Q 中,11Q 、22Q 是θ的偶函数,16Q 、26Q 也是θ的偶函数。
(×) 15.玻璃钢复合材料在拉伸时发生变形,所以是一种塑性材料。
(×)16.利用复合材料的强度准则,可以判断复合材料设计过程的安全性,同时可以计算极限载荷。
(×)17.利用最大应力准则判断材料安全性时,如果判断式大于1,说明材料的机构是安全的。
(×)18.在复合材料中,利用强度比可以计算复合材料的极限载荷。
(√)20.在对称层合板中,)()(z z --=θθ。

结构力学考试题及答案一、选择题1. 结构力学中,关于静定结构的表述,以下哪项是正确的?A. 静定结构的反力和内力可以通过平衡方程直接计算得出。
B. 静定结构在受载后只会产生弹性变形。
C. 静定结构的变形与载荷无关。
D. 静定结构的内力分布不受载荷位置的影响。
答案:A2. 在结构力学中,关于超静定结构的下列说法中,哪一项是错误的?A. 超静定结构的反力和内力不能仅通过平衡方程计算得出。
B. 超静定结构的内力计算需要考虑结构的几何和材料特性。
C. 超静定结构在受载后,除了弹性变形外,还可能产生塑性变形。
D. 超静定结构的内力分布与载荷位置无关。
答案:D3. 以下哪种方法不适用于求解超静定结构的内力?A. 位移法B. 力法C. 能量法D. 随机法答案:D4. 在结构力学中,剪力图和弯矩图是用来表示什么的?A. 结构的几何形状B. 结构的受力状况C. 材料的力学性能D. 结构的稳定性答案:B5. 根据欧拉-伯努利梁理论,梁的弯曲变形主要取决于哪些因素?A. 梁的长度和截面形状B. 梁的材料弹性模量和截面惯性矩C. 载荷的大小和作用位置D. 梁的支撑条件和边界约束答案:B二、填空题1. 结构力学中的__________定理指出,任何结构在受到外部载荷作用下,其变形和内力仅取决于载荷和边界条件,与结构的初始几何形状无关。
答案:虚功2. 在进行结构分析时,__________是用来描述结构在受到横向载荷作用时,抵抗弯曲变形的能力的物理量。
答案:截面模量3. 当一个结构的某一部分被移除后,如果剩余部分仍然保持稳定,那么这个结构是__________的。
答案:超静定4. 在结构力学中,__________是指结构在受到载荷作用后,其变形与载荷成正比的假设。
答案:线性弹性5. 根据__________原理,结构的变形能量等于外部载荷所做的功。
答案:能量守恒三、简答题1. 简述静定结构和超静定结构的区别。
静定结构是指在给定的支撑条件下,结构的反力和内力可以通过平衡方程直接计算得出的结构。

结构力学试题及答案一、选择题1. 结构力学是研究哪个方面的力学?a) 材料力学b) 结构系统c) 动力学d) 热力学答案:b) 结构系统2. 在结构力学中,静力学主要关注哪个方面的力学?a) 动力学b) 运动学c) 静力学d) 热力学答案:c) 静力学3. 在结构力学中,弹性力学主要研究什么?a) 金属的力学性质b) 结构系统的动态响应c) 物体的形变和变形d) 材料的热力学性质答案:c) 物体的形变和变形4. 下面哪个是结构力学中常用的描述物体形变的参数?a) 质量b) 体积c) 长度d) 面积答案:c) 长度5. 结构力学中的受力分析主要用到哪个定律?a) 牛顿第一定律b) 牛顿第二定律c) 牛顿第三定律d) 牛顿万有引力定律答案:b) 牛顿第二定律二、计算题1. 下图所示的结构系统,求杆AC的受力情况。
(插入结构图)答案:根据静力平衡条件,杆AC上的受力平衡,可得:ΣF_x = 0: -F_AC + F_BC = 0ΣF_y = 0: F_AC + F_AD - F_BE = 0解方程得: F_AC = F_BC = F_BE - F_AD2. 已知某杆件的长度为L,材料弹性模量为E,横截面积为A,受力情况如下图所示,求该杆件的应变。
(插入受力图)答案:根据材料的胡克定律,应变ε等于应力σ除以杨氏模量E,即ε = σ / E。
由受力图可知,该杆件受到纵向拉力P,横截面积为A,因此应力σ等于P除以A,所以应变ε = P / (E * A)。
三、解答题1. 简要描述刚体和弹性体的区别。
答案:刚体是指在受力作用下形状和大小不会发生显著变化的物体,它的内部不会发生相对位移。
刚体的形变主要是由于刚体整体的平移或转动引起的。
而弹性体是指在受力作用下会发生形变,但在去除外力后能够恢复到原来形状的物体。
弹性体的形变主要是由于物体内部分子间相对位移引起的。
2. 简要解释结构力学中的静力平衡条件。
答案:结构力学中的静力平衡条件是指一个结构系统中,各个部分受力相互平衡,不会产生任何形状和大小的变化。


《复合材料力学》考试题1.已知玻璃/环氧单向复合材料,玻璃纤维E f =7.5×104MPa,环氧E m =3.5×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =60GPa,E2 =20GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
1.已知玻璃/环氧单向复合材料,玻璃纤维E f =7.0×104MPa,环氧E m =3.0×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =55GPa,E2 =17.5GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。
1.已知玻璃/环氧单向复合材料,玻璃纤维E f =8.0×104MPa,环氧E m =4.0×103MPa。
求V f 分别为30%和70%时复合材料的E1和E2,试用串联、并联公式计算之。
2.已知E1 =65GPa,E2 =22GPa,μ21 =0.25,G12 =10GPa,X t =X c =1000MPa,Y t =50MPa,Y c =150MPa,S=50MPa,规则对称角铺设层合板[±45º]s受单向力N x作用。
试采用局部刚度消减法和Tsai-Hill失效判别式,确定层合板极限荷载(N x /t)。

一. 对材料AS4/3501-6进行设计已知61.1,134.0,3.0,86.6,65.9,2.147======ρυmm t GPa G MPa E MPa E T L MPa S MPa Y MPa Y MPa X MPa X C T c T 105,186,4.49,1468,2356=-==-==最大正应力准则为pi pi Tpi Tpi CpiTSY Y X X R 1222221111,,minσσσσσ=12STEP I Special Stacking Sequence (SSS)(一) 在Task I 载荷作用下已知Longitudinal Load =100 kN ,Transverse Load =-5 kN , Shear Load =30kN外加载荷可等效为{}{}m kN N N N N TT/600502000122211-==对[]0n S 度铺设层合板,{}MPa T447837314925}{-=σ,带入最大正应力准则得N=max{,,}=,所以[]0n S 所需的最小层数为层,且12σ先破坏 对[]90n S 度铺设层合板{}{}MPa T447814925373--=σN=max{,,}=,所以[]90n S 所需的最小层数为层,且22σ先破坏 对[](45)n S ±度铺设层合板45度 {}{}MPa T 3.19125.1801.5496-=σ, N=max{,,}=-45度 {}{}MPa T3.19127.3808.1218=σ, N=max{, ,}=所以对[](45)n S ±度铺设层合板,共需要*4=层,且12σ先破坏对[](0/60)n S ±度铺设层合板0度 {}{}MPa T7.2272.65.6366-=σ, N=max{,,}=+60度{}{}MPa T8.4507.1852267-=σ, N=max{,,}=-60度{}{}MPa 2237.3815.1918T-=σ, N=max{,,}=所以对[](0/60)n S ±度铺设层合板,共需要*6=层,且22σ先破坏 绘制在表格中,如下所示:从上表中可以看到,[]0n s 所需的层数最少,即质量最轻对])45/45/(90/0[z y x-铺层,设+45度和-45度的层数相同(1) 当0度铺层占10%,90度铺层占0%时, 则45度和-45度各占45%时 0度 {}MPa T43987030809}{-=σ, N=+45度 {}MPa T 6.24899.1484.9050}{-=σ, N=-45度 {}MPa T6.24891.5855.268}{-=σ, N=代入最大正应力准则进行校核,经比较得,N=,所以共需要*2=层(2) 当0度铺层占10%,90度铺层占10%时, 则45度和-45度各占40%时 0度,{}MPa T48243327954}{-=σ, N=max{,,}=90度, {}MPa T 482155514524}{-=σ, N=max{,,}=45度, {}MPa T200232211831}{=σ, N=max{,,}=-45度, {}MPa T6.20017.8005.1598}{=σ, N=max{,,}=代入最大正应力准则进行校核,经比较得,N=,所以共需要*2=层(3) 当0度铺层占10%,90度铺层占20%时, 则45度和-45度各占35%时90度 {}MPa T534158310498}{--=σ, N=+45度 {}MPa T 177943414048}{-=σ, N=-45度 {}MPa T17785.9652.2702}{=σ, N=经比较得,N=,所以共需*2=层(4) 当0度铺层占10%,90度铺层占25%时, 45度和-45度各占% 0度,{}MPa T5659027327}{-=σ, N=90度, {}MPa T3.5655.16149092}{--=σ, N=45度, {}MPa T171648115117}{=σ, N=-45度,{}MPa T.1.17169.10427.3118}{=σ, N=经比较得,N=,所以共需要*2=层(5)当0度铺层占10%,90度铺层占30%时, 则45度和-45度各占30%时 0度 {}MPa T606927618}{-=σ, N=90度 {}MPa T8.59916557933}{-=σ, N=+45度 {}MPa T 167552516207}{-=σ, N=-45度 {}MPa T16756.11202.3477}{=σ, N=经比较得,N=,所以共需要*2=层(6)当0度铺层占10%,90度铺层占40%时, 则45度和-45度各占25%时 0度 {}MPa T68313028732}{=σ, N=90度 {}MPa T 6839.17608.6107}{-=σ, N=+45度 {}MPa T164260618561}{-=σ, N= -45度 {}MPa T164212854062}{=σ, N=经比较得,N=,所以共需要*2=层(7)当0度铺层占10%,90度铺层占50%时, 45度和-45度各占20% 0度,{}MPa T79325530507}{=σ, N=90度,{}MPa T5.7936.19028.4691}{--=σ, N=-45度,{}MPa T6.16589.14724888}{=σ, N=经比较得,N=,所以共需要*2=77层(8)当0度铺层占10%,90度铺层占60%时, 则45度和-45度各占15%时 0度 {}MPa T94637832990}{=σ, N=1490度 {}MPa T2.9463.20863607}{--=σ, N= +45度 {}MPa T172076224781}{-=σ, N=-45度 {}MPa T172017024701}{=σ, N=经比较得,N=,所以共需要*2=层(9)当0度铺层占10%,90度铺层占75%时, 则45度和-45度各占%时 0度 {}MPa T145062239942}{=σ, N=90度 {}MPa T8.144925721729.6-}{-=σ, N=+45度 {}MPa T196487734490}{-=σ, N=-45度 {}MPa T5.196323173722}{=σ, N=经比较得,N=,所以共需要*2=层(10)当0度铺层占25%,90度铺层占0%时, 则45度和-45度各占%时 0度 {}MPa T50756820231}{-=σ, N=+45度 {}MPa T16329.1-8284.7}{-=σ, N= -45度 {}MPa T9.16326.4949.2475}{-=σ, N=经比较得,N=,所以共需要*2=层(11)当0度铺层占25%,90度铺层占10%时, 则45度和-45度各占%时0度 {}MPa T56526519118}{-=σ, N=90度 {}MPa T5.5635.10725.9458}{--=σ, N=+45度 {}MPa T134712610829}{-=σ, N=-45度 {}MPa T5.13465.6844.1169}{-=σ, N=经比较得,N=,所以共需要*2=层(12) 当0度铺层占25%,90度铺层占25%时, 则45度和-45度各占25%时0度,{}MPa T6831819099}{-=σ, N=90度,{}MPa T2.68314117.5669}{--=σ, N=45度,{}MPa T116722213964}{-=σ, N=max{,,}=-45度,{}MPa T1.11676.9006.534}{-=σ, N=max{,,}=经比较得,N=,所以共需要*2=层(13)当0度铺层占25%,90度铺层占50%时, 则45度和-45度各占%时 0度 {}MPa T104722721050}{=σ, N=90度 {}MPa T 10473.13271.2452}{--=σ, N=+45度 {}MPa T110725720408}{-=σ, N= -45度 {}MPa T110712978.1809}{-=σ, N=经比较得,N=,所以共需要*2=层(14)当0度铺层占50%,90度铺层占0%时, 则45度和-45度各占25%时0度 {}MPa T68335712870}{-=σ, N=90度 {}MPa T2.6837.4718.9106}{--=σ, N= +45度 {}MPa T6.10351.1823.9131}{--=σ, N=-45度 {}MPa T6.10356.4967.5367}{-=σ, N=经比较得,N=,所以共需要*2=层(15)当0度铺层占50%,90度铺层占10%时, 则45度和-45度各占20%时0度 {}MPa T79312712568}{-=σ, N=90度 {}MPa T793.5-4.7185492.7-}{=σ, N= +45度 {}MPa T 8519811957}{--=σ, N=-45度 {}MPa T8518.6894882}{-=σ, N=经比较得,N=,所以共需要*2=层(16)当0度铺层占50%,90度铺层占25%时, 则45度和-45度各占%时0度 {}MPa T10475212812}{=σ, N=90度 {}MPa T10474.7839.2819}{--=σ, N=+45度 {}MPa T73710216105}{--=σ, N=-45度 {}MPa T6.7366.9379.6112}{-=σ, N=经比较得,N=,所以共需要*2=层在图表中表示如下:的层数最少,为22层,此时的重量最轻。

结构力学的考试题型及答案一、选择题1. 以下哪个选项是结构力学中的基本假设?A. 结构是连续的B. 结构是刚性的C. 结构是弹性的D. 结构是塑性的答案:C2. 梁在受到弯矩作用时,其截面上的应力分布规律是什么?A. 线性分布B. 抛物线分布C. 正弦分布D. 均匀分布答案:B二、填空题3. 在结构力学中,_______是指结构在受到外力作用时,其内部各点的位移和内力满足平衡条件和变形条件。
答案:结构分析4. 悬臂梁自由端受到集中荷载作用时,其最大弯矩为_______。
答案:P*L/2三、简答题5. 简述结构力学中虚功原理的基本思想。
答案:虚功原理的基本思想是,当一个结构处于平衡状态时,任何虚位移所做的虚功都等于零。
这意味着结构在受到任何虚位移时,外力所做的虚功等于内力所做的虚功。
6. 描述梁的剪力和弯矩之间的关系。
答案:梁的剪力是弯矩随梁长度变化的导数,即剪力等于弯矩对梁长度的一阶导数。
具体来说,弯矩是剪力的积分,而剪力是弯矩的微分。
四、计算题7. 已知一简支梁,跨中集中荷载为P,求梁的跨中挠度。
答案:跨中挠度可以通过弯矩方程和挠度方程计算得出,对于简支梁跨中集中荷载的情况,跨中挠度公式为δ_max = (PL^3) / (48EI),其中L为梁长,E为材料的弹性模量,I为截面惯性矩。
8. 计算一端固定一端简支梁在固定端集中荷载作用下的固定端弯矩。
答案:固定端弯矩可以通过弯矩分配法或弯矩方程计算得出。
对于一端固定一端简支梁在固定端集中荷载作用的情况,固定端弯矩公式为M_fixed = (P*L) / 2,其中P为集中荷载,L为梁长。
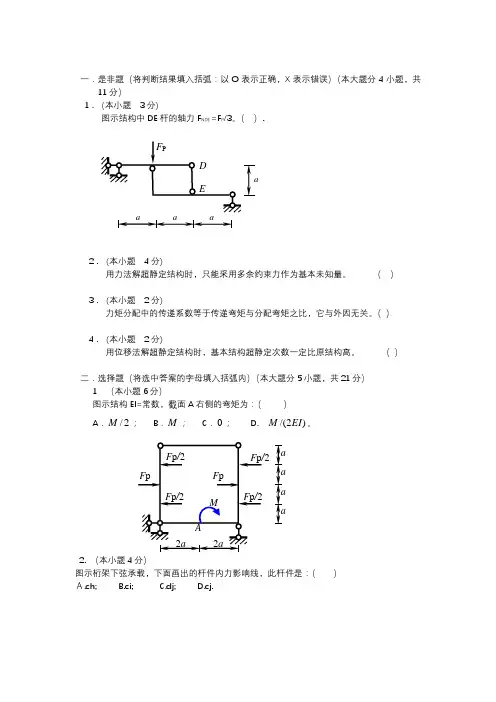
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
结构力学考试题及答案一、选择题1. 结构力学研究的是什么?A. 横截面形状B. 结构设计C. 结构变形和受力关系D. 断裂力学2. 在静力平衡条件下,一个受力结构的总力和总力矩是否为零?A. 是B. 否3. 弹性力学的基本假设是什么?A. 结构材料是均匀、各向同性的B. 结构受力状态是非线性的C. 结构的变形是正比于外力作用下的D. 结构的变形只能是线弹性的4. 一根悬臂梁在悬臂端受到的弯矩最大是在哪个位置?A. 梁的中点B. 梁的一端C. 梁的两端之间的某个位置D. 梁的支点处5. 刚度是衡量什么物理量的指标?A. 应变B. 位移C. 力D. 弯矩二、填空题1. 弹性模量是材料的________力学性质。
2. 杆件在轴向受力作用下长度发生变化的现象称为________。
3. 当材料达到屈服强度时,它会发生________变形。
4. 对于相同截面积的杆件,材料弹性模量越大,其刚度________。
5. 纤维增强复合材料的强度主要取决于________的方向。
三、计算题1. 一个长度为3m、截面积为0.1m²的悬臂梁,承受均匀分布在梁上的荷载为1000N/m。
求最大弯矩和最大挠度。
2. 一根长度为4m的梁,在其一端受到1000N的力作用。
已知该梁的截面积为0.2m²,弹性模量为200GPa。
求梁在作用力作用下的最大挠度和梁的变形方程。
四、解答题1. 简述静力平衡条件的基本原理。
2. 概述结构力学的基本理论。
五、答案选择题:1. C2. A3. A4. D5. B填空题:1. 力学2. 轴向变形3. 塑性4. 越大5. 纤维计算题:1. 最大弯矩:900 N·m,最大挠度:0.05 m2. 最大挠度:0.02 m,梁的变形方程:y = 0.0005x³ + 0.0025x² + 0.002x解答题:1. 静力平衡条件要求一个结构在受力时总力和总力矩为零。
工程力学(静力学与材料力学)习题解答第17章 复合材料的力学行为17-1 图示结构中,两种材料的弹性模量分别为E a 和E b ,且已知E a >E b ,二杆的横截面面积均为bh ,长度为l ,两轮之间的间距为a ,试求: 1.二杆横截面上的正应力;2.杆的总伸长量及复合弹性模量;3.各轮所受的力。
知识点:静不定问题,复合弹性模量 难度:很难 解答:解:1.P Nb Na F F F =+ (1) b a l l ∆=∆ (2) bhE lF l a Na a =∆ (3) bhE lF l b b Nb =∆ (4)将(3)、(4)代入(2),得bNba Na E F E F =(5)(1)、(5)联立解得P b a a Na F E E E F +=,P b a bNb F E E E F +=bh F E E E bh F P b a a Na a +==σ,bh F E E E bh F Pb a b Nb b +==σ2.由(3)式 bhE E lF bh E l F l )(b a P a Na a +==∆ 设复合弹性模量E c)2(c P bh E lF l =∆,由于a l l ∆=∆,比较两式得2ba c E E E +=3.由于F Na >F Nb ,所以,轮C 、轮G 脱离接触面,所以受力为零。
0)(=∑F k M ,022R Nb Na =--a F hF h F H∴ b a b a P R 2E E E E a h F F H +-=,ba ba P R R 2E E E E a h F F F H D +-==17-2 玻璃纤维/环氧树脂单层复合材料由2.5kg 纤维与5kg 树脂组成。
已知玻璃纤维的弹性模量E f =85GPa ,密度f ρ= 2500kg/m 3,环氧树脂的弹性模量E m = 5GPa ,密度m ρ= 1200kg/m 3。
试求垂直于纤维方向和平行于纤维方向的弹性模量E y 和E x 。
结构力学试题及答案一、选择题(每题2分,共20分)1. 下列选项中,哪一个是结构力学中常用的分析方法?A. 能量法B. 静力平衡法C. 动力学分析法D. 热力学分析法答案:A、B2. 梁的弯矩图通常表示的是:A. 剪力B. 弯矩C. 轴力D. 扭矩答案:B3. 悬臂梁在自由端受到垂直向下的集中力作用时,其弯矩图的形状是:A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案:B4. 简支梁在跨中受到垂直向下的集中力作用时,其弯矩图的形状是:A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案:B5. 梁的剪力图通常表示的是:A. 弯矩B. 剪力C. 轴力D. 扭矩答案:B6. 连续梁的内力分布特点是:A. 线性变化B. 非线性变化C. 恒定不变D. 周期性变化答案:B7. 在结构力学中,二阶效应通常指的是:A. 材料的非线性效应B. 几何非线性效应C. 动力效应D. 热效应答案:B8. 桁架结构中,节点的平衡条件是:A. 节点处的力矩平衡B. 节点处的力平衡C. 节点处的力和力矩都平衡D. 节点处的力不平衡答案:C9. 根据结构力学的基本原理,下列说法错误的是:A. 结构的内力与外力有关B. 结构的变形与内力有关C. 结构的稳定性与材料性质有关D. 结构的刚度与外力无关答案:D10. 梁的剪力和弯矩之间的关系是:A. 线性关系B. 非线性关系C. 没有关系D. 互为导数关系答案:D二、填空题(每题2分,共20分)1. 结构力学中,______是结构在荷载作用下产生的位移。
答案:变形2. 梁的剪力和弯矩之间存在______关系。
答案:互为导数3. 在结构力学中,______是结构在荷载作用下产生的内力。
答案:内力4. 悬臂梁在自由端受到垂直向下的集中力作用时,其弯矩图的形状是______。
答案:抛物线5. 简支梁在跨中受到垂直向下的集中力作用时,其弯矩图的形状是______。
答案:抛物线6. 连续梁的内力分布特点是______。
一. 对材料AS4/3501-6进行设计已知61.1,134.0,3.0,86.6,65.9,2.147======ρυmm t GPa G MPa E MPa E T LMPa S MPa Y MPa Y MPa X MPa X C T c T 105,186,4.49,1468,2356=-==-==最大正应力准则为pi pi Tpi Tpi CpiTSY Y X X R 1222221111,,minσσσσσ=12STEP I Special Stacking Sequence (SSS)(一) 在Task I 载荷作用下已知Longitudinal Load =100 kN ,Transverse Load =-5 kN , Shear Load =30 kN 外加载荷可等效为{}{}m kN N N N N TT/600502000122211-== 对[]0n S 度铺设层合板,{}MPa T447837314925}{-=σ,带入最大正应力准则得 N=max{6.3349,2.0054,42.6476}=42.6476,所以[]0n S 所需的最小层数为42.6层,且12σ先破坏对[]90n S 度铺设层合板{}{}MPa T447814925373--=σ N=max{0.2541,302.1255,42.6476}=302.1255,所以[]90n S 所需的最小层数为302.1255层,且22σ先破坏对[](45)n S ±度铺设层合板 45度 {}{}M P aT3.19125.1801.5496-=σ, N=max{2.3328,3.6538,18.2124}=18.2124 -45度{}{}M P a T3.19127.3808.1218=σ, N=max{0.51732,7.7065 ,18.2124}=18.2124所以对[](45)n S ±度铺设层合板,共需要18.21*4=72.84层,且12σ先破坏 对[](0/60)n S ±度铺设层合板 0度{}{}MPa T7.2272.65.6366-=σ, N=max{2.7022,0.0333,2.1686}=2.7022+60度{}{}MPa T8.4507.1852267-=σ, N=max{0.9622,3.7591,4.2933}=4.2933-60度{}{}MPa 2237.3815.1918T-=σ, N=max{1.3069,7.7267,2.1248}=7.37267 所以对[](0/60)n S ±度铺设层合板,共需要7.37*6=44.22层,且22σ先破坏从上表中可以看到,[]0n s 所需的层数最少,即质量最轻对])45/45/(90/0[z y x-铺层,设+45度和-45度的层数相同(1) 当0度铺层占10%,90度铺层占0%时, 则45度和-45度各占45%时 0度 {}M P a T43987030809}{-=σ, N=13.08 +45度 {}MPa T 6.24899.1484.9050}{-=σ, N=23.71-45度 {}MPa T6.24891.5855.268}{-=σ, N=23.71代入最大正应力准则进行校核,经比较得,N=23.71,所以共需要23.71*2=47.42层 (2) 当0度铺层占10%,90度铺层占10%时, 则45度和-45度各占40%时 0度,{}MPa T48243327954}{-=σ, N=max{11.865,2.328,4.5905}=11.86590度, {}MPa T482155514524}{-=σ, N=max{9.8937,31.48,4.5905}=31.4845度, {}MPa T200232211831}{=σ, N=max{5.0216,6.5182,19.07}=19.07 -45度, {}MPa T6.20017.8005.1598}{=σ, N=max{0.6783,16.2085,19.0629}=19.0629代入最大正应力准则进行校核,经比较得,N=31.48,所以共需要31.48*2=62.96层 (3) 当0度铺层占10%,90度铺层占20%时, 则45度和-45度各占35%时 0度 {}M P aT53518327248}{-=σ, N=11.57 90度 {}MPa T534158310498}{--=σ, N=32.04+45度 {}MPa T177943414048}{-=σ, N=16.94 -45度 {}MPa T17785.9652.2702}{=σ, N=19.53 经比较得,N=32.04,所以共需32.04*2=64.08层(4) 当0度铺层占10%,90度铺层占25%时, 45度和-45度各占32.5% 0度,{}MPa T5659027327}{-=σ, N= 11.690度, {}MPa T3.5655.16149092}{--=σ, N= 32.682245度, {}MPa T171648115117}{=σ, N= 16.3429 -45度,{}MPa T.1.17169.10427.3118}{=σ, N= 21.1113经比较得,N=32.68,所以共需要32.68*2=65.36层(5)当0度铺层占10%,90度铺层占30%时, 则45度和-45度各占30%时 0度 {}M P a T606927618}{-=σ, N=11.72 90度 {}MPa T8.59916557933}{-=σ, N=15.95 +45度 {}MPa T167552516207}{-=σ, N=22.67 -45度 {}MPa T16756.11202.3477}{=σ, N=33.49 经比较得,N=33.49,所以共需要33.49*2=66.98层(6)当0度铺层占10%,90度铺层占40%时, 则45度和-45度各占25%时 0度 {}M P aT68313028732}{=σ, N=12.2 90度 {}MPa T6839.17608.6107}{-=σ, N=15.64 +45度 {}MPa T164260618561}{-=σ, N=26.0 -45度 {}MPa T164212854062}{=σ, N=35.65经比较得,N=35.65,所以共需要35.65*2=71.3层(7)当0度铺层占10%,90度铺层占50%时, 45度和-45度各占20% 0度,{}MPa T79325530507}{=σ, N= 12.9590度,{}MPa T5.7936.19028.4691}{--=σ, N= 38.545度,{}MPa T165968521327}{-=σ, N= 15.8 -45度,{}MPa T6.16589.14724888}{=σ, N=14.3经比较得,N=38.5,所以共需要38.5*2=77层(8)当0度铺层占10%,90度铺层占60%时, 则45度和-45度各占15%时 0度 {}M P a T94637832990}{=σ, N=14 90度 {}MPa T2.9463.20863607}{--=σ, N=42.2+45度 {}MPa T172076224781}{-=σ, N=16.3-45度 {}MPa T172017024701}{=σ, N=34.46经比较得,N=42.2,所以共需要42.2*2=84.4层(9)当0度铺层占10%,90度铺层占75%时, 则45度和-45度各占6.25%时 0度 {}M P aT145062239942}{=σ, N=16.95 90度 {}MPa T8.144925721729.6-}{-=σ, N=52.07+45度 {}MPa T196487734490}{-=σ, N=18.7 -45度 {}MPa T5.196323173722}{=σ, N=46.9经比较得,N=52.07,所以共需要52.07*2=104.14层(10)当0度铺层占25%,90度铺层占0%时, 则45度和-45度各占37.5%时 0度 {}M P aT50756820231}{-=σ, N=8.5883 +45度 {}MPa T16329.1-8284.7}{-=σ, N=15.55 -45度 {}MPa T9.16326.4949.2475}{-=σ, N=10.01经比较得,N=15.55,所以共需要15.55*2=31.10层(11)当0度铺层占25%,90度铺层占10%时, 则45度和-45度各占32.5%时 0度 {}M P a T56526519118}{-=σ, N=8.11 90度 {}MPa T5.5635.10725.9458}{--=σ, N=21.71+45度 {}MPa T134712610829}{-=σ, N=13.85 -45度 {}MPa T5.13465.6844.1169}{-=σ, N=12.83经比较得,N=21.71,所以共需要21.71*2=43.42层(12) 当0度铺层占25%,90度铺层占25%时, 则45度和-45度各占25%时 0度,{}MPa T6831819099}{-=σ, N= 8.1 90度,{}MPa T2.68314117.5669}{--=σ, N=23.0945度,{}MPa T116722213964}{-=σ, N=max{5.93,4.5,11.1}=11.1 -45度,{}MPa T1.11676.9006.534}{-=σ, N=max{0.36,18.23,11.1}=18.23经比较得,N=23.09,所以共需要23.09*2=46.18层(13)当0度铺层占25%,90度铺层占50%时, 则45度和-45度各占12.5%时 0度 {}M P aT104722721050}{=σ, N=9.97 90度 {}MPa T10473.13271.2452}{--=σ, N=26.8 +45度 {}MPa T110725720408}{-=σ, N=10.54-45度 {}MPa T110712978.1809}{-=σ, N=26.21 经比较得,N=26.8,所以共需要26.8*2=53.6层(14)当0度铺层占50%,90度铺层占0%时, 则45度和-45度各占25%时 0度 {}M P aT68335712870}{-=σ, N=6.5 90度 {}MPa T 2.6837.4718.9106}{--=σ, N=9.55+45度 {}MPa T6.10351.1823.9131}{--=σ, N=9.86 -45度 {}MPa T6.10356.4967.5367}{-=σ, N=11.05经比较得,N=11.05,所以共需要11.05*2=22.1层(15)当0度铺层占50%,90度铺层占10%时, 则45度和-45度各占20%时 0度 {}M P a T79312712568}{-=σ, N=7.55 90度 {}MPa T793.5-4.7185492.7-}{=σ, N=14.54 +45度 {}MPa T8519811957}{--=σ, N=8.1 -45度 {}MPa T8518.6894882}{-=σ, N=13.96 经比较得,N=14.54,所以共需要14.54*2=29.08层(16)当0度铺层占50%,90度铺层占25%时, 则45度和-45度各占12.5%时 0度 {}M P a T10475212812}{=σ, N=9.9790度 {}MPa T 10474.7839.2819}{--=σ, N=15.85 +45度 {}MPa T73710216105}{--=σ, N=7.01 -45度 {}MPa T6.7366.9379.6112}{-=σ, N=18.97经比较得,N=18.97,所以共需要18.97*2=37.94层需的层数最少,为22层,此时的重量最轻。
结构力学考试题及答案112.3一、选择题(每题2分,共10分)1. 在结构力学中,以下哪个选项不是结构分析的基本假设?A. 平面假设B. 连续性假设C. 均匀性假设D. 刚性假设答案:D2. 确定梁的弯矩图时,以下哪个力不是需要考虑的?A. 集中力B. 分布力C. 温度变化D. 惯性力答案:C3. 对于一个悬臂梁,如果自由端受到一个向下的集中力,那么在固定端的弯矩为?A. 0B. 向上的弯矩C. 向下的弯矩D. 无法确定答案:C4. 在结构力学中,以下哪个方法不适用于求解超静定结构?A. 力法B. 位移法C. 弯矩分配法D. 虚功原理答案:D5. 以下哪个选项不是结构力学中常用的分析方法?A. 矩阵位移法B. 能量法C. 虚功原理D. 牛顿第二定律答案:D二、计算题(每题10分,共40分)1. 给定一个简支梁,跨中点受到一个集中力P,求梁的弯矩图和剪力图。
答案:弯矩图在跨中点为最大值PL/4,剪力图在跨中点为零,两端为P。
2. 计算一个三跨连续梁,中间支座为铰接,两端为固定支座,中间支座受到一个向下的集中力P,求各支座反力。
答案:左端固定支座反力为P/2,右端固定支座反力为P/2,中间铰接支座反力为0。
3. 给定一个悬臂梁,自由端受到一个向下的集中力P和一个顺时针的力矩M,求梁的弯矩图。
答案:弯矩图从固定端到自由端线性增加,自由端弯矩为P*L+M。
4. 计算一个四边形框架,四个角点均为铰接,对角线交点受到一个向下的集中力P,求框架的内力。
答案:对角线交点处的弯矩为0,对角线两侧的梁受到的剪力均为P/2。
三、简答题(每题5分,共10分)1. 简述结构力学中力法的基本思想。
答案:力法的基本思想是通过施加单位载荷,计算出结构的内力影响线,然后根据实际载荷求得实际内力。
2. 什么是结构的稳定性,它与结构的强度有何不同?答案:结构的稳定性是指结构在受到荷载作用时,保持其原有平衡状态的能力。
而结构的强度是指结构在受到荷载作用时,不发生破坏的能力。
Problem Set #1
Handed out: Oct 17th , 2013
Due: Oct 24th , 2013
1. Expand the following tensor equations (Note the Kronecker delta in a and c )
a) 1[(1)]mm T E αβ
αβαβαβευσδσδα=-+-∆ b)
1F F αβσγαβσγαβαβσσσ+= c)
1mn ms n a b δ= d) 1i i B A αα=
(4 points )
2. Based on the ‘Rigorous handling of 2D model’ in the course note, determine for a
volume fraction ()a /a b +equal to 0.6:
a) The stress in the broken fiber
b) The stress in the unbroken fiber
c) The shear stress in the matrix
Try do this for the length equal to 10, 50, 100 fiber diameters. Base on your graphical results, answer the following questions:
a) What is the effect of changing the overall length?
b) What happens when the overall length is 10 fiber diameters?
c) For the case that the fiber total length is more than 50 times of the fiber
diameter, how far from the break point must one go to achieve 99% of the original applied stress in the broken fiber?
(12 points )
Note:
1)
0.083= 2) When max 50ζ≥, max tan()1κζ≈, the equations can be simplified.
3) The purpose of this excise is to learn and practice how to write a small
MATLAB program and draw the scientific figures. More attention should be paid to the following MATLAB commands,
a) FOR… END;
b) IF…ELSE…END
c) PLOT;
d) AXIS;
e) XLABEL,YLABEL;
f) TITLE.
MATLAB’s help will provide more details regarding these commands.
3. Consider the following shear lag problem of a piezoceramic crystal (PZT) surface mounted
on a metal plate. Note that the width of the PZT is less than the width of the plate. When the crystal is activated, a strain is induced. The stress in the PZT can be found from the following equation.
()p p p PZT E σεε=-
where
p E is the modulus of the PZT, p σ and p ε are the stress and the strain in the PZT, and PZT ε is the induced strain due to the external voltage applied.
a) For a given induced strain, what does the displacement look like through the thickness?
(Assume that the strain is constant through the width).
b) Determine the coupled differential equations necessary to solve this problem. (The
independent variables can either be the deflections in the PZT and the plate or the stresses in the PZT and the plate. Assume the shear modulus of the adhesive is a G )
c) What are the boundary conditions?
(8 points)
4. Using micromechanics determine the modulus,T E , of the following three cross sections. The
first elemental volume has a square fiber within a rectangular section of matrix. The fiber has sides of a and the unit volume has a height of 3a . Note that in the first one, the fiber volume fraction is 223a a or 1/3. The dimension of the fibers in the second and third elemental volume is again a . First determine the appropriate dimension of the second and third volume so that the fiber volume fractions of both volumes are equal. In order to determine the modulus of both volumes, you can assume constant strain across any plane perpendicular to the applied load in the 2-direction ( Assume that fiber properties are f E and f ν and the matrix properties are m E and m ν).
(6 points)
a a a σσσσ? ? 2 3 σ
σ。