数学归纳法证明整除
- 格式:docx
- 大小:16.62 KB
- 文档页数:4

数学归纳法及应用举例重点难点分析:(1)第一步递推基础,第二步是递推依据,密切相关缺一不可。
(2)归纳思想充分体现了特殊与一般的思想,数学归纳法体现了有限与无限的辩证关系与转化思想。
(3)归纳—猜想—证明是经常运用的数学方法,观察是解决问题的前提条件,需要进行合理的试验和归纳,提出合理猜想,从而达到解决问题的目的。
(4)数学归纳法的应用通常与数学的其它方法联系在一起,如比较、放缩、配凑、分析和综合法等。
典型例题:例1.证明:=-n(n+1)(4n+3)。
证明:①当n=1时,左,右=-1(1+1)(4+3)=-14,等式成立。
②假设n=k时等式成立,即=-k(k+1)(4k+3)。
n=k+1时,+[(2k+1)(2k+2)2-(2k+2)(2k+3)2] =-k(k+1)(4k+3)-2(k+1)(4k2+12k+9-4k2-6k-2) =-(k+1)[4k2+3k+2(6k+7)]=-(k+1)(4k2+15k+14)=-(k+1)(k+2)(4k+7)=-(k+1)[(k+1)+1][4(k+1)+3],等式成立。
由①②知,当n∈N′时等式成立例2.试证S n=n3+(n+1)3+(n+2)3能被9整除。
证明:①n=1时,S1=4×9,能9整除。
②假设,n=k时,S k能被9整除,则S k+1=(k+1)3+(k+2)3+(k+3)3=S k+(k+3)3-k3=S k+9(k3+3k+3)由归纳假设知S k+1能被9整除,也就是说n=k+1时命题也成立。
综上所述:命题成立。
点评:用数学归纳法证明整除问题时,关键是把n=k+1时的式子分成两部分,其中一部分应用归纳假设,另一部分经过变形处理,确定其能被某数(某式)整除。
例3.通过一点有n个平面,其中没有任何3个平面交于同一条直线,用数学归纳法证明这些平面把空间分成(n2-n+2)个部分。
证明:设适合条件的n个平面把空间分成p n个部分,∴p n=n2-n+2①当n=1时,p1=1-1+2=2,显然符合条件,故命题成立。

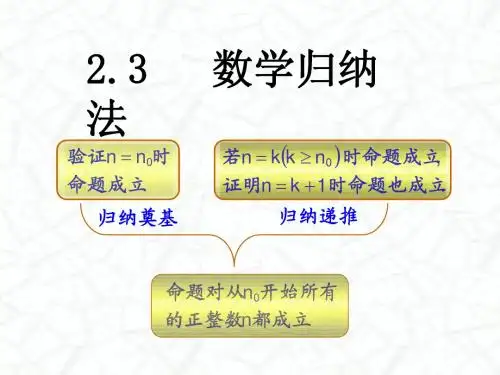
数 学 归 纳 法要点回顾:归纳法是一种由特殊到一般的推理方法,它可以分为完全归纳法和不完全归纳法两种,完全归纳法只局限于有限个元素,而不完全归纳法得出的结论不一定可靠,数学归纳法属于完全归纳法;应用数学归纳法证明的两个步骤: (1)证明当n 取第一个值n 0时结论正确,(2)假设n=k (k ∈N ※,k ≥n 0)时结论正确,证明当n=k+1时结论也正确。
用数学归纳法证题的两个步骤缺一不可,在完成了以上两个步骤以后,就可以断定命题对于从n 0开始的所有正整数n 都正确。
数学归纳法的核心:在验证命题n=n 0正确的基础上,证明命题具有传递性,而第二步实际上是以一次逻辑的推理代替了无限的验证过程.所以说数学归纳法是一种合理、切实可行的科学证题方法,实现了有限到无限的飞跃。
“数学归纳法”中包含着递推思想、类比思想、分类思想、归纳思想.由于数学归纳法是证明与正整数有关的命题,数列是定义在正整数集或其子集上的特殊函数,而导数又是研究函数的重要工具,另外不等式具备传递性,正是这一条知识链注定了数学归纳法必然以数列、不等式、函数与导数等内容为背景。
分析近几年与数学归纳法相关的高考试题,不难得出其命题特点:(1)数学归纳法中的 “归纳—猜想—证明”这一基本思想与方法,考试中可以以各种题型出现,复习中仍需加以重视.但很少单独命制大题,往往作为解答题中某一小问的形式出现,重在体现它的工具性作用。
且常与数列结合去考查,有时还与函数、导数、不等式等内容相关联,以体现“在知识交汇处设计试题”的命题原则。
(2)试题特别注重加强对不完全归纳法的考查,既要求归纳发现结论,又要求能证明结论的正确性,初步形成“观察—归纳—猜想—证明”的思维模式。
(3)高考对数学归纳法主要是‘隐形’考查,也就是说这种方法在题目中往往是“藏而不露”,不明说要用“数归法”,但通常可用“数归法”,也可用其它方法来解决(如果能找到其它解决方法的话)。

数学归纳法证明经典事例数学中的归纳法是很有作用的,关于这些的整除证明是怎样的呢?下面就是店铺给大家整理的数学归纳法证明整除内容,希望大家喜欢。
数学归纳法事例1当n=1 的时候上面的'式子 = 3^4-8-9=64成立假设当n=k 的时候3^(2k+2)-8k-9能够被64整除当n=k+1式子= 3^(2k+4)-8k-17=9[3^(2k+2) -8k-9] +64k+64因为 3^(2k+2)-8k-9能够被64整除∴ 9[3^(2k+2) -8k-9] +64k+64 能够被64整除n=k+1 时,成立根据上面的由数学归纳法3的2n+2次方-8n-9(n属于N*)能被64整除。
数学归纳法事例2n=1时 3^4-8-9=81-17=64 能被4整除·····(特殊性)设当n=k时,仍然成立。
当n=k+1时,·····················(一般性)3^(2(k+1)+2)-8(k+1)-9=3^(2K+2+2)-8K-17 =9*3^(2K+2)-72K+64K-81+64=9(3^(2k+2)-8k-9)+64k+64因为3^(2k+2)-8k-9能被64整除不用写了吧··正确请采纳数学归纳法当n=1 的时候上面的式子 = 3^4-8-9=64成立假设当n=k (k>=1)数学归纳法事例3当3^(2k+2)-8k-9能够被64整除当n=k+1(k>=1)式子= 3^(2k+4)-8k-17=9[3^(2k+2) -8k-9] +64k+64由9[3^(2k+2) -8k-9] +64k+64-(3^(2k+2)-8k-9)可以被64整出n=k+1 时,成立根据上面的由数学归纳法3的2n+2次方-8n-9(n属于N*)能被64整3.证明:对于任意自然数n (3n+1)*7^n-1能被9整除数学归纳法(1)当n=1时 (3*1+1)*7-1=27能被9整除(2)假设当n=k时 (3k+1)*7^k-1能被9整除则当n=k+1时 [3(k+1)+1]*7^(k+1)-1=[21k+28]*7^k-1=(3k+1)*7^k-1+(18k+27)*7^k=[(3k+1)*7^k-1]+9(2k+3)*7^k括号中的代数式能被9整除 9(2k+3)*7^k能被9整除所以当n=k+1时 [3(k+1)+1]*7^(k+1)-1能被9整除综合(1)(2)可知对于任意自然数n 有(3n+1)*7^n-1能被9整除【数学归纳法证明经典事例】。


浅谈数学归纳法的原理及应用姓名:王磊峰单位:砀山县豆集学区范套小学浅谈数学归纳法的原理及应用摘要:数学归纳法是证明与自然数有关命题的一种论证方法,也是数学证明中的一个强有力的工具,无论在初等数学还是高等数学中都有广泛的应用。
本文讨论了数学归纳法的理论依据、应用功能以及应用数学归纳法应注意的问题等。
关键词:数学归纳法;匹阿诺公理;应用;推理;命题;类型数学归纳法是数学中最基本也是最重要的证明方法之一,它在各个数学领域分支中都有极大的应用,因为使用面比较广,所以涉及的知识和技巧比较多,在本文中将介绍数学归纳法的产生、发展和确立并分别举例说明数学归纳法在各个方面的应用。
1数学归纳法的产生、发展和确立1.1数学归纳法的产生数学归纳法的产生经历了一个较长的历史时期,一般认为归纳推理可追溯公元六世纪的毕达哥拉斯时代。
这一时代杰出的数学家毕达哥拉斯利用点子数对级数求和问题进行了探讨,利用经过剖分后的正方形的直观形象,他确信无疑地得出:135+++ (2)-=,这里n n(21)有明显的推理过程,但这种推理只是简单枚举而没有碰到矛盾事实的归纳结果,因此是不完全的归纳推理,或者说只是一种寻求结论的手段,它只是作为一种猜想或假说,而不是可靠的,尽管如此,他仍为数学归纳法的产生奠定了一定的基础。
可靠的归纳推理是欧几里得对系数个数无穷的证明,虽然其中递推过程不甚明显,但基本思想却是按递推归纳原理指导的。
肯定地说,这一关于系数个数无穷的具体证明为后人对数学归纳法的认识提供了原形,促使人们加深了对数学归纳法的理解。
16世纪,经过文艺复兴洗礼的欧洲学者越来越意识到数学的重要性。
意大利数学家毛罗利科首先对全体自然数有关的命题的证明做了深入考察,他认为递归推理是指首先确定命题对于第一个自然数是真的,然后再去验证命题具有后继数也是真的。
于是,根据递推特性,命题对于第一个自然数的后继数为真,则对于第二个自然数也为真;对于第二个自然数为真,则对于第三个自然数也为真。

数学归纳法证明的原理2020-12-07数学归纳法证明的原理数学归纳法证明的原理数学归纳法证明的是与自然数有关的命题,它的依据是皮亚诺提出的自然数的序数理论,就是通常所说的自然数的皮亚诺公理,内容是:(1)l是自然数。
(2)每个自然数a有一个确定的“直接后继”数a’,a也是自然数。
(2)a’≠1,即1不是任何自然数的“直接后继”数。
(4)由a’=b’,推得a=b,即每个自然数只能是另外的唯一自然的“直接后继”数。
(5)任一自然数的集合,如果包含1,并且假设包含a,也一定包含a的“直接后继”数a’,则这个集合包含所有的自然数。
皮亚诺公理中的(5)是数学归纳法的依据,又叫归纳公理数学归纳法的应用及举例。
因为由假设知42k+1+3k+2能被13整除,1342k+1也能被13整除,这就是说,当n=k+1时,f(k+l)能被13整除。
根据(1)、(2),可知命题对任何n∈N都成立。
下面按归纳步中归纳假设的形式向读者介绍数学归纳法的几种不同形式以及它们的应用。
(l)简单归纳法。
即在归纳步中,归纳假设为“n=k时待证命题成立”。
这是最常用的一种归纳法,称为简单归纳法,大家都比较熟悉,这里不再赘述。
(2)强归纳法。
这种数学归纳法,在归纳步中,其归纳假设为“n≥k时待证命题成立”。
我们称之为强归纳法,又叫串值归纳法。
通常,如果在证明p(n+l)成立时,不仅依赖于p(n)成立,而且还可能依赖于以前各步时,一般应选用强归纳法,下面举例说明其应用。
例有数目相等的两堆棋子,两人轮流从任一堆里取几项棋子,但不能不取也不能同时从两堆里取,规定凡取得最后一项者胜。
求证后者必胜。
证:归纳元n为每堆棋子的数目。
设甲为先取者,乙为后取者。
奠基n=l,易证乙必胜。
归纳设Nn≤k时,乙必胜。
现证n=k+l时也是乙必胜。
设甲在某堆中先取r颗,O<r≤k。
乙的对策是在另一堆中也取r颗。
有二种可能:(1)若r<k,经过两人各取一次之后,两堆都只有k-r颗,k-r<k,现在又轮到甲先取,依归纳假设,乙必胜。

多米诺骨牌上的数学——数学归纳法五十多年前,清华大学数学系赵访熊教授在给大学一年级学生讲高等数学课,总要先讲讲数学的基本概念和方法,他在讲解数学归纳法的时候,先讲了这样一个故事:某主妇养小鸡十只,公母各半。
她预备将母鸡养大留着生蛋,公鸡则养到一百天就陆续杀以佐餐。
天天早晨她拿米喂鸡。
到第一百天的早晨,其中的一只公鸡正在想:“第一天早晨有米吃,第二天早晨有米吃,……第九十九天早晨有米吃,所以今天,第一百天的早晨,一定有米吃。
”这时,该主妇来了,正好把这只公鸡抓去杀了。
这只公鸡在第一百天的早晨不但没有吃着米,反而被杀了,虽然它已有九十九天吃米的经验,但不能证明第一百天一定有米吃。
(赵访熊,1908年——1996年,我国最早提倡和从事应用数学与计算数学的教学与研究的学者之一。
)赵先生把这只公鸡的推理戏称为“公鸡归纳法”。
显然这是一种错误的不完全归纳法。
我们经常会遇到涉及全体自然数的命题,对待这种问题,如果要否定它,你只要能举出一个反例即可。
如果要证明它,由于自然数有无限多个,若是一个接一个地验证下去,那永远也做不完。
怎么办?数学家想出了一种非常重要的数学方法来解决这类问题,那就是数学归纳法。
【数学史话】欧几里得的开端实际上,人们很早就遇到了无限集合的问题,而当时具体的推导或计算都只是针对有限对象,实施有限次论证。
怎样在具体的推导或计算中把握无限的难题,很早就摆在数学家面前了。
(欧几里得,公元前330年—公元前275年,古希腊伟大的数学家,被称为数学之父)最先是古希腊数学家欧几里得在他的《几何原本》中采用了近似于数学归纳法的思想。
该书第九卷第20命题是:“素数比任何给定的一批素数都多。
”欧几里得在证明这一命题时采用了独特的“几何”方式,他把数视为线段:设有素数a、b、c,另设d=a·b·c+1,则d或是素数或不是素数。
如果d是素数,则d是与a、b、c三者都不同的素数。
如d不是素数,则它必有素因数e,并且e与a、b、c都不同,所以一定有比给定的素数更多的素数。


被2、3、5整除的数的特征的证明-回复被2、3、5整除的数,即能够同时被2、3、5整除的数,具有一些特征。
我们将一步一步回答以下问题:什么样的数能被2整除?什么样的数能被3整除?什么样的数能被5整除?再进一步分析这三个条件的交集,即同时满足被2、3、5整除的数的特征。
让我们开始证明这些特征吧。
1. 什么样的数能被2整除?一个数能被2整除,意味着它可以被2整除的次数为正整数,即没有余数。
一个数可以被2整除的充分必要条件是,这个数的个位数字为偶数,或者其个位数字为0。
例如,数列2,4,6,8,10...依次都可以被2整除,因为它们的个位数字均为偶数。
0可以被2整除是因为任何数乘以0仍为0。
2. 什么样的数能被3整除?一个数能被3整除,意味着它可以被3整除的次数为正整数,即没有余数。
一个数可以被3整除的充分必要条件是,这个数的各个位数之和能被3整除。
例如,数列3,6,9,12,15...依次都可以被3整除,因为它们的各位数字之和均能被3整除。
3. 什么样的数能被5整除?一个数能被5整除,意味着它可以被5整除的次数为正整数,即没有余数。
一个数可以被5整除的充分必要条件是,这个数的个位数字为5或0。
例如,数列5,10,15,20,25...依次都可以被5整除,因为它们的个位数字均为5或0。
从上面的分析中可以看出,被2、3、5整除的数都有一个共同的特征,即它们的个位数字必须为0或者偶数。
这是因为它们满足了被2整除的条件。
接下来,我们将进一步分析这些数和3的关系。
一个数能被3和2同时整除,意味着它可以被6整除,因为6是2和3的最小公倍数。
因此,被2、3、5整除的数的充要条件是它们的个位数字为0或者偶数,且各个位数之和能被3整除。
下面我们通过数学归纳法证明这个结论。
首先,我们假设一个被2、3、5整除的数可以写为10n,其中n为自然数(即整数且大于等于0)。
这是因为对于任意自然数n,10n的个位数字为0,满足了被2整除的条件。
数学归纳法【学习目标】1.理解数学归纳法的原理及适用范围.掌握数学归纳法证题的思路和特点。
2.能够利用数学归纳法证明与正整数有关的命题。
【要点梳理】知识点一、数学归纳法的原理1.数学归纳法定义:对于某些与自然数n有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0时命题成立;然后假设当n=k(k N*,k≥n0)时命题成立,证明当n=k+1时命题也成立这种证明方法就叫做数学归纳法要点诠释:即先验证使结论有意义的最小的正整数n0,如果当n=n0时,命题成立,再假设当n=k(k≥n0,k∈N*)时,命题成立.(这时命题是否成立不是确定的),根据这个假设,如能推出当n=k+1时,命题也成立,那么就可以递推出对所有不小于n0的正整数n0+1,n0+2,…,命题都成立.2.数学归纳法的原理:数学归纳法是专门证明与正整数集有关的命题的一种方法,它是一种完全归纳法。
它的证明共分两步:①证明了第一步,就获得了递推的基础。
但仅靠这一步还不能说明结论的普遍性.在第一步中,考察结论成立的最小正整数就足够了,没有必要再考察几个正整数,即使命题对这几个正整数都成立,也不能保证命题对其他正整数也成立;②证明了第二步,就获得了递推的依据。
但没有第一步就失去了递推的基础.只有把第一步和第二步结合在一起,才能获得普遍性的结论。
其中第一步是命题成立的基础,称为“归纳基础”(或称特殊性),第二步是递推的证据,解决的是延续性问题(又称传递性问题)。
3.数学归纳法的功能和适用范围1.数学归纳法具有证明的功能,它将无穷的归纳过程根据归纳公理转化为有限的特殊演绎(直接验证和演绎推理相结合)过程.2. 数学归纳法一般被用于证明某些与正整数n(n取无限多个值)有关的数学命题。
但是,并不能简单地说所有与正整数n有关的数学命题都可使用数学归纳法证明。
知识点二、运用数学归纳法的步骤与技巧1用数学归纳法证明一个与正整数有关的命题的步骤:(1)证明:当n取第一个值n0结论正确;(2)假设当n=k(k∈N*,且k≥n0)时结论正确,证明当n=k+1时结论也正确由(1),(2)可知,命题对于从n0开始的所有正整数n都正确2.用数学归纳法证题的注意事项(1)弄错起始n0.n0不一定恒为1,也可能n0=2或3(即起点问题).(2)对项数估算错误.特别是当寻找n=k与n=k+1的关系时,项数的变化易出现错误(即跨度问题).(3)没有利用归纳假设.归纳假设是必须要用的,假设是起桥梁作用的,桥梁断了就过不去了,整个证明过程也就不正确了(即伪证问题).(4)关键步骤含糊不清.“假设n=k时结论成立,利用此假设证明n=k+1时结论也成立”是数学归纳法的关键一步,也是证明问题最重要的环节,推导的过程中要把步骤写完整,另外要注意证明过程的严谨性、规范性(即规范问题).3.用数学归纳法证题的关键:运用数学归纳法由n=k到n=k+l的证明是证明的难点,突破难点的关键是掌握由n=k到n=k+1的推证方法.在运用归纳假设时,应分析由n=k到n=k+1的差异与联系,利用拆、添、并、放、缩等手段,或从归纳假设出发,或从n=k+1时分离出n=k时的式子,再进行局部调整;也可以考虑二者的结合点,以便顺利过渡.知识点三、用数学归纳法证题的类型:1.用数学归纳法证明与正整数n有关的恒等式;对于证明恒等的问题,在由证等式也成立时,应及时把结论和推导过程对比,也就是我们通常所说的两边凑的方法,以减小计算的复杂程度,从而发现所要证明的式子,使问题的证明有目的性.2.用数学归纳法证明与正整数n有关的整除性问题;用数学归纳法证明整除问题时,由到时,首先要从要证的式子中拼凑出假设成立的式子,然后证明剩余的式子也能被某式(数)整除,这是数学归纳法证明问题的一大技巧。
目录1。
前言 (1)2.利用整除性判别法解决整除问题 (1)2.1能被2k或5k整除的判别法 (1)2。
2割尾判别法 (2)3。
利用整除的基本性质解题 (4)4.最大公因数 (6)5.抽屉原理在数论中的应用 (7)6。
致谢 (10)7.参考文献 (11)中学数学中与初等数论相关的几个问题陈琴 (指导老师: 左可正)(湖北师范学院 数学系 湖北 黄石 435002)1。
前言在中学数学中,整数是特殊常用的一类数。
而初等数论是研究整数的性质的、与算术有密切关系的一门学科,可以说初等数论是算术的延续.初等数论问题更是数学竞赛试题多发区.而对于整除性质和抽屉原理的考察一直是中学数学竞赛中应用范围最广的核心内容,作为高中教师,有必要对这些知识进行系统的考查。
2。
利用整除性判别法解决整除问题一个数能不能被另一个数整除,虽然可以用长除法去判别,但当被除数位数较多时,那是很麻烦的。
要判别一个正整数a 能否被另一个正整数d 整除,往往可变为只要找出另一(绝对值)较小的整数b ,而去判别b 能否被d 整除。
这个新的整数b 也就称为判别数。
要看一种整除判别法是否优越,就在于能否用较快的速度而得出很小的判别数。
因为判别数b 越小,就越容易判别能否被d 整除。
下面我将阐述两种判别法。
2。
1能被2k 或5k 整除的判别法令整数01n a a a a =⋯(0<0a ≤9,0≤i a ≤9, i =1,2, ⋯,n)。
i a ∈N.因为210k k |,但k 2不整除110k -,故要判别a 是否能被k 2整除,就是要而且只要判别122n k n k n n a a a a -+-+-⋯能否被k 2整除.我们可以用一个例子来证实这个判别法.例1:试判别51024能否被16整除?解:显然16=42,故相当于来判别a 是否能被42整除.但1024=1000+24而321000∣,42不整除1000,故知以42除1000的余数为8,而8+24=32可被16整除,故知1651024∣.与能被2k 整除的道理一样,判别a 是否能被5k 整除,只需要看122n k n k n n a a a a -+-+-⋯能否被5k 整除就行了。
数学归纳法一、基础知识:1、数学归纳法适用的范围:关于正整数n 的命题(例如数列,不等式,整除问题等),则可以考虑使用数学归纳法进行证明2、第一数学归纳法:通过假设n k =成立,再结合其它条件去证1n k =+成立即可。
证明的步骤如下:(1)归纳验证:验证0n n =(0n 是满足条件的最小整数)时,命题成立(2)归纳假设:假设()0,n k k n n N =³Î成立,证明当1n k =+时,命题也成立(3)归纳结论:得到结论:0,n n n N ³Î时,命题均成立3、第一归纳法要注意的地方:(1)数学归纳法所证命题不一定从1n =开始成立,可从任意一个正整数0n 开始,此时归纳验证从0n n =开始(2)归纳假设中,要注意0k n ³,保证递推的连续性(3)归纳假设中的n k =,命题成立,是证明1n k =+命题成立的重要条件。
在证明的过程中要注意寻找1n k =+与n k =的联系4、第二数学归纳法:在第一数学归纳法中有一个细节,就是在假设n k =命题成立时,可用的条件只有n k =,而不能默认其它n k £的时依然成立。
第二数学归纳法是对第一归纳法的补充,将归纳假设扩充为假设n k £,命题均成立,然后证明1n k =+命题成立。
可使用的条件要比第一归纳法多,证明的步骤如下:(1)归纳验证:验证0n n =(0n 是满足条件的最小整数)时,命题成立(2)归纳假设:假设()0,n k k n n N £³Î成立,证明当1n k =+时,命题也成立(3)归纳结论:得到结论:0,n n n N ³Î时,命题均成立二、典型例题例1:已知等比数列{}n a 的首项12a =,公比3q =,设n S 是它的前n 项和,求证:131n n S n S n++£思路:根据等比数列求和公式可化简所证不等式:321n n ³+,n k =时,不等式为321k k ³+;当1n k =+时,所证不等式为1323k k +³+,可明显看到n k =与1n k =+中,两个不等式的联系,从而想到利用数学归纳法进行证明证明:()11311n nn a q S q -==--,所证不等式为:1313131n n n n+-+£-()()()1313131n n n n +\-£+-1133331n n n n n n n ++Û×-£×+--321n n Û³+,下面用数学归纳法证明:(1)验证:1n =时,左边=右边,不等式成立(2)假设()1,n k k k N =³Î时,不等式成立,则1n k =+时,()()133332163211k k k k k +=׳+=+>++所以1n k =+时,不等式成立n N *\"Î,均有131n n S n S n++£小炼有话说:数学归纳法的证明过程,关键的地方在于寻找所证1n k =+与条件n k =之间的联系,一旦找到联系,则数学归纳法即可使用例2(2015,和平模拟):已知数列{}n a 满足0n a >,其前n 项和1n S >,且()()112,6n n n S a a n N *=++Î(1)求数列{}n a 的通项公式(2)设21log 1n n b a æö=+ç÷èø,并记n T 为数列{}n b 的前n 项和,求证:233log ,2n n a T n N *+æö>Îç÷èø解:(1)2632n n n S a a =++①()21116322,n n n S a a n n N *---=++³Î②①-②可得:()222211116333n n n n n n n n n a a a a a a a a a ----=-+-Þ+=-0n a >Q 所以两边同除以1n n a a -+可得:13n n a a --={}n a \是公差为3的等差数列()131n a a n \=+-,在2632n n n S a a =++中令1n =可得:211116321S a a a =++Þ=(舍)或12a =31n a n \=-(2)思路:利用(1)可求出n b 和n T ,从而简化不等式可得:33633225312n n n +æö×××>ç÷-èøL ,若直接证明则需要进行放缩,难度较大。
多米诺骨牌上的数学——数学归纳法五十多年前,清华大学数学系赵访熊教授在给大学一年级学生讲高等数学课,总要先讲讲数学的基本概念和方法,他在讲解数学归纳法的时候,先讲了这样一个故事:某主妇养小鸡十只,公母各半。
她预备将母鸡养大留着生蛋,公鸡则养到一百天就陆续杀以佐餐。
天天早晨她拿米喂鸡。
到第一百天的早晨,其中的一只公鸡正在想:“第一天早晨有米吃,第二天早晨有米吃,……第九十九天早晨有米吃,所以今天,第一百天的早晨,一定有米吃。
”这时,该主妇来了,正好把这只公鸡抓去杀了。
这只公鸡在第一百天的早晨不但没有吃着米,反而被杀了,虽然它已有九十九天吃米的经验,但不能证明第一百天一定有米吃。
(赵访熊,1908年——1996年,我国最早提倡和从事应用数学与计算数学的教学与研究的学者之一。
)赵先生把这只公鸡的推理戏称为“公鸡归纳法”。
显然这是一种错误的不完全归纳法。
我们经常会遇到涉及全体自然数的命题,对待这种问题,如果要否定它,你只要能举出一个反例即可。
如果要证明它,由于自然数有无限多个,若是一个接一个地验证下去,那永远也做不完。
怎么办?数学家想出了一种非常重要的数学方法来解决这类问题,那就是数学归纳法。
【数学史话】欧几里得的开端实际上,人们很早就遇到了无限集合的问题,而当时具体的推导或计算都只是针对有限对象,实施有限次论证。
怎样在具体的推导或计算中把握无限的难题,很早就摆在数学家面前了。
(欧几里得,公元前330年—公元前275年,古希腊伟大的数学家,被称为数学之父)最先是古希腊数学家欧几里得在他的《几何原本》中采用了近似于数学归纳法的思想。
该书第九卷第20命题是:“素数比任何给定的一批素数都多。
”欧几里得在证明这一命题时采用了独特的“几何”方式,他把数视为线段:设有素数a、b、c,另设d=a·b·c+1,则d或是素数或不是素数。
如果d是素数,则d是与a、b、c三者都不同的素数。
如d不是素数,则它必有素因数e,并且e与a、b、c都不同,所以一定有比给定的素数更多的素数。
数学归纳法的特殊应用解析与归纳数学归纳法是数学中一种常用的证明方法,广泛应用于各个领域。
在此基础上,还可以有一些特殊的应用形式,本文将对数学归纳法的特殊应用进行解析与归纳。
一、奇偶性证明在数学中,奇偶性是一种常见的性质。
我们经常利用数学归纳法来证明某个数学对象的奇偶性。
这里以证明正整数的奇偶性为例:(1)首先,我们需要证明基本情况。
对于最小的正整数1,它是奇数,因此基本情况成立。
(2)假设当n=k时,正整数k是奇数。
我们需要证明当n=k+1时,正整数k+1是偶数。
根据归纳法的思想,我们假设k是奇数,那么k可以表示为2m+1的形式,其中m为整数。
由此可得,k+1=2m+2=2(m+1),即k+1是偶数。
因此,当n=k+1时,正整数k+1是偶数。
(3)综上所述,根据数学归纳法,我们可以得出结论:对于任意正整数n,它都具有相应的奇偶性。
二、整除性证明整除性是数学中另一个重要的性质。
当我们需要证明某个数学对象的整除性时,也可以运用数学归纳法。
(1)首先,我们需要证明基本情况。
对于最小的正整数1,它可以整除任意的正整数,因此基本情况成立。
(2)假设当n=k时,正整数k可以整除某个正整数m。
我们需要证明当n=k+1时,正整数k+1也可以整除某个正整数m+1。
根据归纳法的思想,我们假设k可以整除m,即m=kp,其中p为整数。
由此可得,k+1=1+k=(m+1)p,即k+1可以整除m+1。
因此,当n=k+1时,正整数k+1也可以整除某个正整数m+1。
(3)综上所述,根据数学归纳法,我们可以得出结论:对于任意正整数n,它都具有相应的整除性。
三、恒等式证明恒等式是数学中常见的类似等式的性质。
我们可以利用数学归纳法来证明某个数学恒等式的成立。
(1)首先,我们需要证明基本情况。
对于某个特定的初等函数,我们需要验证当x取某个特定值时,恒等式是否成立。
(2)假设当n=k时,恒等式在某个特定的x值下成立。
我们需要证明当n=k+1时,恒等式在相同的x值下也成立。
数学归纳法证明整除
数学归纳法证明整除数学归纳法
当n=1 的时候
上面的式子 = 3^4-8-9=64
成立
假设当n=k 的时候
3^(2k+2)-8k-9能够被64整除
当n=k+1
式子= 3^(2k+4)-8k-17
=9[3^(2k+2) -8k-9] +64k+64
因为 3^(2k+2)-8k-9能够被64整除
∴ 9[3^(2k+2) -8k-9] +64k+64 能够被64整除
n=k+1 时,成立
根据上面的由数学归纳法
3的2n+2次方-8n-9(n属于N*)能被64整除。
2
当n=1时 3^4-8-9=81-17=64 能被4整除·····(特殊性)
设当n=k时,仍然成立。
当n=k+1时,·····················(一般性)
3^(2(k+1)+2)-8(k+1)-9=3^(2K+2+2)-8K-17 =9*3^(2K+2)-72K+64K-
81+64=9(3^(2k+2)-8k-9)+64k+64
因为3^(2k+2)-8k-9能被64整除
不用写了吧··
正确请采纳
数学归纳法
当n=1 的时候
上面的式子 = 3^4-8-9=64
成立
假设当n=k (k>=1)
3^(2k+2)-8k-9能够被64整除
当n=k+1(k>=1)
式子= 3^(2k+4)-8k-17
=9[3^(2k+2) -8k-9] +64k+64
由9[3^(2k+2) -8k-9] +64k+64-(3^(2k+2)-8k-9)可以被64整出n=k+1 时,成立
根据上面的由数学归纳法
3的2n+2次方-8n-9(n属于N*)能被64整
3.证明:对于任意自然数n (3n+1)*7^n-1能被9整除
数学归纳法
(1)当n=1时 (3*1+1)*7-1=27能被9整除
(2)假设当n=k时 (3k+1)*7^k-1能被9整除
则当n=k+1时 [3(k+1)+1]*7^(k+1)-1=[21k+28]*7^k-1
=(3k+1)*7^k-1+(18k+27)*7^k
=[(3k+1)*7^k-1]+9(2k+3)*7^k
括号中的代数式能被9整除 9(2k+3)*7^k能被9整除
所以当n=k+1时 [3(k+1)+1]*7^(k+1)-1能被9整除
综合(1)(2)可知对于任意自然数n 有(3n+1)*7^n-1能被9整除4证明:
(1)n=1时,3^(6n)-2^(6n) =3^6-2^6=665=19*35,命题成立
(2)假设n=k时命题成立,即
35能整除3^(6k)-2^(6k)
即3^(6k)-2^(6k)=35m (m∈Z+)
则n=k+1时
3^(6n)-2^(6n)
=3^(6k+6)-2^(6k+6)
=(3^6)*3^(6k)-(2^6)*2^(6k)
=64*[3^(6k)-2^(6k)]+(729-64)*3^(6k)
=64*[3^(6k)-2^(6k)]+665*3^(6k)
=64*35m+19*35*3^(6k)
=35*[64m+19*3^(6k)]
即n=k+1时,35能整除3^(6n)-2^(6n)
综合(1)(2)由数学归纳法知:
对于一切正整数n,35能整除3^(6n)-2^(6n)
===============
给定任意正整数n,设d(n)为n的约数个数,证明d(n)证明:
若n存在一个约数a则n/a=b是n的另一个约数,且b>√n
显然a,b是一一对应的
∵a∴a的个数∴b的个数∴d(n)=a的个数+b的个数3^(6k+1)-
2^(6k+1)-3^(6k)+2^(6k)
=(3^6-1)3^(6k)-(2^6-1)*2^(6k)
=728*3^(6k)-63*2^(6k)
=63*(3^(6k)-2^(6k))+665*3^(6k)
因为665/35=19 所以 3^(6k+1)-2^(6k+1)-3^(6k)+2^(6k)可以被35整除
那么由3^(6k+1)-2^(6k+1)-3^(6k)+2^(6k)+3^(6k)-2^(6k)
=3^(6k+1)-2^(6k+1)
可得到
3^(6k+1)-2^(6k+1)
必定可以被35整除
当n=1时3^(6n)-2^(6n)能被35整除
所以证明完成。