王顺荣编高教版社结构化学习题答案第7章

结晶学基础》习题答案目录第章答案7----------- 1第8 章答案 ---------- 12第9 章答案---------- 20第10 章答案25《结晶学基础》第七章习题答案7001 单晶：一个晶体能基本上被一个空间点阵的单位矢量所贯穿。

多晶：包含许多颗晶粒，这些晶粒可能为同一品种，也可能不同品种，由于各晶粒在空间取向可能不同，不能被同一点阵的单位矢量贯穿。

7002 (D ))7004 简单.立方；Cs 和Cl-; 4 G7005 (1) 立方F ⑵A 和B⑶4 个⑷4 组⑸.3 a (6) a/ . 2 7007 4 n 个A, 8 n个B, n为自然数。

7010 dm= 249 p m ; d211= 176 pm 5 doo：=432 pm 7011 六方；D3h 70127013 依次为立方,四方,四方,正交,六方。

7014 立方P,立方I ,立方F；四方P,四方I。

7015 旋转轴，镜面，对称中心，反轴；旋转轴，镜面,对称中心，反轴，点阵，螺旋轴，滑移面；n=123,4,6; 32 个；七个晶系;14种空间点阵型式；230个空间群。

7016 (1) 四方晶系(2) 四方1 (3) D (4) a=b c, ===90°7017 (1) 单斜晶系，单斜P (2) 6 (3) O, m i7018 (2 a,3 b, c):(326); (a,b,c):(111);(6 a,3 b,3c):(122);(2a,-3 b,-3 c):( 322)。

7019 G, C2, C3, C4, C6; 11=i , I 2=m, I 4。

7020 立方晶系：四个按立方体对角线安放的三重轴单斜晶系：一个二重轴或一个对称面。

C2(3), m(3), i 和14, C2(2), m(2)。

7021正交晶系和四方晶系232 个;230 个 7023 四方 I ;四方 P 7025 T , T h , Q O 群 7026 (B)Gv — -- 3mD 2d ---------- 42m T d — --------- 4 3m正交晶系有简单正交，正交面心，正交体心，正交底心，四种点阵型式。

第一章量子力学基础【1.1】.经典物理学在研究黑体辐射、光电效应与氢光谱时遇到了哪些困难？什么叫旧量子论？如何评价旧量子论？[解]：困难：（1)黑体辐射问题。

黑体就是理论上不反射任何电磁波的物体, 黑体辐射是指这类物体的电磁波辐射,由于这类物体不反射,所以由它释放出来的电磁波都来自辐射,实验中在不同的能量区间对黑体辐射规律给出了不同的函数，然而这两个函数无法兼容，是完全不同的，而事实上黑体辐射本该遵循某个唯一的规律。

况且经典理论还无法说明这两个函数中的任意一个.这个问题研究的是辐射与周围物体处于平衡状态时的能量按波长（或频率）的分布。

实验得出的结论是:热平衡时辐射能量密度按波长分布的曲线，其形状和位置只与黑体的绝对温度有关，而与空腔的形状及组成的物质无关。

这一结果用经典理论无法解释。

(2）光电效应。

光照射到金属上时，有电子从金属中逸出。

实验得出的光电效应的有关规律同样用经典理论无法解释。

（3)按照经典电动力学,由于核外电子作加速运动,原子必然坍缩。

经典物理学不能解释原子的稳定性问题。

原子光谱是线状结构的，而按照经典电动力学,作加速运动的电子所辐射的电磁波的频率是连续分布的,这与原子光谱的线状分布不符。

定义：从 1900 年普朗克提出振子能量量子化开始,人们力图以某些物理量必须量子化的假定来修正经典力学,用于解释某些宏观现象,并且给出其微观机制。

这种在量子力学建立以前形成的量子理论称为旧量子论。

评价：旧量子论冲破了经典物理学能量连续变化的框框。

对于黑体辐射、光电效应与氢光谱等现象的解释取得了成功。

但是，旧量子论是一个以连续为特征的经典力学加上以分立为特征的量子化条件的自相矛盾的体系,本质上还是属于经力学的范畴。

由于把微观粒子当作经典粒子，并把经典力学的运动规律应用于微观粒子，因而必然遭到严重的困难。

旧量子论必然会被新的量子论————量子力学所替代。

【1.2】．电子衍射实验如何证明电子的运动具有波动性？［解]：在贝尔实验室工作的戴维逊与革末在一个偶然的机会发现,当一束５4ｅV 的电子束垂直地射向镍单晶表面时,在与入射束成φ＝5０°角的方向上检测到反射的电子数最多。

第七章 过渡金属化合物1. 对于四方配位场(7.1.1), 当点电荷与中心的距离不等, 但符合|±x |<|±y |时, 则中心原子的p 轨道和d 轨道的能级图7.3(a )及(b )将发生什么变化? 请根据你的直觉和简单分析做出最合理的判断, 画出能级图.解:当点电荷距中心距离不等时, 将导致在正四方配位场下的二维不可约表示进一步分裂为两个一维不可约表示,即 p x , p y , 和 d xz , d yz 轨道进一步分裂.若|±x |<|±y |, 则p x 将比p y 感受道更强的来至点电荷的排斥作用, 从而导致p x 能量高于p y .d xz , d yz 轨道的能量也将发生分裂, 但是由于点电荷不在轨道的最大值方向, 感受的排斥相对于p x , p y 要小. 故能级的分裂值较小, d xz 较高, d yz 较低. 能级图如下:2. 反式四配位配合物 t -MA 2B 2, 如[P t C l 2B r 2]2-及P t (NH 3)2B r 2的几何对称性为D 2h ,请以[P t C l 2B r 2]2-为对象, 给出其中的八个对称操作, 并将中心原子的原子轨道:{s , p x ,p y ,p z ,d z 2, d x 2-y 2,d xy ,d xz ,d yz }按D 2h 不可约表示分类;若按D 2h 的子群D 2分类, 结果又如何?(提示:参考特征标表)解:D 2h 的八个对称操作为 I, C 2(x ), C 2(y ), C 2(z ), i , σ(xy ), σ(yz ), σ(zx ). 特征标表为:s 轨道在所有对称操作下不变, 属于全对称表示A g .p x 轨道在I,C 2(x ), σ(xy ), σ(zx )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 1u .p y 轨道在I,C 2(y ), σ(xy ), σ(yz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于p xp yp z原子p x , p y , p zdx 2-y 2dxz dz2原子ddxydyzB 2u ;p z 轨道在I, C 2(z ), σ(xz ), σ(yz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 2u ;d z 2, d x 2-y 2轨道在在所有对称操作下不变, 属于全对称表示A g ;d xy 轨道在I,C 2(z ), i ,σ(xy )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 3g ;d xz 轨道在I,C 2(y ),i , σ(xz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 2g ; d yz 轨道在I,C 2(x ),i , σ(yz )等四个对称操作下不变, 在其余四个对称操作下反号. 属于B 1g .若按D 2群分类, 所有不可约表示将不再按对称性分为 “g ” 和 “u ”, 其它与群D 2h 下的结果相同.3. 顺式四配位配合物c -MA2B2也是平面构型, 它属于什么点群? 请将中心原子的9个价原子轨道按这一点群分类. 解: 平面构型的顺式四配位配合物c -MA2B2属于C 2v 点群.本题可以采用上题同样的分析方法得到各原子轨道所属的不可约表示, 也可参见表5.1所给出的每一个不可约表示的基函数的性质, 直接得到分类结果: s , p z , d z 2, d x 2-y 2属于A 1; d xy 属于A 2; p x , d xz 属于B 1; p y , d yz 属于B 2.4. 请应用中心原子轨道为基的旋转操作的特征标公式(7-10)式,检验表7.2所列特征标数值是否正确无误; 然后由(4-40)式求出各原子轨函(l =0,1,2,3,4)在O h 配位场的约化(分裂)结果.解:根据(7-10)式, 角量子数为l 的原子轨道在绕z 轴旋转角度a 的旋转操作作用下, 特征标为:2s i n)21s i n ()(αααχ+=l ls 轨道, l =0, 12sin 21sin2sin)210sin()(==+=αααααχl,即对于所有不可约表示,特征表皆为1.p 轨道, l =1, 2sin23sin 2sin)211sin()(αααααχ=+=l所以, 321cos2123cos 23lim 21sin23sinlim)(00=⋅⋅=⋅⋅=→→ααααχααI l12121s i n2123s i n)(,03221s i n3223s i n)(,12s i n 23s i n )(432====-==ππχππχππχC C C l l l,说明表7.2中关于s , p 的两行特征标的值是正确的. 关于d , f , g 的特征标的计算过程略. 下面以f 轨道为例, 求解其在O h 群下的分裂.由于f 轨道属于 “u ”类, 所分裂出的不可约表示也将属于“u ”类,)]1(13)1(16)1(16118711[241)()(24111=-⨯⨯+-⨯⨯+-⨯⨯+⨯⨯+⨯⨯==∑R R n l RA Auuχχ1)]1(13)1()1(6)1()1(6118711[241)()(24122=-⨯⨯+-⨯-⨯+-⨯-⨯+⨯⨯+⨯⨯==∑R R n l R A Auuχχ)]1(23)1(06)1(061)1(8721[241)()(241=-⨯⨯+-⨯⨯+-⨯⨯+⨯-⨯+⨯⨯==∑R R n l RE E uuχχ1)]1()1(3)1(16)1()1(6108731[241)()(24111=-⨯-⨯+-⨯⨯+-⨯-⨯+⨯⨯+⨯⨯==∑R R n l RT Tuuχχ1)]1()1(3)1()1(6)1(16108731[241)()(24122=-⨯-⨯+-⨯-⨯+-⨯⨯+⨯⨯+⨯⨯==∑R R n l RT Tuuχχ所以f 分裂为A 2u +T 1u +T 2u .同样方法可以计算s , p , d , g 在O h 群下的分裂情况.5. 在四方配位场中, 中心原子能级(l =0, 1, 2, 3)将按D 4h 群的不可约表示类别约化(分裂)为s =a 1g , p =a 2u +e ud =a 1g +b 1g +b 2g +e g ,f =b 1u +a 2u +b 2u +2e u请按子群D 4计算各类旋转操作的特征标,证明以上结果.(提示:根据D 4h 及D 4特征标表, 仿照题4的计算处理.)解:s , p , d , f 轨道在D 4下的特征标利用(7-10)式计算得到:在D 4中约化得,Γ(s ) =a 1, Γ (p )=a 2+eΓ (d )=a 1+b 1+b 2+e , Γ (f )=b 1+a 2+b 2+2e在D 4h 中考虑原子轨道的 “g ”, “u ”对称性得:Γ (s )= a 1g , Γ (p )= a 2u +e uΓ (d )= a 1g +b 1g +b 2g +e g , Γ (f )= b 1u +a 2u +b 2u +2e u6. 当八面体场很强时, 单电子态(轨函)需按O h 群不可约表示分类, 请问组态 s 2, s 1p 1及p 2应如何表示, 相应的谱项是什么?解: 首先根据表7.2中所列s , p 轨道的特征标求出上述直积表示的O 群各操作的特征标为.再利用O 群的特征标表造出投影算符, 计算上述可约表示的约化结果. 最后得到,Γ(s2)=A1, Γ(s1p1)=T1, Γ(p2)=A1+T1+T2根据s, p轨道的“g”, “u”对称性, 再利用对称性, g×g=g, g×u=u, u×u=g, 就得到在O h 群下的约化结果:Γ(s2)=A1g, Γ(s1p1)=T1u, Γ(p2)=A1g+T1g+T2g7.[VC l6]2-的光谱吸收位置在13800c m-1, [VF6]2-的吸收峰在20120c m-1,请根据配位场理论指认它们属于何种谱项之间的跃迁: 2S+1Γ(基态)→ 2S+1Γ(激发态); 并计算出相应的∆值. 解: [VC l6]2-和[VF6]2-中, 中心原子V的d电子组态为3d1, 基态的对称性属于2t2g,激发态为2e, 光谱项反映从2t2g到2e g的跃迁.g由于上述体系中只有一个d电子,计算组态能量时不涉及库仑积分J和交换积分K, ∆值就是吸收光谱的光子能量: [VC l6]2- ∆值为13800c m-1, [VF6]2- ∆值为20120c m-1.8.正八面体三价钒配离子在可见紫外区有两个吸收峰,数据收集如下(单位:c m-1)[V(CN)6]3-22 200, 28 600;[V(NCS)6]3-16 700, 24 000;[VF6]3-14 800, 23 000;[VC l6]3-11 200, 18 020;请根据弱场方案指认, 求出∆, 排出光谱化学序列; 若采用强场方案, 指认应作何种变动? 解: 上述体系中心原子V的d的组态为d2, 基态谱相为3T1g,, 可见光区的低能量谱带属于3T→3T2g跃迁. 根据弱场方案, 3T1g,3T2g的谱项能量(在表7.4中给出), 以∆为单位分别为1g(-3/5, 1/5), 故上述体系的∆值为低能量谱带的能量乘以(5/4). 分别计算为:[V(CN)6]3-27 750;[V(NCS)6]3-20 870;[VF6]3-18 500;[VC l6]3-14 000.光谱序列为CN- > NC S> F-> C l-.若按强场方案, 3T1g,3T2g的谱项能量能量差即为∆.无需乘以系数(5/4), 所指认光谱化学序列不变.9.请按弱场方案(表7.4和图7.6( c)) ,指认下列光谱数据(单位:c m-1, 求出∆, 排出光谱化学序列.[V(H2O)]2+12 350, 18 500; [V(NCS)6]4-15 500, 22 000; [VC l6]4-7 200, 12 000; [V(NH3)6]2+14 800, 21200; [V(CN)6]4-22 300, 27 700.解:上述体系中心原子V的d的组态为d3, 基态谱相为4A2g,, 可见光区的低能量谱带属于4A→4T2g跃迁. 根据弱场方案, 4A2g,4T2g的谱项能量(在表7.4中给出), 以∆为单位分别2g为(-6/5, -2/5), 故上述体系的∆值为低能量谱带的能量乘以(5/4). 分别计算为:[V(H2O)]2+15 438; [V(NCS)6]4-19 375; [VC l6]4-9 000;[V(NH3)6]2+18 500; [V(CN)6]4-27 875.光谱序列为: CN- > NCS-> NH3 > H2O > C l-.10.请根据7.3.3的简单方法, 求出d5八面体配合物的高自旋和低自旋的能量差. 已知[F e(H2O)6]3+是高自旋, 你能否确定[F e(CN)6]3-究竟是高自旋还是低自旋?解: d5八面体配合物的高自旋组态为(t2g3e g2), 低自旋组态为(t2g5),E(t2g3e g2)=5E0+3(-2/5)∆+2(3/5)∆+10J-10K=5 E0+10J-10KE(t 2g 5)=5E 0+5(-2/5)∆ +10J -4K=5 E 0- 2∆ +10J -4K 两者能量差为E(t 2g 3e g 2) - E(t 2g 5)=2 ∆-6K.由于CN -在光谱化学序列中排在H 2O 的前面, [F e (CN)6]3-的∆要比[F e (H 2O)6]3+的大, 故如果[F e (H 2O)6]3+是高自旋, 则[F e (CN)6]3-一定是高自旋.11. 请通过你的计算, 检验表7.8的d 6与d 7八面体配合物的高自旋和低自旋能量即δ表示式. 解: d 6八面体配合物的高自旋组态为(t 2g 4e g 2), 低自旋组态为(t 2g 6),E(t 2g 4e g 2)=6E 0+4(-2/5)∆+2(3/5)∆+15J -10K=6 E 0-( 2/5) ∆ +15J -10K E(t 2g 6)=6E 0+6(-2/5)∆ +10J -6K=6 E 0-(12/5)∆ +15J -6K两者能量差为E(t 2g 4e g 2) - E(t 2g 6)=2 ∆-4K. d 7八面体配合物的高自旋组态为(t 2g 5e g 2), 低自旋组态为(t 2g 6 e g 1),E(t 2g 5e g 2)=7E 0+5(-2/5)∆+2(3/5)∆+21J -11K=7 E 0-(4/5) ∆ +21J -11K E(t 2g 6 e g 1)=7E 0+6(-2/5)∆ +(3/5)∆+21J -9K=7 E 0-(9/5)∆ +21J -9K 两者能量差为E(t 2g 4e g 2) - E(t 2g 6)= ∆-2K.12. 五配位配合物有两种稳定几何构型(图7.11(a )与(b)), 请根据图7.10中D 3h 和C 4v 能级模式讨论d 6离子为高自旋或低自旋的可能性.解: 由图7.10中所示的d 轨道在D 3h 和C 4v 下的能级分裂的情况容易判断, 在具有D 3h 对称性的双三角锥型配合物种d 6离子为高自旋, 而具有C 4v 对称性的四方锥型配合物种d 6离子为低自旋. 轨道电子填充情况如图所示:13. 在八面体配离子的J ahn -T eller 形变(O h -D 4h )中, 试简单地采用能级图7.12来分析预测, [VC l 6]2- (d 1), [VC l 6]3- (d 2), 和 [C r C l 6]4- (d 4) 的形变模式: 拉长还是压扁? 解:[VC l 6]2- (d 1) 根据图7.12, 若实现拉长形变, 一个电子填充在能量最低的e g 能级上, 总能量降低δ1/3; 若实现压扁形变, 一个电子填充在能量最低的b 2g 能级上总能量降低2δ1/3.从能量的角度看, 应当是压扁形变.[VC l 6]3-(d 2) 若实现拉长形变, 2个电子填充在能量最低的e g 能级上, 总能量降低2δ1/3; 若实现压扁形变, 2个电子填充在能量最低的b 2g 能级上总能量降低4δ1/3.从能量的角度看, 应当是压扁形变. 而且, 若实现拉长形变, 两个填充在能量最低的e g 能级上, 两个电子当取自旋相同的构型, 这样的体系仍是不稳定的还会发生畸变.[C r C l 6]4- (d 4) 若实现拉长形变, 4个电子填充在能量最低的e g 能级上, 总能量降低4δ1/3; 若实现压扁形变, 2个电子填充在能量最低的b 2g 能级上, 另2个电子填充在e g 能级上, 两者的能量升高与降低相抵, 总能量降低2δ1/3. 从能量的角度看, 应当是拉长形变.D3hC 4v14. 按照分子轨道的观点, 正八面体配离子的价电子数等于12+n, n为d电子数. 试由能级图7.15给出[VC l6]2- , [VC l6]3- , [C r C l6]4- , [F e(CN)6]3-,[C o(NH3)6]3+ ,[C o(CN)6]4-, [Ni(H2O)6]2+的基组态.解: 根据能级图7.15,所给出的能级序列, 计算出价电子数后, 可以直接得到基组态.现计算如下:n价电子数基组态[VC l6]2- 1 13 (a1g)2(t1u)6(e g)4(t2g)1[VC l6]3- 2 14 (a1g)2(t1u)6(e g)4(t2g)2[C r C l6]4- 4 16 (a1g)2(t1u)6(e g)4(t2g)4[F e(CN)6]3- 5 17 (a1g)2(t1u)6(e g)4(t2g)5[C o(NH3)6]3+ 6 18 (a1g)2(t1u)6(e g)4(t2g)6[C o(CN)6]4-7 19 (a1g)2(t1u)6(e g)4(t2g)6(e g*)1[Ni(H2O)6]2+ 8 20 (a1g)2(t1u)6(e g)4(t2g)6(e g*)215. 在正八面体配合物的能级序列(图7.15)中, t2g是非键轨道, e g*也可以近似看作非键(d z2,d x2-y2)分子轨道,因此, t2g→e g*的电子跃迁属于中心原子d→d跃迁, 不会伴随M,L之间的电荷转移;但下列跃迁: t2g→a1g*, e g*→t1u*以及e g→t2g, t1u→t2g将伴随电荷转移. 请分别指出它们之中那些属于M→L转移, 那些属于L→M的转移.解:判断电荷跃迁的方向主要根据所涉及的两个分子轨道的组成成分来判断.t2g, e g*是非键轨道, 基本由中心原子的d轨道组成. 电子由它们向其它分子轨道跃迁, 将导致M→L转移, 如t2g→a1g*, e g*→t1u*;t1u, e g是成键轨道,主要由配体原子的轨道组成. 电子由它们向其它分子轨道跃迁, 将导致L→M的转移. 如e g→t2g, t1u→t2g.16.请列举出10个单核配合物满足18电子规则, 再举出5个反例,它们均具有稳定的闭壳组态,表现为反磁性.解:满足18电子规则的例子有:[C o(NH3)6]3+,[C o(H2O)6]3+,[C o(CN)6]3-,[Zn(NH3)4]2+[F e(CN)6]4-,[F e(NCS)6]4-F e(CO)5, Ni(CO)4, F e(C5H5)2, C r(C6H6)2.不满足18电子规则的例子有:[Ni(C5H5N)4]2+, [Cu(NH3)4]2+,17.对于正四面体配合物ML4, [TiC l4, [NiC l4]2-等, 请通过群论方法,造出能级图; 指出与CH4的区别何在?解: 四个配体的轨道在T d群下分解为A1+T2, 若将四个配体原子按图5.7的CH4分子中的H原子的位置放置于立方体的相对的四个顶点, 中心原子按C原子的位置放置于立方体的中心. 造出配体的群轨道同5-8b式,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛------=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛d c b a zy z t t t a 212121212121212121212121212121212221φφφφ中心原子的轨道按对称性分类为s 属于A 1, p 属于T 2, d z 2, d x 2-y 2属于E, d xy ,d yz ,d xz 属于T 2.上述中心原子的轨道按对称性与配体原子的群轨道组合成分子轨道 能级示意图为:与CH 4相比, 中心原子除了s , p 轨道外, 还有d 轨道参加成键. HOMO -LUMO 的能隙变得很小. 从而导致可见光区的吸收光谱带的出现.配体轨道中心离子轨道配合物分子轨道3t。

第七章一选择题1、KCI属于NaCI型晶体，一个晶胞中含（个K+：■A 、1B 、2C 、4D 2、CH属于下列哪类分子点群：（a ）A、Td B D Oh C C3v D C S3、晶包一定是一个：（c ）A、八面体B六方柱体C、平行六面体D正方体4、（312）晶面在a，b，c轴上的截距分别为（c ）:A、3a, b, 2c B 3a, 6b, 2c C、2a, 6b, 3c D 3a, b, c5、空间点阵中下列形式不存在的是（b ）。

A 立方IB 四方C C 四方ID 正交C6、假设有一AB晶体，属于正交底心，每个晶胞中有两个A原子和2个B原子，若A原子的坐标是（000）,（1/2 1/2 0），一个B原子的坐标是（1/4 1/4 1/2），则另一个B原子的分数坐标应是（d ）。

A （1/2 1/2 0）B （1/2 0 1/2）C （1/2 1/2 1/2）D （3/4 3/4 1/2）7、根据正当单位选取原则，下列各组平面格子属于正当格子的组是（c ）。

（1）正方及其带心格子（2）六方及其带心格子（3）平行四边行及其带心格子（4）矩形及其带心格子A （1）⑶⑷B （1）（2）⑷54） D（1）（3）&下列说法正确的是（b ）.A. 凡是八面体配合物，一定属于O点群.B. 异核双原子分子一定没有对称中心•C. 凡是四面体构型分子，一定属于T d点群.D. 在分子点群中，对称性最低的是C,对称性最高的是O群9、空间点阵中下列形式不存在的是（b ）A. 立方IB. 四方CC. 四方ID. 正交C10、有一AB型晶体，属立方晶系，每个晶胞中有一个A和四个B, —个A的坐标是（—，丄，—），四个B的坐标分别是（0，0，0），（—，—，0），（丄，2 2 2 2 2 2 0，1），21 1（0，-，—），此晶体的点阵形式是（b ）2 212. 下列哪一种表述是正确的：（A ）A. 各向异性是晶体区别于非晶体的一种特性.B. 各向同性是晶体区别于非晶体的一种特性.C.晶体的所有性质都是各向异性的.13. 晶胞的两个基本要素是（A ）A. 晶胞的大小、形状及晶胞中原子的位置.B. 晶胞的质量及结构基元数目.C. 晶胞中原子的数目及位置.14. 由正当晶胞抽象出的格子必然是（A ）A.对称性最高. B. 包含点阵点最少. C. 正方体格子.15. 素晶胞是 （B ）A. 只包含一个原子的晶胞.B. 只包含一个结构基元的晶胞.C.只有一种宏观对称元素的晶胞.16.一个点阵点必然对应着晶体中的一个（C ）A.原子 B. 分子 C.结构基元17. 点阵是： （B ）A. 按连接其中任意两点的向量平移而能复原的有限个点 .B. 按连接其中任意两点的向量平移而能复原的无限多个点 .C.按连接其中某些特定点的向量平移而能复原的无限多个点 .18. 干冰是CO 的晶体,其中不被周期性相联系的是（C ）A. 一个结构基元与另一个结构基元.B. 一个晶胞与另一个晶胞.C. CQ 分子中的一个原子与另一个原子.A.立方IB.立方PC. 立方FD. 立方C11、已知配合物MAB 的中心原子 些异构体分别属于的点群是（ M 是d 2SF 3杂化，该分子有2种构造异构体，这 a ） A. C 2V , D 4hB. C 2h , D 4dC.C 3V ,D 6h D.C 3h ,D 6d19 .对于金刚石与立方硫化锌，下列哪种说法是不正确的：（C ）A. 它们的点阵型式都是立方面心.B. 它们的结构基元都包含两个原子（或离子）.C. 它们的结构基元内容相同•20. MgS （NaCI型）与UO （CaF2型）晶体的不同之处是：（B ）A. 正当格子形状•B.负离子堆积方式•C.点阵型式.21 .正、负离子配位比为8 : 8的是下列哪一种晶体：（A ）A. CsCIB.NaCIC. 立方ZnS22 . CeO晶体结构属CaF2型.对于这种晶体，“简单立方” 一词描述的是（A ）A. 氧负离子堆积方式.B.铈正离子堆积方式.C.点阵型式23. 有人把CaF2晶体的点阵型式误认为是点阵点处于负离子位置的立方简单点阵,错误之处就在于（B）A. 立方简单本身违反点阵定义.B. 这种立方简单无法使CaF2晶体复原.C. 这样的立方简单格子比CaF2正当晶胞还要大.24. 当我们说某种离子晶体AB属于CsCI型时，意思是说（B ）A. 它由Cs和CI两种元素组成.B. 它的结构型式与CsCI晶体相同.C. 它的结构基元与CsCI晶体相同.25. 布拉维格子有多少种：（A ）A. 14B. 7C. 3226. 计算立方ZnS正当晶胞中正、负离子总数的算式是：（A ）A. （1/8）X 8 +（1/2）X 6 +4B. （1/8）X 8 +（1/2）X 6C. 8 + 6 + 427. 在A（立方面心）、A（立方体心）、A（金刚石型）三种金属结构中，晶胞边长与原子半径分别与下列三个关系式3a = 4r, 2a= 4r, •• 3a = 8r相符合的是：（B ）A. A 1 A2 A 4B. A2 A1 A 4C. A4 A 1 A28. 从点阵中一个指定的原点到点阵点mnp之间的向量为平移群T mnp=ma+nb+pc（m n、p为整数）,这两点之间的波程差为（A ）A. △ =(mh+nk+pl)入B. △ =(m+n+p)入C. △ =（hx+ky+lz）入（x、y、z 为分数）29. 金单晶为A i型结构（立方面心），每个正当晶胞中原子数、八面体空隙数、四面体空隙数分别为：（C ）A. 1 、1、2B. 2 、2、4C. 4 、4、830. KBr晶体具有立方面心点阵,负离子形成立方最密堆积，其中的正八面体空隙全部被正离子占据.其结构型式为：（A ）A. NaCl 型B.CsCI 型C. 立方ZnS型31. 立方体心点阵的系统消光规律是：（A ）A. h+k+l=奇数B. h+k+l= 偶数C. h 、k、丨奇偶混杂32. 立方底心格子不存在，是由于这种格子（B ）A. 可化为立方体心.B. 破坏了立方晶系的特征对称要素.C. 违反了点阵定义33. 对于二元离子晶体,下列哪一式不成立：（C ）A. n+/n -=Z/Z +B. n-/n += CN/CMC. Z-/Z+=CN/CN!34. HMO 理论适用于处理哪一种体系：（B ）A. c体系B. n体系C. er + n体系35. 轨道对称守恒原理表明,在加热条件下发生顺旋电环化反应的共轭烯烃衍生物具有的n电子数为（A ）A. 4n.B. 4n+2.C. 5n+1.36. 六方晶系的晶胞形状是（C ）A. 六棱柱.B.六个顶点的八面体.C. a = B =90o, 丫=120°的平行六面体37. 晶面与x、y、z轴分别相截于2、3、4,其晶面指标为（C ）A. （234）B. （432）C. （643）38.通过晶胞原点与晶胞中第j 个原子(坐标为为、力、乙)的波程差为(A ) A. △ = (hx j +ky j +lz j )入 B. A = (ax j +by j +cz j )入C. A = (x j +y j +Z j )入39. 由布拉格(Bragg)方程可知,衍射级数n 是(A )A. 数目有限的几个正整数.B. 数目无限的一系列正整数.C. 数目有限的、介于0至1之间的几个分数.40. A 1与A 金属晶体在哪方面不同：(C )A.配位数. B. 空间占有率. C. 点阵型式.41. 离子晶体中正离子配位数 CN 等于6时，离子半径比(r +/r -)的理论值应是44. 下列哪种物质最不可能是晶体(B)A •金刚石B •琥珀C•食盐粉末45. 晶系和晶体学点群各有多少种？ (A) A. 7 种晶系,32种晶体学点群 B. 14 种晶系,32种晶体学点群 C. 7种晶系,14种晶体学点群46. 下列哪一式是晶体结构的代数表示一一平移群： (A)A. T mnp =mc+nb+pc ( m n, p,=0, ± 1, ± 2, ................... )B. r = xa+yb+zcx , y , z 是零或小于1的分数47. 下列哪一种说法是错误的：（B ） A.属于同一晶系的晶体，可能分别属于不同的晶体学点群A. 0.225 < (r +/r J<0.414B. 0.414 < (r +/r -)<0.732C. 0.732 < (r +/r -)<1.00042、 与C 轴垂直的晶面的晶面指标是( (A ) (112)(B ) (100)43、 反式二氯乙烯所属点群为(c(A ) C 3 ( B ) D 3dd )(C ) (010)( D )(001) )C . △ =(mh+ nk+pl)入m n , p和h , k , l均为整数B. 属于同一晶体学点群的晶体，可能分别属于不同的晶系C. 属于同一晶体学点群的晶体，可能分别属于不同的空间群48. 某平面点阵在坐标轴x,y,z上的截数为3，3，5，则平面点阵指标（晶面指标）为（C）A. （335）B. （353）C. （553）49. Bragg方程中的正整数n的物理意义是（A）A.相邻平面点阵衍射波程差的波数B•晶胞中结构基元的数目C•晶胞中原子的数目50. 立方ZnS和六方ZnS晶体的CN/CN都是4:4，那么，它们在下列哪一点上不同？（C）A. 正离子所占空隙种类B. 正离子所占空隙分数C. 负离子堆积方式51. 为了区分素格子与复格子，空间格子中的每个顶点、棱心、面心只分别算作（B）A. 1, 1, 1B. 1/8, 1/4, 1/2C. 1, 1/2, 1/452. CuZn合金（即B黄铜）中两种金属原子的分数坐标分别为0, 0, 0和1/2，1/2，1/2。

第二章原子结构与原子光谱赖才英070601319 何雪萍070601319 陈小娟070601319陈杉杉070601316 肖丽霞070601318 王水金0706013471.n、l、m三个量子数的取值范围、相互关系与物理意义。

取值范围及相互关系：n=1、2、3……共n个l=0、1、2……n-1共n个m=0、±1、±2……±l共2l+1个物理意义：主量子数n决定体系能量的高低、对单电子原子：En=-μe2/8ε2h2*Z2/n2=-13.6Z2/n2(eV)角量子数l决定电子的轨道角动量绝对值|M|=l*(l+1) *h/2π磁量子数m决定电子的轨道角动量在磁量子数方向上的分量Mz：Mz=m*h/2π2．为什么P+1与P-1不是分别对应Px与Py?答：决定复波函数的三个量子数都是确定的，可以用两种方式表示。

实波函数Ψnl| m|的磁量子数仅对应| m|，波函数中既有+| m|的成分又有-| m|的成分。

说明仅在m=0时，复波函数和实波函数是一致的，在m≠0时，是一组复波函数对应于一组实波函数，而不是一一对应的关系。

3.如何由氢原子空间波函数确定轨道的名称,求出En、|M|与Mz等力学量的确定值或平均值。

氢原子空间波函数为：ψ1、0、0=1/π*(Z/a)3/2*e-zr/a=1/π*(1/a)3/2*e-r/a∵n=1、l=0、m=0∴轨道名称应是：1S 此时En=-13.6*Z2/n2（eV）=-13.6ev∵|M|=l*(l+1) *h/2π=0Mz= m*h/2π=04.研究多电子原子结构碰到什么困难？作了那些近似？用了什么模型？答：困难：多电子原子中存在着复杂的电子间瞬时相互作用,其薛定谔方程无法进行变数分离，不能精确求解；多电子原子中存在能级倒臵，一般用屏蔽效应和钻穿效应解释，但是由于这两个效应都是定性的效应，相互又是关联的，所以，定量地解释能级倒臵的原因较为困难；用SCF法似乎解决了问题，但实际上方程仍无法求解，因为解方程需知ψj,而ψi也是未知的.近似:完全忽略电子间的排斥势能即零级近似;体系近似波函数;体系近似总能量;中心势场是近似的球对称势场;在SCF法中,每个电子的运动与其他电子的瞬时坐标无关,即在多电子原子中,每个电子均在各自的原子轨道上,彼此”独立”地运动.模型:中心势场模型是将原子中其他电子对第i个电子的排斥作用看成是球对称的，只与径向有关的力场。

《结晶学基础》习题目录第7章------------------------------------------------------------------------------1第8章----------------------------------------------------------------------------14第9章----------------------------------------------------------------------------20第10章--------------------------------------------------------------------------28《结晶学基础》第七章习题7001 试说明什么是单晶？什么是多晶？7002 有一AB晶胞，其中A和B原子的分数坐标为A(0，0，0)，B(1/2，1/2，1/2)，属于：------------------------------------ ( )(A) 立方体心点阵(B) 立方面心点阵(C) 立方底心点阵(D) 立方简单点阵7004 从CsCl 晶体中能抽出________点阵，结构基元是________，所属晶系的特征对称元素是________。

7005 某AB 型晶体属立方ZnS 型，请回答下列问题：(1) 从该晶体中可抽取出什么空间点阵？(2) 该晶体的结构基元为何？(3) 正当晶胞中含有几个结构基元？(4) 应写出几组B 原子的分数坐标？(5) 晶胞棱长为a，求在C3轴方向上A—A 最短距离；(6) 晶胞棱长为a，求在垂直C4轴的方向上B-B 最短距离。

7007 有一个A1 型立方面心晶体，试问一个立方晶胞中可能含有多少个A 和多少个B。

7010 点阵参数为432 pm的简单立方点阵中，(111)，(211)和(100)点阵面的面间距离各是多少？7011 从某晶体中找到C3，3C2，σh，3σd等对称元素，该晶体属________晶系是_____点群。

第7章 配位聚合
3．
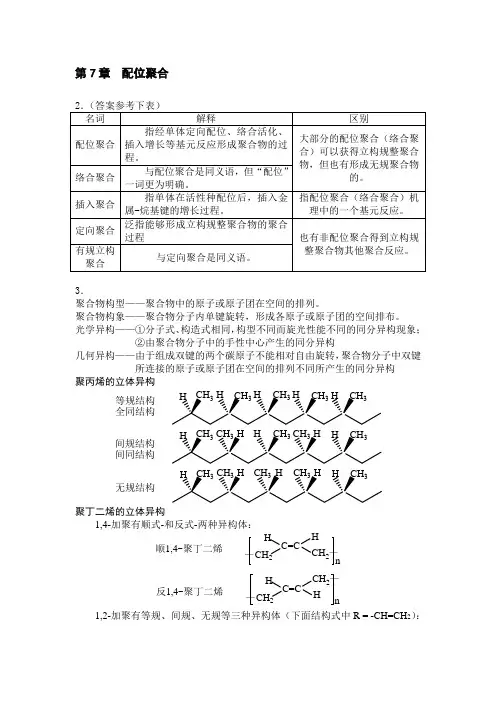
聚合物构型——聚合物中的原子或原子团在空间的排列。

聚合物构象——聚合物分子内单键旋转，形成各原子或原子团的空间排布。

光学异构——①分子式、构造式相同，构型不同而旋光性能不同的同分异构现象；
②由聚合物分子中的手性中心产生的同分异构
几何异构——由于组成双键的两个碳原子不能相对自由旋转，聚合物分子中双键
所连接的原子或原子团在空间的排列不同所产生的同分异构
聚丙烯的立体异构
等规结构全同结构
间规结构间同结构
无规结构
聚丁二烯的立体异构
1,4-加聚有顺式-和反式-两种异构体：
C=C H —CH 2
CH 2—n H
顺1,4-聚丁二烯
C=C
H
—CH 2
CH 2—n H
反1,4-聚丁二烯
1,2-加聚有等规、间规、无规等三种异构体（下面结构式中R = -CH=CH 2）：
等规结构全同结构
间规结构间同结构
无规结构
4．（答案参考P184~185） 5．解：
① 在特定的引发剂和必须的聚合条件下，能够发生配位聚合、生成有规立。

第一章 量子力学基础一、单选题： 1、32/sinx l lπ为一维势箱的状态其能量是：（ a ） 22229164:; :; :; :8888h h h hA B C D ml ml ml ml 2、Ψ321的节面有（ b ）个，其中（ b ）个球面。

A 、3 B 、2 C 、1 D 、03、立方箱中2246m lh E ≤的能量范围内,能级数和状态数为( b ). A.5,20 B.6,6 C.5,11 D.6,174、下列函数是算符d /dx的本征函数的是：（ a ）；本征值为：（ h ）。

A 、e 2x B 、cosX C 、loge x D 、sinx 3 E 、3 F 、-1 G 、1 H 、2 5、下列算符为线性算符的是：（ c ）A 、sine xB 、C 、d 2/dx 2D 、cos2x6、已知一维谐振子的势能表达式为V = kx 2/2，则该体系的定态薛定谔方程应当为（ c ）。

A [-m 22 2∇+21kx 2]Ψ= E ΨB [m 22 2∇- 21kx 2]Ψ= E Ψ C [-m 22 22dx d +21kx 2]Ψ= E Ψ D [-m 22 -21kx 2]Ψ= E Ψ 7、下列函数中，22dx d ,dxd的共同本征函数是（ bc ）。

A cos kxB e –kxC e –ikxD e –kx2 8、粒子处于定态意味着:（ c ）A 、粒子处于概率最大的状态B 、粒子处于势能为0的状态C 、粒子的力学量平均值及概率密度分布都与时间无关系的状态.D 、粒子处于静止状态9、氢原子处于下列各状态 (1)ψ2px (2) ψ3dxz (3) ψ3pz (4) ψ3dz 2 (5)ψ322 ，问哪些状态既是M 2算符的本征函数，又是M z 算符的本征函数?( c )A. (1) (3)B. (2) (4)C. (3) (4) (5)D. (1) (2) (5) 10、+He 离子n=4的状态有（ c ）（A ）4个 （B ）8个 （C ）16个 （D ）20个 11、测不准关系的含义是指（ d ） (A) 粒子太小，不能准确测定其坐标； (B)运动不快时，不能准确测定其动量(C) 粒子的坐标的动量都不能准确地测定； （D ）不能同时准确地测定粒子的坐标与动量12、若用电子束与中子束分别作衍射实验，得到大小相同的环纹，则说明二者（ b ） (A) 动量相同 (B) 动能相同 (C) 质量相同13、 为了写出一个经典力学量对应的量子力学算符，若坐标算符取作坐标本 身，动量算符应是(以一维运动为例) （ a ）(A) mv (B) i x ∂∂ (C)222x ∂-∂14、若∫|ψ|2d τ=K ，利用下列哪个常数乘ψ可以使之归一化：（ c ）(A) K (B) K 2 (C) 1/K15、丁二烯等共轭分子中π电子的离域化可降低体系的能量，这与简单的一维势阱模型是一致的， 因为一维势阱中粒子的能量 （ b ）(A) 反比于势阱长度平方 (B) 正比于势阱长度 (C) 正比于量子数16、对于厄米算符, 下面哪种说法是对的 （ b ）(A) 厄米算符中必然不包含虚数 (B) 厄米算符的本征值必定是实数(C) 厄米算符的本征函数中必然不包含虚数17、对于算符Ĝ的非本征态Ψ （ c ）(A) 不可能测量其本征值g . (B) 不可能测量其平均值<g >.(C) 本征值与平均值均可测量，且二者相等18、将几个非简并的本征函数进行线形组合，结果 （ b ）(A) 再不是原算符的本征函数(B) 仍是原算符的本征函数，且本征值不变 (C) 仍是原算符的本征函数，但本征值改变19. 在光电效应实验中，光电子动能与入射光的哪种物理量呈线形关系：( B )A .波长B. 频率C. 振幅20. 在通常情况下，如果两个算符不可对易，意味着相应的两种物理量( A)A ．不能同时精确测定B ．可以同时精确测定C ．只有量纲不同的两种物理量才不能同时精确测定 21. 电子德布罗意波长为(C )A ．λ=E /h B. λ=c /ν C. λ=h /p 22. 将几个非简并的本征函数进行线形组合，结果( Ａ ） A ．再不是原算符的本征函数B ．仍是原算符的本征函数，且本征值不变C ．仍是原算符的本征函数，但本征值改变23. 根据能量-时间测不准关系式，粒子在某能级上存在的时间τ越短，该能级的不确定度程度ΔE （Ｂ ）A ．越小 B. 越大 C.与τ无关24. 实物微粒具有波粒二象性, 一个质量为m 速度为v 的粒子的德布罗意波长为:A .h/(mv)B. mv/hC. E/h25. 对于厄米算符, 下面哪种说法是对的 ( B )A ．厄米算符中必然不包含虚数B ．厄米算符的本征值必定是实数C ．厄米算符的本征函数中必然不包含虚数 26. 对于算符Ĝ的非本征态Ψ (A ) A ．不可能测得其本征值g. B ．不可能测得其平均值<g>.C ．本征值与平均值均可测得，且二者相等 27. 下列哪一组算符都是线性算符：( C )A ． cos, sinB ． x, logC ． x d dx d dx,,22二 填空题1、能量为100eV 的自由电子的德布罗依波波长为( 122.5pm )2、函数：①xe ，②2x ，③x sin 中，是算符22dxd 的本征函数的是（ 1，3 ），其本征值分别是（ 1，—1；）3、Li 原子的哈密顿算符，在（ 定核 ）近似的基础上是:（()23213212232221223222123332ˆr e r e r e r e r e r e mH +++---∇+∇+∇-= ）三 简答题1. 计算波长为600nm(红光),550nm(黄光),400nm(蓝光)和200nm(紫光)光子的 能量。

第一章 8. )(10088.510593.5891031149811--⨯=⨯⨯==sc λν)(10093.510996.5881031149822--⨯=⨯⨯==scλν)(10696.110593.58911~16911--⨯=⨯==mλν)(10698.110996.58811~16922--⨯=⨯==mλν)(075.203101002.610088.510626.61323143411---⋅=⨯⨯⨯⨯⨯⨯==mol kJ h E ν )(275.203101002.610093.510626.61323143422---⋅=⨯⨯⨯⨯⨯⨯==molkJ h E ν9.)(2102νλυ-=chc m)(10130.8101.9)10464.510300103(10626.62)(215311498340----⋅⨯=⨯⨯-⨯⨯⨯⨯=-=sm mch m νλυ )(10398.710130.8101.9125531---⋅⋅⨯=⨯⨯⨯==s m kg m p m υ )(1096.810398.710626.6102534m ph ---⨯=⨯⨯==λ10. (1))(10626.601.01010626.6221034m m h ph ---⨯=⨯⨯===υλ(2))(1087.2106.11001067.1210626.6212193734m mTh ph ----⨯=⨯⨯⨯⨯⨯⨯===λ(3))(1075.2106.1102101.9210626.622121953134m meVh mTh ph ----⨯=⨯⨯⨯⨯⨯⨯⨯====λ11. 子弹：)(1063.6%10100001.010626.63434m m h x --⨯≥⨯⨯⨯=∆⋅≥∆υ 可忽略花粉：)(1063.6%1011010626.6201334m m h x ---⨯≥⨯⨯⨯=∆⋅≥∆υ可忽略电子：)(1027.7%1010101.910626.6963134m m h x ---⨯≥⨯⨯⨯⨯=∆⋅≥∆υ不能忽略只有不确定关系具有实际意义12. 证明：λ=∆x 因为h m x h p x x ≥∆⋅∆⇒≥∆∆υ υλυ==⋅=∆⋅≥∆m p m h xm h13. meV m eV 2212=⇒=υυυυ1.0=∆10001060219.11091095.021.010626.621.0193034⨯⨯⨯⨯⨯⨯==∆⋅≥∆---Vm h m h x e υ)(1088.310m -⨯= 对成像没有影响 若用π4h p x x ≥∆∆)(1009.311m x -⨯≥∆14.（1）imximxem edx d ⋅-=222)( 是 本征值：2m -（2）x x dx d sin )(sin 22-= 是 本征值：1-（3）2)(2222=+y x dx d 不是（4）)2(])[(22x a eex a dxd xx-+=--- 不是16. φφφφim im im meim iee d d i-=⋅= 是。

资料范本本资料为word版本，可以直接编辑和打印，感谢您的下载有机化学第7、8章习题答案地点：__________________时间：__________________说明：本资料适用于约定双方经过谈判，协商而共同承认，共同遵守的责任与义务，仅供参考，文档可直接下载或修改，不需要的部分可直接删除，使用时请详细阅读内容第7章芳烃及非苯芳烃思考题答案思考题7-1 苯具有什么结构特征? 它与早期的有机化学理论有什么矛盾?答案：苯分子具有高度的不饱和性，其碳氢比相当于同分子量的炔烃，根据早期的有机化学理论，它应具有容易发生加成反应、氧化反应等特性。

但事实上，苯是一种高度不饱和却具异常稳定性的化合物。

因此，要能够很好地解释这一矛盾是当时有机化学家所面临的重大挑战。

[知识点：苯的结构特征]思考题7-2早期的有机化学家对苯的芳香性认识与现代有机化学家对苯的芳香性认识有什么不同?答案：早期的有机化学把那些高度不饱和的苯环类结构并具有芳香气味的化合物称为芳香化合物，这些化合物所具有的特性具称为芳香性。

随着对事物认识的不断深入，人们已经意识到，除了苯环以外还有一些其他类型的分子结构也具有如苯一样的特别性质。

现在仍然迫用芳香性概念，但其内涵已超出了原来的定义范围。

现在对芳香性的定义为：化学结构上环状封闭的共轭大π键，不易被氧化，也不易发生加成反应，但是容易起亲电反应的性质。

[知识点：苯的芳香性]思考题7-3 关于苯分子的近代结构理论有哪些?其中,由Pauling提出的共振结构理论是如何解释苯分子结构?答案：现代价键理论：苯分子中的六个碳原子都以sp2杂化轨道和相邻的碳和氢原子形成σ键，此sp2杂化轨道为平面其对称轴夹角为120°，此外每个碳原子还有一个和平面垂直的p轨道，六个p轨道相互平行重叠形成了一个闭合共轭体系。

分子轨道理论：基态时，苯分子的六个π电子都处在成建轨道上，具有闭壳层电子结构。

离域的π电子使得所有的C-C键都相同，具有大π键的特殊性质因此相比孤立π键要稳定得多。

01.量子力学基础知识【1.1】将锂在火焰上燃烧，放出红光，波长λ=670.8nm ，这是Li 原子由电子组态 (1s)2(2p)1→(1s)2(2s)1跃迁时产生的，试计算该红光的频率、波数以及以k J·mol -1为单位的能量。

解：811412.99810m s 4.46910s 670.8m cνλ−−×⋅===× 41711 1.49110cm 670.810cm νλ−−===××%3414123-1 -16.62610J s 4.46910 6.602310mol 178.4kJ mol A E h N sν−−==×⋅××××=⋅【1.2】 实验测定金属钠的光电效应数据如下：波长λ/nm 312.5 365.0 404.7 546.1 光电子最大动能E k /10-19J 3.41 2.56 1.95 0.75 作“动能-频率”，从图的斜率和截距计算出Plank 常数(h)值、钠的脱出功(W)和临阈频率(ν0)。

解：将各照射光波长换算成频率,并将各频率与对应的光电子的最大动能E k 列于下表：v λ/nm 312.5 365.0 404.7 546.1v /1014s －19.59 8.21 7.41 5.49E k /10－19J 3.41 2.56 1.95 0.75 由表中数据作图，示于图1.2中E k /10-19Jν/1014g-1图1.2 金属的kE ν−图由式 0k hv hv E =+推知0k kE E h v v v Δ==−Δ即Planck 常数等于图的斜率。

选取两合适点，将和v 值带入上式，即可求出h 。

例如： k E −v k E ()()19341412.708.50 1.0510 6.601060010J h J s s −−−×==×−×图中直线与横坐标的交点所代表的即金属的临界频率，由图可知，。

结构化学练习（4-7章）第四章练习(1)I3和I6不是独立的对称元素，因为I3= ,I6= 。

(2)下列等式成立的是A S3=C3+B S3=C6+σhC S3=C3+iD S3=C6+i(3)如果图形中有对称元素S6，那么该图形中必然包含A C6, σhB C3,C C3,iD C6,i(4)下列说法错误的是A 分子中有S n轴，则此分子必然同时存在C n轴和σh。

B 反映面σd一定也是反映面。

C I4是个独立的对称元素。

D 分子既有C n轴又有垂直于C n轴的σh，此分子必有Sn轴。

(5)对称元素C2与σh组合得到，C n轴与垂直于它的C2轴组合可得到。

(6)写出如下点群所具有的全部对称元素及其对称操作:(1)C2h (2)D3 (3)C3i(7)已知配合物MA2B4的中心原子M是d2sp3杂化，该分子中有多少种构造异构体，这些异构体各属于什么点群。

(8)下列说法正确的是A 凡是八面体配合物一定属于Oh点群B 异核双原子分子一定没有对称中心C 凡是四面体构型分子一定属于Td点群D 在分子点群中，对称性最低的是C1，对称性最高的是Oh(9)下列分子具有偶极矩，而不属于C nv群的是A H2O2B NH3C CH2Cl2D H2C=CH2(10)下列各组分子中有极性，但无旋光性的是(1)N3- (2)I3- (3)O3A (1),(2)B (2),(3)C (1),(2),(3)D (3)(11)下列具有相同阶的分子是(1)B2H6 (2)BrCl5 (3)SiF4A (1),(2)B (2),(3) B (1),(3) D 都不同(12)下列分子的点群不是16个群元素的是A CCl4B XeO4C S8D Ni(CN)4(13)(1)SO42- (2)PO43- (3)ClO4-三者中不是T d点群的是A (1)B (2)C (3)D 都是T d点群(14)下列空格中打上“+”或“-”分别表示对与错。