热力学基础第1讲——热力学第一定律及其在理想气体等值过程中的应用

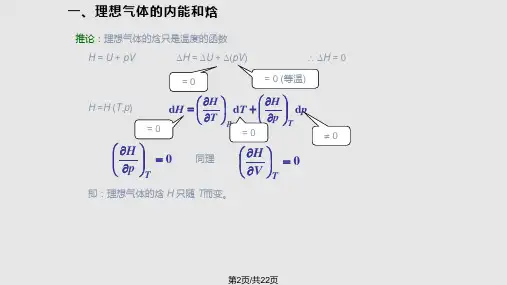
更高更妙的物理专题16热力学基础一、知识概要1、热力学第一定律对于理想气体等值过程的应用等容过程等容过程的特征是气体体积保持不变，V0，故W0，由热力学第一定律可知，在等容过程中，气体与外界交换的热量等于气体内能的增量：QEmimRTCVT。

M2MiR，i为分子的自由度，对于单原子分子气体，i3；对2于双原子分子气体，i5；而对于多原子分子气体i6。

R为摩尔气体常数，R8.31J/(molK)。

mRT，等压过程等压过程的特征是气体压强保持不变，p0，WpVMCV称做定容摩尔比热容，CV由热力学第一定律可得，在等压变化过程中气体与外界交换的热量为mimmi2mRTRTRTCpT。

M2MM2MCi2称为比热容比。

对于单原子分Cp称做定压摩尔比热容，CpCVR，而pCVi578子气体，；而双原子分子气体，；多原子分子气体则有CV、Cp及均356QEpV只与气体分子的自由度有关而与气体温度无关。

等温过程等温过程的特征是气体温度保持不变，T0，由于理想气体的内能取决于温度，故E0，由热力学第一定律可知在等温变化过程中气体与外界交换的热量为QW。

理想气体在等温变化中，pVCTmRT，设气体体积从V1膨胀到V2，压M强从p1减小到p2，所做的功为W，将这个功n（n）等分，每份元功VWCTW，两边取n次方得(Vi1Vi)，即i11nViVinCTV2WnWWTCT。

(1)(1)V1nCTnCTWWTCT当n时，lim(1)eCT，WnCT0nCTnCWWnCWV2mVpmRTln2RTln1，V1MV1Mp2Vpmm则QRTln2RTln1。

MV1Mp2WCTln绝热过程气体在不与外界发生热交换的条件下所发生的状态变化称做绝热过程，其特点是Q0，由热力学第一定律可得WE绝热过程中气体方程为pVmCVT。

MmRT，则对某一元过程有Mpi1Vi1pViipi1(Vi1Vi)Vi(pi1pi)而此元过程气体做元功为mR(Ti1Ti)；MmCV(TiTi1)，Mp(VVi)则有pi1(Vi1Vi)Vi(pi1pi)i1i1R(1)pi1(Vi1Vi)，CVVVipi1pi即有i10。

热力学第一定律对理想气体的应用
热力学第一定律（也称为能量守恒定律）对理想气体的应用提供了重要的物理洞察和计算方法。

以下是热力学第一定律在理想气体中的一些应用：
1.内能变化计算：热力学第一定律表明，理想气体的内能变化等于吸收的热量减去对外界做的功。

根据该定律，我们可以计算理想气体的内能变化，即ΔU = Q - W，其中ΔU 表示内能变化，Q 表示吸收的热量，W 表示对外界做的功。

2.等容过程计算：等容过程是指理想气体在体积不变的条件下发生的过程。

根据热力学第一定律，对于等容过程，ΔU = Q，即内能变化等于吸收的热量。

这使得我们可以根据所吸收的热量计算内能的变化。

3.等压过程计算：等压过程是指理想气体在恒定压力下发生的过程。

根据热力学第一定律，对于等压过程，Q = ΔU + W，即吸收的热量等于内能变化加上对外界所做的功。

这使得我们可以根据所做的功和内能变化计算吸收的热量。

4.等温过程计算：等温过程是指理想气体在恒定温度下发生的过程。

根据热力学第一定律，对于等温过程，Q = W，即吸收的热量等于对外界所做的功。

这意味着在等温过程中，吸收的热量和所做的功相等。

热力学第一定律热力学第一定律是热力学中最基本的定律之一，也被称为能量守恒定律。

它描述了能量在物质系统中的转化和守恒关系。

在本文中，我们将深入探讨热力学第一定律的原理和应用。

1. 热力学第一定律的原理热力学第一定律表明，一个系统的内能的增量等于吸热与做功之和。

简单来说，即能量的增加等于热量输入和功输入之和。

在一个封闭系统中，内能变化可以表示为ΔU = Q + W，其中ΔU表示内能变化量，Q表示吸热，W表示做功。

根据能量的守恒原理，一个系统的能量不会凭空消失或增加，而是转化成其他形式。

2. 热力学第一定律的应用热力学第一定律在各个领域都有广泛的应用。

以下是其中一些常见的应用场景：2.1. 理想气体的过程分析在理想气体的过程分析中，热力学第一定律被广泛应用于计算气体的工作、吸热和内能变化等参数。

根据热力学第一定律的原理，我们可以通过测量系统吸热和做功的量来计算内能的变化。

2.2. 热机效率的计算热力学第一定律也可用于计算热机的效率。

根据热力学第一定律原理，热机的效率可以表示为η = 1 - Q2/Q1，其中Q1表示热机输入的热量，Q2表示热机输出的热量。

通过计算输入和输出的热量可以确定热机的效率。

2.3. 化学反应的能量变化热力学第一定律也可用于描述化学反应的能量变化。

在化学反应中，热力学第一定律可以帮助我们计算反应的吸热或放热量，从而确定反应是否放热或吸热以及能量变化的大小。

3. 热力学第一定律在能源利用中的应用能源利用是热力学第一定律的一个重要应用领域。

通过研究能源的转化过程和能量损失，我们可以更有效地利用能源资源。

3.1. 热力学循环热力学循环是将热能转化为功的过程，如蒸汽轮机和内燃机。

通过分析热力学循环中各个环节的能量转化和损失，可以优化循环系统的效率，提高能源利用率。

3.2. 可再生能源利用热力学第一定律也可以应用于可再生能源的利用。

通过分析可再生能源的收集、转化和储存过程中的能量转化和守恒关系，可以优化利用这些能源的方式，减少能量的损失和浪费。

热力学第一定律及其应用------对理想气体的应用摘要：热力学第一定律是人们生产的理论基础，在此简要叙述热力学第一定律的相关概念及等温，等容，等压，绝热四个过程中功与能量的转化。

关键词：定义等温等容等压绝热热力学第一定律就是能量转化和守恒定律。

十九世纪中期，在长期生产实践和大量科学实验的基础上，它才以科学定律的形式被确立起来。

直到今天，不但没有发现违反这一定律的事实，相反的，大量新的实践不断地证明这一定律的正确性，扩充着它的实践基础，丰富着它所概括的内容。

从1840—1879年,焦耳用大量的、精确的科学实验结果论证了机械能和电能与热能之间的转化关系，他在各种实验中测定的热功当量数值的一致性，给能量转化和守恒定律奠定了不可动摇的基础。

然而，应该指出的是，在十八世纪末和十九世纪，许多国家的科学家都对这一定律的建立作出了一定的贡献。

这是由于当时的历史条件所决定的。

十八世纪初，纽可门制作的大规模把热变为机械能的蒸汽机已在英国煤矿和金属矿使用。

十八世纪后半叶，由瓦特作了重大改进的蒸汽机在英国炼铁业、纺织业广泛采用。

对热机效率以及机器中的摩擦生热问题的研究，大大促进了人们对于能量转化规律的认识。

与此同时，在其他领域内，也分别地发现了各种运动形式之间的相互联系和转化。

如1800年伏打化学电池的发明；1834年法拉第点解定律的发现；1820年奥斯特发现电流的磁效应；1831年法拉第发现电磁感应现象1822年塞贝克发现热电动势并制作出热电源；1840年焦耳发现电流热效应方面的焦耳定律；1840年法拉第还发现了光的偏振面磁致旋转现象。

所有这些，都使各种运动形式间相互联系和相互转化的辩证关系被充分地揭示出来。

正是在这种历史条件下，医生迈尔于1842年曾列举了25种相互转化的形式，并从空气的定压比热与定容比热之差算出了热功当量。

最后，由于焦耳的长期工作，建立了大量可靠的实验资料，能量转化和守恒定律才最终巩固地建立起来。

§2.2 热力学第一定律对理想气体的应用2．2．1、等容过程 气体等容变化时，有=T P 恒量，而且外界对气体做功0=∆-=V p W 。

根据热力学第一定律有△E=Q 。

在等容过程中，气体吸收的热量全部用于增加内能，温度升高；反之，气体放出的热量是以减小内能为代价的，温度降低。

p V i T C n E Q V ∆⋅⋅=∆⋅=∆=2 式中 R i T E v T Q C V ⋅=∆∆=∆=2)(。

2．2．1、等压过程气体在等压过程中，有=T V 恒量，如容器中的活塞在大气环境中无摩擦地自由移动。

根据热力学第一定律可知：气体等压膨胀时，从外界吸收的热量Q ，一部分用来增加内能，温度升高，另一部分用于对外作功；气体等压压缩时，外界对气体做的功和气体温度降低所减少的内能，都转化为向外放出的热量。

且有T nR V p W ∆-=∆-=T nC Q p ∆=V p i T nC E v ∆⋅=∆=∆2定压摩尔热容量p C 与定容摩尔热容量V C 的关系有R C C v p +=。

该式表明：1mol 理想气体等压升高1K 比等容升高1k 要多吸热8.31J ，这是因为1mol 理想气体等压膨胀温度升高1K 时要对外做功8.31J 的缘故。

2．2．3、等温过程气体在等温过程中，有pV =恒量。

例如，气体在恒温装置内或者与大热源想接触时所发生的变化。

理想气体的内能只与温度有关，所以理想气体在等温过程中内能不变，即△E =0，因此有Q=-W 。

即气体作等温膨胀，压强减小，吸收的热量完全用来对外界做功；气体作等温压缩，压强增大，外界的对气体所做的功全部转化为对外放出的热量。

2．2．4、绝热过程气体始终不与外界交换热量的过程称之为绝热过程，即Q=0。

例如用隔热良好的材料把容器包起来，或者由于过程进行得很快来不及和外界发生热交换，这些都可视作绝热过程。

理想气体发生绝热变化时，p 、V 、T 三量会同时发生变化，仍遵循=T pV 恒量。