角接触球轴承主曲率计算公式

角接触球轴承工作游隙计算角接触球轴承是一种常用的轴承类型，其特点是能够承受较大的径向和轴向载荷。

在角接触球轴承的工作过程中，游隙是一个重要的参数，它对轴承的运行性能和寿命有着直接的影响。

游隙是指轴承内圈和外圈之间的间隙，也可以理解为内圈和外圈的相对运动量。

角接触球轴承的游隙是通过调整内圈和外圈之间的间隙来实现的。

正确的游隙设置能够保证轴承在工作时具有适当的刚度和灵活性。

角接触球轴承的游隙计算是一个复杂的过程，需要考虑多个因素。

首先，我们需要确定轴承的类型和尺寸。

不同类型和尺寸的角接触球轴承具有不同的游隙范围。

其次，我们需要考虑轴承在运行时的工作温度和负载情况。

轴承在运行时会因为热胀冷缩而产生变形，这也会影响游隙的大小。

此外，轴承在承受负载时会有一定的弹性变形，这也需要考虑在游隙的计算中。

通常情况下，角接触球轴承的游隙可以通过下列步骤来计算。

首先，在确定轴承类型和尺寸后，可以参考轴承制造商提供的游隙范围表来初步选择游隙。

然后，根据轴承所在的工作温度和负载情况，通过查找相关的修正因子表，计算修正系数。

最后，将初步选择的游隙值与修正系数相乘，得到最终的游隙值。

在进行游隙计算时，需要注意以下几点。

首先，游隙的计算应该满足轴承的使用要求。

一般来说，游隙值越小，轴承的刚度越大，适合承受较大的负载。

但是，如果游隙值过小，可能会影响轴承的灵活性和运转平稳性。

因此，在选择游隙值时，需要综合考虑轴承的使用条件和性能要求。

其次，游隙的计算应尽量准确。

如果游隙值过大或者过小，都会对轴承的工作性能产生不利影响。

角接触球轴承的游隙计算对于轴承的工作性能和寿命具有重要的影响。

正确的游隙设置可以保证轴承在工作时具有适当的刚度和灵活性。

在进行游隙计算时，需要考虑轴承的类型和尺寸、工作温度和负载情况等因素，并参考相关的修正因子表进行计算。

游隙的选择要综合考虑轴承的使用条件和性能要求。

只有合理设置游隙，才能确保角接触球轴承的正常运行和长寿命。

角接触球轴承设计方法优化设计目前已有很多成熟的方法，对于维数不高的具有离散型变量的设计系统，用网格法来进行优化筛选是方便的，该方法将设计变量直接在标准值上进行离散，使设计空间成为一个网格系统，然后在每一个网点上进行约束检验与有关计算，从中可挑选出最佳点，如果将以往的设计经验作为参考点，则优化只需要在附近的局部空间中进行，这便是“局部网格法”的思想。

1主参数优化角接触轴承的优化设计原则是确定Dw、球数Z和球组中心圆直径Dwp 在满足一定约束条件下，使轴承的额定动载荷尽可能地大。

目标函数在充分保证轴承的使用性能的前提下，以轴承径向基本额定动载荷Cr 最大为目标函数。

根据GB/T6391的规定：当Dw≤25.4mm时，约束条件①球径约束：②球数约束：上式表明Kz随Dw的增大而减小，但应满足：Kz≥Kzmin根据设计经验和国外样品分析，可取对金属保持架bmin=1.5，Kzmin=1.11对胶木保持架bmin=1.9，Kzmin=1.134Kz值保持架结构示意图注：若②式不成立，则可按步长0.002（D+d）逐步增大Dwp值。

③球组中心圆直径约束为保证轴承套圈的最小壁厚不小于0.09（D-d），球组中心圆直径受下式约束：0.5（D+d）≤Dwp≤0.515（D+d）④K B ×Dw≤0.96B “C”型冲压保持架K B = 2.8Dw +1.12实体保持架K B=1.14Dw+1.202局部网格法2.1当已知轴承的外形尺寸内径d 、外径D 、宽度B 和公称接触角α（GB/T292）以后，根据设计经验确定球数、球径和球组中心圆直径Z 0，Dw 0，Dwp 0：Dwp 0=0.5（d+D），Dw 0=Kw＇（D-d），Z 0=π×Dwp 0Kz×Dw 0其中Kw＇按下表采用，Kz 按上面的表（Kz 值）采用。

Kw＇值直径系列123Kw＇0.30.310.3172.2将Z 和Dw 各取N 档数值（N 为奇数，一般为5或7），这样就构成一个N×N 的二维网格系统，每个网点的坐标Dwi 和Zj（i，j=1，2，3…，N）按下式取值：设常用钢球表中的每档球径为D Twk （K=1，2，…，M，其中M 为球径总数），将Dw 0与D Twk 按由小到大的顺序逐一进行比较，一旦Dw 0≤D Twk 成立，则停止比较，并记下此时的K 值，则3设计参数的研究一般的轴承设计，如果单纯追求轴承的额定动载荷能力，在限定的轴承横截面积内，一味加大钢球直径和增加球数是不现实的，必须对轴承进行精心的设计，在充分利用轴承横截面积的情况下，选择最佳的结构参数，改善轴承零件接触应力分布状态，采用有利于润滑油膜形成的最优接触形状，来提高轴承的使用性能和使用寿命。

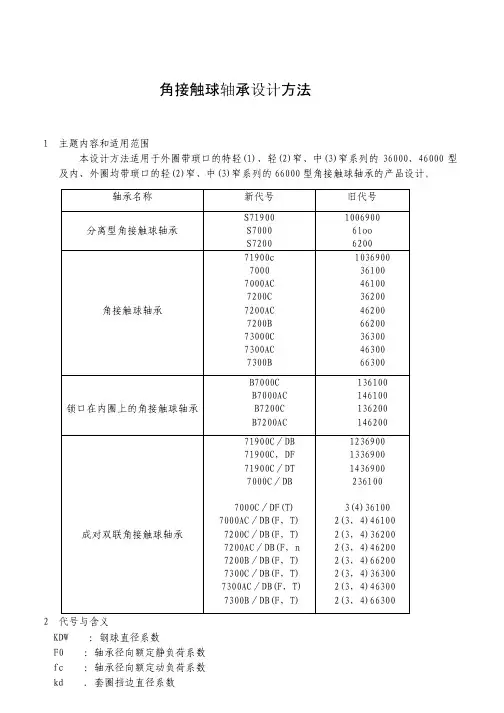
角接触球轴承设计方法1 主题内容和适用范围本设计方法适用于外圈带琐口的特轻(1)、轻(2)窄、中(3)窄系列的36000、46000型及内、外圈均带琐口的轻(2)窄、中(3)窄系列的66000型角接触球轴承的产品设计。

轴承名称 新代号 旧代号分离型角接触球轴承 S71900S7000S720010069006loo6200角接触球轴承 71900c70007000AC7200C7200AC7200B73000C7300AC7300B103690036l0046100362004620066200363004630066300锁口在内圈上的角接触球轴承B7000CB7000ACB7200CB7200AC136100146100136200146200成对双联角接触球轴承71900C／DB71900C，DF71900C／DT7000C／DB7000C／DF(T)7000AC／DB(F，T)7200C／DB(F，T)7200AC／DB(F，n7200B／DB(F，T)7300C／DB(F，T)7300AC／DB(F，T)7300B／DB(F，T)1236900133690014369002361003(4)361002(3，4)461002(3，4)362002(3，4)462002(3，4)662002(3，4)363002(3，4)463002(3，4)663002 代号与含义KDW ：钢球直径系数F0 ：轴承径向额定静负荷系数 fc ：轴承径向额定动负荷系数 kd ．套圈挡边直径系数kt、δt ：装配锁口高度系数Kpi、kpe：内、外圈滚道直径系数εi、ε e：实体保持架内、外径引导间隙kc ：实体保持架内、外径系数3 设计要点整篇文章把dn≥0．6×10^6的称为高速，dn≥1．8×10^6的称为超高速。

结构形式 优 点 缺 点 采用公司外圈单挡边、内圈双挡边．保持架外引导单挡边外圈有利于外圈沟道多余润滑剂流出，不仅减小润滑剂搅动摩擦．而且有利于降低接触SKF-7000FAG-B7000NSK-7000GMN-S6000外圈单挡边、内圈双挡边，保持架内引导 与上面相比，由于采刚内圈烈挡边引导保持架，运动平稳。

轴承滚珠接触角计算公式
在轴承设计和选择中，接触角是一个重要参数。

接触角可以影响轴承的负载能力、转速等性能，因此计算接触角是非常重要的。

下面介绍轴承滚珠接触角的计算公式。

1. 单一滚珠接触角计算公式
单一滚珠接触角是指滚珠在轴承内、外圈之间的接触角。

计算公式如下：
cosα=(d-D)/(2r)
其中，d是滚珠的直径，D是轴承内、外圈的直径，r是轴承的半径。

2. 多滚珠接触角计算公式
在多滚珠轴承中，滚珠数量和排列方式不同，接触角计算也相应有所不同。

一般来说，可以采用Hertz接触理论计算接触角，公式如下：
cosα=(F/(2πER1R2))^(1/2)
其中，F是轴承的额定动载荷，E是轴承材料的弹性模量，R1和R2是轴承内、外圈的半径。

需要注意的是，接触角的计算公式只是一个理论计算值，实际应用中还需要考虑其他因素，如轴承的精度、润滑等条件。

- 1 -。

轴承转速计算公式及方法在机械设备中，轴承是一种常见的零部件，用于支撑和限制旋转或直线运动的机械部件。

轴承的转速是指轴承内圈相对于外圈的旋转速度，通常以每分钟转数（RPM）来表示。

正确地计算轴承的转速对于确保机械设备的正常运行至关重要。

本文将介绍轴承转速的计算公式及方法。

1. 轴承转速的计算公式。

轴承的转速可以通过以下公式来计算：n = (60 × v) / (π× d)。

其中，n代表轴承的转速（RPM），v代表轴承外圈的线速度（m/s），π代表圆周率（约为3.14），d代表轴承的直径（m）。

2. 轴承转速的计算方法。

（1）确定轴承的外圈线速度。

轴承的外圈线速度是指轴承外圈上任意一点的线速度，通常使用以下公式来计算：v = π× d × n / 60。

其中，v代表轴承的外圈线速度（m/s），π代表圆周率（约为3.14），d代表轴承的直径（m），n代表轴承的转速（RPM）。

（2）代入公式计算转速。

将轴承的外圈线速度代入轴承转速的计算公式中，即可得到轴承的转速。

举例说明：假设某个轴承的直径为0.1m，外圈线速度为10m/s，代入公式可得：n = (60 × 10) / (3.14 × 0.1) = 1910 RPM。

因此，该轴承的转速为1910 RPM。

3. 注意事项。

在进行轴承转速的计算时，需要注意以下几点：（1）确保使用正确的单位，在进行计算时，需要使用统一的单位，通常使用国际单位制（SI单位制）来进行计算。

（2）考虑轴承的额定转速，轴承通常会有一个额定转速，超过这个转速可能会导致轴承损坏，因此在计算轴承转速时需要考虑轴承的额定转速。

（3）考虑轴承的工作环境，在实际应用中，轴承的工作环境会对其转速产生影响，例如温度、润滑情况等因素都会对轴承的转速产生影响，因此需要根据实际情况进行适当的修正。

4. 结语。

轴承的转速是保证机械设备正常运行的重要参数，正确地计算轴承的转速对于确保机械设备的正常运行至关重要。

滚动轴承设计原理第二章 滚动轴承的几何学本章内容点、线接触的概念及其对轴承工作的影响；主曲率、主 曲率和函数、主曲率差函数该概念及其计算；游隙、游隙分 类，原始游隙的计算；接触角定义、力学意义；重点：轴承点线接触的判断；会正确计算主曲率、主曲 率和函数、主曲率差函数计算；游隙、接触角定义及其分 类；径向游隙与轴向游隙的关系，轴向游隙与原始接触角的 关系。

第一节 滚动体与滚道的接触状态及密合度 第二节 接触点的主曲率 第三节 游隙与接触角滚动轴承设计原理第二章 滚动轴承的几何学第一节 滚动体与滚道的接触状态及密合度一、点接触球轴承：⎧⎨⎩无轻载载荷荷：：接由触点于扩一展点为一封闭椭圆⎬⎫属于点接触 ⎭球面滚子轴承（调心滚子轴承）：点无载荷：接触于一点接触轻载荷：由点扩展为一封闭的椭圆，如图2-1线中等、重载荷：由点扩展为一非封闭的椭圆，接 触如图2-2滚动轴承设计原理第二章 滚动轴承的几何学想一想：图2-1图2-2滚动轴承设计原理第二章 滚动轴承的几何学二 线接触1.无修缘线接触滚子和滚道表面的母线都是直线⎫滚子和滚道表面的母线不是直线，但是两者曲率相等⎬⎭ ⇒⎧无载荷状态：接触于一条线 ⎨⎩受载后，为一近似的矩形或梯形2.修缘线接触：滚动轴承设计原理第二章 滚动轴承的几何学滚子的母线是小曲率的圆弧（全凸滚子），或者中间是 直线而两端是圆弧。

这种滚子轴承在无负荷状态下，滚子与 滚道接触于一点，或者接触于中间一段线而两端不接触。

受 载后接触面一般是非封闭的椭圆或近似的矩形，消除或减小 了边缘应力集中．这种接触状态称为修正线接触。

图 2-5 为 圆柱滚子轴承修正线接触的情况。

修正线接触滚子轴承由于 消除或减小了边缘应力集中，从而使轴承疲劳寿命有很大提 高。

要消除应力集中，一般采用带凸度的滚子。

滚子的母线 一般为两种：一种是全凸滚子，这种滚子与滚道接触在没有载荷的情 况下为点接触，有载荷的情况下，为椭圆。

角接触球轴承计算机辅助设计计算稿====================================================================== 型号: 71860X2TN1内径 d = 300 外径 D = 380装配高T = 40 宽度 B = 27接触角alfa = 30°最小倒角rsmin = 2.1 r1smin= 1.1====================================================================== 序号计算公式结果(上偏差|下偏差) ====================================================================== ■主参数的确定钢球中心圆直径P ＝0.5*(d+D) 340钢球公称直径Dw'=KDw*(D-d) 26.988（来图）钢球个数Z=πDwp/Kz*Dw=29.74 (Kz=1.33) 取30■额定动负荷Cr(KN) 212当Dw≤25.4mmCr = 1.3fc(cosα)^0.7*Z^(2/3)*Dw^1.8当Dw >25.4mmCr = 1.3*3.647*fc*(cosα)^0.7*Z^(2/3)*Dw^1.4额定静负荷Cor的计算Cor = f0 * i * Z * Dw * Dw * Cosα (KN) 304■套圈的设计内圈滚道曲率半径Ri=fi*Dw 13.9 (+0.08|0)外圈滚道曲率半径Re=fe*Dw 14.17 (+0.08|0)内圈滚道直径di=P-Kpi*Dw Kpi=1.004019 312.904(±0.05)外圈滚道直径De=P+Kpe*Dw Kpe=1.0066987 367.168 (±0.05)内圈挡边直径d2=di+Kd*Dw 328.5 (0|-0.57)外圈挡边直径D2=De-Kd*Dw 351.5 (+0.57|0)内圈滚道中心至基准端面的距离ai:ai = 0.5*B+(Ri-0.5*Dw)sin(α)-2δ20.2 (±0.06)外圈滚道中心至基准端面的距离aeae = 0.5*B+(Re-0.5*Dw)sin(α)-2δ取20.2 (±0.06)δ:滚道位置的上偏差装配锁口高度t的计算t = 0.00053*De + 0.5*gmin+0.5*Ymax 0.45 (0|-0.06)■装配锁口高度的验算（参考）最小锁量应满足下式:Ymin = 2tmin - gmax 0.4最小锁量不得超过表10的规定■标志尺寸的计算外圈标志圆平均直径Dek:Dek=((D-2*r5max)+(D2max+2*r3max))/2 363标志平面有效宽度he:he=((D-2*r5max)-(D2max+2*r3max))/2 7.8■配套径向游隙和装配高的计算配套径向游隙g：gmax=2(Rimin+Remin-Dw)(1-cos(αmax)) αmax=34.464 0.38gmin=2(Rimax+Remax-Dw)(1-cos(αmin)) αmin=23.3554 0.22装配高极限尺寸按下式确定：Tmax=aimax+aemax-(Rimin+Remin-Dw)sin(αmin) 40.09Tmin=aimin+aemin-(Rimax+Remax-D w)sin(αmax) 39.52隔离块设计相邻两球中心距C1 35.540C=Dpw*sin(Pi/Z)外径Dc=0.9*Dw 24内径dc=(0.35～0.45)*Dw 10球兜直径Dcp=(0.8～0.9)*Dc 20.4 (±0.13)球兜曲率半径Rc=0.54*Dw 14.57 (+0.11|0)端面到Rc与dc交点的距离acac=SQR(Rc^2-dc^2/4)-SQR(Rc^2-Dcp^2/4) 3.281球进入兜孔的距离bcbc=0.5*Dw-SQR((Dw^2-dc^2/)4) 0.961隔离块宽度BcBc=C-Dw+2*ac+2*bc=17.14 17(±0.11)隔离块端面到球最远点的距离CpCp=Bc+Dw-ac-bc 39.8===================================================================角接触球轴承计算机辅助设计====================================================================== 型号: 71916ACM标准外形尺寸:轴承内径 d = 80轴承外径 D = 110内圈宽度 B = 16外圈宽度Cs = 16轴承装配高T = 16接触角角度angle=25轴承最小单向倒角rsmin=1r1smin=0.3====================================================================== 序号计算公式结果上偏差下偏差====================================================================== 1. 主参数的确定轴承的外形尺寸d、D、B、γsmin、γ1smin 以及接触角α应符合GB292的规定，γsmin、γ1smin最大尺寸极限应符合GB274的规定。

第41卷第3期2009年6月 南　京　航　空　航　天　大　学　学　报Journal of N anjing U niversity of Aero nautics &Astronautics V ol.41N o.3　Jun.2009角接触球轴承分析模型的数值求解彭　波1　王黎钦1　崔　立1　应丽霞2(1.哈尔滨工业大学机电工程学院,哈尔滨,150001; 2.哈尔滨工程大学机电工程学院,哈尔滨,150001)摘要:建立了内圈静止、外圈旋转的角接触球轴承分析模型,考虑了滚动体的离心力、陀螺力矩以及弹性流体动力润滑作用。

建立了非线性方程组未知量的约束条件,解决了N ew to n-Raphso n 法求解方程易出现不收敛的问题。

以两个角接触球轴承为算例,分析了轴承内、外圈分别旋转对应力的影响,以及转速和径向载荷对轴承工作性能的影响。

结果表明,轴承外圈转时接触应力随转速增大而显著增大,内圈转时则无明显变化;低转速下外圈转的接触应力明显低于内圈转;较小的径向载荷下外圈转的接触应力高于内圈转;轴承微区滑动速度受转速和径向载荷的影响显著。

通过Jones 球轴承拟静力学分析程序计算,验证了模型和程序的有效性。

关键词:角接触球轴承;拟静力学分析;非线性方程组;数值求解中图分类号:T H133.33 文献标识码:A 文章编号:1005-2615(2009)03-0370-05　基金项目:国家自然科学基金(50575054)资助项目。

　收稿日期:2008-03-24;修订日期:2008-05-28　作者简介:彭波,女,博士研究生,1982年12月生;王黎钦(联系人),男,教授,博士生导师,E -mail :lqw ang @hit .edu .cn 。

Numerical Solution of Analysis Model for Angular -Contact Ball BearingsP eng Bo 1,W ang L iqin 1,Cui L i 1,Ying L ix ia2(1.Schoo l o f M echa tro nics Eng ineering ,Har bin Institute o f T echno log y ,Har bin ,150001,China ;2.Co lleg e of M echanical and Elect rical Engineer ing ,Harbin Engineering U niver sity ,Har bin ,150001,China )Abstract :An analy sis mo del of the high-speed angular-contact ball bearing w ith rotatio nal outer race is pr esented.Centrifug al fo rce,g yrosco pic movement and effect o f the elasto -hy dro dynamic lubrication are co nsidered in the mo del .Restrictions ensure that the equations solved by New to n -Raphso n rapidly con-verges .Taking tw o bearings as an ex am ple ,each race ro tating respectiv ely ,the ro tary speed and the ra-dial load on bearing characteristics are studied.Results show that the higher the speed of o uter race,the hig her the stress,but the effect is not distinct w hile the inner race is in r unning ;at the low speed,the stress of the outer race revolve is evidently low er than that of the inner race revo lve ,but it is opposite in the low radial load;the speed and radial loads hav e great influence o n the micr o-slippage.Finally ,the model and the prog ram v er ified by the r esults of Jones computer pro gram are effective.Key words :angular -contact ball bearing ;quasi -static analysis ;nonlinear equations ;numerical so lution 滚动轴承内部复杂的传动力学因素往往是造成轴承失效的主要原因。

角接触球轴承动刚度的计算分析作者：赵耿，刘保国，冯伟，王攀来源：《科技创新与生产力》 2017年第8期赵耿，刘保国，冯伟，王攀（河南工业大学机电工程学院，河南郑州 450001）摘要：通过对轴承运动过程进行物理模型简化以及力学分析，运用MATLAB建立了角接触球轴承的刚度数值计算模型，经实例验证能很好地计算出不同参数下的轴承刚度。

本文通过对7012C型角接触球轴承进行实例计算分析，发现：轴承刚度随着转速的提高呈减小趋势，但各方向刚度变化趋势存在不同；轴承钢球陀螺力矩以及离心作用惯性力随着转速增大逐渐增大；轴承刚度受轴承滚珠离心作用惯性力以及陀螺力矩的影响，轴承的刚度随着轴承滚珠离心作用惯性力及陀螺力矩的增大呈减小趋势。

关键词：轴承；角接触球轴承；轴承刚度；陀螺力矩；离心作用；Matlab中图分类号：TH123；TH133.3 文献标志码：A DOI：10.3969/j.issn.1674-9146.2017.08.075高速电主轴作为高精密机床的核心部件，已成为世界各国的重点研究对象[1]，高速电主轴的研制能够为高精密数控机床系统提供更好的动力系统。

角接触球轴承作为高速电主轴的主要支撑部件，其高速运行情况下的力学特性将会影响电主轴工作性能[2]。

轴承刚度被视为衡量轴承性能的重要指标之一，它对轴承的负载能力、极限转速以及使用寿命有重要的影响。

李纯洁等人研究发现随着预紧力的增大角接触球轴承的等效动刚度也随之增大，且当预紧力增大到一定范围时动刚度受预紧力影响明显变小[3]。

王保民等人通过建立数学模型分析了预紧力对角接触球轴承的接触角、球的离心力和陀螺力矩的影响[4]。

本文通过数值算法建立了轴承刚度计算模型，计算分析了在预紧力一定的情况下，角接触球轴承的动刚度在不同转速下刚度的变化，为高速电主轴主轴系统的模型建立提供数据支持。

1 数学模型的建立该数学模型以Jones滚道控制理论为基础建立，运用Newton-Raphson迭代方法进行数值计算，在模型建立之前先做如下假设：一是轴承的几何形状理想；二是外圈固定，内圈相对于外圈做旋转运动；三是忽略钢球和内外圈沟道之间的摩擦力；四是轴承构件间的相互作用均符合Hertz接触理论；五是不计轴承内部油膜厚度和油膜阻力带来的影响[5]。

nsk角接触球轴承说明书
NSK角接触球轴承说明书
产品简介：
NSK角接触球轴承通常被用作支承较高负载或希望在较小径向空间内获得更高速度的应用。

该产品具有优良的抗疲劳性能和高速度能力。

产品特点：
1. 与其他类型的球轴承相比，NSK角接触球轴承拥有更高的刚性和负载能力。

2. 优秀的滚珠数量分布和球道曲率设计，使得角接触球轴承能够同时承受径向和轴向负载。

3. 角接触球轴承的接触角度较小，因此其摩擦和温升都很低。

4. 适用于高速度使用，提供高转速和低噪音性能。

5. 角接触球轴承的工作寿命较长，也更加可靠。

使用说明：
1. 选择适当的轴承型号和规格，确保适配机器设计要求。

2. 注意轴承的安装方向，不要损坏轴承外露的密封件，保证外部环境无法进入轴承内部。

3. 注意轴承的清洁和润滑，定期维护保养以延长使用寿命。

4. 避免过载和过高速度，否则会影响轴承的寿命和性能。

5. 检查轴承的使用情况，如有异常情况及时更换。

使用注意事项：
1. 不允许在严重的冲击载荷下使用角接触球轴承。

2. 在激烈震动的环境下应注意保护轴承，以避免加速其寿命损耗。

3. 在使用角接触球轴承时应选用专用工具，正确装拆以避免过度载荷带来的轴承局部损伤。

4. 不允许轴承润滑油或润滑脂短缺或污染，应定期清洗更换。

5. 不得在外来渗入和轴承清洁的前提下长期储存轴承，以避免轴承损坏或腐蚀。

以上是关于NSK角接触球轴承的简单说明书，如有更详尽的使用和维护需求，建议咨询相关技术人员。