电路分析基础向量分析法
- 格式:ppt
- 大小:2.18 MB
- 文档页数:32




内蒙古师范大学本科生学年论文题目:相量法在电路中的应用分析学号:20101106316姓名:王菲菲专业:电子信息科学与技术指导教师:张珏2011年5月15日物理与电子信息学院学年论文相量法在电路中的应用分析王菲菲(学号:20101106316)(物理与电子信息学院 10级电子信息科学与技术班,内蒙古呼和浩特 010022)指导老师:张珏摘要:在线性电路的分析中,有很多问题是求电路的稳态解。
相量分析法就是为了简化正弦稳态电路的分析计算而引入的一种电路求解方法。
相量分析法不仅适用于本章只有一种频率的正弦交流电路的分析与计算,同时,它也可推广应用于多个不同频率的正弦激励的线性电路。
关键词:相量分析法;欧姆定律;复功率;复数;正弦中图分类号:TM131.4相量分析法的数学基础是复数运算,因此在研究相量分析法之前,应简要复习复数的概念及其运算法则,并且熟练掌握复数的代数形式、极坐标形式、指数形式之间的变换关系,为应用相量法分析和计算正弦稳态电路打下坚实的基础。
1 复数的概念1.1虚数单位参见图1给出的直角坐标系复数平面。
在这个复数平面上定义虚数单位为虚数单位j又叫做90°旋转因子。
向量法在电路中的应用分析图1在复平面上显示复数1.2复数的表达式一个复数Z有以下四种表达式:1.2.1 直角坐标式(代数式)式中,a叫做复数Z的实部,b叫做复数Z的虚部。
在直角坐标系中,以横坐标为实数轴,纵坐标为虚数轴,这样构成的平面叫做复平面。
任意一个复数都可以在复平面上表示出来。
例如复数A=3+j2在复平面上的表示如图1所示。
1.2.2 三角函数式在图1中,复数Z与x轴的夹角为θ,因此可以写成式中|Z|叫做复数Z的模,又称为Z的绝对值,也可用r表示,即:θ叫作复数Z的辐角,从图1中可以看出复数Z的实部a、虚部b与模|Z|构成一个直角三角形。
1.2.3 指数式利用欧拉公式,可以把三角函数式的复数改写成指数式,即物理与电子信息学院学年论文1.2.4 极坐标式 (相量式)复数的指数式还可以改写成极坐标式,即以上这四种表达式是可以相互转换的,即可以从任一个式子导出其它三种式子。



向量分析法在电气调试中的应用高金磊(河南省安装集有限责任公司,洛阳471000)摘要:在变电站或发电厂电气调试中,为查找电气设备的故障原因,采用向量分析法是最直观、快捷的方法之一。
文中列举几个实例分析,介绍了运用向量图分析计算的方法。
采用该法可以提高查找故障原因的效率,从而避免因设备停运时间过长而造成的经济损失。
关键词:向量电气电压电流互感器极性故障在电气调试过程中,经常遇到电气设备发生故障的现象,这就要求调试人员快速的确定故障性质及产生的原因,然后排除故障。
采用向量分析法配合其他试验手段和检测方法可以直观、快捷的查找出故障原因,从而快速的解决工程现场的技术问题。
下面列举一些实例,简要介绍向量分析法在工程中的应用。
1、电压互感器极性接反在电力系统中,若电压互感器一次极性接反,必然引起二次电压变化,利用向量分析法分析这些数据变化,就能很快的得出结论。
例:某发电站同期系统中,采集的电压为电站侧联络柜电压互感器和母线电压互感器。
电压互感器均为V-V接法,变比为10000/100V且二次侧B相均接地。
倒送电后测得电站侧联络柜电压互感器二次侧电压为:AB=100V,BC=100V,AC=173V。
电站侧联络柜电压互感器与母线电压互感器之间的电压为:AA1=0V,BB1=0V,CC1=200V。
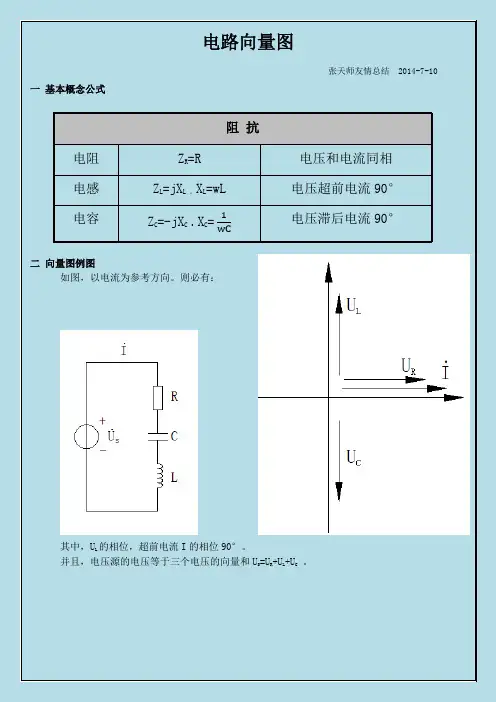
作向量图如下所示:AC O B(a)B相不接地的向量图(b) B相接地的向量图B相不接地系统中性点即为O点,故作其向量图如图(a)所示:由向量图(a)可以看出:|OA|=|OB|=|OC|=57.7V,|AB|=|BC|=|AC|=100V.B相接地系统中因B相接地,所以B点即为O点,故作其向量图如图(b)所示:由向量图(b)可以看出|OA|=|OC|=|AB|=|BC|=|AC|=100VB相接地C相极性反系统中B点即为O点,因C相极性接反,所以C相向量应旋转180度,故作其向量图如图(c)所示:由向量图(c)可以看出:|OA|=|OC|=|AB|=|BC|=100V,|AC|=173V.且|CC′|=200V(C)C(c)B相接地C相极性反的向量图A相极性接反的向量图可参考C相极性接反向量图,将A相向量旋转180度,故:|OA|=|OC|=|AB|=|BC|=100V,|AC|=173V.且|AA1|=200V由所测得数据可知|AB|=|BC|=100V,|AC|=173V,对照所作向量图很容易发现该系统应该是A相或C相极性接反造成的。


第4章向量分析法向量分析是数学中的一门重要分支,主要研究矢量的运算和性质。
它是数学物理学等学科的重要工具,广泛应用于各个领域,例如电磁场理论、流体力学和流形等。
向量分析的基础是对矢量的运算规则的研究。
在直角坐标系中,我们通常将矢量表示为有序三元组(x,y,z),其中x、y、z分别是矢量在x轴、y轴和z轴上的分量。
向量的运算规则包括加法、数乘和点积等。
两个矢量的加法定义为将它们的对应分量相加。
例如,向量A(a1,a2,a3)和向量B(b1,b2,b3)的和为向量C(a1+b1,a2+b2,a3+b3)。
加法满足交换律、结合律和分配律。
加法可以用来表示平移,例如从A点出发,按向量B前进,得到新的点C。
数乘定义为将一个实数与矢量的每一个分量相乘。
例如,实数k与矢量A(a1,a2,a3)的数乘为向量B(ka1,ka2,ka3)。
数乘满足分配律。
数乘可以用来表示伸缩变换,例如一个向量乘以2表示将其长度放大一倍。
点积是两个矢量的乘积与它们夹角的余弦值的乘积。
向量A(a1,a2,a3)和向量B(b1,b2,b3)的点积为a1b1+a2b2+a3b3、点积满足交换律和分配律。
点积可以用来计算矢量的长度、夹角和投影。
向量分析还研究了梯度、散度和旋度等运算。
梯度表示标量场的变化率和方向,散度表示矢量场的源强度,旋度表示矢量场的旋转程度。
这些运算在研究物理现象和解决实际问题时非常有用。
梯度表示标量场f的变化率和方向,定义为梯度算子的作用。
梯度算子是一个矢量算子,由偏导数组成,例如梯度算子∇表示(∂/∂x,∂/∂y,∂/∂z)。
梯度向量的长度表示标量场的变化率,梯度向量的方向表示变化最快的方向。
梯度在微分方程和优化问题中有广泛应用。
散度表示矢量场F的源强度,定义为散度算子的作用。
散度算子是一个标量算子,由偏导数组成,例如散度算子∇·表示(∂/∂x,∂/∂y,∂/∂z)·。
散度的值为正表示矢量场的流出量大于流入量,为负表示流入量大于流出量,为零表示流入流出平衡。