理论力学课后习题答案第11章达朗贝尔原理及其应用
- 格式:doc
- 大小:420.01 KB
- 文档页数:8






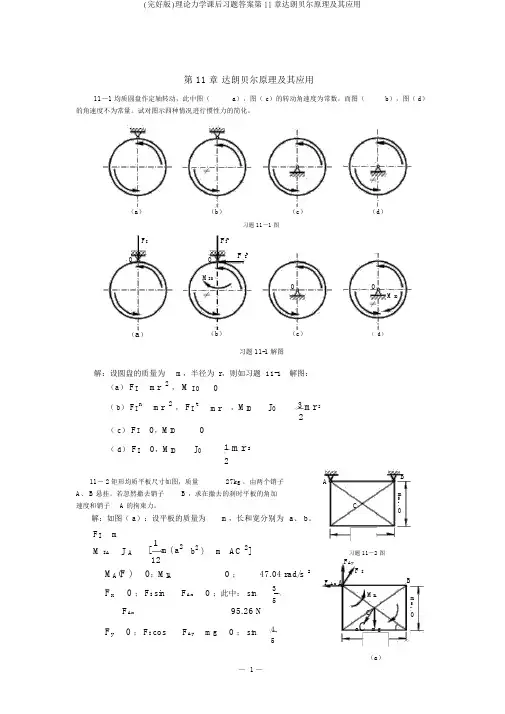
第 11 章 达朗贝尔原理及其应用11-1 均质圆盘作定轴转动,此中图( a ),图( c )的转动角速度为常数,而图( b ),图( d )的角速度不为常量。
试对图示四种情况进行惯性力的简化。
≠≠(a )(b )(c )(d )习题 11-1 图F I F I nOO F I tM I OO O≠M IO≠(a )(b )(c )( d )习题 11-1 解图解:设圆盘的质量为m ,半径为 r ,则如习题 11-1 解图:(a ) F I mr 2 , M I O 0( b ) F I nmr 2 , F I tmr ,M IOJ O3 mr 22( c ) F I 0,M IO 0( d ) F I0,M IOJ O1 mr 2211- 2 矩形均质平板尺寸如图,质量 27kg ,由两个销子AA 、B 悬挂。
若忽然撤去销子 B ,求在撤去的刹时平板的角加速度和销子A 的拘束力。
C解:如图( a ):设平板的质量为 m ,长和宽分别为 a 、 b 。
F I mM I AJ A[ 1m( a 2 b 2 ) m AC 2] 习题 11-2 图122F AyM A (F ) 0;M IA 0 ; 47.04 rad/s F IF Ax AF x0 ; F I sinF Ax0 ;此中: sin3M IA 5CF Ax95.26 NF y0 ; F I cosF Aymg0 ; sin4aC mg5Bm5 1 .Bm51.F Ay 27 9.8 3.375 47.04 0.8 137.6 N11- 3 在均质直角构件 ABC 中, AB 、 BC 两部分的质量各为 AE 保持在图示地点。
若忽然剪断绳索,求此刹时连杆 AD 、 BE已知 l = 1.0m , φ= 30o 。
3.0kg ,用连杆 AD 、 DE 以及绳索所受的力。
连杆的质量忽视不计,C解:如图( a ):设 AB 、 BC 两部分的质量各为 m = 3.0kg 。

第十一章 达朗贝尔原理一. 重点概括1 质点系的达朗贝尔原理在质点系运动的任一瞬时,作用于每一质点上的主动力、约束力和该质点的惯性力在形式上构成一平衡力系。
上式表明,作用在质点系上的外力系和虚加的惯性力系组成平衡力系——质点系的达朗贝尔原理。
用达朗贝尔原理求解非自由质点系动力学问题(已知运动求力或已知力求运动)的方法称为质点系的动静法。
对于空间力系,由这两个矢量式总共可写出6个投影方程;对于平面力系,由这两个矢量式总共可写出3个投影方程。
2 刚体惯性力简化(1) 惯性力系的主矢(2) 惯性力系的主矩I Ni =++i i F F F Ci i i m a m a F F -=-==∑∑)(I IR )(I I i O O F M M ∑=0I e =+∑∑iiF F 0)()(I e=+∑∑iOiOF M FM惯性力系的主矢与刚体的运动形式无关;惯性力系的主矩与刚体的运动形式有关。
3 几种刚体的惯性力(1)平移刚体主矢主矩刚体平移时,惯性力系简化为通过刚体质心的合力。
(2)定轴转动刚体主矢主矢等于刚体质量与质心加速度大小的乘积,方向与质心加速度方向相反。
对转轴的主矩主矩等于刚体对转动轴的转动惯量与角加速度的乘积,方向与角加速度方向相反。
(3)平面运动刚体(具有质量对称面的情形)IR ()i i m ∑F a =- () i C Cm m ∑a a =-=-I 0C M =)(n t R R IR C C C m m F a a a +=-=-αz z J M -=I主矢主矢大小等于刚体质量与质心加速度大小的乘积,方向与质心加速度方向相反。
主矩主矩小等于刚体对通过质心的转动轴的转动惯量与角加速度的乘积,方向与角加速度方向相反。
二. 常见问题和对策常见问题:1.惯性力系出错,表现在方向或大小出错,尤其主矩出错较多;2.质点系运动时,主动力系、约束反力系和惯性力系组成了形式上的平衡力系,切记不含质点之间的内力系(也不要画出内力系);3.质点系的运动参数之间联系出错。

哈尔滨工业大学理论力学教研室理论力学(I)第8版习题答案《理论力学(1 第8版)/“十二五”普通高等教育本科国家级规划教材》第1版至第7版受到广大教师和学生的欢迎。
第8版仍保持前7版理论严谨、逻辑清晰、由浅入深、宜于教学的风格体系,对部分内容进行了修改和修正,适当增加了综合性例题,并增删了一定数量的习题。
本书内容包括静力学(含静力学公理和物体的受力分析、平面力系、空间力系、摩擦),运动学(含点的运动学、刚体的简单运动、点的合成运动、刚体的平面运动),动力学(含质点动力学的基本方程、动量定理、动量矩定理、动能定理、达朗贝尔原理、虚位移原理)。
本书可作为高等学校工科机械、土建、水利、航空、航天等专业理论力学课程的教材,也可作为高职高理论力学(I)第8版哈尔滨工业大学理论力学教研室习题答案专、成人高校相应专业的自学和函授教材,亦可供有关工程技术人员参考。
本书配套的有《理论力学学习辅导》、《理论力学(I)第8版哈尔滨工业大学理论力学教研室习题答案理论力学思考题集》、《理论力学解题指导及习题集》(第3版)、《理论力学电子教案》、《理论力学网络课程》、《理论力学习题解答》、《理论力学网上作业与查询系统》等。
理论力学(I)第8版哈尔滨工业大学理论力学教研室课后答案前辅文静力学关注网页底部或者侧栏二维码回复理论力学(I)第8版答案免费获取答案引言第一章静力学公理哈尔滨工业大学理论力学教研室理论力学(I)第8版课后答案理论力学思考题集》、《理论力学解题指导及习题集》(第3版)、《理论力学电子教案》、《理论力学网络课程》、《理论力学习题解答》、《理论力学网上作业与查询系统》等。
理论力学(I)第8版哈尔滨工业大学理论力学教研室课后答案前辅文静力学引言第一章静力学公理和物体的受力分析第二章平面力系第三章空间力系第四章摩擦理论力学(I)第8版哈尔滨工业大学理论力学教研室习题答案§4-4 滚动摩阻的概念运动学引言第五章点的运动学*§5-5 点的速度和加速度在球坐标中的投影思考题习题第六章刚体的简单运动§6-1 刚体的平行移动§6-2 刚体绕定轴的转动§6-3 转动刚体内各点的速度和加速度§6-4 轮系的传动比§6-5 以矢量表示角速度和角加速度·以矢积表示点的速度和加速度思考题习题第七章点的合成运动第八章刚体的平面运动动力学引言第九章质点动力学的基本方程第十章动量定理第十一章动量矩定理第十二章动能定理第十三章达朗贝尔原理第十四章虚位移原理参考文献习题答案索引Synopsis哈尔滨工业大学理论力学教研室理论力学(I)第8版课后答案第十四章虚位移原理。
(a )习题11-1图第11章 达朗贝尔原理及其应用11-1 均质圆盘作定轴转动,其中图(a ),图(c )的转动角速度为常数,而图(b ),图(d )的角速度不为常量。
试对图示四种情形进行惯性力的简化。
解:设圆盘的质量为m ,半径为r ,则如习题11-1解图:(a )2I ωmr F =,0I =O M(b )2n I ωmr F =,αmr F =tI ,αα2I 23mr J M O O == (c )0I =F ,0I =O M (d )0I =F ,αα2I 21mr J M O O ==11-2矩形均质平板尺寸如图,质量27kg ,由两个销子 A 、B 悬挂。
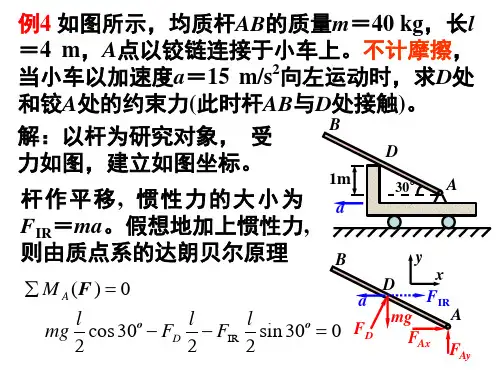
若突然撤去销子B ,求在撤去的瞬时平板的角加 速度和销子A 的约束力。
解:如图(a ):设平板的质量为m ,长和宽分别为a 、b 。
αα375.3I =⋅=AC m Fααα5625.0])(121[222I =⋅++==AC m b a m J M A A∑=0)(F AM ;01.0I =-mg M A ;2rad/s 04.47=α ∑=0x F ;0sin I =-Ax F F θ;其中:6.053sin ==θN 26.956.004.47375.3=⨯⨯=Ax F∑=0y F ;0cos I =-+mg F F Ay θ;8.054sin ==θ习题11-2图习题11-1解图(a )(a )N 6.1378.004.47375.38.927=⨯⨯-⨯=Ay F11-3在均质直角构件ABC 中,AB 、BC 两部分的质量各为3.0kg ,用连杆AD 、DE 以及绳子AE 保持在图示位置。
若突然剪断绳子,求此瞬时连杆AD 、BE 所受的力。
连杆的质量忽略不计,已知l = 1.0m ,φ = 30º。
解:如图(a ):设AB 、BC 两部分的质量各为m = 3.0kg 。
直角构件ABC 作平移,其加速度为a = a A ,质心在O 处。
(a )第11章 达朗贝尔原理及其应用11-1 均质圆盘作定轴转动,其中图(a ),图(c )的转动角速度为常数,而图(b ),图(d )的角速度不为常量。
试对图示四种情形进行惯性力的简化。
r ,0 ,αI (d )I =F ,αα2I 21mr J M O O ==11-2矩形均质平板尺寸如图,质量27kg ,由两个销子A 、B 悬挂。
若突然撤去销子B ,求在撤去的瞬时平板的角加 速度和销子A 的约束力。
解:如图(a ):设平板的质量为m ,长和宽分别为a 、b 。
αα375.3I =⋅=AC m Fααα5625.0])(121[222I =⋅++==AC m b a m J M A A∑=0)(F A M ;01.0I =-mg M A ;2rad/s 04.47=α∑=0xF ;0sin I =-Ax F F θ;其中:6.053sin ==θN 26.956.004.47375.3=⨯⨯=Ax F∑=0yF;0cos I =-+mg F F Ay θ;8.054sin ==θN 6.1378.004.47375.38.927=⨯⨯-⨯=Ay F11-3在均质直角构件ABC 中,AB 、BC 两部分的质量各为3.0kg ,用连杆AD 、DE 以及绳子AE 保持在图示位置。
若突然剪断绳子,求此瞬时连杆AD 、BE 所受的力。
连杆的质量忽略不计,已知l = 1.0m ,φ = 30º。
解:如图(a ):设AB 、BC 两部分的质量各为m直角构件ABC 作平移,其加速度为a = a A ,质心在O 处。
ma F 2I =∑=0)(F O M ;04sin )(43cos 4cos =+--lF F l F l F B A A B ϕϕϕ (1)∑=0AD F ;0cos 2=-+ϕmg F F B A(2) 联立式(1)和式(2),得:A B F mg F 3+=习题((22g m yOAxF ϕg1m xI F AAy F N 38.5)13(41=-=mg F A ;N 5.4538.53=⨯+=mg F B11-4 两种情形的定滑轮质量均为m ,半径均为 r 。
图a 中的绳所受拉力为W ;图b 中块重力为W 。
试分析两种情形下定滑轮的角加速度、绳中拉力和定滑轮轴承处的约束反力是否相同。
解:1、图(a ):① Wr J O =a α Wr mr =a 221αmr W2a =α (1) ②绳中拉力为W (2) ③∑=0x F ,0=Ox F (3) ∑=0y F ,W F Oy = (4) 2、图(b ): ① b 2I 21αmr M O =(5) b I αr gW a g W F ==(6)∑=0O M ,0I I =-+W r r F M O (5)、(6)代入,得)2(2b W mg r Wg +=α(7)②绳中拉力(图c ):∑=0y F ,W F T =+I b W Wmg mg a g W W T 2b +=-= (8) ③轴承反力: ∑=0x F ,0=Ox F(9)∑=0y F ,0I =-+W F F OyW mg mgWF Oy 2+=(10) 由此可见,定滑轮的角加速度a α、b α,绳中拉力,轴承反力均不相同。
11-5 图示调速器由两个质量各为1m 的圆柱状的盘子所构成,两圆盘被偏心地是悬于与调速器转动轴相距a 的十字形框架上,而此调速器则以等角速度ω绕铅垂直轴转动。
圆盘的中心到悬挂点的距离为l ,调速器的外壳质量为2m ,放在这两个圆盘上并可沿铅垂轴上下滑动。
如不计摩擦,试求调速器的角速度ω与圆盘偏离铅垂线的角度ϕ之间的关系。
解:取调速器外壳为研究对象,由对称可知壳与圆盘接 触处所受之约束反力为2/2g m 。
取左圆盘为研究对象,受力如图(a ),惯性力21I )sin (ωϕl a m F +⋅=由动静法∑=0A M ,0cos sin )2(I 21=-+ϕϕl F l gm g m 将I F 值代入,解出abT IF WαFFF F αMF WaIF 0.61m0.102m gm AaONF ϕϕωan t )sin (221212g l a m m m ++=11-6图示两重物通过无重滑轮用绳连接,滑轮又铰接在无重支架上。
已知物G 1、G 2的质量分别为m 1 = 50kg ,m 2 = 70kg ,杆AB 长l 1 = 120cm ,A 、C 间的距离l 2 = 80cm ,夹角θ = 30˚。
试求杆CD 所受的力。
解:取滑轮和物G 1、G 2如图(a )所示,设物G 1、G 2的加速度为a ,则其惯性力分别为: a m F 11I =;a m F 22I =∑=0)(F B M ;0)(212I 1I =-++r g m g m F F ;6120201212gg g m m m m a ==+-=∑=0yF ;0212I 1I =--+-g m g m F F F B ;g g g F B 3350120310=+-= 取杆AB 为研究对象,受力如图(b )所示,∑=0)(F A M;0sin 12='-l F l F B CD θ;kN 43.3N 34303350221==⋅=g l l F CD11-7 直径为1.22m 、重890N 的匀质圆柱以图示方式装置在卡车的箱板上,为防止运输时圆柱前后滚动,在其底部垫上高10.2cm 的小木块,试求圆柱不致产生滚动,卡车最大的加速度?解:图(c )中 ma F =I ∑=0A M22I )102.061.0(61.0)102.061.0(--=-mg F22598.061.0598.0-=⨯mg ma 51.6max ==a a m/s 2讨论:若max a a >,则惯性力引起的对A 点的力矩会大于重力m g 对A 点的矩,使圆柱向后滚动。
原文求min a 不合理。
11-8 两匀质杆焊成图示形状,绕水平轴A 在铅垂平面内作等角速转动。
在图示位置时,角速度3.0=ωrad/s 。
设杆的单位长度重力的大小为100N/m 。
试求轴承A 的约束反力。
解:(1)求A 处约束力重力:303.0100=⨯=P N质量:061.38.9/3.0100=⨯=m kg 质心O 点位置:1333.0=r m2In ωmr F =3.01333.0061.3⨯⨯= =0.122NA B D C G 1 θ G 2B G G AC θ aF F m mF (FF F (Id F 0τI =F (0=α)轴承A 的约束反力122.0=Ax F N (∑=0x F )30=Ay F N (∑=0y F ) (2)求B 截面弯矩考虑BD 段受力,只有惯性力I d F ,在y 方向分量对B 截面弯矩有贡献。
微段质量:100=γN/mx gm d d γ=222I 2.0d d ω+=x m F x x hd 2.03.022+=γθcos d d I I F F y =xx xx x d 8.96d 8.91002.03.0d 2.02.02.08.91003.02222=⨯⨯=++⋅⋅=⎰⎰⨯⨯===05.00205.00I 05.0218.96d 8.96d x x F x M yA=0.000765N·m=0.765N·mm11-9 图示均质圆轮铰接在支架上。
已知轮半径r = 0.1m 、重力的大小Q = 20kN ,重物G 重力的大小P = 100N ,支架尺寸l = 0.3m ,不计支架质量,轮上作用一常力偶,其矩M = 32kN·m 。
试求(1)重物G 上升的加速度;(2)支座B 的约束力。
解:取滑轮和物G 1、G 2如图(a )所示,设物G 1、G 2的加速度为a ,则其惯性力分别为: a m F 11I =;a m F 22I =∑=0)(F B M ;0)(212I 1I =-++r g m g m F F ;6120201212gg g m m m m a ==+-=∑=0yF ;0212I 1I =--+-g m g m F F F B ;g g g F B 3350120310=+-= 取杆AB 为研究对象,受力如图(b )所示,∑=0)(F A M ;0sin 12='-l F l F B CD θ;kN 43.3N 34303350221==⋅=g l l F CD11-10图示系统位于铅直面内,由鼓轮C 与重物A 组成。
已知鼓轮质量为m ,小半径为r ,大半径R = 2r ,对过C 且垂直于鼓轮平面的轴的回转半径ρA 质量为2m 。
试求(1)鼓轮中心C 的加速度;(2)AB 段绳与DE 段绳的张力。
解:设鼓轮的角加速度为α, 在系统上加惯性力如图(a )所示, 则其惯性力分别为: MF ((a 2(e OϕAkyBDr xC 2π=ϕmaxa IF gm FxOαmr F C =I ;αr m F A ⋅=2I ααρα222I 5.1mr m J M C C ===∑=0)(F DM;0)2(I I I =+-++C A C M r mg F F mgg g r a C 2145.132=+==α∑=0y F ;02I I =--+-mg mg F F F A C DE ;mg mr mg F DE 21593=-=α 取重物A 为研究对象,受力如图(b )所示,∑=0y F ;02I =-+mg F F A AB ;mg mg mr mg F AB 2134)2141(222=-=-=α11-11 凸轮导板机构中,偏心轮的偏心距e OA =。
偏心轮绕O 轴以匀角速度ω转动。
当导板CD 在最低位置时弹簧的压缩为b 。
导板质量为m 。
为使导板在运动过程中始终不离开偏心轮,试求弹簧刚度系数的最小值。
解:本题结果与ω转向无关,因讨论加速度。
1、图(a ),导板上点B 的运动代表导板运动r t e y B +=ωsint e y a Bωωsin 2-==&& 当2π=t ω时,a 取极值 2ωe a -=,方向向下。
2、导板受力: 2π=ϕ时,导板上受惯性力I F 2I ωme F =,方向向上。
此力力图使导板与凸轮脱开, 为使不脱开,应使弹簧力F 与板重 力mg 之和大于I F :I F F mg >+2)2(ωme b e k mg >++be g e m k +->2)(2ω讨论:1、当g e ≤2ω时,表示可不加弹簧。
3、板至最低位置时,a 也取极植,但此时惯性力是向下的,不存在脱离凸轮的问题。
11-12图示小车在F 力作用下沿水平直线行驶,均质细杆A 端铰接在小车上,另一端靠在车的光滑竖直壁上。