Romax 箱体有限元应力分析图解流程

连续钢箱梁桥有限元模型的建立及施工阶段应力分析根据X大桥实例，运用有限元软件ANSYS建立西岸水中引桥施工阶段相应工况的精细模型和杆系模型，并对本桥梁施工阶段进行应力分析。

标签：有限元模型；连续钢箱梁桥；应力分析1 工程简介X大桥西岸水中引桥结构形式为等高组合连续箱形梁桥。

桥梁全长480m，计算跨径为79.1m+480m+78.1m，双幅布置，道路平曲线为半径的圆弧。

单箱单室断面，单幅桥宽17m，中央隔离带0.5m，梁高4m，桥面设置2%的横坡。

钢梁为开口槽形截面，顶板板厚20mm-65mm，宽 1.2m；腹板厚度16mm-35mm，曲线内外侧腹板斜率分别为1：2.069和1：2.183；底板板厚14mm-30mm，宽6.6m。

根据板厚以及长度的不同，全桥钢梁共分18种类型。

腹板水平加劲肋采用板式，纵向间断布置，腹板竖向加劲肋采用T型，仅在支点附近布置；底板纵向加劲肋采用板式，沿桥梁纵向连续布置。

在钢梁内部设置横向联结系，全桥包括析架式和隔板式两种类型，除支点位置采用隔板式横向联结系，其余位置均采用析架式。

析架式横向联结系的标准间距为4m，由腹板、底板横向加劲肋、顶板横梁、型钢撑杆组成。

2 有限元模型建立2.1 精细模型运用有限元软件ANSYS建立西岸水中引桥施工阶段相应工况的精细模型。

钢梁顶板、腹板、加劲肋及横向联结系采用she1163单元，网格划分为四边形。

梁底混凝土采用solid45单元，网格划分为四面体。

网格划分边长控制在30cm 以内，保证有限元计算结果的准确性。

全桥钢梁节段类型共18种。

在钢梁处于顶推阶段的最大悬臂状态时，有限元模型为板壳元模型。

就钢梁而言，同时承受着自重荷载及前段导梁的作用。

为了简化模型，将导梁作为集中荷载施加在钢梁前端截面上，竖向力F=-1095.4kN、弯矩M=-21688.9kN、扭矩T=-1.75kN}m。

模型约束条件为，在曲线内外侧顶推设备处，约束竖向平动自由度，沿曲线径向平动自由度。

有限元分析上级报告学院：专业：姓名：班级：学号：均布荷载作用下深梁的变形和应力两端简支，长度l=5m，高度h=1m的深梁，在均布荷载q =5000N/m作用下发生平面弯曲（如图4.1所示）。

已知弹性模量为30Gpa，泊松比为0.3，试利用平面应力单元PLANE82，确定跨中的最大挠度，和上下边缘的最大拉压应力。

4.1 均布荷载作用下深梁计算模型1．理论解具有两个简支支座支承的简支梁，它的变形和应力分布在理论上是没有解析表达式。

在一般的弹性力学教科书中，只有将两边支座简化为等效力的条件，即在两个支座的侧表面上作用有均匀分布的剪力情况，才可以得到理论解答。

(1) 设定应力函数。

获得这种情况下的解答的主要思路是：按照应力解法，考虑到应力分量关于该梁中心位置（x=2.5，y=0.5）有对称和反对称关系。

可以首先假定一个应力函数为：Φ = A(y - 0.5)5+ B(x - 2.5)2 (y -0.5)3 +C(y -0.5)3+ D(x- 2.5)2+ E(x -2.5)2 (y - 0.5) (4.1)依据这个应力函数，可以获得各个应力分量，按照上表面受均布压力作用简支梁的上下表面和左右侧表面的应力边界条件，确定出应力函数（4.1）中的各个待定系数A，B，C，D和E。

按照应力求解平面应力问题方法，应力函数应该满足双调和函数：∇2∇2Φ = 0 (4.2)将（4.1）应力函数代入上式后，得到：24 B( y - 0.5) +120A(y - 0.5) = 0 (4.3)即：B = -5A (4.4)(2)确定应力分量。

应力函数与应力分量之间的关系为：(3) 利用梁的上下表面边界条件确定积分常数。

上表面受均布压力作用简支梁的上表面（y=h=1m）的应力边界条件:下表面(y=0)的应力边界条件:(5) 将梁的左右端面边界条件降低为积分满足。

考察边界条件（4.13）到（4.16），可以看出，无法找到能满足两端侧表面的所有应力边界条件的待定系数。

ProEMechanica有限元分析⼊门教程Pro/E Mechanica有限元分析⼊门教程⼀、进⾏Mechanica分析的步骤：1)建⽴⼏何模型:在Pro/ENGINEER中创建⼏何模型。

2)识别模型类型:将⼏何模型由Pro/ENGINEER导⼊Pro/MECHANICA中，此步需要⽤户确定模型的类型，默认的模型类型是实体模型。

我们为了减⼩模型规模、提⾼计算速度，⼀般⽤⾯的形式建模。

3)定义模型的材料属性。

包括材料、密度、弹性模量、泊松⽐等。

4)定义模型的约束。

5)定义模型的载荷。

6)有限元⽹格的划分：由Pro/MECHANICA中的Auto GEM(⾃动⽹格划分器)⼯具完成有限元⽹格的⾃动划分。

7)定义分析任务，运⾏分析。

8)根据设计变量计算需要的项⽬。

9)图形显⽰计算结果。

⼆、下⾯将上述每⼀步进⾏详解：1、在Pro/ENGINEER模块中完成结构⼏何模型后，单击“应⽤程序”→“Mechanica”,弹出下图所⽰窗⼝，点击Continue继续。

弹出下图，启⽤Mechanica Structure。

⼀定要记住不要勾选有限元模式前⾯的复选框，最后确定。

2、添加材料属性单击“材料”，进⼊下图对话框，选取“More”进⼊材料库，选取材料Name---------为材料的名称；References-----参照Part（Components）-----零件/组件/元件V olumes-------------------体积/容积/容量；Properties-------属性Material-----材料；点选后⾯的More就可以选择材料的类型Material Orientation------材料⽅向，⾦属材料或许不具有⽅向性，但是某些复合材料是纤维就具有⽅向性，可以根据需要进⾏设置⽅向及其转⾓。

点选OK，材料分配结束。

3、定义约束1）：位移约束点击，出现下图所⽰对话框，Name 约束名称Number of Set 约束集名称，点击New可以新建约束集的名称。

有限元分析中如何获得精确的应力解答在强度分析中，除了避免应力奇异问题外，分析人员更关心的问题是应力集中。

为了能够在分析中捕捉到应力集中，提高应力解答的精度，可以通过使用加密网格、应用子模型技术以及收敛性工具等方法。

1.单元选择与网格划分的相关考虑（1）单元的选择对于ANSYS结构分析而言，由于所有的单元均为位移元，即以位移自由度解为基本解，求得单元的节点位移向量后，乘以应变矩阵得到单元积分点上的应变，进而可以通过物理方程计算积分点处的应力。

因此应力相对于位移来说是导出解，其精度不及位移。

一般来说，提高应力解答的精度，一般可以通过加密低阶单元或提高单元阶次这两种方式来实现。

对于线性单元，在单元的边上位移为线性分布，应力则为常数，在应力集中处必须进行加密才能保证应力解答的正确性。

二次单元与线性单元相比，在网格尺寸相当的情况下能够给出更高的应力精度，而且可以避免在模拟弯曲变形中的剪切锁闭问题，因此建议在对更加关注应力结果的分析中优先选用高阶单元。

在ANSYSWorkbench结构分析中，缺省采用SOLID186以及SOLID187这些二次单元划分实体部件，这两种高阶单元经过检验可以获得比线性单元更高的应力精度，特别是10节点的四面体二次单元SOLID187，具有精度高以及适应复杂几何形状的特点，在结构分析中应用广泛。

此外，在结构的塑性分析中，也应优先选用二次单元。

（2）网格划分的相关考虑大量计算实例表明，采用二次单元划分的六面体网格和四面体网格在加密后都能给出满意的解答，为了得到应力集中区域的准确应力分布，需要进行适当的网格加密措施，具体操作时，可通过ANSYSMesh提供的总体及局部控制措施进行网格的加密设置。

①总体控制选项总体控制选项通过Mesh分支的Details设置实现。

ElementSize选项用于指定整体模型的网格尺寸。

Sizing部分提供了一些考虑几何特征的网格尺寸选项。

②局部控制选项局部尺寸选项可通过Mesh分支的右键菜单Insert>Sizing加入。

高中化学学习材料（灿若寒星**整理制作）山东省商河县尹巷镇中学2016届高三下期3月月考化学试卷（鲁教版，解析版）1．下列说法正确的是( )A.已知：H2(g)＋12O2(g)===H2O(l)；ΔH＝－285.8 kJ·mol－1 ，则H2的燃烧热为－285.8kJ·mol－1B. 已知：S(g)＋O2(g)===SO2(g) ΔH1＝－Q1 ；S(s)＋O2(g)===SO2(g) ΔH2＝－Q2，则Q1<Q2C.已知：12H2SO4(浓)＋NaOH(aq)===12Na2SO4(aq)＋H2O(l) ΔH1；CH3COOH(aq)＋NH3·H2O(aq)===CH3COONH4(aq)＋H2O(l) ΔH2，则有|ΔH1|<|ΔH2| D. 已知：Fe2O3(s)＋3C(石墨)===2Fe(s)＋3CO(g)ΔH＝＋489.0 kJ·mol－1CO(g)＋12O2(g)===CO2(g) ΔH＝－283.0 kJ·mol－1C(石墨)＋O2(g)===CO2(g) ΔH＝－393.5 kJ·mol－1则4Fe(s)＋3O2(g)===2Fe2O3(s) ΔH＝－1641.0 kJ·mol－1【答案】D【解析】试题分析：A项H2的燃烧热应该为285.8 kJ·mol－1；B项S(g)转化为S(s)需要放热，所以Q1>Q2；C项浓硫酸遇水放热；CH3COOH反应过程电离吸热，则|ΔH1|>|ΔH2|；D项利用盖斯定律可知正确。

考点：考查热化学方程式的正误及盖斯定律的应用。

点评：特别提醒：方程式相加减，则反应热也要相加减，本题属于简单题。

2．常温下，不能使溴水溶液褪色的是A．甲烷B．乙烯C．乙炔D．苯【答案】A【解析】甲烷属于烷烃，不能使溴水褪色。

乙烯和乙炔属于不饱和的烃，分别含有碳碳双键和碳碳三键，能和溴水发生加成反应而使其褪色。

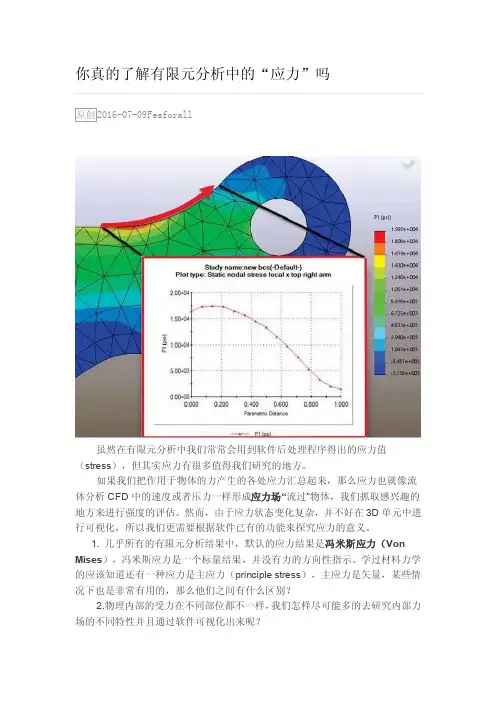
你真的了解有限元分析中的“应力”吗Feaforall虽然在有限元分析中我们常常会用到软件后处理程序得出的应力值（stress），但其实应力有很多值得我们研究的地方。

如果我们把作用于物体的力产生的各处应力汇总起来，那么应力也就像流体分析CFD中的速度或者压力一样形成应力场“流过”物体，我们抓取感兴趣的地方来进行强度的评估。

然而，由于应力状态变化复杂，并不好在3D单元中进行可视化，所以我们更需要根据软件已有的功能来探究应力的意义。

1. 几乎所有的有限元分析结果中，默认的应力结果是冯米斯应力（Von Mises），冯米斯应力是一个标量结果，并没有力的方向性指示。

学过材料力学的应该知道还有一种应力是主应力（principle stress），主应力是矢量，某些情况下也是非常有用的，那么他们之间有什么区别？2.物理内部的受力在不同部位都不一样，我们怎样尽可能多的去研究内部力场的不同特性并且通过软件可视化出来呢？下面我们将探究上面的两个问题。

什么是应力？首先我们先说说什么是应力。

众所周知，应力（stress）是单位面积上作用的力（forces）。

我们并不好感知或者测量应力，但力（force）是实实在在的，我们可以很好的感知和测量。

物质总是由原子构成的，从原子的维度看，原子之间相吸或者相斥。

物体在没有受力的状态下，原子处于自然状态，所有的力互相平衡，如果物体受到外部力的作用，原子就会偏离平衡位置去寻找新的平衡位置来平衡外部力。

如下图所示，相同长度L上分别有两排5对的原子和两排6对的原子，如果假设原子之间的吸引力相同，那么单位长度上6对原子的应力要比5对的大，扩展到宏观的3D情形同样适用。

力和应力单元微积分学科的发展可以使我们通过数学运用无限（无限大或者无限小）的原理来处理很多实际问题，宏观物体的受力是微观单元的叠加。

在材料力学中，我们把一个无限小的立方体（cube）单元来描述某一点的受力情况。

为什么无限小呢？因为由于无限小，小到物体内部力是均匀的，没有应力变化，只有一种应力状态。