下载文档原格式
2.6 四结点四边形单元(The four-node quadrilateral element)前面介绍了四结点的矩形单元其位移函数:xy y x U 4321αααα+++=xy y x V8765αααα+++=为双线性函数，应力，应变在单元内呈线性变化，比常应力三角形单元精度高。
但它对边界要求严格。
本节介绍的四结点四边形等参元，它不但具有较高的精度，而且其网格划分也不受边界的影响。
对任意四边形单元（图见下面）若仍直接采用前面矩形单元的位移函数，在边界上它便不再是线性的（因边界不与x,y 轴一致），这样会使得相邻两单元在公共边界上的位移可能会出现不连续现象（非协调元），而使收敛性受到影响。
可以验证，利用坐标变换就能解决这个问题，即可以通过坐标变换将整体坐标中的四边形（图a ）变换成在局部坐标系中与四边形方向无关的边长为2的正方形。
正方形四个结点i,j,m,p 按反时钟顺序对应四边形的四个结点i j m p 。
正方形的 1-=η 和 1=η 二条边界，分别对应四边形的i ，j 边界和p,m 边界；ξ=-1和ξ=+1分别对应四边形的i ，p 边界和j ，m 边界。
如果用二组直线等分四边形的四个边界线段，使四边形绘成一个非正交网格，那么该非正交网格在正方形上对应着一个等距离的规则网格（见图a, b ）。
当然, 局部坐标上的A 点与整体坐标的A 点对应。
一、四结点四边形等参单元的形函数及坐标变换由于可以将整体坐标下的四边形单元变换成局部坐标下的正方形单元，对于这种正方形单元，自然仍取形函数为： ξηαηαξαα2321+++=U ξηαηαξαα8765+++=V引入边界条件，即可得位移函数：∑=ijmpi i U N Ui ijmpi V N V ∑==写成矩阵形式：{}{}[]{}ee p i p i ed N d N N N N V U f =⎥⎦⎤⎢⎣⎡=⎭⎬⎫⎩⎨⎧=000 式中形函数: ()()()ηηξξηξi i i N ++=1141, ()p m j i ,,, 按照等参元的定义,我们将坐标变换式亦取为: p p m m j j i i i ijmpi x N x N x N x N x N x +++==∑p p m m j j i i i ijmpi y N y N y N y N y N y +++==∑ ()162-- 式中形函数N 与位移函数中的完全一致。
【1】图示弹性力学平面问题，采用三角形常应变元，网格划分及单元、节点编号如图1所示。
试求：(1) 计算系统刚度矩阵的最大带宽；(2) 根据图中结构的边界约束状态，给出约束节点位移值。
【解】(1) 相邻节点号的最大差为d = 4；所以，半带宽为B = 2 ⨯ (4 + 1) = 10。
(2) u1 = 0，v1 = 0，u4 = 0，v4 = 0。
【2】弹性力学平面问题4节点等参元，其单元自由度是多少？单元刚度矩阵是多少阶的？单元刚度矩阵有多少个元素？【解】平面问题4节点等参元，其单元自由度是4 ⨯2 = 8个；单元刚度矩阵是8 ⨯ 8 阶的，单元刚度矩阵有64个元素。
【3】平面刚架结构梁单元（考虑轴向和横向变形）的自由度是多少？单元刚度矩阵是多少阶的？单元刚度矩阵有多少个元素？【解】平面刚架结构梁单元（考虑轴向和横向变形）的自由度是2 ⨯ 3 = 6个；单元刚度矩阵是6 ⨯ 6阶的；单元刚度矩阵有36个元素。
【4】已知一等截面直杆中某一微段的起始点坐标为0.5m，终点坐标为0.6m，起始点的位移为0.2mm，终点的位移为0.3mm。
假定直杆内的位移是线性分布的。
求该微段等截面直杆的位移表达式f(x)。
【解】已知：x i = 0.5m, x j= 0.6m, u i = 0.2mm = 0.2⨯10-3m, u j= 0.3mm = 0.3⨯10-3m。
即【5】已知4节点一维问题中单元①(1, 2)的应力矩阵为结构总体位移列阵为求单元①的应力（用矩阵计算）。
【解】由总体结构位移列阵知，单元①的位移列阵为由{σ} = [C] {∆}e可求得单元①的应力【6】某结构中单元③的单元应力矩阵，节点位移列阵为，求单元3的应力{σ }。
【解】由{σ} = [C] {∆}e可求得单元③的应力【7】已知某结构中三角形常应变单元的单元③的应力矩阵与应变矩阵分别为，单元厚度t = 1，单元面积A = 0.5，求单元③的刚度矩阵[K]3。
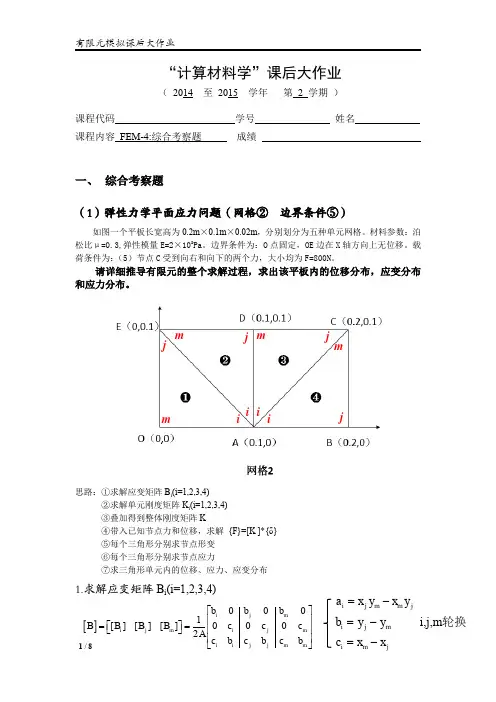
“计算材料学”课后大作业（ 2014 至 2015 学年 第 2 学期 ）课程代码 学号 姓名 课程内容 FEM-4:综合考察题 成绩一、 综合考察题（1）弹性力学平面应力问题（网格② 边界条件⑤）如图一个平板长宽高为0.2m ×0.1m ×0.02m ，分别划分为五种单元网格。
材料参数：泊松比μ=0.3,弹性模量E=2×108Pa 。
边界条件为：O 点固定，OE 边在X 轴方向上无位移。
载荷条件为：（5）节点C 受到向右和向下的两个力，大小均为F=800N 。
请详细推导有限元的整个求解过程，求出该平板内的位移分布，应变分布和应力分布。
思路：①求解应变矩阵B i (i=1,2,3,4)②求解单元刚度矩阵K i (i=1,2,3,4) ③叠加得到整体刚度矩阵K ④带入已知节点力和位移，求解 {F}=[K ]*{δ} ⑤每个三角形分别求节点形变 ⑥每个三角形分别求节点应力⑦求三角形单元内的位移、应力、应变分布1.求解应变矩阵B i (i=1,2,3,4)jim i iijjj mmm i,j,m i j m m ji j m a x y x y b y y =-=-轮换[]0001[][][]0002ij m i j m i j m b b b B B B B c c c A ⎡⎤⎢⎥⎡⎤==⎢⎥⎣⎦各点坐标可从图中读出，对6个点进行逆时针编号：点O坐标（0,0），点A坐标（0.1,0），点B坐标（0.2,0），点C坐标（0.2,0.1），点D坐标（0.1,0.1），点E坐标（0,0.1）。
四个三角形单元面积相等，2A值为：对三角形单元①：B1=12A[0.1000−0.100000.10−0.100.10.10−0.1−0.1]对三角形单元②：B2=12A[0.1000−0.100000.10−0.100.10.10−0.1−0.1]对三角形单元③：B3=12A[000.10−0.100−0.10000.1−0.1000.10.1−0.1]对三角形单元④：2121=0.01 m1i ij jm mx yA x yx y=0 a0 a0.010.1 0 0.10 c0.1 c0.1i j mi j mi j mab b bc======-===-0.01 a0.01 a0.010 0.1 0.10.1 c0.1 c0i j mi j mi j mab b bc==-====-=-==0.01 a0.01 a0.010 0.1 0.10.1 c0 c0.1i j mi j mi j mab b bc==-====-=-==0.02 a0.01 a00.1 0.1 00 c0.1 c0.1i j mi j mi j mab b bc==-==-====-=B4=12A[−0.100.1000000−0.100.10−0.1−0.10.10.10]2.求解单元刚度矩阵K i(i=1,2,3,4)单元刚度矩阵的表达式为：由平面问题物理方程可得：由于[D]中元素是常量，而在线性位移模式下，[B]中的元素也是常量，且因此可得单元刚度矩阵[]e K可记为分块矩阵形式，如下所示，这一点在之后的叠加过程中得以应用，先将矩阵叠加为6*6形式，再展开为12*12的矩阵。
