人教版七年级数学上册整式知识点讲解

13．合并同类项 m－3m＋5m－7m＋…＋1 013m 的结果为( B )
A．0
B．507m
C．m
D．以上答案都不对
14．先合并同类项，再求值：
1
12
(1)4a2b－0.4ab2－2a2b＋5ab2－1，其中 a＝2，b＝－1.
11
2
解：原式＝(4a2b－2a2b)＋(－0.4ab2＋5ab2)－1
易错点 对同类项的判断出错 1
11．计算：2a2b3－2a2b3＋3a3b2－a2b3－2a3b2. 1
解：原式＝2a2b3＋a3b2.
12．(1)(2020·黔南)若单项式 am－2bn＋7 与单项式－3a4b4 的和仍是 一个单项式，则 m－n＝ 9 ．
(2)已知多项式 mx2－4xy－x－2x2＋2nxy－3y 合并同类项后不含 二次项，则 nm 的值是 4 ．
5．计算 3x2－x2 的结果是( B )
A．2
B．2x2
C．2x
D．4x2
6．下列运算中，正确的是( C )
A．3a＋2b＝5ab
B．2a3＋3a2＝5a5
C．3a2b－3ba2＝0
D．5a2－4a2＝1
7．(1)(2021·天津)计算 4a＋2a－a 的结果为 5a ．
1 (2)计算：x5y3－3x5y3＝
知识点 3 合并同类项的应用 10．小明用 3 天看完一本课外读物，第一天看了 a 页，第二天 看的比第一天多 50 页，第三天看的比第二天少 85 页． (1)用含 a 的式子表示这本书的页数． 解：(1)这本书的页数为 a＋a＋50＋a＋50－85＝(3a＋15)页． (2)当 a＝50 时，这本书有多少页？ 解：(2)当 a＝50 时，3a＋15＝3×50＋15＝165. 答：当 a＝50 时，这本书有 165 页．

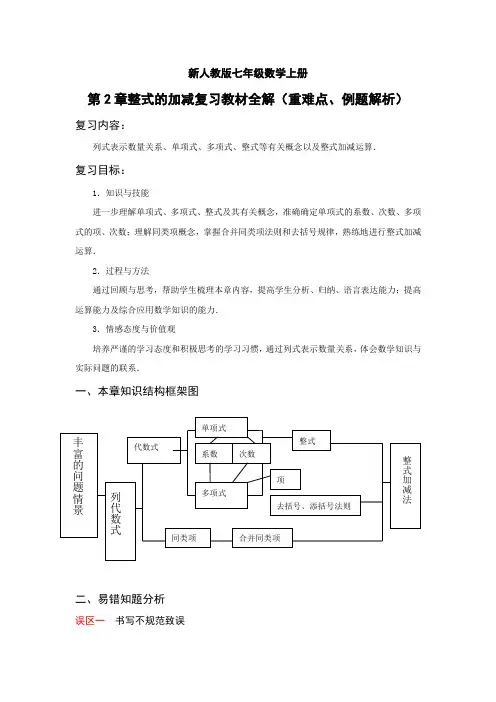
新人教版七年级数学上册第2章整式的加减复习教材全解（重难点、例题解析）复习内容：列式表示数量关系、单项式、多项式、整式等有关概念以及整式加减运算．复习目标：1．知识与技能进一步理解单项式、多项式、整式及其有关概念，准确确定单项式的系数、次数、多项式的项、次数；理解同类项概念，掌握合并同类项法则和去括号规律，熟练地进行整式加减运算．2．过程与方法通过回顾与思考，帮助学生梳理本章内容，提高学生分析、归纳、语言表达能力；提高运算能力及综合应用数学知识的能力．3．情感态度与价值观培养严谨的学习态度和积极思考的学习习惯，通过列式表示数量关系，体会数学知识与实际问题的联系．一、本章知识结构框架图二、易错知题分析误区一书写不规范致误例1 用代数式表示下列语句：（1）比x 与y 的和的平方小x 与y 的和的数 （2）a 的2倍与b 的31的差除以a 与b 的差的立方。

错解（1）（22y x +）－（x+y ） （2）（2a-1/3b ）÷(x+y)剖析：（1）要表示的是“比x 与y 的和的平方小x 与y 的和的数”，应该先求和再求平方即应该是)()(2y x y x +-+，而不应该是（22y x +）－（x+y ）。

（2）是书写不规范，除号要用分数线代替，即应该写成3)(312b a ba --。

正解：（1）)()(2y x y x +-+ （2）3)(312b a ba -- 误区二 概念不清致误例2、判断下列各组是否是同类项：（1）0.2x 2y 与0.2xy 2 （2）4abc 与4ac （3）－130与15 （4）-532m n 与423n m（5）-++()()a b a b 332与 （6）7311pq p q n n n n ++与错解：（1）（3）（4）（6）是同类项，（2）（5）不是同类项。

剖析：（1）0.2x 2y 与0.2xy 2因为字母x 的指数不同，字母y 的指数也不同，所以不是同类项。

千里之行，始于足下。

七年级数学上册第二章整式的加减全章知识点总结新版新人教版以下是七年级数学上册第二章整式的加减的知识点总结（新人教版）：1. 整式的概念：由常数和变量的乘积以及其和差的形式构成的代数式称为整式。

2. 整式的加法：将同类项相加，不同类项保持不变。

3. 同类项：具有相同字母，相同指数的项称为同类项。

4. 倍数和倍式：若正整数a能整除正整数b（即b/a的结果为整数），则a称为b的因数，b称为a的倍数。

a、b都是整数。

5. 同底数幂的加减法：同底数幂相加（或相减）时，保持底数不变，将指数相加（或相减）。

6. 整式的减法：先将被减整式中的各项取相反数，然后按照整式的加法规则进行加法运算。

7. 约束条件：表示一些情况下的特殊要求，一般用等式或不等式表示。

8. 字母运算规则：（1）相同字母的指数相加（或相减）。

（2）不同字母之间的运算，字母之间互不影响。

9. 整式化简：将整式中的同类项合并后，将不同字母之间的项单独放在一起。

第1页/共2页锲而不舍，金石可镂。

10. 内括号化简：使用分配律将多个内括号化简为单个内括号。

11. 外括号化简：使用分配律将外括号前的数分别与里面的每一项进行乘法运算。

12. 同底数幂的运算规则：（1）乘法：底数相同，指数相加。

（2）除法：底数相同，指数相减。

13. 括号内指数的运算规则：括号内的整个表达式的指数乘以括号外数的指数。

14. 幂的指数为负的意义：a的-n次方等于1除以a的n次方。

15. 合并同类项：将整式中相同的同类项相加或相减，得到的结果仍为整式。

16. 合并同底数幂：将整式中的同底数幂相加或相减，得到的结果仍为整式。

这些是七年级数学上册第二章整式的加减的知识点总结，希望对你有帮助！。

＝4(a－b)＋(2a＋b) ＝4a－4b＋2a＋b ＝6a－3b ＝3(2a－b) ＝3×2 ＝6.
(1)用含 x 的式子表示这个三角形的周长． 解：(1)第二条边长为(x＋2)－5＝(x－3)cm， 第三条边长为 2(x－3)＝(2x－6)cm， 则三角形的周长为(x＋2)＋(x－3)＋(2x－6)＝(4x－7)cm.
(2)当 x＝6 时，这个三角形的周长是多少？ 解：(2)当 x＝6 时，4×6－7＝17(cm)． 所以当 x＝6 时，这个三角形的周长为 17 cm.
解：(2)因为 1 米的铝合金的平均费用为 50 元，x＝1.5，y＝2.5， 所以(1)中所需铝合金的总费用为 50×(16×1.5＋14×2.5)＝2 950(元)．
15．定义一种新运算： 1⊙3＝1×4＋3＝7； 3⊙(－1)＝3×4－1＝11； 5⊙4＝5×4＋4＝24； 4⊙(－3)＝4×4－3a－3a)＋(－2＋3)
35 ＝－2a＋2.
知识点 3 去括号化简的应用 7．一块菜地共(6m＋2n)亩，其中(3m＋6n)亩种植白菜，剩下的 地种植黄瓜，则种植黄瓜 (3m－4n) 亩．
8．一个三角形的第一条边长为(x＋2)cm，第二条边长比第一条 边长小 5 cm，第三条边长是第二条边长的 2 倍．
C．8
D．－8
11．当 a 是整数时，整式 a3－3a2＋7a＋7＋(3－2a＋3a2－a3)的
值一定是( C )
A．3 的整数倍
B．4 的整数倍
C．5 的整数倍
D．10 的整数倍
12．(2021·温州)某地居民生活用水收费标准：每月用水量不超
过 17 立方米，每立方米 a 元；超过部分每立方米(a＋1.2)元．该地
区某用户上月用水量为 20 立方米，则应缴水费为( D )

人教版七年级数学上册整式知识点知识点整式加减单项式与多项式统称为整式。

整式是有理式的一部分，在有理式中可以包含加，减，乘，除四种运算，但在整式中除数不能含有字母。

单项式和多项式都统称为整式。

把一个多项式化为几个最简整式的乘积的形式，这种变形叫做把这个多项式因式分解(也叫作分解因式)。

分解因式与整式乘法为相反变形。

(1)单项式：表示数与字母的乘积的代数式，叫做单项式，单独的一个数或一个字母也是单项式，如、2pi;r、a，0……都是单项式。

(2)多项式：几个单项式的和叫做多项式整式的乘法1. 单项式乘法法则:单项式相乘,把它们的系数、相同字母分别相乘，对于只在一个单项式里含有的字母，连同它的指数作为积的一个因式。

单项式乘法法则在运用时要注意以下几点：①积的系数等于各因式系数积，先确定符号，再计算绝对值。

这时容易出现的错误的是，将系数相乘与指数相加混淆;②相同字母相乘，运用同底数的乘法法则;③只在一个单项式里含有的字母，要连同它的指数作为积的一个因式;④单项式乘法法则对于三个以上的单项式相乘同样适用;⑤单项式乘以单项式，结果仍是一个单项式。

2.单项式与多项式相乘单项式乘以多项式，是通过乘法对加法的分配律，把它转化为单项式乘以单项式，即单项式与多项式相乘，就是用单项式去乘多项式的每一项，再把所得的积相加。

单项式与多项式相乘时要注意以下几点：①单项式与多项式相乘，积是一个多项式，其项数与多项式的项数相同;②运算时要注意积的符号，多项式的每一项都包括它前面的符号;③在混合运算时，要注意运算顺序。

3.多项式与多项式相乘多项式与多项式相乘，先用一个多项式中的每一项乘以另一个多项式的每一项，再把所得的积相加。

多项式与多项式相乘时要注意以下几点：①多项式与多项式相乘要防止漏项，检查的方法是：在没有合并同类项之前，积的项数应等于原两个多项式项数的积;②多项式相乘的结果应注意合并同类项;③对含有同一个字母的一次项系数是1的两个一次二项式相乘，其二次项系数为1，一次项系数等于两个因式中常数项的和，常数项是两个因式中常数项的积。

七年级数学上册期末复习整式的加减知识点+易错题整式的加减知识点整式知识点1．单项式：在代数式中，若只含有乘法（包括乘方）运算。

或虽含有除法运算，但除式中不含字母的一类代数式叫单项式.2．单项式的系数与次数：单项式中不为零的数字因数，叫单项式的数字系数，简称单项式的系数；系数不为零时，单项式中所有字母指数的和，叫单项式的次数.3．多项式：几个单项式的和叫多项式.4．多项式的项数与次数：多项式中所含单项式的个数就是多项式的项数，每个单项式叫多项式的项；多项式里，次数最高项的次数叫多项式的次数；注意：（若a、b、c、p、q是常数）ax2+bx+c和x2+px+q是常见的两个二次三项式.5．整式：凡不含有除法运算，或虽含有除法运算但除式中不含字母的代数式叫整式.整式分类为：错误!未找到引用源。

.6．同类项：所含字母相同，并且相同字母的指数也相同的单项式是同类项.7．合并同类项法则：系数相加，字母与字母的指数不变.8．去（添）括号法则：去（添）括号时，若括号前边是“+”号，括号里的各项都不变号；若括号前边是“-”号，括号里的各项都要变号.9．整式的加减：整式的加减，实际上是在去括号的基础上，把多项式的同类项合并.10.多项式的升幂和降幂排列：把一个多项式的各项按某个字母的指数从小到大（或从大到小）排列起来，叫做按这个字母的升幂排列（或降幂排列）.注意：多项式计算的最后结果一般应该进行升幂（或降幂）排列.11. 列代数式列代数式首先要确定数量与数量的运算关系，其次应抓住题中的一些关键词语，如和、差、积、商、平方、倒数以及几分之几、几成、倍等等.抓住这些关键词语，反复咀嚼，认真推敲，列好一般的代数式就不太难了.12.代数式的值根据问题的需要，用具体数值代替代数式中的字母，按照代数式中的运算关系计算，所得的结果是代数式的值.13. 列代数式要注意①数字与字母、字母与字母相乘，要把乘号省略；②数字与字母、字母与字母相除，要把它写成分数的形式；③如果字母前面的数字是带分数，要把它写成假分数。

人教版七年级数学上册整式的加减知识点总结及题型汇总(无答案)整式的加减知识点总结及题型汇总整式知识点1．单项式：在代数式中，若只含有乘法（包括乘方）运算。

或虽含有除法运算，但除式中不含字母的一类代数式叫单项式.2．单项式的系数与次数：单项式中不为零的数字因数，叫单项式的数字系数，简称单项式的系数；系数不为零时，单项式中所有字母指数的和，叫单项式的次数.3．多项式：几个单项式的和叫多项式.4．多项式的项数与次数：多项式中所含单项式的个数就是多项式的项数，每个单项式叫多项式的项；多项式里，次数最高项的次数叫多项式的次数；注意：（若a 、b 、c 、p 、q 是常数）ax 2+bx+c 和x 2+px+q 是常见的两个二次三项式. 5．整式：凡不含有除法运算，或虽含有除法运算但除式中不含字母的代数式叫整式. 整式分类为：⎩⎨⎧多项式单项式整式 .6．同类项：所含字母相同，并且相同字母的指数也相同的单项式是同类项. 7．合并同类项法则：系数相加，字母与字母的指数不变.8．去（添）括号法则：去（添）括号时，若括号前边是“+”号，括号里的各项都不变号；若括号前边是“-”号，括号里的各项都要变号.9．整式的加减：整式的加减，实际上是在去括号的基础上，把多项式的同类项合并.10.多项式的升幂和降幂排列：把一个多项式的各项按某个字母的指数从小到大（或从大到小）排列起来，叫做按这个字母的升幂排列（或降幂排列）.注意：多项式计算的最后结果一般应该进行升幂（或降幂）排列.11. 列代数式列代数式首先要确定数量与数量的运算关系，其次应抓住题中的一些关键词语，如和、差、积、商、平方、倒数以及几分之几、几成、倍等等.抓住这些关键词语，反复咀嚼，认真推敲，列好一般的代数式就不太难了.12.代数式的值根据问题的需要，用具体数值代替代数式中的字母，按照代数式中的运算关系计算，所得的结果是代数式的值. 13. 列代数式要注意①数字与字母、字母与字母相乘，要把乘号省略； ②数字与字母、字母与字母相除，要把它写成分数的形式； ③如果字母前面的数字是带分数，要把它写成假分数。

整式及其加减是数学七年级上册的重要知识点之一，在学生学习过程中往往会遇到一些难点和易错点。

为了帮助学生更好地掌握这一知识点，本文将对人教版数学七年级上册整式及其加减考点进行详细分析和解读。

一、整式的概念及特点1. 整式的定义：整式是由若干个字母与常数通过加、减、乘、乘方等运算符号连接而成的代数表达式。

2. 整式的特点：整式和多项式的区别在于，整式中可能含有有理数指数的正整数次幂，也可能含有有理数指数的负整数次幂，并且可能含有有理数指数的零次幂。

二、整式的加减运算规则3. 整式加减的基本规则：整式的加减运算遵循同类项之间可以相加或相减的法则，即同类项可以合并为一个项。

4. 整式加减的步骤：在进行整式的加减运算时，首先要对整式中的同类项进行合并，然后按照合并后的结果进行简化，最终得到一个最简整式。

5. 整式加减的注意事项：在进行整式的加减运算时，需要注意各项系数的正负、字母的次数和字母的顺序，以免出现计算错误。

三、整式加减的常见类型题目6. 整式加减的基础练习：例如给出一个简单的整式加减题目，让学生通过合并同类项和简化整式来求解。

7. 整式加减的拓展练习：例如给出一个较复杂的整式加减题目，涉及到多个字母和多个项的加减运算，考察学生对整式加减运算规则的掌握程度。

8. 实际问题解决类题目：例如给出一个实际生活中的问题，通过建立整式模型来求解，考察学生运用整式加减进行实际问题求解的能力。

四、整式加减的解题技巧和方法9. 整式加减的化简方法：在进行整式加减运算时，可以通过扩括号、合并同类项、提取公因式等方法进行化简，从而简化整式的计算过程。

10. 整式加减的变形技巧：当遇到复杂的整式加减题目时，可以通过整理项的顺序、利用加法逆元等方法进行整式的变形，使得整式的计算更加简便。

11. 整式加减的实际问题转化方法：对于实际问题解决类的整式加减题目，可以通过建立适当的代数模型，将问题转化为整式加减的求解过程，从而更好地解决实际问题。

2023学年七年级上册数学第二章《2.1整式》讲义【知识点一】单项式【定义】用把数和字母连接而成的式子叫做代数式。

常见运算符号：加、减、乘、除（包括分数线）、乘方注意：单独一个数字或者一个字母也是代数式；π是数字不是字母 【代数式书写规范】（1）数字与字母、字母与字母相乘时，乘号换“”或，数字在，字母在。

若数字是1或－1时，“1” （2）除号改为（3）带分数改为【例1】将下列代数式改为规范的书写形式 （1）m ×2（2）1×x 2（3）（a+1）÷m（4）2x+y 厘米（5）211m（6）-1xy 2【知识点一】单项式一、用含有字母的式子填空，看看列出的式子有什么特点： （1）边长为a 的正方形的表面积为 ；体积为。

（2）铅笔的单价为x 元，圆珠笔的单价是铅笔单价的2.5倍，圆珠笔的单价是 元。

（3）n 表示一个数，则它的相反数是 。

1、单项式的概念：上面列出的式子 6a 2，a 3，2.5x ，-n ，它们都是数或字母的乘积，像这样的式子叫做单项式。

单独一个数或一个字母也是单项式。

【例】指出下列代数式中，哪些是单项式： abc ，261xy ，a 3， ﹣5ab 3， a +b ，a ， 20%m ， ﹣0.6x 2y ， ﹣xy 2，y x −31，﹣12、单项式系数和次数①从单项式的定义可看出单项式由两部分组成：数字因数和字母因数。

②单项式的系数：单项式中的数字因数。

如：单项式500t 的系数是，-2x 2y 的系数是③单项式的次数：单项式中所有字母的指数之和。

如：单项式500t 的t 的指数是，500t 的次数是单项式-2x 2y 的系数是，字母x 与y 的指数的和是，-2x 2y 的次数是【练1】说出下列单项式的系数和次数。

4π２x , 31a 2b 2, ﹣a 2b ,﹣4×105a 6,﹣32x 2y ,2335a b 【例2】用单项式填空，并指出它们的系数和次数：（1）每个书包有12册书本，n 个书包有________册书本；次数是 ，系数是 。

， =
， =
， =

×

×

×

×






=
， =
， 所以第7个数为： =
；

×

×

×
(2)由（1）可得：第n个数是
(3)根据题意可得：


=





(+)

×


，∴


；




(4)解：原式 = − + − + − +
=−
解：ab2−3a2b−3(ab2−a2b)
=ab2−3a2b−(3ab2−3a2b)
=ab2−3a2b−3ab2+3a2b
Байду номын сангаас
直接化简求值法
=−2a2b
当a=2，b=−1时，原式=−2╳22 ╳(−1)=4.
典型例题
(2).若多项式x2+2x−8=0,求2x2+4x−17的值.
分析：没有直接求出的x值，如果把x2+2x看成一个整体，

+
=

+
.
，
是第12个数；



−







+ − + ⋯+ −

+
，
典型例题
②.图形的规律.
一张长方形桌子可坐6人，按图3将桌子拼在一起.
（1）2张桌子拼在一起可坐________人，4张桌子拼在一起可坐
________人，n张桌子拼在一起可坐________人；

感悟新知
知3－讲
2. 去括号的注意事项 (1)括号内的每一项都包含前面的符号，特别是括号外的
数是负数时，注意符号； (2)不要漏乘括号内的项，特别是常数项.
感悟新知
知3－讲
特别解读 1. 去括号的根据是乘法分配律. 2. 括号内多项式本来是和的形式，所以乘括
号外的数所得的结果要相加.
感悟新知
知2－练
例 4 (1)某中学七年级一班数学活动中分为三个组，第一 组有a 人，第二组比第一组的一半多5 人，第三组 人数等于前两组人数的和，则第三组有 _(32_a_＋__5_)人；
解题秘方：先根据数量关系列出整式，然后合并
同类项得到最后结果. 解：因为第一组有a 人，所以第二组有(12a＋5)人. 由a＋ 12a＋5 =32a＋5，可知，第三组有32a＋5 人.
知2－讲
感悟新知
知2－讲
4.
升降幂排列：把一个多项式各项按某个字母的指数从大 ••
到小的顺序排列，叫作这个多项式按这个字母的降幂排
••
•••
列• . 若按某个字母的指数从小到大的顺序排列，叫作这
个多项式按这个字母的升幂排列. ••••
感悟新知
特别解读
知2－讲
1. 合并同类项法则可简记为“一相加，两不变”.其中，“一相
知2－练
感悟新知
知2－练
3-1.[期末·广州天河区] 下列各式中正确的是( C ) A．2x＋2y=4xy B．3x2 － x2=2 C．3xy － 2xy=xy D．2x＋4x=6x2
感悟新知
知2－练
3-2.[中考·黄冈] 先化简，再求值：4xy－2xy－(－3xy)， 其 中x=2，y=－1. 解：4xy－2xy－(－3xy)＝4xy－2xy＋3xy＝5xy. 当x＝2，y＝－1时，原式＝5×2×(－1)＝－10.

2.1 整式
第一课时 用字母表示数
0
1.了解字母表示数的意义; 2.掌握列式书写的规范性； 3.会用含有字母的式子表示实际问题中的数量关系．
掌握列式书写的规范性。
会用含有字母的式子表示实际问题中的数量关系。
0
青藏铁路线上,在格尔木到拉萨之间有一段很长的冻
土地段,列车在冻土地段的行驶速度是100千米/时,在非冻
长是a mm，小正方形的边长是b mm，用式子表示剩余部分的面
积.
(a2 b2 )mm2
0
知识回顾 问题探究 课堂小结 随堂检测
如a×b表示为ab或 a·b.
②数与字母相乘时，数必须写在字母前面，
当这个数为1时可以省略不写， 如1ab表示为ab；
当这个数是-1时，只省略1，但“负号”不能省略， 如-1ab表示为-ab；
当这个数是带分数时必须把这个数化为假分数，
如 3 2 ab 应表示为 17 ab .
550ຫໍສະໝຸດ 知识回顾 问题探究 课堂小结 随堂检测
思考：式子中m、x、a在各自实际问题中分别表示什么意义？
0
知识回顾 问题探究 课堂小结 随堂检测
探究一：字母表示数的意义
难点知识▲
活动1
总结：用字母表示数，虽然字母在不同的实际 问题中表示的意义不一样，但与数一样可以参 与各种运算，可以用式子把数量关系简明地表 示出来。字母比数字更具有一般性。
0
知识回顾 问题探究 课堂小结 随堂检测
可得到这所住宅的建筑面积(单位:m2 )是 (x2 2x 18)m2.
0
知识回顾 问题探究 课堂小结 随堂检测
探究三：会用列式表示实际问题中简单的数量关系 重点、难点知识★▲
活动3 练习：(1)某种商品每袋4.8元,在一个月内的销售量是m袋, 用式子表示在这个月内销售这种商品的收入. 4.8m元

米，宽为 (10－x) 米．
(2)菜地的面积为
(18－2x)(10－x)
平方米．
16．(2021·石家庄长安区期末)小明跟同学在某餐厅吃饭，下图 为此餐厅的菜单：
套餐一：一份重庆小面 套餐二：一份重庆小面加一杯饮料 套餐三：一份重庆小面加一杯饮料和一份沙拉 若他们一共点了 10 份重庆小面、x 杯饮料、y 份沙拉，则他们 点了 (10－x) 份套餐一．
(2)若把 n 张这样的餐桌拼接起来，四周可坐多少人？ 解：(2)n 张餐桌按上述方式拼接，四周可坐(4n＋2)人．
51 解：(1)2a－3b. (2)x 与 4 的商的平方．
x 解：(2)(4)2.
1 12．用字母表示“x 的 2 倍与 y 的差的平方的3”，正确的是( D )
1 A．(2x2－y)·3
1 B．2x－3y2
1 C．(2x－3y)2
1 D．3(2x－y)2
6 13．某件夏装的原价是 a 元，因过季打折，以(10a－20)元出售．下 列说法中，能正确表述该夏装出售价格的是( A ) A．原价打六折后再降低 20 元 B．原价打四折后再降低 20 元 C．原价降低 20 元后再打六折 D．原价降低 20 元后再打四折
知识点 3 用含字母的式子表示实际问题中的数量关系
5．已知苹果每千克 m 元，则 2 千克苹果共
元( D )
A．m－2
B．m＋2
m C． 2
D．2m
6．一列火车从甲站出发，5 h 后行驶了 m km，则这列火车的平 m
均速度是 5 km/h.
7．小何买了 4 本笔记本，10 支圆珠笔，设笔记本的单价为 a 元，
C．5 个 a 的和
D．5 个 a 的积
3．用式子表示“a 的 2 倍与 3 的和”正确的是( B )

2.1整式知识点归纳由数和字母经过有限次加、减、乘、除、乘方等代数运算所得的式子叫做代数式。

单独一个数或者字母也是代数式。

、a5、2x2y3、100、x都是代数式。

例1、2a、3+x、5a-6b、3(a+b)÷c、1x代数式的书写规范：①字母与字母相乘、数字与字母相乘，可以省略“×”号，也可以写成“·”。

例2、a×b可以写成a·b或者ab；7×a可以写成7·a或者7a 。

②数字与数字相乘，必须写“×”号，不能省略。

例3、3×7不能写成3·7 。

③数字与字母相乘，数字写在字母的前面，字母按英文字母的顺序排列。

例4、a×6不能写成a6，而应该写成6a 。

例5、3×m×a×n可以写成3amn 。

④数字、字母与含有括号的式子相乘时，数字和字母都要放在括号前面。

例6、(a+b)×4不能写成(a+b)4，而应该写成4(a+b) 。

⑤如果数字因数是1，则要省略。

例7、1a要省略数字因数1，直接写成a即可。

⑥当代数式后面要跟单位时，如果这个代数式是几个数的和或差的形式，则要用括号括起来。

例8、(a+b)个、(x-y)元、(a+2b-3c)条⑦要表示除法运算时，不使用“÷”号，而是把式子写成分数的形式。

例9、3÷a 要写成3a ；x ÷y 要写成x y 。

⑧带分数要写成假分数。

例10、213要写成73 。

代数式可以有绝对值，但一定不能有等号、不等号、约等号。

例11、|a|+2是代数式；x+y=6、3+a ＞b 、6-x ≈3都不是代数式。

由数和字母的积组成的代数式叫做单项式。

单独一个数或者字母也是单项式。

例12、3a 、a 4、4a 2b 3、50、x 都是单项式。

单项式的数字因数叫做这个单项式的系数，所有字母的指数之和叫做这个单项式的次数。

整式的概念【要点梳理】要点一、单项式1.单项式的概念：如22xy -，13mn ，-1，它们都是数与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式．要点诠释：（1）单项式包括三种类型：①数字与字母相乘或字母与字母相乘组成的式子；②单独的一个数；③单独的一个字母．（2）单项式中不能含有加减运算，但可以含有除法运算．如：2st 可以写成12st 。

但若分母中含有字母，如5m就不是单项式，因为它无法写成数字与字母的乘积． 2.单项式的系数：单项式中的数字因数叫做这个单项式的系数．要点诠释：（1）确定单项式的系数时，最好先将单项式写成数与字母的乘积的形式，再确定其系数；（2）圆周率π是常数．单项式中出现π时，应看作系数；（3）当一个单项式的系数是1或-1时，“1”通常省略不写；（4）单项式的系数是带分数时，通常写成假分数，如：2114x y 写成254x y ． 3.单项式的次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数．要点诠释：单项式的次数是计算单项式中所有字母的指数和得到的，计算时要注意以下两点：（1）没有写指数的字母，实际上其指数是1，计算时不能将其遗漏；（2）不能将数字的指数一同计算．要点二、多项式1.多项式的概念：几个单项式的和叫做多项式．要点诠释：“几个”是指两个或两个以上．2. 多项式的项：每个单项式叫做多项式的项，不含字母的项叫做常数项． 要点诠释：（1）多项式的每一项包括它前面的符号．（2）一个多项式含有几项，就叫几项式，如：2627x x --是一个三项式．3. 多项式的次数：多项式里次数最高项的次数，叫做这个多项式的次数．要点诠释：（1）多项式的次数不是所有项的次数之和，而是多项式中次数最高的单项式的次数．（2）一个多项式中的最高次项有时不止一个，在确定最高次项时，都应写出． 要点三、 整式单项式与多项式统称为整式．要点诠释：（1）单项式、多项式、整式这三者之间的关系如图所示．即单项式、多项式必是整式，但反过来就不一定成立．（2）分母中含有字母的式子一定不是整式．【典型例题】类型一、整式概念辨析1．指出下列各式中哪些是单项式？哪些是多项式？哪些是整式？ 22x y +，x -，3a b +，10，61xy +，1x ，217m n ，225x x --，22x x +，7a举一反三： 【变式】下列代数式：322332111;;;;2;-232a x y ab x x y x y y x+--++π①②③④⑤⑥，其中是单项式的是_______________，是多项式的是_______________.类型二、单项式2．指出下列代数式中的单项式，并写出各单项式的系数和次数．234a b -，a -，442x ，a mn ，223a y π，a -3，5-3，82-310tm ⨯，2x y举一反三：【变式1】单项式3x 2y 3的系数是 ．【变式2】下列结论正确的是( )．A ．没有加减运算的代数式叫做单项式．B ．单项式237xy 的系数是3，次数是2． C ．单项式m 既没有系数，也没有次数．D ．单项式2xy z -的系数是-1，次数是4．类型三、多项式3.多项式24242153x y x y x -+-+，这个多项式的最高次项是什么？一次项的系数是什么？常数项是什么？这是几次几项式?4. 已知多项式32312246753m x xy x y y x y ---+--． (1)求多项式各项的系数和次数．(2)如果多项式是七次五项式，求m 的值．举一反三：【变式】多项式()34ba x x xb --+-是关于x 的二次三项式，求a 与b 的差的相反数．类型四、整式的应用5. 用整式填空：(1)某商场将一种商品A 按标价的9折出售(即优惠10%)仍可获利10%，若商场商品A 的标价为a 元，那么该商品的进价为________元(列出式子即可，不用化简)．(2)甲商品的进价为1400元，若标价为a 元，按标价的9折出售；乙商品的进价是400元，若标价为b 元，按标价的8折出售，列式表示两种商品的利润率分别为甲：________ 乙：________．举一反三：【变式】（2014秋•栖霞市期末）对下列代数式作出解释，其中不正确的是（ ）A. a ﹣b ：今年小明b 岁，小明的爸爸a 岁，小明比他爸爸小（a ﹣b ）岁B. a ﹣b ：今年小明b 岁，小明的爸爸a 岁，则小明出生时，他爸爸为（a ﹣b ）岁C. ab ：长方形的长为acm ，宽为bcm ，长方形的面积为abcm2 D. ab ：三角形的一边长为acm ，这边上的高为bcm ，此三角形的面积为abcm2【巩固练习】一、选择题1．（2014秋•章丘市校级期末）下面的说法正确的是（ ）A. ﹣2不是代数式B. ﹣a 表示负数C. 的系数是3D. x+1是代数式2．已知单项式243x y -，下列说法正确的是( )． A ．系数是-4，次数是3B ．系数是43-，次数是3 C ．系数是43，次数是3 D ．系数是43-，次数是2 3．如果一个多项式的次数是3，那么这个多项式的任何一项的次数( )．A ．都小于3B ．都等于3C ．都不小于3D ．都不大于34．下列式子：a+2b ，2a b -，221()3x y -，2a，0中，整式的个数是( )． A ．2个 B ．3个 C ．4个 D ．5个 5.．关于单项式3222x y z -，下列结论正确的是( )．A ．系数是-2，次数是4B ．系数是-2，次数是5C ．系数是-2，次数是8D ．系数是-23，次数是56．一组按规律排列的多项式：a b +，23a b -，35a b +，47a b -，…，其中第10个式子是( )．A ．1019a b +B ．1019a b -C ．1017a b -D ．1021a b -二、填空题7．代数式23mn ，2353x y ，2x y -，23ab c -，0，31a a +-中是单项式的是________，是多项式的是________．8.关于x 的多项式3(1)23nm x x x --+的次数是2，那么______,______m n ==． 9．多项式2x 2-3x+5是_ 次______项式．10．（2015•长春模拟）今年五．一假期，张老师一家四口开着一辆轿车去长春市净月潭森林公园度假．若门票每人a 元，进入园区的轿车每辆收费20元，则张老师一家开车进入净月潭森林公园园区所需费用是 元（用含a 的代数式表示）． 11．有一组单项式：2a ，32a -，43a ，…，请观察它们的构成规律，用你发现的规律写出第10个单项式：________．12．关于x 的二次三项式的一次项的系数为5，二次项的系数为-3，常数项为-4，按照x 的次数逐渐降低排列，这个二次三项式为________．13．某校生物教师李老师在生物实验室做试验时，将水稻种子分组进行发芽试验：第1组取3粒，第2组取5粒，第3组取7粒，第4组取9粒……按此规律，请你推测第n 组应该取种子数是________粒．。