当前位置：文档之家 › 形式语言与自动机理论--第七章(蒋宗礼)

形式语言与自动机理论--第七章(蒋宗礼)

  • 格式：ppt
  • 大小：453.00 KB
  • 文档页数：51

下载文档原格式

  / 51

合集下载

形式语言与自动机2009-11-30

形式语言与自动机2009-11-30


4. 王柏, 杨娟. 形式语言与自动机. 北京: 北京邮电大学出版社, 2003.2
5. Thomas A.Sudkamp著. 孙家骝等译. 语言与机器—计算机 科学理论导论 (第3版).北京: 机械工业出版社, 2008年
4
构造文法G，使L(G)={wwT|w∈{0,1,2,3}+}。 S00 | 11 | 22 | 33 | 0S0 | 1S1 | 2S2 | 3S3 构造文法G，使L(G12)={w|w是十进制有理数}。 SR | +R | -R RN | B BN.D N0 | AM D0 | MA A1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 Mε | 0M | 1M | 2M | 3M | 4M | 5M | 6M | 7M | 8M | 9M
形式语言与自动机理论
Formal Languages and Automata Theory
1
主要内容
语言的文法描述。 RL
RG、 FA、RE、RL的性质 。
CFL
CFG(CNF、GNF)、PDA、CFL的性质。
TM
基本TM、构造技术、TM的修改。
CSL
CSG、LBA。
2
主要内容
抽象模型 自动机 变种 不确定 NFA 对应语言 •正则语言 •3型 相当于程序或算法 If ,case ,goto, 无变量（内 存）无数组
Байду номын сангаас
下推机
不确定下推机 不确定线性界限 下推机
前后文无关语 言， 2型 前后文有关语 言1型 语言
增加： 堆栈。仍无变量 （内存）无数组
一定停机的 图灵机 图灵机 数学模型， 简洁，易分 析
蒋宗礼送形式语言与自动机理论-资料

蒋宗礼送形式语言与自动机理论-资料


2019/10/15
19
补集(Complementary Set)
A是论域U上的一个集合，A补集是由U中的、 不在A中的所有元素组成的集合
AUA
U
U
9/10/15
20
补集(Complementary Set)
如果AB，则 B A
AAU
AA
B A A B U & A B
2019/10/15
8
1.1.2 集合之间的关系
•集合相等
– 如果集合A，B含有的元素完全相同，则称集 合A与集合B相等(Equivalence)，记作A=B。
•对任意集合A、B、C： ⑴ A=B iff AB且BA。 ⑵ 如果AB，则|A|≤|B| ⑶ 如果AB，则|A|≤|B|。 ⑷ 如果A是有穷集，且AB，则|B|>|A|。
2019/10/15
12
交(Intersection)
• ⑷ A∩B=A iff A B • ⑸ Φ∩A=Φ • ⑹ |A∩B|≤min{|A|，|B|} • ⑺ A∩(B∪C)=(A∩B)∪(A∩C) • ⑻ A∪(B∩C)=(A∪B)∩(A∪C) • ⑼ A∩(A∪B)=A • ⑽ A∪(A∩B)=A
2019/10/15
30
1.2.3递归定义与归纳证明
• 归纳证明
– 与递归定义相对应
– 归纳证明方法包括三大步
• 基础(Basis)：证明最基本元素具有相应性质
• 归纳(Induction)：证明如果某些元素具有相 应性质，则根据这些元素用所规定的方法得 到的新元素也具有相应的性质。
• 根据归纳法原理，所有的元素具有相应的性 质
形式语言与自动机理论
形式语言与自动机蒋宗礼答案

形式语言与自动机蒋宗礼答案

形式语言与自动机蒋宗礼答案形式语言与自动机蒋宗礼答案【篇一：形式语言第四章参考答案(蒋宗礼)】p> 解：所求正则表达式为：(0+1)*。

+⑵ {0, 1}。

解：所求正则表达式为：(0+1)+。

⑶ { x│x∈{0,1}且x中不含形如00的子串 }。

解：根据第三章构造的fa，可得所求正则表达式为：1*(01+)*(01+0+1)。

⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。

++ +q1为终态时的正则表达式：0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式：0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式：0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式：0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)* 将以上5个正则表达式用“+”号相连，就得到所要求的正则表达式。

⑺ { x│x∈{0,1}且当把x看成二进制数时，x模5与3同余和x为0时，│x│=1且x≠0时，x的首字符为1}。

解：先画出状态转移图，设置5个状态q0、q1、q2、q3、q4，分别表示除5的余数是0、1、2、3、4的情形。

另外，设置一个开始状态q.由于要求x模5和3同余，而3模5余3,故只有q3可以作为终态。

由题设，x=0时，│x│=1，模5是1，不符合条件，所以不必增加关于它的状态。

下面对每一个状态考虑输入0和1时的状态转移。

q: 输入1，模5是1，进入q1。

+q0: 设x=5n。

输入0，x=5n*2=10n，模5是0，故进入q0输入1，x=5n*2+1=10n+1，模5是1，故进入q1q1：设x=5n+1。

输入0，x=(5n+1)*2=10n+2，模5是2，故进入q2输入1，x=(5n+1)*2+1=10n+3，模5是3，故进入q3 q2：设x=5n+2。

形式语言与自动机答案蒋宗礼

形式语言与自动机答案蒋宗礼

形式语言与自动机答案蒋宗礼【篇一：形式语言第四章参考答案(蒋宗礼)】p> 解：所求正则表达式为：(0+1)*。

+⑵ {0, 1}。

解：所求正则表达式为：(0+1)+。

⑶ { x│x∈{0,1}且x中不含形如00的子串 }。

解：根据第三章构造的fa，可得所求正则表达式为：1*(01+)*(01+0+1)。

⑷ { x│x∈{0,1}*且x中不含形如00的子串 }。

++ +q1为终态时的正则表达式：0*1(1*(0(10)*111*1)*(0(10)*00*1)*)* q2为终态时的正则表达式：0*11*0((10)*(111*11*0)*(00*11*0)*)*q3为终态时的正则表达式：0*11*0(10)*1(11*11*0((10)*(00*11*0)*)*1)* q4为终态时的正则表达式：0*11*0(10)*11(1*(11*0((00*11*0)*(10)*)*11)*)*将以上5个正则表达式用“+”号相连，就得到所要求的正则表达式。

⑺ { x│x∈{0,1}且当把x看成二进制数时，x模5与3同余和x为0时，│x│=1且x≠0时，x的首字符为1}。

解：先画出状态转移图，设置5个状态q0、q1、q2、q3、q4，分别表示除5的余数是0、1、2、3、4的情形。

另外，设置一个开始状态q.由于要求x模5和3同余，而3模5余3,故只有q3可以作为终态。

由题设，x=0时，│x│=1，模5是1，不符合条件，所以不必增加关于它的状态。

下面对每一个状态考虑输入0和1时的状态转移。

q: 输入1，模5是1，进入q1。

+q0: 设x=5n。

输入0，x=5n*2=10n，模5是0，故进入q0输入1，x=5n*2+1=10n+1，模5是1，故进入q1q1：设x=5n+1。

输入0，x=(5n+1)*2=10n+2，模5是2，故进入q2输入1，x=(5n+1)*2+1=10n+3，模5是3，故进入q3 q2：设x=5n+2。

形式语言与自动机理论--第七章(蒋宗礼)

形式语言与自动机理论--第七章(蒋宗礼)


7.1 基本定义
• 符号使用约定 • 英文字母表较为前面的小写字母，如a，b， c，…，表示输入符号； • 英文字母表较为后面的小写字母，如x，y， z，…，表示由输入字符串； • 英文字母表的大写字母，表示栈符号； • 希腊字母α，β，γ，…，表示栈符号串。
7.1 基本定义
• 即时描述(instantaneous description，ID) (q，w，γ)∈(Q，∑*，Γ*)称为M的一个 即时描述。它表示M处于状态q，w是当前 还未处理的输入字符串，而且M正注视着w 的首字符，栈中的符号串为γ，γ的最左符 号为栈顶符号，最右符号为栈底的符号， 较左的符号在栈的较上面，较右的符号在 栈的较下面。
• CSL
– CSG、LBA。
教材及主要参考书目
1.蒋宗礼，姜守旭. 形式语言与自动机理论. 北京： 清华大学出版社，2003年 2. John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001 3. John E Hopcroft, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, 1979
第7章下推自动机
• 主要内容
– – – – PDA的基本概念。 PDA的构造举例。 用终态接受语言和用空栈接受语言的等价性。 PDA是CFL的接受器。
形式语言与自动机-经典教学课件(完整版)资料讲解

形式语言与自动机-经典教学课件(完整版)资料讲解

3. John E Hopcroft, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, 1979
2020/6/20
5
第1章 绪论
2020/6/20
8
1.1.2 集合之间的关系
⑸ 如果AB，则对x∈A，有x∈B。 ⑹ 如 果 AB ， 则 对 x∈A ， 有 x∈B 并 且
x∈B，但xA。 ⑺ 如果AB且BC，则AC。 ⑻ 如果AB且BC，或者AB且BC，或者
AB且BC，则AC。 ⑼ 如果A=B，则|A|=|B|。
2020/6/20
⑵ (A× B)× C≠A× (B× C)。 ⑶ A× A≠A。
⑷ A× Φ=Φ。
2020/6/20
15
笛卡儿积(Cartesian product)
Ai
i1
A{a|AS,aA}
AS
2020/6/20
10
交(intersection)
• 集合A和B中都有的所有元素放在一起构成 的集合为A与B的交 ，记作A∩B。
A∩B={a|a∈A且a∈B}
• “∩”为交运算符，A∩B读作A交B。
• 如果A∩B=Φ，则称A与B不相交。
• ⑴ A∩B= B∩A。 ⑵ (A∩B)∩C=A∩(B∩C)。 ⑶ A∩A=A。
• 1.1 集合的基础知识 • 1.1.1 集合及其表示
– 集合：一定范围内的、确定的、并且彼此可以区 分的对象汇集在一起形成的整体叫做集合(set)， 简称为集(set)。
– 元素：集合的成员为该集合的元素(element)。 – 集合描述形式。 – 基数。 – 集合的分类。
形式语言与自动机理论FormalLanguagesandAutomataTheory

形式语言与自动机理论FormalLanguagesandAutomataTheory


2020/7/10
14
笛卡儿积(Cartesian product)
❖ A与B的笛卡儿积(Cartesian product)是一个集合， 该集合是由所有这样的有序对(a，b)组成的：其中 a∈A，b∈B ，记作A× B。
A× B={(a，b)|a∈A& b∈B }。
❖ “× ”为笛卡儿乘运算符。A× B读作A叉乘B。
❖ A与B的并(union)是一个集合，该集合中的元素要么 是A的元素，要么是B的元素，记作A∪B。
A∪B={a|a∈A或者a∈B}
A1∪A2∪…∪An={a|i，1≤i≤n，使得a∈Ai} A1∪A2∪…∪An ∪…={a|i，i∈N,使得a∈Ai}
Ai
i 1
A {a | A S, a A}
2020/7/10
7
1.1.2 集合之间的关系
❖集合相等
如果集合A，B含有的元素完全相同，则称集合 A与集合B相等(equivalence)，记作A=B。
❖对任意集合A、B、C： ⑴ A=B iff AB且BA。 ⑵ 如果AB，则|A|≤|B|。 ⑶ 如果AB，则|A|≤|B|。 ⑷ 2020/7/10 如果A是有穷集，且AB，则|B|>|A|。 8
❖ 计算思维能力
逻辑思维能力和抽象思维能力
构造模型对问题进行形式化描述
理解和处理形式模型
2020/7/10
2
课程目的和基本要求
❖ 知识
掌握正则语言、下文无关语言的文法、识别模型 及其基本性质、图灵机的基本知识。
❖ 能力
培养学生的形式化描述和抽象思维能力。
使学生了解和初步掌握“问题、形式化描述、自 动化（计算机化）”这一最典型的计算机问题求 解思路。
形式语言与自动机理论--目录

形式语言与自动机理论--目录

形式语言与自动机理论（第2版）作者：蒋宗礼、姜守旭第1章绪论11.1集合的基础知识21.1.1集合及其表示21.1.2集合之间的关系51.1.3集合的运算61.2关系121.2.1二元关系121.2.2等价关系与等价类131.2.3关系的合成141.2.4递归定义与归纳证明151.2.5关系的闭包181.3图191.3.1无向图191.3.2有向图211.3.3树231.4语言241.4.1什么是语言241.4.2形式语言与自动机理论的产生与作用25 1.4.3基本概念281.5小结35习题35第2章文法422.1启示432.2形式定义482.3文法的构造582.4文法的乔姆斯基体系682.5空语句792.6小结82习题82第3章有穷状态自动机863.1语言的识别863.2有穷状态自动机893.3不确定的有穷状态自动机1023.3.1作为对DFA的修改1023.3.2NFA的形式定义1043.3.3NFA与DFA等价1063.4带空移动的有穷状态自动机1103.5FA是正则语言的识别器1153.5.1FA与右线性文法1153.5.2FA与左线性文法1203.6FA的一些变形1223.6.1双向有穷状态自动机1223.6.2带输出的FA1233.7小结125习题126第4章正则表达式1314.1启示1314.2正则表达式的形式定义1334.3正则表达式与FA等价1354.3.1正则表达式到FA的等价变换1354.3.2正则语言可以用正则表达式表示1444.4正则语言等价模型的总结1504.5小结152习题153第5章正则语言的性质1565.1正则语言的泵引理1565.2正则语言的封闭性1625.3Myhill Nerode 定理与DFA的极小化170 5.3.1Myhill Nerode 定理1705.3.2DFA的极小化1805.4关于正则语言的判定算法1895.5小结190习题191第6章上下文无关语言1946.1上下文无关文法1956.1.1上下文无关文法的派生树1956.1.2二义性2026.1.3自顶向下的分析和自底向上的分析2056.2上下文无关文法的化简2076.2.1去无用符号2086.2.2去ε 产生式2126.2.3去单一产生式组2166.3乔姆斯基范式2196.4格雷巴赫范式2236.5自嵌套文法2296.6小结230习题230第7章下推自动机2357.1基本定义2357.2PDA与CFG等价2427.2.1PDA用空栈接受和用终止状态接受等价243 7.2.2PDA与CFG等价2467.3小结257习题257第8章上下文无关语言的性质2608.1上下文无关语言的泵引理2608.2上下文无关语言的封闭性2678.3上下文无关语言的判定算法2738.3.1L空否的判定2738.3.2L是否有穷的判定2748.3.3x是否为L的句子的判定2768.4小结278习题278第9章图灵机2809.1基本概念2819.1.1基本图灵机2829.1.2图灵机作为非负整函数的计算模型2899.1.3图灵机的构造2939.2图灵机的变形3009.2.1双向无穷带图灵机3009.2.2多带图灵机3049.2.3不确定的图灵机3069.2.4多维图灵机3089.2.5其他图灵机3109.3通用图灵机3139.4几个相关的概念3159.4.1可计算性3159.4.2P与NP相关问题3169.5小结316习题317第10章上下文有关语言32010.1图灵机与短语结构文法的等价性32010.2线性有界自动机及其与上下文有关文法的等价性323 10.3小结325习题325附录A教学设计327附录B缩写符号338词汇索引340参考文献348。

最新形式语言与自动机理论-蒋宗礼-第二章参考答案

最新形式语言与自动机理论-蒋宗礼-第二章参考答案

2．1回答下面的问题： （周期律 02282067） （1）在文法中，终极符号和非终极符号各起什么作用？✓ 终结符号是一个文法所产生的语言中句子的中出现的字符，他决定了一个文法的产生语言中字符的范围。

✓ 非终结符号又叫做一个语法变量，它表示一个语法范畴，文法中每一个产生式的左部至少要还有一个非终结符号，（二，三型文法要求更严，只允许左部为一个非终结符号）他是推导或归约的核心。

（2）文法的语法范畴有什么意义？开始符号所对应的语法范畴有什么特殊意义？ ✓ 文法的非终结符号A 所对应的语法范畴代表着一个集合L （A ），此集合由文法产生式中关于A 的产生式推导实现的✓ 开始符号所对应的语法范畴则为文法G = {V ，T ，P ，S}所产生的语言L （G ）={w S T w w **|⇒∈且}（3）在文法中，除了的变量可以对应一个终极符号行的集合外，按照类似的对应方法，一个字符串也可以对应一个终极符号行集合，这个集合表达什么意义？✓ 字符串对应的终极符号行集合表示这个字符串所能推导到的终极字符串集合，为某个句型的语言。

（4）文法中的归约和推导有什么不同？✓ 推导：文法G = {V ，T ，P ，S}，如果,)(,,* T VP ∈∈→δγβα则称γαδ在G 中推导出了γβδ。

✓ 归约：文法G = {V ，T ，P ，S}，如果,)(,,*T VP ∈∈→δγβα则称γβδ在G 中归约到γαδ。

✓ 这他们的定义，我个人理解两个概念从不同角度看待文法中的产生式，推导是自上而下（从产生式的左边到右边），而归约是自下而上（从产生式的右边到左边），体现到具体实际中，如编译中语法分析时语法树的建立，递归下降，LL （1）等分析法采用自开始符号向下推导识别输入代码生成语法树，对应的LR （1），LALR 等分析法则是采用自输入代码（相当于文法中语言的句子）自底向上归约到开始符号建立语法树，各有优劣。

（5）为什么要求定义语言的字母表上的语言为一个非空有穷集合？ ✓ 非空：根据字母表幂的定义：εε,}{0∑=为字母表中０个字符组成的。

形式语言与自动机教学提纲

形式语言与自动机教学提纲

用计算机进行问题求解的基本途径是，首先要用适当的数据对问题进行抽象和形式化表示，然后采用适当的算法对数据进行变换得到求解结果。形式语言和自动机理论给出了对一类基本问题的抽象的基本描述和计算模型，并研究这些模型的性质和变换方法。由此展示了一个典型的问题求解的基本思想和方法。另外，它还是研究算法及编译技术的理论基础。
实践环节
无
其他需要说明的内容：无
第八章上下文有关语言
教学目的
与要求
了解识别CSL的装置—线性有界自动机（LBA）。
教学重点
图灵机与短语结构文法的等价性，线性有界自动机及其与上下文有关文法的等价性
教学难点
图灵机与短语结构文法的等价性，线性有界自动机及其与上下文有关文法的等价性
教学具体
内容
1、图灵机与短语结构文法的等价性
知识要点：Myhill-Nerode定理，DFA的极小化。
4、关于正则语言的判定算法
知识要点：算法。
实践环节
无
其他需要说明的内容：无
第六章上下文无关语言
教学目的
与要求
理解上下文无关文法的性质、作用，掌握该文法的化简方法。
教学重点
二义性，自顶向下的分析和自底向上的分析
教学难点
文法的二义性，上下文无关文法的派生树
/view/c06b4a2d3169a4517723a33e.html（电子教案）
/p-4032290717788.html（相关论文）
课程教学进程
教材章节
或课次
课题
授课周次
授课课时
课时
累计
1
绪论
1
2
2
2
文法
2
2
4
3
教
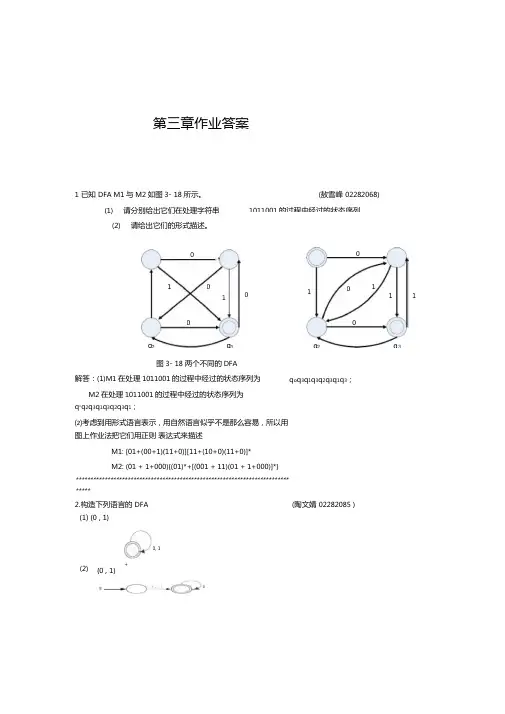
形式语言与自动机理论-蒋宗礼-参考答案

形式语言与自动机理论-蒋宗礼-参考答案

第三章作业答案1 已知 DFA M1与M2如图3- 18所示。

(1) 请分别给出它们在处理字符串 (2)请给出它们的形式描述。

图3- 18 两个不同的DFA解答：(1)M1在处理1011001的过程中经过的状态序列为M2在处理1011001的过程中经过的状态序列为 q °q 2q 3q 1q 3q 2q 3q 1；⑵考虑到用形式语言表示，用自然语言似乎不是那么容易，所以用图上作业法把它们用正则 表达式来描述M1: [01+(00+1)(11+0)][11+(10+0)(11+0)]* M2: (01 + 1+000){(01)*+[(001 + 11)(01 + 1+000)]*}*******************************************************************************2.构造下列语言的 DFA (陶文婧 02282085 )(1) {0 , 1}*1 0 011111(敖雪峰 02282068)1011001的过程中经过的状态序列。

q o q 3q 1q 3q 2q 3q 1q 3；(2) 0, 1+{0 , 1}(3) {x|x {0, 1}+且x中不含00的串}(设置一个陷阱状态，一旦发现有00的子串，就进入陷阱状态)(4) { x|x • {0 , 1}*且x 中不含00的串}(可接受空字符串，所以初始状态也是接受状态)(6) {x|x^{0, 1}+且x 中不含形如10110的子串}(设置一个陷阱状态，一旦发现有 00的子串，就进入陷阱状态)(7){x|x {0，1}+且当把x 看成二进制时，x 模5和3同余，要求当x 为0时，|x|=1,且x=0 时，x 的首字符为1 }1.以0开头的串不被接受，故设置陷阱状态，当 DFA 在启动状态读入的符号为 0,则进入陷阱状态2.设置7个状态：开始状态q s ,q °:除以5余0的等价类，除以5余1的等价类口2:除以5余2的等价类，q 3：除以5余3的等价类，q 4：除以5余4的等价类，接受状态 q t3.状态转移表为状态0 1 q 0 q 1 q 2 q 1 q 3 q 2 q 2 q 0 q 4 q 3q 1q 21(5){x|x ・{0, 1}+且x 中含形如10110的子串}q4 q3 q4 (8) {x|x {0 , 1}+且x的第十个字符为1}(设置一个陷阱状态，一旦发现x的第十个字符为(9){x|x • {0，1}+且x以0开头以1结尾}(设置陷阱状态，当第一个字符为1时，进入陷阱状态)0,进入陷阱状态)(10){x|x {0，1}+且x中至少含有两个1}(11) {x|x ■ {0 , 1}+且如果x以1结尾，则它的长度为偶数；如果为奇数}可将{0 , 1}+的字符串分为4个等价类。

形式语言与自动机理论电子教案

– (a，b) ∈R，也可表示为：aRb。
– A称为定义域(domain)，B称为值域(range)。
– 当A=B时，则称R是A上的二元关系。
• 二元关系的性质
– 自反(reflexive)性、反自反(irreflexive)性、对称 (symmetric)性、反对称(asymmetric)性、传递 (transitive)性。
• 归纳证明 – 与递归定义相对应。 – 归纳证明方法包括三大步： • 基础(basis)：证明最基本元素具有相应性质。 • 归纳(induction)：证明如果某些元素具有相 应性质，则根据这些元素用所规定的方法得 到的新元素也具有相应的性质。
• 根据归纳法原理，所有的元素具有相应的性 质。
S的满足如下要求的划分：S1、S2、S3、…、Sn…称 为S关于R的等价划分，Si称为等价类。
⑴ S= S1∪S2∪S3∪…∪Sn∪…； ⑵ 如果i≠j，则Si∩Sj=Φ； ⑶ 对任意的i，Si中的任意两个元素a、b，aRb恒成
立；
⑷ 对任意的i，j，i≠j，Si中的任意元素a和Sj中的任 意元素b，aRb恒不成立
• CFL
– CFG(CNF、GNF)、PDA、CFL的性质。
• TM
– 基本TM、构造技术、TM的修改。
• CSL
– CSG、LBA。
2020/1/10
5
教材及主要参考书目
1.蒋宗礼，姜守旭. 形式语言与自动机理论. 北京： 清华大学出版社，2003年
2. John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001

形式语言与自动机理论-蒋宗礼-参考答案

ij求索-百度文库2.1回答下面的问题：（周期律02282067）（1）在文法中，终极符号和非终极符号各起什么作用？/终结符号是一个文法所产生的语言中句子的中出现的字符,他决上了一个文法的产生语言中字符的范围。

/ 非终结符号又叫做一个语法变量，它表示一个语法范畴，文法中每一个产生式的左部至少要还有一个非终结符号，（二，三型文法要求更严，只允许左部为一个非终结符号）他是推导或归约的核心。

（2）文法的语法范畴有什么意义？开始符号所对应的语法范畴有什么特殊意义？/ 文法的非终结符号A所对应的语法范畴代表着一个集合L （A）,此集合由文法产生式中关于A的产生式推导实现的/ 开始符号所对应的语法范畴则为文法G = （V, T, P, S}所产生的语言L （G）*={ vvl w e 厂且S =► w }（3）在文法中，除了的变量可以对应一个终极符号行的集合外，按照类似的对应方法，一个字符串也可以对应一个终极符号行集合，这个集合表达什么意义？/字符串对应的终极符号行集合表示这个字符串所能推导到的终极字符串集合，为某个句型的语言。

（4）文法中的归约和推导有什么不同？/ 推导：文法G = {V, T, P, S},如果则称gd在G中推导岀了汐5。

/ 归约：文法G={V, T, P, S},如果则称汐5在G中归约到*7》。

/ 这他们的左义，我个人理解两个槪念从不同角度看待文法中的产生式，推导是自上而下（从产生式的左边到右边），而归约是自下而上（从产生式的右边到左边），体现到具体实际中，如编译中语法分析时语法树的建立，递归下降，LL （1）等分析法采用自开始符号向下推导识別输入代码生成语法树，对应的LR （1）, LALR等分析法则是采用自输入代码（相当于文法中语言的句子）自底向上归约到开始符号建立语法树，各有优劣。

（5）为什么要求左义语言的字母表上的语言为一个非空有穷集合？/ 菲空：根据字母表幕的立义：工°={£},£为字母表中0个字符组成的。

认知方法在形式语言与自动机理论教学中的应用

认知方法在形式语言与自动机理论教学中的应用摘要：在形式语言和自动机理论的教学活动中，合理地应用归纳和演绎方法，对于计算思维能力的培养有重要作用。

本文介绍了我院这方面的教学实践和经验。

关键词：计算思维能力；归纳和演绎；理论教学1归纳和演绎是两种认知的科学方法以学校为例，最初认识是“学校”这样一个词。

在对其进行分类的过程中就可以不断理解这一词的含义。

进一步知道学校有大学、中专、中学和小学之分；再进一步又知道大学分综合性大学，理、工、农、医、文科大学等；每一学科分又为不同专业，专业分为不同方向。

这就是从一般到特殊的演绎方法。

一条黄狗，一条白狗，除了颜色不一样外，其他有关狗的特征完全一样，这样，可以构造一个类：“狗”，其中描述了狗的所有共同特征，比如：会叫，具有犬齿，嗅觉灵敏，具有颜色，忠实等。

这就是从特殊到一般的归纳方法，在本科阶段的学习过程中，学生以观察、描述、比较、分类、推断、应用、创造思维等科学思维过程为主，强调自学的能力在培养；研究生阶段，需要对学生进一步进行抽象思维、逻辑思维、创造思维能力的培养。

计算机科学与技术学科强调4个方面的专业能力：计算思维能力、算法设计与分析能力、程序设计与实现能力、计算机系统的认知、分析、设计和运用能力。

这也是计算机科学与其他学科的重要区别。

相关的理论是计算机学科的基础[1]。

计算机科学与技术学科要求学生具有形式化描述和抽象思维能力，要求掌握逻辑思维方法。

这种能力就是计算思维能力或计算机思维能力。

形式语言与自动机理论课程是培养计算思维能力的重要课程。

认知方法提供了从一般到特殊的演绎手段，又提供了从特殊到一般的归纳形式。

这种分类、归纳的方法在在形式语言与自动机理论课程的教学中是很重要的。

2形式语言理论中的归纳和演绎采用一般到特殊的演绎方法，提出比较通用的文法构造方法，再具体讨论不同语言对典型文法的应用情况。

进一步总结文法一般性的构造方法，学生难以理解和掌握的文法构造方法，不再是难题。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

7.1 基本定义
• δ——状态转移函数(transition function)，有 时候又叫做状态转换函数或者移动函数。 δ：Q×(∑∪{ε})×Γ
2
Q *
7.1 基本定义
δ(q ， a ， Z)={(p1 ， γ1) ， (p2 ， γ2) ， … ， (pm，γm)} • 表示M在状态q，栈顶符号为Z时，读入字 符a，对于i=1，2，…，m，可以选择地将 状态变成pi，并将栈顶符号Z弹出，将γi中 的符号从右到左依次压入栈，然后将读头 向右移动一个带方格而指向输入字符串的 下一个字符。
主要内容
• 语言的文法描述。 • RL
– RG、 FA、RE、RL的性质 。
• CFL
– CFG(CNF、GNF)、PDA、CFL的性质。
• TM
– 基本TM、构造技术、TM的修改。
• CSL
– CSG、LBA。
教材及主要参考书目
1.蒋宗礼，姜守旭. 形式语言与自动机理论. 北京： 清华大学出版社，2003年 2. John E Hopcroft, Rajeev Motwani, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation (2nd Edition). Addison-Wesley Publishing Company, 2001 3. John E Hopcroft, Jeffrey D Ullman. Introduction to Automata Theory, Languages, and Computation. Addison-Wesley Publishing Company, 1979
• 计算思维能力
–逻辑思维能力和抽象思维能力 –构造模型对问题进行形式化描述 –理解和处理形式模型
课程目的和基本要求
• 知识
–掌握正则语言、下文无关语言的文法、识别模 型及其基本性质、图灵机的基本知识。
• 能力
–培养学生的形式化描述和抽象思维能力。 –使学生了解和初步掌握“问题、形式化描述、 自动化（计算机化）”这一最典型的计算机问 题求解思路。
7.1 基本定义
• 符号使用约定 • 英文字母表较为前面的小写字母，如a，b， c，…，表示输入符号； • 英文字母表较为后面的小写字母，如x，y， z，…，表示由输入字符串； • 英文字母表的大写字母，表示栈符号； • 希腊字母α，β，γ，…，表示栈符号串。
7.1 基本定义
• 即时描述(instantaneous description，ID) (q，w，γ)∈(Q，∑*，Γ*)称为M的一个 即时描述。它表示M处于状态q，w是当前 还未处理的输入字符串，而且M正注视着w 的首字符，栈中的符号串为γ，γ的最左符 号为栈顶符号，最右符号为栈底的符号， 较左的符号在栈的较上面，较右的符号在 栈的较下面。
7.1 基本定义
• Z0——Z0∈Γ叫做开始符号(start symbol)， 是 M 启动时候栈内惟一的一个符号。所以， 习惯地称其为栈底符号； • q0——q0∈Q，是M的开始状态(initial state)， 也可叫做初始状态或者启动状态； • F——FQ，是M的终止状态(final state)集 合，简称为终态集。q∈F，q称为M的终 止状态，也可称为接受状态(accept state)， 简称为终态。
第7章下推自动机
• PDA描述CFL，所以它应该与CFG等价。 • PDA应该包含FA的各个元素，或者包含那 些可以取代FA的各个元素的功能的元素。 • PDA按照最左派生的派生顺序，处理处于 当前句型最左边的变量，因此，需要采用 栈作为其存储机构。 • 按照FA的“习惯”，PDA用终态接受语言。 • 模拟GNF的派生PDA用空栈接受语言。
7.1 基本定义
如果(p，γ)∈δ(q，a，Z)，a∈∑，则 (q，aw，Zβ)├M(p，w，γβ) 表示M做一次非空移动，从ID(q，aw，Zβ)变 成ID(p，w，γβ)。 如果(p，γ)∈δ(q，ε，Z)，则 (q，w，Zβ)├M(p，w，γβ) 表示M做一次空移动，从ID(q，aw，Zβ)变成 ID(p，w，γβ) 。
第7章下推自动机
• 主要内容
– – – – PDA的基本概念。 PDA的构造举例。 用终态接受语言和用空栈接受语言的等价性。 PDA是CFL的接受器。
• 重点
– PDA的基本定义及其构造，PDA是CFL的等价描述。
• 难点
– 根据PDA构造CFG。
7.1 基本定义
• PDA的物理模型
7.1 基本定义
课程目的和基本要求
• 课程性质
–技术基础
• 基础知识要求
–数学分析（或者高等数学），离散数学
• 主要特点
–抽象和形式化 –理论证明和构造性 –基本模型的建立与性质
课程目的和基本要求
• 本专业人员4种基本的专业能力
–计算思维能力 –算法的设计与分析能力 –程序设计和实现能力 –计算机软硬件系统的认知、分析、设计与应用能力
7.1 基本定义
δ(q ， ε ， Z)={(p1 ， γ1) ， (p2 ， γ2) ， … ， (pm，γm)} • 表示M进行一次ε-移动(空移动)，即M在状 态q，栈顶符号为Z时，无论输入符号是什 么，对于i=1，2，…，m，可以选择地将状 态变成pi，并将栈顶符号Z弹出，将γi中的 符号从右到左依次压入栈，读头不移动。
• PDA应该含有三个基本结构
– 存放输入符号串的输入带。 – 存放文法符号的栈。 – 有穷状穷状态控制器的控制下根据它的当前状态、 栈顶符号、以及输入符号作出相应的动作，在 有的时候，不需要考虑输入符号。
7.1 基本定义
• 下推自动机(pushdown automaton，PDA) M= (Q，∑，Γ，δ，q0，Z0，F) Q——状态的非空有穷集合。q∈Q，q称为 M的一个状态(state)； ∑——输入字母表(input alphabet)。要求M的 输入字符串都是∑上的字符串； Γ——栈符号表(stack alphabet)。A∈Γ，叫 做一个栈符号；