级硕士矩阵分析试卷

海大2013数学专业硕士研究生《矩阵分析》试题姓 名__________ 学 号 _________________ 分 数___________一、 计算题 (共30分)1. （8分）设函数矩阵61cos t A(t)sin2t 0cot tarc t ⎛⎫ ⎪= ⎪ ⎪⎝⎭试求 A(t )d t ⎰.2. （8分）设矩阵200A 211021⎛⎫ ⎪= ⎪ ⎪⎝⎭试求 Ate .3. (8分) 将矩阵A 谱分解 133353664A -⎛⎫ ⎪=- ⎪ ⎪-⎝⎭.4. （6分）设123,,ααα是三维空间V 的一个基，V 的线性变换T 在这个基下的矩阵为123A 234012⎛⎫ ⎪= ⎪ ⎪⎝⎭求T 的核空间Ker T 和T 的像空间Im T .二、 证明题（共40分）1．（20分）证明：在连续函数构成的线性空间Ｃ［ａ，ｂ］定义：(),()[,]f x g x C a b ∀∈1(),()()()f x g x f x g x dx πππ-=⎰（） 则在此定义下，该线性空间构成一个内积空间。

并验证nx nx x x x x sin ,cos ,,2sin ,2cos ,sin ,cos 1， 构成它的一组标准正交基。

2．（20分）设T 是复内积空间V 中的线性变换，则下面的叙述是等价的：（1） ((),())(,),;T T V ααααα=∀∈ （2）若12,,,n e e e 是V 的标准正交基，且T 是在这个基下的矩阵为A ，即1212(,,,)(,,,)n n T e e e e e e A = 则A 是酉阵。

即T T A A AA E ==。

三、简单论述题(共30分)1. 在相似变换下，一个复矩阵最后相似的矩阵的标准形式是怎么样的？给出结论，并简单说明理由。

2. 简谈你对利用建立空间来研究矩阵的认识。

广东工业大学考试试卷
课程量 ， ， ， ， ，令 ，
试求：
(1) 的一组基与维数。
(2) 的一组基与维数。
2(满分14分)设 表示所有正实数集合，在 中定义加法 和数乘 分别为：
试证明 构成数域 上的线性空间，并分析该空间的基和维数。
3（满分12分）设 与 是 上的两种范数，试证明 也构成 上的范数。
4（满分12分）设 是酉空间V的一组向量，令
试证明矩阵 可逆的充要条件是向量组 线性无关。
5（满分12分）设 ， 是 上的线性变换，定义如下：
试求线性变换 在基 ， ， 下的矩阵表示；并判断该矩阵是否为单纯矩阵。
6（满分12分）验证下面矩阵 是正规矩阵，并求酉矩阵 ，使得 为对角矩阵，其中
7（满分12分）已知矩阵 ，试求矩阵A的谱分解表达式。
8（满分14分）已知 ， ， ，
试求

第一套试题答案一（10分）、证明：（1）设11k x +22k x +33k x =0， ①用σ作用式①两端，有111k x λ+222k x λ+333k x λ=0 ②1λ⨯①-②，有21223133()()0k x k x λλλλ-+-= ③再用σ作用式③两端，有2122231333()()0k x k x λλλλλλ-+-= ④ ③⨯2λ-④，有313233()()0k x λλλλ--=。

由于123,,λλλ互不相等，30x ≠，因此30k =，将其代入④，有20k =，利用①，有10k =。

故1x ，2x ，3x 是线性无关的。

（2）用反证法。

假设1x +2x +3x 是σ的属于特征值λ的特征向量，于是有123123()()x x x x x x σλ++=++即112223123()x x x x x x λλλλ++=++112223()()()0x x x λλλλλλ-+-+-=由于1x ，2x ，3x 线性无关，因此123λλλλ===，这与123,,λλλ互不相等矛盾。

所以，1x +2x +3x 不是σ的特征向量。

二（10分）、解:2312321232()()1;()(2);()(2)()1;()(2);()(2)1()(2)(2)A D D D d d d A λλλλλλλλλλλλλλλλλλλλ==-=-==-=-⎛⎫⎪- ⎪ ⎪-⎝⎭的行列式因子分别为，不变因子分别为，于是的Smith 标准形为.三（10分）、解:11121634E A λλλλ+⎛⎫ ⎪-= ⎪ ⎪---⎝⎭210001000(1)λλ⎛⎫ ⎪≅- ⎪ ⎪-⎝⎭A λλ2矩阵的初等因子为: -1, (-1)，100:011001J ⎛⎫⎪= ⎪ ⎪⎝⎭故约当标准形为。

四（12分）、解：令()()()1120,E A λλλλ-=-++=得特征值123112λλλ==-=-，，，解齐次方程组()0,E A x -=()2;Tii α=1得基础解系解齐次方程组()0,E A x --=()101;Tα=-2得基础解系解齐次方程组()20,E A x --=()1;T ii α=-3得基础解系αααααα123123由于，，已两两正交，将，，单位化得()()()11121011623T T Tp i i p p i i --123=，=，= ()1,(2)1.3H U p p p U AU ⎛⎫⎪==- ⎪ ⎪⎝⎭123令分，则五（10分）、解：(){}11(1),01,()TAx o i N A span ξξ===解齐次方程组得基础解系，，；又(){}{}()232323010,,,,100,,00H H R A span o span A o i ξξξξξξ⎛⎫⎪===-= ⎪ ⎪-⎝⎭这里，； 显然(),0,iji j ξξ=≠当时；()().HN A R A ⊥故有()()()()()()()()()333(2)dim dim dim 3dim ,Q H H H H N A R A C N A R A N A R A C N A R A C ++=+==+=是的子空间且故。

B.
1 2 1
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
0 0 0
五、(15 分)求矩阵
的满秩分解：
1 0 1 2 A 1 2 1 1
2 2 2 1
解：
A
E


1 1
0 2
1 1
2 1

1 0
0 1
0 0
2 2 2 1 0 0 1
1 0 1 2 1 0 0
令 g n n2 2 1 n2 2 1 2 1
2 1 n2 1 2 1 1 n3 n4 1 3
由 Hamilton-Cayley 定理知 gA 0
et e 2t
a0 a0
a1 2a1
于是解得：
a0 a1
2et e2t

e 2t et
从而：
f A e At gA a0 E a1 A

1 3 A4 1 2
下的坐标.
试燕 卷山
大 学 研 究 生 课 程 考 试
姓名
专业
学院
密 封 线
二．（10 分）设 AC mn ，证明 A 的伪逆矩阵是惟一的.
三．（10 分）求实二次型 X T AX 对 X 的导数，其中 A AT 为 n n实常数矩阵，
X Fn.
四．（15 分）若 ( X , Y ) 为酉空间V n (C,U ) 上的内积， X 为 X 的模，证
1 0 1 1
A
0
2
2
2
1 4 5 3
求矩阵 A 的伪逆矩阵 A .
密 封 线
试燕 卷山
大 学 研 究 生 课 程 考 试
密 封 线
七．（15 分）设
2 1 0 0
A 4 1 0 0
2 1 2 2 7 6 1 0
求下列矩阵范数： A , A , A , A , A
m1
m2
m
阵，且 A 正定. 证明 AB 的特征值都为实 数
级硕士矩阵分析试卷
Final approval draft on November 22, 2020
座位号
学号
题号 一 二 三 四 五 六 七 八 总分
得分
一．（10 分）在线性空间 R 22 中，求向量
密
封 线
在基
1 2 A 1 0
2 1
0
A1 0 1 , A2 2
1 2
，
A3
2
1
1 2,
明：
(X,Y) X Y
X ,Y V n (C,U )
密 封 线
试燕 卷山
大 学 研 究 生 课 程 考 试

1 3 A4 1 2
下的坐标.
燕 山 大 学 研 究 生 课 程 考 试 试 卷
学号
姓名
专业
学院
密 封 线
第1页共6页
二．（10 分）设 AC mn ，证明 A 的伪逆矩阵是惟一的.
三．（10 分）求实二次型 X T AX 对 X 的导数，其中 A AT 为 n n 实常数矩阵，
X Fn.
第2页共6页
求下列矩阵范数： A , A , A , A , A
m1
m2
m
1
八. （10 分）设 A 、 B 均为埃尔米特矩阵，且 A 正定. 证明 AB 的特征值都为实数
第6页共6页
四．（15 分）若 ( X , Y ) 为酉空间V n (C,U ) 上的内积， X 为 X 的模，证明：
(X,Y) X Y
X ,Y V n (C,U )
密 封 线
燕 山 大 学 研 究 生 课 程 考 试 试 卷
密 封 线
第3页共6页
五．（15 分）求下列矩阵的 Smith 标准型、若尔当（Jordan）标准形、初等因子、 不变因子和各阶行列式因子，设：
座位号
燕山大学 2016 年秋季学期研究生课程考试试卷
课程名称： 矩阵分析
考试时间： 2016 年 11 月 26 日
题号 一 二 三 四 五 六 七 八 总分
得分
一．（10 分）在线性空间 R 22 中，求向量
密 封
线 在基
A
1 1
2 0பைடு நூலகம்
2 1
0
A1 0 1 , A2 2
1 2
，
A3
2
1
1 2,
3 0 8

解：（1）由 (T1,T2 ,T3 ) (1,2 ,3 )A, 可得 1 2 1 1 0 1 1
A (1 , 2 , 3 )1 (T1 ,T 2 ,T 3 ) 0 1 1 1 1 2 1 1 1 1 0 1
0 1 10 1 1 0 1 1 1 2 1 1 1 2 1 3 2. 1 3 11 0 1 2 4 4
2 1, 1, 3, 7T ，求W1 W2 与W1 W2 的维数，并求W1 W 2 。（10 分）
解： W1 W2 L1, 2 L1 2 L1, 2 , 1, 2
1 1 2 1
1 -1 2 1
A1,2,1,2 12
设 W1 W2, x11 x22 x33 x44,化为齐次线性方程组
1 1 2 1
(1,2 ,1,2 )X 41

0
，即
2 1
1 1
1 0
1 3
X

0
。
0 1 1 7
x1 k, x2 4k, x3 3k, x4 k, k1 4k2 k5,2,3,4T ,即 解得 W1 W2 k5,2,3,4T .
注：计算W1 W2 维数 4 分，计算W1 W2 的维数 2 分，求集合W1 W 2 4 分。
3. 设 R3 中 ， 线 性 变 换 T 为 ： Ti i , i 1, 2, 3, 其 中 1 (1, 0, 1)T , 2 (2,1,1)T , 3 (1,1,1)T 与
2

1

1 0
1 1
12
注：矩阵 B, C, 各 3 分, A BC 计算 2 分。
1 0 0 -1

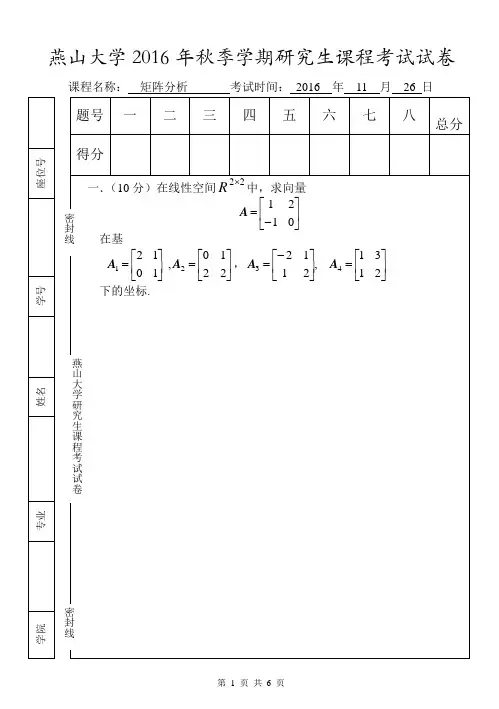
一、（10分）设矩阵121021110A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，计算||A ||1，max{||Ax ||∞：||x ||∞=2}、cond 1(A )。

解： ||A ||1=5 （3分）；max{||Ax ||∞：||x ||∞=2}=2 ||A ||∞=8 （6分）1110111212A --⎡⎤⎢⎥=-⎢⎥⎢⎥--⎣⎦（8分）cond 1(A )= ||A ||1⋅||A -1||1=20 （10分） 二、（12分）已知矩阵308212205A -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦，试求A 不变因子、初等因子，并写出A 的Jordan 标准形。

解：不变因子d 1=d 2=1；d 3=(λ+1)3；……6分；初等因子为(λ+1)3 (9分)A 的Jordan 标准形为110011001A J -⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦(12分) 三、（8分）利用盖尔圆定理证明25822131114A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦有三个互异实特征值。

解：取D =diag(2,1,1),则A 与B=D -1AD 特征值相同，而B 的三个行盖尔圆彼此孤立，故每个盖尔圆内有且仅有1个特征值，而B 是实矩阵，而各盖尔圆均关于实轴对称，因而其中特征值均是实的。

……………8分四、（10分）用LU 分解求解方程组 102311001111x ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦解:系数矩阵A 的LU 分解如下102100102110110012111111001⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ （5 分）求解得到(1,1,1)T x =- （１0分）五、（10）利用幂法计算矩阵210131114A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦按模最大的特征值及特征向量的近似值：设初始向量v 0=[1 1 1]T ，迭代2次，保留4位小数。

解: λmax ≈5.3333, 特征向量[0.3438 0.7500 1.0000] ( 10分)六、（20分）已知1011202,11100A b ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦，（1）求A 的满秩分解；（2）求A +；（3）用广义逆矩阵方法判断线性方程组Ax b =是否有解；（4）求Ax b =的极小范数解或极小范数最小二乘解，并指出所求的是哪种解．解：(1)101012001-111A ⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎢⎥⎣⎦ (6分) (2)1251121015245A +⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦(12分) (3) []0.6 1.20TA b b A +=≠,方程组无解； (16 分)（4）极小范数最小二乘解为[]011125T x A b +==- ( 20分) 七、（15分）对于如下线性方程组，201101011021x ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ （1）试证明其Jacobi 迭代收敛；（2）并用Jacobi 迭代法计算其近似解，设初始向量为x (0)=[0 0 0]T , 迭代四次，结果用分数或小数（保留到小数点后第四位）表示。

2 3 4 A 4 6 8 6 7 8 。 一（20 分） （1）设
2010 ~ 2011 学年《矩阵论》 课程考试 A 卷
（i）求 A 的特征多项式和 A 的全部特征值； （ii）求 A 的行列式因子，不变因子和初等因子； （iii）写出 A 的 Jordan 标准形；
1 A* A2 A* （3）证明： n 。
1 1 1 1 A 0 0 0 0 四、 （20 分）已知矩阵
（1）求矩阵 A 的 QR 分解；
1 2 0 1 b 1 1 2 1 ，向量 ，
（2）计算 A ；
17 6 14 60 A , B 45 16 3 13 ，试问 A 和 B 是否相似？并说明 （2）设
原因。
2 1 A 1 2 3 1 ，求 A 1 ， A 2 ， A ， A F ； 二（20 分） （1）设

（3）用广义逆判断方程组 Ax b 是否相容？若相容,求其通解;若不相容,求其极小最小二乘解。
五、 （20 分）
（1）设矩阵
问当 t 满足什么条件时, A B 成立？
5 3 2 0 1 A 3 2 t , B 1 1 2 t 2 2 0 .5 t
五（20 分）设
A ( a ij )
为 n 阶 Hermite 矩阵，证明：
3
存在唯一 Hermite 矩阵 B 使得 A B ；
2
（2）
（3） 如果 A 0 ，则 tr ( A)tr ( A ) n 。
1
如果 A 0 ，则 tr ( A ) (tr ( A)) ；
2

考试方式：闭卷
太原理工大学矩阵分析试卷（A）
题号
一
二
三
四
总 分
得分
适用专业：2015级硕士研究生考试日期：时间：120分钟 共8页
得分
1、填空选择题（每小题3分，共30分）
1-5题为填空题：
1.已知 ， ，则 ， ， 。
2.若矩阵 ，则矩阵 的谱半径
3．已知矩阵函数 ，则
4.设矩阵 ，则
5．若矩阵 ，且列向量组是两两正交的单位向量，则
得分
五．解答题（每小题10分，共20分）
16.已知 .
(1)求 的Smith标准型 ；(2)求 的Jordan标准型 .
17.已知 ，
(1)求 ；(2)求解微分方程组 ，
11.设 ，判断 是否收敛，若收敛求其和.
得分
三、证明题（每小题10分，共20分）
12.设 是线性空间 的基， 是 上的两个线性变换： ，且 .
（1）证明： .
（2）如果 也是线性空间 的一个基，证明 到 的过度矩阵A等于 在基 下的矩阵B，也等于于 中的列向量 ，定义映射 ，其中 表示向量2-范数，
(A) (B)
(C) 但 (D)
9.设 是线性空间 上的一个线性变换，则下列命题正确的是 （ ）
（A） （B）
（C） （D） .
10.与命题“ 阶矩阵 相似”不等价的命题是（）
(A) 具有相同的特征多项式(B) 具有相同的初级因子
(C) 具有相同的不变因子(D) 的特征矩阵 等价
得分
二、解答题（10分）
6-10题为单项选择题：
6．设 是正规矩阵，则下列说法不正确的是（）.
(A) 一定可以对角化；（B） 的特征值全为实数

矩陣論2012年試題一、 填空題：（每個空3分，共27分）1、設矩陣⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+---=i i i i i A 1013122131,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111X ,其中1-=i ，則______,1=AX .______1=A 2、設矩陣1000030012-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=P P A ，則______;)(dim =A N .______)(λA m 3、矩陣⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000a a a a a a A ，則a 滿足條件______時，矩陣冪級數∑∞=0k k A 收斂. 4、論矩陣⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=221132332211A ，則A 的LDV 分解為.______= 5、設⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=3/10002/10001A ,)sin(A 的Jordan 矩陣______;)sin(=A J .______)sin(lim =∞>-n n A6、設⎥⎦⎤⎢⎣⎡=201a A ，⎥⎦⎤⎢⎣⎡=1203B ，則矩陣方程0=+XB AX 有非零解的條件是.______≠a 二、（15分）設線性空間3R 上的線性變換T 在基},,{321e e e 下的變換矩陣為⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=333231232221131211a a a a a a a a a A ， （1） 求變換T 在基},3,{321e e e 下的變換矩陣.（2） 求變換T 在基},,{3211e e e e +下的變換矩陣.三、（15分）設矩陣⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=000012A （1）求矩陣A 的奇異值分解.（2）求矩陣A 的P M -廣義逆+A .四、（15分）設⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=111,011L W 是空間3R 的子空間， （1）求空間3R 上的正交投影變換P ，使得P 的象空間.)(W P R =（2）求空間3R 的向量T]3,2,1[=α在投影變換P 下的象. 五、（15分）設⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=502613803A ，計算矩陣函數.At e 六、證明題：（1）（7分）設A 是可逆矩陣，n σ是矩陣A 的最小奇異值，證明n A σ121=-（2）（6分）設矩陣A 和B 都是n 階方正，證明)()()(B rank A rank B A rank ⋅=⊗。

二、 证明：线性变换在不同的基下所对应的矩阵相似。
三、假设V = R[x]2 表示实数域上次数不超过 2 的多项式和零多项式构成的线性空间。在V 中
∫ 定义内积:
( f (x), g(x)) =
1
f (x)g(x)dx 。
−1
(1). 求基 x2 , x,1 的度量矩阵；
(2). 将基 x2 , x,1 转化为标准正交基；
ix1 x3
+
2 x2
x2
3;
1 2
x3
x3
(1). 写出 Hermite 二次型对应的矩阵； (2). 求酉矩阵 U ，使得二次型变为标准二次型。
2
六、已知
A
=
0
0
i
0
，求
A
的奇异值分解。
0
2 1 0
七、 已知=A
1
−1
0
，求
A、 ∞
A、 1
A 、A 。
2
F
0 0 1
2018工程数学(矩阵分析)试题-A卷
一.设 R3 中向量α = ( x1, x2 , x3 ) ，对 ∀x ∈ R3 定义变换 f ： f ( x) =(−2 x1 + x2 + x3 , x1 − 2 x2 + x3 , x1 + x2 − 2 x3 ) (1). 证明： f 是线性变换； (2). 求 f= 在基 e1 (1= , 0, 0);e2 (= 0,1, 0);e3 (0, 0,1) ,下的矩阵 A ； (3). 求 f 的值域 R( f ) 及核子空间 N ( f ) 的基及它们的维数。
(3). 求η = x2 在子空间W = L(1, x) 中的正投影η0 ，使得 η −η0=

13 ） 设 求 积 公 式
1 0 0 0
3 ⎞ ⎛2 5 ⎟ T ⎟ ; LL 分解中 L= ⎜ ⎜3 4 ⎜ − ⎟ ⎟ ⎝2 5⎠
1 1 2 2
0 ⎞ ⎟ 7 ⎟。 ⎟ 2 ⎠
Gauss 求 积 公 式 ， 则
1 ∫ x + 1 f (x ) dx ≈ A f (x ) + A f (x ) + A f (x ) 为
2）为使二点数值求积公式 积节点和求积系数应为 (A) x0 = −
∫
1
f ( x) 1 − x2
.
−1
dx ≈ A0 f ( x0 ) + A1 f ( x1 ) 具有最高的代数精度，其求
B
2 2 π 1 1 1 , x1 = ; A0 = A1 = ； (B) x0 = − , x1 = ; A0 = A1 = ； 2 2 2 2 2 2
⎛ ⎜ 即 V = ( v1 v2 ) = ⎜ ⎜ ⎜ ⎝ ⎛ ⎜ V1 = V = ⎜ ⎜ ⎜ ⎝ 1 2 1 2 1 ⎞ ⎛ ⎟ ⎜ 2⎟ 或 V = ( v1 v2 ) = ⎜ −1 ⎟ ⎜ ⎟ ⎜ 2⎠ ⎝ 1 2 1 2 ⎛ ⎜ ⎜ ⎜ ⎜ ⎝ −1 ⎞ 2⎟ ⎟ ，因 rank(A)=1，故有 1 ⎟ ⎟ 2⎠ 1 ⎞ ⎛ 1 ⎞ ⎟ ⎜ ⎟ 2⎟ (1) = ⎜ 2 ⎟ , 由 U = (U1U 2 ) , 则 1 ⎟ ⎜ 1 ⎟ ⎟ ⎜ ⎟ 2⎠ ⎝ 2⎠
17）. 为了减少运算次数，应将表达式.
4 x3 − 3x 2 − 2 x − 1 改写为 x4 + x2 + x − 1
( ( 4 x − 3) x − 2 ) x − 1 ； ( ( ( x + 0 ) x + 1) x + 1) x − 1

X ,Y V n (C,U )
密 封 线
燕 山 大 学 研 究 生 课 程 考 试 试 卷
密 封 线
五．（15 分）求下列矩阵的 Smith 标准型、若尔当（Jordan）标准形、初等因子、 不变因子和各阶行列式因子，设：
3 0 8
A
3
1
6
2 0 5
六.（15 分) 设
1 0 1 1
座位号
学号
题号 一 二 三 四 五 六 七 八 总分
得分
一．（10 分）在线性空间 R 22 中，求向量
密 封
线 在基
1 2 A 1 0
2 1
0
A1 0 1 , A2 2
1 2
，
A3
2
1
12,
1 3 A4 1 2
下的坐标.
燕 山 大 学 研 究 生 课 程 考 试 试 卷
姓名
专业
密 封 线
Aபைடு நூலகம்
0
2
2
2
1 4 5 3
求矩阵 A 的伪逆矩阵 A .
密 封 线
燕 山 大 学 研 究 生 课 程 考 试 试 卷
密 封 线
七．（15 分）设
2 1 0 0
A 4 1 0 0
2 1 2 2 7 6 1 0
求下列矩阵范数： A , A , A , A , A
m1
m2
m
1
八. （10 分）设 A 、 B 均为埃尔米特矩阵，且 A 正定. 证明 AB 的特征值都为实数
学院
二．（10 分）设 AC mn ，证明 A 的伪逆矩阵是惟一的.
三．（10 分）求实二次型 X T AX 对 X 的导数，其中 A AT 为 n n 实常数矩阵，

H
D 0 ，这里 0 0
D diag d1 , d2 ,
, dr ，且 d1 d2
dr 0 。 di i 1, 2,
, r 称为 A 的奇异值，而
D 0 H （P84） A P Q 称为矩阵 A 的奇异值分解式。 0 0
2
0 0 3、 ( 1) 2
1
4、下列命题不正确的是 。 （A）有相同特征多项式的两个矩阵一定相似； （B）有相同不变因子的两个矩阵一定相似； （C）有相同初级因子的两个矩阵一定相似； （D）有相同行列式因子的两个矩阵一定相似。 【分析】A。由 C 或 D 都能得到 B，而不变因子唯一确定矩阵的约当形。若矩阵的约当形相同， 则矩阵相似。A 的反例是显然的： M1
3
1
3
，
d1 1, d2 1 1 , d3 1 1
2
2
，
则
Smith
标 准
型 为
1
1 1
。 2 2 1 1
4、 lim A 0 的充要条件是： 其特征值的模的最大值（谱半径） A 1 。换言之， A 的所
3
0 1 1 2 0 0 1 2 阵 P 0 2 1 ， 约 当 标 准 形 J 0 1 1 （ 或 取 P3 0 ， 则 P2 4 ， 此 时 1 1 0 0 0 1 1 2 0 2 P 0 4 1 2 1 ） 。都有 P 1 AP J 。 0 1

2

1 1, 1 1 , 1 1
2
x,1 1 x 0 x 1dx 1 x 1 , 2 , 1 2 x 2 2 2 1 2 12 1,1 1 1 dx

|
xn
xn
|
an1
|
x1xnx2 Nhomakorabeaxn
| a12 | x2 x1
| a22 |
| an2 | x2
xn
| a1n | xn
x1
| a2n | xn
x2
| ann |
∑ →
D−1BD 的每个
Gerschgorin
圆为
Si
={z ∈ C
:|
z−
|
aii
||≤
Ri },
Ri
(
)
= 例如 x (0,1, 0,, 0) ≠ 0 ，但 || x ||= 0
4、|| x ||∞ ≤|| x ||1≤ n || x ||∞ .
n
∑
||
x
||∞
=max i
|
xi
|≤
i =1
|
xi
|
= || x ||1≤
n max i
|
xi
|=n ||
x ||∞
5、设 A 为 n 阶酉矩阵，则 A= A+ A= + A E.
=
0 AH
A
0
，则
||
B
||2
=||
A
||2
.
（5 分）
0
证：
B
=
AH
A
0
→
BH
=
0
AH
A
0
→
BB H
=
AAH
0 AH A
→
r ( BB H
)
=
r( AAH )
→ || B ||2 =|| A ||2

解：(B)是定理的结论.其它，例如取 V R[ x ]n ， Tf ( x ) f ( x ) ，则有 R (T ) R[ x ]n 1 ， ker(T ) R ， 从而 R (T ) ker(T ) R[ x ]n 1 R R[ x ]n 1 R[ x ]n V ．知(A)不成立，因此其它命题也不成立． 10.与命题“ n 阶矩阵 A, B 相似”不等价的命题是 (A) A, B 具有相同的特征多项式； (C) A, B 具有相同的不变因子； 解：反例， A ( A ) (B) A, B 具有相同的初等因子；
2 2
(e1 e2 ) (e1 e2 ) (e e ) (e1 e2 ) x2 1 2 V 2 ， 2 2 又因为对线性变换 T1 , T2 有 T1 (e1 ) 1 ， T1 (e2 ) 2 ， T2 (e1 e2 ) 1 2 ， T2 (e1 e2 ) 1 2 ，

e At dt
t 0
0 1 . 2 3
4.设矩阵 A
1 0 1 0 ，则 A 1 1 ； 1 1 2
2
解：因为 E A ( 1) ( ) 是 A 的最小多项式，所以设 由
A a0 E a1 A ，
解：因为 V 为酉空间，(A) (B)都差共轭，而(C)应 ( x, x) 0 ，只有(D)成立. 9.设 T 是线性空间 V 上的一个线性变换，则下列命题正确的是 (A) R (T ) ker(T ) V ； (B) dim( R(T )) dim(ker(T )) dim V ； (C) R (T ) ker(T ) 0 ； (D) R (T ) ker(T ) R (T ) ker(T ) . ( B )