奥数 之和差倍 年龄问题 鸡兔同笼
- 格式:pdf
- 大小:4.01 MB
- 文档页数:34
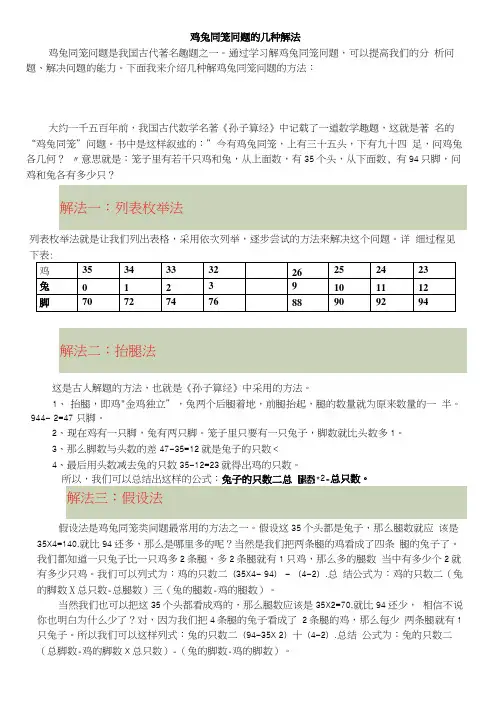
鸡兔同笼冋题的几种解法鸡兔同笼问题是我国古代著名趣题之一。
通过学习解鸡兔同笼冋题,可以提高我们的分析问题、解决问题的能力。
下面我来介绍几种解鸡兔同笼问题的方法:大约一千五百年前,我国古代数学名著《孙子算经》中记载了一道数学趣题,这就是著名的“鸡兔同笼”问题。
书中是这样叙述的:”今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何?〃意思就是:笼子里有若干只鸡和兔,从上面数,有35个头,从下面数, 有94只脚,问鸡和兔各有多少只?解法一:列表枚举法列表枚举法就是让我们列出表格,采用依次列举,逐步尝试的方法来解决这个问题。
详细过程见下表:鸡3534333226252423兔01239101112脚7072747688909294解法二:抬腿法这是古人解题的方法,也就是《孙子算经》中采用的方法。
1、抬腿,即鸡"金鸡独立”,兔两个后腿着地,前腿抬起,腿的数量就为原来数量的一半。
944- 2=47 只脚。
2、现在鸡有一只脚,兔有两只脚。
笼子里只要有一只兔子,脚数就比头数多1。
3、那么脚数与头数的差47-35=12就是兔子的只数<4、最后用头数减去兔的只数35-12=23就得岀鸡的只数。
所以,我们可以总结岀这样的公式:兔子的只数二总*2-总只数。
解法三:假设法假设法是鸡兔同笼类间题最常用的方法之一。
假设这35个头都是兔子,那么腿数就应该是35X4=140,就比94还多,那么是哪里多的呢?当然是我们把两条腿的鸡看成了四条腿的兔子了。
我们都知道一只兔子比一只鸡多2条腿,多2条腿就有1只鸡,那么多的腿数当中有多少个2就有多少只鸡。
我们可以列式为:鸡的只数二(35X4- 94) - (4-2).总结公式为:鸡的只数二(兔的脚数X总只数-总腿数)三(兔的腿数-鸡的腿数)。
当然我们也可以把这35个头都看成鸡的,那么腿数应该是35X2=70,就比94还少,相信不说你也明白为什么少了?对,因为我们把4条腿的兔子看成了2条腿的鸡,那么每少两条腿就有1只兔子。

鸡兔同笼问题知识点来源:已知两个人或若干个人的年龄,求他们年龄之间的某种数量关系,包括大小,倍数等. 或者,开始知道两个人的年龄之间的关系,最后通过和差倍问题求解两个人或者多个人的年龄。
1.解题方法:年龄问题的三大规律:1.两人的年龄差是不变的;2.两人年龄的倍数关系是变化的量;3.随着时间的推移,两人的年龄都是增加相等的量.2.年龄问题的类型:1.转化为和差问题的年龄问题;2.转化为和倍问题的年龄问题;3.转化为差倍问题的年龄问题.4.这类问题也可以用画图法来解决。
3.易错点:年龄问题里面不变的是年龄差,不是年龄的倍数,找准年龄差,再去考虑和倍,差倍的问题。
典型例题例1、小明今年6岁,妈妈今年36岁,再过6年,小明读初中时,妈妈比小明大多少岁?【练习1】今年姐姐13岁,弟弟今年10岁,当姐弟年龄之和达101岁时,姐姐是多少岁?【练习2】姐姐、妹妹二人的年龄和是33岁,四年后姐姐比妹妹大5岁.那么今年姐姐______岁,妹妹______岁?(答案格式:数字中间请用一个空格隔开(从前到后))【练习3】小明爸爸妈妈现在的年龄和是72岁;五年后,爸爸比妈妈大6岁.今年爸爸______岁,妈妈______岁?(答案格式:数字中间请用一个空格隔开(从前到后))例2、小明今年6岁,妈妈今年36岁,再过多少年之后,小明妈妈的年龄是小明年龄的2倍?1.明明比爸爸小28岁,爸爸今年的年龄是明明年龄的5倍,明明今年多少岁,爸爸今年多少岁?【练习4】爸爸比小强大30岁,明年爸爸的年龄是小强的3倍,今年小强多少岁?【练习5】父亲比儿子大27岁,4年后父亲的年龄是儿子的4倍,那么儿子今年多少岁?例3、5年前爸爸和儿子的年龄和是40岁,今年爸爸的年龄是儿子的4倍,今年爸爸和儿子各多少岁?【练习6】父子俩今年的年龄和是48岁,父亲的年龄是儿子的5倍,父亲今年______岁,儿子今年______岁?(答案格式:数字中间请用一个空格隔开(从前到后))【练习7】3年前,妈妈与女儿的年龄和是46岁,,今年妈妈的年龄是女儿的3倍,今年妈妈______岁,女儿______岁?(答案格式:数字中间请用一个空格隔开(从前到后))【练习8】姐姐今年22岁,弟弟今年15岁,几年前姐姐的年龄是弟弟的两倍?例4、小刚4年前的年龄与小明7年后的年龄之和是39岁,小刚5年后的年龄等于小明3年前的年龄,求小刚、小明今年的年龄是多少?【练习9】哥哥5年前的年龄等于7年后弟弟的年龄,哥哥4年后的年龄与弟弟3年前的年龄和是35岁,求哥哥今年______岁,弟弟今年______岁。

鸡兔同笼问题板块一、两个对象的“鸡兔同笼”【例 1】鸡兔同笼,头共46,足共128,鸡兔各几只【巩固】点点家养了一些鸡和兔子,同时养在一个笼子里,点点数了数,它们共有35个头,94只脚.问:点点家养的鸡和兔各有多少只【巩固】鸡兔共有45只,关在同一个笼子中.每只鸡有两条腿,每只兔子有四条腿,笼中共有100条腿.试计算,笼中有鸡多少只兔子多少只【巩固】动物园里有一群鸵鸟和大象,它们共有36只眼睛和52只脚,问:鸵鸟和大象各有多少【巩固】鸡兔同笼,上有35头,下有94足,求笼中鸡兔各几只【例 2】动物园里养了一些梅花鹿和鸵鸟,共有脚208只,鸵鸟比梅花鹿多20只,梅花鹿和鸵鸟各有多少只【巩固】一个养殖园内,鸡比兔多36只,共有脚792只,鸡兔各几只【巩固】鸡兔同笼,鸡、兔共有107只,兔的脚数比鸡的脚数多56只,问鸡、兔各多少只【巩固】鸡、兔共100只,鸡脚比兔脚多20只.问:鸡、兔各多少只?【巩固】鸡、兔共60只,鸡脚比兔脚多60只.问:鸡、兔各多少只【巩固】鸡、兔同笼,鸡比兔多26只,足数共274只,问鸡、兔各几只【巩固】鸡与兔共100只,鸡的脚数比兔的脚数少28.问鸡与兔各几只【例 3】在一个停车场上,现有车辆41辆,其中汽车有4个轮子,摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆【巩固】体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、裤子每件19元,问老师买上衣和裤子各多少件【巩固】小建和小雷做仰卧起坐,小建先做了3分钟,然后两人各做了5分钟,一共做仰卧起坐136次.已知每分钟小建比小雷平均多做4次,那么小建比小雷多做了多少次【例 4】(中国古代僧粥问题)一百个和尚刚好喝一百碗粥,一个大和尚喝三碗粥,三个小和尚喝一碗粥,那么大和尚有多少个,小和尚有多少个【巩固】100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人【巩固】100个和尚160个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人【解析】从前有座山,山里有个庙,庙里有许多小和尚,两个小和尚用一根扁担一个桶抬水,一个小和尚用一根扁担两个桶挑水,共用了38根扁担和58个桶,那么有多少个小和尚抬水多少个挑水【例 5】工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个倒赔100元.运完这批花瓶后,工人共得4400元,则损坏了多少个【巩固】乐乐百货商店委托搬运站运送100只花瓶.双方商定每只运费1元,但如果发生损坏,那么每打破一只不仅不给运费,而且还要赔偿1元,结果搬运站共得运费92元.问:搬运过程中共打破了几只花瓶【巩固】有一辆货车运输2000只玻璃瓶,运费按到达时完好的瓶子数目计算,每只2角,如有破损,破损瓶子不给运费,还要每只赔偿1元.结果得到运费379.6元,问这次搬运中玻璃瓶破损了几只【例 6】(2008年第八届“春蕾杯”小学数学邀请赛决赛)甲、乙两人进行射击比赛,约定每中一发得20分,脱靶一发扣12分,两人各打10发,共得208分,最后甲比乙多得64分,乙打中发。

【鸡兔同笼】是我国著名的趣味数学题之一,实际上这题的答案多样化,可以培养学生们的思维能力。
题目是这样的:鸡兔同一个笼子,头35,脚34只,请问鸡兔各有多少只?01方程法一元一次方程解:设兔有x只,则鸡有(35-x)只。
4x+2(35-x)=944x+70-2x=942x=94-702x=24x=1235-12=23(只)或解:设鸡有x只,则兔有(35-x)只。
2x+4(35-x)=942x+140-4x=942x=46x=2335-23=12(只)答:兔子有12只,鸡有23只。
02抬腿法法一假如让鸡抬起一只脚,兔子抬起2只脚,还有94除以2=47只脚。
笼子里的兔就比鸡的头数多1,这时,脚与头的总数之差47-35=12,就是兔子的只数。
法二假如鸡与兔子都抬起两只脚,还剩下94-35×2=24只脚,这时鸡是屁股坐在地上,地上只有兔子的脚,而且每只兔子有两只脚在地上,所以有24÷2=12只兔子,就有35-12=23只鸡03二元一次方程解:设鸡有x只,兔有y只。
x+y=352x+4y=94(x+y=35)×2=2x+2y=70(2x+2y=70)-(2x+4y=94)=(2y=24)y=12把y=12代入(x+y=35) x+12=35x=35-12(只)x=23(只)答:兔子有12只,鸡有23只。
小学四年级数学奥数练习题(八)鸡兔同笼问题基本公式是:兔数=(实际脚数-每只鸡脚数×鸡兔总数)÷(每只兔子脚数-每只鸡脚数)鸡兔同笼问题例题透析11、有若干只鸡和兔子,它们共有88个头,244只脚,鸡和兔各有多少只?解:我们设想,每只鸡都是“金鸡独立”,一只脚站着;而每只兔子都用两条后腿,像人一样用两只脚站着.现在,地面上出现脚的总数的一半,也就是244÷2=122(只).在122这个数里,鸡的头数算了一次,兔子的头数相当于算了两次.因此从122减去总头数88,剩下的就是兔子头数122-88=34,有34只兔子.当然鸡就有54只.答:有兔子34只,鸡54只. 上面的计算,可以归结为下面算式:总脚数÷2-总头数=兔子数. 上面的解法是《孙子算经》中记载的.做一次除法和一次减法,马上能求出兔子数,多简单!能够这样算,主要利用了兔和鸡的脚数分别是4和2,4又是2的2倍.可是,当其他问题转化成这类问题时,“脚数”就不一定是4和2,上面的计算方法就行不通.因此,我们对这类问题给出一种一般解法.还说此题. 如果设想88只都是兔子,那么就有4×88只脚,比244只脚多了88×4-244=108(只).每只鸡比兔子少(4-2)只脚,所以共有鸡(88×4-244)÷(4-2)= 54(只).说明我们设想的88只“兔子”中,有54只不是兔子.而是鸡.因此可以列出公式鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数).当然,我们也可以设想88只都是“鸡”,那么共有脚2×88=176(只),比244只脚少了244-176=68(只).每只鸡比每只兔子少(4-2)只脚,68÷2=34(只).说明设想中的“鸡”,有34只是兔子,也可以列出公式兔数=(总脚数-鸡脚数×总头数)÷(兔脚数-鸡脚数). 上面两个公式不必都用,用其中一个算出兔数或鸡数,再用总头数去减,就知道另一个数.假设全是鸡,或者全是兔,通常用这样的思路求解,有人称为“假设法”.鸡兔同笼问题例题透析2红铅笔每支0.19元,蓝铅笔每支0.11元,两种铅笔共买了16支,花了2.80元.问红、蓝铅笔各买几支?解:以“分”作为钱的单位.我们设想,一种“鸡”有11只脚,一种“兔子”有19只脚,它们共有16个头,280只脚. 现在已经把买铅笔问题,转化成“鸡兔同笼”问题了.利用上面算兔数公式,就有蓝笔数=(19×16-280)÷(19-11)=24÷8=3(支).红笔数=16-3=13(支). 答:买了13支红铅笔和3支蓝铅笔. 对于这类问题的计算,常常可以利用已知脚数的特殊性.例2中的“脚数”19与11之和是30.我们也可以设想16只中,8只是“兔子”,8只是“鸡”,根据这一设想,脚数是8×(11+19)=240.比280少40.40÷(19-11)=5.就知道设想中的8只“鸡”应少5只,也就是“鸡”(蓝铅笔)数是3。

授课内容:一、课前小测1、笼子里有若干只鸡和兔。
从上面数,有8个头,从下面数,有26只脚。
鸡和兔各有多少只?2、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?3、光明小学开展冬季体育比赛,参加跳绳比赛的人数是踺子人数的3倍,比踢踺子的多36人。
参加跳绳和踢踺子比赛的各有多少人?二、例题讲解与练习(1)鸡兔同笼基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)例1、某次数学竞赛共20道题,评分标准是:每做对一题得5分,每做错或不做一题扣1分.小华参加了这次竞赛,得了64分.问:小华做对几道题?练习1、一只货船载重260吨,容积1000米3,现装运甲、乙两种货物,已知甲种货物每吨体积是8米3,乙种货物每吨体积2米3,要使这只船的载重量与容积得到充分利用,甲、乙两种货物应分别装多少吨?练习2、自行车越野赛全程 220千米,全程被分为 20个路段,其中一部分路段长14千米,其余的长9千米.问:长9千米的路段有多少个?(2)和差倍问题和差问题:公式①(和-差)÷2=较小数较小数+差=较大数和-较小数=较大数②(和+差)÷2=较大数较大数-差=较小数和-较大数=较小数和倍问题:公式:和÷(倍数+1)=小数小数×倍数=大数和-小数=大数例1、甲班和乙班共有图书160本.甲班的图书本数是乙班的3倍,甲班和乙班各有图书多少本?例2、光明小学有学生760人,其中男生比女生的3倍少40人,男、女生各有多少人?练习1、禽养场今年养鸡和鸭共4600只,养的鸡比鸭的4倍还多100只,禽养场今年的鸡鸭各多少只?练习2、姐姐和妹妹共做了340朵小红花,后来姐姐把她做的红花送给了小明30朵,妹妹自己又做了20朵,这时姐姐做的小红花是妹妹的5倍。

1. 熟悉雞兔同籠的“砍足法”和“假設法”.2. 利用雞兔同籠的方法解決一些實際問題,需要把多個對象進行恰當組合以轉化成兩個對象.一、雞兔同籠這個問題,是我國古代著名趣題之一.大約在1500年前,《孫子算經》中就記載了這個有趣的問題.書中是這樣敘述的:“今有雞兔同籠,上有三十五頭,下有九十四足,問雞兔各幾何?這四句話的意思是:有若干只雞兔同在一個籠子裏,從上面數,有35個頭;從下麵數,有94只腳.求籠中各有幾只雞和兔?你會解答這個問題嗎?你想知道《孫子算經》中是如何解答這個問題的嗎?二、解雞兔同籠的基本步驟解答思路是這樣的:假如砍去每只雞、每只兔一半的腳,則每只雞就變成了“獨腳雞”,每只兔就變成了“雙腳兔”.這樣,雞和兔的腳的總數就由94只變成了47只;如果籠子裏有一只兔子,則腳的總數就比頭的總數多1.因此,腳的總只數47與總頭數35的差,就是兔子的只數,即473512-=(只).顯然,雞的只數就是351223-=(只)了.這一思路新穎而奇特,其“砍足法”也令古今中外數學家讚歎不已.除此之外,“雞兔同籠”問題的經典思路“假設法”.假設法順口溜:雞兔同籠很奧妙,用假設法能做到,假設裏面全是雞,算出共有幾只腳,和腳總數做比較,做差除二兔找到.解雞兔同籠問題的基本關係式是:如果假設全是兔,那麼則有:雞數=(每只兔子腳數×雞兔總數-實際腳數)÷(每只兔子腳數-每只雞的腳數)兔數=雞兔總數-雞數如果假設全是雞,那麼就有:兔數=(實際腳數-每只雞腳數×雞兔總數)÷(每只兔子腳數-每只雞的腳數)雞數=雞兔總數-兔數知識精講 教學目標6-1-9.雞兔同籠問題(一)當頭數一樣時,腳的關係:兔子是雞的2倍當腳數一樣時,頭的關係:雞是兔子的2倍在學習的過程中,注重假設法的運用,滲透假設法的重要性,在以後的專題中,如工程,行程,方程等專題中也都會接觸到假設法例題精講模組一、兩個量的“雞兔同籠”問題——雞兔同籠問題【例 1】雞兔同籠,頭共46,足共128,雞兔各幾只?【巩固】點點家養了一些雞和兔子,同時養在一個籠子裏,點點數了數,它們共有35個頭,94只腳.問:點點家養的雞和兔各有多少只?【巩固】雞兔共有45只,關在同一個籠子中.每只雞有兩條腿,每只兔子有四條腿,籠中共有100條腿.試計算,籠中有雞多少只?兔子多少只?【巩固】老虎和雞共l0只,腳共26只.雞()只.【例 2】動物園裏有一群鴕鳥和大象,它們共有36只眼睛和52只腳,問:鴕鳥和大象各有多少?【例 3】一隊獵手一隊狗,兩隊並著一起走。

题目:现有一笼子,里面有鸡和兔子若干只,数一数,共有头14个,腿38条,球鸡和兔子各有多少只?(请用尽量多的方法解答)腿5650464238...根据上面的表格,我们可以看出,鸡为9只,兔子为5只。
我们在列表的时候不要按顺序列,否则做题的速度会很慢,比如说列完鸡为0只,兔子为14只,发现腿的数量56条,和实际38条相差较大,那么下一个你可以跳过鸡的数量为2只这种情况,直接列鸡的数量为3只,这样做速度会快一些哦!『方法二:最快乐的画图法』画图可以让数学变得形象化,而且经常画图还有助于创造力的培养!假设14只全部是鸡,先把鸡给画好。
14×2=28条,差38-28=10条,而每一只鸡补2条腿就变成兔子,需要把5只鸡每只补2条腿,所以有5只兔子,14-5=9只鸡。
『方法三:最酷的金鸡独立法』分析:让每只鸡都一只脚站立着,每只兔都用两只后脚站立着,那么地上的总脚数只是原来的一半,即19只脚。
鸡的脚数与头数相同,而兔的脚数是兔的头数的2倍,因此从19里减去头数14,剩下来的就是兔的头数19-14=5只,鸡有14-5=9只。
『方法四:最逗的吹哨法』分析:假设鸡和兔接受过特种部队训练,吹一声哨,它们抬起一只脚,还有38-14=24只腿在站着,再吹一声哨,它们又抬起一只脚,这时鸡都一屁股坐地上了,兔子还有两只脚立着。
这时还有24-14=10只腿在站着,而这10只腿全部是兔子的,所以兔子有10÷2=5只,鸡有14-5=9只。
(惊现跑男中包贝尔的抬脚法有木有!)『方法五:最常用的假设法』分析:假设全部是鸡,则有14×2=28条腿,比实际少38-28=10只,一只鸡变成一只兔子腿增加2条,10÷2=5只,所以需要5只鸡变成兔子,即兔子为5只,鸡为14-5=9只。
『方法六:最常用的假设法』分析:假设全部是兔子,则有14×4=56条腿,比实际多56-38=18只,一只兔子变成一只鸡腿减少2条,18÷2=9只,所以需要9只兔子变成鸡,即鸡为9只,兔子为14 - 9=5只。

例1:解方程-)(x35-18=963+-xx6=(4)156(=)94(++xx)8-(4x213515)+x+6=)25(⨯-x+x3080=-1350-x4()-)87(=25)(4(=)1⨯-xx8++⨯⨯(x12)2560)47(=--x⨯-例2:甲、乙、丙三个数,乙比甲的3倍少15,丙比甲的5倍多10,丙比乙多35。
求甲、乙、丙各是多少?例3:甲、乙、丙三个数,乙比甲的3倍少15,丙比甲的5倍少10,乙比丙少35。
求甲、乙、丙各是多少?例4:学校买来大、小学桌120张,共用去11600元。
大学桌每张110元,小学桌每张70元。
大、小学桌各买来多少张?例5:电影院有座位1200张,一次演出,座无虚席。
前排票每张10元,后排票每张6元。
前排票比后排票多收入5600元,电影院有前排、后排座位各多少张?例6:面值10元和面值5元的钞票若干张,共175元。
10元的张数是5元的张数的3倍。
这两种钞票各几张?例7:学校买来3元、4元和5元的电影票共200张,用去780元,其中4元票与5元票张数相等,每种票各买多少张?例8:一分币、二分币、五分币共100枚,共200分钱,其中二分币的枚数是五分币枚数的6倍。
三种硬币各几枚?例9:王大爷卖了公鸡、母鸡、小鸡共25只,共得146元。
已知每只公鸡、母鸡、小鸡的价格分别为10元、6元、4元,母鸡比小鸡少4只。
问公鸡、母鸡、小鸡各有多少只?1.解方程()35=4-xx30-⨯x435+x15)(6=-174(--x14-x53=))+17164(53=7612)(=4(+xx20-+4))35(156=-xx40-18)4(40x)-x--5(=183(12)36)5(=+x-+x60⨯(=12)+-141-x⨯4x43=)67(⨯(-3+x14)2+-x⨯-x⨯)1238)32(43(=2.甲、乙、丙三个数,乙比甲的3倍多15,丙比甲的5倍多10,丙比乙多35。

9.年龄问题年龄问题:将差为一定值的两个数作为题中的一个条件,这种应用题被称为“年龄问题”。
解题关键:年龄问题与和差、和倍、差倍问题类似,主要特点是随着时间的变化,年岁不断增长,但大小两个不同年龄的差是不会改变的,因此,年龄问题是一种“差不变”的问题,解题时,要善于利用差不变的特点。
例:父亲 48 岁,儿子 21 岁。
问几年前父亲的年龄是儿子的 4 倍?分析:父子的年龄差为 48-21=27 (岁)。
由于几年前父亲年龄是儿子的 4 倍,可知父子年龄的倍数差是( 4-1 )倍。
这样可以算出几年前父子的年龄,从而可以求出几年前父亲的年龄是儿子的 4 倍。
列式为: 21( 48-21 )÷( 4-1 ) =12 (年)(1) 6年前,母亲的年龄是儿子的5倍,6年后母子年龄的和事78岁,问:母亲今年多少岁?(2) 2005年爷爷的年龄是孙子的10倍,再过12年爷爷的年龄是孙子的4倍,2005年孙子是多少岁?(3)小丽今年的年龄比小娜的3倍小2岁。
而小丽8年前与小娜6年后的年龄相等,求小丽和小娜今年各几岁?(4)姐姐对妹妹说“当我是你今年的岁数时,你才6岁。
”妹妹对姐姐说“当我的岁数是你现在的岁数时,你将21岁。
”姐姐和妹妹今年各几岁?10.鸡兔问题鸡兔问题:已知“鸡兔”的总头数和总腿数。
求“鸡”和“兔”各多少只的一类应用题。
通常称为“鸡兔问题”又称鸡兔同笼问题解题关键:解答鸡兔问题一般采用假设法,假设全是一种动物(如全是“鸡”或全是“兔”,然后根据出现的腿数差,可推算出某一种的头数。
基本公式:(总腿数-鸡腿数×总头数)÷一只鸡兔腿数的差=兔子只数兔子只数=(总腿数-2×总头数)÷2如果假设全是兔子,可以有下面的式子:鸡的只数=(4×总头数-总腿数)÷2 兔的头数=总头数-鸡的只数例:鸡兔同笼共 50 个头, 170 条腿。
问鸡兔各有多少只?解:兔子只数( 170-2 × 50 )÷ 2 =35 (只)鸡的只数 50-35=15 (只)(1)一个停车场上,汽车、摩托车共停了60量,一共有190个轮子。

一、和差倍问题例1:三、四年级的同学们一共制作了318件航模,四年级同学制作的航模件数是三年级的2倍,三、四年级的同学各制作了多少件航模?例2:小强和小明共有28本练习本,小强的练习本比小明的2倍少2本。
小强和小明各有几本练习本?例3:李爷爷家养的鸭比鹅多18只,鸭的只数是鹅的3倍,你知道李爷爷家养的鸭和鹅各有多少只吗?练习:1、停车场的轿车数量是面包车的8倍,轿车比面包车多56辆,问轿车和面包车各有多少辆?2、小林和小军下棋,两人共下了24盘,小林赢的盘数是小军的2倍,小林和小军各赢了几盘棋?二、年龄问题例1:小华今年12岁,他妈妈今年48岁,多少年以前妈妈的年龄是小华的5倍?多少年以后妈妈的年龄是小华的3倍?例2:父亲今年38岁,母亲今年36岁,儿子今年11岁,多少年后,父母亲的年龄之和是儿子的年龄的4倍?例3:爸爸今年30岁,儿子小明和小强分别是5岁和6岁,再过几年小明和小强的年龄和与爸爸的年龄相等?练习:1、父亲今年54岁,儿子今年18岁,几年前父亲的年龄是儿子年龄的7倍?2、姐姐与妹妹3年后的年龄和是33岁,妹妹今年的年龄等于两人的年龄差,姐姐今年多少岁?三、植树问题例1:在一个1890米的池塘边每隔2米种一棵树,一共要种多少棵树?例2:在一条长150米的水泥路上,从头开始每隔3米摆一盆花,一共摆了多少盆花?例3:少先队员在路的两旁每隔2米栽一棵树,起点和终点都栽,一共栽了42棵,这条路长多少米?练习:1、平平在桌子摆小棒,每隔12厘米摆一根,到600厘米处可摆几根?2、一座桥长625米,在它的两边每隔5米有一盏灯,第一盏灯在桥的起点,最后一盏灯在桥的终点,桥上一共有几盏灯?四、周期问题例1:2004年的1月4日是星期日,问1月28日是星期几?例2:有同样大小的黄、红、蓝弹子共180个,按先4个红的,再2个黄的,再3个蓝的排到底,三种颜色的弹子各有多少个?例3:全体自然数排成四列,101在哪个字母下面?练习:1、有同样大小的红、白、黑珠共160个,按先4个红的,再3个白的,再2个黑的顺序排列。
三年级奥数5-1鸡兔同笼训练题【例1】鸡兔同笼,头共46,足共128,鸡兔各几只?【巩固】点点家养了一些鸡和兔子,同时养在一个笼子里,点点数了数,它们共有35个头,94只脚.问:点点家养的鸡和兔各有多少只?【巩固】鸡兔共有45只,关在同一个笼子中.每只鸡有两条腿,每只兔子有四条腿,笼中共有100条腿.试计算,笼中有鸡多少只?兔子多少只?【巩固】动物园里有一群鸵鸟和大象,它们共有36只眼睛和52只脚,问:鸵鸟和大象各有多少?【巩固】鸡兔同笼,上有35头,下有94足,求笼中鸡兔各几只?【例2】动物园里养了一些梅花鹿和鸵鸟,共有脚208只,鸵鸟比梅花鹿多20只,梅花鹿和鸵鸟各有多少只?【巩固】一个养殖园内,鸡比兔多36只,共有脚792只,鸡兔各几只?【巩固】鸡兔同笼,鸡、兔共有107只,兔的脚数比鸡的脚数多56只,问鸡、兔各多少只?【巩固】鸡、兔共100只,鸡脚比兔脚多20只.问:鸡、兔各多少只?【巩固】鸡、兔共60只,鸡脚比兔脚多60只.问:鸡、兔各多少只?【巩固】鸡、兔同笼,鸡比兔多26只,足数共274只,问鸡、兔各几只?【巩固】鸡与兔共100只,鸡的脚数比兔的脚数少28.问鸡与兔各几只?【例3】在一个停车场上,现有车辆41辆,其中汽车有4个轮子,摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆?【巩固】体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、裤子每件19元,问老师买上衣和裤子各多少件?【巩固】小建和小雷做仰卧起坐,小建先做了3分钟,然后两人各做了5分钟,一共做仰卧起坐136次.已知每分钟小建比小雷平均多做4次,那么小建比小雷多做了多少次?【例4】(中国古代僧粥问题)一百个和尚刚好喝一百碗粥,一个大和尚喝三碗粥,三个小和尚喝一碗粥,那么大和尚有多少个,小和尚有多少个?【巩固】100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人?【巩固】100个和尚160个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人?【解析】从前有座山,山里有个庙,庙里有许多小和尚,两个小和尚用一根扁担一个桶抬水,一个小和尚用一根扁担两个桶挑水,共用了38根扁担和58个桶,那么有多少个小和尚抬水?多少个挑水?【例5】工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个倒赔100元.运完这批花瓶后,工人共得4400元,则损坏了多少个?【巩固】乐乐百货商店委托搬运站运送100只花瓶.双方商定每只运费1元,但如果发生损坏,那么每打破一只不仅不给运费,而且还要赔偿1元,结果搬运站共得运费92元.问:搬运过程中共打破了几只花瓶?【巩固】有一辆货车运输2000只玻璃瓶,运费按到达时完好的瓶子数目计算,每只2角,如有破损,破损瓶子不给运费,还要每只赔偿1元.结果得到运费379.6元,问这次搬运中玻璃瓶破损了几只【例6】(2008年第八届“春蕾杯”小学数学邀请赛决赛)甲、乙两人进行射击比赛,约定每中一发得20分,脱靶一发扣12分,两人各打10发,共得208分,最后甲比乙多得64分,乙打中发。
和差倍、年龄及鸡兔同笼问题1.果园里有梨树和苹果树共324 棵,苹果树的棵树是梨树的5 倍,苹果树比梨树多多少棵?2.商店运来桔子、苹果、香蕉共53 千克,桔子的重量是苹果的3 倍少3 千克,香蕉的重量是苹果的2 倍多2 千克,桔子重多少千克?3.甲乙两筐梨,甲筐比乙筐重48 千克,甲筐每天可以卖出的数量是乙筐的2 倍,4 天后两筐梨的重量一样多,甲筐每天卖出多少梨。
4.小刚4年前的年龄与小明7年后的年龄之和是39岁,小刚5年后的年龄等于小明3前的年龄,求小刚、小明今年的年龄是多少?5.10年前父亲的年龄是儿子年龄的7倍,15年后父亲的年龄是他儿子的2倍,问今年父子二人各多少岁?6.今年小刚的年龄是明明年龄的5倍,25年后, 小刚的年龄比明明的年龄的2倍少16岁,今年小刚、明明各多少岁?7. 鸡兔共35只,每只鸡2条腿,每只兔4条腿,共有100条腿,请问几只鸡?几只兔?8.现有车辆24辆,其中汽车有4个轮子,摩托车有3个轮子,这些车共有86个轮子,那么三轮摩托车有多少辆?二、解答题11.根据题意看图,我们可以知道39岁为粗线表示的部分.如果我们以小刚5年后的年龄,也就是小明3年前的年龄为1倍量的话,只要我们能找到2倍对应的数据就可以了.从图中可知,如果小刚4年前的年龄加4加5就是5年后的年龄,如果小明7年后的年龄减7减3就是3年前的年龄,总数变为39+4+5-3-7=38(岁)相当于2倍量,这样,问题就可以解决了.39+4+5-3-7=38(岁)38÷2=19(岁)19-5=14(岁)19+3=22(岁)答:小明今年22岁,小刚今年14岁.12. 根据题意看图,我们可以知道35岁为粗线表示的部分.如果我们把弟弟7年后的年龄作为1倍量,那么哥哥5年前的年龄也是1倍量.只要我们找到这两倍量所对应的数量,就可以先求出1倍量,使问题得解.35+3+7-5-4=36(岁)36÷2=18(岁)18-7=11(岁)14+5=23(岁)答:哥哥今年23岁,弟弟今年11岁.13.小刚: 5年 今年 3年 小明: 今年 4年 ? 岁 ? 岁39岁 7年 弟弟: 7年 今年 5年 哥哥:今年年 35岁 4年父亲:儿子: 10年 今年 10年 今年15年 ? 岁 ? 岁“1” 15年(“1”) 7倍 (2倍)因为15年后父亲的年龄是他儿子年龄的2倍,所以父子当时的年龄差为儿子当时的年龄,即10+15+儿子10年前的年龄.因为10年前父亲的年龄是儿子年龄的7倍,父子的年龄差为儿子当时年龄的6倍,由于年龄差不变,25+儿子10年前年龄=儿子10年前年龄的6倍.所以25相当于儿子10年前年龄的5倍,可求出儿子10年前的年龄,使问题得解.7-1-1=510+15=25(岁)25÷5=5(岁)5+10=15(岁)5×7=35(岁)35+10=45(岁)答:儿子今年15岁,父亲今年45岁.14.看图,25年后,小刚的年龄是明明的2倍,如果明明的年龄乘2就和小刚的年龄相等,如下图:从上图可以清楚地看出,当两人年龄相等时,明明今年年龄的3倍对应的是:25×2-25-16=9(年),由此可以求出明明今年的年龄,使问题得解.25×2-25-16=9(年)5-1×2=39÷3=3(岁)3×5=15(岁)答:明明今年3岁,小刚今年15岁.小刚: 明明:16年 25年 ? 岁 ? 岁 “1” 25年 (“1”) 5倍 (2倍)小刚: 明明: 16年 25年 “1”“1” 25年 (“1”)5倍 25年。
三年级奥数5-1鸡兔同笼训练题【例 1】鸡兔同笼,头共46,足共128,鸡兔各几只【巩固】点点家养了一些鸡和兔子,同时养在一个笼子里,点点数了数,它们共有35个头,94只脚.问:点点家养的鸡和兔各有多少只【巩固】鸡兔共有45只,关在同一个笼子中.每只鸡有两条腿,每只兔子有四条腿,笼中共有100条腿.试计算,笼中有鸡多少只兔子多少只【巩固】动物园里有一群鸵鸟和大象,它们共有36只眼睛和52只脚,问:鸵鸟和大象各有多少【巩固】鸡兔同笼,上有35头,下有94足,求笼中鸡兔各几只【例 2】动物园里养了一些梅花鹿和鸵鸟,共有脚208只,鸵鸟比梅花鹿多20只,梅花鹿和鸵鸟各有多少只【巩固】一个养殖园内,鸡比兔多36只,共有脚792只,鸡兔各几只【巩固】鸡兔同笼,鸡、兔共有107只,兔的脚数比鸡的脚数多56只,问鸡、兔各多少只【巩固】鸡、兔共100只,鸡脚比兔脚多20只.问:鸡、兔各多少只【巩固】鸡、兔共60只,鸡脚比兔脚多60只.问:鸡、兔各多少只【巩固】鸡、兔同笼,鸡比兔多26只,足数共274只,问鸡、兔各几只【巩固】鸡与兔共100只,鸡的脚数比兔的脚数少28.问鸡与兔各几只【例 3】在一个停车场上,现有车辆41辆,其中汽车有4个轮子,摩托车有3个轮子,这些车共有127个轮子,那么三轮摩托车有多少辆【巩固】体育老师买了运动服上衣和裤子共21件,共用了439元,其中上衣每件24元、【巩固】小建和小雷做仰卧起坐,小建先做了3分钟,然后两人各做了5分钟,一共做仰卧起坐136次.已知每分钟小建比小雷平均多做4次,那么小建比小雷多做了多少次【例 4】(中国古代僧粥问题)一百个和尚刚好喝一百碗粥,一个大和尚喝三碗粥,三个小和尚喝一碗粥,那么大和尚有多少个,小和尚有多少个【巩固】100个和尚140个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人【巩固】100个和尚160个馍,大和尚1人分3个馍,小和尚1人分1个馍.问:大、小和尚各有多少人【解析】从前有座山,山里有个庙,庙里有许多小和尚,两个小和尚用一根扁担一个桶抬水,一个小和尚用一根扁担两个桶挑水,共用了38根扁担和58个桶,那么有多少个小和尚抬水多少个挑水【例 5】工人运青瓷花瓶250个,规定完整运到目的地一个给运费20元,损坏一个倒赔100元.运完这批花瓶后,工人共得4400元,则损坏了多少个【巩固】乐乐百货商店委托搬运站运送100只花瓶.双方商定每只运费1元,但如果发生损坏,那么每打破一只不仅不给运费,而且还要赔偿1元,结果搬运站共得运费92元.问:搬运过程中共打破了几只花瓶【巩固】有一辆货车运输2000只玻璃瓶,运费按到达时完好的瓶子数目计算,每只2角,如有破损,破损瓶子不给运费,还要每只赔偿1元.结果得到运费元,问这次搬运中玻璃瓶破损了几只【例 6】(2008年第八届“春蕾杯”小学数学邀请赛决赛)甲、乙两人进行射击比赛,约定每中一发得20分,脱靶一发扣12分,两人各打10发,共得208分,最后甲比乙多得64分,乙打中发。
小学数学知识点总结汇编包含经典问题(和差倍问题、年龄问题、植树问题、鸡兔同笼问题等)1、和差倍问题差与倍数2、年龄问题的三个基本特征:①两个人的年龄差是不变的;②两个人的年龄是同时增加或者同时减少的;③两个人的年龄的倍数是发生变化的;3、归一问题的基本特点:问题中有一个不变的量,一般是那个“单一量”,题目一般用“照这样的速度”……等词语来表示。
关键问题:根据题目中的条件确定并求出单一量;4、植树问题5、鸡兔同笼问题基本概念:鸡兔同笼问题又称为置换问题、假设问题,就是把假设错的那部分置换出来;基本思路:①假设,即假设某种现象存在(甲和乙一样或者乙和甲一样):②假设后,发生了和题目条件不同的差,找出这个差是多少;③每个事物造成的差是固定的,从而找出出现这个差的原因;④再根据这两个差作适当的调整,消去出现的差。
基本公式:①把所有鸡假设成兔子:鸡数=(兔脚数×总头数-总脚数)÷(兔脚数-鸡脚数)②把所有兔子假设成鸡:兔数=(总脚数一鸡脚数×总头数)÷(兔脚数一鸡脚数)关键问题:找出总量的差与单位量的差。
6、盈亏问题基本概念:一定量的对象,按照某种标准分组,产生一种结果:按照另一种标准分组,又产生一种结果,由于分组的标准不同,造成结果的差异,由它们的关系求对象分组的组数或对象的总量.基本思路:先将两种分配方案进行比较,分析由于标准的差异造成结果的变化,根据这个关系求出参加分配的总份数,然后根据题意求出对象的总量.基本题型:①一次有余数,另一次不足;基本公式:总份数=(余数+不足数)÷两次每份数的差②当两次都有余数;基本公式:总份数=(较大余数一较小余数)÷两次每份数的差③当两次都不足;基本公式:总份数=(较大不足数一较小不足数)÷两次每份数的差基本特点:对象总量和总的组数是不变的。
关键问题:确定对象总量和总的组数。
7、牛吃草问题基本思路:假设每头牛吃草的速度为“1”份,根据两次不同的吃法,求出其中的总草量的差;再找出造成这种差异的原因,即可确定草的生长速度和总草量。