范德坡振荡电路Matlab相图
- 格式:pdf
- 大小:115.74 KB
- 文档页数:3

范德坡振荡电路Van der Pol oscillator简介在动态电路中,范德坡振荡是非保守的、非线性阻尼振荡。
它在时间域上的二阶微分方程:d 2x d t 2−µ(1−x 2)d x d t+x =0其中x 是位置坐标,也是关于时间t 的函数,µ是一个标量参数表示非线性和阻尼强度。
Liénard 定理可以证明系统存在一个极限环,运用Liénard 转换y =x −x 3/3−˙x /µ,其中点表示对时间的导数,可以将范德坡振荡写成其二维形式:˙x =µ(x −13x 3−y )˙y =1µx 电路RLC 串联电路,其中LC 为线性元件,R 为非线性电阻,u R =13i 3R −i R ,令τ=1√LCt ,ε=√CL 根据KCL ,VCR 得:d u c d τ=−1εi L d i L d τ=ε[u c −(13i 3L−i L )]令u C (0+)=6V ,i L (0+)=1A ,ε分别取0.1,0.05,0.01,作u C −t ,i L −t 和u C −i L 关系图:ε=0.1ε=0.05ε=0.01源代码一阶微分方程组1%%filename:vdp.m2function yd=vdp(t,y)3epsilon=0.1;%test values:0.1,0.05,0.014yd=[-1.0/epsilon*y(2);5epsilon*(y(1)-(1.0/3.0*y(2)^3-y(2)))];数值计算和画图1%%filename:solve.m2tspan=[0,40];3u_C0=6;4i_L0=1;56y0=[u_C0;i_L0];7[t,YY]=ode45('vdp',tspan,y0);89figure10plot(t,YY(:,1));11grid on;12xlabel('t'),ylabel('u_C'); 1314figure15plot(t,YY(:,2));16grid on;17xlabel('t'),ylabel('i_L'); 1819figure20plot(YY(:,1),YY(:,2),'-');21grid on;22xlabel('u_C'),ylabel('i_L');。

Vanderpol系统的电路设计与实现摘要:Vanderpol系统是非线性系统中常用的混沌模型之一。
本论文通过介绍Vanderpol系统的背景,利用Matlab软件中Simulink模块搭建方程进行仿真,并且利用Mutisim软件进行电路设计与模拟,得到了理想的结果。
关键词:Vanderpol系统;Matlab仿真;模拟电路仿真中图分类号:TN702 文献标识码:A 文章编号:1001-828X(2015)008-000-01一、Vanderpol系统的背景介绍范德坡尔系统是一种典型且具有重要意义的自激振荡[1,2]。
它是由范德坡尔在1926年研究电子管振荡回路时发现的,经典Vanderpol方程的具体描述如下:(1)可见,方程只有一个奇点(0,0),我们将方程线性化,如下:(2)由上式可以得到:(3)由此,可以分析得到以下几种情况:(1)当时,方程具有两个实数根,且为负数,平衡点(0,0)为稳定的结点;(2)当时,方程具有两个复数根,并且实部为负,平衡点(0,0)为稳定的焦点;(3)当时,方程具有两个虚数根,平衡点是中心;(4)当时,方程具有两个具有正实部的复数根,平衡点是不稳定的焦点;(5)当时,方程有两个正实根,平衡点为不稳定的结点。
另外,从稳定性分析,可以看出(0,0)点是不稳定点。
当位移很小时,正的阻尼项因为很小,所以忽略不计。
项起主要作用,负阻尼因子使得系统的能量增加,偏离原点,位移变大,由此可以知道,系统在原点不稳定。
而当位移很大时,作为负阻尼项相对较小,正的阻尼项起主要作用,正阻尼使得系统的产生能量耗散,偏向原点,位移变小。
同时,由方程可以看出,系统有且只有原点一个不动点,没有别的奇点,运动轨道被局限在一个范围内,也就是一条闭合的曲线,即极限环型的周期振荡。
二、Vanderpol方程Matlab仿真模型的建立根据式(2)提供的范德坡尔的理论数学模型,利用Matlab软件中的Simulink模块对范德坡尔系统进行初步的计算机仿真,仿真模型如图1所示:保守系统运动的振幅和系统的初值有关,并且运动形成的闭合轨迹是一圈一圈围绕而成的,而自激振荡不同于周期运动,无论系统的初值如何取值,自激振荡的运动轨迹最终会趋向于一个孤立极限圆,也就是极限环。

实验六 基于MATLAB 控制系统的Nyquist 图及其稳定性分析 一、实验目的1、熟练掌握使用MATLAB 命令绘制控制系统Nyquist 图的方法。
2、能够分析控制系统Nyquist 图的基本规律。
3、加深理解控制系统乃奎斯特稳定性判据的实际应用。
4、学会利用奈氏图设计控制系统。
二、实验原理奈奎斯特稳定性判据(又称奈氏判据)反馈控制系统稳定的充分必要条件是当从变到时,开环系统的奈氏曲线不穿过点且逆时针包围临界点点的圈数R 等于开环传递函数的正实部极点数。
奈奎斯特稳定性判据是利用系统开环频率特性来判断闭环系统稳定性的一个判据,便于研究当系统结构参数改变时对系统稳定性的影响。
1、对于开环稳定的系统,闭环系统稳定的充分必要条件是:开环系统的奈氏曲线不包围点。
反之,则闭环系统是不稳定的。
2、对于开环不稳定的系统,有个开环极点位于右半平面,则闭环系统稳定的充分必要条件是:当从变到时,开环系统的奈氏曲线逆时针包围点次。
三、实验内容1、绘制控制系统Nyquist 图例1、系统开环传递函数,绘制其Nyquist 图。
210()210G s s s =++M-fileclcclear all den=[10]; num=[1 2 10]; sys=tf(den,num) nyquist(sys);2、根据奈氏曲线判定系统的稳定性例2、已知绘制Nyquist 图,判定系统的稳定性。
M-fileclc320.5()()20.5G s H s s s s =+++clearden=[0.5];num=[1 2 1 0.5];sys=tf(den,num);nyquist(sys)roots(num)ans =-1.5652-0.2174 + 0.5217i-0.2174 - 0.5217i【分析】由于系统奈氏曲线没有包围且远离(-1,j 0)点,且p=0,因此系统闭环稳定。
四、实验能力要求1、熟练使用MATLAB绘制控制系统Nyquist曲线的方法,掌握函数nyquist ( )的三种调用格式,并灵活运用。

目录目录 (I)摘要 (II)第一章绪论 (1)第二章简单电力网络的稳态运行及振荡 (3)2.1 常见简单故障分析 (3)2.2 振荡分析 (5)2.2.1 电力系统振荡的概念 (5)2.2.2 电力系统振荡时电流、电压的变化规律 (5)第三章MATLAB及其仿真工具simulink简介 (8)3.1 MATLAB简介 (8)3.2 MATLAB的主要组成部分 (8)3.3 Simulink简介 (9)3.4 simpowersys 模块介绍 (10)3.4.1特点 (11)3.4.2强大功能 (11)3.4.3 与Simulink 和MATLAB集成在一起 (12)3.4.4 交互式参数设定 (13)3.4.5 仿真和分析 (13)3.4.6 完善的文档和示例 (13)第四章简单电力网络建模与仿真 (15)4.1 仿真模型的建立和参数设定 (15)4.2 仿真波形及分析 (19)4.2.1 正常状况下各点波形 (19)4.2.2电力系统网络发生故障时波形分析 (21)4.2.3网络发生振荡时波形分析 (22)结论 (23)谢辞 (25)参考文献 (26)附录 (28)附录一译文: (28)摘要这篇文章首先介绍了电力系统稳态运行的原理以及MATLAB的组成和功能。
然后,利用MATLAB中的SIMULINK模块建立了电力系统的模型。
通过在不同的地点设置观测点,观测正常情况下稳态运行以及简单故障、震荡时各点的各相波形,从而验证课本上的稳态运行理论。
本文以IEEE5节点模型为例,制作了界面有好的图形界面窗口,可以方便的选择观测点以及模拟振荡情况,并将各相的波形显示在图形窗口之上,有利于教师在课堂上演示稳态运行的各种特点,增加教学的趣味性。
通过对不同参数下线路稳态运行及振荡情况的计算机模拟,可以提高课程教学的直观效果,使同学们对稳态运行及振荡时各点电气量的变化情况有一个形象的认识。
关键词simulink 电力系统稳态运行振荡仿真AbstractFirst of all,the principles of power system steady-state operation and the blocks of MATLAB was introduced in this paper.then, use the simulink software of MATLAB to construct the model of the power system.set observation points in different places,and observe the figure in the normal situation and the oscillation is happened,in this way ,we can prove the principles of the textbook.what’s more,we use the IEEE5 model as an example to make a GUI software which is more friendly to us,we can select the observation points and simulate the oscillations conveniently,and display the figure of the sequences in the GUI.this is good for the teacher to demonstrate all kinds of steady-state operation in the class and make the lesson more interesting.Simulating the transmission line steady-state operation and oscillation in different parameters by computer,we can make the lesson more interesting and let the students have a detail impression on the steady-state operation and oscillation.Keywords: simulink power system steady-state operationoscillation simulation第一章绪论我们经常讨论电力系统的稳定性问题。

使用matlab求解vanderpol方程的研究方法研究van der pol方程是一种重要的非线性动力学问题,它描述了一些自振系统的运动行为。
这个方程由物理学家布里尔·范·德·波尔在1920年首次提出,并广泛用于描述电路、生物和化学系统中的自振现象。
van der pol方程的一般形式如下:d^2x/dt^2 - μ(1 - x^2)dx/dt + x = 0其中,x是系统的状态变量,t是时间,而μ是一个非负常数,代表了系统的非线性因素。
为了研究van der pol方程的行为,我们可以使用MATLAB进行求解和分析。
下面将介绍几种常用的方法。
1. 数值解法:通过数值方法求解van der pol方程是最常用的研究方法之一、MATLAB中可以使用ode45函数来进行求解。
该函数基于Adams-Bashforth-Moulton方法,可以自动选择适当的步长,并给出较高的数值精度。
例如,我们可以定义一个匿名函数来表示van der pol方程,并使用ode45来求解:```MATLABmu = 1; % 设置μ的值[t, x] = ode45(f, [0, 10], [0.1; 0]); % 求解方程plot(t, x(:,1)); % 绘制解的图像xlabel('t'); ylabel('x');```这段代码定义了一个匿名函数f,其中t是时间,x是状态变量。
通过ode45函数对该方程进行求解,给定了初始条件[0.1; 0],求解时间范围为[0, 10]。
最后,使用plot函数对解进行可视化。
2. 分岔和稳定性分析:van der pol方程是一个具有非线性耗散的系统,因此它可以表现出各种动力学行为,如周期振荡、混沌和吸引子等。
MATLAB提供了一些函数用于分析方程的分岔和稳定性。
例如,可以使用bifurcation函数分析van der pol方程的分岔图:```MATLABmu = linspace(0, 10, 100); % 设定μ的取值范围x = linspace(-2, 2, 100); % 设定x的取值范围bifplot(bif_x, bif_par); % 绘制分岔图xlabel('μ'); ylabel('x');```这段代码根据设定的μ和x范围,使用bifurcation函数计算系统的分岔图,并使用bifplot函数进行可视化。
利用M a t l a b分析运算放大器电路(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--目录摘要 (1)1题目来源................................................... . (1)2研究意义................................................................... .. (2)3系统分析................................................................... .. (3)任务及要求 (3)分析与计算 (3)电路频率响应分析 (3)自激分析 (4)4编程和仿真 (5)5仿真结果与分析................................................. 6、7 6小结.. (8)7心得体会 (9)参考文献 (10)附录 (11)1题目来源matlab是一种科学计算软件,在数学类科技应用软件中在数值计算方面首屈一指。
它可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
而且的应用范围非常广,包括信号和图像处理、通讯、控制系统设计、测试和测量、财务建模和分析以及计算生物学等众多应用领域。
由于它使用方便,输入简捷,运算高效,内容丰富等特点,并且很容易由用户自行扩展,因此,matlab现已成为国外发达国家大学教学和科学研究中必不可少的工具。
结合我们所学的模拟电子技术,对其中的集成电路运算放大器求解电压增益和频率响应都不是一件容易的事情。
但是运用matlab函数对其处理求解便变得容易,而且形象直观。
让我们对电路的增益、频率响应以及自激现象的模拟更为简便。
基于MATLAB的非线性电路特性仿真研究作者:李佳伦来源:《科技视界》2019年第24期【摘要】实际电路都是非线性的。
非线性电路具有很多和线性电路完全不同的特性,表现出非线性电路独有的一些行为。
论文利用MATLAB搭建了不同的非线性电路模型,然后利用数值仿真,分析了非线性电路稳态不唯一、极限环、混沌等三个典型特性,直观展现了非线性电路中稳定与不稳定平衡点、极限环、混沌等不同行为的具体表现,分析了非线性电路轨迹与初始点的相关性,为了解非线性电路特殊的行为提供参考。
【关键词】非线性电路;平衡点;极限环;混沌中图分类号: TN710 文献标识码: A 文章编号: 2095-2457(2019)24-0047-004DOI:10.19694/ki.issn2095-2457.2019.24.023【Abstract】All actual circuits are nonlinear. Nonlinear circuits have many different characteristics from linear circuits, and some special behaviors would appear. The paper uses MATLAB to build different nonlinear circuit models, and then uses numerical simulation to analyze three typical characteristics of nonlinear circuits, i.e. multiple steady states, limit cycle and chaos, and visually shows the stable equilibrium point and unstable equilibrium point, limit cycle, chaos and other characteristics in nonlinear circuits. The paper also analyzes the dependence of trajectories of nonlinear circuits on the initial points. The results provide a reference for understanding the special behaviors of nonlinear circuits.【Key words】Non-linear circuit; Equilibrium point; Limit cycle; Chaos0 引言在線性电路中,线性元件的特点是其参数不随电压或电流而变化。
范德坡振荡电路Van der Pol oscillator
简介
在动态电路中,范德坡振荡是非保守的、非线性阻尼振荡。
它在时间域上的二阶微分方程:
d 2x d t 2−µ(1−x 2)d x d t
+x =0其中x 是位置坐标,也是关于时间t 的函数,µ是一个标量参数表示非线性和阻尼强度。
Liénard 定理可以证明系统存在一个极限环,运用Liénard 转换y =x −x 3/3−˙x /µ,其中点表示对时间的导数,可以将范德坡振荡写成其二维形式:
˙x =µ(x −13x 3−y )˙y =1µ
x 电路
RLC 串联电路,其中LC 为线性元件,R 为非线性电阻,u R =13i 3R −i R ,令τ=1√LC
t ,ε=√CL 根据KCL ,VCR 得:d u c d τ=−1ε
i L d i L d τ=ε[u c −(13i 3L
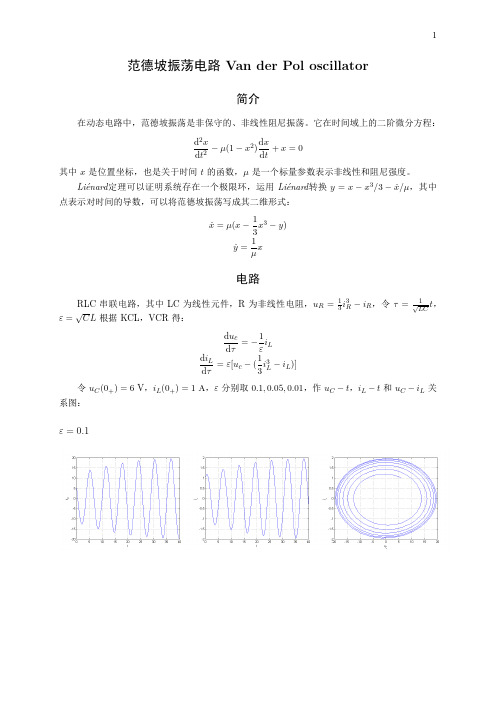
−i L )]令u C (0+)=6V ,i L (0+)=1A ,ε分别取0.1,0.05,0.01,作u C −t ,i L −t 和u C −i L 关系图:
ε=0.1
ε=0.05
ε=0.01
源代码
一阶微分方程组
1%%filename:vdp.m
2function yd=vdp(t,y)
3epsilon=0.1;%test values:0.1,0.05,0.01
4yd=[-1.0/epsilon*y(2);
5epsilon*(y(1)-(1.0/3.0*y(2)^3-y(2)))];
数值计算和画图
1%%filename:solve.m
2tspan=[0,40];
3u_C0=6;
4i_L0=1;
5
6y0=[u_C0;i_L0];
7[t,YY]=ode45('vdp',tspan,y0);
8
9figure
10plot(t,YY(:,1));
11grid on;
12xlabel('t'),ylabel('u_C'); 13
14figure
15plot(t,YY(:,2));
16grid on;
17xlabel('t'),ylabel('i_L'); 18
19figure
20plot(YY(:,1),YY(:,2),'-');
21grid on;
22xlabel('u_C'),ylabel('i_L');。