知识讲解 气体热现象的微观意义
- 格式:doc
- 大小:174.01 KB
- 文档页数:7

气体热现象的微观意义一、气体热现象微观意义的趣味解读咱们来唠唠气体热现象的微观意义哈。
这气体热现象啊,就像是微观世界里的一场热闹派对。
你想啊,气体分子就像一群调皮的小精怪。
当温度升高的时候呢,这些小精怪就像是被打了兴奋剂一样,开始疯狂地跑来跑去,活力四射。
它们的运动速度加快,相互之间的碰撞也变得更加频繁。
就好比在一个热热闹闹的舞会上,大家随着音乐节奏加快,跳舞的动作幅度变大,碰撞到彼此的几率也大大增加了。
从微观角度看,气体压强的产生也很有趣。
这些分子不停地撞击容器壁,就像一群小皮球不停地砸向墙壁。
分子越多,撞击得就越频繁,压强也就越大。
而且啊,分子运动速度越快,撞击的力量就越大,压强也会增大。
这就像是一群孩子扔球,如果扔球的速度快,而且孩子的数量还多,那墙壁受到的冲击力肯定就大。
还有气体的体积和温度的关系。
温度升高的时候,分子们需要更大的空间来撒欢儿,就像人热的时候想伸展四肢一样,所以气体体积会膨胀。
相反,温度降低的时候,分子们就没那么活跃了,就会收缩起来,气体体积也就变小了。
气体分子之间的距离相对比较大,它们之间的作用力比较小。
这就使得气体能够充满整个容器,而且还能被压缩。
这就好比是一群散漫的小动物,彼此之间联系不太紧密,所以可以被赶到更小的空间里,也可以让它们在很大的空间里自由活动。
在热传递方面呢,当两个温度不同的气体相互接触时,热的气体分子运动快,就像热情的舞者,它们会把能量传递给运动慢的分子,就像是带着那些比较慵懒的分子一起嗨起来。
这样就实现了热量从高温物体向低温物体的传递。
我们生活中很多现象都和气体热现象的微观意义有关。
比如说,夏天的时候自行车胎容易爆胎,就是因为温度高,分子运动剧烈,气体压强增大。
还有热气球能够飞起来,是因为加热空气后,空气分子运动加快,密度变小,从而产生向上的浮力。
反正就是说,气体热现象的微观意义就隐藏在这些微观粒子的一举一动之中,理解了这些,就好像打开了微观世界的一扇小窗户,可以看到那些奇妙的景象。








第四节气体热现象的微观意义气体热现象的微观意义指的是通过研究气体的分子结构和运动,来解释和理解气体的热传导、热膨胀、热传递等热现象的行为。
这种研究方法能够从微观的角度出发,揭示出气体热现象的根本原理,对于我们更深入地理解气体的性质和行为具有重要意义。
首先,气体热现象的微观意义在于揭示了气体分子的运动特性。
根据动理论,气体分子在运动过程中的速度、方向和碰撞等行为对于气体的热传导、热膨胀等现象具有重要影响。
通过研究气体分子的平均速度、能量分布以及碰撞的频率和方式,我们可以更准确地预测和解释气体的热传导和热膨胀现象。
这对于相关领域的研究和应用具有重要意义,例如热工学、热力学、材料科学等。
其次,气体热现象的微观意义在于揭示了气体的热传导机制。
气体的热传导是指热能从高温区域向低温区域的传递过程。
在微观尺度上,气体分子之间通过碰撞和相互作用传递能量。
通过研究气体分子之间的碰撞方式和能量传递机制,我们可以理解气体热传导的原理和规律。
例如,通过研究气体分子的自由路径和碰撞概率,我们可以计算气体的热导率和热传导速率,从而更好地控制和应用气体的热传导性能。
此外,气体热现象的微观意义还在于揭示了气体的热膨胀机制。
在微观尺度上,气体分子的运动导致气体的体积随着温度的变化而发生变化。
通过研究气体分子的运动规律和热膨胀机制,我们可以解释和预测气体的体积随温度变化的规律。
这对于工程设计和材料选择具有重要意义,例如在设计汽车内燃机时需要考虑气体的热膨胀对引擎的影响,同时在材料选择时需要考虑气体的热膨胀系数以及材料的热稳定性。
最后,气体热现象的微观意义还在于揭示了气体的热传递机制。
热传递是指热能从高温区域向低温区域的传递过程,它由传导、对流和辐射三种方式组成。
通过研究气体分子的运动和能量的传递规律,我们可以理解气体的传导、对流和辐射热传递机制,从而更准确地预测和解释气体的热传递行为。
这对于能源利用和热工学应用具有重要意义,例如在工业生产中的热能转换和传输过程中需要考虑气体的热传递性能,同时在设计和优化热力系统时要考虑气体传导、对流和辐射的综合影响。

气体热现象的微观意义[要点导学]1.这堂课学习教材第四节的内容。
主要要求如下:了解气体分子运动的特点,能用分子运动论的观点理解温度、压强的物理意义,能运用分子运动论对气体定律作出微观解释。
2.气体分子之间存在很大的空间,分子距离很大,所以分子之间的分子力十分微弱,可以忽略。
气体分子可以自由地运动。
由于气体分子运动有这样的特点,宏观上表现出:(1)气体可以充满整个容器。
一定质量的气体,不管用多大的容器装它,它的体积总等于容器的容积。
(2)气体很容易被压缩,气体的体积很容易改变。
3.分子做无规则热运动,速率有大有小,但按一定规律分布;分子运动的剧烈程度与温度有关,温度越高,分子热运动的平均速率就越大;理想气体的分子平均动能与气体的热力学温度成正比;温度是分子平均动能的标志。
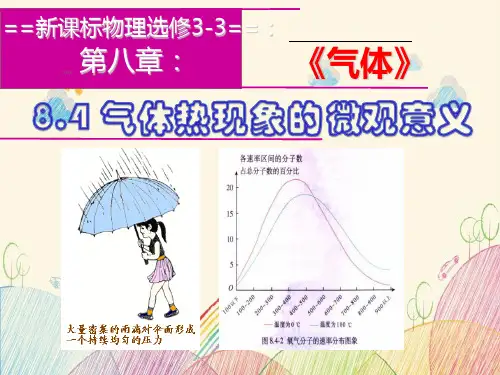
4.气体分子做无规则运动时,对容器壁撞击产生冲力,单个分子撞击容器壁的冲力是短暂的,大量的分子连续不断地撞击容器壁,就产生了持续的均匀的压力。
气体对容器壁的压力就是由于气体分子频繁碰撞器壁而产生的,单位面积上的压力就是压强。
气体压强的大小,从微观上来看,与两个因素有关,一是气体分子的密集程度,一是气体分子的平均动能。
平均动能越大,分子对容器壁的冲力就越大,分子密集程度则反映了单位时间内单位面积上撞击容器壁的分子数量。
5.对一定质量的气体来说,反映分子密集程度的宏观量就是气体体积;分子平均动能的宏观标志是温度,所以气体压强与温度和体积有关系。
对气体定律进行微观解释就是要将宏观现象与微观分子运动联系起来。
如:对于气体等温变化的解释就是:温度不变,分子平均运动的速率不变,也就是每个分子撞击容器壁的平均冲力一定,当一定质量的气体体积变小,分子的密集程度就________,撞击单位面积容器壁上的分子数_________,所以气体压强增大。
[范例精析]例1一位同学用橡皮帽堵住了注射器前端的小孔,用活塞封闭了一部分空气在注射器中,他把注射器竖直放入热水中(如图所示),发现注射器的活塞向上升起.试用分子动理论解释这个现象.解析:由题意可知,在实验过程中封闭的气体压强保持不变.当注射器放入热水中时,气体的温度升高,分子的平均速率增大了,要保持压强不变,只有使一定时间内撞击单位面积容器壁的分子数减少,也就是使气体分子密集程度减小,即气体的体积增大。
高中气体热现象的微观意义学案教案Document number【980KGB-6898YT-769T8CB-246UT-18GG08】气体热现象的微观意义[学习目标]1、了解统计规律及其在科学研究和社会生活中的作用。
2、知道分子运动的特点,掌握温度的微观定义。
3、掌握压强、实验定律的微观解释。
[自主学习]一、气体分子运动的特点1、从微观的角度看,物体的热现象是由的热运动所决定的,尽管个别分子的运动有它的不确定性,但大量分子的运动情况会遵守一定的。
2、分子做无规则的运动,速率有大有小,由于分子间频繁碰撞,速率又将发生变化,但分子的速率都呈现的规律分布。
这种分子整体所体现出来的规律叫统计规律。
3、气体分子运动的特点(1)分子的运动杂乱无章,在某一时刻,向着运动的分子都有,而且向各个方向运动的气体分子数目都。
(2)气体分子速率分布表现出“中间多,两头少”的分布规律。
温度升高时,速率大的分子数目,速率小的分子数目,分子的平均速率。
4、温度是的标志。
用公式表示为。
二、气体压强的微观意义1、气体的压强是而产生的。
气体压强等于大量气体分子作用在器壁。
2、影响气体压强的两个因素:,。
从两个因素中可见一定质量的气体的压强与,两个参量有关。
三、对气体实验定律的微观解释1、一定质量的气体,温度保持不变时,分子的平均动能是的,在这种情况下,体积减小时,分子的,气体的压强就这就是玻意耳定律的微观解释。
2、这就是查理定律的微观解释。
3、是盖·吕萨克定律的微观解释。
[典型例题]1、有关气体的压强,下列说法正确的是()A、气体分子的平均速率增大,则气体的压强一定增大B、气体分子的密集程度增大,则气体的压强一定增大C、气体分子的平均动能增大,则气体的压强一定增大D、气体分子的平均动能增大,气体的压强有可能减小2、以查理定律为例,用分子动理论从微观的角度作出解释[当堂达标]1、下列哪些量是由大量分子热运动的整体表现所决定的()A、压强B、温度C、分子密度D、分子的平均速率2、对一定质量的理想气体,下列说法正确的是()A、体积不变,压强增大时,气体分子的平均动能一定增大B、温度不变,压强减小时,气体的密度一定减小C、压强不变,温度降低时,气体的密度一定减小D、温度升高,压强和体积都可能不变3、从气体压强的微观意义,解释在图中,竖直放置两端封闭的玻璃管升温时液柱的移动方向。
气体热现象的微观意义今天我和大家一起学习第八章第4节,《气体热现象的微观意义》首先我们一起来欣赏一个发生在飞机上的笑话,谁愿意给大家表演一下?(学生表演大屏幕上的笑话)笑话欣赏完了,当然,这仅仅是一个笑话,不可能把炸弹带上飞机。
我们先不评价飞机上的这个人是聪明还是愚蠢,但是我们看到了一个概念,那就是“概率”,“概率”,也就是前面提到的“统计规律”,今天就从统计规律开始学习。
(板书:随机性与统计规律)首先我们学习几个概念:1、在一定条件下,若某事件必然出现,这个事件叫做必然事件2、若某件事不可能出现,这个事件叫做不可能事件3、若在一定条件下某事件可能出现,也可能不出现,这个事件叫做随机事件举个简单例子,我手里有一枚硬币,如果我从静止释放,那么这枚硬币落地,就应该是“必然事件”,这枚硬币飞上天,就应该是“不可能事件”,而硬币落地后,有可能正面朝上,也有可能背面朝上,那正面朝上就应该是“随机事件”必然事件和随机事件我们这里不做研究,大家想一想,这里的随机事件,也就是硬币正面朝上,如果我多次做这个实验,随机事件的出现有没有规律呢?正面朝上的概率大概能确定吗?(学生,百分之五十)下面我们就做一个类似的实验,来看看随机事件的出现是否存在规律性。
(学生看实验内容)我对这个实验做一个简单的解释:如果我们投掷4枚硬币,可能出现的情况是:有1个正面朝上、2个正面朝上、3个、4个或者0个。
各种情况都有可能发生,也就是说这个事件为随机事件,具有偶然性,如果我们进行多次投掷,会不会存在着一定的规律性呢?我们每人做10次,看看1个正面朝上的有几次,2个正面朝上的有几次等,然后填入课本26页的表格中,分析一下是否存在规律性。
我们的大组长负责统计你们大组的全部数据。
现在开始。
(学生实验)实验做完了,在大组长统计的同时,我们找几个同学把自己的数据给大家展示一下(4位同学展示自己数据)大家看看有什么规律性吗?为了更加清晰地分析这些数据,我做一下柱形图。
气体热现象的微观意义编稿:张金虎 审稿:李勇康【学习目标】1.知道气体分子的运动特点,知道气体分子的运动遵循统计规律.2.知道气体压强的微观意义.3.知道三个气体实验定律的微观解释.4.了解气体压强公式和推导过程.【要点梳理】要点一、统计规律1.统计规律由于物体是由数量极多的分子组成的,这些分子并没有统一的运动步调,单独看来,各个分子的运动都是不规则的,带有偶然性,但从总体来看,大量分子的运动却有一定的规律,这种规律叫做统计规律.2.分子的分布密度分子的个数与它们所占空间的体积之比叫做分子的分布密度,通常用n 表示.3.气体分子运动的特点(1)气体分子之间的距离很大,失约是分子直径的10倍.因此除了相互碰撞或者跟器壁碰撞外,气体分子不受力的作用,在空间自由移动.(2)分子的运动杂乱无章,在某一时刻,向着任何一个方向运动的分子都有,而且向各个方向运动的气体分子数目都相等.(3)每个气体分子都在做永不停息的运动,常温下大多数气体分子的速率都达到数百米每秒,在数量级上相当于子弹的速率.(4)气体分子的热运动与温度的关系○1温度越高,分子的热运动越激烈.○2理想气体的热力学温度T 与分子的平均动能k E 成正比,即:k T aE (式中a 是比例常数),因此可以说,温度是分子平均动能的标志.要点诠释:理想气体没有分子势能,所以其内能仅由温度决定,温度越高,内能越大,温度越低,内能越小.要点二、对气体的微观解释1.气体压强的微观意义(1)气体压强的大小等于气体作用在器壁单位面积上的压力.(2)产生原因:大量气体分子无规则运动碰撞器壁,形成对器壁各处均匀的持续的压力而产生.(3)决定因素:一定气体的压强大小,微观上决定于分子的平均动能和单位体积内的分子数;宏观上决定于气体的温度T 和体积V2.对气体实验定律的微观解释(1)一定质量的气体,分子的总数是一定的,在温度保持不变时,分子的平均动能保持不变,气体的体积减小到原来的几分之一,气体的密度就增大到几倍,因此压强就增大到几倍,反之亦然,所以气体压强与体积成反比,这就是玻意耳定律.(2)一定质量的气体,体积保持不变而温度升高时,分子的平均动能增大,因而气体压强增大,温度降低时,情况相反,这就是查理定律所表达的内容.(3)一定质量的气体,温度升高时要保持压强不变,只有增大气体体积,减小分子的分布密度才行,这就是盖一吕萨克定律所表达的内容.要点三、分子的平均动能1.分子的平均动能物体分子动能的平均值叫分子平均动能.温度是分子平均动能的标志,温度越高,分子平均动能越大.物体内部各个分子的运动速率是不相同的,所以分子的动能也不相等.在研究热现象时,有意义的不是一个分子的动能,而是物体内所有分子动能的平均值——分子平均动能.物体的温度是大量分子热运动剧烈程度的特征,分子热运动越剧烈,物体的温度越高,分子平均动能就越大,所以说温度是分子平均动能的标志这是对温度这一概念从物体的冷热程度的简单认识,进一步深化到它的微观含义、本质的含义.2.判断气体分子平均动能变化的方法(1)判断气体的平均动能的变化,关键是判断气体温度的变化,因为温度是气体分子平均动能的标志.(2)理解气体实验定律的微观解释关键在于理解压强的微观意义.要点四、宏观、微观的区别与联系1.宏观、微观的区别与联系从宏观上看,一定质量的气体仅温度升高或仅体积减小都会使压强增大,从微观上看,这两种情况有没有什么区别?分析:因为一定质量的气体的压强是由单位体积内的分子数和气体的温度决定的.气体温度升高,即气体分子运动加剧,分子的平均速率增大,分子撞击器壁的作用力增大,故压强增大.气体体积减小时,虽然分子的平均速率不变,分子对容器的撞击力不变,但单位体积内的分子数增多,单位时间内撞击器壁的分子数增多,故压强增大,所以这两种情况下在微观上是有区别的.2.气体压强的公式现在从分子动理论的观点推导气体压强的公式.设想有一个向右运动的分子与器壁发生碰撞(图8-5-1),碰撞前的速率为v ,碰撞前的动量为mv ,碰撞后向左运动。
速率为'v ,碰撞后的动量为'mv -.碰撞前后的动量变化为'mv mv --.设分子与器壁的碰撞没有能量损失,分子碰撞前后的速率相等,即'v v ,因而碰撞前后的动量变化量为2mv -.这个动量变化量2mv -等于器壁对分子的冲量,从牛顿第三定律知道,分子对器壁也有一个大小相等方向相反的冲量.可见,气体分子每碰撞一次器壁,就给器壁2mv 的冲量.单位时间内大量分子对器壁的总冲量等于器壁所受的平均压力,对单位面积器壁的总冲量就等于气体的压强.怎样算出这个总冲量呢?单靠力学知识不行,需要用到统计方法.大量气体分子做无规则的热运动,它们沿各个方向运动的机会是均等的,从统计的观点来看,可以认为各有1/6的分子向着上、下、前、后、左、右这六个方向运动,气体分子的速率是按照一定的统计规律分布的,可以认为所有分子都以平均速率v 向着各个方向运动.计算出大量气体分子碰撞器壁的总冲量,就可以进一步求出器壁所受的压力,进而求出气体的压强来.如图所示,在气体内部设想一个柱体,底面积为单位面积,高度为分子平均速率v 的数值,设气体单位体积中的分子数为0n ,则在这个柱体中有016n v 个向右运动的分子.因此,在单位时间内,这016n v 个分子会与器壁发生碰撞.分子每碰撞一次器壁,给器壁的冲量为2mv .因此,单位时间内分子给单位面积器壁的总冲量等于20011263n v mv n mv ⋅=. 单位时间内气体对器壁的总冲量等于器壁所受的平均压力,单位器壁所受的平均压力就等于气体的压强p (如图).于是我们得到气体的压强公式:2013p n mv =. 气体分子的平均动能 212E mv =, 上式化为 023p n E =. 从这个公式可以知道,单位体积内的分子数越多,气体分子的平均动能越大,气体的压强就越大. 要点四、知识归纳与提升1.知识梳理(1)气体分子沿各个方向运动的机会均等,分子速率按一定的“中间多,两头少”的统计规律分布.(2)影响气体压强的两个因素是:分子的平均动能和单位体积内的分子数,而且气体的压强正比于二者的乘积.2.规律方法总结(1)判断气体的平均动能的变化,关键是判断气体温度的变化,因为温度是气体分子平均动能的标志.(2)理解气体实验定律的微观解释关键在于理解压强的微观意义.【典型例题】类型一、微观解释例1.(2016 聊城模拟)对于一定质量的理想气体,下列论述中正确的是()A.若单位体积内分子个数不变,当分子热运动加剧时,压强一定变大B.若单位体积内分子个数不变,当分子热运动加剧时,压强可能不变C.若气体的压强不变而温度降低时,则单位体积内分子个数一定增加D.若气体的压强不变而温度降低时,则单位体积内分子个数可能不变E.气体的压强由温度和单位体积内的分子个数共同决定【答案】ACE【解析】单位体积内分子个数不变,当分子热运动加剧时,单位面积上的碰撞次数和碰撞的平均力都增大,因此这时气体压强一定增大,故A正确,B错误;若气体的压强不变而温度降低时,气体分子热运动的平均动能减小,则单位体积内分子个数一定增加,故C正确,D错误;气体的压强与气体的温度和单位体积内的分子个数共同决定,E正确。
举一反三:【变式1】容积不变的容器内封闭着一定质量的理想气体,当温度升高时().A.每个气体分子的速率都增大B.单位时间内气体分子撞击单位面积器壁的次数增多C.气体分子对器壁的撞击在单位面积上每秒钟内的个数增多D.气体分子在单位时间内,作用于单位面积器壁的总冲量增大【答案】B、C、D【解析】气体温度增加时,从平均效果来说,物体内部分子的热运动加剧,是大量分子热运动的集体表现.而对单个的分子而言,说它的温度与动能之间有联系是没有意义的,故选项A不正确.理想气体的温度升高,分子的无规则热运动加剧,使分子每秒钟与单位面积器壁的碰撞次数增多,因分子平均动能增大,分子每次碰撞而施于器壁的冲量也增大,因而气体分子在单位时间内,作用于单位面积器壁的总冲量也增大,故选项B、C、D正确.举一反三:【变式2】对于一定量的稀薄气体,下列说法正确的是( )A.压强变大时,分子热运动必然变得剧烈B.保持压强不变时,分子热运动可能变得剧烈C.压强变大时,分子间的平均距离必然变小D.压强变小时,分子间的平均距离可能变小【答案】BD【解析】一定质量的稀薄气体可以看做理想气体,分子运动的剧烈程度与温度有关,温度越高,分子运动的越剧烈;压强变大可能是的原因是体积变小或温度升高,所以压强变大,分子热运动不一定剧烈,AC 项错误,B 项正确;压强变小时,也可能体积不变,可能变大,也可能变小;温度可能降低,可能不变,可能升高,所以分子间距离不能确定,D 项正确。
例2.一定质量的某种理想气体,当它的热力学温度升高为原来的1.5倍、体积增大为原来的3倍时,压强将变为原来的多少?请你从压强和温度的微观意义来说明.【思路点拨】气体的压强在微观意义上正比于单位体积内气体分子个数和气体分子平均动能的乘积.【答案】见解析【解析】在微观意义上,气体的压强等于单位面积上气体碰撞器壁的作用力,找出单位时间内碰撞器壁作用力的决定因素,即可求解.若单位体积内的分子数为n 0个,则单位面积上单位时间内能碰撞器壁的分子所占的体积V v =,所以碰撞器壁的分子个数n ∝n 0V ,即0n n v ∝.每个气体分子以平均速率v 碰撞器壁时的速率变化量为2v ,则由牛顿第二定律得F ma mv =∝.气体的压强等于在单位面积上的器壁受的碰撞力,则有20p nF n mv =∝, 即0k p n E ∝. ①由于热力学温度升高为原来的1.5倍,由k E aT =得' 1.5k k E E =. ②体积增大为原来的3倍,则气体单位体积内的分子个数减为原来的13,即001'3n n =, ③ 由①②③式得 1'2p p =,即气体的压强变为原来的12倍. 【总结升华】气体的压强在微观意义上正比于单位体积内气体分子个数和气体分子平均动能的乘积.举一反三:【变式】对于一定质量的理想气体,下列论述中正确的是( ).A .当分子热运动变得剧烈时,压强必变大B .当分子热运动变得剧烈时,压强可以不变C .当分子间的平均距离变大时,压强必变小D .当分子间的平均距离变大时,压强必变大【答案】B【解析】解此题应把握以下两个方面:①分子热运动的剧烈程度由温度高低决定;②对一定质量的理想气体,pV T=恒量.选项A、B中,“分子热运动变得剧烈”说明温度升高。
但不知体积变化情况,所以压强变化情况不确定,所以A错。