下载文档原格式
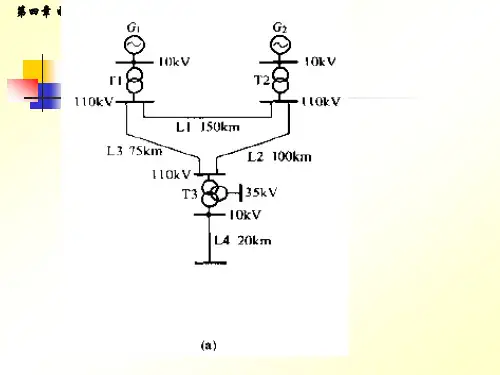
第四章 复杂电力系统的潮流计算复杂电力系统是一个包括大量母线、支路的庞大系统。
对这样的系统进行潮流分析时，采用第三章中人工计算的方法已不适用。
目前，随着计算机技术的发展，计算机算法已逐渐成为分析复杂系统潮流分布的主要方法，其中包括建立数学模型、确定计算方法和编制计算程序三方面的内容。
本章主要讲述前两方面的内容，同时为了方便分析，针对计算机解法作如下规定：⑴ 所有参数（功率、电压、电流、阻抗或导纳）都以标幺值表示；⑵ 电力系统稳态运行时，可以把负荷作恒定功率处理，也可作恒定阻抗处理；⑶ 所有电源（发电机、调相机、电力电容器等）均向母线注入功率（或电流），取正号；⑷ 作恒定功率处理的负荷，均为从母线“吸取”功率，是向母线注入负的功率（或电流），取负号； ⑸ 母线总的注入功率（或电流）为电源注入功率（或电流）与负荷“吸取”功率（或电流）代数和； ⑹ 输电线路、变压器用П型等值电路表示。
第一节 电力网络的数学模型电力网络的数学模型是指将网络的有关参数和变量及其相互关系归纳起来所组成的、可反映网络性能的数学方程组。
电力网络属于线性网络， 因此，电路理论中关于线性网络的分析方法也适用于分析电力网络。
目前，普遍采用的有两种方法：一是节点电压法；二是回路电流法。
一、节点电压方程和回路电流方程1.节点电压方程是依据基尔霍夫电流定律，通过节点导纳矩阵（或节点阻抗矩阵）反映节点电流与节点电压之间关系的数学模型。
⑴ 用节点导纳矩阵描述的节点电压方程：B B B U Y I = （4-1）一般地，当网络中的独立节点数（即母线数）为n 时，在式（4-1）中：B I =（1•I ，2•I ，… i I •，… n I •）T 为节点注入电流的n 维列向量；B U =（1•U ，2•U ， … i U • … n U •）T 为节点电压列向量； Y 11 Y 12 … Y 1i … Y 1nY 21 Y 22 … Y 2i … Y 2nB Y = … … … 为n ×n 阶节点导纳矩阵 （4-2）Y i1 Y i2 … Y ii … Y in… … …Y n1 Y n2 … Y ni … Y nn由以上分析可知，对n 母线电力系统有n 个独立的节点电压方程式（以大地为参考节点）。
电力系统分析第04章复杂电力系统潮流计算潮流计算是电力系统分析的一个重要工具，用于计算电力系统中各节点的电压幅值和相角，以及各支路的功率潮流分布情况。
复杂电力系统潮流计算主要包括节点潮流计算和线路潮流计算两部分。
节点潮流计算是指计算电力系统各节点的电压幅值和相角。
节点潮流计算的基本原理是根据节点复功率方程和节点电流平衡方程，建立节点潮流计算的数学模型。
该模型可以用于计算电力系统中各节点的电压幅值和相角，并找出潮流计算过程中出现的问题。
线路潮流计算是指计算电力系统中各支路的功率潮流分布情况。
线路潮流计算的基本原理是根据支路潮流方程，建立线路潮流计算的数学模型。
该模型可以用于计算电力系统中各支路的功率潮流，包括有功功率、无功功率和视在功率等。
在复杂电力系统潮流计算中，需要考虑以下几个方面。
首先，需要确定电力系统的潮流计算方法，常用的有直接法、迭代法和改进迭代法。
直接法适用于小型电力系统，计算速度较快，但对于大型电力系统不太适用。
迭代法采用不断迭代的方式计算潮流，适用于大型电力系统，计算精度较高。
改进迭代法是对迭代法的改进，可以提高计算速度和精度。
其次，需要确定电力系统的节点类型。
电力系统中的节点可以分为平衡节点、PQ节点、PV节点和参考节点。
平衡节点的有功功率和无功功率都为零，用于维持整个系统的功率平衡。
PQ节点的有功功率和无功功率是已知的，需要通过潮流计算来确定该节点的电压幅值和相角。
PV节点的有功功率是已知的，需要通过潮流计算来确定该节点的无功功率和电压幅值。
参考节点是一个已知电压值的节点，作为其他节点电压相角的参考点。
最后，需要考虑电力系统潮流计算的收敛性和稳定性。
收敛性是指潮流计算的结果是否能够收敛到一个稳定的值。
如果潮流计算不能收敛，则需要调整潮流计算的参数或算法，以提高收敛性。
稳定性是指潮流计算结果对电力系统的扰动是否具有稳定的响应。
如果潮流计算结果不稳定，则需要进一步分析系统的动态行为，以寻找稳定的解决方案。
