弹簧振子的振幅是

机械振动（五）答案1. 图为同一实验中甲、乙两个单摆的振动图象，从图象可知（）A.两摆球质量相等B.两单摆的摆长相等C.两单摆相位相差π4D.在相同的时间内，两摆球通过的路程总有s甲=2s 乙【解析】根根据图线得到振幅和周期的情况，然后结合单摆的周期公式进行分析讨论．【解答】解：A、从单摆的位移时间图象可以看出两个单摆的周期相等，根据周期公式T=2π√Lg可知，两个单摆的摆长相等，周期与摆球的质量无关，故A错误，B正确；C、从图象可以看出，t=0时刻，甲到达了正向最大位移处而乙才开始从平衡位置向正向的最大位移处运动，所以两单摆相位相差为π2，故C错误；D、由于两个摆的初相位不同，所以只有从平衡位置或最大位移处开始计时时，而且末位置也是平衡位置或最大位移处的特殊情况下，经过相同时间，两球通过的路程才一定满足s甲=2s乙，若不能满足以上的要求，则不一定满足：s甲=2s乙．故D错误；故选：B2. 某质点在0∼4s的振动图象如图所示，则下列说法正确的是（）A.质点沿振动曲线运动B.在0∼1s内质点做初速度为0的加速运动C.在0∼4s内质点通过的路程为20cmD.振动图象是从平衡位置开始计时的【解析】由图象直接读出．根据质点位移的变化，不能确定其轨迹的形状．加速度方向总与位移方向相反．分析质点振动的过程，确定其路程．质点的振幅等于位移x的最大值，由图象直接读出．【解答】解：A、振动图象反映质点的位移随时间的变化情况，不是质点的运动轨迹，该图并不表示质点沿曲线运动．故A错误．B、在0∼1s内质点从平衡位置向正向最大位移处运动，做初速度不为0的减速运动，故B错误．C、在0∼4s内质点通过的路程等于四倍振幅，为4A=40cm，故C错误．D、由图知，t=0时，x=0，可知振动图象是从平衡位置开始计时的．故D正确．故选：D．3. 一列简谐横波沿直线由A向B传播，相距10.5m的A、B两处的质点振动图象如图a、b所示，则（）A.该波的振幅一定是20cmB.该波的波长可能是14mC.该波的波速可能是10.5m/sD.该波由a传播到b可能历时7s【解析】根据振动图象读出质点的振幅，即为该波的振幅．由图读出同一时刻a、b两质点的位置和速度方向，结合波形分析质点间的距离与波长的关系，得到波长的通项，再求解波长的特殊值，求出波速的通项，求解波速的特殊值．【解答】解：A、由图读出，该波的振幅为A=10cm，周期为4s．故A错误．B、C、由图看出，在t=0时刻，质点a经过平衡位置向上运动，质点b位于波谷，波由a向b传播，结合波形得到a、b间距离与波长的关系为：△x=(n+14)λ，(n=0, 1, 2,…)，得到波长为：λ=4△x4n+1=424n+1m，如果λ=14m，则n=0.5，不是整数，矛盾；故B错误；当n=1时，λ=8.4m，波速为：v=λT=8.44=2.1m/s，当n=0时，λ=42m，波速为：v=10.5m/s．故C正确．D、该波由a传播到b的时间为t=(n+14)T=(4n+1)s，(n= 0, 1, 2,…)，由于n是整数，t不可能等于7s．故D错误．故选：C．4. 如图为一水平弹簧振子的振动图象，由此可知（）A.在t2时刻，振子的速度方向沿x轴正方向B.在t4时刻，振子的速度最大，加速度最大C.在0−t1时间内，振子的速度逐渐增大，位移逐渐增大D.在t2−t3时间内，振子做加速度逐渐增大的减速运动【解析】振动图象是位移时间图象，其切线斜率等于速度，斜率的正负表示速度的方向；直接读出振子的位置随时间的变化关系，结合运动的方向和位移判定加速度的变化与速度的变化．【解答】解：A、t2时刻图象切线的斜率为负，说明振子处于平衡位置且速度方向沿x轴负方向，故A错误．B、在t4时刻，振子位于平衡位置处，的速度最大，加速度是0，故B错误．C 、在0−t 1时间内，振子的位移逐渐增大，速度逐渐减小．故C错误； D 、由图可知在t 2−t 3时间内，振子的位移向负方向逐渐增大，由a =−kx m振子做加速度逐渐增大的减速运动，故D 正确．故选：D5. 如图所示为某弹簧振子在0∼5s 内的振动图像，由图可知，下列说法中正确的是（ ）A.振动周期为5s ，振幅为8cmB.第2s 末振子的速度为零，加速度为负向的最大值C.第3s 末振子的速度为正向的最大值D.从第1s 末到第2s 末振子在做加速运动 【解析】 此题暂无解析 【解答】解：A ．由图知，质点的振幅是8cm ，周期是4s ，故A 错误； B ．在t =2s 时，物体到达负向最大位移处，速度为零，加速度为正向最大值，故B 错误；C ．第3s 末振子在平衡位置处，其速度为正向的最大值，故C 正确；D ．从第1s 末到第2s 末振子在平衡位置向负向移动，振子在做减速运动，故D 错误． 故选C ．6. 关于简谐振动，下列说法正确的是（ ）A.如果质点振动的位移与时间的关系遵从正弦函数的规律，这样的振动叫做简谐振动B.如果质点做简谐振动，则质点振动的动能和弹性势能的总和保持不变C.回复力F =−kx ，是简谐振动的条件，回复力F 只能是弹力D.弹簧振子的振动在考虑空气阻力时，做的也是简谐振动 【解析】简谐振动的位移与时间的关系遵从正弦函数的规律；回复力可以在弹力，也可以是其他的力；回复力是做简谐运动的物体所受到的指向平衡位置的合力，方向总是指向平衡位置；回复力公式F =−kx 中的k 是比例系数；回复力是变力． 【解答】解：A 、根据简谐振动的特点可知，如果质点振动的位移与时间的关系遵从正弦函数的规律，这样的振动叫做简谐振动．故A 正确； B 、如果质点做简谐振动，则质点振动的动能、重力势能、弹性势能等的总和保持不变．故B 错误；C 、回复力F =−kx ，是简谐振动的条件，但是回复力F 不一定只是弹力，可以会有其他的外力．故C 错误；D 、弹簧振子的振动在考虑空气阻力时，做阻尼振动．故D 错误． 故选：A7. 图为某弹簧振子的简谐运动图象，由图可知（ ）A.周期为3s ，振幅为20cmB.1s 末质点的速度最大、加速度最小C.2s 末质点的速度最大，势能最小D.4s 末质点的速度为零，回复力为正的最大 【解析】由位移的最大值读出振幅，相邻两个最大值之间的时间间隔读出周期．根据质点的位置分析速度大小．根据质点位置的变化，判断其速度方向．根据回复力与位移方向间的关系，判断回复力做功的正负． 【解答】解：A 、由图读出周期为T =4s ，振幅为A =10cm ．故A 错误． B 、1s 末质点位于平衡位置；速度为最大值，加速度最小；故B 正确；C 、2s 末质点的位移沿负方向且为最大值，速度为零；故C 错误；D 、4s 末质点的位移沿正方向且为最大值，速度为零，回复力为负的最大．故D 错误． 故选：B8. 有一弹簧振子，振幅为0.8cm ，周期为0.5s ，初始时具有正方向的最大位移，则它的振动方程是（ ） A.x =8×10−3sin(4πt +π2)m B.x =8×10−3sin(4πt −π2)m C.x =8×10−1sin(πt +3π2)mD.x =8×10−1sin(π4t +π2)m 【解析】t =0时刻振子的位移是正向最大．由周期求出圆频率ω，即可由x =Asin(ωt +φ0)求出简谐振动方程． 【解答】解：周期为0.5s ，则角速度为：ω=2πT=2π0.5rad/s =4πrad/s振子的初始位移是正向最大，则位移表达式x =Asin(ωt +φ0)中，φ0=π2；则位移表达式为x =Asin(ωt +φ0)=0.8sin(4πt +π2)(cm)=8×10−3sin(4πt +π2)m ．故A 正确，BCD 错误， 故选：A ．9. 一列简谐横波沿x 轴负方向传播，甲图是该横波t =2s 时的波形图，乙图是波中某质点位移随时间变化的振动图线，则乙图可能是甲图中哪个质点的振动图线（ ）A.x =0处的质点B.x =1m 处的质点C.x =2m 处的质点D.x =3m 处的质点【解析】由振动图象乙读出t =2s 时刻质点的运动状态，在波动图象甲上找出相对应的质点．【解答】解：由图知周期为T=4s，波长λ=4m；图乙上t=2s时质点位于平衡位置正向上运动．图甲上，t=2s时刻，只有x=1m处质点、x=3m处质点经过平衡位置．简谐横波沿x轴负方向传播，根据波形平移法可知，x=1m处质点经平衡位置向上，与图乙t=2s时刻质点的状态相同．故选：B．10. 如图所示，做简谐运动的弹簧振子从平衡位置O向B 运动过程中，下述说法中正确的是（）A.振子做匀减速运动B.振子的回复力指向BC.振子的位移不断增大D.振子的速度不断增大【解析】振子做远离平衡位置的运动，位移增加，加速度增大，做减速运动．【解答】解：AB、弹簧振子从平衡位置O向B运动过程中，弹簧的弹力与速度方向相反，做减速运动．随着位移的增大，加速度增大，做变减速运动．故A错误．B、振子的回复力是始终指向平衡位置的，所以指向O，故B错误；C、振子的位移起点是平衡位置，则知弹簧振子从平衡位置O向B运动过程中，振子的位移不断增大，故C正确．D、由上分析知振子做减速运动，速度不断减小，故D错误．故选：C．11. 如图所示为弹簧振子的振动图象，关于振子振动的判断正确的是（）A.振幅为8cmB.周期为1sC.在0.25s时刻振子正在作减速运动D.若0.25s时刻弹簧处于伸长状态，弹簧未形变时振子处于平衡位置，则在0.75s时刻处于压缩状态【解析】根据图象可直接读出周期和振幅．根据位移的变化即可分析振子速度的变化．根据对称性和平衡位置的特点分析弹簧的状态．【解答】解：AB、由图看出振子的振幅为4cm，周期为2s，故A、B错误；C、在0.25s时刻振子的位移正在减小，向平衡位置靠近，速度在增大，故B错误；D、若0.25s时刻弹簧处于伸长状态，弹簧未形变时振子处于平衡位置，则根据对称性可知在0.75s时刻处于压缩状态．故D正确．故选：D 12. 一质点做简谐运动的图象如图所示，下列说法正确的是（）A.质点振动频率是4HzB.质点在任意2s内的路程不一定都是4cmC.第6s末质点的速度有负向最大值D.在t=3s和t=5s两时刻，质点位移相同【解析】由图可读出质点振动周期、振幅及各点振动情况，求频率；再根据振动的周期性，可得质点振动的路程及各时刻物体的速度．【解答】解：A、由图可知，质点振动的周期为4s，故频率为f=1T=14Hz=0.25Hz，故A错误；B、振动的振幅为A=2cm，质点做简谐运动，一个周期内通过的路程一定是4A，半个周期即2s内，通过的路程一定是2A=4cm，故B错误；C、第6s末质点处于平衡位置处，故质点的速度最大，图象的斜率为负，则第6s末质点的速度有负向最大值．故C正确；D、在t=3s和t=5s两时刻，质点的位移大小相等，方向相反，所以位移不同．故D错误；故选：C13. 某个质点做简谐振动，得到如图所示的振动图象，下列说法错误的是（）A.质点的振动周期为2sB.质点在0.5s时具有最大的加速度C.质点在1s时受到的回复力为零D.质点在1.5s时具有最大的动能【解析】振动物体完成一次全振动的时间叫做周期，由振动图象直接读出．质点在最大位移处时速度为零，加速度最大，加速度方向与位移方向相反．【解答】解：A、由图，周期为2s，故A正确；B、质点在0.5s时的位移最大，具有最大的加速度，故B正确；C、质点在1s时处于平衡位置处，位移是零，所以受到的回复力为零．故C正确；D、质点在1.5s时位移最大，势能最大，故动能为零，速度最小．故D错误．本题选择错误的，故选：D．14. 弹簧振子做简谐运动的过程中（）A.当加速度最大时，速度最大B.当速度最大时，位移最大C.当位移最大时，回复力最大D.当回复力最大时，速度最大【解析】简谐运动的平衡位置是回复力为零的位置，速度最大，加速度最小；【解答】解：A、根据a=−kxm，当加速度最大时，位移最大，而位移最大时速度为零，故A错误；B、当速度最大时，位移为零，B 错误；C、当位移最大时，回复力F=kx最大，C正确；D、当回复力最大时，位移最大，速度为零，D错误；故选：C．15. 如图所示，下述说法正确的是（）A.第0.2s末加速度为正，速度为0B.第0.6s末加速度为0，速度为正最大C.质点振动的频率是1.25HzD.质点振动的振幅是10cm【解析】根据振动图象得到位移情况，根据a=−kxm判断加速度情况，切线的斜率表示速度．【解答】解：A、第0.2s末位移为正向最大，根据a=−kxm，加速度为负的最大；最大位移处速度为零；故A错误；B、第0.6s末位移为负向最大；加速度最大，速度为零；故B错误；C、振动周期为0.8s；则频率f=10.8=1.25Hz；故C正确；D、由图可知，振幅为5cm；D错误；故选：C．16. 如图是一正弦式交变电流的电流图象．由图可知，这个电流的（）A.最大值为10AB.最大值为5√2AC.频率为100HzD.频率为200Hz【解析】根据图象可以直接得出电流的最大值和周期的大小，根据周期与频率的关系得出频率的大小．【解答】解：由图象可知，电流的最大值为10A，周期T=0.02s，则交流电的频率f=1T=50Hz．故A正确，B、C、D错误．故选：A．17. 如图所示为同一地点质量相同的甲、乙两单摆的振动图象，下列说法中正确的是（）A.甲、乙两单摆的摆长不相等B.甲摆的振幅比乙摆大C.甲摆的机械能比乙摆大D.在t=0.5s时有正向最大加速度的是乙摆【解析】由图读出两单摆的周期，由单摆的周期公式分析摆长关系；由位移的最大值读出振幅；由于两摆的质量未知，无法比较机械能的大小；根据加速度与位移方向相反，确定加速度的方向．【解答】解：A、由图看出，两单摆的周期相同，同一地点g相同，由单摆的周期公式T=2π√Lg得知，甲、乙两单摆的摆长L相等．故A错误．B、甲摆的振幅为10cm，乙摆的振幅为7cm，则甲摆的振幅比乙摆大．故B正确．C、尽管甲摆的振幅比乙摆大，两摆的摆长也相等，但由于两摆的质量未知，无法比较机械能的大小．故C错误．D、在t=0.5s时，甲摆经过平衡位置，振动的加速度为零，而乙摆的位移为负的最大，则乙摆具有正向最大加速度．故D正确．故选：BD．18. 如图所示，在同一地点的A、B两个单摆做简谐运动的图象，其中实线表示A的简谐运动图象，虚线表示B的简谐运动图象．关于这两个单摆的以下判断中正确的是（）A.摆球质量一定相等B.单摆的摆长一定不同C.单摆的最大摆角一定相同D.单摆的振幅一定相同【解析】根据图线得到振幅和周期的情况，然后结合单摆的周期公式进行分析讨论，分析时要抓住单摆的周期与摆球质量、振幅无关．【解答】解：AD、由图知，A的周期小于B的周期，两摆的振幅相同，但单摆的周期与摆球质量无关，所以不能确定摆球质量关系，故A错误，D正确．C、由单摆的周期公式T=2π√Lg知，周期不同，则摆长一定不同，故B正确．D、单摆的摆长不同，振幅相同，则单摆的最大摆角一定不同，故C错误．故选：BD19. 如图所示是某弹簧振子的振动图象，由图可知（）A.质点的振幅是5cm，周期是2sB.在t=1.5s时，质点的速度和加速度方向相同C.在t=1.0s时，质点的位移最大，速度为零，加速度−x方向最大D.在t=4.0s时，质点的速度为零【解析】由振动图象能直接振幅和周期．根据图象的斜率读出速度的方向．根据位移的方向分析加速度方向．质点通过平衡位置时速度最大．【解答】解：A、由图知，质点的振幅是5cm，周期是4s，故A错误．B、在t=1.5s时，图象的斜率为负值，质点的速度沿负向．位移为正值，由a=−kxm知，加速度为负向，所以质点的速度和加速度方向相同，故B正确．C 、在t=1.0s时，质点的位移为正向最大，速度为零，由a=−kxm知，加速度−x方向最大，故C正确．D、在t=4.0s时，质点的位移为0，表示质点通过平衡位置，速度最大，故D错误．故选：BC．20. 关于振动图象和波的图象，下列说法正确的是（）A.波的图象反映的是很多质点在同一时刻的位移B.通过波的图象可以找出任一质点在任一时刻的位移C.它们的横坐标都表示时间D.它们的纵坐标都表示质点的位移【解析】振动图象反映同一质点在不同时刻的位移，而波动图象反映同一时刻介质中各个质点的位移．【解答】解：A、波的图象反映的是介质中很多质点在同一时刻的位移，故A正确．B、运用波形的平移法，通过波的图象可以找出任一质点在任一时刻的位移，故B正确．C、振动图象横坐标表示时间，波的图象横坐标质点的平衡位置，故C错误．D、它们的纵坐标都表示质点的位移．故D正确．故选：ABD．21. 如图为某物体做简谐运动的图象，以下说法正确的是（）A.1.2s时刻物体的回复力与0.4s时刻的回复力相同B.0.2s时刻的速度与0.4s时刻的速度相同C.0.7s到0.9s时间内加速度在减小D.1.1s到1.3s时间内的势能在增大【解析】简谐运动的图象中图线切线的斜率表示速度，加速度和位移的关系是a=−kxm，物体经过平衡位置时动能最大，在最大位移处时动能为零．根据这些知识进行分析【解答】解：A、由图知物体在1.2s与0.4s时刻位移相同，由F=−kx知，A正确．B、物体在0.2s时刻与0.4s时刻的位移相对于平衡位置对称，由运动特点可得故速度大小方向均相同，故B正确．C、0.7s∼0.9s时间内物体的位移增大，由a=−kxm，可知物体的加速度在增大，故C错误．D、1.1s∼1.3s时间内物体的位移增大，物体远离平衡位置，则势能在增大，故D正确．故选：ABD22. 如图所示是一弹簧振子在水平面内作简谐运动的x−t图象，则下列说法正确的是（）A.t1时刻和t2时刻具有相同的动能B.t2到1.0s时间内加速度变小，速度减小C.弹簧振子的振动方程是x=0.10sinπt(m)D.t2数值等于3倍的t1数值【解析】振动图象中图象的纵坐标表示质点运动位移，根据位移情况分析摆球的位置，分析摆球的速度和拉力大小，当摆球在平衡位置时速度最大，回复力最小，则加速度最小，当摆球在最大位移处速度为零，回复力最大，则加速度最大，根据图象得出周期和振幅，从而写出弹簧振子的振动方程，根据t2、t1时刻位移都是5cm求出时间，从而求出t2、t1的关系．【解答】解：A、根据图象可知，t1时刻和t2时刻在同一个位置，速度大小相等，但方向相反，所以动能相同，故A正确；B、t2到1.0s时间内振子由正向位移处向平衡位置处振动，加速度减小，速度增大，平衡位置处速度最大，故B错误；C、根据图象可知，振动的周期T=2s，则角速度ω=2πT=πrad/s，振幅A=10cm=0.1m，则弹簧振子的振动方程是x=0.10sinπt(m)，故C正确；D、当x=5cm=0.05m时，根据振动方程是x=0.10sinπt(m)得：t1=16s，t2=56s，则t2数值等于5倍的t1数值，故D错误．故选：AC23. 如图所示为一水平弹簧振子做简谐运动的振动图象，由图可以推断，振动系统（）A.t1和t3时刻具有相等的动能和相同的加速度B.t3和t4时刻具有相同的速度C.t4和t6时刻具有相同的位移和速度D.t1和t6时刻具有相等的动能和相反方向的速度【解析】在简谐运动的振动图象上，某点斜率的大小代表速度的大小，斜率的正负代表速度的方向．【解答】解：A、v−t图象的斜率表示速度，在t1和t3时刻，速度大小相等，动能相等；另外，相同位置处振子的加速度是相等的，故A正确；B、v−t图象的斜率表示速度，在t3和t4时刻，速度相等，方向也相同，故速度相同，故B正确；C、在t4和t6时刻具有相同的位移，均为负值；但速度大小相等，方向相反，故不同，故C错误；D、v−t图象的斜率表示速度，在t1和t6时刻，速度相等，方向也相同，故速度相同，故D错误；故选：AB．24. 如图所示为某物体做简谐运动的振动图象，在所画的曲线范围内，下列关于物体的判断中正确的是（）A.在0到t1时间内，速度变大，加速度变小B.在t1到t2时间内，速度变大，加速度变小C.在t2到t3时间内，动能变大，势能变小D.在t3到t4时间内，动能变大，势能变小【解析】由振动图象直接读出质点的位移及其变化情况，能判断质点的振动方向．根据简谐运动特征：F=−kx、a=−kxm分析回复力和加速度．动量P=mv，根据速度分析．【解答】解：A、由图知，在0到t1时间内质点远离平衡位置，速度变小，加速度变大．故A错误．B、在t1到t2时间内质点靠近平衡位置，速度变大，加速度变小．故B正确．C、在t2到t3时间内质点远离平衡位置，动能变小，势能变大．故C错误．D、在t3到t4时间内，动能变大，势能变小．故D正确．故选：BD25. 如图表示某质点做简谐运动的图象，以下说法中正确的是（）A.t1、t2时刻的速度相同B.从t1到t2这段时间内，速度与加速度同向C.从t2到t3这段时间内，速度变大，加速度变小D.t1、t3时刻的加速度相同【解析】简谐运动中质点的加速度a=−kxm．加速度方向总是与质点的位移方向相反，而速度与位移变化情况相反．根据位移的变化进行分析．【解答】解：A、t1时刻图象切线的斜率为负值，说明质点的速度沿负方向，而t2时刻切线斜率为零，速度为零，则这两个时刻质点的速度不同．故A错误．B、从t1到t2这段时间内，质点的位移增大，离开平衡位置，速度沿负方向，位移为负方向，由a=−kxm，则知加速度沿正方向，所以速度与加速度方向相反．故B错误．C、从t2到t3这段时间内，质点的位移减小，靠近平衡位置，速度变大，加速度变小，故C正确．D、t1、t3时刻质点经过平衡位置，加速度都为零，故D正确．故选：CD．26. （多选）如图所示为某物体做简谐运动的图象，下列说法中正确的是（）A.由P→Q位移在增大B.由P→Q速度在增大C.由M→N位移是先减小后增大D.由M→N位移始终减小【解析】简谐运动的质点位移随时间按正弦规律变化，由图象可得振幅和周期以及振子的运动方向及位移变化情况．【解答】A、由图可知，由P→Q，位移在增大，故A正确；B、由P→Q，位移在增大，速度在减小，故B错误；C、由M→N，中间越过了平衡位置，位移先减小后增大，故C正确；D、由C分析得，D错误。

大学物理(第四版)课后习题及答案机械振动13 机械振动解答13-1 有一弹簧振子，振幅A=2.0×10-2m，周期T=1.0s，初相ϕ=3π/4。

试写出它的运动方程，并做出x--t图、v--t 图和a--t图。

13-1分析弹簧振子的振动是简谐运动。

振幅A、初相ϕ、角频率ω是简谐运动方程x=Acos(ωt+ϕ)的三个特征量。

求运动方程就要设法确定这三个物理量。

题中除A、ϕ已知外，ω可通过关系式ω=2π确定。

振子运动的速度T和加速度的计算仍与质点运动学中的计算方法相同。

解因ω=2π，则运动方程 T⎛2πt⎛x=Acos(ωt+ϕ)=Acos t+ϕ⎛⎛T⎛根据题中给出的数据得x=(2.0⨯10-2m)cos[(2πs-1)t+0.75π]振子的速度和加速度分别为v=dx/dt=-(4π⨯10-2m⋅s-1)sin[(2πs-1)t+0.75π] a=d2x/dt2=-(8π2⨯10-2m⋅s-1)cos[(2πs-1)t+0.75πx-t、v-t及a-t图如图13-l所示π⎛⎛13-2 若简谐运动方程为x=(0.01m)cos⎛(20πs-1)t+⎛，求：（1）振幅、频率、角频率、周期和4⎛⎛初相；（2）t=2s 时的位移、速度和加速度。

13-2分析可采用比较法求解。

将已知的简谐运动方程与简谐运动方程的一般形式x=Acos(ωt+ϕ)作比较，即可求得各特征量。

运用与上题相同的处理方法，写出位移、速度、加速度的表达式，代入t值后，即可求得结果。

解（l）将x=(0.10m)cos[(20πs-1)t+0.25π]与x=Acos(ωt+ϕ)比较后可得：振幅A= 0.10 m，角频率ω=20πs-1，初相ϕ=0.25π，则周期T=2π/ω=0.1s，频率ν=1/T=10Hz。

（2）t= 2s时的位移、速度、加速度分别为x=(0.10m)cos(40π+0.25π)=7.07⨯10-2m v=dx/dt=-(2πm⋅s-1)sin(40π+0.25π)a=d2x/dt2=-(40π2m⋅s-2)cos(40π+0.25π)13-3 设地球是一个半径为R的均匀球体，密度ρ5.5×103kg•m。

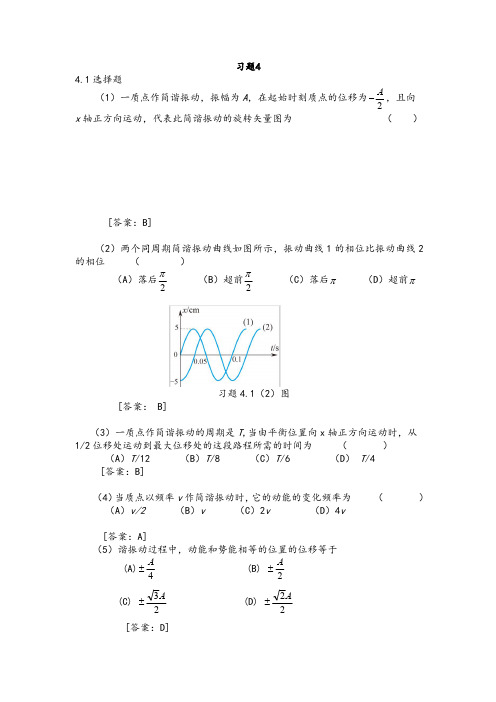
一、选择题1．一弹簧振子做简谱运动，它所受的回复力F 随时间t 变化的图象为正弦曲线，如图所示，下列说法正确的是（ ）A ．在t 从0到2s 时间内，弹簧振子做加速运动B ．在t 1=3s 和t 2=5s 时，弹簧振子的速度大小相等，方向相同C ．在t 2=5s 和t 3=7s 时，弹簧振子的位移大小相等，方向相同D ．在t 从0到4s 时间内，t =2s 时刻弹簧振子所受回复力做功瞬时功率最大C 解析：CA ．在t 从0到2s 时间内，回复力逐渐变大，说明振子逐渐远离平衡位置，做减速运动，A 错误；B ．在t 1=3s 和t 2=5s 时，弹簧振子的速度大小相等，方向相反，B 错误；C ．在t 1=5s 和t 2=7s 时，回复力相等，根据公式F kx =-所以位移相同，C 正确；D ．在t 从0到4s 时间内，t =2s 时刻弹簧振子的速度为零，所以功率为零，D 错误。

故选C 。

2．如图甲所示为以O 点为平衡位置。

在A 、B 两点间做简谐运动的弹簧振子，图乙为这个弹簧振子的振动图像，由图可知下列说法中正确的是（ ）A ．在0.2s t =时，弹簧振子一定运动到B 位置B ．在0.3s t =与0.7s t =两个时刻，弹簧振子的速度相同C ．从0到0.2s t =的时间内，弹簧振子的动能持续地减少D ．在0.2s t =与0.6s t =两个时刻，弹簧振子的加速度相同C解析：CA ．在t =0.2s 时，弹簧振子位移最大，但没有规定正方向，故可能在A 点，也可能在B 点，故A 错误；B ．x -t 图象的切线斜率表示速度，在t =0.3s 与t =0.7s 两个时刻，弹簧振子的速度大小相等，方向相反，故B 错误；C ．从t =0到t =0.2s 的时间内，位移增加，远离平衡位置，故动能减小，故C 正确；D ．在t =0.2s 与t =0.6s 两个时刻，位移相反，根据kx a m=-可知，加速度大小相等，方向相反，故D 错误。

振幅周期和频率
各种不同的机械运动都需要用位移、速度、加速度等物理量来描述，但是不同的运动具有不同的特点，需要引入不同的物理量表示这种特点．描述圆周运动就引入了角速度、周期、转速等物理量．描述简谐运动也需要引入新的物理量，这就是振幅、周期和频率．
振动物体总是在一定范围内运动的．在图9-1中，振子在水平杆上的 A点和A′点之间做往复运动，振子离开平衡位置的最大距离为OA或者OA′．振动物体离开平衡位置的最大距离，叫做振动的振幅．在图9-1中，OA或OA′的大小就是弹簧振子的振幅．振幅是表示振动强弱的物理量．
简谐运动具有周期性．在图9-1中，如果振子由A点开始运动，经过O点运动到A′点，再经过O点回到A点，我们就说它完成了一次全振动．此后振子不停地重复这种往复运动．实验表明，弹簧振子完成一次全振动所用的时间是相同的．做简谐运动的物体完成一次全振动所需要的时间，叫做振动的周期．单位时间内完成的全振动的次数，叫做振动的频率．
周期和频率都是表示振动快慢的物理量．周期越短，频率越大，表示振动越快．用T表示周期，用f表示频率，则有
在国际单位制中，周期的单位是秒，频率的单位是赫兹，简称赫，符号是Hz．1Hz=1s-1．
上面我们说过，振子完成一次全振动所用的时间是相同的．如果改变弹簧振子的振幅，弹簧振子的周期或频率是否改变呢？
观察弹簧振子的运动可以发现，开始拉伸(或压缩)弹簧的程度不同，振动的振幅也就不同，但是对同一个振子，振动的频率(或周期)却是一定的．可见，简谐运动的频率与振幅无关．简谐运动的频率由振动系统本身的性质所决定．如弹簧振子的频率由弹簧的劲度和振子的质量所决定，与振幅的大小无关，因此又称为振动系统的固有频率．。

专练机械振动机械波1.一位游客在千岛湖边欲乘游船，当日风浪很大，游船上下浮动．可把游艇浮动简化成竖直方向的简谐运动，振幅为20 cm，周期为3.0 s．当船上升到最高点时，甲板刚好与码头地面平齐．地面与甲板的高度差不超过10 cm时，游客能舒服地登船．在一个周期内，游客能舒服地登船的时间是()A．0.5 s B．0.75 s C．1.0 s D．1.5 s2．一弹簧振子的位移y随时间t变化的关系式为y＝0.1sin2.5πt，位移y的单位为m，时间t的单位为s.则()A．弹簧振子的振幅为0.2 mB．弹簧振子的周期为1.25 sC．在t＝0.2 s时，振子的运动速度为零D．在任意0.2 s时间内，振子的位移均为0.1 m3.如图所示，是简谐运动的回复力随时间变化规律的图象，根据图象判断以下说法正确的是()A．0至t1时间内，质点向着远离平衡位置方向运动，速率越来越大B．t1至t2时间内，质点的加速度方向与运动方向相反C．t2至t3时间内，质点向着靠近平衡位置方向运动，速率越来越小D．t3至t4时间内，质点的加速度方向与运动方向相同4．(多选)下表中给出的是做简谐运动的物体的位移x或速度v 与时间的对应关系，T是振动周期．则下列选项中正确的是()时刻状态物理量0 14T12T34TT甲零正向最大零负向最大零乙零负向最大零正向最大零丙正向最大零负向最大零正向最大丁负向最大零正向最大零负向最大A.若甲表示位移x，则丙表示相应的速度vB．若丁表示位移x，则甲表示相应的速度vC．若丙表示位移x，则甲表示相应的速度vD．若乙表示位移x，则丙表示相应的速度v5．(多选)水平弹簧振子，每隔时间t，振子的位移总是大小和方向都相同，每隔t2的时间，振子的速度总是大小相等、方向相反，则有()A．弹簧振子的周期可能小于t2B．每隔t2的时间，振子的加速度总是相同的C．每隔t2的时间，振子的动能总是相同的D．每隔t2的时间，弹簧的长度总是相同的6．关于简谐运动与机械波的下列说法中，正确的是()A．同一单摆，在月球表面做简谐运动的周期大于在地球表面做简谐运动的周期B．受迫振动物体的振幅与它的振动频率无关C．在同一种介质中，不同频率的机械波的传播速度不同D．在波的传播过程中，质点的振动方向总是与波的传播方向垂直7.如图，沿同一弹性绳相向传播的甲、乙两列简谐横波，波长相等，振幅分别为10 cm、20 cm，在某时刻恰好传到坐标原点．则两列波相遇叠加后()A．不可能产生稳定的干涉图样B．在x＝2 m的质点振动始终减弱C．在x＝0.5 m的质点振幅为零D．坐标原点的振幅为30 cm8.(多选)图甲为一列简谐横波在t＝2 s时的波形图，图乙为媒质中平衡位置在x＝1.5 m处的质点的振动图象，P是平衡位置为x＝2 m 的质点．下列说法中正确的是()A．波速为0.5 m/sB．波的传播方向向右C．0～2 s时间内，P运动的路程为8 cmD．0～2 s时间内，P向y轴正方向运动E．当t＝7 s时，P恰好回到平衡位置9.如图所示为一列简谐横波在t＝0时刻的波的图象(图中仅画出0～12 m范围内的波形)，经过Δt＝1.2 s时间，恰好第三次出现图示的波形．根据以上信息，不能得出的结论是()A．波的传播速度的大小B．Δt＝1.2 s时间内质点P经过的路程C．t＝0.6 s时刻质点P的速度方向D．t＝0.6 s时刻的波形10．在“用双缝干涉测光的波长”实验中(实验装置如图甲所示)：甲乙(1)下列说法正确的是()A．调节光源高度使光束沿遮光筒轴线照在屏中心时，应放上单缝和双缝B．测量某条干涉亮纹位置时，应使目镜分划板中心刻线与该亮纹的中心对齐C．为了减少测量误差，可用目镜测出n条亮纹间的距离a，求出相邻两条亮纹间距Δx＝a n－1(2)测量某亮纹位置时，手轮上的示数如图乙所示，其示数为________ mm.11.设B、C为两列机械波的波源，它们在同种介质中传播，其振动表达式分别为y B＝0.1cos(2πt)cm和y C＝0.1cos(2πt＋π)cm，发出的波的传播方向如图中的虚线所示．它们传到P点时相遇，2 s末P点开始起振.PB＝40 cm，PC＝50 cm.试求：(1)这两列波的波长；(2)P点形成合振动的振幅．12.如图所示，一列沿x轴正方向传播的简谐横波在t＝0时刻的波形如图中的实线所示，此时这列波恰好传播到P点，且再经过1.2 s，坐标为x＝8 m的Q点开始起振，求：(1)该列波的周期T；(2)从t＝0时刻到Q点第一次达到波峰时，振源O点相对平衡位置的位移y及其所经过的路程s.练高考——找规律1．(多选)(课标Ⅰ)某同学漂浮在海面上，虽然水面波正平稳地以1.8 m /s 的速率向着海滩传播，但他并不向海滩靠近．该同学发现从第1个波峰到第10个波峰通过身下的时间间隔为15 s ．下列说法正确的是( )A ．水面波是一种机械波B ．该水面波的频率为6 HzC ．该水面波的波长为3 mD ．水面波没有将该同学推向岸边，是因为波传播时能量不会传递出去E ．水面波没有将该同学推向岸边，是因为波传播时振动的质点并不随波迁移2．(多选)(课标Ⅲ)由波源S 形成的简谐横波在均匀介质中向左、右传播．波源振动的频率为20 Hz ，波速为16 m /s .已知介质中P 、Q 两质点位于波源S 的两侧，且P 、Q 和S 的平衡位置在一条直线上，P 、Q 的平衡位置到S 的平衡位置之间的距离分别为15.8 m 、14.6 m ．P 、Q 开始振动后，下列判断正确的是( )A ．P 、Q 两质点运动的方向始终相同B ．P 、Q 两质点运动的方向始终相反C ．当S 恰好通过平衡位置时，P 、Q 两点也正好通过平衡位置D ．当S 恰好通过平衡位置向上运动时，P 在波峰E ．当S 恰好通过平衡位置向下运动时，Q 在波峰3.(多选)(天津理综)在均匀介质中坐标原点O 处有一波源做简谐运动，其表达式为y ＝5sin ⎝ ⎛⎭⎪⎫π2t ，它在介质中形成的简谐横波沿x 轴正方向传播，某时刻波刚好传播到x ＝12 m 处，波形图象如图所示，则( )A ．此后再经6 s 该波传播到x ＝24 m 处B ．M 点在此后第3 s 末的振动方向沿y 轴正方向C ．波源开始振动时的运动方向沿y 轴负方向D ．此后M 点第一次到达y ＝－3 m 处所需时间是2 s4．(北京理综)如图所示，弹簧振子在M 、N 之间做简谐运动．以平衡位置O 为原点，建立Ox 轴．向右为x 轴正方向．若振子位于N 点时开始计时，则其振动图象为( )5．(·课标Ⅱ)一列简谐横波在介质中沿x 轴正向传播，波长不小于10 cm .O 和A 是介质中平衡位置分别位于x ＝0和x ＝5 cm 处的两个质点．t ＝0时开始观测，此时质点O 的位移为y ＝4 cm ，质点A 处于波峰位置；t ＝13 s 时，质点O 第一次回到平衡位置，t ＝1 s 时，质点A 第一次回到平衡位置．求：(1)简谐波的周期、波速和波长；(2)质点O 的位移随时间变化的关系式．6．(·课标Ⅰ)甲、乙两列简谐横波在同一介质中分别沿x 轴正向和负向传播，波速均为v ＝25 cm /s .两列波在t ＝0时的波形曲线如图所示．求(1)t ＝0时，介质中偏离平衡位置位移为16 cm 的所有质点的x坐标；(2)从t ＝0开始，介质中最早出现偏离平衡位置位移为－16 cm 的质点的时间．练模拟——明趋势7．(多选)(广东深圳一调)一个质点经过平衡位置O ，在A 、B 间做简谐运动，如图(a )所示，它的振动图象如图(b )所示，设向右为正方向，下列说法正确的是( )A ．OB ＝5 cmB ．第0.2 s 末质点的速度方向是A →OC ．第0.4 s 末质点的加速度方向是A →OD ．第0.7 s 末时质点位置在O 点与A 点之间E ．在4 s 内完成5次全振动8．(多选)(湖北孝感调研)一列简谐横波沿x 轴正方向传播，周期为T.在t ＝0时的波形如图所示，波上有P 、Q 两点，其纵坐标分别为y P ＝2 cm ，y Q ＝－2 cm ，下列说法中正确的是( )A ．P 点的振动形式传到Q 点需要T 2B ．P 、Q 在振动过程中，位移的大小总相等C ．在5T 4内，P 点通过的路程为20 cmD ．经过3T 8，Q 点回到平衡位置E ．在相等时间内，P 、Q 两质点通过的路程相等9．(·湖北襄阳二联)如图所示，a 、b 、c 、d …为传播简谐横波的介质中一系列等间隔的质点，相邻两质点间的距离均为0.1 m ．若某时刻向右传播的波到达a 质点，a 开始时先向上运动，经过0.2 s d 质点第一次达到最大位移，此时a 正好在平衡位置(已知质点振幅为2 cm ，a 、d 沿传播方向上的距离小于一个波长)．则该简谐横波在介质中的波速可能值为________ m /s ，此时质点j 的位移为________cm .10．(河北邯郸一模)图甲为一列简谐横波在t ＝0.20 s 时刻的波形图，P 是平衡位置在x ＝1.0 m 处的质点，Q 是平衡位置在x ＝4.0 m 处的质点；图乙为质点Q 的振动图象．这列波的传播速度是________ m /s ，质点P 简谐运动的表达式为________．11．(辽宁名校模拟)如图所示，S是水面波的波源，x、y是挡板，S1、S2是两个狭缝(SS1＝SS2，狭缝的尺寸比波长小得多)，试回答以下问题：(1)若闭上S1，只打开S2会看到什么现象？(2)若S1、S2都打开，会发生什么现象？(3)若图中实线和虚线分别表示波峰和波谷，那么在A、B、C、D各点中，哪些点振动最强，哪些点振动最弱？12．(山西右玉一模)如图所示，图中的实线是一列简谐横波在t＝0时刻的波形图，虚线对应的是t＝0.5 s时的波形图．求：(1)如果波沿x轴负方向传播，且周期T>0.5 s，则波的速度多大？(2)如果波沿x轴正方向传播，且周期T满足0.3 s<T<0.5 s，则波的速度又是多大？课练 机械振动 机械波1．C由题意知，游船在做简谐运动，振动图象如图所示，根据振动方程y ＝A sin(ωt ＋φ)，结合振动图象知地面与甲板的高度差不超过10 cm 的时间有三分之一周期，故C 正确，A 、B 、D 错误．2．C 由y －t 关系式可知，弹簧振子的振幅为0.1 m ，选项A 错误；弹簧振子的周期为T ＝2πω＝2π2.5π s ＝0.8 s ，选项B 错误；在t ＝0.2s 时，y ＝0.1 m ，即振子到达最高点，此时振子的运动速度为零，选项C 正确；只有当振子从平衡位置或者从最高点(或最低点)开始计时时，经过T /4＝0.2 s ，振子的位移才为0.1 m ，选项D 错误．3．D 由图知，0至t 1时间内，回复力变大，位移增大，故质点远离平衡位置，速率减小，所以选项A 错误；t 1至t 2时间内，回复力减小，故位移减小，质点向平衡位置加速运动，加速度方向与运动方向相同，所以选项B 错误；t 2至t 3时间内，回复力增大，所以位移增大，质点远离平衡位置，速率减小，所以选项C 错误；t 3至t 4时间内，回复力减小，所以位移减小，质点向平衡位置做加速运动，加速度方向与运动方向相同，所以选项D 正确．4．AB 先讨论选项A ：当t ＝0时，位移为零，这时速度为正向最大，当t ＝14T 时，甲的位移为正向最大，这时速度为零．由此可知，若甲表示位移，丙表示相应速度，满足简谐运动规律，故A 正确．同样可推出B 正确，C 、D 错误．5．AC 由题意可知，t ＝nT ，n 可以是1,3，…，当n ＝1时，T＝t ；当n ＝3时，T ＝t 3<t 2，选项A 正确．讨论B 、C 、D 时，以t ＝T为例．每隔T 2时间，振子的位置关于平衡位置对称，振子的加速度大小总是相等，方向总是相反，振子的动能总是相同，弹簧的长度不相同，选项C 正确，选项B 、D 错误．6．A根据单摆的周期公式T ＝2π l g ，月球表面的重力加速度小于地球表面的重力加速度，所以A 正确；做受迫振动的物体的振动频率等于驱动力的频率时振幅最大，振幅与振动频率间的关系如图所示，所以B 错误；机械波的传播速度由介质决定，故在同一种介质中，不同频率的机械波的传播速度相同，所以C 错误；在纵波的传播过程中，质点的振动方向总是与波的传播方向在一条直线上，所以D 错误．7．D 由图可知，两波的波长相等，又波速相等，则频率相等，能发生干涉，能产生稳定的干涉图样，故A 错误；两列波相遇后，在叠加区域x ＝2 m 的质点，振动方向相同，则振动始终加强，故B 错误；两列波在x ＝0.5 m 的质点振动方向相反，则振幅为两列波的振幅之差，即为10 cm ，故C 错误；根据矢量叠加原则，两列波在原点振动方向相同，则原点的振幅为两列波的振幅之和，即为30 cm ，故D 正确．8．ACE 由振动图象知，周期T ＝4 s ，由波的图象知，波长λ＝2 m ，波速v ＝λT ＝0.5 m/s ，A 正确；又由振动图象知，x ＝1.5 m处的质点在t ＝2 s 时在平衡位置且向下振动，则波应该向左传播，B 错误；则0～2 s 内P 运动的路程为8 cm ，C 正确；由于t ＝2 s 时的波形如题图甲，则0～2 s 内P 向y 轴负方向运动，D 错误；Δt ＝7 s ＝134T ，P 质点恰好回到平衡位置，E 正确．9．C 由波的图象读出波长λ＝8 m ．因为经过整数倍周期，图象重复，所以根据经过1.2 s 该波形恰好第三次出现，得到2T ＝1.2 s ，则周期T ＝0.6 s ，由公式λ＝v T 确定出波速v ＝403 m/s ，A 不符合题意；质点经过一个周期，通过的路程是四个振幅，则经过1.2 s ，即两个周期，质点P 通过的路程是s ＝8A ＝80 cm ，B 不符合题意；由于波的传播方向不确定，P 点的速度方向不确定，C 符合题意；t ＝0.6 s 时的波形图与图示时刻相差一个周期，波形确定，D 不符合题意．10．解题思路：(1)摆放各光具时应保证光线沿直线通过各光具的中心(轴线)，所以摆放时并不放单缝和双缝，A 项错误；测量亮纹位置时，为了准确，应该将目镜分划板的中心刻线与亮纹中心对齐，s ，频率f ＝1T ＝0.6 Hz ，波长λ＝v T ＝1.8×53 m ＝3 m ，故B 错、C 正确．2．BDE 由波速公式：v ＝λf 得λ＝v f ＝0.8 m ，L SP ＝15.80.8λ＝1934λ，L SQ ＝14.60.8λ＝1814λ，由波动的周期性，采用“去整留零”的方法，可在波形图上标出S 、P 、Q 三点的位置，如图所示，由图可知，P 、Q 两点的运动方向始终相反，A 项错误、B 项正确；S 在平衡位置时，P 、Q 一个在波峰，一个在波谷，C 项错误；当S 恰通过平衡位置向上运动时，P 在波峰，Q 在波谷，反之则相反，故D 、E 项正确．3．AB 由波源振动表达式可知ω＝π2，而ω＝2πT ，所以T ＝4 s ，由波形图知λ＝8 m ，波速v ＝λT ＝2 m/s ，Δx ＝v ·Δt ＝12 m ，故A 项正确；经过Δt ′＝3 s ，波向前传播的距离为Δx ′，Δx ′＝v ·Δt ′＝6 m ，画出这一时刻的波形图如图中虚线所示，由图可知，M 点振动方向沿y 轴正方向，B 项正确； 在波的传播过程中，各质点的起振方向都与波源的起振方向相同，可得波源起振方向沿y 轴正方向，C 项错误；此时M 点在y ＝3 m处且沿y 轴负方向振动，第一次到达y ＝－3 m 处所用时间小于T 2，故D 项错误．4．A 振子在N 点时开始计时，其位移为正向最大，并按正弦规律变化，故选项A 正确．5．解题思路：(1)设振动周期为T .由于质点A 在0到1 s 内由最大位移处第一次回到平衡位置，经历的是14个周期，由此可知T ＝4 s ①由于质点O 与A 的距离5 cm 小于半个波长，且波沿x 轴正向传动到波谷的时间大于T 8，再从波谷运动到平衡位置的时间为T 4，所以经过38T ，Q 点没有回到平衡位置，故D 错误．由于P 、Q 两点的振动步调总是相反，所以在相等时间内，P 、Q 两质点通过的路程相等，故E 正确．9．解题思路：由题意可知介质中质点起振方向向上，所以d 质点第一次达到最大位移时处于波峰位置，又a 、d 沿传播方向上的距离小于一个波长，则可知a 、d 间的波形如图所示有两种情况：图甲：x ad ＝14λ甲t ＝12T 甲v 甲＝λ甲T 甲 解得v 甲＝3 m/s图乙：x ad ＝34λ乙t ＝T 乙v 乙＝λ乙T 乙解得v 乙＝2 m/s结合甲、乙两图可知此时质点j 还没有起振，所以位移为零． 答案：3或2 010．解题思路：由图可知波长λ＝8 m ，周期T ＝0.2 s ，则波的传播速度v ＝λT ＝40 m/s ，ω＝2πT ＝10π rad/s ，由图甲、乙可知波沿x 轴。