连续周期正弦信号
- 格式:ppt
- 大小:384.00 KB
- 文档页数:1



FS,FT,DFS,DTFT,DFT,FFT的联系和区别对于初学数字信号处理(DSP)的人来说,这几种变换是最为头疼的,它们是数字信号处理的理论基础,贯穿整个信号的处理。
学习过《高等数学》和《信号与系统》这两门课的朋友,都知道时域上任意连续的周期信号可以分解为无限多个正弦信号之和,在频域上就表示为离散非周期的信号,即时域连续周期对应频域离散非周期的特点,这就是傅里叶级数展开(FS),它用于分析连续周期信号。
FT是傅里叶变换,它主要用于分析连续非周期信号,由于信号是非周期的,它必包含了各种频率的信号,所以具有时域连续非周期对应频域连续非周期的特点。
FS和FT 都是用于连续信号频谱的分析工具,它们都以傅里叶级数理论问基础推导出的。
时域上连续的信号在频域上都有非周期的特点,但对于周期信号和非周期信号又有在频域离散和连续之分。
在自然界中除了存在温度,压力等在时间上连续的信号,还存在一些离散信号,离散信号可经过连续信号采样获得,也有本身就是离散的。
例如,某地区的年降水量或平均增长率等信号,这类信号的时间变量为年,不在整数时间点的信号是没有意义的。
用于离散信号频谱分析的工具包括DFS,DTFT和DFT。
DTFT是离散时间傅里叶变换,它用于离散非周期序列分析,根据连续傅里叶变换要求连续信号在时间上必须可积这一充分必要条件,那么对于离散时间傅里叶变换,用于它之上的离散序列也必须满足在时间轴上级数求和收敛的条件;由于信号是非周期序列,它必包含了各种频率的信号,所以DTFT对离散非周期信号变换后的频谱为连续的,即有时域离散非周期对应频域连续周期的特点。
当离散的信号为周期序列时,严格的讲,离散时间傅里叶变换是不存在的,因为它不满足信号序列绝对级数和收敛(绝对可和)这一傅里叶变换的充要条件,但是采用DFS(离散傅里叶级数)这一分析工具仍然可以对其进行傅里叶分析。
我们知道周期离散信号是由无穷多相同的周期序列在时间轴上组成的,假设周期为N,即每个周期序列都有N个元素,而这样的周期序列有无穷多个,由于无穷多个周期序列都相同,所以可以只取其中一个周期就足以表示整个序列了,这个被抽出来表示整个序列特性的周期称为主值周期,这个序列称为主值序列。





常用公式第一章判断周期信号方法两个周期信号x(t),y(t)的周期分别为T1和T2,若其周期之比T1/T2为有理数,则其和信号x(t)+y(t)仍然是周期信号,其周期为T1和T2的最小公倍数。
2/2/2/(2/),/N N M M N πβπβπβπβπβ==仅当为整数时正弦序列才具有周期当为有理数时 正弦序列仍具有周期性, 其周期为取使为整数的最小整数当2为无理数时 正弦序列不具有周期性,1、连续正弦信号一定是周期信号,而正弦序列不一定是周期序列。
2、两连续周期信号之和不一定是周期信号,而两周期序列之和一定是周期序列。
信号的能量 def2()E f t dt +∞-∞=⎰信号的平均功率 def2/2/21lim ()T T T P f t dt T +-→∞=⎰ 冲激函数的特性'''()()(0)()(0)()f t t f t f t δδδ=- ()()(0)()f t t f t δδ=()()()()f t t a f a t a δδ-=- ()()(0),f t t dt f δ∞-∞=⎰()()()f t t a dt f a δ∞-∞-=⎰()()11()()n n n at t a a δδ=g 001()()t at t t a aδδ-=- 000()()()()f k k k f k k k δδ-=-()()()()(1)(0)n n n t f t dt f δ∞∞=-⎰- ''()()(0)t f t dt f δ∞∞=-⎰-动态系统是线性系统的条件可分解性 {}{}{}{}()()()0,()(0),0f x y y y T f T x •=•+•=•+⎡⎤⎡⎤⎣⎦⎣⎦ 零状态线性 {}{}{}{}{}{}12120,()()0,()0,()T af t bf t aT f bT f +=•+•⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦ 零输入线性 {}{}{}{}{}{}1212(0)(0),0(0),0(0),0T ax bx aT x bT x +=+⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦判断系统时不变、因果、稳定的方法。

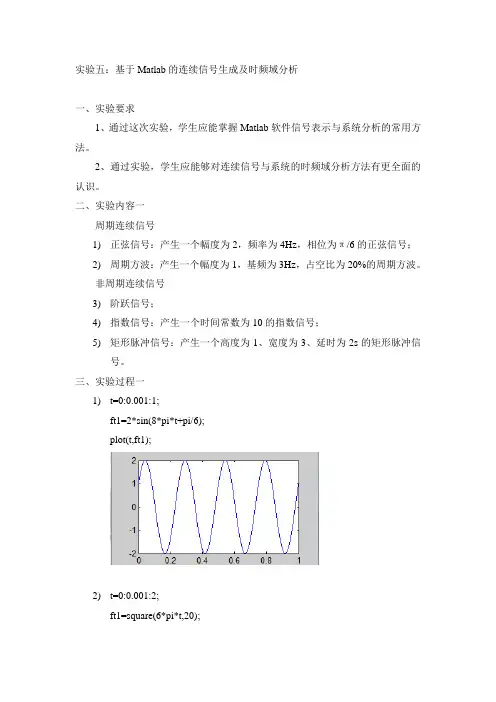
实验五:基于Matlab的连续信号生成及时频域分析一、实验要求1、通过这次实验,学生应能掌握Matlab软件信号表示与系统分析的常用方法。
2、通过实验,学生应能够对连续信号与系统的时频域分析方法有更全面的认识。
二、实验内容一周期连续信号1)正弦信号:产生一个幅度为2,频率为4Hz,相位为π/6的正弦信号;2)周期方波:产生一个幅度为1,基频为3Hz,占空比为20%的周期方波。
非周期连续信号3)阶跃信号;4)指数信号:产生一个时间常数为10的指数信号;5)矩形脉冲信号:产生一个高度为1、宽度为3、延时为2s的矩形脉冲信号。
三、实验过程一1)t=0:0.001:1;ft1=2*sin(8*pi*t+pi/6);plot(t,ft1);2)t=0:0.001:2;ft1=square(6*pi*t,20);plot(t,ft1),axis([0,2,-1.5,1.5]);3)t=-2:0.001:2;y=(t>0);ft1=y;plot(t,ft1),axis([-2,2,-1,2]);4)t=0:0.001:30;ft1=exp(-1/10*t);plot(t,ft1),axis([0,30,0,1]);5)t=-2:0.001:6;ft1=rectpuls(t-2,3);plot(t,ft1),axis([-2,6,-0.5,1.5]);四、实验内容二1)信号的尺度变换、翻转、时移(平移)已知三角波f(t),用MATLAB画信号f(t)、f(2t)和f(2-2t) 波形,三角波波形自定。
2)信号的相加与相乘相加用算术运算符“+”实现,相乘用数组运算符“.*”实现。
已知信号x(t)=exp(-0.4*t),y(t)=2cos(2pi*t),画出信号x(t)+y(t)、x(t)*y(t)的波形。
3)离散序列的差分与求和、连续信号的微分与积分已知三角波f(t),画出其微分与积分的波形,三角波波形自定。

正弦调制波信号ur 和三角载波uc 的波形1.引言1.1 概述概述正弦调制波信号(ur)和三角载波(uc)是通信领域中广泛使用的两种波形信号。
正弦调制波信号(ur)是通过改变正弦波的振幅、频率或相位来传输信息的一种调制方式。
而三角载波(uc)是一种具有一定频率和幅度的三角波形信号。
在通信系统中,正弦调制波信号(ur)可以通过调制源信号来实现信息的传输。
它具有波形周期性、连续平滑的特点,能够有效地传输不同频率和频带的信号。
通过调制源信号与正弦波进行调制,可以改变正弦波的振幅或频率,从而实现信号的传输和解调。
正弦调制波信号(ur)可以用于无线通信、广播电视、调频调幅等领域。
三角载波(uc)是一种具有渐变特性的波形信号。
它的波形由上升阶段和下降阶段组成,具有逐渐增大和减小的特点。
三角载波(uc)可以通过电子电路或数学函数进行生成,是一种常用的调制载波信号。
与正弦调制波信号(ur)不同,三角载波(uc)的频率和斜率是可以调节的,因此在不同的应用场景中具有更灵活的适应性。
本文将深入探讨正弦调制波信号(ur)和三角载波(uc)的波形特点。
我们将通过分析它们的波形周期、振幅和频率等参数,了解它们在信号传输中的重要性和应用前景。
此外,我们还将介绍正弦调制波信号(ur)和三角载波(uc)的生成方法和调制原理,以增进对它们的理解和应用。
作者希望通过本文的阐述,能够帮助读者对正弦调制波信号(ur)和三角载波(uc)有更深入的了解,并在相关领域的研究和应用中发挥积极的作用。
在文章的后续部分,我们将详细探讨它们的波形特点、生成方法,并总结它们在通信领域的应用前景。
1.2 文章结构文章结构的主要部分如下:本文主要分为引言、正文和结论三个部分。
下面将对每个部分进行详细的介绍。
引言部分主要包括三个小节:概述、文章结构和目的。
概述部分简要介绍了正弦调制波信号ur 和三角载波uc 的波形,并指出了它们在通信领域中的重要性。
文章结构部分则是介绍文章的整体架构,包括各个部分的内容和次序。
⼀个周期信号分解为若⼲个正弦信号⼀个周期信号分解为若⼲个正弦信号,就是傅⾥叶级数,不过我对傅⾥叶级数了解不多,⼀⽅⾯是懒得去细看,⼀⽅⾯也是为了保持神秘感。
我们把⼀个周期信号,甚⾄⾮周期信号,记为 y = Src ( t ) ,也称为源信号。
傅⾥叶级数的⼀般形式可以写为: Sin [ 1 ] + Sin [ 2 ] + Sin [ 3 ] + …… + Sin [ n ] , n -> ⽆穷Sin [ n ] = An * sin ( ωn * t + ψn ) + bn , A 为振幅,ω为⾓速度, t 为时间,ψ为初始相位, b 为增量, n 为项的序号(下标), An 是第 n 项的振幅,ωn 是第 n 项的⾓速度,ψn 是第 n 项的初始相位, bn 是第 n 项的增量。
那么,将 y = Src ( t ) 展开为傅⾥叶级数可以这样表⽰:Src ( t ) = Sin [ 1 ] + Sin [ 2 ] + Sin [ 3 ] + …… + Sin [ n ] , n -> ⽆穷只要确定了每⼀项的 A 、ω、ψ、b ,就得到源信号对应的傅⾥叶级数了。
那么,每⼀项的 A 、ω、ψ、b 怎么确定?记 Sins ( t ) = Sin [ 1 ] + Sin [ 2 ] + Sin [ 3 ] + …… + Sin [ n ] , n -> ⽆穷可以写⼀个定积分,ʃ | Src (t) - Sins (t) | dt , [ t1, t2 ] ,[ t1, t2 ] 是定积分的区间,也是源信号的区间,| Src (t) - Sins (t) | 表⽰ Src (t) - Sins (t) 的绝对值。
我们只要找出让ʃ | Src (t) - Sins (t) | dt , [ t1, t2 ] 这个定积分的值等于 0 的条件就可以了。
就是说,我们要为每⼀项找到合适的 A 、ω、ψ、b ,使得ʃ | Src (t) - Sins (t) | dt , [ t1, t2 ] = 0 。
实验四 信号的频谱分析一.实验目的1.掌握利用FFT 分析连续周期,非周期信号的频谱,如周期,非周期方波,正弦信号等。
理解CFS ,CTFT 与DFT (FFT )的关系。
2.利用FFT 分析离散周期,非周期信号的频谱,如周期,非周期方波,正弦信号等。
理解DFS ,DTFT 与DFT (FFT )的关系,并讨论连续信号与离散信号频谱分析方法的异同。
二.实验要求1.编写程序完成任意信号数字谱分析算法;2.编写实验报告。
三.实验内容1.利用FFT ,分析并画出sin(100),cos(100)t t ππ频谱,改变采样间隔与截断长度,分析混叠与泄漏对单一频率成分信号频谱的影响。
(1)sin (100*pi*t )产生程序:close all;clc;clear;t=0:0.0025:0.5-0.0025;f=400*t;w0=100*pi;y=sin(w0*t);a=fft(y);b=abs(a)/200;d=angle(a)*180/pi; subplot(311);plot(t,y);title('y=sin(wt)'); xlabel('t');ylabel('y(t)'); subplot(312); stem(f,b);title('振幅'); xlabel('f');ylabel('y(t)'); subplot(313); stem(f,d);title('相位'); xlabel('t');ylabel('y(t)');混叠close all;clc;clear;t=0:0.0115:0.46-0.0115; f=(t/0.0115)*2;w0=100*pi;y=sin(w0*t);a=fft(y);b=abs(a)/40;d=angle(a)*180/pi; subplot(311);plot(t,y);title('y=sin(wt)'); xlabel('t');ylabel('y(t)'); subplot(312); stem(f,b); title('振幅'); xlabel('f'); ylabel('y(t)'); subplot(313); stem(f,d); title('相位'); xlabel('t'); ylabel('y(t)');泄漏close all; clc;clear;t=0:0.0025:0.5-0.0075; f=800*t;w0=100*pi;y=sin(w0*t);a=fft(y);b=abs(a)/198;d=angle(a)*180/pi; subplot(311);plot(t,y);title('y=sin(wt)'); xlabel('t');ylabel('y(t)');subplot(312);stem(f,b);title('振幅');xlabel('f');ylabel('y(t)');subplot(313);stem(f,d);title('相位');xlabel('t');ylabel('y(t)');(2)cos(100*pi*t); close all;clc;clear;t=0:0.0025:0.5-0.0025; f=800*t;w0=100*pi;y=cos(w0*t);a=fft(y);b=abs(a)/200;d=angle(a)*180/pi; subplot(311);plot(t,y);title('y=cos(wt)'); xlabel('t');ylabel('y(t)');grid on; hold on; subplot(312); stem(f,b); title('振幅'); xlabel('f'); ylabel('y(t)'); grid on; hold on; subplot(313); stem(f,d); title('相位'); xlabel('f'); ylabel('y(t)');混叠close all;clc;clear;t=0:0.0115:0.46-0.0115; f=(t/0.0115)*2;w0=100*pi;y=cos(w0*t);a=fft(y);b=abs(a)/40;d=angle(a)*180/pi; subplot(311);plot(t,y);title('y=cos(wt)'); xlabel('t');ylabel('y(t)');subplot(312);stem(f,b);title('振幅');xlabel('f');ylabel('y(t)');subplot(313);stem(f,d);title('相位');ylabel('y(t)');泄漏close all;clc;clear;t=0:0.0025:0.5-0.0075; f=800*t;w0=100*pi;y=cos(w0*t);a=fft(y);b=abs(a)/198;d=angle(a)*180/pi; subplot(311);plot(t,y);title('y=cos(wt)');ylabel('y(t)');subplot(312);stem(f,b);title('振幅');xlabel('f');ylabel('y(t)');subplot(313);stem(f,d);title('相位');xlabel('t');ylabel('y(t)');2.利用FFT,分析并对比方波以及半波对称的正负方波的频谱,改变采样间隔与截断长度,分析混叠与泄漏对信号频谱的影响。
正弦信号的频率-回复
正弦信号的频率是指每秒钟重复出现的正弦波的周期次数。
频率的量纲为赫兹(Hz),表示每秒钟发生的周期变化的次数。
频率决定了信号的高低音调,对于音频信号而言,频率越高,音调越高;频率越低,音调越低。
在信号处理领域,正弦信号是一种具有周期性的波形信号,由一个恒定频率的正弦波表达。
正弦信号可以表示为A*sin(2πf*t+φ),其中A是振幅,f是频率,t是时间,φ是相位。
频率的测量可以通过直接计数周期的数量来实现,然后将周期数除以时间的测量点数以获得频率。
在实际应用中,我们使用频谱分析技术来确定信号的频率。
频谱分析是一种将信号分解为不同频率成分的方法。
通过对信号进行傅里叶变换,可以将信号转换到频率域,也就是将信号表示为一系列不同频率的正弦波的叠加。
傅里叶变换产生的结果称为频谱,它显示了信号中不同频率成分的幅度和相位信息。
在频谱中,我们可以通过查找信号的主要频率成分来确定正弦信号的频率。
使用峰值检测算法,可以找到频谱中幅度最高的频率成分,该频率即为信号的主频率。
此外,我们还可以使用基频法来确定正弦信号的频率。
基频是信号中最低频率的周期,也是信号的基本频率。
通过计算基频的倒数,可以得到信号的频率。
基频法适用于周期性较好的信号,但对于非周期性信号,基频法可能无法准确测量频率。
通过以上方法,我们可以准确地测量正弦信号的频率。
频率对于许多领域的应用至关重要,如音频处理、通信系统、医学诊断等。
了解信号的频率特性有助于我们理解和分析信号,从而优化信号处理和应用。
正弦型模拟信号和正弦序列
正弦型模拟信号和正弦序列是通信工程领域中经常用到的两种信号形式。
正弦型模拟信号(Sinusoidal Analog Signal)是一种连续变化的信号形式,它的波形是正弦函数,具有周期性、波形简单、易于处理等特点。
在实际应用中,正弦型模拟信号被广泛用于模拟电路、通信电路、音频信号等领域。
通常用A表示信号的幅度,f表示信号的频率,θ表示信号的相位。
因为正弦型模拟信号是连续变化的,所以在处理过程中需要经过模拟信号采样、量化等步骤,将其转化为数字信号并进行数字处理。
正弦型模拟信号和正弦序列在通信工程领域中都扮演着重要的角色,它们虽然在信号形式上有所区别,但在处理方法上有很多相似之处。
对于正弦型模拟信号,在数字处理时需要进行采样、量化、离散化等转换操作,对于正弦序列,在处理时需要进行离散化、傅里叶变换等操作。
在实际应用中,正弦型模拟信号和正弦序列互相转化也是常见的操作,比如在数字滤波中,将正弦型模拟信号离散化后就变成了正弦序列,然后再进行数字滤波处理;而在数字合成音乐中,正弦序列可以被合成成为复杂的音乐信号,而正弦型模拟信号则可以被用于模拟乐器的声音。
总之,正弦型模拟信号和正弦序列是通信工程领域中十分重要的信号形式,它们在模拟信号处理和数字信号处理中得到了广泛应用,对于工程师来说掌握这两种信号形式的定义、表示、转换和处理方法是非常重要的。