下载文档原格式
曲线的曲率与弯曲性质的解析几何描述曲线是解析几何中的重要概念，它在数学以及其他领域中都有广泛的应用。
曲线的曲率和弯曲性质是描述曲线形状的重要指标，它们可以帮助我们理解曲线的特征和性质。
在本文中，我们将从解析几何的角度出发，对曲线的曲率和弯曲性质进行详细的描述和解释。
一、曲线的曲率曲线的曲率是描述曲线弯曲程度的量度，它反映了曲线在某一点的弯曲程度。
要计算曲线的曲率，我们首先需要了解曲线的切线和法线。
1. 切线：曲线上的任意一点，都可以通过该点的切线来描述曲线在该点的方向。
切线的斜率等于曲线在该点的导数，即切线的斜率等于曲线的导数。
切线的方向与曲线在该点的切线方向相同。
2. 法线：曲线上的任意一点，都可以通过该点的法线来描述曲线在该点的垂直方向。
法线与切线垂直，即切线和法线的斜率的乘积等于-1。
曲线的曲率可以通过计算曲线在某一点的切线与曲线的夹角来得到。
曲线的曲率越大，说明曲线在该点的弯曲程度越大；曲率越小，则说明曲线在该点的弯曲程度越小。
二、曲线的弯曲性质曲线的弯曲性质描述了曲线的整体形状和特征，包括曲线的凸性和凹性。
1. 凸曲线：如果曲线上的任意两点的连线都位于曲线的上方或者曲线上，那么这条曲线被称为凸曲线。
凸曲线的弯曲方向向外，如圆的外弯部分。
2. 凹曲线：如果曲线上的任意两点的连线都位于曲线的下方或者曲线上，那么这条曲线被称为凹曲线。
凹曲线的弯曲方向向内，如圆的内弯部分。
曲线的弯曲性质可以通过曲线的曲率来判断。
如果曲线的曲率在某一点大于零，则该点属于凸曲线；如果曲率小于零，则该点属于凹曲线。
三、曲线的解析几何描述在解析几何中，我们可以使用数学模型来描述曲线的曲率和弯曲性质。
常见的数学模型包括参数方程和隐式方程。
1. 参数方程：曲线的参数方程是用参数表示曲线上的点的坐标。
例如，对于平面上的曲线，可以使用参数方程x=f(t)和y=g(t)来描述曲线上的点的坐标，其中t为参数。
通过对参数方程求导，我们可以计算曲线在某一点的切线和曲率。
直线和曲线的认识和区分直线和曲线是数学中常见的几何概念，它们在几何图形的描述和分析中起着重要的作用。
本文将从数学角度出发，对直线和曲线的认识和区分进行探讨。
一、直线的认识直线是指没有弯曲和拐角的无限延伸的轨迹。
从数学的角度来看，直线可以通过两点确定，任意两点都可以确定一条唯一的直线。
直线上的任意两点之间的距离是恒定的，而且两点之间的连线是直的，没有任何弯曲。
直线的特点在于其方向和直线上的点的无限性。
直线可以水平、垂直或倾斜，方向由直线的斜率所决定。
同时，直线上的点是无限多的，可以沿着直线无限地延伸。
二、曲线的认识曲线是指有弯曲和拐角的轨迹。
与直线不同，曲线不能用两点来确定，而是需要用函数或方程来描述。
曲线上的点之间的距离是不恒定的，两点之间的连线会出现弯曲和变化。
曲线的特点在于其弯曲和多样性。
曲线可以呈现出各种形状，如圆形、椭圆形、抛物线形等。
曲线上的点具有一定的规律性，可以通过方程或函数来描述其变化规律。
三、直线和曲线的区分直线和曲线的主要区别在于弯曲程度和形状的多样性。
直线是最简单的几何形状，没有任何弯曲和拐角。
而曲线则包含有弯曲和拐角，形状多样，可以呈现出各种复杂的图形。
此外，直线可以通过两点来确定，而曲线需要用函数或方程来描述。
直线上的点之间的距离是恒定的，而曲线上的点之间的距离是不恒定的，会出现弯曲和变化。
总结起来，直线是没有弯曲和拐角的轨迹，可以通过两点来确定，而曲线是有弯曲和拐角的轨迹，需要用函数或方程来描述。
直线具有方向性和无限性，而曲线具有多样性和变化性。
四、应用领域举例直线和曲线在各个领域中都有广泛的应用。
在几何学中，直线和曲线是基本的几何概念，用于描述和分析各种图形。
在物理学中，直线和曲线是描述物体运动轨迹的重要工具。
在工程学和建筑学中，直线和曲线被广泛应用于设计和构造中。
在计算机图形学中，直线和曲线是描述图像和动画的基础。
在经济学和统计学中，直线和曲线是分析和预测数据的重要方法。
平面几何的基本图形平面几何是几何学中的一个分支，研究平面上的点、线、面及其相互关系。
在平面几何中，有一些基本图形是我们常见且重要的，它们是点、线、线段、射线、角、多边形、圆和曲线。
本文将会逐一介绍这些基本图形及其特征。
一、点（Point）点是平面上最基本的图形，用一个大写字母表示，如A、B、C。
点没有长度、面积和方向，只有位置。
点只有一个，不同的点可以有不同的位置。
在平面几何中，点是构成其他几何图形的基础。
二、线（Line）线由无数个点组成，无限延伸，没有宽度。
线段是有限的线，有两个端点。
线用两个大写字母表示，如AB、CD。
在平面几何中，线是连接两个点的直线路径。
三、线段（Line Segment）线段是两个点之间的有限线，有固定的长度。
线段用两个大写字母表示，并在两个字母之间加一条横线，如AB。
与线相比，线段具有确定的长度。
四、射线（Ray）射线起始于一个点，无限延伸，只有一个端点。
射线用一个大写字母及一个端点所在的小写字母表示，如OA，其中O为起点。
五、角（Angle）角是由两条射线共同起点组成的图形。
角用三个字母表示，中间的字母代表角的顶点，两边的字母分别代表两条射线。
例如∠ABC表示以点B为顶点，射线BA和射线BC所夹的角。
角可以根据其大小分为锐角、直角、钝角和平角。
六、多边形（Polygon）多边形是由多条线段连接而成的封闭图形。
多边形由至少三条线段组成，每个线段称为边，相邻边之间的交点称为顶点。
根据边的数量，多边形可以分为三角形、四边形、五边形等。
最常见的多边形是三角形、四边形和五边形。
七、圆（Circle）圆是由一条曲线和平面上的一个点组成的图形，其中曲线称为圆周，点称为圆心。
圆周上的任意一点到圆心的距离都相等，这个距离称为半径。
用一个大写字母表示圆心，用圆心字母上方加一个小写字母表示圆周，如O、OA。
八、曲线（Curve）曲线在平面上呈现出曲折或弯曲的形状，没有直线的性质。
曲线可以是闭合的，也可以是不闭合的。
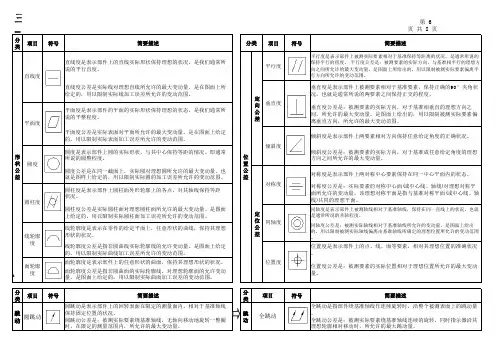
三-1、常用的几何形位公差符号及简要描述第 6 页 共 8 页分类项目符号项目符号平行度分类项目符号分类符号跳动圆跳动跳动形状公差直线度平面度圆度分类定向公差垂直度位置度公差是：被测要素的实际位置相对于理想位置所允许的最大变动量。
面轮廓度线轮廓度平面度是表示部件的平面的实际形状保持理想的状态。
是我们通常所说的平整程度。
平面度公差是实际表面对平面所允许的最大变动量。
是在图面上给定的，用以限制实际表面加工误差所允许的变动范围。
圆度是表示部件上圆的实际形状，与其中心保持等距的情况。
即通常所说的圆整程度。
圆度公差是在同一截面上，实际圆对理想圆所允许的最大变动量。
也就是图样上给定的，用以限制实际圆的加工误差所允许的变动范围。
圆柱度简要描述平行度是表示部件上被测实际要素相对于基准保持等距离的状况。
是通常所说的保持平行的程度。
平行度公差是：被测要素的实际方向，与基准相平行的理想方向之间所允许的最大变动量。
是图面上所给出的，用以限制被测实际要素偏离平行方向所允许的变动范围。
位置公差圆柱度是表示部件上圆柱面外形轮廓上的各点，对其轴线保持等距状况。
圆柱度公差是实际圆柱面对理想圆柱面所允许的最大变动量。
是图面上给定的，用以限制实际圆柱面加工误差所允许的变动范围。
线轮廓度是表示在零件的给定平面上，任意形状的曲线，保持其理想形状的状况。
线轮廓度公差是指非圆曲线实际轮廓线的允许变动量。
是图面上给定的，用以限制实际曲线加工误差所允许的变动范围。
简要描述直线度是表示部件上的直线实际形状保持理想的状况。
是我们通常所说的平行直度。
直线度公差是实际线对理想直线所允许的最大变动量。
是在图面上所给定的，用以限制实际线加工误差所允许的变动范围。
面轮廓度是表示部件上的任意形状的曲面，保持其理想形状的状况。
面轮廓度公差是指非圆曲面的实际轮廓线，对理想轮廓面的允许变动量。
是图面上给定的，用以限制实际曲面加工误差的变动范围。
垂直度是表示部件上被测要素相对于基准要素，保持正确的90°夹角状况。
几何形的坐标表示几何学是研究空间中的点、线、面和体量等几何对象的性质和关系的学科。
而在几何学中，坐标表示是一种重要的方法，它能够通过使用数学中的坐标系统来描述和分析几何形状。
本文将探讨几何形的坐标表示，介绍常见的几何形状及其坐标表示方法。
1. 点的坐标表示在二维直角坐标系中，点是由两个坐标值(x, y)表示的。
其中，x表示点在x轴上的水平距离，y表示点在y轴上的垂直距离。
例如，点A的坐标为(2, 3)，表示它在x轴上距离原点2个单位，而在y轴上距离原点3个单位。
在三维空间中，点的坐标表示需要使用三个坐标值(x, y, z)。
其中，z表示点在z轴上的垂直距离。
例如，点B的坐标为(1, 2, 3)，表示它在x轴上距离原点1个单位，y轴上距离原点2个单位，z轴上距离原点3个单位。
2. 直线的坐标表示直线是由无数点组成的，因此需要使用直线上两个点的坐标表示来确定一条直线。
在二维坐标系中，通过两个点的坐标(x1, y1)和(x2, y2)，可以确定一条直线的方程。
常见的直线方程有斜截式方程、点斜式方程和标准式方程等。
斜截式方程表示为y = kx + b，其中k为直线的斜率，b为直线与y轴的截距。
例如，直线L的斜截式方程为y = 2x + 3，表示直线L的斜率为2，与y轴的截距为3。
点斜式方程表示为y - y1 = k(x - x1)，其中(x1, y1)为直线上一点的坐标，k为直线的斜率。
例如，过点P(2, 4)且斜率为3的直线的点斜式方程为y - 4 = 3(x - 2)。
在三维空间中，直线的坐标表示需要使用参数方程。
例如，直线L过点A(1, 2, 3)且与向量v(2, -1, 1)平行，那么直线L的参数方程可以表示为x = 1 + 2t，y = 2 - t，z = 3 + t，其中t为参数。
3. 平面的坐标表示平面是由无数的点组成的，因此需要使用平面上三个点的坐标表示来确定一个平面。
在三维空间中，通过平面上三个点的坐标(x1, y1, z1)，(x2, y2, z2)和(x3, y3, z3)，可以确定一个平面的方程。
几何形的坐标表示在几何学中，我们经常遇到需要表示和描述不同形状的问题。
为了方便准确地表示这些形状，我们使用了坐标系和坐标来进行描述和计算。
本文将介绍几何形的坐标表示方法，包括点、直线和曲线的表示方式。
一、点的坐标表示在平面几何中，我们通常使用二维坐标系来表示点的位置。
在笛卡尔坐标系中，平面上的每个点都可以用一个有序对(x, y)来表示，其中x表示点在x轴上的投影，y表示点在y轴上的投影。
例如，点A的坐标为(3, 4)，表示它在x轴上的投影为3，在y轴上的投影为4。
二、直线的坐标表示直线可以用不同的方式来表示，最常见的是使用两个点来确定一条直线。
我们可以通过两点的坐标来求解直线的斜率和截距，从而得到直线的方程。
例如，经过点A(1, 2)和点B(3, 4)的直线可以表示为y =mx + b的形式，其中m为斜率，b为截距。
除了通过两点来表示直线，我们还可以使用一般式方程来表示直线。
一般式方程的形式为Ax + By + C = 0，其中A、B、C为常数，代表了直线的一般性质。
通过一般式方程，我们可以方便地判断点是否在直线上，以及求解直线的交点等问题。
三、曲线的坐标表示曲线的坐标表示方法与直线有所不同，通常我们使用参数方程来描述曲线的轨迹。
参数方程是将曲线上每个点的坐标表示为参数t的函数形式。
例如，二阶曲线圆的参数方程为x = r*cos(t)和y = r*sin(t)，其中r为半径，t为参数。
除了参数方程，还有一些常见的曲线可以使用其他的坐标表示方法。
例如，椭圆可以使用中心点坐标和长度、宽度来表示；抛物线可以使用焦点和直线的距离来表示；双曲线可以使用焦点和准线的距离来表示。
结语几何形的坐标表示方法对于准确描述和计算几何形状非常重要。
不同的形状可以采用不同的表示方法，包括点的坐标、直线的方程和曲线的参数方程等。
通过熟练掌握这些表示方法，我们可以更好地理解和应用几何学中的各种概念和定理。
通过本文的介绍，希望读者对几何形的坐标表示有了更清晰的了解，并能够在实际问题中应用这些知识。
曲线知识点曲线是数学中的重要概念，也是许多学科领域中的基础知识。
它在几何学、物理学、经济学等多个领域中扮演着重要的角色。
本文将介绍曲线的基本概念、特点和一些常见应用，帮助读者更好地理解和掌握曲线知识点。
一、曲线的定义曲线是平面上的一条连续的路径。
从数学的角度来看，曲线可以通过参数方程、隐式方程或者显式方程进行表示。
曲线可以是直线、圆、椭圆、双曲线等各种形状。
曲线的形状和特征由方程的形式和参数的取值决定。
二、曲线的特点 1. 曲线的长度：曲线的长度可以通过曲线的参数方程或者函数的导数计算得出。
曲线的长度可以是有限的或者无限的，取决于曲线的形状。
2.曲线的斜率：曲线在某一点的斜率可以通过曲线的导数计算得出。
斜率表示了曲线在该点的变化速率。
曲线的斜率可以用来描述曲线的陡峭程度。
3. 曲线的凹凸性：曲线的凹凸性可以通过曲线的二阶导数来判断。
凹曲线在任意一点的二阶导数大于零，而凸曲线在任意一点的二阶导数小于零。
三、曲线的常见应用 1. 几何学：曲线在几何学中有广泛的应用，如描述平面上的点的运动轨迹、刻画曲面的形状等。
例如，椭圆曲线在几何学中用来描述平面上的点，可以应用于密码学、椭圆曲线加密等领域。
2. 物理学：曲线在物理学中可以用来描述运动的路径。
例如，自由落体运动中物体的运动轨迹可以用抛物线来描述。
3. 经济学：曲线在经济学中常常用来表示供求关系、生产函数等。
例如，需求曲线和供给曲线的交点可以表示市场平衡点。
4. 统计学：曲线在统计学中被广泛应用于数据分析和模型拟合。
例如，正态分布曲线可以用来描述许多自然现象的概率分布。
总结：曲线是数学中的基本概念，具有广泛的应用。
掌握曲线的基本概念和特点对于理解和应用曲线知识点至关重要。
通过本文的介绍，相信读者已经对曲线有了更深入的了解，可以在实际问题中灵活运用曲线知识点。
对于进一步学习和研究曲线，可以深入探索曲线的性质、曲率、弧长等更高级的内容。
解析几何中的曲线与双曲线几何学是数学中的一个重要分支，主要研究空间中的图形和形状。
而解析几何则是将几何问题用坐标和代数方法进行描述和解决的一种方法。
在解析几何中，曲线是一个重要的概念，而双曲线则是曲线中的一种特殊类型。
本文将会对曲线与双曲线进行详细的解析和分析。
一、曲线的定义与特点在解析几何中，曲线是指由一系列点组成的连续图形。
通常我们可以通过方程来表示和描述曲线。
曲线有许多种类，包括直线、圆、椭圆、双曲线等等。
不同类型的曲线具有不同的数学模型和特点。
对于一条曲线来说，我们可以通过以下几个要素来描述它：1. 方程：我们可以通过一个数学方程来表示曲线。
例如，对于直线来说，它的方程可以写成y = kx + b的形式；对于圆来说，它的方程可以写成(x-a)² + (y-b)² = r²的形式。
2. 曲线的形状：通过观察曲线的形状，我们可以了解到曲线是直线、圆、椭圆还是双曲线等等。
3. 相对位置：我们可以通过曲线与坐标轴的相交关系来了解曲线在空间中的位置。
4. 参数方程：有些复杂的曲线需要用参数方程来进行描述，参数方程可以用一组参数来描绘曲线上的每一个点。
二、双曲线的定义与性质双曲线是解析几何中的一种重要曲线，它是由两个分离的曲线组成的。
双曲线的方程通常可以写成下面的形式：(x-h)²/a² - (y-k)²/b² = 1 或者 (y-k)²/b² - (x-h)²/a² = 1其中(a, b)为椭圆的中心点，而a,b则分别为椭圆沿x轴和y轴的半轴长度。
双曲线有以下几个重要性质：1. 双曲线的中心点：双曲线的中心点为(h, k)。
2. 对称轴：双曲线包含两条对称轴，分别是以中心点为中心的水平对称轴和垂直对称轴。
3. 渐近线：双曲线还有两条渐近线，它们是双曲线与其两个分支的切线。
双曲线的形状和特点取决于参数a和b的大小和正负。
