陕西省西安市昆仑中学高考数学一轮复习讲义 第70课时 算法初步 理

课题：数列求和教学目标：1.熟练掌握等差数列与等比数列的求和公式； 2.能运用倒序相加、错位相减、拆项相消等重要的数学方法进行求和运算；3.熟记一些常用的数列的和的公式． 教学重点：特殊数列求和的方法．（一） 主要知识：1.等差数列与等比数列的求和公式的应用；2.倒序相加、错位相减，分组求和、拆项求和等求和方法；（二）主要方法：1.基本公式法：()1等差数列求和公式：()()11122n n n a a n n S na d +-==+ ()2等比数列求和公式：()111,11,111n n n na q S a q a a qq qq =⎧⎪=-⎨-=≠⎪--⎩ ()3()()2221121216n n n n +++=++L ；()4()23333112314n n n ++++=+⎡⎤⎣⎦L ； ()50122n nn n n n C C C C ++++=L .2.错位相消法：给12n n S a a a =+++L 各边同乘以一个适当的数或式，然后把所得的等式和原等式相减，对应项相互抵消，最后得出前n 项和n S .一般适应于数列{}n n a b 的前n 向求和，其中{}n a 成等差数列，{}n b 成等比数列。

3.分组求和：把一个数列分成几个可以直接求和的数列，然后利用公式法求和。

4.拆项（裂项）求和：把一个数列的通项公式分成两项差的形式，相加过程中消去中间项，只剩下有限项再求和. 常见的拆项公式有：()1若{}n a 是公差为d 的等差数列，则111111n n n n a a d a a ++⎛⎫=- ⎪⎝⎭； ()2()()1111212122121n n n n ⎛⎫=- ⎪-+-+⎝⎭；()3()()()()()1111122112n n n n n n n ⎡⎤=-⎢⎥+++++⎣⎦；()41a b=-；()51k=；()611m m mn n n C C C -+=-；()7()!1!!n n n n ⋅=+-；()811,1,2n nn S n a S S n -=⎧=⎨-⎩≥ 5.倒序相加法：根据有些数列的特点，将其倒写后与原数列相加，以达到求和的目的。

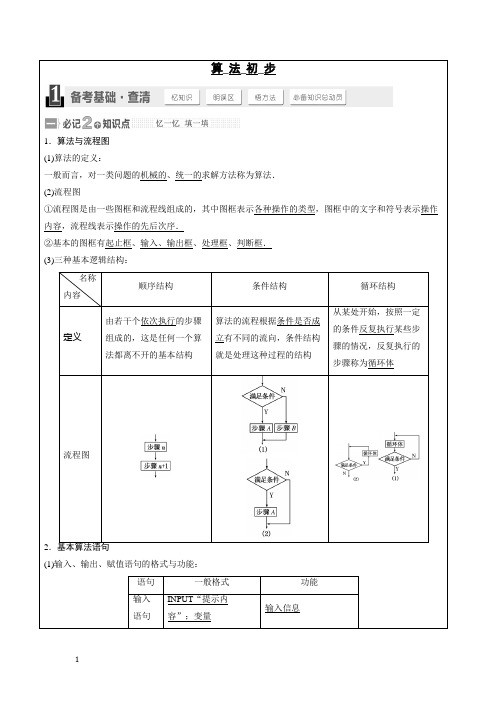
算_法_初_步1．算法与流程图(1)算法的定义：一般而言，对一类问题的机械的、统一的求解方法称为算法．(2)流程图①流程图是由一些图框和流程线组成的，其中图框表示各种操作的类型，图框中的文字和符号表示操作内容，流程线表示操作的先后次序．②基本的图框有起止框、输入、输出框、处理框、判断框．(3)三种基本逻辑结构：名称内容顺序结构条件结构循环结构定义由若干个依次执行的步骤组成的，这是任何一个算法都离不开的基本结构算法的流程根据条件是否成立有不同的流向，条件结构就是处理这种过程的结构从某处开始，按照一定的条件反复执行某些步骤的情况，反复执行的步骤称为循环体流程图2．基本算法语句(1)输入、输出、赋值语句的格式与功能：语句一般格式功能输入语句INPUT“提示内容”；变量输入信息输出语句PRINT“提示内容”；表达式输出常量、变量的值和系统信息赋值语句变量＝表达式将表达式所代表的值赋给变量(2)条件语句的格式及框图：①IF－THEN格式：②IF－THEN－ELSE格式：(3)循环语句的格式及框图：①UNTIL语句：②WHILE语句：1．易混淆处理框与输入框，处理框主要是赋值、计算，而输入框只是表示一个算法输入的信息．2．易忽视循环结构中必有条件结构，其作用是控制循环进程，避免进入“死循环”，是循环结构必不可少的一部分．3．易混淆当型循环与直到型循环．直到型循环是“先循环，后判断，条件满足时终止循环”；而当型循环则是“先判断，后循环，条件满足时执行循环”；两者的判断框内的条件表述在解决同一问题时是不同的，它们恰好相反．[试一试]1．执行如图所示的算法流程图，若输入x＝2，则输出y的值为________．2．如图是一个算法流程图，则输出的k的值是________．识别算法流程图运行和完善流程图的步骤识别运行算法流程图和完善流程图是高考的热点．解答这一类问题，第一，要明确流程图的顺序结构、条件结构和循环结构；第二，要识别运行流程图，理解框图所解决的实际问题；第三，按照题目的要求完成解答．对流程图的考查常与数列和函数等知识相结合，进一步强化框图问题的实际背景．[练一练]1．(2014·深圳调研)若执行图中的框图，输入N＝13，则输出的数等于________．2．运行如图所示的流程图，若输出的结果是62，则判断框中整数M的值是________．考点一算法的基本结构1．(2012·江苏高考)下图是一个算法流程图，则输出的k的值是________．2．(2013·安徽高考改编)如图所示，程序框图(算法流程图)的输出结果为________．3．(2014·南昌模拟)若如下框图所给的程序运行结果为S＝20，那么判断框中应填入的关于k的条件是________．[类题通法]1．解决流程框图问题要注意几个常用变量：(1)计数变量：用来记录某个事件发生的次数，如i＝i＋1.(2)累加变量：用来计算数据之和，如S＝S＋i.(3)累乘变量：用来计算数据之积，如p＝p×i.2．处理循环结构的框图问题，关键是理解并认清终止循环结构的条件及循环次数．考点二算法的交汇性问题算法是高考热点内容之一，算法的交汇性问题是新课标高考的一大亮点，归纳起来常见的命题角度有：(1)与统计的交汇问题；(2)与函数的交汇问题；(3)与概率的交汇问题.角度一与统计的交汇问题1．(2014·荆州模拟)图(1)是某高三学生进入高中三年来的数学考试成绩茎叶图，第1次到第14次的考试成绩依次记为A1，A2，…，A14.图(2)是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图．那么算法流程图输出的结果是________．角度二与函数的交汇问题2．(2014·北京海淀模拟)执行如图所示的算法流程图，输出的k值是________．角度三与概率的交汇问题3．如图是用模拟方法估计圆周率π值的流程图，P表示估计结果，则图中空白框内应填入________．[类题通法]解决算法的交汇性问题的方法(1)读懂流程图、明确交汇知识；(2)根据给出问题与流程图处理问题；(3)注意框图中结构的判断．考点三基本算法语句[典例](2013·南京、盐城一模)如图是一算法的伪代码，执行此算法，最后输出的n的值为________．n←6s←0While s<15s←s＋nn←n－1End WhilePrint n[类题通法]1．输入语句、输出语句和赋值语句基本对应于算法的顺序结构．2．在循环语句中也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套格式，这些语句需要保证算法的完整性，否则就会造成程序无法执行．[针对训练]运行下面的程序时，WHILE循环语句的执行次数是________．N←0WHILE N<20N←N＋1N←N*NWENDPRINT NEND[课堂练通考点]1．(2013·济南模拟)阅读算法流程图，运行相应的程序，输出的结果为________．2．(2014·福州模拟)执行如图所示的流程图，若输入的x值为2，则输出的x值为________．3．(2013·广东高考改编)执行如图所示的程序框图，若输入n的值为4，则输出s的值为________．4．(2013·惠州模拟)如图所示是一个算法的流程图，则输出S的值是________．[课下提升考能]1．(2014·大连模拟)在如图所示的流程图中，输入A＝192，B＝22，则输出的结果是________．2．当a＝1，b＝3时，执行完如图的一段程序后x的值是________．IF a<b THENx←a＋bELSEx←a－bEND IF3．图中的算法伪代码运行后，输出的S为________．I←1While I<8S←2×I＋3I←I＋2End WhilePrint S4．按如图所示的流程图运行后，输出的结果是63，则判断框中的整数M的值是________．5．(2013·东城模拟)某算法流程图如图所示，执行该程序，若输入的x值为5，则输出的y值为________．6．(2014·南通调研)已知实数x∈[1,9]，执行如图所示的流程图，则输出的x不小于55的概率为________．7．(2014·徐州摸底)已知某算法的流程图如图所示，则程序运行结束输出的结果为________．8．(2013·长春第三次调研)执行如图所示的流程图，若输出的k＝5，则输入的整数p的最大值为________．9．(2014·台州模拟)按如图所示的流程图运算，若输入x＝20，则输出的k＝________. 10．(2013·湖南高考)执行如图所示的程序框图，如果输入a＝1，b＝2，则输出的a的值为________．11．(2014·湖北八校联考)执行如图所示的流程图，输出的S的值为________．12．(2014·湘潭模拟)执行如图所示的流程图，输出的结果是________．。

第十一章算法初步高考导航知识网络11.1 算法的含义与程序框图典例精析题型一 算法的含义【例1】已知球的表面积是16π，要求球的体积，写出解决该问题的一个算法. 【解析】算法如下： 第一步，s ＝16π. 第二步，计算R ＝s 4π. 第三步，计算V ＝4πR 33.第四步，输出V .【点拨】给出一个问题，设计算法应该注意：(1)认真分析问题，联系解决此问题的一般数学方法，此问题涉及到的各种情况； (2)将此问题分成若干个步骤； (3)用简练的语句将各步表述出来.【变式训练1】设计一个计算1×3×5×7×9×11×13的算法.图中给出程序的一部分，则在横线①上不能填入的数是( )A.13B.13.5C.14D.14.5【解析】当I ＜13成立时，只能运算 1×3×5×7×9×11.故选A.题型二 程序框图【例2】图一是某县参加高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A 1，A 2，…，A 10(如A 2表示身高(单位：cm)在[150,155)内的学生人数).图二是统计图一中身高在一定范围内学生人数的一个算法流程图.现要统计身高在160～180 cm(含160 cm ，不含180 cm)的学生人数，那么在流程图中的判断框内应填写的条件是( )A.i ＜6？B.i ＜7？C.i ＜8？D.i ＜9？图一【解析】根据题意可知，i 的初始值为4，输出结果应该是A 4＋A 5＋A 6＋A 7，因此判断框中应填写i ＜8？，选C.【点拨】本题的命题角度较为新颖，信息量较大，以条形统计图为知识点进行铺垫，介绍了算法流程图中各个数据的引入来源，其考查点集中于循环结构的终止条件的判断，考查了学生合理地进行推理与迅速作出判断的解题能力，解本题的过程中不少考生误选A ，实质上本题中的数据并不大，考生完全可以直接从头开始限次按流程图循环观察，依次写出每次循环后的变量的赋值，即可得解.【变式训练2】(辽宁)某店一个月的收入和支出，总共记录了N 个数据a 1，a 2，…，a N .其中收入记为正数，支出记为负数，该店用如图所示的程序框图计算月总收入S 和月净盈利V ，那么在图中空白的判断框和处理框中，应分别填入下列四个选项中的( )A.A ＞0？，V ＝S －TB.A ＜0？，V ＝S －TC.A ＞0？，V ＝S ＋TD.A ＜0？，V ＝S ＋T 【解析】选C.题型三 算法的条件结构【例3】某快递公司规定甲、乙两地之间物品的托运费用根据下列方法计算： f ＝⎩⎨⎧⨯-+⨯).50＞(85.0)50(53.050),50≤＜0(53.0ωωωω 其中f (单位：元)为托运费，ω为托运物品的重量(单位：千克)，试写出一个计算费用f 的算法，并画出相应的程序框图.【解析】算法如下：第一步，输入物品重量ω.第二步，如果ω≤50，那么f＝0.53ω，否则，f＝50×0.53＋(ω－50)×0.85.第三步，输出托运费f.程序框图如图所示.【点拨】求分段函数值的算法应用到条件结构，因此在程序框图的画法中需要引入判断框，要根据题目的要求引入判断框的个数，而判断框内的条件不同，对应的框图中的内容或操作就相应地进行变化.【变式训练3】(天津)阅读如图的程序框图，若输出s的值为－7，则判断框内可填写()A.i＜3？B.i＜4？C.i＜5？D.i＜6？【解析】i＝1，s＝2－1＝1；i＝3，s＝1－3＝－2；i＝5，s＝－2－5＝－7.所以选D.题型四算法的循环结构【例4】设计一个计算10个数的平均数的算法，并画出程序框图.【解析】算法步骤如下：第一步，令S＝0.第二步，令I＝1.第三步，输入一个数G.第四步，令S＝S＋G.第五步，令I＝I＋1.第六步，若I＞10，转到第七步，若I≤10，转到第三步.第七步，令A＝S/10.第八步，输出A.据上述算法步骤，程序框图如图.【点拨】(1)引入变量S作为累加变量，引入I为计数变量，对于这种多个数据的处理问题，可通过循环结构来达到；(2)计数变量用于记录循环次数，同时它的取值还用于判断循环是否终止，累加变量用于输出结果.【变式训练4】设计一个求1×2×3×…×10的程序框图.【解析】程序框图如下面的图一或图二.图一图二总结提高1.给出一个问题，设计算法时应注意：(1)认真分析问题，联系解决此问题的一般数学方法；(2)综合考虑此类问题中可能涉及的各种情况；(3)借助有关的变量或参数对算法加以表述；(4)将解决问题的过程划分为若干个步骤；(5)用简练的语言将各个步骤表示出来.2.循环结构有两种形式，即当型和直到型，这两种形式的循环结构在执行流程上有所不同，当型循环是当条件满足时执行循环体，不满足时退出循环体；而直到型循环则是当条件不满足时执行循环体，满足时退出循环体.所以判断框内的条件，是由两种循环语句确定的，不得随便更改.3.条件结构主要用在一些需要依据条件进行判断的算法中.如分段函数的求值，数据的大小关系等问题的算法设计.11.2 基本算法语句典例精析题型一 输入、输出与赋值语句的应用【例1】阅读程序框图(如下图)，若输入m ＝4，n ＝6，则输出a ＝ ，i ＝ .【解析】a ＝12，i ＝3.【点拨】赋值语句是一种重要的基本语句，也是程序必不可少的重要组成部分，使用赋值语句，要注意其格式要求.【变式训练1】(陕西)如图是求样本x 1，x 2，…，x 10的平均数x 的程序框图，则图中空白框中应填入的内容为( )A.S ＝S ＋x nB.S ＝S ＋x nnC.S ＝S ＋nD.S ＝S ＋1n【解析】因为此步为求和，显然为S ＝S ＋x n ，故选A. 题型二 循环语句的应用【例2】设计算法求11×2＋12×3＋13×4＋…＋199×100的值.要求画出程序框图，写出用基本语句编写的程序.【解析】这是一个累加求和问题，共99项相加，可设计一个计数变量，一个累加变量，用循环结构实现这一算法.程序框图如下图所示：程序如下：语句编写程序解决问题时，一定要注意格式和条件的表述方法，WHILE语句是当条件满足时执行循环体，UNTIL语句是当条件不满足时执行循环体.(2)在解决一些需要反复执行的运算任务，如累加求和、累乘求积等问题中应注意考虑利用循环语句来实现.(3)在循环语句中，也可以嵌套条件语句，甚至是循环语句，此时需要注意嵌套的这些语句，保证语句的完整性，否则就会造成程序无法执行.【变式训练2】下图是输出某个有限数列各项的程序框图，则该框图所输出的最后一个数据是 .【解析】由程序框图可知，当N ＝1时，A ＝1；N ＝2时，A ＝13；N ＝3时，A ＝15，…，即输出各个A值的分母是以1为首项以2为公差的等差数列，故当N ＝50时，A ＝11＋(50－1)×2＝199，即为框图最后输出的一个数据.故填199.题型三 算法语句的实际应用【例3】某电信部门规定：拨打市内电话时，如果通话时间3分钟以内，收取通话费0.2元，如果通话时间超过3分钟，则超过部分以每分钟0.1元收取通话费(通话不足1分钟时按1分钟计算).试设计一个计算通话费用的算法，要求写出算法，编写程序.【解析】我们用c (单位：元)表示通话费，t (单位：分钟)表示通话时间， 则依题意有⎩⎨⎧⨯+=,3＞2],[0.10.23,≤＜0,2.0t t-t c算法步骤如下： 第一步，输入通话时间t .第二步，如果t ≤3，那么c ＝0.2；否则c ＝0.2＋0.1×[t －2]. 第三步，输出通话费用c . 程序如下：【点拨】法步骤，画出程序框图，最后准确地编写出程序，同时要注意结合题意加深对算法的理解.【变式训练3】(江苏)下图是一个算法流程图，则输出S 的值是 .【解析】n＝1时，S＝3；n＝2时，S＝3＋4＝7；n＝3时，S＝7＋8＝15；n＝4时，S＝15＋24＝31；n ＝5时，S＝31＋25＝63.因为63≥33，所以输出的S值为63.总结提高1.输入、输出语句可以设计提示信息，加引号表示出来，与变量之间用分号隔开.2.赋值语句的赋值号左边只能是变量而不能是表达式；赋值号左右两边不能对换，不能利用赋值语句进行代数式计算，利用赋值语句可以实现两个变量值的互换，方法是引进第三个变量，用三个赋值语句完成.3.在某些算法中，根据需要，在条件语句的THEN分支或ELSE分支中又可以包含条件语句.遇到这样的问题，要分清内外条件结构，保证结构的完整性.4.分清WHILE语句和UNTIL语句的格式，在解决一些需要反复执行的运算任务，如累加求和，累乘求积等问题中应主要考虑利用循环语句来实现，但也要结合其他语句如条件语句.5.编程的一般步骤：(1)算法分析；(2)画出程序框图；(3)写出程序.11.3 算法案例典例精析题型一求最大公约数【例1】(1)用辗转相除法求840与1 764的最大公约数；(2)用更相减损术求440与556的最大公约数.【解析】(1)用辗转相除法求840与1 764的最大公约数：1 764＝840×2＋84，840＝84×10＋0.所以840与1 764的最大公约数是84.(2)用更相减损术求440与556的最大公约数：556－440＝116，440－116＝324，324－116＝116＝92，116－92＝24，92－24＝68，68－24＝44，44－24＝24－，＝16，16－4＝12，12－4＝8，8－4＝4.所以440与556的最大公约数是4.【点拨】(1)辗转相除法与更相减损术是求两个正整数的最大公约数的方法，辗转相除法用较大的数除以较小的数，直到大数被小数除尽结束运算，较小的数就是最大公约数；更相减损术是用两数中较大的数减去较小的数，直到所得的差和较小数相等为止，这个较小数就是这两个数的最大公约数.一般情况下，辗转相除法步骤较少，而更相减损术步骤较多，但运算简易，解题时要灵活运用.(2)两个以上的数求最大公约数，先求其中两个数的最大公约数，再用所得的公约数与其他各数求最大公约数即可.【变式训练1】求147,343,133的最大公约数.【解析】先求147与343的最大公约数.343－147＝196，196－147＝49，147－49＝98，98－49＝49，所以147与343的最大公约数为49.再求49与133的最大公约数.133－49＝84，84－49＝35，49－35＝14，35－14＝21，21－14＝7，14－7＝7.所以147,343,133的最大公约数为7.题型二秦九韶算法的应用【例2】用秦九韶算法写出求多项式f(x)＝1＋x＋0.5x2＋0.016 67x3＋0.041 67x4＋0.008 33x5在x＝－0.2时的值的过程.【解析】先把函数整理成f(x)＝((((0.008 33x＋0.041 67)x＋0.166 67)x＋0.5)x＋1)x＋1，按照从内向外的顺序依次进行.x＝－0.2，a5＝0.008 33，v0＝a5＝0.008 33；a4＝0.041 67，v1＝v0x＋a4＝0.04；a3＝0.016 67，v2＝v1x＋a3＝0.008 67；a2＝0.5，v3＝v2x＋a2＝0.498 27；a1＝1，v4＝v3x＋a1＝0.900 35；a0＝1，v5＝v4x＋a0＝0.819 93；所以f(－0.2)＝0.819 93.【点拨】秦九韶算法是多项式求值的最优算法，特点是：(1)将高次多项式的求值化为一次多项式求值；(2)减少运算次数，提高效率；(3)步骤重复实施，能用计算机操作.【变式训练2】用秦九韶算法求多项式f(x)＝8x7＋5x6＋3x4＋2x＋1当x＝2时的值为.【解析】1 397.题型三进位制之间的转换【例3】(1)将101 111 011(2)转化为十进制的数；(2)将53(8)转化为二进制的数.【解析】(1)101 111 011(2)＝1×28＋0×27＋1×26＋1×25＋1×24＋1×23＋0×22＋1×21＋1＝379.(2)53(8)＝5×81＋3＝43.所以53(8)＝101 011(2).【点拨】将k进制数转换为十进制数，关键是先写成幂的积的形式再求和，将十进制数转换为k进制数，用“除k取余法”，余数的书写是由下往上，顺序不能颠倒，k进制化为m进制(k，m≠10)，可以用十进制过渡.【变式训练3】把十进制数89化为三进制数.【解析】具体的计算方法如下：89＝3×29＋2，29＝3×9＋2，9＝3×3＋0，3＝3×1＋0，1＝3×0＋1，所以89(10)＝10 022(3).总结提高1.辗转相除法和更相减损术都是用来求两个数的最大公约数的方法.其算法不同，但二者的原理却是相似的，主要区别是一个是除法运算，一个是减法运算，实质都是一个递推的过程.用秦九韶算法计算多项式的值，关键是正确的将多项式改写，然后由内向外，依次计算求解.2.将k进制数转化为十进制数的算法和将十进制数转化为k进制数的算法操作性很强，要掌握算法步骤，并熟练转化；要熟练应用“除基数，倒取余，一直除到商为0”.。

课题：函数的周期性教学目标：掌握周期函数的定义及最小正周期的意义教学重点：了解常见的具有周期性的抽象函数(一)主要知识：1. 周期函数的定义：对于f(x)定义域内的每一个x，都存在非零常数T，使得f (x・T) =f(x)恒成立，则称函数f (x)具有周期性，T叫做f(x)的一个周期，则kT ( Z,k=O)也是f (x)的周期，所有周期中的最小正数叫 f (x)的最小正周期.2. 几种特殊的抽象函数：具有周期性的抽象函数：函数y二f x满足对定义域内任一实数x (其中a为常数)，①fx二fx・a，贝U y二fx是以T=a为周期的周期函数；②f x • a二-f x，则f x是以T =2a为周期的周期函数；1 ,③f x • a，贝U f x是以T =2a为周期的周期函数；f (x)④f x a =f x -a，则fx是以T =2a为周期的周期函数；⑤ f (x a) J 一f(x)，贝V f x是以T =2a为周期的周期函数.1+ f(x)⑥ f (x • a) = -1一f (x)，贝y f x是以T =4a为周期的周期函数.1 + f (x)⑦ f (X a) J f(x)，贝y f x是以T =4a为周期的周期函数.1-f(x)⑧函数y = f (x)满足f (a • x) = f (a -x) ( a 0)，若f (x)为奇函数，则其周期为T =4a , 若f (x)为偶函数，则其周期为T =2a.⑨函数y二f(x) R的图象关于直线x二a和x二b a ：：： b都对称，则函数f (x)是以2 b-a为周期的周期函数；⑩函数y二f (x) R的图象关于两点A a,y0、B b, y^\ \a ::: b都对称，贝U函数f (x)是以2 b -a为周期的周期函数；(11)函数y二f(x) * R的图象关于A a,y0和直线x二b a :: b都对称，则函数f (x)是以4 b - a为周期的周期函数；(二)主要方法：1. 判断一个函数是否是周期函数要抓住两点：一是对定义域中任意的x恒有f(x T^ f (x);二是能找到适合这一等式的非零常数T, 一般来说，周期函数的定义域均为无限集.2. 解决周期函数问题时，要注意灵活运用以上结论，同时要重视数形结合思想方法的运用，还要注意根据所要解决的问题的特征来进行赋值。

课题：集合的概念教学目标：集合、子集的概念，能利用集合中元素的性质解决问题，掌握集合问题的常规处理方法. 教学重点：集合中元素的3个性质，集合的3种表示方法，集合语言、集合思想的运用. 教学过程：（一）主要知识：1.集合、子集、空集的概念；两个集合相等的概念2. 集合中元素的3个性质，集合的3种表示方法；3. 若有限集A有n个元素，则A的子集有2n个，真子集有2n一1,非空子集有2n -1个, 非空真子集有2n -2个.4. 空集是任何集合的子集，空集是任何非空集合的真子集5. 若A B, B C，则A C6. A A U B,A「IB A,A D B A U B.7. A B= A U B=B;A B= A“B=A.（二）主要方法：1. 解决集合问题，首先要弄清楚集合中的元素是什么，即元素分析法的掌握.2. 弄清集合中元素的本质属性，能化简的要化简；3. 抓住集合中元素的3个性质，对互异性要注意检验；4. 正确进行“集合语言”和普通“数学语言”的相互转化.（三）典例分析：I、可题1：已知集合M ={xx=3 n,n e1}, N={xx = 3 n+1, n^z }, Phxx=3 n—1, n Z?,且a M , b N , c P，设d=a—b c，贝yAd M B. d N C. d P D. d MUN问题2：设集合A={xx=a2+2a+4}, B=<yy=b2—4b+7}.1若a，R , b R，试确定集合A与集合B的关系；2 若a N , b R, 的关系.问题3:2008年第29届奥运会将在北京召开，现有三个实数的集合，既可以表示为「a，b，"，也可以表示为〈a2,a b,0 ?,则a2008 - b2008二______________N ={x|x = £舟,k Z}问题4：（02新课程）设M={x|x=：2 {，匕Z},则A. M 二N B. M = N C. M Y N D. M 门N =：_问题5：①若A =| x2• ax • 1 =0, x • R1 , B - ",2?，且A。

课题：抛物线教学目标：理解抛物线的定义，抛物线的标准方程，抛物线的几何性质。

教学重点： 抛物线的定义、四种方程及几何性质；四种方程的运用及对应性质的比较、辨别和应用，抛物线的几何性质的应用.（一） 主要知识及主要方法：1.（课本115P ）P （0p >）的几何意义是抛物线的焦准距（焦点到准线的距离）.2.（课本115P ）抛物线的通径：通过焦点并且垂直于对称轴的直线与抛物线两交点之间的线段叫做抛物线的通径.通径的长为2p ,通径是过焦点最短的弦.（二）典例分析：问题1.求满足下列条件的抛物线的标准方程，并求对应抛物线的准线方程：()1过点P ()3,2-；()2焦点在直线240x y --=上；()3顶点在原点，对称轴为x 轴，抛物线上的点()3,M m -到焦点的距离等于5；()4顶点在原点，对称轴为x 轴且截直线210x y -+=问题2．()1在抛物线24y x =上找一点M ，使MA MF+最小，其中()3,2A ，()1,0F ，求M 点的坐标及此时的最小值；()2已知抛物线22y x =和定点103,3A ⎛⎫ ⎪⎝⎭，抛物线上有一动点P ，P 到点A 的距离为1d ，P 到抛物线准线的距离为2d ，求12d d +的最小值及此时P 点的坐标.问题3．()1(05全国Ⅱ)抛物线24x y =上一点A 的纵坐标为4，则点A 与抛物线焦点的距离为 .A 2 .B 3 .C 4 .D 5()2（07海南）已知抛物线22y px =(0)p >的焦点为F ，点111222()()P x y P x y ，，，，333()P x y ，在抛物线上，且2132x x x =+， 则有.A 123FP FP FP += .B 222123FPFP FP += .C 2132FP FP FP =+ .D 2213FPFP FP =g()3定长为3的线段AB 的端点A 、B 在抛物线2y x =上移动，求线段AB 的中点M 到y 轴距离的最小值.()4(06全国Ⅰ)抛物线2y x =-的点到直线4380x y +-=距离的最小值是.A 43.B 73.C 85.D 3问题4．（98全国）直线1l 和2l 相交于点M ，12l l ⊥，点1N l ∈.以A 、B 为端点的曲线段C 上的任一点到2l 的距离与到点N 的距离相等.若AMN △为锐角三角形，17AM =，3AN =，且6BN =.建立适当的坐标系，求曲线段C 的方程.问题5．(05全国Ⅲ) 设()11A x y ，，()22B x y ，两点在抛物线22y x =上，l 是AB的垂直平分线。

课题：指数函数教学目标：1•掌握指数函数；2•掌握指数函数的图象和性质教学重点：指数函数的图象及性质的简单应用.（一）主要知识：指数函数的图象和性质：1. y=a x（a 0且a=1）的定义域为R，值域为.2. y=a x（a 0且a=1）的单调性：a 1时，y = a x在R上为增函数；0 ::: a ：：：1时，y = a*在R上是减函数.3. y = a x（a - 0且a = 1）的图像特征：a 1时，图象像一撇，过点0,1 - 且在y轴左侧a越大，图象越靠近y轴（如图1）；0 ：a <1时，图象像一捺,过点0,1 ，且在y轴左侧a越小，图象越靠近y轴（如图2）；y =a x与y =a "的图象关于y轴对称（如图3）.图1 图2 图3（二）主要方法：1. 指数方程，指数不等式：常要转化为同底数的形式，在利用指数函数的单调性求解；2. 确定与指数有关的函数的单调性时，常要注意针对底数进行讨论；3. 要注意运用数形结合思想解决问题.（三）典例分析：问题 1 1 （05福建）函数f（x）=a x J b的图象如图，其中a、b为常数，则下列结论正确的是A. a 1, b < 0B. a 1,b 0C. 0 :: a ：：1,b 0D. 0 ■a :: 1,b :: 0（2 股x>0，且a x£b x£1（a>0，b>0），贝y a 与b 的关系是A. b ::: a ::: 1B. a ::: b ::: 1C. 1 ：：：b ：： aD. 1 ：：： a ::: b3若函数y =2」“ •m的图象不经过第一象限，贝U m的取值范围是A. m _ -2B. m^. -2C. m _ -1D. m〕：：「1x(4 )( 06山东模拟)设f(x) = 3 -1 , ccbva且f (c) a f (a) a f (b)，则下列关系式一定成立的是 A. 3c. 3b B. 3b3a C. 3c3a2 D. 3c- 3^：： 2x — 2问题2. ( 06上海模拟)已知函数f(x)二a x(a 1),x十11证明函数f (x)在(-1,7)上为增函数；2用反证法证明f(x)=O没有负数根问题3 .要使函数y =1 +2x +a 4x在(—比, 1上y > 0恒成立，求a的取值范围I、可题4. （04全国川理）解方程：4%十1一2x=11（四）巩固练习：（1羊*1. 不等式3"的解集为13丿2 f [" ................2. 函数v 的递减区间为；最大值是12丿（五）课后作业：1.如图为指数函数（1）y 二a x,（2）y 二b x,（3）y 二c x,（4）y 二d x，则a,b,c,d 与1 的大小关系为A. a :: b ::: 1■c:：dC. 1 :: a :: b :： cB. b a :: 1 ：： d :: c：：：2.若函数f(x) =2»4_m的图象与x轴有交点，则实数m的范围是3.已知函数f (x^ ax2 bx c a 0，满足f (1 一x) = f (1 • x)，贝U f (2x)与f (3x) 的大小关系是A. f (2x) f (3x)B. f(2x p： f(3x)C. f (2x) > f(3x)D. f(2x) w f (3x)4.若直线y=2a与函数y=a x—1(a=0且a^1)的图象有两个公共点，贝U a的范围是5.已知函数y =4x -3 2x3的值域为1,7 1,则x的范围是A. 2,4 1B.(- ：,6.函数y = 2 的定义域为___________ ，值域为_______________7.设a • 0, a = 1，如果函数y = a2x 2 a x -1在L 1,1】上的最大值为14，求a的值/ 、x_28.已知八’1求函数『八的值域x -Xa —a9.已知f(x) x x0 a 1 . 1证明：f(x)是定义域上的减函数; a +a2求f (x)的值域.(a 0，且a=1) . 1求f (x)的定义域;10.已知f(x)a x -12讨论f(x)的奇偶性；3求a的范围，使f(x) 0在定义域上恒成立（六）走向高考：1. （06山东）函数y =1 • a x 0 ：：： a 1的反函数的图象大致是(A) (B) ( C) ( D)A. B. C. D.2. ( 04湖北文)若函数f (x)二a x• b -1 ( a 0，且a =1)的图象经过第二、四象限，则一定有 A. 0 :: a :: 1且b 0 ； B. a 1且b 0C. Ovacl 且b£0 ；D. a>1 且b£03. （05全国川文）设3x=扌，则① 0 ■ b ::: a :② a ::: b ::: 0 :③ 0 ：： a ：： b :④ b ■ a ■ 0 :⑤ a = b 其中不可能成立的关系式有y = x 3与y 二- 的图象的交点为 y 2 B. (1,2) C. (2,3)A. 一2 ：： x ：： -1B. —3 ：： x ：： -2C. -1 ：：： x ::: 0D. 0 .. x :: 1 4. ( 07山东)已知集合 M -「-1,1 ,A^-1,1? B^-1? 1 x-W f N =?x -<2 <4, X E Z '，则 M“N = I 2 ? J C. {0} D. {—1,0}5. ( 07北京)函数A. (0, •:：) x f (x) = 3 ( 0 ：：： x w 2 )的反函数的定义域为B. (1,9]C. (0,1)D.[9,：：)6. ( 05江西)已知实数A. 1个B.2个C.3个D.4个7.( 07山东)设函数是 A (0,1) (x 0, y °)，则x 0所在的区间 D. (3,4) a 、b 满足等式x8. ( 04全国川理)已知函数y = f(x)是奇函数，则当X—0时，f(x) = 3 -1，设f (x) 的反函数是y =g(x)，则g(-8) 口9.( 05全国I)设0 ：：：a ：：：1 ,函数f (x) =log a(a2x -2a x -2)，则使f (x) ：：：0 的x 的取值范围是A.(-：：,0)B. (0, ：：)C. (_：：,log a3)D.(log a3,：：)10. ( 06 天津)如果函数f (x) =a x(a x-3a2-1) ( a 0且a=1)在区间〔0,= 上是增函数，那么实数a的取值范围为A. 0,2B.弓,1C. 0,J3D. 2,13」.3丿- ]2丿。

课题：多面体和球教学目标：1.了解多面体、凸多面体的概念 了解正多面体的概念，知道欧拉公式2V F E +-=和五种正多面体的顶点数、面数及棱数2.要使学生理解两点的球面距离，掌握球的表面积及球的体积公式、求球面面积、球的体积及两点的球面距离.3.球是最常见的几何体.高考对球的考查主要在以下四个方面：()1球的截面的性质；()2球的表面积和体积；()3球面上两点间的球面距离；()4球与其他几何体的组合体.而且多以选择题和填空题的形式出现.第（4）方面有时用综合题进行考查. 教学重点：（一） 主要知识及主要方法：1.每个面都是有相同边数的正多边形，每个顶点为端点都有相同棱数的凸多面体，叫做正多面体.2.正多面体有且只有5种.分别是正四面体、正六面体、正八面体、正十二面体、正二十面体.3.简单多面体：考虑一个多面体，例如正六面体，假定它的面是用橡胶薄膜做成的，如果充以气体，那么它就会连续（不破裂）变形，最后可变为一个球面.如图：象这样，表面经过连续变形可变为球面的多面体，叫做简单多面体.说明：棱柱、棱锥、正多面体等一切凸多面体都是简单多面体5.欧拉定理（欧拉公式）：简单多面体的顶点数V 、面数F 及棱数E 有关系式：V F E +-= 计算棱数E 常见方法：()1 2E V F =+-；()2 E =各面多边形边数和的一半；()3E =顶点数与共顶点棱数积的一半.6.球的概念： 与定点距离等于或小于定长的点的集合，叫做球体，简称球定长叫球的半径与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示，例如球O7.球的截面：用一平面α去截一个球O ，设OO '是平面α的垂线段，O '为垂足，且OO d '=，所得的截面是以球心在截面内的射影为圆心，以r =为半径的一个圆，截面是一个圆面.球面被经过球心的平面截得的圆叫做大圆，被不经过球心的平面截得的圆叫做小圆 8.两点的球面距离：球面上两点之间的最短距离，就是经过两点的大圆在这两点间的一段劣弧的长度，我们把这个弧长叫做两点的球面距离.l R ϕ=(ϕ为球心角的弧度数).9.球的表面积和体积公式：24S R π=，343V R π=. （二）典例分析：问题1．()1（05辽宁）棱长为a 的正方体，连结相邻面的中心，以这些线段为棱的八面体的体积为 .A 23a .B 24a .C 26a .D 212a()2已知一个正四面体和一个正八面体的棱长相等且为1，把它们拼起来，使一个表面重合，所得的多面体有多少个面？问题2．()1(07天津）一个长方体的各顶点均在同一球的球面上，且一个顶点上的三条棱的长分别为1,2,3，则此球的表面积为()2(07全国Ⅰ文)正四棱锥S ABCD -，点,,,,S A B C D都在同一个球面上，则该球的体积为()3（07江西文）四面体ABCD的外接球球心在CD上，且2CD=，3AB=，在外接球面上两点A、B间的球面距离是.Aπ6.Bπ3.C2π3.D5π6()4（06陕西）水平桌面α上放有4个半径均为2R的球，且相邻的球都相切(球心的连线构成正方形).在这4个球的上面放1个半径为R的小球，它和下面4个球恰好都相切，则小球的球心到水平桌面α的距离是问题3．（07四川）设球O的半径是1，A、B、C是球面上三点，已知A 到B 、C 两点的球面距离都是2π，且二面角B OA C --的大小为3π，则从A 点沿球面经B 、C 两点再回到A 点的最短距离是 .A 67π .B 45π .C 34π .D 23π问题4．三棱锥A BCD -的两条棱6AB CD ==，其余各棱长均为5，求三棱锥的内切球半径和外接球半径.问题5．已知球的半径为R ，在球内作一个内接圆柱，这个圆柱底面半径与高为何值时，它的侧面积最大?侧面积的最大值是多少?（三）课后作业：1.正方体、正多面体、凸多面体、简单多面体是什么关系？2.已知凸多面体每个面都是五边形，每个顶点都有三条棱相交，试求该凸多面体的面数、顶点数和棱数.3.一个广告气球被一束入射角为 的平行光线照射，其投影是一个长半轴为5m的椭圆，则制作这个广告气球至少需要的面料是4.在球面上有四个点P 、A 、B 、C ，如果PA 、PB 、PC 两两互相垂直，且PA PB PC a ===，那么这个球面的面积是 .A 22a π .B 23a π .C 24a π.D 26a π5.北纬30︒的圆把北半球面积分为两部分，这两部分面积的比为.A 1:1 .B 2:1 .C .D6.已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半， 且2AB BC CA ===，则球面面积是.A 9π16 .B 3π8 .C 4π .D 9π647.正八面体的相邻两个面所成二面角的大小为.A 1arccos 3 .B 1arccos 3π- .C 1arccos 23π- .D 1arccos 3-（四）走向高考：8.（07陕西）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是 .A 433 .B 33 .C 43 .D 1239.（07辽宁）若一个底面边长为2，的正六棱柱的所有顶点都在一个平面上，则此球的体积为10.（07全国Ⅱ）一个正四棱柱的各个顶点在一个直径为2cm 的球面上。

高三数学第一轮复习讲义高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式；2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 . 例 4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式；2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 .例4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式；2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 . 例 4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式；2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比.例3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 .例4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式； 2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 .例4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式； 2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 . 例 4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式； 2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 .例4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式； 2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 . 例 4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式； 2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 .例4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名高三数学第一轮复习讲义直线的方程一．复习目标： 1．深化理解倾斜角、斜率的观点，娴熟掌握斜率公式； 2 ．掌握直线方程的点斜式、斜截式、两点式、截距式和一般式，并能娴熟写出直线方程．二．知识重点： 1．过两点、的直线斜率公式：．2．直线方程的几种形式：点斜式：；斜截式：；两点式：；截距式：；一般式：．三．课前预习： 1 ．设，则直线的倾斜角为（）2．已知，则过不一样三点，，的直线的条数为（）多于 3．已知的极点 ,，重心，则边所在直线方程为；经过点且与轴、轴围成的三角形面积是的直线方程是；过点，且它的倾斜角等于已知直线的倾斜角的一半的直线的方程是.4．若直线的方向向量是, 则直线的倾斜角是；若点，，直线过点且与线段订交，则直线的斜率k的取值范围为.四．例题剖析：例1．已知直线的方程为，过点作直线，交轴于点，交于点，且，求的方程 . 例 2．⑴已知，试求被直线所分红的比λ；⑵已知，，若直线与直线订交于点，不与重合，求证：点分的比 . 例 3．过点引一条直线，使它在两条坐标轴上的截距都是正数，且它们的和最小，求直线的方程 . 例 4．的一个极点，两条高所在直线方程为和，求三边所在直线方程．五．课后作业：班级学号姓名。

课题：映射与函数教学目标：了解映射的概念，在此基础上加深对函数概念的理解；能根据函数的三要素判断两个函数是否为同一函数；理解分段函数的意义.教学重点：函数是一种特殊的映射，而映射是一种特殊的对应；函数的三要素中对应法则是核心，定义域是灵魂.（一）主要知识：1. 映射与函数的概念；2. 函数的三要素及表示法，两个函数相同的条件；3. 正确理解函数值的含义，掌握函数值的求法，会灵活解决有关函数值的问题；特别是涉及分段函数或复合函数的值的问题•（二）主要方法：1. 对映射有两个关键点：一是有象，二是象惟一，缺一不可；2. 对函数三要素及其之间的关系给以深刻理解，这是处理函数问题的关键；3. 理解函数和映射的关系，函数式和方程式的关系.（三）典例分析：问题1.已知集合P =^x Q<x<4｝ , Q=｛x0^x^2｝，下列不.表.示.从P到Q的映射是A. f : x > y =2xB. f : x》y=3xC. f : x—；y =£xD. f : x—y = x问题2. （05黄岗模拟）下列从M到N的各对应法则f i（i =1,2,3,4 ）中哪些是映射？哪些是函数？哪些不是映射？为什么？1 M -｛直线Ax By ^0｝, N 二R , f1：求直线Ax By C =0 的斜率；2 M =｛直线Ax By 0 ｝, N -0 —：：J , f2:求直线Ax By C = 0 的倾斜角；3当M=N=R , f3:求M中每个元素的正切；4 M二N = x 一0 ?, f4:求M中每个元素的算术平方根.5 M =｛平面〉内的矩形｝, N =｛平面〉内的圆｝, f s :作矩形的外接圆（此小题为编者自拟）问题3. 1已知x,y在映射f作用下的象是x y,xy .①求-2,3在f作用下的象②若在f作用下的象是2,3，求它的原象2设集合A和B都是实数集，映射f : A》B把集合A中的元素x映射到集合B中的元素x3 -x 1，则在映射f下，象1的原象组成的集合是A 4 BJ-1,0,V C.（0 D.「—2,—1,0l问题4. 下列各对函数中，相同的是丄2 / ------A. f(x) =x, g(x) =：〔x2B. f(x) =、1-x2, g(x)=1-x , x 1-1,11C. y = f(x), g(x) = f(x+1) , x^RD. f(x) = lg(打,g(x)=lg2，x问题5.①（05浙江文）设f （x） = x T - x ,则f -f （；）］=A. -2B. 0C. 4D. 1笑(05山东)函数sin（兀x2）, 一1 c x < 0, 卄一八一“小f（xH x；，若f 1 f a =2,$xJL,xZ0.则a的所有可能值为A. 1 B•血 C. 1 丘 D. 1 丘2 ，2 ，2问题 6.矩形ABCD的长AB =8，宽AD =5，动点E、F分别在BC、CD上，且CE二CF二x , 1将厶AEF的面积S表示为x的函数f(x)，求函数S=f(x)的解析式；2求S的最大值.(四)巩固练习:21. 1 A 二 R ， B ={ y | y 0}， f : x — y =|x| ；2 A ={x |x _2,x 二 N }， B -〔y | y _ 0,y 二 N ?, f : x —； y = x 2-2x 2 ；3 A = {x | x 0}， B = {y | y R}， f : x —； y 二 x .上述三个对应 ______________ 是A 到B 的映射.1 12. 给定映射f : (x, y)r (2x y,xy)，点(一，)的原象是 _______________ __ _____6 6 3.下列函数中，与函数 y 二x 相同的函数是2A y = — B. y=(、. x)2 C.y=lg10xD.y = 2xx-3,(^10)□上4.设函数f (x)，则f (5)=lf(f(x+5)),(x<10)5. ( 06湖北八校一联)设 f ,g 都是由表一映射f 的对应法则 则与f1相同的是 A 6. ( 06灌云模拟)设 M Ma,b,c?，从M 到N 的映射f 满足f (a) • f(b) 一 f(c),试确定这样的映射 f 的个数为A. 1B. 2C.3D.4(五) 课后作业：1.设A =「x|O 乞x 乞2},B =「y|1乞2二在下图中，能表示从集合 A 到集合B 的映射是原象 1 2 3 4 象4 3 2 1lOg2X原象1 2 3 4 象 3 4 2 1A 到A 的映射，其对应法则如下表(从上到下)表二 映射f 的对应法则B. g 〔f(2)lC. g 〔f(3)lD.g[f(4)] A.B .z z = (x, y ),x, y € R,x2+ y2—12y + 27 兰0〉到集合B = R 的映射2.已知从集合A =：2f : z > -，则该映射的象集为xA一：：，_-、3 U .3, ：： B. 卜-』3, -3 C. -.3, .3 D.以上都不对3. ( 04北京东城模拟)设映射 2—X - 2x是实数集M到实数集N的映射，若对于实数p • N，在M中不存在原象，则p的取值范围是A. 1, ：：B. 1, ：：C. 一：：,1D. -：：,114.设集合A」1,2,3，B-4,5,6?，定义映射 f : A > B，使对任意2 2X - f (x) X f (x)是奇数，则这样的映射f的个数为A. 7B. 9C. 10D. 1825.若g(x) =1 -2x, f (g(x))晋& = 0)，则f(A )A. 1B. 3C. 15D. 306•已知f(x) = P "王0)，则不等式x+(x + 2)f(x+2)兰5的解集是[-1 (xcO)2x +17.设A=R , B=R , f : x 是A—；B 的映射，21设a • A，则a在B中的象是什么？s在映射f的象是什么?2设r A，那么t 1在B中的象是什么？3设s，A，若s-1在映射f下的象为5，则s应是多少?(六)走向高考:1. ( 06陕西)为确保信息安全,信息需加密传输,发送方由明文T 密文(加密),接收方由密文 T 明文(解密),已知加密规则为：明文 a 、b 、c 、d 对应密文a 2b , 2b c , 2c 3d , 4d .例如：明文1,2,3,4对应密文5,7,18,16.当接收方收到密文14,9,23,28时，则解密得 到的明文为A. 4,6,1,7B. 7,6,1,4C. 6,4,1,7D. 1,6,5,72. ( 06浙江)函数f : “,2,3丨一；；1,2,3 [满足f(f(x)) = f(x)，则这样的函数个数共有A. 1个B. 4个C. 8个D.10个3. ( 06广东文)对于任意的两个实数对(a,b)和(c,d)，规定：(a,b)=(c,d),当且仅当 a 二c,b =d ；运算"：”为：(a,b) ： (Gd) =(ac 「bd,bc ad)； 运算“二”为：(a,b)二(c,d) =(a c,b d)，设 p,q R ，若(1,2)： (p,q)=(5,0),则(1,2)二(p,q)=A. (4,0)B. (2,0)C. (0,2)D. (0,-4)4. ( 03全国)已知f 5『(x ) =lgx ，则f(2)二( )A. lg2B. lg 32C. lg丄1 D.-lg23252e x",x ：25. ( 06山东文)设1 f (X ) 2,则 f (f (2))的值为[log 3 (x -1 ,x_2A. 0B. 1C. 2D. 36. ( 07北京)已知函数f (x) , g(x)分别由下表给出:则f[g(1)]的值为___________ ；满足f[g(x)] g[f(x)]的x 的值是 ______________。